Abstract
A microfluidic device denoted the Phase Chip has been designed to measure and manipulate the phase diagram of multi-component fluid mixtures. The Phase Chip exploits the permeation of water through poly(dimethylsiloxane) (PDMS) in order to controllably vary the concentration of solutes in aqueous nanoliter volume microdrops stored in wells. The permeation of water in the Phase Chip is modeled using the diffusion equation and good agreement between experiment and theory is obtained. The Phase Chip operates by first creating drops of the water/solute mixture whose composition varies sequentially. Next, drops are transported down channels and guided into storage wells using surface tension forces. Finally, the solute concentration of each stored drop is simultaneously varied and measured. Two applications of the Phase Chip are presented. First, the phase diagram of a polymer/salt mixture is measured on-chip and validated off-chip and second, protein crystallization rates are enhanced through the manipulation of the kinetics of nucleation and growth.
Keywords: microfluidics, PDMS, water permeation, high throughput protein crystallization, phase diagram, nucleation, growth, Ostwald ripening
Microfluidic instruments are capable of precisely manipulating sub-nanoliter quantities of fluids. Their purpose is to vastly reduce the amount of fluids used in chemical processing and provide accurate delivery of fluids in a defined geometry on the micron length scale with a temporal accuracy of milliseconds. A microfluidic device can include channels for transporting fluids, valves for controlling flow, nozzles to create drops, pumps to propel fluids, storage chambers, and mixers to homogenize multiple fluid streams and drops 1–4. To this panoply of components we add the abilities to store drops and to controllably vary the water content of stored drops. Each of these primitive functions can be combined in numerous ways to create complex devices optimized for specific tasks. Other powerful features of microfluidics are the ease and rapidity of their construction and the low cost of materials.
This paper reports the development of a microfluidic device, the Phase Chip shown in Figure 1a, which is designed to determine the phase diagram of multi-component fluid mixtures. The Phase Chip consists of a number of distinct microfluidic modules, which in sequence are used to formulate drops, generate drops, mix drops, store drops in specific docking sites, and reversibly and controllably vary the amount of water in the drops and thereby regulate the concentration of solutes in the drops. The Phase Chip is a poly(dimethylsiloxane) (PDMS) device, which utilizes hydrodynamic focusing to produce drops of aqueous solution inside a continuous oil stream 2–5. A movie of the drop formation is in the supplement, S4.1. There are several important reasons why drops are an attractive solution to high throughput applications; each drop can be independently formulated to have a given composition, when the drops are dispersed in an immiscible carrier fluid there is no cross-contamination between drops and each drop can be transported with its contents remaining intact4, 6. To this list of desirable features we demonstrate in this paper that when the solutes in the drops are impermeable to the carrier fluid and PDMS, measurement of the drop volume can be used to determine the solute concentration. The ability to simultaneously vary and measure the solute concentration is an important advance in microfluidics and enables the two phase transition studies described below. While this paper was under review an implementation of reversible permeation similar to ours was reported7.
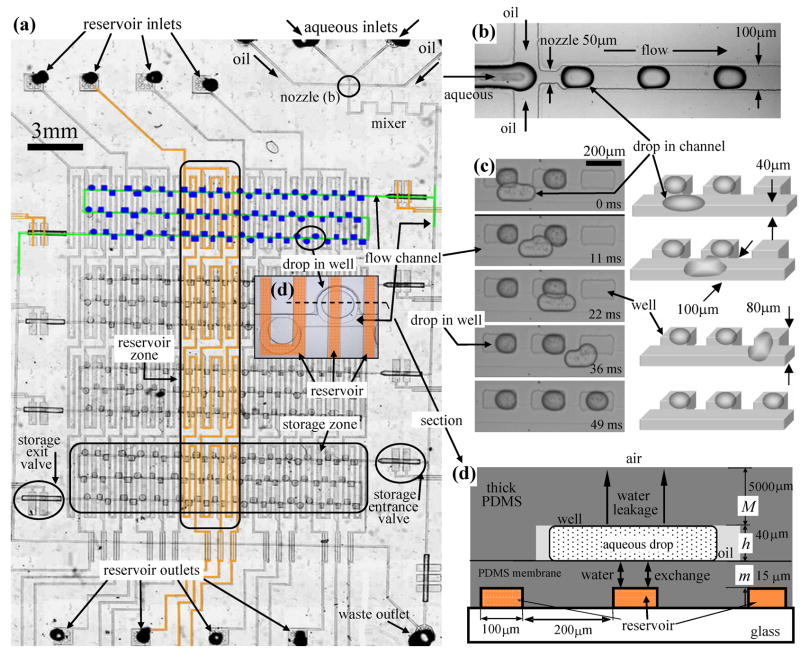
Figure 1.
(a) Plan view of the Phase Chip. (b) Drop formation at nozzle. Confined drops are flattened and elongated in the flow channels. A movie, S4.1, is in the supplement. (c) Photographs of surface tension guided storage of aqueous drops into rectangular wells. Movies are shown in the supplement S4.2, S4.3 and S4.4. These pictures are taken on a chip without a reservoir and have different dimensions than the device portrayed in the rest of this figure. (d) Vertical section of the Phase Chip corresponding to the insert in (a). The device is constructed from two PDMS layers and subsequently sealed together. In the upper, thick (5 mm) layer there are flow channels and storage wells. In the lower, thin (40 μm) layer there is a reservoir sealed by a 15 μm thick PDMS membrane. The reservoir is formed by spin coating a 40 μm thick layer PDMS over a 25 μm high photoresist mold. The principle path for water permeation is between the drop and the reservoir, but there is also a small flux through the 5 mm thick PMDS layer between the drop and the device exterior.
Surface tension guided drop storage
The first innovation of the Phase Chip is our method of storing drops in wells using surface tension forces as illustrated in Figure 1c and in the movie in the supplement, S4.2. After formation (Figure 1b), drops are forced to flow through wide rectangular channels (100μm) of narrow height (40μm), which flattens the drops creating a large surface area and because of the oil-water interface, a large surface energy. Deep wells are fabricated on the chip that are adjacent to, but still connected to the flow channel. Because the wells are deeper and wider than the channel, a drop inside a well will be less confined then when in the channel allowing the surface area of the drop to be reduced. The gradient in the height of the microfluidic device produces a gradient in the drop’s surface area, and therefore a gradient in the drop’s interfacial energy, which generates a force on the drop driving it out of the confining channel into the deeper well. The change in interfacial energy in transforming a flattened drop, such as shown in Figure 1c, into a spherical one is approximately 104 times greater than the change in gravitational energy. The shape with minimal surface area is a sphere, but any geometric change in the channel that allows a reduction in the confined drop’s surface area will create a force on the drop and the channel shape will have the potential to store drops. Furthermore, because the well is located to the side of the channel the hydrodynamic stress on the drop in the well is much weaker than in the channel. When the well is about twice the depth of channel then the drop will remain in the well permanently even when oil is flowing rapidly through the channel. Drops fill the wells in sequence with the first drop docking into the first empty well and the last drop docking into the last well. If surfactant is added to stabilize the drops against coalescence then the drops pass over filled wells without mixing. In figure 1c, stable drops of water in hexadecane (Sigma-Aldrich) are formed by adding Span80 (2% v/w, Sigma-Aldrich) to the oil. Care must be made to match the volume of the drop to the wells. If the docked drop is too large it will protrude into the channel and the next drop will dislodge it. If the docked drop is too small, a second drop will share its well. And for drops that are half the size of the wells an amusing cascade can be created as illustrated in the movie supplement, S4.3.
Not all oil/water drops can be stabilized. For example, we have not found commercially available surfactants that can stabilize fluorocarbon oil/water or silicone oil/water microdrops. Therefore we have developed a method to dock drops without having to stabilize against coalescence. When the well is shallow in depth, comparable with the height of the flow channel, the drops pass by wells if the speed of drops is fast (≈1.1cm sec ). When the flow stops the drops spontaneously dock into the nearest well. In this method the first drop docks into the last well and the last drop docks into the first well. Without surfactant to stabilize the drop some mixing of drops occurs and typically the contents of about three or four adjacent drops are shared. In our experiments a fluorinated oil (FC-43, 3M) mixed with a surfactant (12%w/w, Tridecafluoro octanol, Sigma-Aldrich) are used. The surfactant lowers surface tension making it easy to create drops and simultaneously slows coalescence of drops. A movie illustrating this storage method is shown in the supplement, S4.4.
Controlling solute concentration
Concentration is a key thermodynamic variable for aqueous solutions. The other important thermodynamic variable, temperature, can only be varied over a relatively narrow range because the freezing and boiling temperatures of water are close, and/or because the solute may only be stable over a small temperature range, as is the case for proteins. Unfortunately, it is experimentally challenging to prepare droplets of accurate composition in the pico and nanoliter range due to dispensing difficulties and to evaporation. Once drops are formulated it is even more difficult to vary the solute concentration as this involves opening the sample container and adding still smaller amounts of solvent and solutes. In contrast, changing temperature is experimentally straight forward because heat flows through sealed containers. The second innovation of the Phase Chip is to controllably vary the water content of stored drops inside the sealed Phase Chip, thus rendering concentration as convenient a thermodynamic variable as temperature. As illustrated in Figure 1d, this is accomplished by fabricating the bottom of the wells from a thin PDMS membrane (15 μm thick) that is slightly permeable to water 7–11, but impermeable to proteins, poly(ethylene glycol) (PEG), and salts. The fluids in the layer containing the reservoir and in the layer containing the flow channels and wells are not directly connected to each other in any way. Water is transported between these two layers solely via permeation through the PDMS membrane. Across the membrane from the well is a 100 nano-liter reservoir. During operation dry air or an aqueous salt solution is flowed through the reservoir, which produces a chemical potential gradient between the solution stored in the well and the reservoir. When the reservoir is filled with dry air or a solution whose salt concentration is greater than that of the drop, water permeates from the stored drops in the wells through the membrane into the reservoir thereby increasing the concentration of the PDMS-impermeable solutes inside the drop. In contrast, if pure water is introduced in the reservoir, then the chemical potential gradient is reversed and water permeates through the membrane from the reservoir to the drop, thereby diluting each PDMS-impermeable component as the drops swell. Because the drops stored in the wells are confined in one dimension, they have a disklike shape (Figure 1d) so that when the drops are shrinking and swelling only the area of drops is changing, not the height.
The example of the Phase Chip illustrated in Figure 1 has four independent regions for drop storage. Each region contains 84 wells and drops can be directed to a particular storage region from the nozzle by selecting on-chip valves. For example, each region could be used to store drops containing different solutes, while within each region the wells could contain drops with different ratios of solutes. Five independent reservoirs are constructed as parallel channels located underneath the well layer. These can be filled with different salt concentrations in order to generate a large combinatoric set of initial and final compositions of the stored drops, making the Phase Chip a device suitable for high-throughput screening of phase transitions of multicomponent aqueous solutions.
Modeling of Water Permeation in the Phase Chip
As shown in Figure 1d, there are two paths through which the water permeates; the principal one is through the thin PDMS membrane separating the wells and reservoir, and the secondary one is a leakage path through the thick PDMS above the wells to the exterior of the device. The flux of water along each of these paths, assuming ideal solution behavior, is Ji = P∇Bci with P = kD where P is the permeation coefficient, k = 7.1 × 10−4 and D = 8.5 × 10−10 [m2/s] are the solubility and diffusion constant of water in PDMS 8, 9, respectively, and ∇Bci are the gradients in water concentration along each path. When the aqueous drops are in fluorinated oil, which is the case for the following experiments, we have evidence that the drops wet the PDMS because the shape of the drops indicates that the PDMS/water/oil contact line is pinned, as shown in Figure 5d. But even if the oil wets the PDMS we assume that the oil layer is so thin as to have a negligible effect on the permeation of water.
Figure 5.
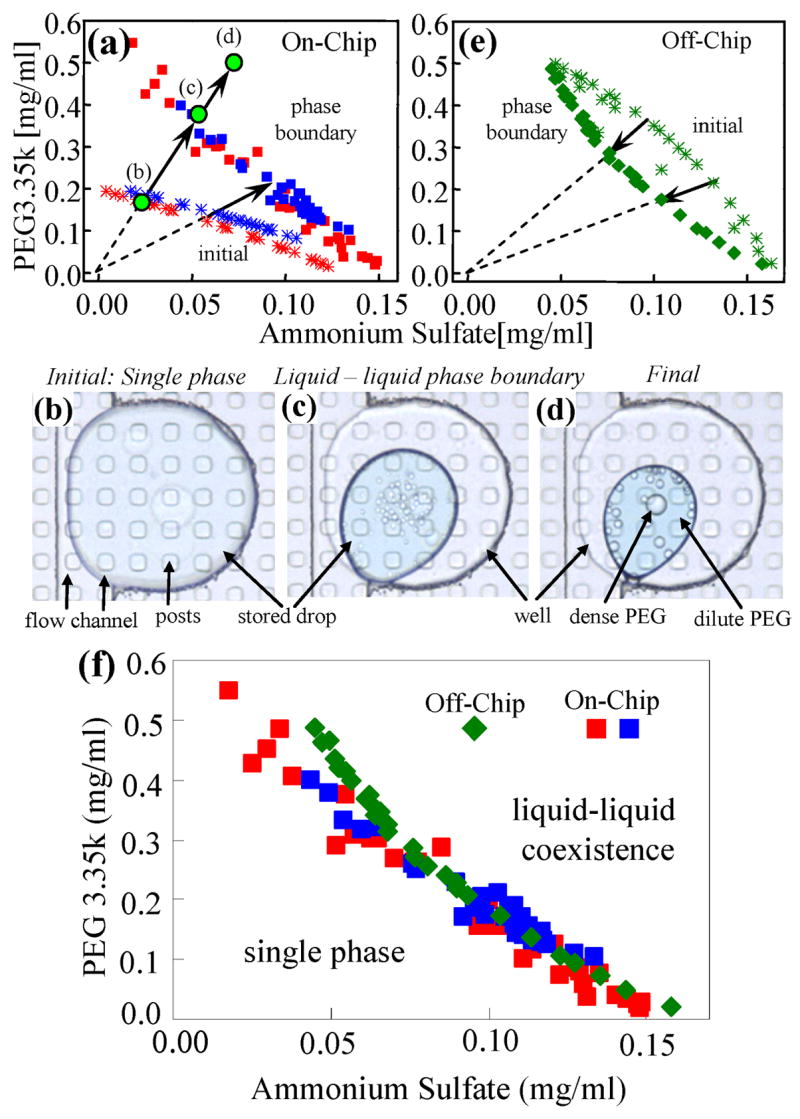
(a) The phase diagram of a mixture of PEG 3.35k and ammonium sulfate measured on the Phase Chip. The asterisks represent the initial conditions of drops stored on-chip. Different colors correspond to independent trials. Squares denote the phase boundary. The mixture is single liquid phase below the boundary and two liquid phases co-exist above the boundary. Water, but not salt or PEG is removed from the drops so the solute concentrations evolve along lines emanating from the origin. 5(b),5(c),5(d). The photos show the appearance of the drops while the water is leaving the drop. The initially homogeneous solution (5b), which corresponds to the green circle in (5a) denoted by the letter (b), separates into two phases shown in (5c), corresponding to the point on the phase boundary indicated by point (c) in (5a). In (5d) the drop has moved deeper into the two-phase region at the end of the experiment when the drop has achieved steady state. A movie is in the supplement, S4.5. 5(e). The plot shows the phase diagram of the mixture measured off-chip. The initial solutions (green asterisks) are prepared in the vial with concentrations above the phase boundary so they are in the two-phase state and have a cloudy appearance. Then water is added to the solution until it becomes clear, which signals a single, homogenous phase. The final concentration is calculated from the initial condition and the amount of water added onto the solution. 5(f). The two phase diagrams measured on- and off-chip are plotted together. The blue and red squares represent the on-chip measurements, the green diamonds represent the off-chip data.
Our reservoirs have two basic designs. One consists of a series of serpentine, parallel channels of width varying between 100 μm to 200 μm running beneath the storage wells, as shown in Figure 1. The second design consists of a single rectangular chamber, 16 mm by 7 mm, where the membrane is supported by 30 μm square posts patterned on a 100 μm square, as shown in Figures 4 and 5. For both geometries the flux of water between the drop and reservoir through the thin PDMS membrane can be considered as 1-dimensional planar diffusion as the disk shaped drops have a typical diameter of 300 μm and height of 40 μm, while the thickness of the membrane is 15 μm (Fig. 1d). We will see that the planar approximation for modeling the flux between the reservoir and drop is highly accurate.
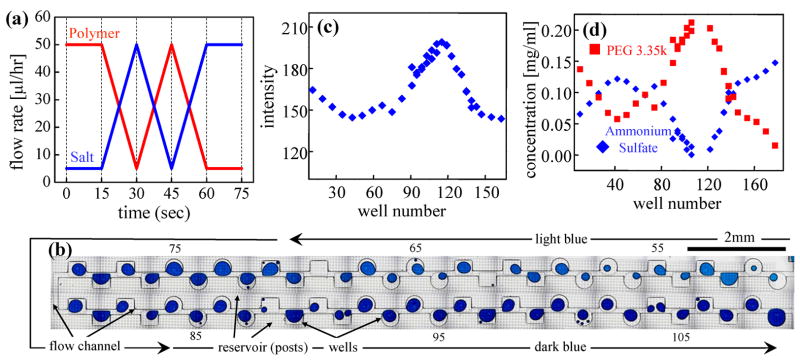
Figure 4.
(a) Drop formulation. Flow rate profiles of polymer (PEG 3.35k) and salt (ammonium sulfate) of co-flowing aqueous streams being fed into the drop generating nozzle by syringe pumps. The polymer and salt concentrations of the stock solutions are 0.21 mg/ml and 0.14 mg/ml, respectively. (b) Drop storage. A portion of the Phase Chip containing blue dyed drops of the polymer/salt mixture solution stored in the wells. The concentration of ammonium sulfate is determined by measuring the light intensity passing through each stored drop and the concentration of polymer is calculated from the salt concentration because the relative volumetric compositions of each drop are known from Figure 4a. A movie is in S4.4 (c) Light transmittance of the stored drops. The plot shows the light intensity transmitted through each drop in arbitrary units. The brighter drops contain less blue dye, which is proportional to the concentration of ammonium sulfate. (d) Initial concentrations of polymer and salt of the drops stored in wells. Blue diamond; Ammonium Sulfate. Red square; PEG 3.35k.
In order to model the leakage flux from the reservoir and wells through the thick PDMS slab to the exterior of the device (Fig 1d) we note that the wells are located on a planar periodic lattice. Each well can be thought of as a source for the water, which diffuses through the PDMS. The water concentration varies periodically in planes parallel to the wells and the amplitude of the water concentration variation decays exponentially with distance from the plane of the wells with the decay length the order of the spacing between wells 12. Because the wells are separated by a distance small (0.5 mm) compared to the thickness of the entire PDMS device (5 mm) and the wells are distributed over an area with linear dimensions much greater than the thickness of the PDMS device it is valid to approximate the leakage flux between the wells and exterior of the device as planar diffusion, although we will see that this approximation is not quantitative. However, the crudeness of our approximation is unimportant when we operate the chip in a regime where the leakage flux is much less than the reservoir flux.
The gradient of water concentration across the thin PDMS membrane separating the drop and the reservoir is ∇Bcres = Δc/m = (cdrop − creservoir )/m while the gradient in water concentration between the drop and the exterior of the device is ∇Bcext = Δc/M = (cdrop − cexterior)/M with cdrop, creservoir and cexterior the concentration of water in the drop, reservoir, and exterior of the device respectively, while m is the thickness of the PDMS membrane separating the drop and reservoir and M is the thickness of the PDMS separating the drop and exterior of the device. The molar concentration of water can be expressed in terms of the molar concentration of solutes as cα = W − Xα where α is either the drop, reservoir, or external environment, W = 55 M is the molar concentration (mol/liter) of pure water, and Xα is the molar concentration of solute, such as salt or PEG. Thus −∇Bcres = (Xdrop − Xres)/m and −∇Bcext = (Xdrop − Xext)/M. If the device is operated in the laboratory environment then the water concentration in the air exterior to the device cannot be greater than the vapor saturation value, which at 20 oC is cexterior = 10−3[M]. This is negligible compared to the maximum concentration W of pure water so the equivalent solute concentration can be approximated as Xext = W − cexterior ~ 55 M. The total molar flux (J [m M s-1]) of water out of the drop is calculated with the 1-dimensional diffusion equation; J = −P·∇BCwater = kD·((Xdrop − Xres)/m+(Xdrop − Xext)/M). Assuming that only water and not the solute permeates through the PDMS allows use of mass conservation to relate the volume change of the drop to the molar flux of water from the drop; dV/dt[m3s−1] =h dA(t)/dt = J A(t)/W with V[m3] = A(t) · h the volume of a drop, A(t) the area of the drop and h the constant height of the confined, disk-shaped drop. Since we assume only water leaves the drop, the concentration of solute in the drop is inversely proportional to the drop’s volume; thus the solute concentration of the drop as a function of time is Xdrop = Xo · Vo/V(t) = Xo · Ao/A(t) with Vo, Ao, and Xo the initial volume, area and concentration of a drop, respectively.
The change in size of a drop placed in dialytic contact with a reservoir is derived by combining the 1-dimensional diffusion and mass conservation equations; dA(t)/dt = J A(t)/(hW) =kD/hW · {(Ao · Xo − A(t) · Xres)/m+(Ao · Xo − A(t) · Xext)/M}. The solution to this differential equation describes how the area, A(t), of a drop of initial area Ao and initial solute concentration Xo that is placed in contact with a reservoir and exterior environment of constant solute concentration Xres and Xext, respectively, at time t = 0 evolves with time. As the drop volume changes so does the drop concentration, from an initial concentration Xo to the final concentration X∞. The dimensionless relative drop area is
| Equation (1) |
where α is the ratio of the final area to the initial area, or equivalently, the ratio of the initial solute concentration, Xo, to the final solute concentration, X∞;
| Equation (2) |
and τ−1 is the time constant for changing the drop’s concentration;
| Equation (3) |
Measurement of Water Permeation in the Phase Chip
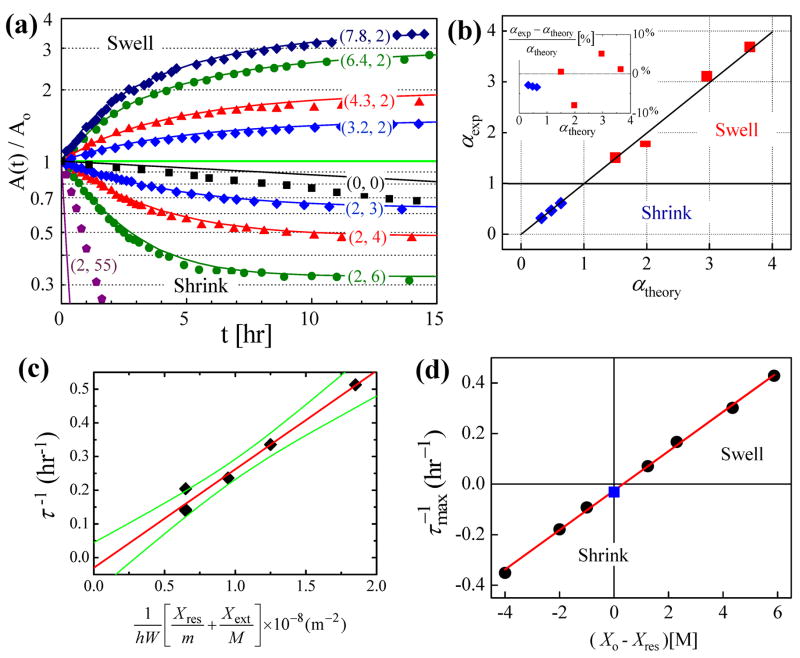
Figure 2a shows the normalized areas of a series of stored drops of initial concentration, Xo, as a function of time following a change in the reservoir salt concentration, Xres. If Xres = Xext then τ is the time constant for the drop to equilibrate with the reservoir. If Xres ≠ Xext then water is always permeating through the device and τ is the time constant for the steady state drop size to be reached at which time the flux from the reservoir to drop equals the flux from the drop to the exterior of the device. If the reservoir is filled with a much higher (lower) salt concentration than in the drops, then the drops will shrink (swell). Each data set, obtained from a single drop, was fitted to Eqn. (1) and the parameters α and τ were extracted. In Figure 2b the fitted values of α (αexp) are compared with the theoretical values of α (αtheory) given in Equation (2). As all the parameters in αtheory are independently known, there are no free variables. The straight line of slope one shows theory and experiment agree within an experimental variation of 5%. In Figure 2c the fitted rate τ−1 is plotted vs. the theory given in Equation (3). All the parameters except for the permeation constant P = k D are measured independently of the fitting. The proportionality between τ−1 and as predicted by Equation (3) is observed in Figure 2c. The proportionality constant, P, is found to be P = k D = 7.4 × 10−13[m2/s], which is consistent with literature values 8. This agreement between theory and experiment further validates our model. In Figure 2a the solid lines are not fits to the data, but are the theory with the same fitted permeation coefficient (P) obtained from in Figure 2c. The solid lines in Figure 2a are plots of Equation (1) for each of nine experiments performed using different values of the salt concentration of reservoir, Xres, and initial drop concentration, Xo, and constant values of the independently measured device parameters (h = 40 μm, m = 15 μm, M = 5 mm, Xext = 55 M, W = 55 M) and the one fitted parameter, P = k D = 7.4 × 10−13[m2/s]. Seven of the nine experiments closely match theory; the discrepancies will be discussed later.
Figure 2.
(a) The relative areas of saline drops (A(t)/Ao) stored in wells as a function of time (t) after a change in reservoir salt concentration. The vertical axis is a logarithmic scale. The numbers next to each curve represent the initial salt concentration [M] of the drop and reservoir; (Xo, Xres). The solid lines are the theory using the same single adjustable parameter (P) for each curve. (b) The ratio of final to initial drop area for experiment vs. theory. The experimental values (αexp) are obtained by fitting the data of (a) to Equation (1). The theoretical values (αtheory) are obtained using Equation (2) and the known experimental parameters. (c) The rate of change of the τ−1, is plotted vs. which equation (3) predicts is a line passing through the origin with slope P = k D. The experimental values of τ−1 are obtained by fitting the data of (a) to Equation (1). The green lines mark 90% confidence levels. (d) The initial (maximal) rate of change of the relative area, , given in equation 4 as a function of the difference between the initial salt concentration of the drop and reservoir; Xo − Xres.
For practical applications it is useful to know how quickly the concentration of a drop be changed. The maximum rate of change, , for an exponential process is the initial rate found by expanding Equation (3) for t ≪ τ ; A(t)/Ao ~ 1+t/τmax with
| Equation (4) |
In our experiment we use NaCl salt solutions in the drop and in the reservoir. The saturation concentration of NaCl is about 6 M, which sets the salt concentration range for the drop to be 0 ≤ Xo ≤ 6. The reservoir can contain salt solutions of this range, or contain air, which has an equivalent salt concentration of 55 M. Therefore the difference in drop and reservoir salt concentrations can range from 0 ≤ Xo − Xres ≤ 55[M]. If we operate the device in air (Xext = 55 [M]) then the difference in drop and external concentration ranges from −55[M]≤Xo − Xext≤−49[M]. Consequently, the gradient in salt concentration between the drop and reservoir has a large range from while the gradient in salt concentration between the drop and exterior of the device has a small range from . The Phase Chip is designed such that the reservoir flux will M primarily set the final concentration of the drop, with the leakage flux to the exterior of the device being a small correction. In order to test whether or not the gradient in salt concentration between the drop and reservoir is controlling the drop concentration we plot the initial rate of change of the area of the drop, , as a function of Xo − X res in Figure 2d. The initial rates are calculated as where α and τ−1 are obtained from fits to the data as shown in Figs 2b and 2c.
As shown in Figure 2d, the initial rates are well approximated by the linear function: . Fitting the slope of the line in Figure 2d to Equation (4) yields a = kD/mhW = 0.078(M−1hr−1) from which the permeability of water in PDMS is calculated, P = 7.2 × 10−13[m2/s], similar to the value we obtained from fitting only τ−1 in Figure 2c, while the intercept yields the leakage flux rate . As discussed in the previous paragraph the fact that b can only vary by at most 10% and that the chip is operated under conditions where the flux of water from the reservoir dominates the leakage flux allows us to approximate the leakage flux as a constant and treat the reservoir flux as the independent variable. The interpretation of the data in Figure 2d is that the initial rate of change of concentration of the drop, , varies linearly with the difference in concentration between the drop and reservoir. For example, with a four molar initial difference in salt concentration between the reservoir and drop, the drop concentration will initially change by 30% per hour. When the drop and reservoir are initially set to have the same salt concentration, the drop will still increase concentration at a rate of 2.6% per hour due to the leakage path to the exterior of the device. The drop will not change volume if the drop contains a salt solution that is 0.33 M more concentrated than the reservoir solution because then the flux to the reservoir is balanced by the leakage flux to the exterior of the device. If we make the more extreme approximation of ignoring the leakage flux altogether, or set M → ∞in Equation (4), we find . This predicts that Figure 2d will be a straight line with zero intercept, which is a reasonable approximation when |Xo − Xres| >1[M]. There is considerable experimental freedom to vary . While the parameters k, D, and W are material constants h, m, and Xo − Xres can be chosen over a wide range of values.
As mentioned previously the solid curves in Figure 2a are not fits to the experiment, but rather the theory with all the parameters except for P independently measured. There are seven curves for which the theory and experiment have excellent agreement, corresponding to when the difference Xo − Xres is large. The other two curves show significant deviations from theory. One (black squares) is for the case when Xo = Xres = 0. In this case the initial flux out of the drop is only due to the leakage flux. The drop concentration does not accurately follow an exponential time variation indicating that the 1-dimensional planar approximation for the leakage flux is not as accurate as for the flux to the reservoir. The planar approximation underestimates the experimental transient leakage rate by a factor of 2 to 3. However, most of our experiments are done in a regime where the leakage flux is small compared to the reservoir flux. A more extreme approximation is to completely ignore the leakage in the theory, which is done by considering the device to be infinitely thick and setting M → ∞ in Equations (2) and (3). Then the final drop concentration, X∞, is predicted to equal the reservoir concentration, Xres. Instead, as shown in Figure 3 the measured value of X∞ is found to be about 5% higher than Xres when |Xo − Xres| >1[M]. These systematic offsets are caused by the unidirectional leakage flux. When the device is operated in an air-filled laboratory water always permeates from the drop to the exterior of the device while the reservoir can either source or sink water from the drop. While the transient time dependence of the leakage flux does not match the theory, the steady state leakage flux and final drop concentration do agree with theory, as shown in Figure 3.
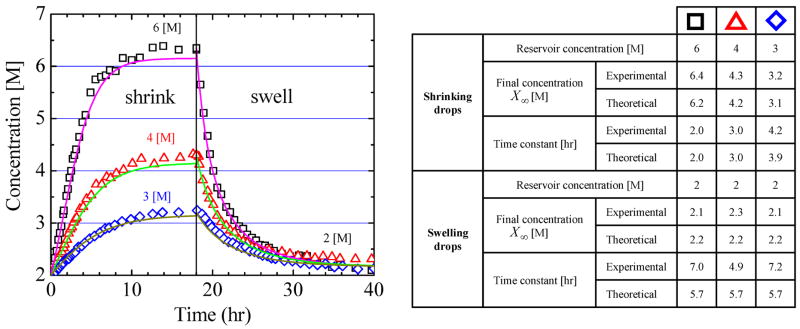
Figure 3.
(a) The concentration of saline drops stored in wells with respect to time after a change in reservoir salt concentration. Drop concentrations are inferred by measuring the drop area: Xdrop (t) = Xo · Ao/A(t). The data are identical to Figure 2a. First, all drops had the same initial sodium chloride concentration, Xo = 2 M, and at t = 0 were exposed to different reservoir conditions (Xres) for 18 hours: 6 M (square), 4 M (triangle), 3 M (diamond). Next, the reservoir conditions were changed to the same concentration; Xres = 2 M. The solid lines are theory (Eq. 1); all six curves are generated with the same value of the single fitting parameter, P = 7.4 × 10−13[m2/s] and the other parameters are given in the text. (b) The table shows the experimental steady state concentration X∞ and time constant τ obtained by fitting Equation (1) to the data in Fig 2a, while the theoretical values are calculated from Equations (2) and (3), respectively.
The other curve that shows deviation from theory is for the case of when the reservoir contains dry air. In this case the concentration of water in the reservoir is zero and we consider this equivalent to filling the reservoir with a salt solution of Xres = 55[M]. In the experiment air is driven through the 30 μm deep reservoir by applying a pressure of 10 psi. The data shows that the rate of drop shrinkage is much slower than predicted. We speculate that this is due to the air forming a boundary layer inside the reservoir effectively making the membrane thicker than m. This hypothesis suggests that if the air flow were increased so as to reduce the thickness of the boundary layer then a faster shrinking rate would be obtained10.
The conclusion of this section is that the concentration of solutes in drops can be predicted as a function of time for all times to 5% accuracy as long as the difference between the initial drop and reservoir concentration is greater than 1M. Furthermore, the final drop concentration can be predicted to within 5% for all initial drop and reservoir concentrations.
Impermeability of PDMS to Salt and PEG
A central assumption of our model is that only water and none of the solutes permeate through the PDMS membrane. Figure 3 demonstrates that this is the case for sodium chloride (NaCl), which shows the time evolution of the concentration of drops containing NaCl solution as a function of reservoir concentration. The initial NaCl concentration in the drops was 2 [M] and the reservoir was filled with a greater NaCl concentration (3 [M], 4 [M], and 6 [M]) than the initial drop concentration. In these cases water leaves the drop, which shrinks in volume. For these conditions it takes approximately 15 hours for the drops to reach steady-state. Once the drops attain their final concentration, the reservoir concentration is replaced with 2 [M] of NaCl solution. This reverses the chemical potential difference between the reservoir and drop causing water to be transported from the reservoir to drops. In response the drops swell until a steady state drop size is established with the flux of water from the reservoir to drop matched by the flux of water from the drop to the exterior of the device. We assume that none of the salt leaves the drop during the forty hour experiment. The final measured drop volume implies a final salt concentration in the range of 2.1 [M] – 2.2 [M], which is slightly larger than that in the reservoir. The final salt concentration is higher than the reservoir concentration due to the small leakage flux and is in quantitative agreement with Equation (2). Had some salt left the drop by dissolving into either the oil or PDMS, then the drop would be smaller than predicted, which would be interpreted as a higher than predicted salt concentration. Since experiment and theory agree we conclude that only water molecules, and not sodium or chloride ions, permeate through PDMS.
We tested the molecular weight dependence of PEG permeability by creating salt free drops containing 18%w/v, of PEG 400 M.W. and 24%w/v of PEG 1,000 and 8,000 M.W. We performed similar experiments to those shown in Figure 3 in which we docked drops in wells containing salt-free PEG solutions and reversibly varied the reservoir ionic strength to cycle the volume of the stored drop by a factor of two over a five day period. The assumption was that if the drops returned to their initial volume when the reservoir conditions were the same as initially then this would prove that the PEG remained in the drop and did not permeate through the PDMS membrane into the reservoir or oil. For example, if all the PEG left the drop, then the drop would contain only pure water and consequently would not be able to attain a steady state volume when in contact with a reservoir containing a finite salt concentration and the drop would completely evaporate. Because of the large molecular weight of PEG compared to NaCl the chemical potential difference between PEG solutions and pure water is much less than the chemical potential difference between salt solutions and pure water on a weight basis. A 20% by weight solution of PEG 8,000 has an osmotic pressure that is equivalent to a 0.15 [M] solution of NaCl. Extensive tables of the osmotic pressure of PEG solutions are available online (http://www.brocku.ca/researchers/peter_rand/osmotic/osfile.html). Because of the small chemical potential difference between PEG solutions and pure water, the flux of water between the reservoir and docked PEG containing drops was small and comparable to the leakage flux to the exterior of the device, which led to noisy data. However, the conclusion (within 10% experimental resolution) was that PEG, over a five day period, does not permeate through PDMS. We emphasize that this was true for all molecular weights, even for the 400 molecular weight solutions.
Measuring the Phase Diagram of a Salt/Polymer Mixture
To demonstrate the performance of the Phase Chip, the phase diagram of a polymer and salt mixture is measured. For certain compositions, mixtures of poly(ethylene glycol) (PEG) and ammonium sulfate in water will phase separate into two liquid phases, with one phase rich in polymer, the other phase salt rich13.
Figure 4 illustrates the procedure by which we initially prepare the samples and measure the salt and PEG concentrations on the Phase Chip. First, a series of drops is generated on the Phase Chip containing mixtures of PEG (molecular weight 3.35k, Sigma-Aldrich) and salt (Ammonium Sulfate, Sigma-Aldrich) whose concentrations vary in a linear fashion. To formulate the drops we employ a technique developed for protein crystallization 5. In this method two co-flowing aqueous streams, one of PEG and one of salt, merge with two opposing oil streams at a nozzle, creating drops of the aqueous solution in the continuous oil phase, as shown in Figures 1a & b. The flow rates of the PEG and salt are periodically varied, with one increasing and one decreasing such that the total flow rate remains constant. Thus when drops are formed at the nozzle each drop has a different ratio of PEG to salt, but the volume of each drop is the same. Figure 4 demonstrates how drops whose ratio of PEG to salt varies linearly with time are created. The time scale of the experiment is 45 seconds. Each well has a volume of 0.6 nl and a total of 250 wells were filled.
In Figure 4b a sequence of 60 wells filled with drops are shown. These wells are only slightly deeper than the channels so the surface tension forces holding the drops in place are weak. When the flow rate is high the drops flow past the wells, but when the flow is suddenly stopped by closing on-chip valves, surface tension forces lead the drops to dock into the nearest available well. No surfactant is used to stabilize the drops against coalescence. A movie illustrating the filling process is shown in the supplement, S4.4. In order to measure the salt concentration in each drop, 5%(w/v) of a blue food dye (McCormic Corp.) is added into the Ammonium Sulfate stock solution. The intensity of each drop indicates the concentration of Ammonium Sulfate; the darker the drop the higher the salt concentration. The intensity of transmitted light was measured using a video camera and 8-bit digitizer, as shown in Figure 4d. The salt concentration is calculated from the intensity using a calibration table determined by filling the exact same microfluidic device with drops that all have the same known concentration of dye. The polymer concentration of each drop is calculated from the salt concentration since there is a specific volumetric relation between the ingredients as given by Figure 4a.
As shown in Figure 4b the color of each drop gradually changes from the light blue (upper-right) to the dark blue (lower-right) along the flow channel. The intensity varies smoothly with the index of drops as shown in Figure 4c demonstrating that drop formulation and storage were working as designed. Although some coalescence and breakage of drops occurs between drop formation at the nozzle and drop storage in the wells, Figure 4c demonstrates that this mixing of drops is not enough to homogenize the composition gradient.
After preparing the initial conditions by formulating and storing drops and determining their composition by analyzing the intensity of the blue dye, the next step is to induce the liquid-liquid phase transition and to determine the PEG/salt composition at the phase boundary. We drive the phase transition by removing water from the drops. This is accomplished by filling the reservoir with a 6 M NaCl solution. Initially, the salt concentration inside each of the drops is much less than 6 M so water flows out of the drops into the reservoir. As we concluded previously, the drops retain all the salt and PEG placed there initially, which means the ratio of salt to PEG remains constant and the solute concentrations increase as water leaves the drops and the drops shrink in volume. Because only water permeates through the PDMS and because the height of the docked disk-shaped drops remains constant we can determine each solute concentration by measuring the area of the drop as a function of time: , with Ao and A(t) the initial and time dependent area of the drop, respectively, and with and the time dependent and initial concentration of the solutes, respectively, where i represents PEG or Ammonium Sulfate. This method of determining concentration by measuring the drop area is more accurate than measuring the transmitted light intensity due to the presence of the blue dye.
In this experiment 250 wells were filled with drops of different composition as illustrated in Figure 4. As we are interested in determining the area of each drop and hence the concentration of its solutes as a function of time, automated data acquisition and processing is desired. Automated imaging of each of the drops was performed using a robotic system designed for protein crystallization, the Rock Imager (Formulatrix, Waltham, MA). This system consists of a stepping motor driven XY translation stage and a digital camera with a zoom lens and Kohler illumination. The Rock Imager can be programmed to acquire images as a function of time and location and stores the images in a data base. After acquisition we process the images using an image recognition software package to measure the area of each drop (LabView, National Instruments).
After the reservoir is filled with 6 M salt solution the drops are allowed to shrink and reach a steady state size. After the initial concentration of the drops is determined by analyzing the intensity of transmitted light, the concentration of each of the solutes in the drop is subsequently calculated by measuring the area of the drop. The images of the drops are viewed and the point at which liquid-liquid phase separation is observed is noted as the phase boundary. Figure 5 illustrates this process and a movie is also in the supplement, S4.5. In Figure 5b an image of a drop at the beginning of the experiment is shown. The solution is a homogenous single-phase liquid and the composition of the drop is indicated by point (b) in the phase diagram of Figure 5a. As the drop shrinks the concentrations of each solute in the drop increase, but because none of the solutes leave the drop the ratio of solute concentrations remain constant. This constrains the solute concentration to increase linearly and the concentrations evolve along a line emanating from the origin of the phase diagram in Figure 5a. In Figure 5c the appearance of two liquid phases is first observed. By measuring the area of this drop, the concentration of the solutes is determined and noted as point (c) in Figure 5a. The drop continues to shrink until it reaches a steady state volume when the reservoir flux equals the leakage flux. After phase separation we assume that the flux of water from the PEG-rich and PEG-poor regions is equal, which allows us to indicate the final composition of the drop as point (d) in Figure 5a. Note that this assumption does not effect the location of the phase boundary. A photograph of the final state is shown in Figure 5d. This process is repeated in parallel for the 250 wells on the Phase Chip for each initial composition as shown in Figure 5a in order to determine a complete phase diagram. The entire experiment was repeated with a different set of drops, which demonstrates reproducibility, as illustrated in Figure 5a.
We validated the phase diagram obtained with the Phase Chip by measuring the phase diagram off-chip. Here a series of samples in the two phase region was prepared and then diluted with water until the system became a single phase. We performed a dilution experiment because it is easier to add solvent than to remove it when off-chip. Similarly to the on-chip case, the ratio of solute concentrations remains constant as water is added to the mixture and the initial solute concentrations evolve along lines extrapolating to the origin. The phase diagram obtained off-chip is shown in Figure 5e and the on-chip and off-chip phase diagrams are compared in Figure 5f. The on- and off-chip phase diagrams match except for low salt concentration. Measurement of the initial concentration of Ammonium Sulfate is inaccurate in this region because the blue dye is very dilute and is at the limits of sensitivity of our 8-bit digital camera. Off-chip measurements consumed 30 ml of solution in contrast to the on-chip measurements which consumed 50 μl. Further optimization of the Phase Chip can readily reduce the volume consumed by at least an order of magnitude.
Separating Nucleation and Growth in Protein Crystallization
A second application of the Phase Chip is to address the problem of separating nucleation and growth of protein crystals. The motivation to study this comes from structural biology as it is necessary to crystallize a protein in order to reveal its three dimensional molecular structure by x-ray diffraction14. Currently protein crystals are produced by trial and error methods, which necessitates exploring a large number of conditions consuming milligrams of protein. Non-microfluidic methods require about 1 μl of solution per trial14, while microfluidic devices have reduced the volume per trial to 1 nl or less2, 3.
Reducing protein consumption, although important, is not the most pressing problem facing crystallographers. Recently attention has turned to understanding the underlying phase behavior of protein crystallization as a rational approach 15. However, even knowledge of the equilibrium phase behavior is not enough to produce crystals, because crystallization, in general, is an activated process16. Even when the protein solution is supersaturated so that the chemical potential of a protein molecule in the liquid is greater than in the crystal (Δμ >0 ), a small crystal will be unstable. Due to the surface tension, γ, between the crystal and the fluid there is an energy barrier, ΔG*, that causes crystals below a certain size to dissolve17. The free energy (ΔG) of a spherical crystal nucleus of radius r in a protein solution of concentration ρ is ΔG = γ4π r2 − ρ Δμ 4 π r3/3 leading to a barrier of height ΔG* = 16πγ3/3ρ2 Δμ2 that occurs at a radius r* = 2γ/ρ Δμ as shown in Figure 6. Crystals that spontaneously form with a radius r < r* lower their free energy by dissolving and only crystals larger than r* grow. The free energy barrier often is quite large for proteins 18, so to achieve a finite nucleation rate, Γ ~ exp(ΔG */kT), protein solutions in crystallization conditions are highly supersaturated. However, under these circumstances both the nucleation and growth rate are high, leading to the formation of many small and defect laden crystals that are unsuitable for x-ray diffraction. The conundrum facing the crystallographer is that while the nucleation of crystals requires high supersaturation, the converse is true to grow large, defect free crystals.
Figure 6.
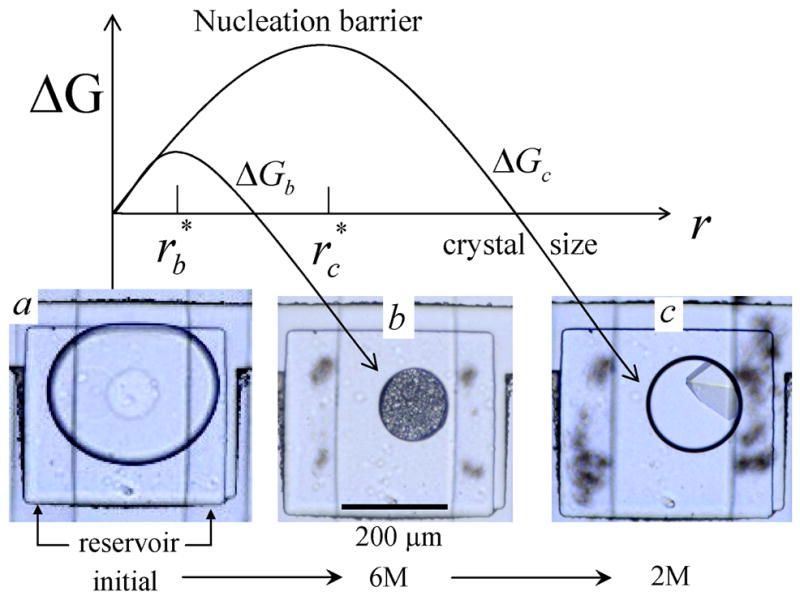
The free energy of crystal formation ΔG as a function of crystal radius r. ΔGb and ΔGc correspond to high and low Δμ, respectively. (a) Initially the protein solution stored in the well is a stable single phase and ΔG > 0 for all r. (b) The chemical potential reservoir (Fig 1), located below the well, is filled with 6M NaCl causing water to osmotically flow out of the drop, raising Δμ and creating a free energy, ΔGb, with a small nucleation barrier leading to production of many small crystals of minimum size . (c) Next, the reservoir is filled with 2M NaCl, causing water to flow back into the drop, lowering Δμ and raising the nucleation barrier, ΔGc. Only crystals larger than grow while smaller crystals melt. This transforms the small precipitates in (b) into a single large crystal, a process known as Oswald ripening. Five times fewer crystals were observed when the protein drop in (a) was quenched directly to final condition (c), indicating the importance of controlling the kinetic pathway for protein crystallization. The protein solution was a mixture of 20 mg/ml lysozyme and 10 %(w/w) poly(ethylene) glycol (PEG) of molecular weight 8000 g/mol dissolved in 0.2 M sodium acetate trihydrate and 0.1 M sodium cacodylate at pH 6.5.
Free interface diffusion, microbatch, and vapor diffusion are popular crystallization methods, which partially decouple the physical mechanisms of nucleation and growth 19, 20. While these methods have been successfully implemented in microfluidics 3, 21–23, their drawback is that they rely on irreversible kinetic processes, which are difficult to control and optimize and they do not measure the solute concentration.
Crystal seeding 24 is a method practiced in protein crystallization that permits independent optimization of nucleation and growth. In the crystal seeding method, solution conditions are first highly supersaturated in order to nucleate many small crystals, or “seeds”. Then a few seeds are transferred to a solution of low supersaturation that is optimized for growth. A microfluidic version of seeding has recently been implemented 25.
Microdialysis 14, 26, 27 is a second method practiced in protein crystallization that permits independent optimization of nucleation and growth. In microdialysis, several microliters of protein solution are sealed in a container by a semi-permeable membrane and subsequently submerged in a reservoir of fixed chemical potential. Microdialysis allows changing of solvent conditions so that nucleation and growth can be independently optimized. However, these methods as currently practiced are not sufficiently controlled, nor are they conducive to high-throughput screening. To overcome these deficiencies we utilize the Phase Chip, which incorporates the attributes of high-throughput, precision, and low volume that are characteristics of microfluidics and allows reversible control and measurement of solute concentrations. Recently an implementation of reversible permeation was utilized to find the solubility limit of protein solutions7 and to titrate protein and solute concentrations to just below this point. In contrast, we purposely reversibly cycle through supersaturation conditions to induce nucleation and then lower supersaturation to Oswald ripen numerous, small crystals into few, or even a single large crystal.
Our strategy for decoupling nucleation and growth in protein crystallization on the Phase Chip is to first create and store drops of protein solutions in a manner similar to that used in the salt/PEG study. As a proof of concept we used a protein solution that was a mixture of 20 mg/ml lysozyme and 10 %(w/w) poly(ethylene) glycol (PEG) of molecular weight 8000 g/mol dissolved in 0.2 M sodium acetate trihydrate and 0.1 M sodium cacodylate at pH 6.5. In order to collect statistics we made all the drops with identical composition. For this experiment the oil was a 10:1 mixture of 3M Fluorinert FC-43 and Tridecafluoro-1-octanol from Aldrich. The drops do not form stable emulsions in this oil; drops merged and broke apart as they passed over occupied wells.
Protein solutions are notorious for their large region of metastability 18 and deep supersaturations are required to nucleate crystals. Immediately after loading the wells with drops of the above protein solution the reservoir was filled with a 6 [M] NaCl salt solution, which causes water to flow out of the protein drop to the reservoir, shrinking the drop and thereby concentrating the protein solution. The drop will shrink until the chemical potential inside the drop approximately equals the chemical potential inside the reservoir. As the protein drop shrank a large number of small crystals or small drops of protein gel appeared, shown in Figure 6b. A schematic representation of the free energy of the concentrated drop is also plotted in Figure 6 as ΔGb with a small barrier height and small critical radius, consistent with the observation of the nucleation of many small crystals. We regard this precipitated material as seeds for crystallization and subsequently change reservoir conditions by introducing a 2 [M] salt solution into the reservoir. Water permeates from the reservoir into the protein solution, swelling the drop (Figure 6c) and reduces the protein and salt concentrations. This lowers the chemical potential difference between the protein in solution and in the crystal, which raises the height of the nucleation barrier, shown in Figure 6 as ΔGc and also increases the critical radius r* causing all smaller nuclei to dissolve and the larger crystals to grow, thereby transforming many small defected crystals (Figure 6b) into one large single crystal (Figure 6c)
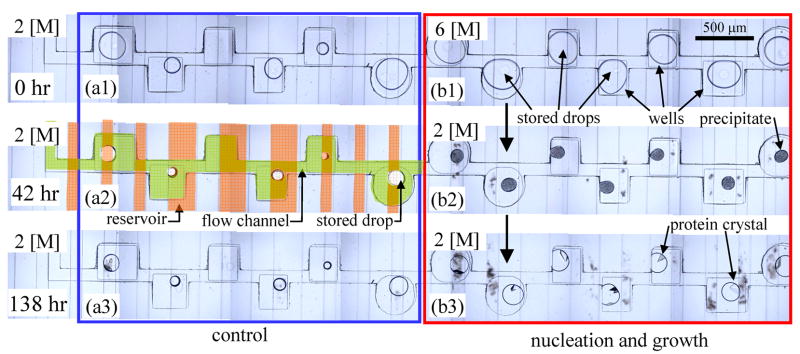
Figure 7 illustrates in more detail how the kinetic path of the protein solution through the phase diagram influences the crystallization process. Eleven drops containing the same lysozyme solution described above are divided into two sets. At t = 0 hours, the first set of drops was placed in dialytic contact with a 2 [M] salt solution immediately after the drops are docked in the wells. After 42 hours the drops had reached their steady state concentration and none had crystallized. Finally, after 139 hours, one of five of the drops had a single crystal. In parallel, at t = 0 hours, the second set of drops was placed in dialytic contact with a 6 [M] salt reservoir for 42 hours, which drove the protein solution deep into supersaturation, inducing precipitation in all of the six drops. We did not measure the concentration or characterize the composition of the precipitates. After 42 hours in contact with the 6 [M] reservoir, we reduced the salt concentration of the reservoir to 2 [M], the same condition as for the first set of drops. We observed that the precipitate dissolved as the drops swelled and the drops became clear. Within 24 hours, three of the seven drops contained a single crystal and after another 72 hours the remaining four drops also crystallized. After 138 hours the second set of drops had all crystallized with six of the seven drops containing a single crystal and the seventh drop containing two crystals. A time lapse movie of the second from the rightmost well in Figure 7 is shown in the supplement, S4.6. In contrast, during the same 138 hours the control set of drops, which were quenched immediately from the initial to final state, produced crystals in only one out of five drops. The two sets of drops had the same initial composition, the same final composition and were observed for the same amount of time, but the number of crystals (20% in the first set, 100% in the second set) depended on the temporal trajectory through the phase diagram. These experiments demonstrate that the decoupling of nucleation and growth through the process of temporally tuning the protein supersaturation improves the crystallization process.
Figure 7.
Protein crystallization as a function of kinetic path. Each row of photographs was taken at the same moment; the first row just upon filling, while the 2nd and the 3rd row were taken at 42 and 138 hours later, respectively. (a) A 2M NaCl solution flows through the reservoir for 138 hours. Although the protein solution is supersaturated, after 138 hours only one protein crystal out of five drops is found. (b) The reservoir is filled with 6M NaCl solution for 42 hours. The protein precipitates indicating this condition is deep in the supersaturation region. After 42 hours the reservoir is replaced with a 2M NaCl solution. The drops first became clear and then a single crystal grew at the oil/water interface. At the end, five of the sixs drops contained a single crystal, while the remaining drop had two crystals. A time lapse movie of the second from the rightmost well is in the supplement, S4.6.
As a final application of the Phase Chip, we reversibly grow and dissolve a crystal of the protein xylanase by varying the salt concentration of the reservoir, illustrated in the supplement S4.7. When the reservoir contains high salt, water flows out of the protein solution, dehydrating the protein solution and the crystal grows. When the reservoir contains low salt, water flows into the protein solution and the crystal dissolves. This demonstrates the ability to precisely control and measure crystal growth conditions.
Conclusion
We have manufactured a class of microfluidic devices designed to manipulate and measure the phase diagrams of multi component aqueous systems. The device consists of a solute formulation stage, a droplet creation stage, and a droplet storage stage in which the solute concentration can be reversibly varied. The storage compartment contains a semi-permeable membrane through which water passes, but not protein, PEG, or salt. The water content of the stored drop is controllably varied by filling a reservoir located across the membrane from the storage well with a salt solution of a specific molarity. The water permeability of the Phase Chip was experimentally investigated and quantitatively modeled with transport theory. Because the PDMS membranes are thin and the protein drops are small, the diffusion times are short and permeation is rapid. Phase Chips were built that were able to store 1 nl drops in wells at a density of 200/cm2 with up to 10 independent dialysis reservoirs. The Phase Chip, with its ability to reversibly control the water content of drops stored in wells renders the control and measurement of solute concentrations as convenient as the manipulation and measurement of temperature. As a first application of the Phase Chip the phase diagram of a mixture of PEG and ammonium sulfate was measured on-chip and validated off-chip. In a second application, temporal variation of the supersaturation of a protein solution was demonstrated to enhance crystallization and control crystal growth. Protein crystallization is a non-equilibrium process requiring one set of conditions for crystal nucleation and another set for crystal growth. The Phase Chip, which allows dynamic control over the key thermodynamic variable, concentration, is an ideal platform for optimization of this process.
Supplementary Material
Details of device fabrication, movies of Phase Chip in action.
Acknowledgments
SF acknowledges support from the NSF Major Research Instrumentation program, DMR-0420921, the NIH-NIGMS, R21 RGM075052A, and the CIMS at Harvard University (now the Center for Nanoscale Science).
References
- 1.Sia SK, Whitesides GM. Electrophoresis. 2003;24(21):3563–3576. doi: 10.1002/elps.200305584. [DOI] [PubMed] [Google Scholar]
- 2.Squires TM, Quake SR. Reviews Of Modern Physics. 2005;77(3):977–1026. [Google Scholar]
- 3.Zheng B, Gerdts CJ, Ismagilov RF. Current Opinion In Structural Biology. 2005;15(5):548–555. doi: 10.1016/j.sbi.2005.08.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Song H, Chen DL, Ismagilov RF. Angewandte Chemie-International Edition. 2006;45(44):7336–7356. doi: 10.1002/anie.200601554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zheng B, Roach LS, Ismagilov RF. Journal Of The American Chemical Society. 2003;125(37):11170–11171. doi: 10.1021/ja037166v. [DOI] [PubMed] [Google Scholar]
- 6.Song H, Ismagilov RF. Journal of the American Chemical Society. 2003;125(47):14613–14619. doi: 10.1021/ja0354566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lau BTC, Baitz CA, Dong XP, Hansen CL. Journal of the American Chemical Society. 2007;129(3):454–455. doi: 10.1021/ja065855b. [DOI] [PubMed] [Google Scholar]
- 8.Watson JM, Baron MG. Journal Of Membrane Science. 1995;106(3):259–268. [Google Scholar]
- 9.Randall GC, Doyle PS. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2005;102(31):10813–10818. doi: 10.1073/pnas.0503287102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Leng J, Lonetti B, Tabeling P, Joanicot M, Ajdari A. Physical Review Letters. 2006;96(8):084503. doi: 10.1103/PhysRevLett.96.084503. [DOI] [PubMed] [Google Scholar]
- 11.Urbanski JP, Thies W, Rhodes C, Amarasinghe S, Thorsen T. Lab on a Chip. 2006;6(1):96–104. doi: 10.1039/b510127a. [DOI] [PubMed] [Google Scholar]
- 12.Feynman RP, Leighton RB, Sands ML. The Feynman Lectures on Physics. II. Addison - Wesley; 1964. Chap. 7-5. [Google Scholar]
- 13.Zaslavsky BY, Gulaeva ND, Djafarov S, Masimov EA, Miheeva LM. Journal Of Colloid And Interface Science. 1990;137(1):147–156. [Google Scholar]
- 14.McPherson A. Crystallization of biological macromolecules. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 1999. p. 586. [Google Scholar]
- 15.Anderson MJ, Hansen CL, Quake SR. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(45):16746–16751. doi: 10.1073/pnas.0605293103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Garcia-Ruiz JM. Journal of Structural Biology. 2003;142(1):22–31. doi: 10.1016/s1047-8477(03)00035-2. [DOI] [PubMed] [Google Scholar]
- 17.Debendetti PG. Metastable Liquids: Concepts and Principles. Princeton University Press; 1996. [Google Scholar]
- 18.Berland CR, Thurston GM, Kondo M, Broide ML, Pande J, Ogun O, Benedek GB. Proceedings Of The National Academy Of Sciences Of The United States Of America. 1992;89(4):1214–1218. doi: 10.1073/pnas.89.4.1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chayen NE. Progress In Biophysics & Molecular Biology. 2005;88(3):329–337. doi: 10.1016/j.pbiomolbio.2004.07.007. [DOI] [PubMed] [Google Scholar]
- 20.Chayen NE. Current Opinion In Structural Biology. 2004;14(5):577–583. doi: 10.1016/j.sbi.2004.08.002. [DOI] [PubMed] [Google Scholar]
- 21.Hansen CL, Sommer MOA, Quake SR. Proceedings of the National Academy of Sciences of the United States of America. 2004;101(40):14431–14436. doi: 10.1073/pnas.0405847101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hansen CL, Skordalakes E, Berger JM, Quake SR. Proceedings Of The National Academy Of Sciences Of The United States Of America. 2002;99(26):16531–16536. doi: 10.1073/pnas.262485199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hansen CL, Classen S, Berger JM, Quake SR. Journal of the American Chemical Society. 2006;128(10):3142–3143. doi: 10.1021/ja0576637. [DOI] [PubMed] [Google Scholar]
- 24.Bergfors T. Journal Of Structural Biology. 2003;142(1):66–76. doi: 10.1016/s1047-8477(03)00039-x. [DOI] [PubMed] [Google Scholar]
- 25.Gerdts CJ, Tereshko V, Yadav MK, Dementieva I, Collart F, Joachimiak A, Stevens RC, Kuhn P, Kossiakoff A, Ismagilov RF. Angewandte Chemie-International Edition. 2006;45(48):8156–8160. doi: 10.1002/anie.200602946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Smith HW, Delucas LJ. Journal Of Crystal Growth. 1991;110(1–2):137–141. [Google Scholar]
- 27.Lee SSJ, Cudney R. Journal Of Applied Crystallography. 2004;37:504–505. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Details of device fabrication, movies of Phase Chip in action.