An increase in AMPA and a decrease in SK conductance increase burst firing by different mechanisms in a model of a dopamine neuron in vivo

Abstract

A stylized, symmetric, compartmental model of a dopamine neuron in vivo shows how rate and pattern can be modulated either concurrently or differentially. If two or more parameters in the model are varied concurrently, the baseline firing rate and the extent of bursting become de-correlated, which provides an explanation for the lack of a tight correlation in vivo, and is consistent with some independence of the mechanisms that generate baseline firing rates versus bursts. We hypothesize that most bursts are triggered by a barrage of synaptic input, and that particularly meaningful stimuli recruit larger numbers of synapses in a more synchronous way.

An example of concurrent modulation is that increasing the short-lived AMPA current evokes additional spikes without regard to pattern, producing comparable increases in spike frequency and fraction fired in bursts. On the other hand, blocking the SK current evokes additional bursts by allowing a depolarization that previously produced only a single spike to elicit two or more, and elongates existing bursts by the same principle, resulting in a greater effect on pattern than rate. A probabilistic algorithm for the random insertion of spikes into the firing pattern produces a good approximation to the pattern changes induced by increasing the AMPA conductance, but not by blocking the SK current, consistent with a differential modulation in the latter case. Furthermore, blocking SK produced a longer burst with a greater intra-burst frequency in response to a simulated meaningful input, suggesting that reduction of this current may augment reward-related responses.

Introduction

Importance of burst firing in dopamine neurons

Midbrain dopamine (DA) neurons are involved in motivation and the control of movement, and dysfunctional dopaminergic signaling has been implicated in Parkinson’s disease (Bernheimer et al. 1973), schizophrenia (Weinberger 1987), and drug abuse (Koob et al. 1997). The firing pattern in these neurons determines the amount of dopamine released in the projection areas, and a bursting firing pattern releases more dopamine than a tonic one (Chergui et al. 1996; Gonon 1998). Therefore, an understanding of dopaminergic signaling must include an understanding of how the firing pattern is regulated. Dopamine neurons in vivo can exhibit one of several firing modes (Grace and Bunney 1984a,b; Hyland et al. 2002): silence, regular single-spike firing, irregular single-spike firing, and bursting. In a bursting cell, the percentage of spikes fired in bursts is variable. DA neurons also exhibit interesting activity in the context of a behavioral task. Recordings from awake, behaving monkeys during reward-mediated learning (Schultz 1998) show that dopamine neurons fire a population burst in response to the delivery of an unexpected primary reward or to a reward-predicting stimulus.

Correlation between pattern and rate

The definition of a burst in midbrain dopamine neurons in vivo is based on experimental observations (Grace and Bunney 1984b). The criterion is that a burst begins with an ISI (inter-spike interval) less than 80 ms but terminates when the ISI exceeds 160 ms. The spikes identified by this criterion as occurring within a burst are consistent with the perception of bursts upon visual inspection; not only the original investigators, but essentially all subsequent ones use the same definition, except that some studies consider a doublet to be a burst whereas others stipulate a minimum of three spikes. Based on the operational definition of a burst, an increase in frequency might reasonably be expected to increase the fraction of spikes occurring in bursts without increasing the tendency to cluster. Since an increase in frequency decreases the average ISI, the probability that an ISI less than 80 ms would occur and be followed by an ISI less than 160 ms might be increased by this mechanism alone.

When a single parameter (such as levels of iontophoresis of glutamate or haloperidol) is manipulated in a single neuron while holding all other parameters constant (Grace and Bunney 1984b), the correlation between rate and pattern (fraction of spikes fired in bursts) is excellent (r=0.99). On the other hand, several studies (Grace and Bunney 1984b; Hyland et al. 2002; Paladini and Tepper 1999) found only a weak correlation (r = 0.14-0.38) between pattern and rate across a population of DA neurons. Furthermore, in one study burst firing was increased by pressure ejection of bicucculine, and the correlation across the population between changes in the pattern and changes in frequency the same neuron before and after the manipulation was very low (r=0.14) (Paladini and Tepper 1999).

These findings and others (Charlety et al. 1991; Overton and Clark 1992) suggest that the rate and pattern can be modulated independently in dopamine neurons, consistent with some independence of the mechanisms generating baseline firing rates and bursts (Hyland et al. 2002). However, if only cells firing above 6 Hz are examined, a positive linear relationship emerges between rate and pattern (Hyland et al. 2002; Smith and Grace 1992; Zhang et al. 1994). This relationship seems to be an artifact of the definition of bursting using intervals for burst initiation and termination that are unusual at the range of firing rates usually observed (Hyland et al. 2002), but not necessarily at higher rates. Therefore, one challenge was to separate the effects of chance increases in bursting due to increases in frequency and of increases due to enhancing burst firing selectively.

In this study, we examine two different types of modulations. The two modulations were to increase the α-amino-3-hydroxy-5-methylisoxazole-4-proprionate (AMPA) conductance and to block the small conductance (SK) Ca²⁺-activated K⁺ channel conductance. In the model, increasing AMPA modulates rate and pattern concurrently, but blocking SK modulates the firing pattern in a manner that is largely independent of the rate.

Rationale for examining the effect of doubling the AMPA conductance

A doubling of the AMPA component of the synaptic current evoked by glutamate is an example of plasticity that has been observed in dopamine neurons in response to the administration of drugs of abuse, both in vivo (Zhang et. al. 1997) and in vitro (Borgland et al. 2004). The ratio of the peak EPSC (excitatory postsynaptic current) evoked by the stimulation of AMPA and NMDA receptors can be measured by blocking all other synaptic currents pharmaceutically, voltage clamping the cell to +40 mV, then stimulating the slice. Under these conditions, the ratio of the peak AMPA EPSC to the peak NMDA EPSC can be increased from 0.38 to 0.75 by a single injection of cocaine (Ungless et al. 2001). An increase in the AMPA component was responsible for this change. The AMPA/NMDA ratio was positively correlated with locomotor activity, and Jones and Bonci (2005) speculated that an increase in the synaptic AMPA response could result in an enhancement of the response of dopamine neurons to reward related stimuli. In addition, iontophoretic administration of AMPA has been shown to increase both the frequency and the fraction of spikes fired in bursts in chloral hydrate anesthetized rats (Christoffersen and Meltzer 1995).

Rationale for examining the effect of blocking the SK conductance

Hyland et al. (2002) found a greater intra-burst frequency for bursts in the context of a task within operant behavior experiments than for those occurring at other times. They suggested that a reduction of spike after-hyperpolarization, similar to that produced by the application of the SK blocker apamin, may be involved in the mechanism of inducing bursts in behaving animals. SK channel blockers have been shown to facilitate bursting in vivo in rats under chloral hydrate anesthesia (Waroux et al. 2005; Ji and Shepard 2006). The proportion of spikes fired in three or more spike bursts in the VTA was increased from 20 to 52% with only a slight if any increase in rate. In addition, differential expression of the small-conductance, calcium activated potassium channel SK3 accounts for differences in the regularity of firing in dopaminergic midbrain neurons (Wolfart et al. 2001). The SK3 subtype is preferentially expressed in the monoamine cell group regions, and some studies have found an association between abnormalities in the SK3 channel gene and schizophrenia (Liegeois et al. 2003). The SK3 channel is not known to be directly modulated, but there are several known modulators of the second messenger cascades that release calcium from internal stores that can activate the SK channel (Fiorillo and Williams 1998). Acetylcholine (Fiorillo and Williams 2000), norepinephrine, dopamine (Paladini et al. 2001), and serotonin (Brodie et al. 1999) have all been postulated to reduce the access of the SK channel to calcium activation in dopamine neurons, hence these modulators may act to reduce current flow through the SK channel in vivo.

Methods

Compartmental Model

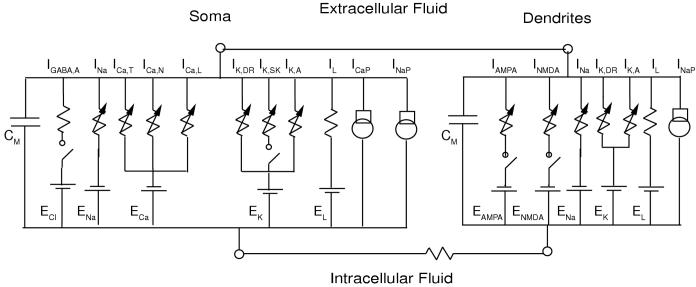
The three-compartment model of Komendantov et al. (2004) was used with a few modifications (see Fig. 1). Computation was minimized by utilizing a stylized, symmetric model neuron with a soma, four primary, and eight secondary dendrites. Using symmetry, only one compartment of each type was integrated and the electrotonic currents were scaled accordingly (Canavier 1999). All compartments contain a fast sodium current (I_Na), a delayed rectifying potassium channel (I_K,DR), a transient outward potassium current (I_K,A), a leak current (I_L), and a sodium pump (I_NaP). Each compartment is capable of spiking (Hausser et al. 1995). All compartments contain sodium dynamics and a sodium balance. The soma also contains calcium dynamics and a calcium balance that includes the voltage-activated T, N, and L-type calcium currents (I_Ca,T, I_Ca,N and I_Ca,L), a calcium component of the leak current (I_L), and a calcium pump (I_CaP). Calcium entry in the soma activates the SK channel current (I_K,SK). The glutamatergic synapses that produce the AMPA and NMDA currents (I_AMPA and I_NMDA) are located exclusively on the dendrites, and the GABAergic synaptic conductance that produces the GABAergic current (I_GABA,A) is located primarily on the soma. As in Komendantov et al. (2004), some I_GABA,A is located on the dendrites, but the conductance is one tenth that on the soma, and is not shown in Fig. 1 in order emphasize that the bulk of the inhibitory input in the model is on the soma.

Figure 1.

Equivalent circuit diagram. The somatic compartment contains the conductances shown (see text for a listing) in parallel with a membrane capacitance, and both the proximal and dendritic compartments contain the conductances shown for the dendritic compartment, again in parallel with a membrane capacitance.

The model was originally calibrated using in vitro data¹ and is capable of emulating both regular pacemaking in the absence of any synaptic input or external stimulus current and the slow oscillatory potential (SOP) seen in the slice in the presence of TTX. The interplay between the calcium currents and the SK channel drive the SOP that underlies pacemaking (Amini et al. 1999; Wilson and Callaway 2000). The model also emulates NMDA-induced burst firing based on an oscillation in dendritic sodium concentration that in the model is driven by the interplay between sodium entering via the voltage-dependent NMDA receptor channel and exiting via the electrogenic sodium pump. The value of the SK conductance was changed from the 900 μS/cm² reported in Komendantov et al. (2004) to 800 μS/cm² in order to obtain robust pacemaker firing, and the axial resistance (R_a) was changed to 400 Ω cm. Full equations and parameters are given in Appendix I.

Glutamatergic Synaptic Current Dynamics

A two-state kinetic scheme was used for both AMPA and NMDA receptor dynamics. The rate constants α and β for binding and unbinding, respectively for AMPA (1100 s^-1 mM^-1, 190 s^-1) and NMDA (72 s^-1 mM^-1,6.6 s^-1) were taken from Table 1 of Destexhe et al. (1995). Assuming the law of mass action, the explicit solution for the fraction of the population of receptors activated at a synapse is

$$\mathrm{r}\left(\mathrm{t}\right)={\mathrm{r}}_{\infty }+(\mathrm{r}\left(t_n\right)-{\mathrm{r}}_{\infty })(\exp ((t_n-\mathrm{t})∕\tau )$$

during a pulse of transmitter, and otherwise it is

$$\mathrm{r}\left(\mathrm{t}\right)=[{\mathrm{r}}_{\infty }+\left(\mathrm{r}\left({\mathrm{t}}_{\mathrm{n}}\right)-{\mathrm{r}}_{\infty }\right)(\exp (\mathrm{d}∕\tau )]\exp (\beta \left(d+t_n-t\right)$$

where d is the transmitter pulse duration, r(t_n) is the value of r(t) at the time the pulse of transmitter is emitted, r_∞ is the steady state value α[T]/(α[T]+β) in the presence of transmitter concentration [T], and τ is the time constant during the pulse, 1/(α[T]+β). A 1 mM, 1 ms pulse in glutamate concentration in the cleft ([T]) was presumed to occur at the time of a synaptic event. During most simulations, r(t_n) was assumed to be zero, hence the potential unavailability of receptors due to a previous recent input at the same synapse was not considered. In order to take this potential unavailability into account, one would have to assume a fixed number of synapses and generate a dedicated input train for each input. For the simulations of transient inputs, we did assume that a fixed number of synapses were activated, however we assumed a common input train for all synapses that was the result of a reward-related stimulus, and r(t_n) was calculated for each input in the train .

Table 1.

Cutoff Frequency (Hz)	4	5	6	7	8
Control	0.55	0.66	0.74	0.81	0.86
SK set to zero	0.80	0.86	0.91	0.94	0.95
Increased AMPA	0.59	0.65	0.71	0.79	0.85
Prediction	0.57	0.64	0.73	0.80	0.86

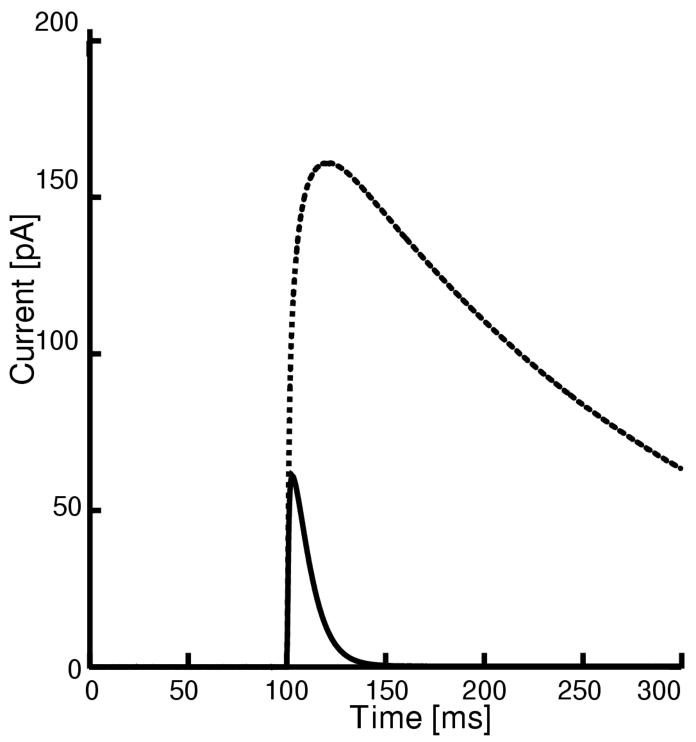
In midbrain slice preparations, there are no prominent, easily identifiable tracts consisting of bundles of axons. Hence, in order to stimulate a particular afferent, a cocktail of pharmaceutical agents designed to block all synaptic inputs, except the one(s) under study, is applied, and then the slice is stimulated at an arbitrary point. The time course and relative amplitudes of the AMPA and NMDA synaptic currents were calibrated using experimental data from the literature obtained under voltage clamp conditions (Borgland et al. 2004) generated using a strong stimulus that presumably activated a number of glutamatergic synapses. The model EPSCs (see Fig. 2) were measured under simulated somatic voltage clamp to +40 mV in order to mimic the conditions in Fig. 1B of Borgland et al. (2004). The delayed rectifier conductance (g_K,DR) was set to zero because the patch-clamp electrodes contained TEA, and both internal and external TEA block this current (Lenaeus et al. 2005). Using the kinetic parameters given above, the AMPA conductance (g_AMPA) and the NMDA receptor channel permeability (P_NMDA) to sodium were scaled to match the ratio of the peak AMPA EPSC to peak NMDA EPSC in Fig. 1B of Borgland et al. (2004), which was 0.38 under control conditions and 0.75 after exposure to cocaine. In the absence of precise knowledge of how many synapses were activated, we assumed that ten minimal synaptic events were simultaneously activated by the stimulus during the voltage clamp simulation.

Figure 2.

Calibration of Glutamatergic Synaptic Dynamics. Simulated EPSCs mediated by AMPA and NMDA. The larger amplitude EPSC (dotted curve) is the NMDA current, and the smaller (solid curve) is AMPA. The soma was voltage clamped at +40 mV. The delayed rectifier conductance was set to zero to simulate the application of TEA.

For a minimal synaptic event, the permeability to sodium ions (P_NMDA) was set to 0.23e-6 × 10^-6 cm/s. The sodium component of the AMPA conductance (g_AMPA,Na) for a minimal event was set to 2.68 μS/cm² and the potassium component (g_AMPA,K) was set to 3.37 μS/cm². Due to the simplified, stylized and symmetric nature of this model, the synaptic input was assumed to be evenly distributed across the proximal and dendritic compartments. Only two dendritic compartments are integrated but conceptually twelve compartments (four proximal and eight distal) are represented.

The Nernst potential for sodium was allowed to vary based on internal cytosolic concentration in order to calculate the contribution of I_AMPA,Na to the sodium balance. The apparent conductance of the NMDA receptors in the model was estimated by measuring the slope of the linear portions of the current/voltage (IV) curve generated using the Goldman Hodgkin Katz (GHK) equation for this current. Since the internal sodium and calcium are variable, the slope conductance of the NMDA current associated with a minimal event varies somewhat but is approximately 100-150 μS/cm² in the concentration ranges observed during simulations, with a reversal potential near 0 mV. The total AMPA conductance (sodium plus potassium) that we assumed for a minimal event is 6.05 μS/cm². In order to determine that the values chosen for a minimal event, the actual conductances were calculated from the densities. The area of the proximal compartment is 14.1 × 10^-6 cm² and that of the distal compartment is 16.5 × 10^-6 cm², for a total dendritic surface area of 188.5 × 10^-6 cm². Thus the minimum distributed synaptic conductance is 1.140 nS for AMPA and 28.275 nS for NMDA. However, in order to match the peak conductance ratios for the EPSC generated in response to a single strong input, the scaling by the peak r(t) achieved during a pulse of transmitter must be taken into account: the peak r(t) for AMPA is 0.618 compared to only 0.069 for NMDA, resulting in peak conductances for a single input of 705 and 1951 pS respectively. A recent study (Dalby and Mody 2003) using spontaneous EPSCs in rat dentate gyrus cells estimated the single channel conductance of an NMDA receptor as 60 pS, and the number of channels open as 4, for a minimum event conductance of 240 pS. Hence, the minimum synaptic input to the model corresponds to about eight spontaneous events as measured in dentate gyrus. The magnitude of the smallest synaptic event in the model, distributed across the twelve conceptual compartments, seems reasonable in view of the simplicity of the model and the lack of precise knowledge regarding the convergence and coherence of the glutamatergic inputs to dopamine neurons. In simulations of the drug-induced plasticity described in the Introduction in which the AMPA/NMDA ratio increased from 0.38 to 0.75, both components of g_AMPA were doubled.

Glutamatergic Synaptic Event Statistics

The interevent intervals for the glutamatergic synaptic events were selected using a simulated Poisson process. The input was symmetrically distributed between the proximal and distal compartments. Each event generated a 1 ms pulse of transmitter at a synapse. The output r(t) from all prior events were summed at each time point to produce the cumulative receptor activation R(t). A maximum time step of 0.1ms was used with the integration package CVODE. The first 90 seconds of each simulation was discarded to allow the system to equilibrate, and data analysis was performed on the next 90 seconds of simulated data. The same 90 seconds of random receptor activation history was used for the discarded 90 sec and the 90 sec that was analyzed. To speed computation, this input was pre-computed and discretized at 0.1 ms, and used for all simulation runs at a given average P_NMDA regardless of the value of the GABA and SK conductances or the AMPA/NMDA ratio.

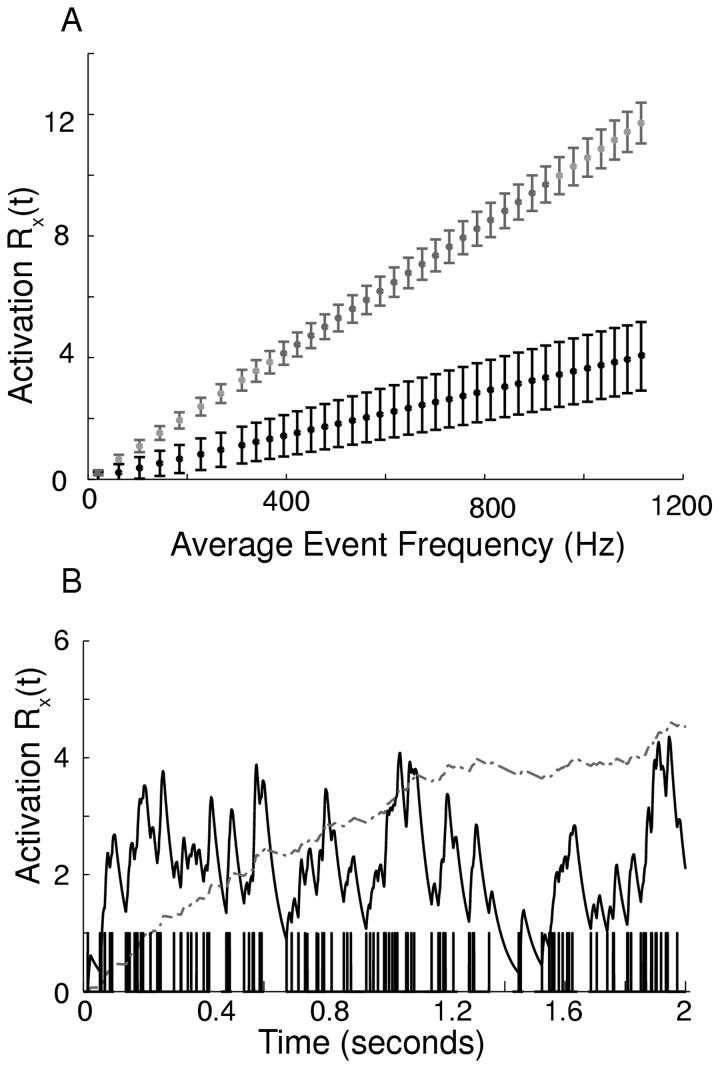
In this study, the relative background levels of activation of AMPA and NMDA depend upon the average interevent interval (IEI) given in ms. Since we have assumed that a given synapse is not activated often enough to saturate, there is an approximately linear relationship between the average level of NMDA receptor activation (R_NMDA) and the reciprocal of the mean interevent interval, [R_NMDA] =10.503 [IEI], where [] indicates the average value. If this relationship is multiplied by the permeability of a single synapse to sodium, we obtain an expression for the average total permeability to sodium, [P_NMDA×10^-6 cm/s ]= 2.4157×10^-9 cm [IEI]. The relationship is different for AMPA, which has a faster time constant, such that [R_AMPA] =3.626 [IEI] and [g_,AMPA] = 21.937 ms μS/cm²[IEI]. Figure 3A plots the average value and standard deviation of the synaptic activation of both AMPA and NMDA receptors calculated from a simulation. The linear relationship is evident. NMDA receptor activation summates much more effectively than AMPA, especially as the frequency of the synaptic events is increased. An example at an IEI of 1.6981 ms (588 Hz) is given in Fig. 3B. As stated above, the same set of random event times was used for all values of the GABA_A conductance at a given average value of P_NMDA.

Figure 3.

Receptor Dynamics. A. Mean steady-state NMDA (gray, upper) and AMPA (black, lower) cumulative receptor activation R_x(t) and standard deviation as a function of average input frequency. The subscript denotes AMPA or NMDA. B. Summation of AMPA (solid black) and NMDA (dot-dashed gray) cumulative receptor activation R_x(t) during a simulation of mixed bursting and single spike firing with a comb plot of event times on the x axis. The average input frequency was 589 Hz ([IEI] = 1.6981 ms).

Data Analysis

A spike was counted when the somatic potential became more depolarized than -30 mV. Occasionally a spike would have two peaks very close together due to electrical coupling of compartments with a slightly different spike time. These false doublets were eliminated by requiring a hyperpolarization below -30 mV between spikes. A burst was initiated by an ISI of 80 ms and terminated by an ISI of less than 160 ms. These criteria were based on the experimental literature (Grace and Bunney 1984b). Our previous study (Komendantov et al. 2004) used a similar definition, but required a 5 mV hyperpolarization between bursts. In order to make a better comparison with in vivo data, in this study a minimum hyperpolarization between bursts was not required.

Probabilistic algorithm for random insertion of spikes into the firing pattern

The number of spikes that occur in bursts, which in this analysis have a minimum of three spikes, can be increased in several ways. The most obvious is to add a spike during a burst. In addition, a spike that occurs less than 80 ms prior to, or less than 160 ms after, an existing burst will be counted as occurring within a burst and will extend the burst duration. A doublet, or two spikes separated by less than 80 ms, can be converted to a new three-spike burst by a spike occurring before, during, or after the doublet. Finally, spikes in bursts can be added by concatenation of bursts or doublets. Two bursts are separated more than 160 ms by definition, and if they are separated by an interval between 160 and 320 ms, a spike occurring in a window equal to the interval less 160 ms can concatenate the two bursts. A spike is added to the bursting fraction in the process. Similarly, two doublets are separated by more than 80 ms by definition and can be concatenated in a similar fashion. New doublets can be created if a spike is inserted within 80 ms of an existing spike. A probabilistic algorithm was developed that took as its input the number of bursts, the number of doublets, the number of single spikes, the cumulative duration of the bursts, and the cumulative duration of the doublets plus the number of spikes added by the manipulation.

A constant probability density for spike occurrence is assumed throughout the interval except that a refractory period is assumed after each spike. Thus the probability of a spike occurring during a burst or a doublet or immediately before or after is the fraction of the total non-refractory duration of the train comprised by the relevant interval. For the purposes of calculating the probability of concatenations, each pair of events was assumed to have its inter-event intervals distributed evenly over the entire interval. In order to obtain pairs of events, the largest integer smaller than the current expectation value for the number of events was used. In an actual trial a spike is added to one category to the exclusion of all others, but in the probabilistic algorithm the expectation value of spikes in each category was computed instead. Therefore the actual values when plotted against the values predicted by the probabilistic algorithm should scatter evenly above and below the diagonal if the increase in spikes that occur within a burst is a result of the random insertion of spikes. The complete algorithm is given in Appendix II.

Results

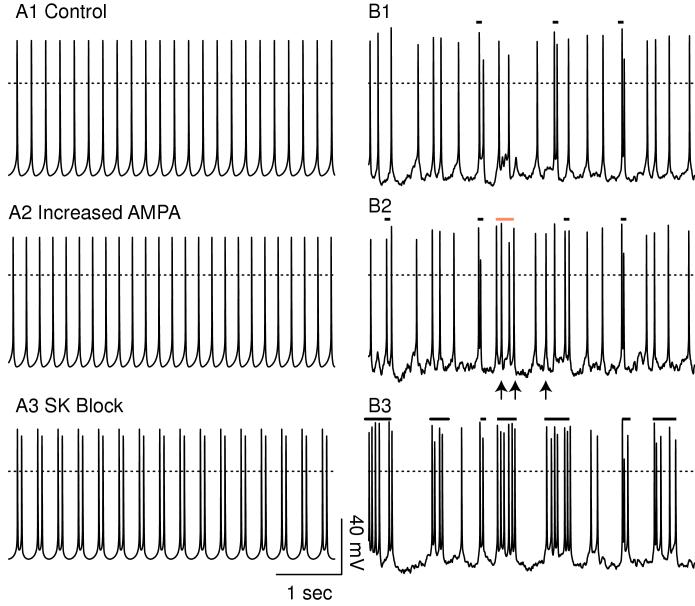
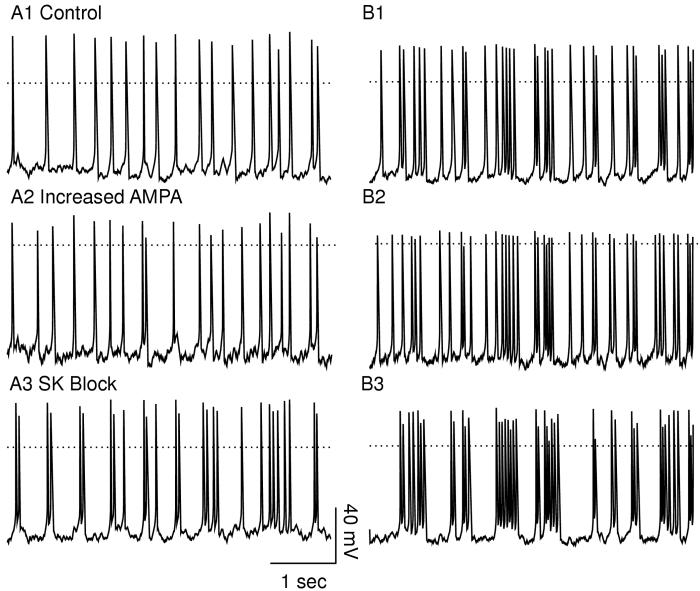
Figure 4 contrasts the firing patterns obtained by holding the AMPA conductance and NMDA permeability constant at their average values (left-hand side) versus the firing patterns produced in the presence of randomly timed synaptic inputs (right-hand side). The latter clearly produces a better approximation to the firing patterns most often observed in vivo. Figure 4A1 shows pacemaker-like firing under control conditions with constant permeability of the NMDA receptors and constant AMPA-mediated conductance. Using constant values, doubling g_AMPA (Fig. 4A2) produced a slight increase in the frequency (25 vs 23 spikes in 5 sec). The sub-threshold oscillation is slightly reduced in amplitude by the linear, ohmic synaptic current, resulting in a slightly faster frequency. In the presence of randomly timed inputs, the number of spikes is increased from 23 under control conditions (Fig. 4B1) to 26 with g_AMPA doubled Fig. 4B2); however, the timing of many spikes is nearly the same, in large part because the same synaptic input pattern was used for all simulations on the right-hand side. Therefore the increase in frequency does not appear to be achieved by a uniform reduction in ISI as in B1, but rather by the addition of spikes in a random manner. The arrows in Fig. 4B2 indicate the spikes that appear to have been inserted as a result of the increase in g_AMPA. The bars over the panels indicate which spikes meet the criteria for being included in a doublet or burst. The red bar in Fig. 4B2 indicates a four-spike burst in which the first and third spikes were concatenated into a burst by the addition of the second spike, and the addition of the fourth spike extended the burst. This figure illustrates the value of modeling-a physiological experiment could never be run twice keeping everything the same, including the pattern of synaptic activation, and just changing one parameter between the two experiments.

Figure 4.

Comparison of in vitro and in vivo models. Average P_NMDA = 1.086 × 10^-6 cm/s ([IEI] = 2.2237 ms) and g = 500 μS/cm² _GABA,A,s. The dotted line indicates 0 mV. A. The lefthand side shows simulations with the level of activation of AMPA and NMDA held constant at their average values. A1. Pacemaker control. A2. Doubling g_AMPA slightly increases the frequency. A3. Blocking SK induces doublets. B. The right-hand side shows receptors activated with random synaptic dynamics. Bursts and doublets are indicated by the solid bars. B1. Much less regular, mostly single spiking is observed when excitation and inhibition are balanced in simulations of activity in vivo. B2. Doubling g_AMPA increases the number of spikes evoked by inserting additional spikes (arrows), in one case creating a burst by concatenating spikes (red bar). B3. Blocking SK strongly increases the tendency of spikes to cluster in bursts.

In contrast to doubling g_AMPA, setting g_K,SK to zero in Fig. 4B3 causes a pronounced increase in the tendency of spikes to cluster into bursts that are frequently followed by relatively long hyperpolarized intervals. Note that the same manipulation in the presence of a tonic level of receptor activation converts singlet firing to periodic doublets (Fig. 4A3) rather than bursts, underestimating the actual increase in bursting observed in the presence of noisy synaptic input pattern. The noise causes unpredictable switches between the hyperpolarized and depolarized phases, resulting in singlets and bursts in addition to doublets. However, the underlying mechanism is the same. The SK current usually generates a hyperpolarizing current in response to a depolarization, and blocking this current allows the sub-threshold oscillation to increase in the amplitude and duration so that not just one but two spikes occur on each cycle. The slower frequency of the sub-threshold oscillation in Fig. 4A3 compared to Fig. 4A1 results from the increased amplitude of the sub-threshold oscillation (see explanation of intrinsic mechanisms in Fig. 5).

Figure 5.

Intrinsic versus synaptic influences on the firing pattern. Average P_NMDA = 0.149×10^-6 cm/s (IEI = 16.1079 ms) and g_GABA,A,s= 100 μS/cm². A. Pacemaker-like activity (black) at low levels of synaptic activation under control conditions. An oscillation in cytosolic somatic Ca²⁺(green) and the level of NMDA receptor activation (blue) both influence the firing pattern. The green arrow indicates a particularly long ISI resulting from a period of lower than average synaptic activation, and the blue arrow indicates a short one due to a spike in the synaptic input (blue). B. Setting g_K,SK to zero disrupts the oscillation in Ca²⁺ and causes the activity to become less regular and more bursty. In the model, the interplay between Na⁺ accumulation (red) and Na⁺ pump activation becomes the dominant intrinsic process under these conditions. The blue arrows indicate spikes or bursts that are triggered at higher than average values of Na because of local peaks in the synaptic activation. Conversely, the red arrows indicate relatively low values of Na⁺ immediately before a spike or burst that is not triggered by any apparent increase in synaptic activation. In sum, the level of synaptic activation required to allow the initiation of a spike or a burst is variable, depending upon the levels of Na⁺ and Ca²⁺ concentration and on the levels of the hyperpolarizing currents that these ions activate. These levels reflect the immediate past firing history of the neuron.

On the left-hand side of Fig. 4, intrinsic dynamics control spike timing. On the right-hand side of Fig. 4 both synaptic and intrinsic dynamics contribute to the timing of bursts. Hence if a spike is “added”, subsequent spikes can be occluded or delayed due to refractoriness. Figure 5 illustrates how intrinsic and synaptic dynamics interact. Figure 5A illustrates an example of nearly pacemaker-like activity at low levels of synaptic activation under control conditions (the somatic membrane potential is shown in black). The green trace reveals an oscillation in cytosolic somatic Ca²⁺, whereas the blue trace indicates the level of NMDA receptor activation. When sufficient Ca²⁺ is removed subsequent to an action potential to adequately deactivate the SK current, a slow depolarization is initiated. The level to which Ca²⁺ has to be removed before a slow depolarization that precedes an action potential is triggered is variable. For example, in Fig. 5A the green arrow indicates a particularly long ISI resulting from a period of lower than average synaptic activation that required a lower than usual level of Ca²⁺ and a lower than usual level of SK activation before an action potential could be initiated. Conversely, the blue arrow indicates a shorter than usual ISI due to a local peak in synaptic activation. This peak is able to overcome the SK current activated at a higher than usual level of Ca²⁺ just prior to action potential initiation. The interaction between intrinsic and synaptic dynamics is similar in the case of doubled g_AMPA (not shown). In Fig. 5B, setting g_K,SK to zero disrupts the oscillation in Ca²⁺ that drives pacemaker-like activity and causes the activity to become less regular and more bursty. In the model, the interplay between Na⁺ accumulation and Na⁺ pump activation becomes the dominant intrinsic process under these conditions. The NMDA receptor activation is still shown in blue, and the Na⁺ concentration is shown in red. The blue arrows indicate spikes or bursts that are triggered at higher than average values of Na⁺ and thus hyperpolarizing Na⁺ pump activation because of local peaks in the synaptic activation. Conversely, the red arrows indicate relatively low values of Na⁺ immediately before a spike or burst that is not triggered by any apparent increase in synaptic activation. In sum, the level of synaptic activation required to allow the initiation of a spike or a burst is variable, depending upon the levels of Na⁺ and Ca²⁺ concentration and on the levels of the hyperpolarizing currents that these ions activate. These levels reflect the immediate past firing history of the neuron. Thus, both synaptic and intrinsic factors are required to account for the firing pattern.

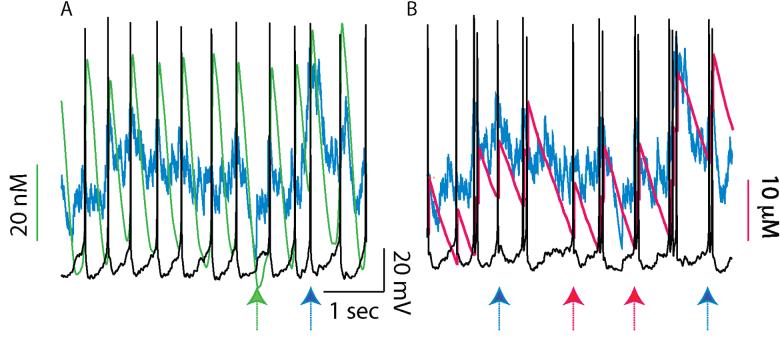
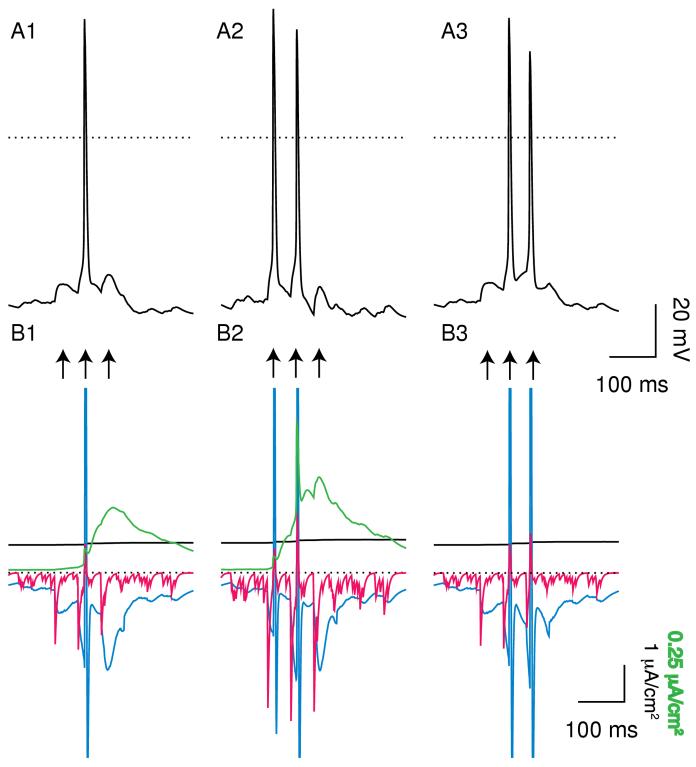
In order to more clearly delineate this interaction, Fig. 6 illustrates the response of a quiescent model neuron to a weak transient input. The idea is to predict the alteration in response to a coherent, reward-related activation of glutamatergic receptors. A train of three EPSPs was applied with an IEI of 50 ms, assuming that the inputs were received concurrently at 10 synapses activated as described in the Methods. Under control conditions (Fig. 6A1), only the second input elicits an action potential. The current elicited by stimulation of the NMDA receptors (blue trace Fig. 6B) summates and is opposed by an increase in I_K,SK (green trace in Fig 6B) and the sodium pump current (black trace in Fig. 6B). The first EPSP does not elicit an action potential because temporal summation is required to reach threshold in this instance, and the third does not elicit and action potential because I_K,SK has become strong enough to prevent it. The current elicited by stimulation of the AMPA receptor is short-lived (red trace in Fig. 6B). Doubling g_AMPA (Fig. 6A2) allows the first EPSP to elicit an action potential in addition to the second by allowing a subthreshold EPSP to become supratheshold. Setting g_K,SK to zero (Fig. 6A3) instead allows the third EPSP to elicit an action potential in addition to the second.

Figure 6.

Burst responses to a weak input train. A train of 3 inputs (arrows) spaced 50 ms apart was applied simultaneously at 10 minimal synapses on a quiescent neuron. Average P_NMDA = 0.251×10^-6 cm/s (IEI = 9.6203 ms) and g_GABA,A,s = 500 μS/cm². A. Membrane potential. The dotted line indicates 0 mV. A1. Under control conditions only the middle EPSP evoked a spike. A2. Doubling g_AMPA allowed the first EPSP to also evoke a spike. A3. Blocking SK caused the second and third EPSPs to evoke a spike. B. Currents. The dotted line indicates 0 μA. The EPSPs and the spike (s) allow calcium entry that activates the somatic SK current (green). The AMPA components of the EPSC (red) is short-lived and the NMDA component (blue) is long-lasting. The dendritic sodium pump current density (solid black) increases slightly during the simulation. B1 Control. B2. The larger AMPA current (red) allows the first EPSP to become suprathreshold. B3. The absence of the hyperpolarizing SK current allows the long-lasting NMDA current (blue) to continue to depolarize the neuron above threshold. Note that the somatic I_K,SK is shown on a different scale than the dendritic currents. The full amplitude of some currents was truncated in Figs. 6B and 7B during action potentials in order to better illustrate the time course in between spikes.

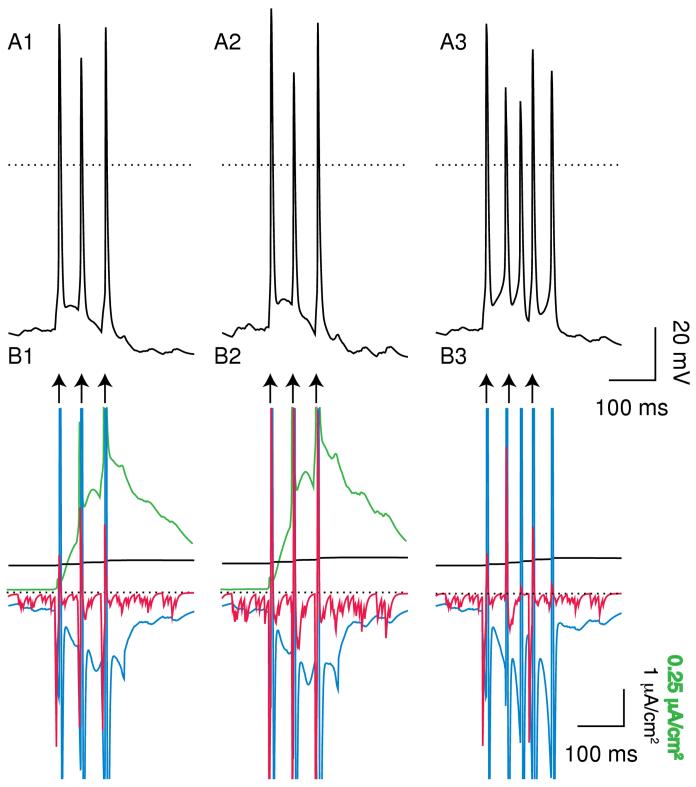
Figure 7 illustrates the response of a quiescent model neuron to a stronger transient input; in this case the inputs were received concurrently at 22 synapses activated as described in the Methods. Under control conditions (Fig. 7A1), each of the three EPSPs elicits an action potential. Note the summation of the SK current (green) and NMDA current (blue) in Fig. B1. Doubling g_AMPA (Fig. 7A2) has no effect in this case, because each EPSP is already suprathreshold so the increase in the short-lived AMPA current (red) in Fig. 7B2 is irrelevant. On the other hand, setting g_K,SK to zero (Fig. 7A3) increases the intra-burst frequency and extends the burst, resulting in five spikes rather than just three. Note the larger amplitude and duration of the NMDA current (blue) when it is not opposed by the SK current (Fig. 7B3).

Figure 7.

Burst Responses to a stronger input train. This train (arrows) was applied simultaneously at 22 minimal synapses on the same neuron. A. Membrane potential. The dotted line indicates 0 mV. A1. Under control conditions all three EPSPs evoked a spike. A2. Doubling g_AMPA had no effect. A3. Blocking SK caused an increase in intra-burst frequency and extended the burst by two spikes. B. Currents. The dotted line indicates 0 μA. B1. Control. B2 The increase in the short-lived AMPA current (red) had no effect because all three EPSPs were already supra-threshold. C2. The residual depolarizationof the NMDA receptors (blue) is unmasked in the presence of SK block.

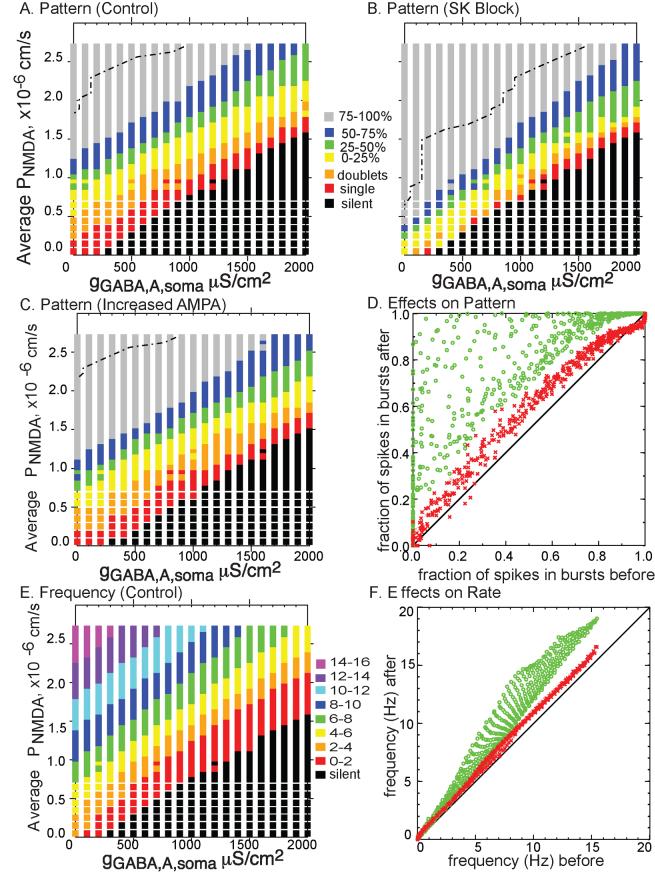
The results presented in Figs. 4, 5, 6 and 7 suggest the hypothesis that increasing g_AMPA evokes additional spikes without regard to pattern, whereas blocking SK extends existing bursts and creates new bursts and doublets by intensifying and extending the depolarization underlying doublets and single spikes. We next performed a search of the parameter space defined by the background levels of glutamatergic excitation and glutamatergic inhibition (Fig. 8). The colored band in Fig. 8A indicates a region in which excitation and inhibition are roughly balanced, producing activity with 0 to 75% of the spikes in three spike bursts. Figure 8B clearly shows that this band is narrower in the presence of simulated SK block, and the bands corresponding to pure single spike firing (red) and a mix of single spikes and doublets (orange) are nearly eliminated. The colored band is also shifted downward, because lower levels of excitation are required to produce the same amount of burst firing with the SK current blocked. Therefore the black region denoting quiescence is correspondingly smaller. Furthermore, the gray region that denotes greater than 75% bursting (rarely seen in vivo) is expanded. Above the dashed lines, only extreme bursting cases with clear “up” and “down” states are observed, and these cases occupy a greater fraction of the parameter space in the presence of simulated SK block.

Figure 8.

Effect of Blocking SK or Doubling g_AMPA on pattern and rate. A-C. Patterns exhibited at various values of glutamatergic and gabaergic input (parameter space). The dot dashed lines in panels A-C demarcate regions above and to the left that appear to have distinct up and down states. A. Control. B. SK blocked. The regions of single spiking and doublets are nearly eliminated and that for bursting is extended. C. Doubling g_AMPA. D. Percent spikes in burst plotted before and after block of SK (green circles) or doubling g_AMPA (red crosses). E. Frequency under control conditions. F. Frequency before and after block of SK (green circles) or an increase in the AMPA/NMDA ratio (red crosses).

Figure 8C shows that doubling g_AMPA shifts all the bands downward because once again, a lower level of excitation of NMDA receptors is required to support the same level of burst firing. However, the colored band is not noticeably narrower in this case. Figure 8D summarizes the effect of both manipulations on the pattern, showing the fraction of spikes fired in bursts after each manipulation as a function of the spikes fired in bursts under control conditions. Doubling g_AMPA (red) produces a modest increase in the fraction of spikes fired in bursts, whereas the effect of setting g_K,SK to zero (green) is a much more pronounced and variable increase. Figure 8E shows the average frequency under control conditions across the parameter space, and Fig. 8F summarizes the effect of each manipulation on frequency. The effect of doubling g_AMPA (red) on frequency seems similar to the effect on pattern, whereas the effect of setting g_K,SK to zero (green) is quite small at low frequencies and increases at higher frequencies, which often correspond to high bursting rates. The banded appearance of the green symbols in 8F is an artifact of the sampling grid in Fig. 8E, and can be made to appear continuous by reducing the grid spacing (not shown).

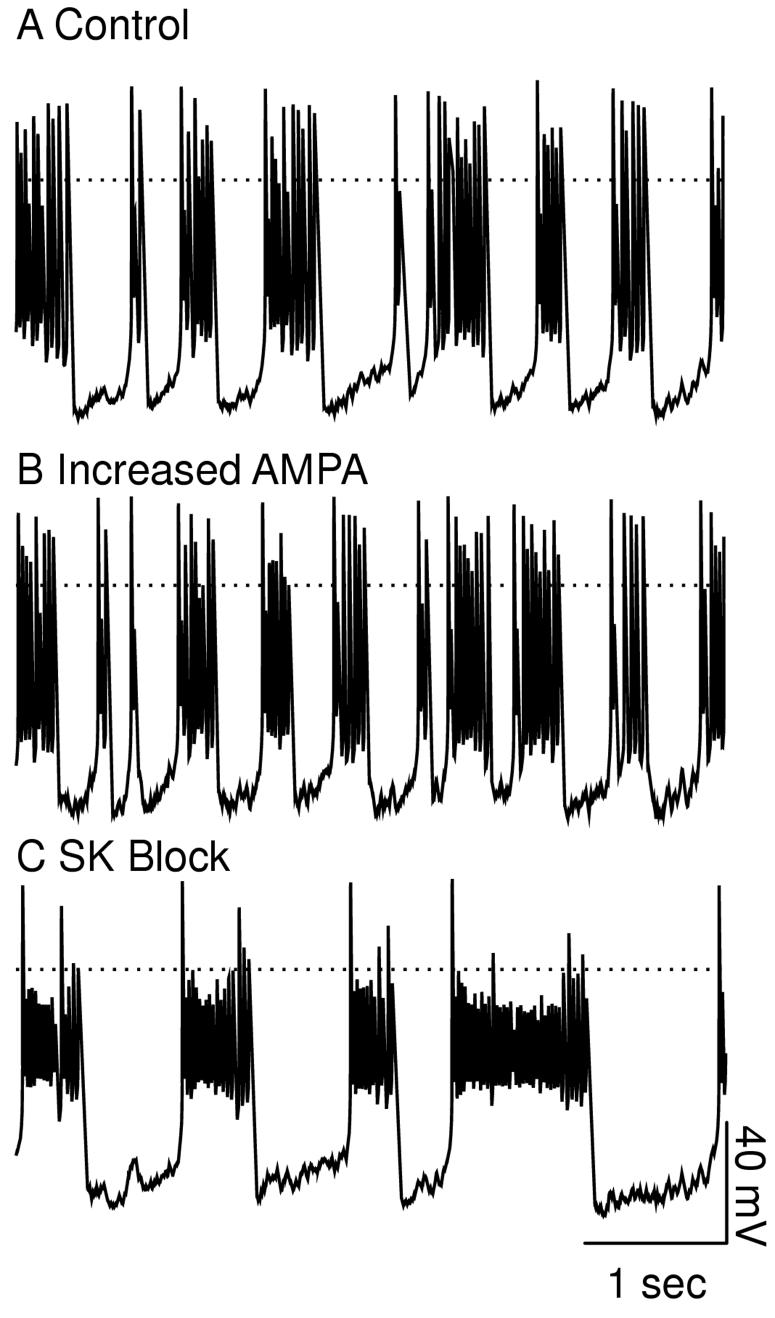
Figure 9 shows more examples of the effects of these manipulations on the firing pattern. On the left-hand side, doubling g_AMPA (A2) inserts a few spikes into the control single spike pattern shown in A1, including one that produces a doublet. Setting g_K,SK to zero (A3) converts numerous single spike into doublets, including a pair that are concatenated into a burst. As stated above, since there are significant intrinsic dynamics at work in addition to the synaptic dynamics, an explanation based solely on random spike insertion is clearly an over-simplification, in but the case of manipulating the AMPA conductance, it appears to be a reasonable starting point. On the right hand side, the control pattern (B1) is already quite bursty, with over half its spikes in bursts of three or more spikes and nearly a quarter in doublets. Once again, doubling g_AMPA (B2) appears to insert a few spikes into the control pattern, but here setting g_K,SK to zero (B3) results in longer bursts with more spikes, to the near exclusion of single spikes and doublets.

Figure 9.

Examples of the effect of SK block and doubling g_AMPA on the electrical activity exhibited by the model in different parameter ranges. The top traces show the model output under control conditions with g_K,SK set to 800 μS/cm², the middle traces show the output with g_AMPA doubled and the bottom traces show the model output with g_K,SK set to 0. The random synaptic input was exactly the same for each of the three cases. The dotted line indicates 0 mV. Left-hand side: average P_NMDA = 0.885×10^-6 cm/s (IEI = 2.7271 ms) and g_GABA,A,s = 500 μS/cm². Right-hand side: average P_NMDA = 2.028×10^-6 cm/s (IEI = 1.1898 ms) and g_GABA,A,s = 1100 μS/cm². A1. Mostly single spikes. A2. Doubling g_AMPA adds two spikes and shifts the timing of many others. A3. A burstier firing mode with a number of doublets and bursts of 3 or more that did not appear under control conditions. B1. Control firing with several doublets and most spikes in bursts of 3 or more. B2. Once again, increasing adds some spikes and shifts the timing of others. B3. Longer bursts with larger interburst intervals than under control conditions.

The parameter region above the dashed lines in Fig. 8A-C exhibits continuous bursting activity. Fig. 10A shows that the model behaves like a relaxation oscillator in this regime (Canavier 1999), except that the switches between spiking and quiescence appear random rather than periodic due to the random nature of the synaptic input. Increasing the relative contribution of nonlinear regenerative currents (such as I_NMDA) favors a larger amplitude oscillation in the underlying slow variable (such as accumulation of sodium in the dendrites) with a slower frequency. On the other hand, increasing the linear currents dampens the oscillation causing a decrease in amplitude and a concomitant increase in frequency. Hence increasing the linear I_AMPA current (Fig. 10B) produces more and shorter bursts whereas blocking the SK current (Fig. 10C) produces fewer and longer bursts. Blocking SK exerts its effects by removing its opposition to the regenerative I_NMDA. The larger depolarization experienced in the larger amplitude bursts reduces the amplitude of the spikes. A similar reduction of spike amplitude during bursts has been observed in vitro (Wang et al. 1994) in the presence of 30 μM NMDA.

Figure 10.

Continuous bursting with randomized burst lengths. Average P_NMDA = 2.294×10^-6 cm/s (IEI = 1.0520 ms) and g_GABA,A,s = 300 μS/cm². The dotted line indicates 0 mV. Distinct “up” and “down” states are recognizable in all panels. A. Control firing with nearly all spikes in bursts of 3 or more. B Doubling g_AMPA. Shorter bursts with shorter interburst intervals, nearly all spikes in bursts of 3 or more. C. SK Block. Longer bursts with reduced amplitude spikes and longer interburst intervals, all spikes in bursts of 3 or more.

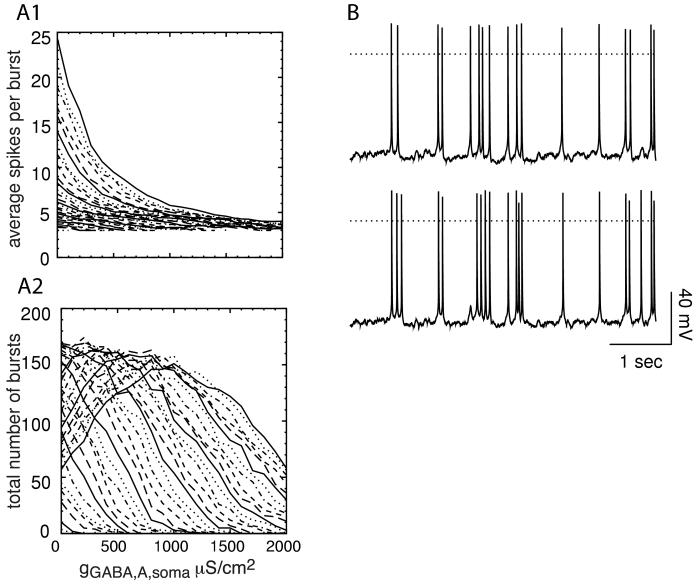
The effects of modulating the GABA_A conductance are illustrated in Fig. 11. Each curve in both A1 and A2 represents a different value of average P_NMDA from Fig. 8. Increasing g_GABA,A (Fig. 11A1) consistently decreases the number of spikes per burst, as shown experimentally by Paladini and Tepper (1999). On the other hand, Fig. 11A2 shows that for lower values of P_NMDA, the total number of bursts in a 90 s simulation consistently decreases as g_GABA,A is increased, whereas for higher values there is an initial increase followed by a decrease. The increase occurs in the continuously bursting regime by decreasing the amplitude and increasing the frequency of bursts analogously to the effect of increasing g_AMPA in Fig. 10. As g_GABA,A continues to increase, the amplitude of some bursts is decreased to the point that they no longer can sustain burst firing. Fig 11B shows an example of blocking the SK current at high levels of g_GABA,A. The top trace (B1) shows control conditions and the bottom trace (B2) shows SK block. Three additional spikes are inserted, two of them in bursts, but the effect is not as dramatic as at lower values of g_GABA,A (Figs. 4 and 9).

Figure 11.

Effect of increasing the GABA_A conductance. A. Each curve represents one of 6 representative average values of P_NMDA in panel A at 21 values of g_GABA,A,s. The legend in A1 gives each value of P_NMDA×10^-6 cm/s for both A1 and A2. A1. Average number of spikes per burst decreases as g_GABA,A,s is increased. A2. The total number of bursts usually but not always decreases as g_GABA,A,s is increased (see text). B. Average P = 2.028×10^-6 cm/s (IEI = 1.1898 ms) and g_{NMDA GABA,A,s}= 1700 μS/cm². The dotted line indicates 0 mV. B1: control. B2: SK block. At this high level of g_GABA,A,s, SK block results in three additional spikes in five seconds, two of which occur in bursts. The effect is much less dramatic than that at lower values of g_GABA,A,s.

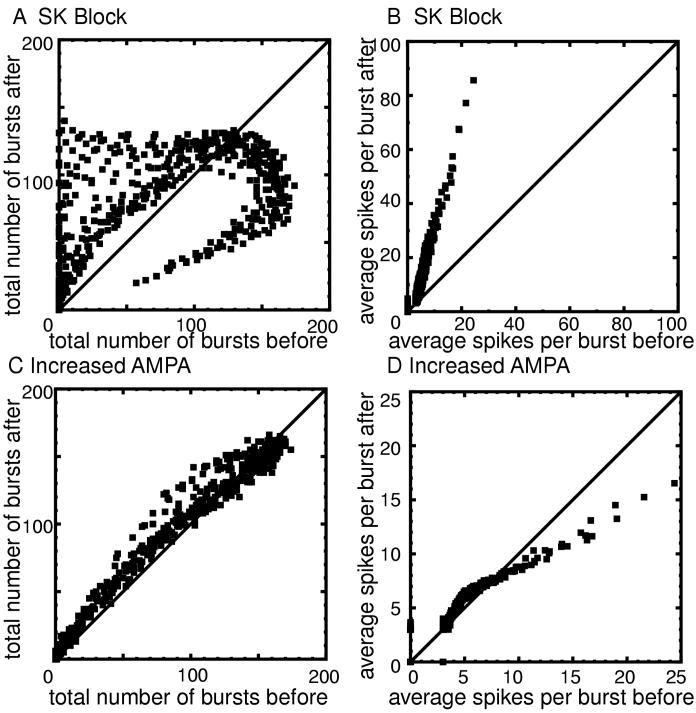
The effects of modulating the AMPA and SK conductances on burst frequency and on the number of spikes per burst are summarized in Fig. 12. Panel A shows the total number of bursts in a 90 s simulation after g_K,SK is set to zero as a function of the number of bursts under control conditions for each simulation. A point above the diagonal indicates an increase in the number of bursts. Most points fall above the diagonal, except for a branch in which the number of bursts is reduced. This branch corresponds to parameter regions that produce activity of the type illustrated in Fig. 10C. The bursts become so long that fewer can be accommodated in a given time period. Panel B shows that the number of spikes per burst uniformly increases, and that the increase is proportional to the control number of bursts.

Figure 12.

Effect of blocking SK or doubling g_AMPA on burst frequency and average number of spikes per burst. Points that fall above the 45° were increased by the manipulation, and those below decreased. A. Number of bursts fired (after the transients die out) in 90 seconds before (x-axis) and after (y-axis) blocking SK. The number of bursts decreased in some cases because the bursts became so long that more would not fit in the interval. B. The average number of spikes per bursts before and after blocking SK is clearly increased. C. Number of bursts fired (after the transients die out) in 90 seconds before and after doubling g_AMPA. D. The average number of spikes per bursts before and after doubling g_AMPA is only slightly affected except in spikes with many bursts.

Panel C and D contain similar information regarding the effects of doubling g_AMPA. There is a tendency for the number of bursts to increase, and for control bursts with fewer than about seven spikes there is a tendency for the number of spikes per burst to increase. However, control bursts with large numbers of spikes tend to have fewer spikes after doubling g_AMPA. The explanation again lies in Fig. 10. In parameter regions where the “up” and “down” states are exhibited, increasing g_AMPA increases burst frequency but decreases the burst length and intra-burst frequency, resulting in fewer spikes per burst.

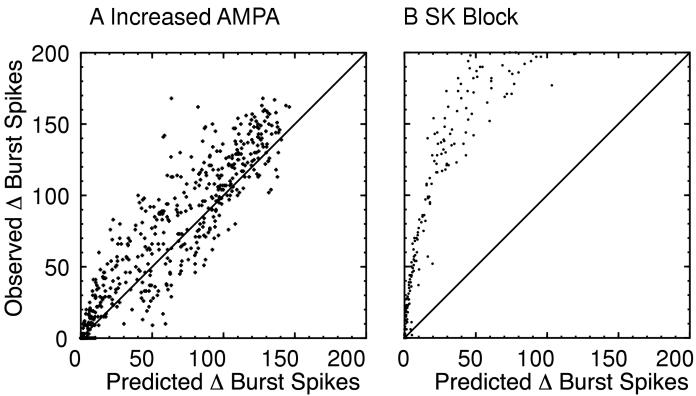
We used the probabilistic algorithm described in the Methods and in Appendix II to test whether the addition of spikes randomly throughout the spike train can explain the effects of modulating g_AMPA or g_K,SK and to quantify whether the rate and pattern are truly being modulated differentially. The main assumption is that the probability of a spike being inserted anywhere in the spike train is uniform, except during the refractory period. Figure 13 plots the actual number of spikes added in bursts compared to the predicted number of spikes added in bursts. A perfect prediction would fall along the diagonal line (slope =1). For doubling g_AMPA (Fig. 13A), the slope of the best fit line was 1.06 (r=0.93), whereas for blocking the SK current (Fig. 13B) it was 2.56 (r=0.89). These slopes are significantly different because their 95% confidence intervals do not overlap. It is evident from Fig. 13A that the increase in spike frequency can reasonably account for the increased number of spikes in bursts caused by doubling g_AMPA, and it is equally evident from Fig. 13B that when g_K,SK is set to zero, the change in pattern is far greater than the change in that is expected simply due to an increase in frequency. In order to make an appropriate comparison between the two manipulations, only simulations in which blocking SK added less than 200 spikes in bursts were used in the analysis shown in Fig. 13. However, in every case when g_K,SK was set to zero, the observed values were greater then the predicted values. A potential confound for the algorithm are the extreme bursting cases in which there are clear “up” and “down” states, because the probability of a spike occurring during the down state is very low. Eliminating these extreme cases in which 95% or more spikes were fired in bursts made little difference to the analysis, however; for doubling g_AMPA we obtained a slope of 1.07 (r=0.95) and a slope of 2.53 (r=0.90) for setting g_K,SK to zero.

Figure 13.

Prediction Algorithm Based on Random Insertion of Spikes Without regard to Pattern. A. Doubling g_AMPA. The algorithm produced a reasonable prediction. B SK Block. Clearly, many more spikes were added in bursts than predicted by the algorithm.

The correlations between the firing pattern and rate in the model, shown in Table 1, were weak to moderate, depending upon the frequency range examined. In the model, very high spiking rates are only observed in the continuously bursting regimes (Fig. 10), therefore at high frequencies the fraction of spikes in bursts is always 1, and it only makes sense to look for linear correlations in the frequency range corresponding to less than 100% of the spikes fired in bursts. Increasing the AMPA conductance made no consistent difference in the correlation. Interestingly, the correlation of the pattern for increased AMPA conductance, predicted using the probabilistic algorithm described above, with the rate was indistinguishable from that of the correlation of the observed pattern with the rate. Thus a probabilistic algorithm can generate similar levels of correlation as those observed in the model despite the nonlinearity of the transformation from known changes in rate to predicted changes in pattern (see Appendix II). In the model, blocking SK tightens the correlation between rate and pattern by eliminating the non-bursters (red and orange bands in Fig. 8AB) that could be found at many different rates. The correlation of changes in firing rate with changes in pattern were weak: r=0.18 for doubling g_AMPA and r=0.18 for blocking SK.

Discussion

Differential Modulation of Pattern and Rate

In the absence of intracellular membrane potential recordings, it is not possible to confirm the presence of a depolarizing wave underlying bursting and often extending beyond the last spike in a burst (Grace and Bunney 1984b). Instead, an operational definition of a burst (Grace and Bunney 1984b) that relies only upon successive ISIs is employed. Although rhythmic bursting has been observed under certain conditions in vitro, it is the exception in vivo (Freeman et al. 1985, Fig 3B), and most burst episodes are transient and intermixed with single spikes in vivo. If the firing rate is increased, then more spikes occur in a fixed time interval. In order for burst firing to be modulated truly independently of the rate, then more spikes should be added in bursts than one would expect by random insertion of spikes regardless of the firing pattern. To our knowledge, this type of analysis has not yet been applied to physiological data. However, in the model presented in this study, the assumption of random insertion accounts for most of the effects of the modulation of the AMPA conductance but not the SK conductance. Therefore, rate and pattern are modulated concurrently in the first instance but independently in the second. The results of this modeling study suggest that the increases in burst firing caused by increasing g_AMPA are mostly due to increasing the tendency for EPSPs to summate above threshold, with the EPSPs that are promoted from sub to suprathreshold located nearly uniformly throughout the spike trains. There may be a small bias towards clustering spikes in bursts since the confidence interval for the slope of the best fit line between actual and predicted values based on the assumption of random insertion did not include 1. On the other hand, the SK current is activated by depolarization with a delay so that it directly suppresses bursts but not single spikes, therefore blocking this current modulates pattern preferentially by facilitating the underlying burst mechanism. This mechanism is consistent with recent data (Ji and Shepard 2006) showing that apamin-treated DA neurons in vivo have more bursts with three or more spikes and fewer doublets than control cells.

A linear correlation analysis between pattern and rate is not particularly helpful, because the dependency of pattern on rate increases is highly nonlinear and a linear correlation analysis does not directly address whether the proportion of spikes fired in bursts is changed by chance or by modulating the underlying mechanisms for burst generation. Even in the cases that the increase in rate was used to predict the change in pattern, changes in pattern and rate were weakly correlated. The dependence of pattern on rate as a single parameter is changed in the same neuron is linear in both physiological (Grace and Bunney 1984b) and model dopamine neurons (see Results), but becomes nonlinear as more than one parameter is varied simultaneously. This explains the weak correlation between pattern and observed across a population of physiological (Grace and Bunney 1984b; Hyland et al. 2002; Paladini and Tepper 1999) or model neurons (see Table 1). One study (Zhang et al. 1994) obtained an r=0.68 for the correlation between pattern and rate, which is close to the values obtained in the model in physiological frequency ranges. The correlation between changes in pattern and rate in the model is a close match to the data of Paladini and Tepper, 1999. The model predicts that blocking SK will tighten the correlation between pattern and rate (Table 1) by eliminating the low bursters that occur at many frequencies and also predicts that high levels of tonic GABAergic receptor activation could occlude the effects of blocking the SK channel.

How do the statistics of the model compare to real dopamine neurons?

At least 70% of identified dopamine neurons were spontaneously active in chloral hydrate-anesthetized and gallamine paralyzed rats (Grace and Bunney 1984a), and more active DA neurons per track were identified in freely moving rats (Freeman et al. 1985) than in paralyzed or anesthetized rats, consistent with an enhancement of GABAergic transmission and an inhibition of glutamate-mediated excitation by chloral hydrate anaesthesia (Fa et al. 2003). DA neurons in awake, freely moving rats fired an average of 46% (range 1-81%) of their spikes in bursts (Freeman et al. 1985). In freely moving rats, 20% of all spikes were fired in bursts but nearly half of these occurred as doublets (Hyland et al. 2002). A subset of high bursters had 45% of their spikes in bursts. In chloral hydrate anesthetized rats (Grace and Bunney 1984b), 55% of the spontaneously firing neurons fired on average 30% of their spikes in bursts of two or more spikes, but usually six or less. A recent study (Fa et al. 2003) found that the proportion of spikes fired in bursts in the conscious, head-restrained rat was 23 %, compared to 13% in rats lightly anesthetized with choral hydrate and only 0.5% in deeply anesthetized rats. Based on the statistics given above, most physiological dopamine neurons fall in the region of the colored diagonal bands in Fig. 8A, in which spontaneous activity ranging from single spike firing to up to 75% burst firing is observed. The implication is that in vivo the excitatory and inhibitory inputs to the dopamine neurons are balanced.

Comparison to Other Models

Recently, Kuznetsov et al. (2006) proposed a multicompartmental model of transient burst firing in dopamine neurons. Our results are in agreement with those of Kuznetsov et al. (2006) in that the activation of the dendritic AMPA and NMDA receptors are essential for the transient bursting in both models. The restriction of calcium dynamics to the soma in the model in this study is an oversimplification, and it has been suggested that dendritic calcium dynamics drive pacemaking (Chan et al. 2005). However, dopamine neurons with only small stumps of dendrites remaining after trituration (Cardozo and Bean 1995) still fire regularly at about 3Hz, as do acutely isolated neurons (Silva et al. 1990). The model in this paper, unlike Kuznetsov et al (2006) does not depend upon the dendritic calcium entry and activation of the SK current alone to prevent depolarization block at high rates of firing, because our model produces increased bursts in the presence of SK blockers, consistent with experimental evidence (Ji and Shepard 2006; Waroux et al. 2005).

The model presented in this paper is an extension of a previous model (Komendantov et al. 2004) that simulated the situation in vivo with constant levels of both glutamatergic and GABAergic input. The results of the previous paper underestimated the effects of blocking SK because the deterministic model could only burst or fire in single spikes. In constrast, the stochastic model with realistic synaptic dynamics presented in this study can burst transiently like real dopamine neurons. The effects of SK channel blockers in promoting burst firing are more prominent in the presence of synaptic noise (see Fig. 4C). The effects of increasing AMPA are fundamentally different as well (see Fig. 4B).

Theoretical Framework

The mechanisms of burst firing in dopamine neurons are not fully understood. The regenerative, nonlinear inward current mediated by NMDA receptors has been implicated in burst firing both in vivo (Chergui et al. 1993) and in vitro (Johnson et al. 1992; Wang et al. 1994; Mereu et al. 1997; Prisco et al. 2004). SK channel blockers facilitated NMDA-induced bursting in several studies (Johnson et al. 1992; Seutin et al. 1993; Prisco et al. 2004). Recently, Johnson and Wu (2004) were able to generate both NMDA-dependent and NMDA independent burst firing experimentally. The latter was induced by the application of the SK blocker apamin alone, is analogous to similar bursting observed previously by Ping and Shepard (1996), and is probably dependent upon the L-type calcium channel since it is abolished in the presence of nifedipine. In the model in this study, the NMDA receptor current and other nonlinear, regenerative, inward currents, such as the L-type calcium current, can contribute to the depolarizations underlying spike and burst firing in our model. Their regenerative nonlinearity enables repetitive oscillations, and both linear currents (Canavier 1999) and the nonlinear SK channel current tend to reduce the amplitude of these oscillations. In addition to a process that produces a regenerative depolarization, a delayed repolarizing process is required in order to produce an oscillation such as that underlying bursting or repetitive single spike firing. The SK channel current provides a repolarizing force, and in its absence, the model sodium pump provides much of the repolarizing drive. Other, as yet unidentified currents, may also contribute in physiological dopamine neurons.

The underlying nonlinear dynamics of the model provide a theoretical framework for understanding the effects of pharmacological manipulations on the firing rate. The effect of GABA to reduce the number of spikes per burst (Fig. 11A1) until there are no bursts can be explained in terms of the linear dampening (Canavier 1999) that removes any region of positive feedback or negative conductance associated with the regenerative inward currents from the steady state IV curve. Blocking SK has the opposite effect (Fig 12B), which is even more pronounced because SK has a supralinear dependence on voltage, that is, the hyperpolarization becomes more pronounced with increasing depolarization than one would expect from an increase in driving force alone because calcium entry is voltage-activated. In general, a large negative conductance excursion in the IV curve results in a large amplitude oscillation with a long period, thus effects on amplitude also change the period (Fig. 10).

Effect on Reward-Related Responses

Increasing g_AMPA in the model has little if any effect on the train of strong inputs in Fig. 7 that were meant to simulate reward-related synaptic inputs signaling reward-related stimuli received by dopamine neurons. Since increasing g_AMPA also increases the background firing rate and percent spikes fired in bursts (Fig. 8), such transient stimuli might seemed weaker than normal rather than enhanced as hypothesized by Jones and Bonci (2005). However, increasing g_AMPA also lowers the threshold for stimuli to evoke a response in model DA cells. Behaviorally, the implications might be to cause a small subset of stimuli that would otherwise be ignored to elicit an expectation of reward. On the other hand, a reduction in the SK conductance is predicted to consistently intensify the response to reward-mediated stimuli by increasing the duration of bursts and the intra-burst frequency, resulting in a larger release of dopamine in the projection areas. Hyland et al. (2002) observed a greater intra-burst frequency in bursts related to reward compared to bursts in a context unrelated to reward, so we suggest that modulation of the SK current may convey reward-related information.

Appendix I: Equations and Parameters for Compartmental Model

Equations governing membrane potential in each compartment:

-C_m ( dV_d/dt) = I_Na,d + I _A,d + I_KDR,d + I_NaP,d + I_L,d + I_dp + I _NMDA,d + I_AMPAd + I _GABA,A,d

-C_m ( dV_p/dt) = I_Na,p + I_A,p + I_KDR,p + I_NaP,p + I_L,p + I_pd + I_ps + I _NMDA,p + I_AMPAp + I _GABA,A,p

-C_m ( dV_s/dt) = I_Na,s + I_A,s + I _KDR,s + I_K,SK + I_NaP,s + I_Ca,T +I_Ca,L + I_Ca,N + I_CaP + I_L,s + I_sp + I _GABA,A,s

The subscript “i” indicates a nonspecific compartment, whereas subscripts “d”, “p”, and “s” indicate distal dendritic compartment, proximal dendritic compartment and somatic compartment respectively.

NMDA-induced current:

I_NMDA= I_NMDA,Na + I_NMDA,K + I_NMDA,Ca

I_NMDA,Na = P_NMDA R_NMDA(t) p (VF2/RT)[λ[Na]_in - λ[Na]_out exp(-VF/RT)] /[1-exp(-VF/RT)]

I_NMDA,K = P_NMDA R_NMDA (t) _p (VF²/RT) [λ[K]_in - λ[K]_out exp(-VF/RT)] /[1-exp(-VF/RT)]

I_NMDA,Ca = 2.65 P_NMDA R_NMDA (t) _p (4VF²/RT){[Ca]_in - λ_Ca[Ca]_out exp(-2VF/RT)} /[1-exp(-2VF/RT)]

dp/dt = (p_∞ - p)/1.0

p_∞ = 0.0225+ 0.9775/(1+([Mg]_out/K_m,Mg)exp(-V/q))

AMPA current:

I_AMPA,i = I_AMPA,Na,i + I_AMPA,K,i; I_AMPA,K,i = g _AMPA,K,i R_AMPA(t) (V_i- E _K); I_AMPA,Na,i = g _AMPA,Na,i R_AMPA(t) (V_i - E_Na,i);

GABA current:

I_GABA,A,i = g_GABA,A,i (V_i - E_Cl); g_GABA,A,p = g_GABA,A,d = g_GABA,A,s /10

Linear leakage current:

I_L,i = I_L,Na,i + I_L,K,i + I_L,Ca,i; I_L,K,i = g _L,K,i (V_i- E _K); I_L,Na,i = g _L,Na,i (V_i - E_Na,i); I_L,Ca,i = g_L,Ca,i (V_i- E _Ca); I_L,Ca,i is only nonzero in the somatic compartment

E _Na,i = (RT/F) ln ([Na]_out/[Na]_in,i)

Sodium pump current:

I_NaP,i = I_NaP,max,i / (1+ (K _m,Na/[Na]_in,i)^1.5)

Sodium balance:

d[Na]_in,d/dt = 4 × f_d (-I_Na,d - I_L,Na,d - I_NMDA,Na,d - I_AMPA,Na,d - 3I_NaP,d)/ (d_d F)

d[Na]_in,p/dt = 4 × f_p (-I_Na,p - I_L,Na,p - I_NMDA,Na,p - I_AMPA,Na,p - 3I _NaP,p)/(d_p F)

d[Na]_in,s/dt = 4 × f_s (-I_Na,s - I _L,Na,s - 3_{I NaP,s})/( d_s F)

Calcium pump current:

I_CaP = I_CaP,max [Ca²⁺]_in / ([Ca²⁺]_in + K _m,CaP)

Calcium Balance:

d[Ca²⁺]_in/dt = 2 × f_Ca (I_Ca,T + I_Ca,L + I_Ca,N + I_CaP + I_L,Ca )/( d_s F)

Fast sodium current:

I_Na,i = g_Na,i m³ _ih_i (V_i - E_Na,i)

dm_i/dt =(1/{1+ exp[(V _half,m,i- V_i)/6.0]} - m_i )/τ_m

dh_i/dt = (1/{1 + exp[(V _half,h,i - V_i)/7.8]} - h_i)/τ_h

τ_m = 1.0/{1 + exp[(V_i + 45.0)/ 1.5]} - 1.0/{1+exp[(V_i +65)/0.5]} + 0.04

τ_h = 56.0/{1 + exp[(V_i - 27.8 - V _half,h,i)/ 4.5]} - 56.0/{1+exp([V_i - 7.8 - V _half,h,i)/2.0]} + 1.0

Calcium currents:

I_Ca,T = g_Ca,T d_T f_T (V_s - E_Ca)

dd_T/dt = (1/{1 + exp[-(V_s + 63.5)/1.5]} - d_T)/τ_dT

df_T/dt = (1/{1 + exp[(V_s + 76.2)/3.0]} - f_T)/τ_fT

τ_dT = 65.0 exp[-(V_s + 66.0)/40.0] + 3.5

τ_fT = 50.0 exp[-(V_s + 72.0)/100.0] +10.0

I_Ca,N = g_Ca,N d_N f_Ca,N (V_s - E_Ca)

dd_N/dt = (1/{1 + exp[-(V_s + 45.0)/7.0)]} - d_N)/τ_dN

τ = 18.0 exp[-(V_s + 70.0)/5.0] + 0.3

f_Ca,N = K_{M, fCaN}/( K_{M, fCaN} + [Ca]_in)

I_Ca,L = g_Ca,L d_L f_Ca,L (V_s - E_Ca)

dd_L/dt = (1/{1 + exp[-(V_s + 50.0)/20.0]} - d_T)/τ_dL

τ_dL = 18.0 exp[-(V_s + 45.0)/400] + 1.5

f_Ca,L = K _{M, fCaL}/( K_{M, fCaL} + [Ca]_in)

Delayed rectifier current:

I_KDR,i = g_KDR,i n_i (V_i - E_K)

dn_i/dt = (1/{1+exp[(-35.0 - V_i)/12.0]} - n_i)/10.0

Transient outward potassium current:

I_A,i = g_A,i q_i s_i (V_i - E_K)

dq_i/dt=(1/{1+exp[(-V_i - 42.0)/4.0]} - q_i)/ τ_q

ds_i/dt= (1/{1+exp[(V_i + 63.0)/4.0]} - s_i)/50.0

τ_q = 5.5 exp[-(V_s + 42.0)/100.0] + 4.0

SK potassium current:

I_K,SK = g_K,SK /[1 + (K_M,SK/[Ca²⁺]_in) 4 ] (V_s - E_K)

Interneuronal coupling currents:

G_sp = 10² π d_p ² d_s ² /[ 2 R_a (L_p d_s² + L_s d_p ²)]; G_pd = 10² π d_p ² d_d² / [2 R_a (L_p d_d 2 + L_d d_p ²) ]

g_sp = 4 × 10⁸ G_sp / (π d_s L_s); g_ps = 10⁸ G^sp / (π d_p L_p)

g_pd = 2 × 10⁸ G_pd / (π d_p L_p); g_dp = 10⁸ G_pd / (π d_d L_d)

I_dp = g_dp(V_d - V_p) ; I_pd = g_pd(V_p - V_d); I_ps = g_ps(V_p - V_s); I_sp = g_sp (V_s - V_p)

Parameters

g_Na,i = 5500 μS/cm² ; g_L,Na,i = 9.5 μS/cm² ; g_L,Ca = 0.6 μS/cm²

g_Ca,T = 1044 μS/cm² ; g_Ca,N = 171 μS/cm² ; g_Ca,L = 216 μS/cm²

g_KDR,i = 1000 μS/cm²; g_L,K,i = 18 μS/cm²

g_A,d = 1000 μS/cm² ; g_A,p = 300 μS/cm² ; g_A,s = 100 μS/cm²

V_half,m,d = -26.6 mV ; V_half,m,p = -34.6 mV ; V_half,m,s = -44.6 mV

V_half,h,d = -48.8 mV ; V_half,h,p = -56.8 mV ; V_half,h,s = -66.8 mV

C_m = 1 mF/cm²

E_K = - 100 mV; E_Cl = -70 mV; E_Ca = 120 mV;

[Na]_out = 145 mM; [K]_out = 2.5 mM; [K]_in = 140 mM

[Ca]_out = 2.0 mM; [Mg]_out = 1.2 mM

K_M,fCa,N = 0.0001 mM; K_M,fCa,L = 0.00045 mM; K_M,SK = 0.00019 mM;

K_M,CaP = 0.0005 mM; K_M,Na = 10 mM; K_M,Mg = 50.7 mM; q = 9 mV;

d_d = 1.5 μm; d_p = 3 μm; d_s = 15 μm; L_d = 350 μm; L_p = 150 μm; L_s = 25 μm

f_p = 1; f_d = 1 ; f_s = 4; f_Ca = 0.005; I _CaP,max = 0.0312 mA/cm²;

I _NaP,max,s = 0.0036 mA/cm²; I _NaP,max,p = 0.0072 mA/cm²; I _NaP,max,d = 0.009 mA/cm²;

R_a = 400 Ω cm ; R = 8,314 J/kg mol K; F = 96520 C/mol; T = 308.15 K;

λ = 0.75 ; λ _Ca = 0.3

Appendix II: Probabilistic algorithm for random insertion of spikes into the firing pattern

N number of total additional spikes due to manipulation

Nb[n] number of bursts

Nd[n] number of doublets

Nsb[n] number of spikes in bursts

Nsd[n] number of spikes in doublets

Nss[n] number of single spikes that are not in a burst or a doublet

r refractory period (0.030 s)

T total time (90 s)

Tb[n] sum of time periods in which an additional spike would become part of an existing burst

Td[n] sum of time periods in which an additional spike would convert a doublet to a burst

Ts[n] sum of time periods in which an additional spike would be a singlet

Tbr [n] Tb[n] corrected for refractory period

Tdr[n] Td[n] corrected for refractory period

Tsr[n] Ts[n] corrected for refractory period

ΔNb[n] change in the expected number of bursts due to addition of spike n

ΔNbs[n] change in the expected number of spikes in bursts due to addition of spike n

ΔNd[n] change in the expected number of doublets due to addition of spike n

ΔNss[n] change in the expected number of single spikes due to addition of spike n

ISIb expected duration added to a burst by a spike occurring just before or just after a burst or doublet

ISId expected interspike interval within a new doublet

Cb[n] expected number of concatenated bursts-includes for each pair of bursts the probability that the interval between them will be in the range 0.160 to 0.320 and the probability that the spike will occur in the right part of that interval so that the interval between the spike and each burst is less than 0.160.

Cd[n] expected number of concatenated doublets

Cbs[n] expected number of spikes concatenated into bursts

Cds[n] expected number of spikes concatenated into doublets

Cbd[n] expected number of doublets concatenated into bursts

dd[n] expected doublet duration

db[n] expected burst duration

w = 0.160 ms or Ts[n]/Nss[n], whichever is smaller, for the expected interval between single spikes

ISIb = 0.080/6 + 0.0160/3

ISId = 0.080/2

Input to algorithm: Nb[0],Nd[0],Nsb[0],Nss[0], Tb[0], Td[0], N

Nsd[n] = 2 Nd[n]

Tbr[n] = Tb[n] - Nb[n] r

Tdr[n] = Td[n] - Nd[n] r

Ts[n] = 1 -Tb[n] - Td[n]

Tsr[n] = Ts[n] - Nss[n] r

dd[n] = Td[n]/Nd[n]

db[n] = Tb[n]/Nb[n]

ΔNsb[n] = Tbr[n]/(Tsr[n] + Tdr[n] + Tbr[n])

ΔNb[n] = Tdr[n]/(Tsr[n] + Tdr[n] + Tbr[n])

ΔNd[n] = Nss[n] (w[n] - 2 r)/(Tsr[n] + Tdr[n] + Tbr[n])

ΔNss[n] = Tsr[n]/(Tsr[n] + Tdr[n] + Tbr[n]) - ΔNd[n]

Cb[n] = Nb[n] (Nb[n] - 1) ( 0.160)/(T - 2 db[n]) (0.080/(Tsr[n] + Tdr[n] + Tbr[n]))

Cd[n] = Nd[n] (Nd[n] - 1) ( 0.160)/(T - 2 dd[n]) (0.080/(Tsr[n] + Tdr[n] + Tbr[n]))

Cbd[n] = Nb[n] Nd[n] ( 0.160)/(T - db[n] - dd[n]) (0.080/(Tsr[n] + Tdr[n] + Tbr[n]))

Cbs[n] = Nb[n] Ns[n] ( 0.120)/(T - db[n] ) (0.060/(Tsr[n] + Tdr[n] + Tbr[n]))

Cbs[n] = Nb[n] Ns[n] ( 0.120)/(T - db[n] ) (0.060/(Tsr[n] + Tdr[n] + Tbr[n]))

Nsb[n+1] = Nsb[n] + ΔNsb[n] + 3 ΔNb[n] + 5 Cd[n] + Cb[n] + 3 Cbd[n] + 2 Cbs[n] + 4 Cds[n]

Nb[n+1] = Nb[n] + ΔNb[n] - Cb[n] + Cd[n]

Nd[n+1] = Nd[n] + ΔNd[n] - ΔNb[n] - 2 Cd[n] - Cbd[n] - Cds[n]

Tb[n+1] = Tb[n] + ΔNd[n] ( 2 ISIb + 0.080 +0.160) + Nb[n] ISIb (0.240/(Tsr[n] + Tdr[n] + Tbr[n]))

Td[n+1] = Td[n] + ISId ΔNd[n] - dd[n] (ΔNb[n] + 2 Cd[n] + Cbd[n] + Cds[n])

Nsd[n+1] = 2 Nd[n+1]

Nss[n+1] = Nss[n] + ΔNss[n] - ΔNd[n] - Cd[n] - Cb[n] - Cbd[n] - 2 Cbs[n] - 2 Cds[n]

Output : predicted increase in number of spikes in bursts is Nsb[N] - Nsb[0]