A Porous SiO₂ Interferometric Biosensor for Quantitative Determination of Protein Interactions: Binding of Protein A to Immunoglobulins Derived from Different Species

Abstract

Determination of kinetic and thermodynamic protein binding constants using interferometry from a porous Si Fabry-Perot layer is presented. A protein A capture probe is adsorbed within the pores of an oxidized porous Si matrix, and binding of immunoglobulin G (IgG) antibodies derived from different species is investigated. The relative protein A/IgG binding affinity is human > rabbit > goat, in agreement with literature values. The equilibrium binding constant (K_a) for human IgG binding to surface-immobilized protein A is determined to be 3.0 ± 0.5 × 10⁷ M^-1 using an equilibrium Langmuir model. Kinetic rate constants are calculated to be k_d = 2.1 ± 0.2 × 10^-4 s^-1 and k_a = 1.2 ± 0.4 × 10⁴ M^-1s^-1 using non-linear least squares analysis, yielding an equilibrium binding constant of K_a = 5.5 ± 1.5 × 10⁷ M^-1. Both steady state and time-dependent measurements yield equilibrium binding constants that are consistent with literature values. Kinetic rate constants determined through non-linear least squares analysis are also in agreement with protein A/IgG binding on a surface. Dosing with a high concentration of analyte leads to deviations from ideal binding behavior, interpreted in terms of restricted analyte diffusion within the porous SiO₂ matrix. It is shown that the diffusion limitations can be minimized if the kinetic measurements are performed at low analyte concentrations or under conditions in which the protein A capture probe is not saturated with analyte. Potential limitations of the use of porous SiO₂ interferometers for quantitative determination of protein binding constants are discussed.

Introduction

Biosensor research is driven by the desire to classify and sense biological interactions for medical applications, environmental monitoring, and basic mechanistic studies. Optical techniques have received significant attention for label-free biosensing,¹ and sensitive methods employing surface plasmon resonance (SPR),^2-6 thin-film interference spectroscopy,^7-9 or optical waveguides^10-13 have been developed to measure biological interactions. It is especially desirable to develop biosensing methods that are inexpensive, simple to use, manufacturable, portable, and that can be incorporated into high-throughput arrays. Optical biosensors based on porous Si interferometers meet these requirements, and many label-free biological sensing applications have been demonstrated.^14-21 Porous Si is an attractive material for biological sensing due to its compatibility with conventional silicon microfabrication methods, its tunable pore sizes across biologically relevant length scales,^{19, 22} and its convenient covalent and non-covalent surface chemistry.^23-29 The electrochemically controlled synthesis allows construction of complex photonic structures; for example porous Si devices that include an internal reference channel (to correct for zero-point drift)^{27, 30} or a resonant cavity (to increase sensitivity)^{18, 20} have been demonstrated.

Qualitative measurement of the binding of human IgG to a protein A capture probe on porous Si films has been reported,¹⁷ and recently, determination of equilibrium binding has been demonstrated for rabbit IgG binding to non-covalently bound protein A on porous Si.³⁰ One of the primary advantages of biosensors based on refractive index changes is that quantitative kinetic and equilibrium binding constants can be determined in real-time.^{12, 31, 32} The optical signal change that is measured upon analyte binding within a porous Si Fabry-Pérot film scales with analyte mass,¹⁷ and therefore it should be possible to use porous Si interferometry to quantify protein binding kinetics.

In this report, we demonstrate that the spectral response from a porous SiO₂ film correctly determines relative binding affinities for a series of IgG molecules derived from different species. Equilibrium binding constants for the protein A/human IgG interaction are determined using a Langmuir model, while kinetic and equilibrium constants are determined using non-linear least-squares analysis of time-dependent data.^{12, 31, 32} One of the significant potential limitations of working with a microporous sensing matrix is that restricted diffusion may interfere with binding kinetics. This limitation is explored in the present study, and it is found that a porous SiO₂ interferometer can accurately determine kinetic rate constants by performing measurements at short times and by limiting the concentration of analyte. The ultimate detection limit of the method is not probed in this study, though it has been reported to be of the same order of magnitude as surface plasmon resonance, the standard label-free method for measuring protein binding interactions.³³

Experimental

Reagents

Phosphate buffered saline (PBS) was obtained from Mediatech Inc. (1X solution, Cellgro, Cat. No. MT 21-040-CM). IgG from human (Cat. No. I 4506), rabbit (Cat. No. I 5006), and goat (Cat. No. I 5256) sera and bovine serum albumin (BSA) were obtained from Sigma-Aldrich (> 95% purity). Molecular weight for all IgG species was assumed to be 146 kDa. Protein A from Staphylococcus Aureus (Cat. No. 539202) was obtained from Calbiochem. Aqueous hydrofluoric acid (48%) was supplied by Fisher Scientific.

Porous Si Preparation

Porous Si samples were prepared from single-crystal, highly doped p-type Si (boron doped, polished on the (100) face, from Siltronix Corp.). Resistivity was determined with a 4-point probe (Cascade Microtech), and only wafers with resistivity between 0.0005-0.0006 Ω-cm were used for this work. Porous Si samples were prepared by electrochemical etch in a 3:1 solution of 49% aqueous hydrofluoric acid:ethanol (CAUTION: Hydrofluoric acid is highly toxic and contact with the skin should be treated immediately). Samples were etched at a current density of 485 mA/cm² for 20 s, yielding pore sizes of approximately 50-150 nm. Immediately after etching, samples were rinsed with ethanol. Before the ethanol was allowed to dry, the porous Si layer was rinsed with hexane to prevent cracking due to capillary stresses on the porous network during evaporation. The porous layer was then thermally oxidized by heating to 800 °C for 1 hour in a tube furnace (Lindberg/Blue M) under ambient atmosphere. Thermally oxidized porous Si chips were found to be stable; the samples retained their sensing characteristics for at least several months when stored in ambient atmosphere. Fresh porous SiO₂ chips were used for each experiment and they were not recycled for use in subsequent experiments.

Porous Si Interferometry

The method for collecting reflectivity spectra from porous SiO₂ Fabry-Pérot films has been described.²⁷ White light from a tungsten lamp (Ocean Optics) is fed through one end of a bifurcated fiber optic cable and focused through a lens onto the porous SiO₂ substrate at normal incidence (See Supporting Information Figure S1 for schematic representation of experimental design). A 2.5 cm-diameter lens with a long focal distance (∼18 cm) is used to minimize angular dispersion effects. Reflected light is collected through the same optics, and the distal end of the bifurcated fiber optic cable is input to a CCD spectrometer (Ocean Optics S-2000). Spectra were not corrected for spectral response of the instrument or the lamp. The quantity nL, referred to as the optical thickness (OT) in this work, is determined from the Fabry-Pérot relationship:

$$\text{m}\lambda =2\text{nL}$$ (1)

where λ is the wavelength of maximum constructive interference for spectral fringe of order m, n is the index of refraction of the porous layer and its contents, and L is the thickness of the porous layer. The value of OT was determined by Fourier transformation of the reflectivity spectrum. The wavelength axis of the spectrum from the Ocean Optics spectrometer was inverted and a linear interpolation applied such that the data were spaced evenly in units proportional to frequency (nm^-1). A Hanning window was applied to the spectrum, it was redimensioned to 4096 data points and then zero padded to the power of two. A discrete Fourier transform using a multidimensional fast prime factor decomposition algorithm from the Wavemetrics, inc (www.wavemetrics.com) IGOR program library (FFT) was applied. Fourier transformation results in a sharp peak whose position is equal to the quantity (2nL) of eq. 1.

The quantity OT is related to the amount of protein in the pores.^15-17 The refractive index of the porous layer derives from the refractive index of the as-prepared Si oxide and the material in the pores (PBS, media, and/or protein). Replacement of aqueous media (n ∼ 1.3) by protein (n ∼ 1.5) leads to a larger value of the optical thickness.

Steady-State Biosensing Experiments

Equilibrium protein binding constants were determined in a static cell, with the sensor chip immersed in a reservoir of analyte that was not circulated. Porous SiO₂ samples were mounted in a Teflon cell similar to the one used to electrochemically etch the porous layer. The reservoir of this cell is ∼1.2 cm in diameter with a ∼ 2 mL capacity. 2 mL of PBS buffer was first added to the cell to establish a baseline spectrum. The protein A capture probe was immobilized by replacing a 200 μL aliquot of the PBS solution with 200 μL of 1 mg/mL protein A (0.1 mg/mL final concentration) and the chip was maintained in this solution for 2 h. The protein A solution was then removed and the sample rinsed three times with PBS. A 2 mL aliquot of PBS solution was then added to the reservoir. The PBS solution was adjusted to the proper IgG concentration by removing an aliquot of PBS and adding an equal aliquot of concentration 1 mg/mL or 0.1 mg/mL in IgG to achieve the desired final concentration. The solution was vigorously stirred after addition of IgG. Reflectivity spectra were acquired until the value of the optical thickness reached a constant value, indicating establishment of equilibrium. The equilibrium change in optical thickness (denoted ΔOT_f) was measured as the difference between the average OT (using an average of 20 points upon attaining the steady-state optical thickness value after IgG addition) and the initial OT (measured as the average of 20 points immediately preceding addition of the IgG solution).

Time-Resolved (Flow Cell) Biosensing Experiments

A custom-built flow cell system, described previously,¹⁶ was used in the time-dependent protein binding experiments. A schematic of the flow cell configuration can be found in the Supporting Information (Figure S2). Briefly, the porous Si sample was mounted in a plexiglass sample holder containing inlet and outlet ports, and solutions were introduced at a flow rate of ∼1 mL/min using a peristaltic pump (Fisher Scientific) from a reservoir with a total volume of ∼3-4 mL. Protein solutions (protein A or IgG) were continuously recirculated from this reservoir during the course of an experiment while buffer solutions were not recirculated. The spectrometer was focused onto the porous SiO₂ surface through the plexiglass sample holder.

After establishing an initial baseline in PBS, protein A was directly adsorbed onto the oxidized surface through non-covalent interactions by recirculating 3 mL of a 0.1 mg/mL (∼2.4 μM) solution of protein A (in PBS buffer) over the porous SiO₂ chip for 20 minutes. A steady-state response in the reflectivity spectrum was obtained more quickly in the flow cell (20 min) compared with the static experiments (∼120 min). After loading with protein A, free protein was removed by flushing the cell with PBS buffer solution until a stable baseline was achieved. At this point, the protein A-coated surface was found to be quite stable; only negligible changes in OT were observed upon rinsing with PBS over the time scale of the protein-binding experiments.

For the association phase of the experiments, 4 mL of solution containing the relevant IgG molecule was continuously circulated through the flow cell from the reservoir. Separate experiments using larger volumes of IgG solution yielded identical results, indicating that IgG was not depleted significantly from the test solutions at the concentrations studied, and therefore constant [IgG] was assumed in the models used to obtain kinetic and thermodynamic binding constants. The ΔOT values presented in this work represent the shift in optical thickness (OT) relative to the initial OT value at [IgG] = 0. Time point 0 represents a data point obtained 2 minutes after introduction of a new solution (pure buffer or IgG) to account for the time for solution to travel from the inlet port to the sample.

Determination of Equilibrium Binding Constant from Steady-State Experiments

The reaction of surface adsorbed protein A with IgG was modeled by the expression

$${\text{A}}_{\text{ads}}+\text{IgG}\underset{k_d}{\overset{k_a}{\rightleftarrows }}\text{AG}$$ (2)

where A_ads represents the available adsorbed protein A binding sites, IgG represents free IgG in solution, AG represents the surface-bound protein A/IgG complex, and k_a and k_d are the kinetic rate constants for protein A/IgG binding and dissociation, respectively. The equilibrium dissociation constant (K_d) is defined as

$${\text{K}}_{\text{d}}=\frac{{\text{A}}_{\text{ads}}[\text{IgG}]}{\text{AG}}$$ (3)

and can be represented by the following equation (See Supporting Information):

$$\Delta {\text{OT}}_f=\frac{\Delta {\text{OT}}_{max}[\text{IgG}]}{{\text{K}}_{\text{d}}+[\text{IgG}]}$$ (4)

Where ΔOT_max represents the signal obtained when all protein A binding sites are occupied and ΔOT_f is the steady-state value of ΔOT for a given [IgG]. K_d is obtained from a numerical fit to the plot of [IgG] vs. ΔOT_f (see Data Analysis section).

Determination of Kinetic Parameters from Time-Resolved Data

Protein binding inside the porous SiO₂ matrix is directly related to the refractive index of the film, which can be monitored in real-time with the reflection spectrometer used in the present study. Kinetic parameters are obtained from a nonlinear least-squares fit of the data to the time-dependent form of the rate law.^{12, 31, 32} It is assumed that the kinetics are not diffusion-limited in the time scale over which the data are fit.

The rate law for eq. 2 is given by:

$$\frac{d[\text{AG}]}{dt}={\text{k}}_{\text{a}}[\text{A}][\text{IgG}]-{\text{k}}_{\text{d}}[\text{AG}]$$ (5)

which can be solved to give the expression (See Supporting Information):

$$\Delta \text{OT}=\text{C}[1-e^{{-\text{k}}_{\text{x}}\text{t}}]$$ (6)

Here C and k_x (k_x = k_a[IgG]+k_d) are constants determined by numerical fit of the adsorption data to eq. 6. The dissociation constant k_d is determined from a least-squares fit of the desorption data to the equation:

$$\Delta \text{OT}=\Delta {\text{OT}}_{\text{0}}{e}^{{-\text{k}}_{\text{d}}\text{t}}$$ (7)

where ΔOT₀ is the sensor response measured immediately after changing the flow stream to pure buffer.³¹ The use of eq. 7 to obtain k_d is valid if the PBS solution is continually refreshed to prevent reassociation of unbound IgG molecules, and therefore only fresh (not recirculated) PBS was used to flush the sample during the dissociation phase of the experiments.

Data analysis

All data analysis was performed using the IGOR software package (Wavemetrics, Inc). A Levenberg-Marquardt algorithm was used to iteratively search for the coefficients that best fit the data, determined by minimization of the χ² value. Residuals represent the difference between the raw data and the fitted curves. All reported values represent an average of at least 3 trials unless otherwise noted. For the time-dependent equations, the results of the fitting algorithm are somewhat dependent on the initial guesses input for the unknown coefficients k_x and C, and it is possible for the fitting routine to find only a local minimum of the χ² values. The initial guesses for C and k_x were thus chosen such that k_d/k_a yielded an equilibrium binding constant similar to that obtained using steady-state data. Iterative analysis in which calculated values were used as the initial guesses for subsequent iterations was performed until the calculated constants reached an unchanging value and χ² was minimized. For the data shown in Figure 6, C was held at a constant value equal to the value of ΔOT_f determined in a separate experiment (performed using the same concentration of IgG).

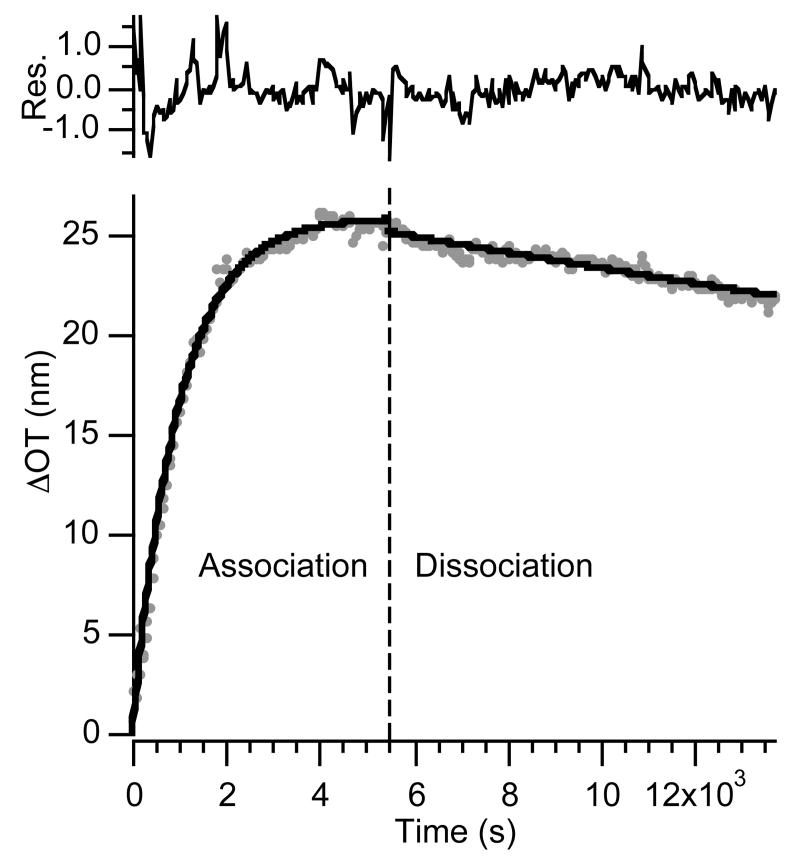
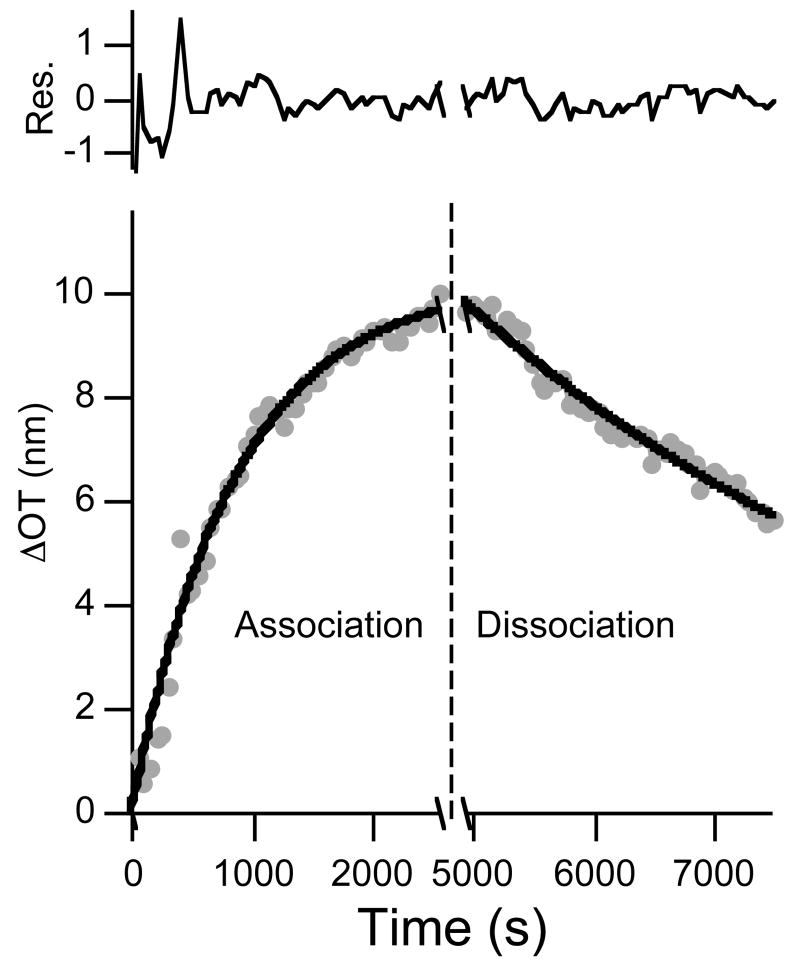
Figure 6.

Association (dots, left of dashed line) and dissociation (dots, right of dashed line) curves and corresponding fit to the time-dependent equations 6 and 7 (solid lines) for a protein A-coated porous SiO₂ surface dosed with 171 nM human IgG for a short period of time (4 min). Residuals represent the difference between the fit line and the data. The initial 180 s of dissociation data were not used in the fit, to account for clearing of the tubing and chamber of the flow cell upon switching from IgG to buffer solution.

Results and Discussion

Relative Binding of Human, Rabbit, and Goat IgG to Protein A

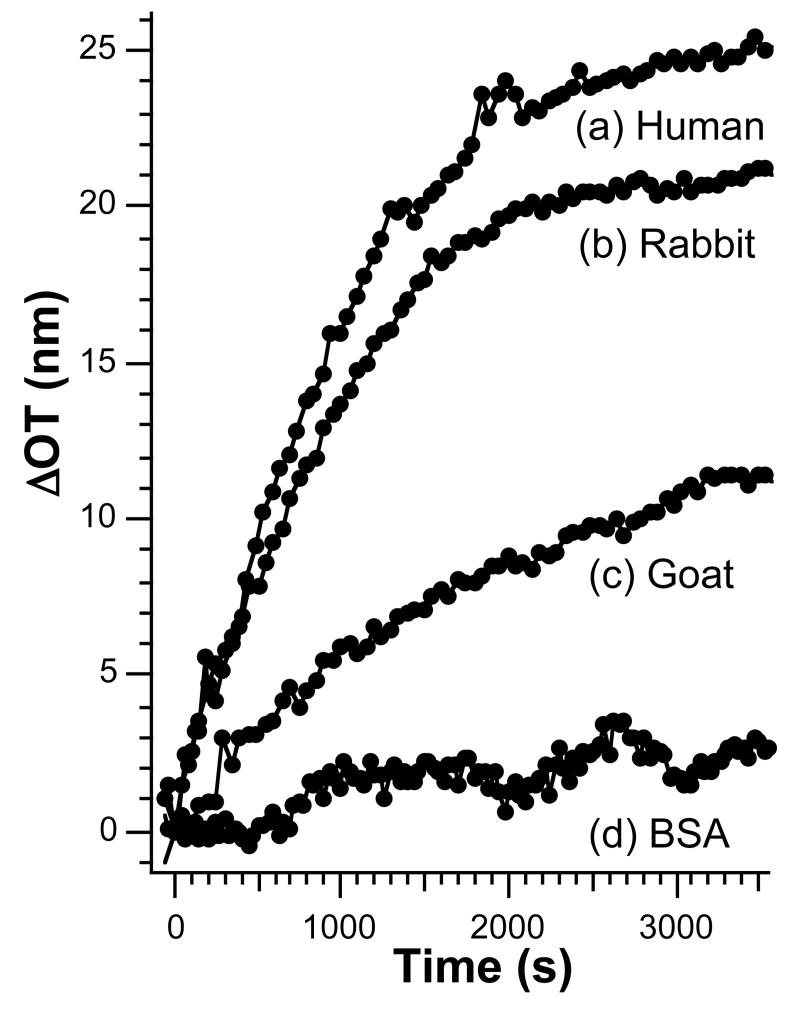
Protein A binds specifically to the Fc region of certain species of IgG. The species-dependence of the binding constant is used in the present study to test the response of optical interferometric sensors constructed from porous SiO₂. Figure 1 shows a comparison of binding curves for protein A-coated porous SiO₂ films exposed to solutions 171 nM (0.025 mg/mL) in (a) human IgG, (b) rabbit IgG, and (c) goat IgG. The affinity of IgG binding to protein A based on the ΔOT measurement is human > rabbit > goat. Exposure of a sample to a solution 725 nM (0.05 mg/mL) in bovine serum albumin (BSA) (Figure 1d) leads to a significantly smaller shift in OT, even when it is present at twice the concentration (by mass) of the IgG molecules. These results are consistent with previously published data on the competitive binding of protein A to the three types of IgG molecules.^{34, 35}

Figure 1.

Comparison of time-dependent binding curves for different IgG species. Protein A-coated porous SiO₂ samples dosed with 171 nM (a) human IgG, (b) rabbit IgG, and (c) goat IgG and (d) 725 nM bovine serum albumin (BSA).

Several control experiments were performed to test the hypothesis that the optical changes observed correspond to specific binding of IgG with protein A. The introduction of any protein solution is expected to result in an increase in OT, because the solution will have a higher index of refraction than the protein-free buffer solution. However, for the relatively low concentration of IgG used in the present experiments, this change is expected to be very small unless the molecule is concentrated in the porous film (either by specific or non-specific interactions). Two key controls on the protein A-coated samples address this issue. First, addition of goat IgG, which has a weaker interaction with protein A and so is not expected to be as concentrated in the pores as human IgG,^34-37 shows an OT change (Figure 1c) that is significantly smaller than that observed for an equivalent dose of human IgG (Figure 1a). Second, the addition of a greater quantity (by mass) of BSA to a protein A-coated sample exhibits only a small OT change (Figure 1d). BSA is a smaller molecule than IgG and is expected to infiltrate the pores of the matrix more effectively. Thus the BSA results establish that the observed OT changes cannot be attributed to simply a change in the refractive index of the bulk solution.

Two additional control experiments performed on films that were not pre-coated with protein A support the specific binding hypothesis. When a chip is exposed to a 171 nM dose of human IgG without pre-adsorption of protein A, the net shift in OT is significantly smaller (< 6 nm) than when protein A is present. The small shift in OT is attributed to non-specific binding. This result also indicates that the non-specific binding of protein A to the bare chip surface is more efficient than the non-specific binding of human IgG. An additional control in which the chip is first dosed with 725 nM BSA, followed by a 171 nM dose of human IgG, yields a total OT shift of < 6 nm, further supporting the hypothesis that the OT changes > 6 nm observed for the various IgG molecules in Figure 1 arise from specific binding to the immobilized protein A capture probe.

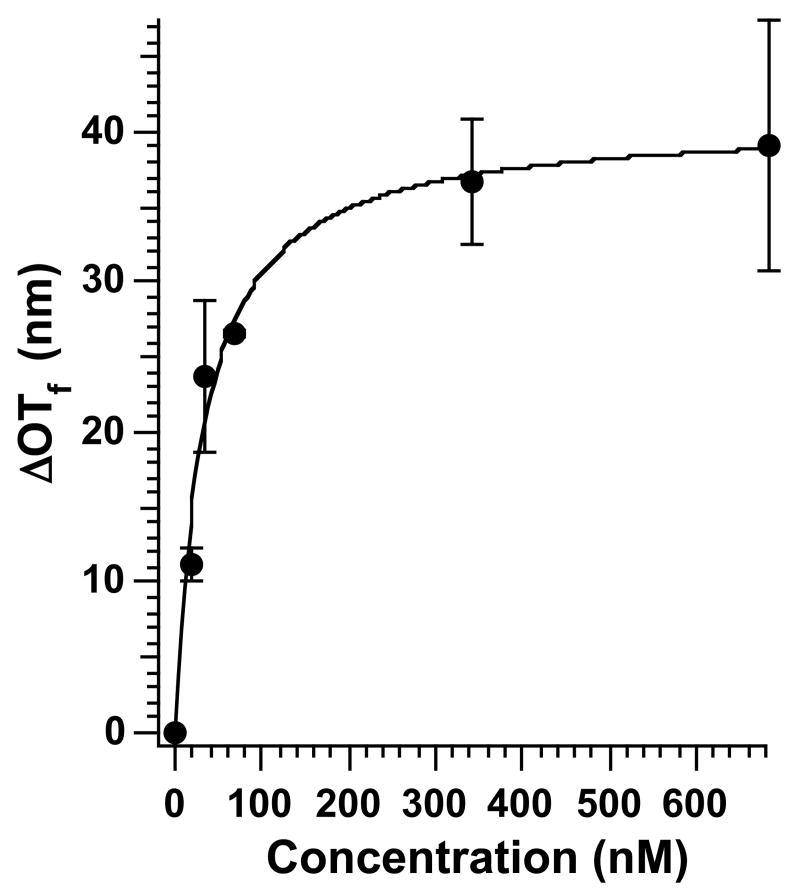
Equilibrium IgG/Protein A binding constants can be obtained by measurement of the equilibrium value of ΔOT (ΔOT_f) as a function of [IgG]. Figure 2 shows a plot of human IgG concentration vs. ΔOT_f and the corresponding line generated by fitting the average ΔOT_f values to eq. 4. The data were collected by placing a protein A-modified porous SiO₂ sample in 2 mL of buffer, adding an aliquot of IgG solution under static (no flow) conditions, and monitoring the value of OT in the reflectivity spectrum until it reached a constant value. The quantity ΔOT_f is defined as equilibrium OT (measured after addition of IgG) - baseline OT (measured in PBS buffer before IgG addition). An average of at least 3 data points (measured on separate porous SiO₂ chips prepared from the same Si wafer) were fit to eq. 4 for each concentration of IgG. The value ΔOT_max in eq. 4 represents the saturation value of ΔOT, corresponding to the condition in which all the protein A receptor sites on the sensor surface are bound to analyte. Fitting the experimental data to a Langmuir plot (eq. 4) yields a K_d value for protein A/human IgG binding of 3.3 ± 0.6 × 10^-8 M (K_a = 3.0 ± 0.5 × 10⁷ M^-1). The equilibrium binding constant obtained for human IgG binding to a protein A-coated porous Si surface is consistent with previously determined values for IgG binding to protein A immobilized on cell walls (K_a ∼ 4–9.4 × 10⁷ M^-1)^38-40 or solid supports (K_a ∼ 1.8–4.8 × 10⁷ M^-1).^{41, 42}

Figure 2.

Plot of concentration of human IgG vs. ΔOT_f measured on a protein A-coated porous SiO₂ film. The quantity ΔOT_f is the final, steady-state value of ΔOT obtained after exposure of the sample to the indicated concentration of IgG. The solid line represents a fit of the average values to eq. 4. The calculated K_d value is 3.3 ± 0.6 × 10^-8 M (K_a =3.0 ± 0.5 × 10⁷ M^-1).

Time-Resolved Measurement of Binding of Human IgG to Protein A

While the steady-state Langmuir model is useful for determining equilibrium binding constants, determination of kinetic rate constants requires the use of the time-dependent form of the equation. For optical biosensors that monitor changes in refractive index such as SPR and RIFS, both kinetic and equilibrium binding constants can be obtained using non-linear least squares analysis of the time dependent protein binding curve.^{12, 31, 32} In this work, we investigated the time-dependent response of the porous SiO₂ sensor to see if it reflects the protein A/human IgG binding kinetics.

Figure 3 shows the change in optical thickness vs. time for a protein A-coated porous SiO₂ surface exposed to 171 nM human IgG (association) followed by flushing with PBS buffer (dissociation). The black solid lines represent fits to the association (eq. 6) and dissociation (eq. 7) equations. From the values of the experimentally determined kinetic rate constants k_a (1.1 ± 0.6 × 10⁴ M^-1s^-1) and k_d (2.1 ± 1.0 × 10^-5 s^-1), the equilibrium association constant (K_a) is calculated to be 5.2 ± 2.7 × 10⁸ M^-1. This value is significantly larger than that obtained from the steady-state Langmuir model above (3.0 ± 0.5 × 10⁷ M^-1), and the published values for binding of human IgG to cell wall bacteria and other immobilized protein A systems (1.8 – 9.4 × 10⁷ M^-1).^38-41 The overestimate of the equilibrium binding constant determined from the kinetic parameters can be attributed to the significantly smaller dissociation rate constant (k_d = 2.1 × 10^-5 s^-1) determined in the present system, relative to the value previously observed for protein A/IgG binding at a surface (k_d ∼2.77 × 10^-4 s^-1).⁴² The analogous rabbit and goat IgG kinetic data (also using analyte concentrations of 171 nM) similarly overestimate equilibrium binding (K_a) and underestimate the dissociation rate constants (k_d) compared with previous results.⁴²

Figure 3.

Adsorption and desorption curves for human IgG dosed on a protein A-coated surface. Adsorption and desorption curves (dots) and corresponding fit to the time-dependent eqs 6 and 7 (solid lines) for a protein A-coated porous SiO₂ surface dosed with 171 nM human IgG. Residuals represent the difference between the fit line and the data.

Deviations from Ideal Binding Behavior at High [IgG]

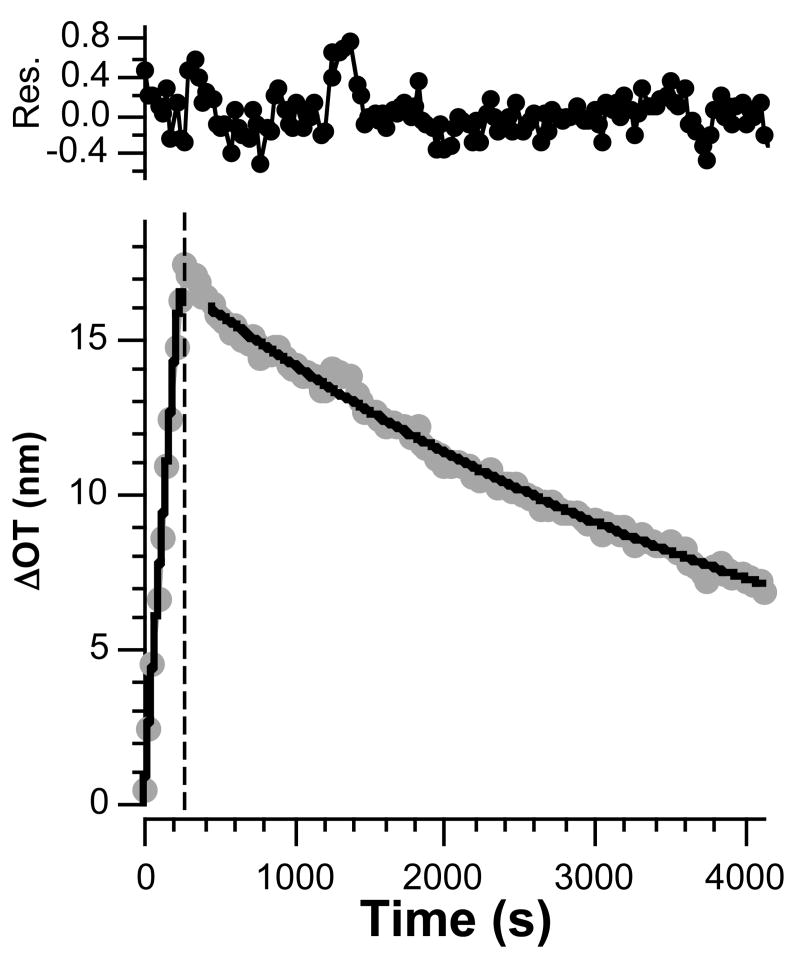
For porous systems, the accurate measurement of kinetic rate constants can be limited by mass transport within the pores.^43-47 Hindered diffusion is expected to lead to significant deviations from ideal protein binding behavior for both association and dissociation phases,⁴⁶ and in extreme cases, measured rate constants can be solely due to transport limitations.⁴⁵ In the present system, more consistent kinetic data are obtained when the measurements are made at lower analyte concentrations. Thus the association and dissociation curves obtained when the sensor is exposed to a solution of human IgG at a concentration of 51 nM (Figure 4) instead of 171 nM (Figure 3) provide a more reliable fit to the ideal equations (eq. 6 and 7), and the resulting kinetic rate constants (k_a = 1.6 ± 0.3 × 10⁴ M^-1s^-1 and k_d = 2.2 ± 0.1 × 10^-4 s^-1) are more consistent with the published values. The equilibrium binding constant (K_a = 7.4 ± 1.7 × 10⁷ M^-1, determined from two replicate trials) is closer to the value obtained from the steady-state experiments and in the range of previously reported values.^38-42

Figure 4.

Association and dissociation curves (dots) and corresponding fit to the time-dependent eqs 6 and 7 (solid lines) for a protein A-coated porous SiO₂ surface dosed with a 51 nM human IgG solution. Residuals represent the difference between the fit line and the data.

Analysis of Kinetic Data: Dissociation Derivative Plots

The deviation from ideal 1:1 protein binding behavior observed in the data obtained at high (171 nM) analyte concentration is likely attributed to restricted diffusion in the ∼100 nanometer diameter pores of the sensor film. Other potential causes of deviation from ideal behavior include steric hindrance of binding sites by the adsorbing protein,^{48, 49} multiple binding interactions due to surface heterogeneity,⁵⁰ and two-state binding⁵¹. Dissociation derivative plots (ln(ΔOT₀/ΔOT) vs. time) can provide insight into the cause of deviation from ideal 1:1 binding behavior.^{45, 47, 49} The dissociation derivative plot has the effect of normalizing the data to account for non-equivalent surface coverage due to different analyte concentrations or different dosing times.

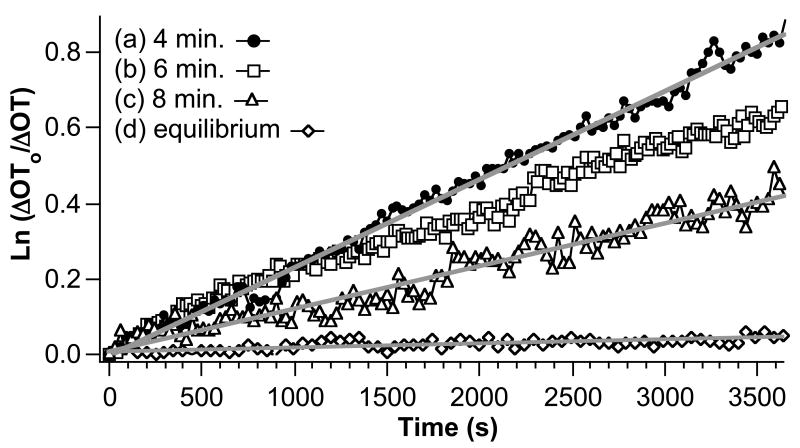
Figure 5 shows dissociation derivative plots for protein A-coated porous SiO₂ surfaces exposed to a solution containing 171 nM human IgG for different periods of time. The total amount of bound IgG decreases with decreasing dose time. For ideal 1:1 protein binding, dissociation derivative plots should be independent of the amount of time for which the sample was dosed. The data presented in Figure 5 shows that the dissociation process is distinctly dependent on the amount of time dosed. In particular, larger dose periods lead to slower dissociation, indicated by a smaller slope in the ln(ΔOT₀/ΔOT) curve. Each set of data can be fit to a line with the exception of the 6 minute dose. The 6 minute dose displays a dissociation rate that is initially almost identical to the 4 minute dose, but then becomes slower after ∼1500 s.

Figure 5.

Dissociation derivative plots (ln(ΔOT₀/ΔOT) vs time) for dosing of a protein A-coated porous SiO₂ film with a 171 nM solution in human IgG. The quantity ΔOT₀ is the change in OT observed after exposure of the sensor to human IgG for the time periods indicated in the inset. The quantity ΔOT is then determined as a function of time, where time = 0 corresponds to 180 s after changing the IgG solution to pure buffer. The 180 s delay accounts for clearing of the tubing and chamber of the flow cell. A larger slope indicates a faster rate of dissociation.

There are several factors that lead to dose time-dependent dissociation kinetics. For example, previous studies have shown that rebinding effects during the dissociation phase become most pronounced as more surface sites become available, i.e. with a smaller number of protein molecules adsorbed to the surface.^{44-47, 49} Figure 5 shows that the rate of IgG dissociation is slower at higher initial surface loading, the opposite of what is expected if analyte rebinding is occurring. In addition, the 4 minute dose shows a linear dissociation derivative plot, while deviations due to rebinding are expected to yield non-linear plots due to the time-dependent increase in available binding sites.^{44, 47, 49} Therefore, the data are not consistent with an analyte rebinding mechanism.

The presence of multiple binding sites with significantly different dissociation constants (for example, due to different protein A conformations) can also be ruled out. At low dose times or low concentration dosing, the stronger binding complex would form preferentially, with increased contribution from the weaker binding species at longer dose times or higher concentration dosing. However, contribution from a weaker binding species is expected to lead to nonlinear, biphasic dissociation derivative plots. At longer dissociation times, the ln(ΔOT₀/ΔOT) traces should display similar slopes for all the dissociation plots, corresponding to dissociation of the more tightly bound component. In the work presented here, most of the ln(ΔOT₀/ΔOT) curves are linear (Figure 5), and the plots do not display similar slopes at long dissociation times.

Dissociation derivative traces that display an increasing slope with decreasing dose time have been attributed to steric crowding effects⁴⁹ and two-state reactions.⁵¹ Steric crowding can be expected if bound analyte molecules block the openings of small pores or limit access of additional analyte molecules to available binding sites deeper in the pores.⁴⁸ In addition to being attributed to dose-dependent dissociation,⁴⁹ steric crowding has been attributed to deviations in the ideal association phase that become more pronounced at higher concentration dosing,⁴⁸ similar to what is observed in the present case. The smaller apparent rate of dissociation observed when the sample is exposed to analyte for a longer period of time can also be attributed to two-state binding, in which surface-bound proteins form a more stable species due to reorganization,⁵¹ self-association,^{52, 53} or silica surface aggregation and conformational changes.^{54, 55} Therefore, a two-state mechanism in which IgG initially binds to protein A and then reorganizes to form a more stable surface complex cannot be ruled out, and it is possible that both effects (diffusional limits imposed by steric crowding in the pores and two-state binding) play a role in the observed deviations from ideal behavior.

Effect of Analyte Concentration and Exposure Time on the Accuracy of Kinetic Rate Constant Determination

Deviations from ideal behavior are typically handled by analyzing only the initial portions of the association and dissociation curves.⁵⁶ Both restricted diffusion and surface interaction limitations can be minimized by limiting the association phase to sub-saturation dosing so that all binding sites are not occupied. The observation that the 6 minute dose of 171 nM IgG shows two dissociation regimes could indicate a transition in which steric hindrance or protein interactions begin to dominate. There is little difference between the initial slopes of either the 4 minute or the 6 minute IgG dosing runs, indicating that the dissociation rate reaches a limiting value at shorter times. Also of note is the observation that the 4 minute dissociation derivative plot is linear, suggesting that rebinding is not significant in this regime.^{44, 47, 49} Therefore, limiting the time the sensor is exposed to analyte is expected to allow the acquisition of meaningful kinetic and thermodynamic binding data when solutions containing high analyte concentrations are tested.

Figure 6 shows plots of ΔOT vs. time for a sensor film dosed with a solution 171 nM in human IgG for 4 minutes followed by a PBS flush. Dosing with human IgG produces a large change in optical thickness that can be attributed to protein A/IgG binding. Also shown in Figure 6 are the fit lines (black lines) for association (eq. 6) and dissociation (eq. 7) phases. The 4 minute human IgG dose data provide excellent fits to eqs. 6 and 7.

Table 1 summarizes the binding constants obtained from the various time-resolved and steady-state measurements used in this work. The dissociation rate constant calculated from a 4 minute dose of IgG (k_d = 2.1 ± 0.2 × 10^-4 s^-1) is higher than the value obtained when the system is allowed to reach equilibrium (2.1 ± 1.0 × 10^-5 s^-1), and is similar to the value obtained from a 51 nM equilibrium dose and from the literature (for protein A/IgG binding on a surface: ∼2.77 × 10^-4 s^-1)⁴². Additionally, the value of the equilibrium association constant, K_a, determined from the 4 minute IgG dosing experiments (5.5 ± 1.5 × 10⁷ M^-1) agrees with the literature values for protein A/IgG binding (K_a ∼ 1.8 – 9.4 × 10⁷ M^-1),^38-42 and it is close to the value calculated using the steady-state Langmuir model (Figure 2, K_a = 3.0 ± 0.5 × 10⁷ M^-1). We therefore conclude that through proper choice of reaction conditions and method of analysis, porous Si interferometry can yield reliable kinetic and equilibrium binding constants.

Table 1.

Comparison of kinetic and equilibrium binding constants for human IgG binding to protein A.

	ka (M-1s-1)	kd (s-1)	Ka (M-1)	Kd (M)
Time-resolved data:
171 nM equilibrium dose	1.1 ± 0.6 × 104	2.1 ± 1.0 × 10-5	5.2 ± 2.7 × 108	1.9 ± 1.0 × 10-9
51 nM equilibrium dose	1.6 ± 0.3 × 104	2.2 ± 0.1 × 10-4	7.4 ± 1.7 × 107	1.4 ± 0.3 × 10-8
171 nM 4 minute dose	1.2 ± 0.4 × 104	2.1 ± 0.2 × 10-4	5.5 ± 1.5 × 107	1.9 ± 0.5 × 10-8
Steady-state data:
171 nM equilibrium dose	-	-	3.0 ± 0.5 × 107	3.3 ± 0.6 × 10-8
Published valuesa	-	-	1.8-9.4 × 107	-
Published value, Protein A/IgG, surfaceb	8.02 × 103	2.77 × 10-4	2.9 × 107	-

^aReferences 36-⁴⁰.

^bReference 42, unknown IgG species.

Conclusions

The capabilities and limitations of porous SiO₂ Fabry-Perot interferometers to act as label-free optical biosensors were studied. A protein A capture probe/IgG analyte test system was used, and the kinetic and thermodynamic binding constants obtained were compared with literature values. The porous SiO₂ system correctly determines relative affinity of binding to a protein A capture probe for a series of IgG molecules derived from different species (human>rabbit>goat IgG). The equilibrium binding constant (K_a) for human IgG/protein A binding is determined to be 3.0 ± 0.5 × 10⁷ M^-1 using a steady-state binding model. In the determination of kinetic association and dissociation constants, significant deviations from ideality are observed. These errors are attributed to restricted diffusion in the nanometer-scale pores of the interferometer film, and they can be minimized if the capture probe is not allowed to become saturated with analyte. Thus, dosing analyte for short times or using low analyte concentrations minimizes deviations from ideal behavior, providing kinetic and thermodynamic binding constants that are self-consistent and in agreement with the previously published values.

In this work, the protein A capture probe was immobilized on an oxidized porous SiO₂ sample through non-covalent interactions, but the method could be adapted to incorporate covalent attachment schemes through standard silica^{17, 29} and silicon^{23-25, 57, 58} chemistry. Interferometry on porous Fabry-Perot layers provides a means to qualitatively and quantitatively study protein binding.

Supplementary Material

si20061016_070. Supporting Information Available.

Schematic representation of experimental design and flow cell, representative reflectance and FT spectra, and detailed derivation of equations used for fitting. This information is available free of charge via the Internet at http://pubs.acs.org.