Prediction of uterine rupture associated with attempted vaginal birth after cesarean delivery

Abstract

Objective

To predict individual-specific risk of uterine rupture during an attempted vaginal birth after cesarean (VBAC).

Methods

Women with one prior low-transverse cesarean delivery who underwent a trial of labor with a term singleton were identified in a multi-center concurrently collected database of deliveries occurring during a four-year period. We analyzed different techniques to develop an accurate prediction model for uterine rupture.

Results

Of the 11,855 women analyzed, 83 (0.7%) had a uterine rupture. The optimal model, based on a logistic regression,included: any prior vaginal delivery (OR 0.44, 95% CI 0.27 – 0.71) and labor induction(OR 1.73, 95% CI 1.11 – 2.69). This model, with a c-statistic of .627, had poor discriminating ability and does not allow the determination of a clinically useful estimate of the probability of uterine rupture for an individual patient.

Conclusion

Patient-specific factors cannot be used to accurately predict the relatively small proportion of women who will incur a uterine rupture during an attempted VBAC after 36 weeks of gestatation.

Condensation

Factors available before or at admission for delivery cannot be used to accurately predict uterine rupture during an attempted vaginal birth after cesarean.

Even though uterine rupture during an attempted vaginal birth after cesarean (VBAC) occurs infrequently, the potential ramifications, such as hysterectomy and neonatal neurodevelopmental disability or death, are of great clinical significance.¹ Correspondingly, when pregnant women with a prior cesarean delivery are confronted with the decision of whether to attempt a trial of labor (TOL), the possibility of a uterine rupture is particularly relevant to their decision-making process. In an effort to aid this process, investigators have studied the different factors that are associated with the occurrence of uterine rupture.^2–5

The identification of factors associated with uterine rupture may allow physicians to provide general guidance to a woman regarding her chance of uterine rupture during a TOL. However, even though certain factors may be associated with uterine rupture, it does not necessarily follow that those associations can be combined to allow accurate prediction of the probability of a uterine rupture for an individual woman. The development of such a prediction model could further aid women and their caregivers in counseling regarding the decision to attempt a VBAC.

Macones et al attempted to develop a model for the prediction of uterine rupture, but were unable to construct an accurate one.⁶ We have recently demonstrated a methodological technique for developing a graphical nomogram that can be used to accurately predict the probability of another important component of the decision to undergo a TOL, namely, the chance of achieving a vaginal delivery.⁷ We hypothesized that this technique also could allow the development of an accurate prediction model for uterine rupture. In this study, we have investigated that possibility.

Methods

Between 1999 and 2002, 19 academic medical centers participating in the National Institute of Child Health and Human Development’s Maternal-Fetal Medicine Units Network participated in a study of pregnant women with a prior cesarean. At each center, trained and certified research nurses concurrently identified women who were admitted for delivery and who had a history of prior cesarean delivery. Those women who were identified had their charts abstracted for demographic data, medical and obstetric history, and intrapartum and postpartum events. Uterine rupture was defined as disruption of the uterine muscle and visceral peritoneum or a uterine muscle separation with extension to the bladder or broad ligament found at the time of cesarean delivery or laparotomy. Reports of uterine rupture underwent secondary review at each clinical center as well as centrally to ensure accuracy of diagnosis. Further details of the methodology of this study have been previously described.¹ Approval for the study was obtained from the Institutional Review Board of each institution.

This analysis concerns those women in the registry with a vertex singleton gestation and one prior low-transverse cesarean delivery who underwent a trial of labor after 36 6/7 weeks of gestation. Women with an antepartum intrauterine fetal demise were excluded. For development of the predictive model, patient factors were considered for inclusion if they could be ascertained at the first prenatal visit or upon admission for the TOL. These factors included: demographic variables (maternal age, ethnicity, body mass index); variables related to the prior cesarean delivery (recurrent indication, length of time since cesarean); variables related to prior obstetric history (any prior vaginal delivery, number of prior vaginal deliveries, any vaginal delivery subsequent to cesarean, prior preterm vaginal deliveries only, maximal birth weight of a prior child); variables reflective of medical conditions (pre-gestational or gestational diabetes mellitus, asthma, chronic hypertension, renal or heart disease, or a connective tissue disorder); and intrapartum variables ascertainable at the start of labor (induction of labor, cervical exam upon admission, estimated gestational age at delivery, pregnancy-induced hypertension) . Recurrent indication for a cesarean delivery was defined as arrest of dilation or descent as the indication for the prior cesarean.

In the initial phase of the development of the predictive model, the original data set was randomly and approximately equally divided into a training set and a test set. The classification errors were estimated through a cross-validation procedure. Once the training set was used to identify predictive factors for uterine rupture and build the predictive model, the independent test set was used to estimate the classification errors. Marginal exploratory analysis was performed on continuous variables to analyze whether these were best represented in the model as continuous or categorical variables. We first built a logistic regression model based on the training set with stepwise variable selection, and then used the test set to evaluate the model.^{8, 9} A receiver operating characteristics (ROC) curve was generated from this regression and a c-statistic (representing the “area under the curve”) was determined. In addition to the logistic regression, other classification techniques, such as classification tree, random forest, support vector machine, and boosting analysis were evaluated to determine if they provided a more accurate model. ^10–12 These techniques, however, did not improve predictive capability.

The logistic regression model developed from the training set was validated as follows. After applying the regression model to the test set, the predicted probabilities of uterine rupture were partitioned into 10 groups (i.e. 0–0.5%, 0.5–1.0%,…4.5 – 5%). The mid points of these probability ranges (e.g. 0.25%, 0.75%, etc.) were used to represent these groups. In each group, the proportion of women with a uterine rupture was calculated to estimate the empirical probability of uterine rupture. The scatter plots of the predicted and empirical VBAC probabilities were smoothly connected to form a curve. The ideal validation would generate a 45-degree straight line. Corresponding 95% confidence intervals for the curve were calculated from the normal approximation. The validation curve provides additional and important insight into the predictive strength of a model that the ROC curve alone cannot provide. The ROC curve indicates how effectively one can predict whether an individual will or will not have a uterine rupture. Yet, even if a prediction model could not accurately predict this dichotomous outcome, it may allow good estimation of an individual’s specific risk for an outcome. It is the validation curve that provides insight into this estimation of specific risk. SAS version 8.2 (SAS Institute, Cary, NC) was used for analysis.

Results

During the study period, 11,855 women met inclusion criteria. Uterine rupture occurred in 83 (0.7%) of these women. Descriptive characteristics of the population are presented in Table 1. Eleven thousand six hundred and seventy-six women had a complete set of values for all variables under consideration and this comprised the final population used for analysis.

Table 1.

Descriptive characteristics of the study population.

Variable	N (data available)
Maternal age (years)	11,855	28.6 ± 5.8
BMI at first prenatal visit (kg/m2)	7998	26.4 ± 6.3
BMI at delivery (kg/m2)	11,070	32.2 ± 6.7
Duration since prior cesarean delivery(years)	11,347	5.2 ± 3.6
Maternal race	11,855
Caucasian		4589 (38.7%)
Latina		2362 (19.9%)
African American		4300 (36.3%)
Other		604 (5.1%)
Recurring indication for cesarean	11,329	4108 (36.3%)
Any prior vaginal delivery	11,816	5617 (47.5%)
Prior preterm vaginal delivery only	11,816	290 (2.5%)
Vaginal delivery after prior cesarean	11,855	3996 (33.7%)
Maximum birth weight of prior child (pounds)	8792	7.2 ± 1.5
Pre-existing medical condition
Diabetes mellitus	11,854	99 (0.8%)
Other*	11,855	1205 (10.2%)
Complications of pregnancy
Gestational diabetes mellitus	11,854	525 (4.4%)
Pregnancy-induced hypertension	11,855	249 (2.1%)
Induction of labor	11,715	3239 (27.7%)
Cervical exam at admission for delivery
Dilation (cm)	11,432	3.2 ± 2.0
Effacement (%)	11,225	68.7 ± 26.9
Station < 0	10,921	9954 (91.2%)
EGA at admission for delivery	11,855	39.2 ± 1.2

Data are presented as mean ± standard deviation or N (%)

^*Other preexisting medical conditions include chronic hypertension, cardiac disease, asthma, renal disease, or a connective tissue disorder

BMI = body mass index; EGA = estimated gestational age

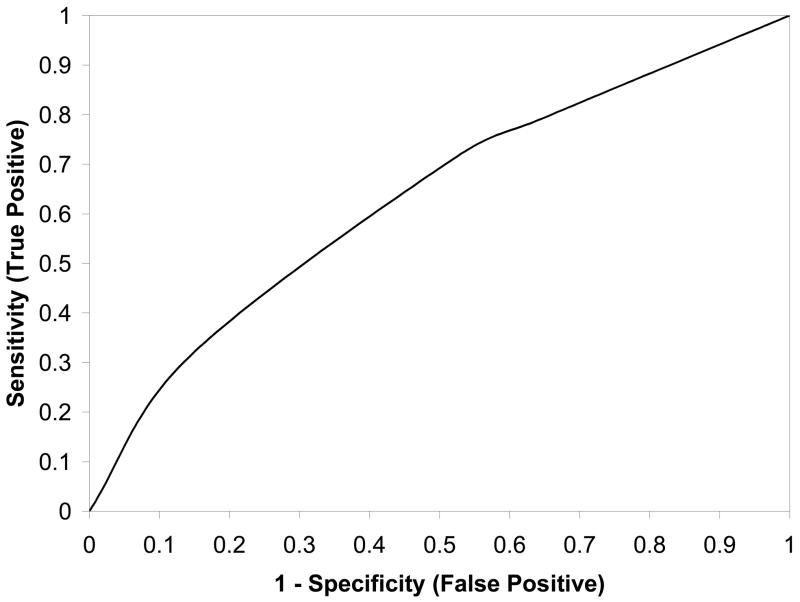
The specific regression equation that was determined to best predict the probability of uterine rupture was: exp (w)/[1+exp (w)], where w = −4.81 – 0.82(prior vaginal delivery) + 0.55 (induction of labor). As can be seen in this equation, only two factors, namely the occurrence of a prior vaginal delivery or induction of labor, were found to contribute to an optimal final prediction model. The addition of further factors did not materially improve the ability to accurately predict uterine rupture. Table 2 reveals the odds ratio and 95% confidence interval derived from the regression equation for each predictive factor. As indicated by the odds ratios, history of a prior vaginal delivery was associated with a lower probability of uterine rupture, while induction of labor was associated with a higher probability of uterine rupture. The corresponding receiver operating characteristic curve, with an area under the curve of 0.627 (95% confidence interval 0.568–0.686) is presented in Figure 1.

Table 2.

Factors associated with uterine rupture in multivariable logistic regression

Variable	Odds ratio	95% confidence interval
Any prior vaginal delivery	0.44	0.27 – 0.71
Induction of labor	1.73	1.11 – 2.69

Figure 1.

Receiver-operating characteristic curve for the logistic regression model for prediction of uterine rupture associated with a trial of labor.

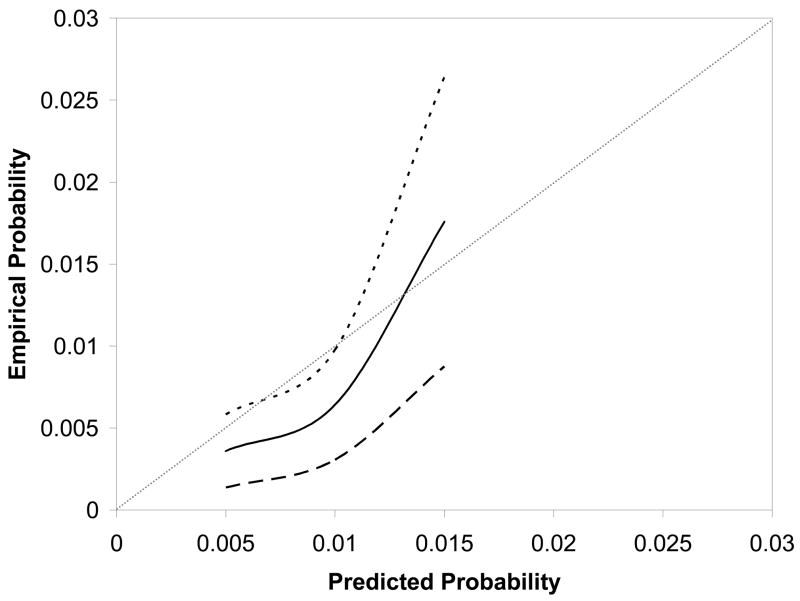
The cross-validation procedure showed that the performance of the model on the test set was similar to that originally determined from the training set, with an area under the curve that was determined to be 0.603. Figure 2 compares the predicted rates of uterine rupture with the empirical probabilities of uterine rupture for women in the test set. The estimated curve and its 95% confidence band demonstrate two important features. First, the predicted probabilities of uterine rupture do not accurately reflect the empirical probabilities that the patient experienced. Second, the 95% confidence intervals are relatively wide given the point probability of uterine rupture. For example, an empirical probability of rupture of 1.3% has a 95% confidence interval ranging from 0.6% to 1.8%. Although the absolute difference in these frequencies is small, the range of the confidence interval is nearly 100% of the point estimate. Thus, the prediction model is neither accurate nor discriminating. Given that an adequate prediction model could not be obtained, a graphical nomogram ⁷ was not constructed, as it would have little clinical value.

Figure 2.

Nomogram calibration: The reference line, which an ideal nomogram would produce, is represented by the diagonal line; the solid line represents the actual performance of the current nomogram; the two dashed lines represent its 95% confidence band.

Comment

Faced with the prospect of undergoing delivery after a low-transverse cesarean, women must choose an intended route of delivery. The decision to undergo a TOL depends upon how women balance the benefits and risks of that trial. On one hand, women can achieve a vaginal delivery, an outcome with a shorter recovery and fewer long-term reproductive consequences than a cesarean.¹³ On the other hand, however, is the possibility of uterine rupture, a potentially catastrophic event for the health of both the mother and neonate.¹ In order to make the most informed choices, women should have information that allows them to understand the magnitude of the probability of these outcomes.

Traditionally, women have been counseled using outcome probabilities that are based on population averages.⁴ If women could be provided with individual-specific probabilities for the benefits and risks of a TOL, the counseling provided to them and their ability to make the most informed decision would be enhanced. To date, however, a predictive model has not been developed that allows the discernment of individual-specific risks of uterine rupture.

Recently, we have demonstrated how a technique employing a graphical nomogram can be used to establish and validate a predictive model for the probability of achieving a VBAC after a TOL.⁷ The results of this approach suggested that it could be equally useful in establishing a predictive model for individual-specific risks of uterine rupture, and we attempted to develop such a model. In an effort to optimize the model, we incorporated patient characteristics that were available both at the initiation of prenatal care and at the time of admission to labor and delivery. However, this approach still failed to yield a model that could establish an accurate estimate of uterine rupture, and discriminate one woman from another with regard to this risk.

Our results echo those of Macones et al.⁶ Their methodology was somewhat different than ours, as they used a case-control design and evaluated a logistic regression only. Also, they included data from women with more than one prior cesarean delivery and women who were having a preterm delivery. By studying women at term with only one prior cesarean, we hoped that the greater homogeneity of the group and the reduced potential for variable interactions would enhance our model’s predictive accuracy. Nevertheless, our results were similar to theirs and confirm their findings. In both studies, the predictive models that were developed revealed prior vaginal delivery as a factor associated with a decreased risk of uterine rupture and labor induction as a factor associated with an increased risk of uterine rupture. The model of Macones et al also suggested that increasing maternal age was associated with an increased uterine rupture risk. Regardless of the similarities and differences, neither model could ultimately provide accurate prediction of this relatively uncommon event.

The inability of the present investigation to establish an accurate prediction model for uterine rupture raises the concern that such a model may not be achievable. We had the benefit of a data set that was gathered over 4 years at multiple academic sites with large delivery volumes. Such a collection of concurrently collected data, from women undertaking a TOL, is unlikely to be accumulated again. Also, we evaluated multiple types of statistical analyses (e.g. logistic regression, random forest analysis) to discern the optimal statistical basis for a model, and we utilized a technique that has a demonstrated ability to establish a usable predictive model for certain outcomes.

The difficulty in achieving a useful prediction model highlights the fact that associations between exposures and outcomes cannot always be translated into accurate prediction of these outcomes. Several authors, including in the present study, have demonstrated that multiple factors may be associated with uterine rupture.^1–5 Yet, because these associations are not of great magnitude and the occurrence of uterine rupture is relatively uncommon, these associations cannot be translated into accurate person-specific risks. As shown in the results of our analysis, although a “risk” can be calculated, this probability has a confidence interval that is so wide, and a potential deviation from the observed risk that is so large, that a truly accurate prediction is not achieved.

These results do not imply that a woman considering a TOL can be given no information regarding uterine rupture. The associations that do exist allow at least population-level insight into factors that may decrease or increase a woman’s risk for a uterine rupture. Yet, in contrast to the prediction of successful VBAC, these associations cannot be used to provide the accurate woman-specific probability of uterine rupture.

Appendix

The authors would like to thank the following people for their contribution to the manuscript: protocol/data management and statistical analysis (Elizabeth Thom, PhD and Sharon Gilbert, MS, MBA), protocol development and coordination between clinical research centers (Francee Johnson, BSN, Julia Gold BSN/APN), and manuscript oversight (Alan M. Peaceman, MD).

In addition to the authors, other members of the National Institute of Child Health and Human Development Maternal-Fetal Medicine Units Network are as follows:

• Ohio State University — J. Iams, F. Johnson, S. Meadows, H. Walker

• University of Alabama at Birmingham — J. Hauth, A. Northen, S. Tate

• University of Texas Southwestern Medical Center — S. Bloom, J. Gold, D. Bradford

• University of Utah — M. Belfort, F. Porter, B. Oshiro, K. Anderson, A. Guzman

• University of Chicago — J. Hibbard, P. Jones, M. Ramos-Brinson, M. Moran, D. Scott

• University of Pittsburgh — K. Lain, M. Cotroneo, D. Fischer, M. Luce

• Wake Forest University — P. Meis, M. Swain, C. Moorefield, K. Lanier, L. Steele

• Thomas Jefferson University — A. Sciscione, M. DiVito, M. Talucci, M. Pollock

• Wayne State University — M. Dombrowski, G. Norman, A. Millinder, C. Sudz, B. Steffy

• University of Cincinnati — T. Siddiqi, H. How, N. Elder

• Columbia University — F. Malone, M. D’Alton, V. Pemberton, V. Carmona, H. Husami

• Brown University — H. Silver, J. Tillinghast, D. Catlow, D. Allard

• Northwestern University — A. Peaceman, M. Socol, D. Gradishar, G. Mallett

• University of Miami, Miami, FL — G. Burkett, J. Gilles, J. Potter, F. Doyle, S. Chandler

• University of Tennessee — W. Mabie, R. Ramsey

• University of Texas at San Antonio — D. Conway, S. Barker, M. Rodriguez

• University of North Carolina — K. Moise, K. Dorman, S. Brody, J. Mitchell

• University of Texas at Houston — L. Gilstrap, M. Day, M. Kerr, E. Gildersleeve

• Case Western Reserve University — P. Catalano, C. Milluzzi, B. Slivers, C. Santori

• The George Washington University Biostatistics Center — E. Thom, S. Gilbert, H. Juliussen-Stevenson, M. Fischer

• National Institute of Child Health and Human Development — D. McNellis, K. Howell, S. Pagliaro