Abstract
Neuron-machine interfaces such as dynamic clamp and brain-implantable neuroprosthetic devices require real-time simulations of neuronal ion channel dynamics. Field Programmable Gate Array (FPGA) has emerged as a high-speed digital platform ideal for such application-specific computations. We propose an efficient and flexible component-based FPGA design framework for neuronal ion channel dynamics simulations, which overcomes certain limitations of the recently proposed memory-based approach. A parallel processing strategy is used to minimize computational delay, and a hardware-efficient factoring approach for calculating exponential and division functions in neuronal ion channel models is used to conserve resource consumption. Performances of the various FPGA design approaches are compared theoretically and experimentally in corresponding implementations of the AMPA and NMDA synaptic ion channel models. Our results suggest that the component-based design framework provides a more memory economic solution as well as more efficient logic utilization for large word lengths, whereas the memory-based approach may be suitable for time-critical applications where a higher throughput rate is desired.
Index Terms: FPGA, neuronal ion channel, dynamic clamp, brain-machine interface, neuroprosthetic device
I. Introduction
Real-time simulation of neuronal ion channel dynamics is an important step in the implementation of neuron-machine interaction, which is fundamental to several emerging neuromorphic and biomimetic applications. For example, in electrophysiological studies of neuronal membrane properties using the dynamic clamp technique [1] a digital computer is used to generate virtual ion channel conductances which continuously interact with a biological neuron in real time. Such software-based experimental applications are highly computation-intensive and often require judicious choice of operating systems [2] and/or numerical procedures [3] to improve the computational speed and flexibility. A hardware-based, application-specific implementation of the dynamic clamp technique would circumvent the limitations of general-purpose computers.
Another example of real-time neuronal ion channel dynamics computation is found in neuroprosthetic devices using brain-machine interface (BMI). For example, a robotic arm controlled by central brain activity has been shown to be capable of generating complex motions [4], and such capability may find important applications in patients with Parkinson's disease, essential tremor, dystonia, multiple sclerosis, muscular dystrophy and other motor dysfunctions [5]. Future applications of such neuroprosthetic devices might incorporate brain-implantable biomimetic electronics as chronic replacements for damaged neurons in central regions of the brain [6-8]. One such technology is neuromorphic analog VLSI circuits [9]. Towards this end, we have previously proposed a neuromorphic Hebbian synapse design using analog CMOS circuits operating in subthreshold regime [10, 11]. However, the relatively long design and fabrication cycles for analog CMOS circuits can be a bottleneck in the development of such devices.
In recent years, Field Programmable Gate Array (FPGA) technology has emerged as a high-speed digital computation platform [12]. The flexibility of the FPGA's programmable logic combined with its high-speed operation potentially allows it to control neuroprosthetic devices and dynamic clamp systems in real time. Additionally, FPGAs can be used to accelerate prototyping of analog hardware models of brain processes by quickly building a simulation platform to study the functional behavior of the proposed model in a much shorter design cycle. The applicability of FPGAs for neuronal ion channel dynamics simulation was first proposed in [13, 14]. Specifically, FPGAs offer an advantage of high-speed signal processing which could be orders of magnitude faster than software-based approaches to simulating biological neuronal signals. This technology can potentially be an effective prototyping tool or permanent platform for dynamic clamp experiments or neuroprosthetic device applications.
However, neuronal ion channel models involve computation-intensive functions which present a challenge for FPGA implementation. Currently, FPGA development toolkits do not always provide efficient build-in operators or basic building blocks for computation-intensive functions such as exponentiation and division. To circumvent this difficulty, a memory-based approach that stores the pre-computed function values in look-up tables was adopted in previous implementations [13] and expounded upon in [14-16]. This simple approach has a number of limitations that call for a more flexible and hardware-economical design methodology.
In this paper, we propose a component-based FPGA design framework for the modeling and simulation of ion channel dynamics. Under this framework, computational algorithms for exponentiation and division are implemented using FPGA digital logics [17] instead of look-up tables. These FPGA basic arithmetic components provide the computational primitives for constructing any ion channel models readily. In Section II, the background of neuronal ion channel dynamics and the alternative FPGA design approaches are reviewed. The component-based FPGA design framework is presented in Section III, where two design alternatives for achieving maximum speed or minimum resource consumption are introduced. Section IV illustrates this design approach with component-based FPGA implementations of the NMDA and AMPA excitatory synapse ion channel models. Section V concludes with a summary of the findings.
II. Background
A. Neuronal Ion Channel Models
The current Ii(t) flowing through an ion channel i at time t can be thought of as an ohmic relationship with a time-varying conductance gi(t) and membrane potential Vm(t):
| (1) |
where Ei is the reversal potential of the i-th ion channel. The time-varying conductance gi(t) can be modified accordingly to model voltage-dependent and ligand-dependent ion channels [18]. Computational intensive functions, such as exponential function and division, are frequently used in modeling the time-varying conductance.
The ion channel dynamics can be modeled by using first-order differential equation that captures the evolution of the membrane potential,
| (2) |
where Cm is the membrane capacitance, gleak is the leak conductance of the membrane patch, Vrest is the resting membrane potential, and ΣiIi(t) sums all the currents from different membrane ion channels.
B. Memory-based Versus Component-based Approaches
For the memory-based approach, key computational steps of the above neuronal models are pre-computed and stored in the FPGA internal memory such that during playback these values can be retrieved readily at a high rate [14, 16]. The ion channel equations are evaluated with predefined parameters and with a time increment that is indexed in the look-up table. There are two major advantages with memory-based model realizations: (i) small computational delay, and (ii) design simplicity. However, the simplicity and high-speed memory retrieval come with a cost, in that the size of the pre-computed look-up table grows exponentially with increasing accuracy and input resolution requirements. On-chip memory could be easily exhausted when dealing with large-scale neuronal models with multiple ion channels.
One obvious way to conserve memory is by decreasing the time and output resolutions. An efficient way of restoring time resolution is to use linear interpolation on 2n intervals between two stored values, say, yt and yt+1. By simply shifting the difference Δy = yt+1-yt leftward by n bits and then adding Δy to yt iteratively, the intermediate y values between yt and yt+1 can be approximated. Such an interpolation procedure requires only minimal additional FPGA logic hardware, namely a shifter and adder. An alternative way is by using the bipartite or multipartite table method in which two or more tables are introduced to reduce the required memory while improving the error bound [19]. Nevertheless, memory consumption is still a limiting factor when large-scale models with high resolution are involved.
In addition, with the memory-based approach it is difficult to change the model parameters in run-time. This is because all functions are pre-computed in advance assuming predefined parameters. This is a limitation for certain applications such as dynamic clamps, where the ability to modify parameters at run-time is highly desirable.
For the component-based approach, basic model functions such as exponentiation and division are evaluated with computational components and implemented using digital logics. Several algorithms are available for mapping these functions to FPGA embedded logics to form basic components [20, 21]. The requirement for on-chip memory can be greatly reduced with this approach. Further, model parameters can be adjusted and adapted in real time. This is because the model functions are evaluated directly at run-time using FPGA computational primitives. A drawback of the component-based approach is the latency overhead but the computation speed can be improved by introducing parallelism to the calculations.
Table I summarizes the differences between the memory-based and component-based approaches for neuronal ion channel model implementation. For the memory-based approach, large on-chip memory is required. For the component-based approach, there is a well balance between memory and logic resources utilization. For computational speed, the memory-based approach is generally faster than the component-based approach but the latter has a greater flexibility in allowing optimal tradeoff between speed and resource utilization. For scalability, availability of hardware resources would be the limiting factor for the memory-based approach with respect to improving resolution and model complexity. Lastly, since the model simulation results from the component-based approach is directly evaluated in run-time, this approach is more adaptable to changing parameter settings.
TABLE I. Summary of Memory-Based Versus Component-Based Approaches.
| Memory-based approach | Component-based approach | |
|---|---|---|
| Hardware resources | Requires additional logics and substantial memory storage | Reasonably balanced between logics and memory |
| Computational speed | Faster | Slower |
| Scalability | Exponential growth of memory with accuracy | Linear growth of both logics and memory |
| Flexibility | Fixed parameters only | Adaptable to new parameters at run-time |
| Ease of design | Easier | Integration of components |
III. Component-Based Approach
A. FPGA Design Flow
FPGA systems can be designed with high-level programming languages. Several commercial design platforms and environments provide automatic compilation of high-level programming languages, such as C, C++, Matlab, into FPGA digital logics. Alternatively, FPGAs can also be programmed by using VHDL or Java under a low-level design scheme. Readers are directed to [22] for a detailed survey on FPGA design flow. Our logic-level design makes extensive use of Xilinx's System Generator (SG) that works under MATLAB's Simulink environment [23]. The latter provides a schematic design environment of logic gate blocks which are used to implement the FPGA model. SG automatically synthesizes the Simulink model from the schematic design to a bit stream file, which can be readily used to configure the FPGA hardware. FPGA as a standalone simulation device can be properly interfaced with different kinds of software, such as MATLAB and LabView. Analog signals can be converted to digital by using an external Analog-to-Digital conversion (ADC) chipset before inputting to FPGA.
B. System Architecture
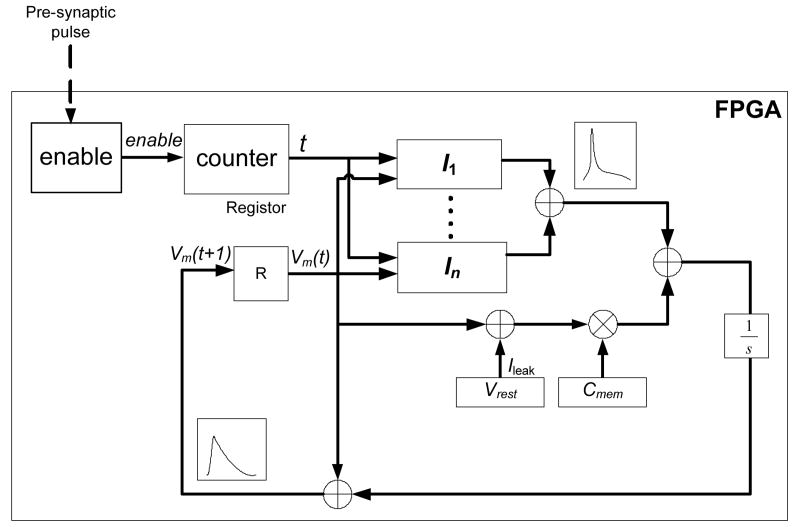
The basic equations (Eqs. 1-3) require iterative computations at each time increment (Δt), from t =0 with the given initial conditions. A common technique for realizing this time-increment requirement in FPGA design is to construct a counter block, to be triggered by an external ENABLE pulse (the rising edge of which defines the instant t=0). This approach can effectively mimic the time increment with little hardware needed. The trigger starts the counting at a frequency specified by the FPGA clock, and can be used to provide a steady stream of values of t at regular intervals for subsequent calculations.
Fig. 1 shows the data flow of an overall design with n ion-channel compartments. We use a register R to store the membrane voltage Vm. The membrane leak conductance is regulated by the differences between the membrane potential and the rest potential. The ion channel blocks run in parallel and generate the net membrane current. The accumulator (1/s) effectively models the conversion of electric charge into a voltage, acting as an R-C circuit emulating the effects of Cm and gleak.
Figure 1.
Dataflow diagram for ion channels dynamics simulations using FPGA.
C. Implementation of Exponentiation and Division Using Factoring Approach
FPGAs offer programmable on-chip logics, embedded multipliers and interconnect fabric. There are no readily adaptable hardware resources for the exponentiation (exp(X)) and division (Y/X) operations required for the neuronal ion channel models (Eqs. 1-2). Traditional software routines provide accurate evaluations of these functions given enough time for iterative operations. Most of these routines require repeated multiplicative operations, which are hardware resource expensive in digital logics. Alternatively, a hardware-efficient routine known as the factoring approach, or additive normalization, approximates the exponential and division functions successively with only shift-and-add operations [17, 20]. Specifically, multiplication of 2i, where i is an integer, would become simple i-bit shifting operations in digital logics, which are highly hardware-economical. Basic component or arithmetic units for exponentiation and division can be implemented with the factoring algorithm in a cost-effective manner (see Appendix).
D. Maximum Speed vs. Minimum Resource Consumption
FPGA hardware resources can be configured by the designer in various ways. Software support with a full-spectrum library of different granular entities (e.g., basic logic gates, flip flops, counters, multiplexers, adders, multipliers) is now widely available, along with a high-level hierarchical design platform and graphic interface. This helps tremendously our component-based modeling approach with flexible design options to achieve either maximum speed or minimum resource consumption.
To take full advantage of available hardware resources, functional operators may be executed in parallel in order to gain greater speed. This is known as the maximum speed design [24]. The drawback of this approach is that extra hardware resources are required. Alternatively, execution in a sequential order can reduce the required number of hardware operators, as some of them may be used for different operations at different time stamps. This minimum resource consumption design option is useful when hardware resources are scarce or when implementing large-scale or complex ion channel models. Table II compares the advantages and disadvantages between the maximum speed and minimum resource consumption schemes.
TABLE II. Summary of Maximum Speed Versus Minimum Resources Consumption.
| Maximum speed | Minimum Resources Consumption | |
|---|---|---|
| Hardware resources | More logics and arithmetic operators | Less logics and arithmetic operators |
| Computational speed | Faster | Slower |
| Scalability | Poorer | Better |
| Ease of design | Easier | Requires proper scheduling |
IV. Implementation Examples and Testing Results
In this section, we illustrate the above design principles with the FPGA-based modeling of two types of synaptic ion channels: N-methyl-D-aspartate (NMDA) and alpha-amino-3-hydroxy-5-methyl-4-isoxazole propionic acid (AMPA) receptor-gated ion channels (Fig. 2). Both ion channels are present in glutamatergic excitatory synapses and play an important role in synaptic plasticity such as long-term potentiation and depression [25-27]. AMPA channels, which carry the bulk of the excitatory synaptic current IAMPA(t), can be modeled by using Eqs. (1) and the time-varying conductance gAMPA(t) can be modeled by using an alpha function as follows [18]:
Figure 2.
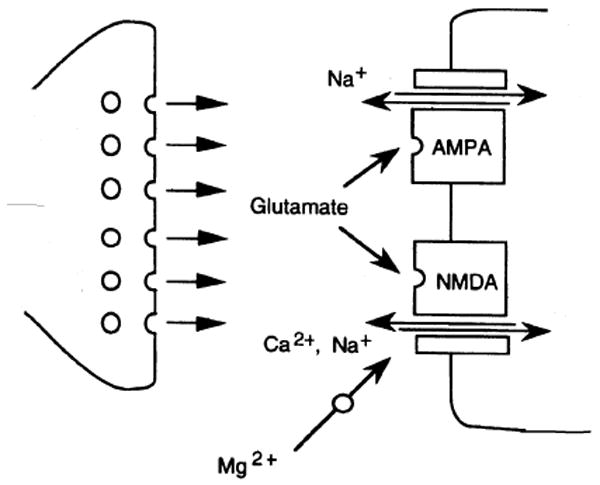
Biological synapse model with excitatory neurotransmitter glutamate activating AMPA and NMDA receptor gated ion channels to generate an excitatory postsynaptic potential (EPSP)
| (3) |
NMDA channels with excitatory current INMDA(t) are the major source of Ca+2 influx into the postsynaptic cell. They have the interesting property that their gating is jointly controlled by neurotransmitter binding and by a voltage-dependent blockage of the channel by Mg+2 ions. This bivariate gating function is characterized by the membrane reversal potential Esyn and other parameters:
| (4) |
where gn is the maximal channel conductance, τ1 and τ2 are the channel's activation and deactivation time constants, [Mg+2] is the extracellular magnesium concentration, η and γ are constants. Because of their unique dependence on both presynaptic and postsynaptic activation, NMDA channels are generally thought to be a biophysical implementation of the Hebbian adaptation rule [10, 25, 26, 28].
A. Component-Based FPGA Implementations of APMA and NMDA Ion Channel Models
For convenience of analysis, the binary operators for addition/subtraction, multiplication, division via FPGA logic hardware implementations are denoted as ⊕(x,y), ⊗(x,y), Ø(x,y), respectively; the unary operator for exponential is exp(x). Also, T⊗ refers to the latency for multiplication and Texp refers to the latency for exponentiation. Parallelization of independent processes Pi and Pj is denoted as Pi || Pj, such that processes Pi and Pj are independent.
Computing IAMPA(t): Using the above notations, Eqs. (1,3) for calculating IAMPA(t) may be rewritten as:
| (5) |
| (6) |
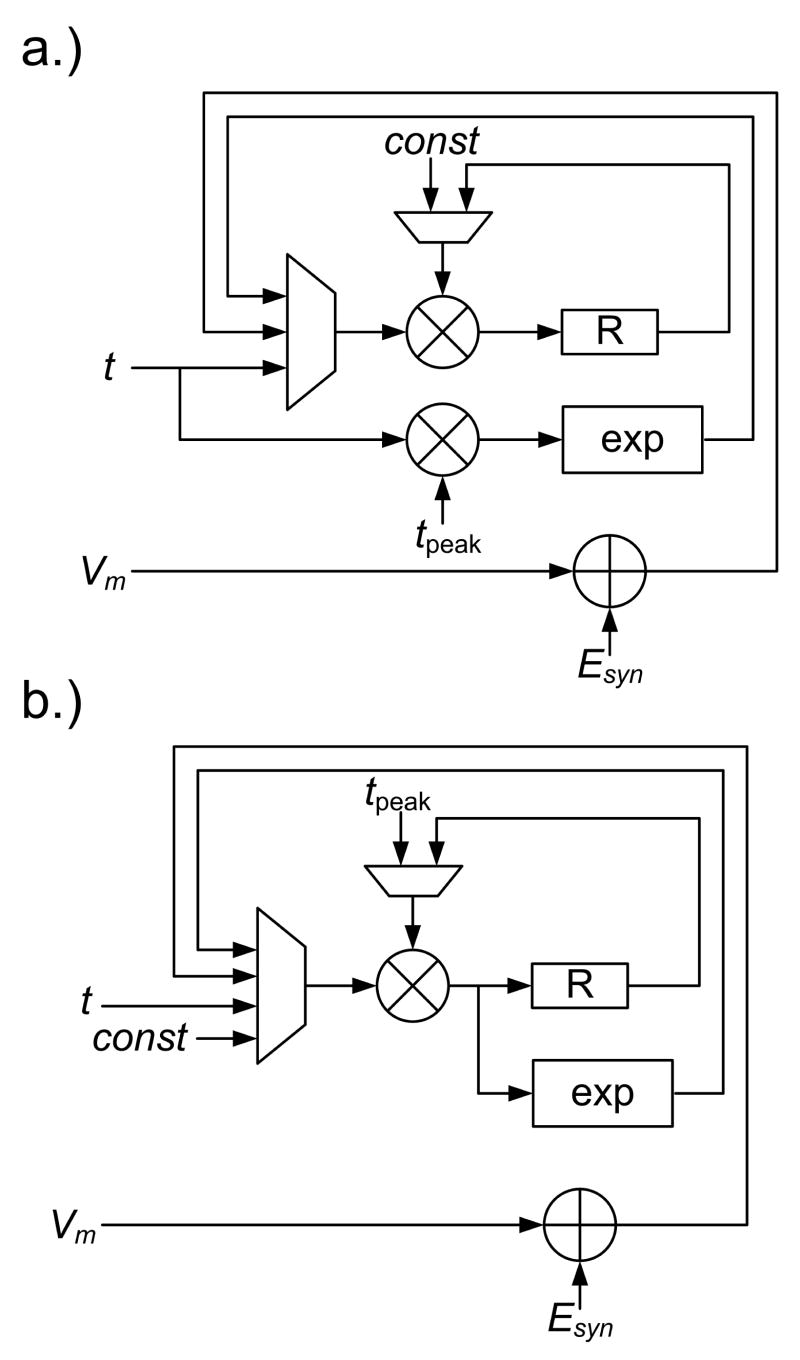
where Pi denotes the i-th independent process, which can be realized by using dedicated hardware resource. Fig. 3 shows the maximum speed (a.) and minimum resources consumption (b.) hardware mapping strategies for the implementation of Eqs. (5,6). For the maximum speed design, multiplications are parallelized to obtain the speed-up. Alternatively, multiplication operators are time-shared to conserve hardware resources. It is the designer's discretion to decide which approach is appropriate.
Figure 3.
Implementation of AMPA ion channel with (a) maximum speed and (b) minimum resource consumption approaches
Computing INMDA(t): Reformulating Eq. 4 for calculating INMDA(t) gives:
| (7) |
| (8) |
| (9) |
Table III compares the computational delay and resource requirements for the maximum speed and minimum resource consumption implementations of the IAMPA(t) and INMDA(t).
TABLE III. Theoretical Estimation of Computational Delay and Resources Consumption for the Maximum Speed and Minimum Resources Approaches.
| Maximum Speed | Minimum Resources Consumption | |||
|---|---|---|---|---|
| Function | Delay | Resources | Delay | Resources |
| AMPA | 3T⊗ + Texp | 2 ⊗ + exp+ ⊕ | 4T⊗ + Texp | ⊗ + exp +⊕ |
| NMDA | 3T⊗ +TØ +Texp+T⊕ | 4⊗+Ø+3exp+2⊕ | 7T⊗+TØ +3Texp +3T⊕ | ⊗+Ø +exp+⊕ |
| Vm | T⊗ + 2T⊕ | 2 ⊗ +3⊕ | 2T⊗ + 3T⊕ | ⊗ + ⊕ |
Table IV shows the experimental results for the tradeoffs between computational delay and resource consumption for these two design alternatives implemented on the Xilinx Virtex-II FPGA the Xilinx Virtex-II FPGA. The metric for computational delay is the number of clock cycles required to finish the task. For modern FPGAs, such as the Xilinx Virtex-II, dedicated multipliers and RAM are also embedded into the FPGA fabric, which can highly improve the computational efficiency. Therefore, counts of these three important hardware resources, (i) slice (or logics), (ii) RAM and (iii) multipliers become the metric of resources evaluation. The experimental results for the computational delay and resources binding for the memory and multipliers are generally in good agreement with the theoretical bounds. However, the number of binding multipliers are double that expected from the above theoretical analysis. This is because the evaluation of exponential functions itself requires a multiplier, which is not counted in the theoretical analysis. Addition and division are realized by using logic slices. It can be seen that the NMDA circuit requires substantially more logic units than the AMPA circuit, as predicted by the theoretical bound. Further, the computing speed for the maximum speed design is double the other design, while most of the logic slices requirements are 87% more than the other design.
TABLE IV. Experimental Results of Maximum Speed and Minimum Resources Approaches.
| format | Max speed | Min Resources Consumption | ||
|---|---|---|---|---|
|
| ||||
| AMPA | Time (clock cycles) | 8-bit | 21 | 30 |
| 16-bit | 27 | 38 | ||
|
| ||||
| Resourcesa | 8-bit | sl=228, rm=1, mu=4 | sl=160, rm=1, mu=2 | |
| 16-bit | sl=391, rm=1, mu=4 | sl=210, rm=1, mu=2 | ||
|
| ||||
| NMDA | Time (clock cycles) | 8-bit | 37 | 68 |
| 16-bit | 51 | 107 | ||
|
| ||||
| Resources | 8-bit | sl=1492, rm=3, mu=12 | sl=657, rm=1, mu=2 | |
| 16-bit | sl=1935, rm=3, mu=12 | sl=1002, rm=1, mu=2 | ||
sl is number of slices, which is the basic configurable logic unit in FPGA. rm is number of on-chip Block RAM (BRAM) and mu is number of embedded multipliers
B. Resources Utilization of Memory-based and Component-based FPGA Designs
Both the memory-based and component-based approaches require look-up tables of certain sizes which are mapped into FPGA internal memory, such as block RAMs (BRAMs). It is possible to use the number of BRAMs being occupied as a metric for memory consumption. However, the size of BRAMs varies for different FPGAs and technologies. For example, the Xilinx Virtex-II XC2V2000 has a total of 1008 kbits memory and each BRAM has 18 kbits. Greater BRAM capacity is now available for more powerful FPGAs such as Virtex-5 XC5VLX330, the latest from Xilinx's, with 10368 kbits. Alternatively, we can directly compare the sizes of the look-up tables in bits for each implementation use.
The size of a look-up table is dependent on both the word length (number of bits) of the output signal (L) and the required word length precision of the input (N). Both L and N may directly affect data precision and the quality of the computational results. We compare the sizes of look-up tables required for the two approaches by varying L and N. The comparison results are presented in Table V-VI, in which the numbers are in bits. The memory-based approach requires a much larger look-up table. The table size is two to three orders of magnitude more than the component-based approach. Also, its look-up table size increases exponentially with increasing N. This may be a problem for a moderate-size FPGA, i.e. Xilinx Virtex-II, which can only support a design with N up to 14 bits and L up to 12 bits, by exhausting all memory. In contrast, for the component-based approach the look-up table size increases linearly with both L and N. In this case, memory will not become a bottleneck as in the memory-based design.
TABLE V. Comparison of Memory Consumption for Memory-based and Component-based Approaches.
| Memory-Based | Component-Based | ||||
|---|---|---|---|---|---|
| N | NMDA | AMPA | NMDA | AMPA | |
|
| |||||
| L=8 | 4 | 256 | 128 | 96 | 32 |
| 8 | 4096 | 2048 | 192 | 64 | |
| 12 | 65536 | 32768 | 288 | 96 | |
| 14 | 262144 | 131072 | 336 | 112 | |
| 16 | 1048576 | 524288 | 384 | 128 | |
| 18 | 4194304 | 2097152 | 432 | 144 | |
|
| |||||
| L=12 | 4 | 384 | 192 | 144 | 48 |
| 8 | 6144 | 3072 | 288 | 96 | |
| 12 | 98304 | 49152 | 432 | 144 | |
| 14 | 393216 | 196608 | 504 | 168 | |
| 16 | 1572864 | 786432 | 576 | 192 | |
| 18 | 6291456 | 3145728 | 648 | 216 | |
L is the bit-length of the output values. N is the input resolution. Values are number of bits
TABLE VI. Comparison of Memory Consumption for Memory-based and Component-based Approaches.
| Memory-Based | Component-Based | ||||
|---|---|---|---|---|---|
| L | NMDA | AMPA | NMDA | AMPA | |
|
| |||||
| 4 | 2048 | 1024 | 96 | 32 | |
| 8 | 4096 | 2048 | 192 | 64 | |
| N=8 | 12 | 6144 | 3072 | 288 | 96 |
| 14 | 7168 | 3584 | 336 | 112 | |
| 16 | 8192 | 4096 | 384 | 128 | |
| 18 | 9216 | 4608 | 432 | 144 | |
|
| |||||
| 4 | 32768 | 16384 | 144 | 48 | |
| 8 | 65536 | 32768 | 288 | 96 | |
| N=12 | 12 | 98304 | 49152 | 432 | 144 |
| 14 | 114688 | 57344 | 504 | 168 | |
| 16 | 131072 | 65536 | 576 | 192 | |
| 18 | 147456 | 73728 | 648 | 216 | |
L is the bit-length of the output values. N is the input resolution. Values are number of bits
Another important on-chip resource is logic gates, each of which is realized using a 4-input look-up table known as slices. In contrast to look-up tables, the logic gates consumption is mainly dependent on the word length. The results are shown in Fig. 4. The memory-based approach consumes less logic slices than the component-based approach for word lengths smaller than 16. This is because more primitive logics are needed to realize the algebraic components in the component-based approach, whereas logics are required only for memory retrieval and proper scaling for the output in the memory-based approach.
Figure 4.
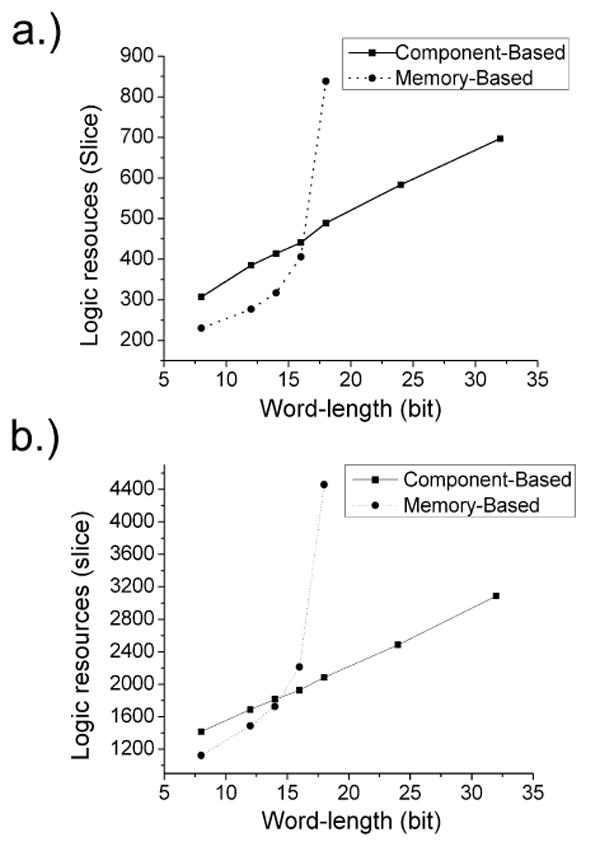
Comparison of logic consumption in terms of slice between memory-based and component-based approaches that logic slices are the basic configurable logic unit in FPGA. (a) Implementation of AMPA receptor (b) Implementation of NMDA receptor.
However, when the word length is longer than 16 bits (for the case of AMPA) and 14 bits (for the case of NMDA), logic slices consumption grows explosively for the memory-based implementation. This is because, to obtain such word length accuracy, a large look-up table is needed. A total of 256 and 1024 BRAMs are required for the AMPA and NMDA circuit, respectively. A large amount of logic units are also needed to construct the communication bus architecture and the necessary data representation conversion. For word lengths over 24 bit, the memory requirement is > 1Mbits, which represents a significant portion of FPGA embedded memory capacity currently available. On the other hand, logics usage for component-based approach increases linearly with increasing word length.
A well-known drawback of the component-based approach is the computation delay overhead. In the present design framework, the exponentiation and division operations require only addition and shifting operations, which are relatively economical time-wise. Still, when compared to the memory-based approach, which directly retrieves pre-computed results form RAM, the maximum speed component-based approach takes a longer time as reflected by the number of clock cycles needed (Table VII). The computational delay for the component-based approach depends on the word length, as more iteration loops are required for higher accuracy requirement. In contrast, memory retrieval time is not necessarily dependent on bit accuracy, as all signals are retrieved in parallel. Results show that the memory-based approach could be 3 to 4 times faster than the component-based approach.
TABLE VII. Comparison of Computational Delay for Memory-based and Component-based Approaches.
| Memory-Based | Component-Base | |||
|---|---|---|---|---|
| All-bit | 8-bit | 12-bit | 16-bit | |
|
| ||||
| AMPA | 8 | 15 | 19 | 23 |
| NMDA | 10 | 23 | 29 | 37 |
Values are the number of clock cycles to finish the functional evaluation
Specifically, since the FPGA is driven by a global clock signal, the computational speed of the model is dependent on the frequency of the digital clock f and the implementation strategy for the model equations. The amount of time it takes to evaluate the model equations can be expressed as p/f, where p is the number of clock cycles needed. For a Xilinx Virtex-II XCV2000 FPGA, the maximum frequencies for the memory-based and component-based approaches are 70 MHz and 68 MHz respectively due to differences in signal flow critical paths. The model using the memory-based approach requires 4950 clock cycles to generate an output, which means that each presynaptic pulse generates a postsynaptic signal in 70.7 μs. For the component-based approach, the model requires 18315 clock cycles or equivalently, 269.3 μs to generate a postsynaptic signal. Software computation of the model equations on a Pentium-4 desktop computer with 2.8 GHz clock rate takes ∼4.7 ms, making FPGA faster by 66 and 17 times with the memory-based and component-based approaches respectively.
Overall, the component-based model provides a more memory economic solution, as well as more efficient logic utilization for large word lengths (> 16). Although there is a cost in computational delay for the arithmetic evaluations, the savings in hardware resources may be critical for model scaling. Thus, multiple ion channel models may be simulated in parallel on one chip without overshooting either the memory or logic slice limit. In contrast to multiplexing, which switches different inputs and outputs and reuses the same logics, parallel implementation could better utilize the available input/output ports for higher performance. On the other hand, the memory-based approach may be suitable for time-critical applications where a higher throughput rate is desired.
C. Simulation Results
Fig. 5 shows the comparison between biological recordings (EPSCs) mediated by either NMDA channels alone or both AMPA and NMDA channels in a cultured hippocampal neuron from a neonatal rat. The FPGA simulation results from the memory-based approach and the maximum speed component-based approach both adequately mimicked in real time the actual NMDA and AMPA currents from the experimental data in [29]. Both memory-based and component-based approaches adopt a 16-bit output resolution. Especially, memory-based is with 8-bit addresses resolution. However, close-up views of both simulation curves (Fig. 5c, d) reveal significant truncation errors from the memory-based approach (but not the component-based approach) when compared to a reference curve generated by using a simulation software with floating point precision on a digital computer. The truncation errors are attributed to the limited resolution of the lookup table Next, we used double precision floating point arithmetic as a reference to systematically evaluate the relative errors of both FPGA approaches, defined as the normalized errors averaged (±standard deviations) for the first 5000 time stamps of the simulation runs for: (i) component-based approach (Comp) with 16-bit input and output; (ii) memory-based approach (Mem8) with 8-bit memory address and 16-bit output; (iii) memory-based (Mem14) with 14-bit memory address and 16-bit resolution. Fig. 6 shows the relative errors of the three implementations for varying tpeak and τ1, which are parameters in Eqs. (3,4), respectively. For tpeak> 600 or τ1 > 600 the relative errors of Mem8 and Mem14 are much larger than Comp. The relative error of Comp increased with tpeak but decreased with τ1. This is because when tpeak increases, the AMPA current will decrease and hence the relative error will increase for a given truncation error, whereas the NMDA current increases with τ1. For Mem8, there were large variances in the relative errors for the AMPA simulation but not the NMDA simulation, the reason being that AMPA current is very sensitive to tpeak while NMDA current is less sensitive to τ1.
Figure 5.
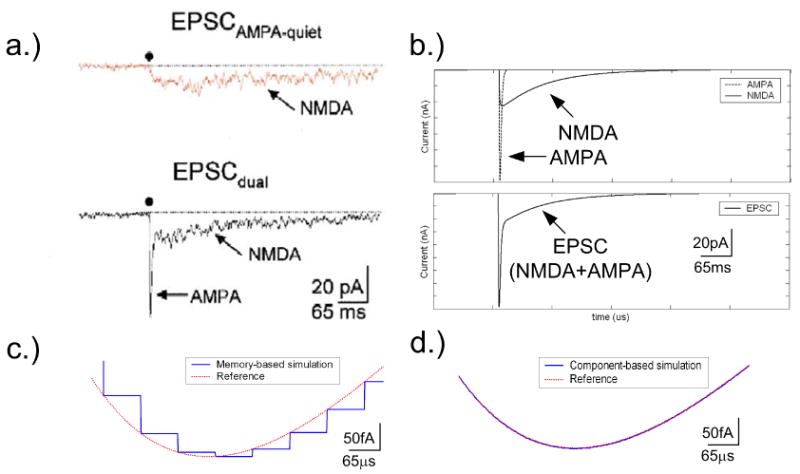
(a) Biological recording of individual NMDA channels and excitatory postsynaptic currents (EPSCs) from AMPA and NMDA channels. (Data adapted from [29] with permission.) (b) Simulation of FPGA circuits for the EPSCs from AMPA and NMDA channels separately (upper panel) and together (lower panel). Both memory-based and component-based approaches show nearly identical results which are qualitatively similar to the experimental data in (a). (c) Close-up view for the simulation results with the memory-based approach. (d) Close-up view of the simulation results with the component-based approach.
Figure 6.
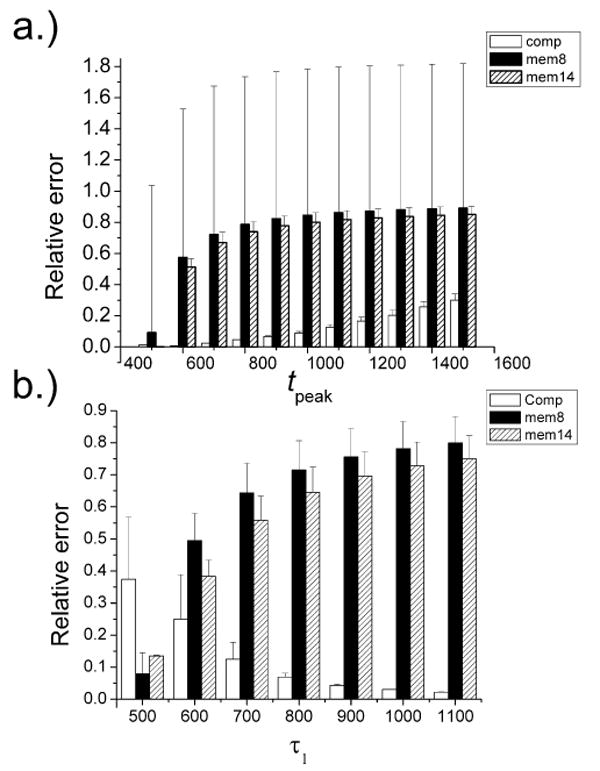
(a) Normalized error for AMPA computation for different tpeak. (b) Normalized error for NMDA computation for different τ1.
V. Conclusion
A component-based FPGA design framework for digital simulation of neuronal ion channel dynamics has been presented. The FPGA realization computes with comparable accuracy as digital computer implementations while operating at much higher speeds. The programmability and high-speed capability of the FPGA system allow it to prototype analog circuit designs with a much shorter design cycle. The proposed component-based design strategy overcomes the inflexibility and memory limitations of the memory-based design approach. This technology can potentially be used as a valuable tool for dynamic clamp experiments or for controlling neuroprosthetic devices, or for chronic replacement of damaged neurons in central regions of the brain in future.
Acknowledgments
This work was supported in part by NIH grant EB005460. T. Mak was a recipient of a US Office of Naval Research Global travel award and a Croucher Foundation scholarship. G. Rachmuth was a recipient of a US National Defense Science and Engineering Graduate Fellowship.
VI. Appendix
A. Exponentiation Using Factoring Approach
Consider exponentiation function eX, which can be approximated by product of n factors with judicious choice of sj, such that
| (10) |
where X ≥ 0 and sj ε {0,1}.
Suppose we have a table storing log(1+2-j) for j=0,1,2,…,n. Thus, sj can be determined by comparing Xj and log(1+2-j) for all j=0,1,2,…,n. If Xj is larger than log(1+2-j) for some j, sj will be one and otherwise sj will be zero. Successively, the product term will converge to eX. The algorithm is shown as follows
The input domain of factoring algorithm assumes that X ε (0,1.38]. It is necessary to reformulate the exp function to fit the input number range of the neuronal modeling. For the ion channel models, the input X for exp function is -t/τ, which is a negative number. A method is needed to transform the input into an acceptable domain for factoring algorithm.
By rearranging the index term, the exp function can be formulated as a product of two terms. One of the terms can be simply evaluated by multiplications of constant and the other is with input at the acceptable domain of factoring algorithm. We let X equals to −A−B, where A, B are positive integers. Therefore, we have
| (11) |
Since A is an integer, the first term, e-A-1 can be evaluated by simple multiplications. The second term can be evaluated by using factoring algorithm, as 1–B is a positive number less than one.
In addition, the comparison between look-up-table and factoring approaches for eX is shown in Table VIII. The mean and standard deviation of their corresponding normalized error are shown that the floating point exponentiation function from Matlab is used as a reference. The column address is the memory addresses resolution in bits and the iteration column is the number of operation cycles of the algorithm.
TABLE VIII. Table-look-up (LUT) and Factoring (Fact) Approaches.
| Address (bit) | Iteration (cycle) | Error (mean) | Error (std) | |
|---|---|---|---|---|
| Fact | 14 | 14 | 3.07e-5 | 1.76e-5 |
| Fact | 16 | 16 | 7.72e-6 | 4.39e-6 |
| Fact | 20 | 18 | 4.87e-7 | 2.75e-7 |
| LUT | 28 | - | 3.34e-4 | 2.02e-4 |
| LUT | 210 | - | 3.79e-5 | 5.06e-5 |
| LUT | 214 | - | 3.62e-6 | 3.16e-6 |
Solutions from the Matlab build-in functions are used as references for the error computation of the LUT and FACT methods
B. Division Using factoring Approach
Factoring is also an effective approach for division approximation, such as (Y/X) [17]. Division can be considered as a reciprocal computation, as reciprocal is a special case of division with (Y=1). Similar to the exponentiation, division can be formulated as product of n factors as follows,
| (12) |
where sj = -1. Similarly, the algorithm approximates the reciprocal with successive evaluation of partial results, .
Eventually, pj·X converges to one, while pj converges to Y/X. The algorithm is shown as follows
Factoring Algorithm for Exponentiation.
| 1 | x0=X, y0=1, g(i)=log(1+2-i), i=1,2,…,n | ||
| 2 | for i=1 to n | ||
| 3 | a = xi – g(i) | ||
| 4 | if a > 0 | ||
| 5 | xi+1 = a | ||
| 6 | yi+1 = yi + yi·2-i | ||
| 7 | else | ||
| 8 | xi+1 = xi | ||
| 9 | yi+1 = yi | ||
| 10 | end if | ||
| 11 | end for | ||
Factoring Algorithm for Division.
| 1 | x0=X, y0=1, i=1,2,…,n | ||
| 2 | for i=1 to n | ||
| 3 | a = xi - xi·2-i | ||
| 4 | if a > 1 | ||
| 5 | xi+1 = a | ||
| 6 | yi+1= yi - yi·2-i | ||
| 7 | else | ||
| 8 | xi+1 = xi | ||
| 9 | yi+1 = yi | ||
| 10 | end if | ||
| 11 | end for | ||
Contributor Information
Terrence S. T. Mak, Department of Systems Engineering & Engineering Management, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong. (Current address of T. Mak: Department of Electrical and Electronic Engineering, Imperial College, London, UK.)
Guy Rachmuth, Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, USA..
Kai-Pui Lam, Department of Systems Engineering & Engineering Management, The Chinese University of Hong Kong, Shatin, N.T., Hong Kong..
Chi-Sang Poon, (corresponding author; e-mail: cpoon@mit.edu) Harvard-MIT Division of Health Sciences and Technology, Massachusetts Institute of Technology, Cambridge, MA, USA..
References
- 1.Sharp AA, O'Neil MB, Abbott LF, Marder E. Dynamic clamp: computer-generated conductances in real neurons. Journal of Neurophysiology. 1993;69:992–995. doi: 10.1152/jn.1993.69.3.992. [DOI] [PubMed] [Google Scholar]
- 2.Dorval AD, Christini DJ, White JA. Real-Time linux dynamic clamp: a fast and flexible way to construct virtual ion channels in living cells. Annals of biomedical engineering. 2001;29:897–907. doi: 10.1114/1.1408929. [DOI] [PubMed] [Google Scholar]
- 3.Butera RJ, McCarthy ML. Analysis of real-time numerical integration methods applied to dynamic clamp experiments. Journal of Neural Engineering. 2004;1:187–194. doi: 10.1088/1741-2560/1/4/001. [DOI] [PubMed] [Google Scholar]
- 4.Taylor DM, Tillery SIH, Schwartz AB. Direct Cortical Control of 3D Neuroprosthetic Devices. Science. 2002;296:1829–1832. doi: 10.1126/science.1070291. [DOI] [PubMed] [Google Scholar]
- 5.Isaacs RE, Weber DJ, Schwartz AB. Work toward real-time control of a cortical neural prothesis. IEEE Trans Rehabil Eng. 2000;8:196–8. doi: 10.1109/86.847814. [DOI] [PubMed] [Google Scholar]
- 6.Berger TW, Baudry M, Brinton RD, Liaw JS, Marmarelis VZ, Park AY, Sheu BJ, Tanguay AR., Jr Brain-implantable biomimetic electronics as the next era in neuralprosthetics. Proceedings of the IEEE. 2001;89:993–1012. [Google Scholar]
- 7.Simpson M, Sayler G, Patterson G, Nivens E, Bolton E, Rochells J, Arnott J, Applegate B, Ripp S, Guillorn M. An integrated CMOS microluminometer for low-level luminescence sensing in the bioluminescent bioreporter integrated circuit. Sensors and Actuators B. 2002;72:134–140. doi: 10.1016/s0925-4005(00)00641-9. [DOI] [PubMed] [Google Scholar]
- 8.Song YK, Patterson WR, Bull CW, Beals J, Hwang N, Deangelis AP, Lay C, McKay JL, Nurmikko AV, Fellows MR, Simeral JD, Donoghue JP, Connors BW. Development of a chipscale integrated microelectrode/microelectronic device for brain implantable neuroengineering applications. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2005;13:220–226. doi: 10.1109/TNSRE.2005.848337. [DOI] [PubMed] [Google Scholar]
- 9.Mead CA. Neuromorphic electronic systems. Proceedings of the IEEE. 1990;78:1629–1636. [Google Scholar]
- 10.Rachmuth G, Poon CS. Design of a neuromorphic Hebbian synapse using analog VLSI. presented at Neural Engineering, 2003. Conference Proceedings. First International IEEE EMBS Conference on; Capri, Italy. 2003. [Google Scholar]
- 11.Rachmuth G, Poon CS. Design of a neuromorphic Hebbian synapse using analog VLSI. presented at First International IEEE EMBS Conference on Neural Engineering; Capri, Italy. 2003. [Google Scholar]
- 12.Cheung PYK, Constantinides GA, deSousa JT. Introduction: Field Programmable Logic and Applications. IEEE Transactions on Computers. 2004;53:1361–1362. [Google Scholar]
- 13.Graas EL, Brown EA, Lee RH. An FPGA-Based Approach to High-Speed Simulation of Conductance-Based Neuron Models. Neuroinformatics. 2004;2:417–436. doi: 10.1385/NI:2:4:417. [DOI] [PubMed] [Google Scholar]
- 14.Mak TST, Rachmuth G, Lam KP, Poon CS. Field Programmable Gate Array Implementation of Neuronal Ion Channel Dynamics. presented at The 2nd International IEEE EMBS Conference on Neural Engineering; 2005. [Google Scholar]
- 15.Weinstein RK, Lee RH. Design of High Performance Physiologically-Complex Motoneuron Models in FPGAs. presented at The 2nd International IEEE EMBS Conference on Neural Engineering; 2005. [Google Scholar]
- 16.Weinstein RK, Lee RH. Architectures for high-performance FPGA implementations of neural models. Journal of Neural Engineering. 2006;3:21–34. doi: 10.1088/1741-2560/3/1/003. [DOI] [PubMed] [Google Scholar]
- 17.Ercegovac MD, Lang T. Digital Arithmetic. Morgan Kaufmann; 2004. [Google Scholar]
- 18.Koch C, Segev I. Methods in Neuronal Modeling: From Ions to Networks. MIT Press; 1998. [Google Scholar]
- 19.Schulte MJ, Stine JE. Approximating Elementary Functions with Symmetric Bipartite Tables. IEEE Transactions on Compututers. 1999;48:842–847. [Google Scholar]
- 20.Chen CY, Chen RL. Pipelined Computation of Very Large Word-Length LNS Addition/Subtraction with Polynomial Hardware Cost. IEEE Transactions on Computers. 2000;49:716–726. [Google Scholar]
- 21.Mencer O, Semeria L, Morf M, Delosme JM. Application of Reconfigurable CORDIC Architectures. The Journal of VLSI Signal Processing (Special Issue on Reconfigurable Computing) 2000 [Google Scholar]
- 22.Todman TJ, Constantinides GA, Wilton SJE, Mencer O, Luk W, Cheung PYK. Reconfigurable Computing: Architectures, Design Methods, and Applications. IEE Proceedings on Computers and Digital Techniques. 2005;152:193–207. [Google Scholar]
- 23.Hwang J, Milne B, shirazi N, Stroomer J. System Level Tools for DSP in FPGAs. presented at 11th International Conference on Field-Programmable Logic and Applications; 2001. [Google Scholar]
- 24.Dehon A, Wawrzynek J. Reconfigurable computing: what, why, and implications for design automation. presented at Design Automation Conference; 1999. [Google Scholar]
- 25.Kitajima T, Hara K. A model of the mechanisms of long-term potentiation in the hippocampus. Biological Cybernetics. 1990;64:33–39. doi: 10.1007/BF00203628. [DOI] [PubMed] [Google Scholar]
- 26.Zador A, Koch C, Brown TH. Biophysical model of a Hebbian synapse. Proceedings of the National Academy of Sciences USA. 1990;87:6718–6722. doi: 10.1073/pnas.87.17.6718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhou Z, Champagnat J, Poon CS. Phasic and long-term depression in brainstem nucleus tractus solitarius neurons: differing roles of AMPA receptor desensitization. The Journal of Neuroscience. 1997;17:5349–56. doi: 10.1523/JNEUROSCI.17-14-05349.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hebb D. The Organization of Behavior. New York: Wiley; 1949. [Google Scholar]
- 29.Renger JJ, Egles C, Liu G. A Developmental Switch in Neurotransmitter Flux Enhances Synaptic Efficacy by Affecting AMPA Receptor Activation. Neuron. 2001;29:469–484. doi: 10.1016/s0896-6273(01)00219-7. [DOI] [PubMed] [Google Scholar]