Importance of Tensor Asymmetry for the Analysis of ²H-NMR Spectra from Deuterated Aromatic Rings

Abstract

We have used ab initio calculations to compute all of the tensor elements of the electric field gradient for each carbon-deuterium bond in the ring of deuterated 3-methyl-indole. Previous analyses have ignored the smaller tensor elements perpendicular to principal component V_zz which is aligned with the C-²H bond (local bond z-axis). At each ring position, the smallest element V_xx is in the molecular plane and V_yy is normal to the plane of the ring. The asymmetry parameter η = (|V_yy|-|V_xx|)/|V_zz| ranges from 0.07 at C4 to 0.11 at C2. We used the perpendicular (off-bond) tensor elements, in concert with an improved understanding of the indole ring geometry¹, to analyze prototype ²H-NMR spectra from well-oriented, hydrated peptide/lipid samples. For each of the 4 tryptophans of membrane-spanning gramicidin A (gA)² channels, the inclusion of the perpendicular elements changes the deduced ring tilt by nearly 10° and increases the ring principal order parameter S_zz for overall ‘wobble’ with respect to the membrane normal (molecular z-axis). With the improved analysis, the magnitude of S_zz for the outermost indole rings of Trp¹³ and Trp¹⁵ is indistinguishable from that observed previously for backbone atoms (0.93 ± 0.03). For the Trp⁹ and Trp¹¹ rings, which are slightly more buried within the membrane, S_zz is slightly lower (0.86 ± 0.03). The results show that the perpendicular elements are important for the detailed analysis of ²H-NMR spectra from aromatic ring systems.

Introduction

Solid-state NMR methods permit investigations of liquid-crystalline lipid/protein systems using uniaxially oriented samples³ and/or unoriented samples⁴. Dynamic as well as structural information can be deduced from the spectra of appropriately labeled samples⁵. For example, the orientations and dynamics of the symmetric aromatic rings of Phe and Tyr can be characterized^6-9. The asymmetric indole ring of Trp is of particular interest as a membrane-anchoring residue^10,11 and has been investigated^1,12,13 using ¹³C, ¹⁵N and ²H labels. In this article, we refine the analysis of the ²H quadrupole spin interaction for each relevant position on a ²H-labeled indole ring.

The ²H quadrupolar spin interaction is due to electrostatic interaction between the deuterium nuclear quadrupole moment and the electric field gradient at the deuterium nucleus. Because deuterium has a large quadrupole coupling constant and a small gyromagnetic ratio, the deuterium resonance is determined largely by the quadrupole interaction. The electric field gradient is characterized by a symmetric second rank tensor. As the tensor trace does not affect the spectra, it is usually given in the traceless form, V_xx+V_yy+V_zz=0, with |V_xx|<|V_yy|<|V_zz|. In an appropriately chosen coordinate system the field gradient tensor is diagonal. In aromatic systems including the indole ring, the local principal axis z is approximately along the C-²H bond, y is perpendicular to the plane of the ring and x is in the ring plane⁶, perpendicular to both y and z. Corresponding to the approximate cylindrical nature of the C-²H bond, the tensor components V_yy and V_xx are roughly equal, and smaller in absolute value than the axial component V_zz. The deviation from strict cylindrical symmetry (V_yy=V_xx) is characterized by the asymmetry parameter η, defined as (|V_yy|-|V_xx|)/|V_zz|. For an aliphatic C-²H bond, η is expected to be close to zero due to the approximate cylindrical symmetry of the bond. For methyl groups (C-²H₃), η should be negligible for a different reason: the rapid methyl rotation⁷. For aromatic C-²H bonds, η is not necessarily negligible, due to the markedly different electronic structure in the ring plane and perpendicular to it. Nevertheless, it has been generally assumed that η is quite small and often η has been ignored. For a phenyl ring, Opella and coworkers⁶ measured an average η of 0.05 for the uniformly deuterated ring of phenylalanine at 100 K.

Recently¹ we reported a need for a refined geometry for the planar indole ring, with specific attention to the C2-²H bond direction, when interpreting solid-state ²H-NMR spectra. Our earlier study revealed that considerations of the indole ring geometry were important to determine consistent orientation parameters for the indole ring. When the indole's C2-²H bond direction was corrected by 5.8°, based upon a close agreement between ab initio calculations and experimental data¹, it was found that the analytical fits to typical observed spectra for labeled Trp indole rings were much improved—such that the rms deviations between observed and calculated ²H-quadrupolar splittings around a ring were, for the first time, as low as the inherent uncertainties of the experimental measurements themselves. With a correct refined indole ring geometry in hand, it seemed prudent to revisit the question of non-zero values of the asymmetry parameter of the electric field gradient tensor η that has been neglected in most prior work, including ours. At the same time it was possible to assess the extent of alignment of V_zz with the C-²H bond direction. In this article, we present ab initio calculations of not only the axial component of the electric field gradient tensor V_zz , but also of the perpendicular components V_xx and V_yy, for each relevant C-²H bond on a deuterated 3-methyl indole ring. Ab initio calculations are well suited to determine electric field gradients that are typical one-electron quantities, if proper attention is paid to the basis set. The cost of these calculations, which formerly was a major deterrent to their use, is now insignificant. We will address two questions: First, is the assumption that the principal axis of the electric field gradient is aligned with the C-²H bond correct? Second, how large is the asymmetry parameter η, and how important is it in determining the orientation of the indole ring? We will show that the first assumption is valid. However, the asymmetry parameter is not negligible. The perpendicular tensor elements lead to values of η that range from 0.07 at C4 to 0.11 at C2 of the indole ring. As proof of principle, we use the off-bond (perpendicular) tensor elements to analyze the ²H quadrupolar splittings for each of the four Trp indole rings of membrane-spanning gramicidin channels (whose sequence is formyl-VGALAVVVWLWLWLW-ethanolamide, with D-residues underlined). The main finding is that the rings exhibit even less motional libration than previously thought. Concerning the ring orientations, the main effect relates to a ring's rotational tilt about an in-plane axis normal to the ring bridge. The inclusion of the theoretically computed electric field gradient asymmetry parameters is important for correct interpretation of deuterium NMR spectra with respect to the average orientations and principal order parameters of Trp indole rings in membrane-spanning proteins.

Materials and Methods

Ab initio calculations

All ab initio calculations were performed with the PQS suite of programs¹⁴. The geometry of the 3-methyl indole was optimized at the B3LYP/6−311G** level, i.e. using density functional theory with Becke's 3-parameter exchange correlation functional¹⁵ and the polarized triple zeta 6−311G** basis set of Pople and coworkers¹⁶. This level of theory is quite accurate for the geometries of rigid organic molecules¹⁷. Electric field gradients are fairly sensitive properties, and we have calculated them by larger basis sets: the 6−311++G(2df,2pd) basis, augmented with a set of compact (exponent=6 a₀⁻²) p polarization functions on the hydrogens. In the Pople nomenclature, this is denoted as B3LYP/6−311++G(2df,2pd)//B3LYP/6−311G** (method/basis set for the property//method/basis set for the geometry). To approach the basis set limit, we used the aug-cc-pVTZ basis¹⁸, further augmented by compact p (exponent 5.1) and d (exponent 4.5) functions on the hydrogens. We denote this basis as aug+cc-pVTZ; it contains 739 contracted basis functions for 3-methyl-indole. For the aug+cc-pVTZ calculations, we have optimized the geometry at the B3LYP/6−311G(2df,2pd) level.

NMR spectroscopy

Samples of gA that incorporate a single partially or fully labeled tryptophan indole ring were synthesized on a 0.1 mmole scale as previously described¹⁹, using 5-fold molar excess of the labeled or unlabeled amino acids. Oriented samples of specifically ²H-labeled gA in hydrated DMPC (1/10 to 1/40 molar ratio of peptide/lipid) were prepared on glass plates, and NMR spectra were recorded according to earlier methods¹. The spectra have been presented previously^13,20, and the spectral assignments have been established using selectively labeled Trp rings¹.

Indole ring geometry and orientation analysis

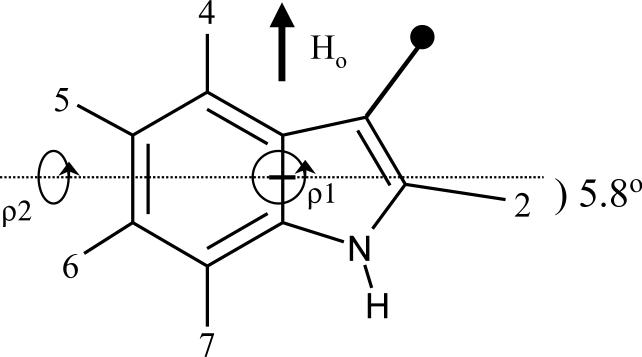
In a recent work, we refined the geometry of the indole ring using ab initio calculations. Our main finding was that the C2-²H bond makes an angle of about 6° with the normal to the C8-C9 bridge (Figure 1)¹. Based upon this ring geometry, the quadrupolar splittings from ²H-NMR spectra of labeled Trp indole ring side chains were analyzed using a method which is independent of any information or assumptions concerning the polypeptide backbone conformation¹. In this method, a hypothetical “free” indole ring, whose assigned ²H-NMR spectrum is known, is first aligned with its bridge parallel to the external magnetic field, H₀ (Figure 1). For comparisons with the observed spectra, the two rotation angles ρ₁ and ρ₂ in Figure 1 serve to tip the ring through all possible orientations with respect to H₀.

Figure 1.

3-Methyl-indole ring geometry and rotational degrees of freedom ρ₁ and ρ₂ for orienting the ring with respect to an external magnetic field H₀. The positions of deuteration are numbered. A critical geometrical feature is the 5.8° angle of the C2-²H bond with respect to the normal to the ring bridge¹.

In addition to the static description of the C-²H bond orientations, dynamics are important. In the case of a gramicidin channel spanning a liquid-crystalline lipid bilayer, gA undergoes rapid reorientation (on the NMR timescale) around an axis that is perpendicular to the membrane plane. The molecular long axis (helix axis, or molecular z-axis) is approximately aligned with the axis of rapid global molecular reorientation. The dynamic extent of (mis)alignment between the molecular z-axis and the membrane normal is characterized by the time average S_zz = <3cos²α − 1>/2 where α is the instantaneous angle between these two directions. The quadrupolar splittings associated with the C-²H bonds will be influenced by fluctuations (wobbling) of the orientation of the molecular z-axis, combined with other more localized motions, here expressed in terms of the (motional) order parameters S_zz, S_yy, and S_xx.

As a ring is rotated, the variation of the calculated deuterium quadrupolar splitting for each deuteron is expressed by the equation^20,21:

$$\Delta {\nu }_{\mathrm{q}}=(3∕8)(e^{2}qQ∕h)[{\mathrm{S}}_{\mathrm{zz}}(3{\cos }^2\theta -1)+\eta \left({\mathrm{S}}_{\mathrm{xx}}\text{-}{\mathrm{S}}_{\mathrm{yy}}\right)\left({\sin }^2\theta \right)\left(\cos 2{\rho }_2\right)](3{\cos }^2\beta -1)$$ (1)

in which e²qQ/h is the static C-²H quadrupolar coupling constant (QCC; ∼180 kHz for aromatic deuterons⁶); θ is the angle between a C-²H bond and the average direction of the molecular z axis (the membrane normal); β is the angle between the membrane normal and the magnetic field, H₀; ρ₂ is the angle between the ring plane and the magnetic field, defined in Figure 1; and η is the asymmetry parameter, η = (|V_yy|-|V_xx|)/|V_zz| in the local coordinate system of a C-²H bond; ref.6,13,21,22. In a previous analysis¹, η was assumed to be zero.

Using a zero-value asymmetry parameter, the principal order parameter S_zz has been found to be 0.93 ± 0.03 for backbone atoms at numerous positions along the gramicidin sequence^22-26. This would also represent an upper limit to the motion experienced by the side-chain indole rings. The significant, but generally smaller, contribution to the quadrupolar splitting associated with the non-zero asymmetry parameter has a different sensitivity to the motion: (S_xx – S_yy). Individual values for S_xx and S_yy can range from −0.5 to 1.0 and, for the planar indole ring, are likely to be quite different from each other. We examined a range of values of (S_xx – S_yy) for each of the four rings and found that an estimated value of 1.1 for the difference (S_xx – S_yy) was a reasonable compromise which could fit data for all of the rings. With the aim of not ‘over fitting' the experimental data, the quantity (S_xx – S_yy) was therefore fixed at 1.1 in calculations for all rings. For each indole ring, values of (ρ₁, ρ₂) and S_zz were then determined which gave the best fit to the ensemble of quadrupolar splittings representing all of the ring C-²H bonds.

Results and discussion

For polycrystalline ring-(²H)₅ labeled phenylalanine at 100 K, the measured static quadrupolar coupling constant (e²qQ/h) is ∼180 kHz, and the average η is 0.05 for the five ring positions⁶. A somewhat lower average η of 0.037 was measured for ring-labeled Phe-d₅ at 300 K. In part because of the low η values measured for Phe, the asymmetry parameter has largely been ignored in the analysis of ²H-NMR spectra from labeled indole rings^13,20,27,28. We now fill this void, with the present report of the position-dependent values of η based on ab initio calculations for a 3-methyl-indole ring.

In Table 1 we show the calculated principal values of the tensor elements as a function of the position of each deuteron in the 3-methyl-indole ring. The exact tensor orientations are not given because the local x (ring plane) and y (normal to the ring) directions are fixed by symmetry, and the local z direction practically coincides with the C-²H bond direction. (The angle between the two is negligible, less than 0.05°). The results obtained using the modest 6−311G** basis are not shown; the effect of enlarging the basis set to the augmented 6−311++G(2df,2pd) set is noticeable, and consists mainly in a uniform 4−7 % decrease of the absolute magnitudes of the field gradients, and therefore of the quadrupole coupling constants. Going to the large aug+cc-pVTZ basis diminishes the electric field gradients further by about 3 %. Because of the almost uniform scaling, the calculated asymmetry parameters, which range from 0.07 to 0.11, change less than 0.002 when going from the 6−311G** to the 6−311++G(2df,2pd) basis, and less than 0.003 when going further to the augmented aug+cc-pVTZ basis. We have tested several popular exchange-correlation functionals, and have found that they produce values that are quite close to each other. Non-hybrid functionals produce field gradients that are systematically 1−2 % higher than the B3LYP values for 3-methyl-indole. When converted to the kHz scale (see below), the average quadrupolar coupling constant is ∼200 kHz at the B3LYP/6−311++G(2df,2pd)//B3LYP/6−311G** level, and 194 kHz at the B3LYP/aug+cc-pVTZ//B3LYP/6−311G(2df,2pd) level; i.e. the calculations overestimate quadrupolar coupling by 7−10 %. The conversion factor can be derived from the quadrupole moment of the deuteron²⁹, eQ = 2.86×10⁻³¹ m² e = 4.582×10⁻⁵⁰ Cm² (e = elementary charge), and the atomic unit of the electric field gradient, 1 au = e(4πε₀)⁻¹a₀⁻³ = 9.71736×10²¹ Vm⁻², yielding (eQ×au/h) = 672.0 kHz (h = Planck's constant); i.e. the quadrupole splitting ν is related to the V_zz component of the traceless electric field gradient as ν/kHz = 672.0 (V_zz/au). This is the same factor used by Gerber and Huber³⁰.

Table 1.

Electric field gradient tensor elements for 3-methyl-indole^a.

Ring Position	Vxx (perpendicular to bond, in plane)	Vyy (normal to ring)	Vzz (along C-2H bond)	η
2	−0.1357	−0.1678	0.3037	0.106
	−0.1310	−0.1633	0.2943	0.110
4	−0.1380	−0.1586	0.2966	0.069
	−0.1335	−0.1534	0.2869	0.069
5	−0.1371	−0.1608	0.2979	0.080
	−0.1326	−0.1557	0.2883	0.080
6	−0.1373	−0.1600	0.2973	0.076
	−0.1330	−0.1550	0.2880	0.076
7	−0.1365	−0.1610	0.2975	0.082
	−0.1321	−0.1558	0.2879	0.082

^aIn atomic units, 1 au = 1 e(4πε₀)⁻¹a₀⁻³ = 9.71736×10²¹ Vm⁻².

Top row: B3LYP/6−311++G(2df,2pd)//B3LYP/6−311G** values; bottom row: B3LYP/aug+cc-pVTZ//B3LYP/6311F(2df,2pd) values. See Methods. The asymmetry parameter (η) is calculated as (|V_yy|−|V_xx|)/|V_zz|. The local principal axis z is aligned in all cases to within 0.05° with the C-²H bond.

To understand the origin of the discrepancy, we compare our quadrupole coupling constants for a few small molecules (Table 2) with the results of Gerber and Huber³⁰, and also with more recent density functional theory (B3LYP) results of Bailey³¹, and with experiment. Gerber and Huber use a method very different from ours: fourth-order Møller-Plesset perturbation theory (MP4) versus density functional theory (DFT). Their molecular geometry is also different. For consistency, we used geometries optimized at the B3LYP/6−311G(2df,2pd) while Gerber and Huber do not define the geometries, except that they are “experimental” (presumably microwave r_s values). In spite of this, their raw results are remarkably close to ours.

Table 2.

Calculated deuterium quadrupole coupling constants (kHz) for small molecules.

Molecule	Method Aa	Method Bb	MP4c	B3LYPd	Expt.c
H2O	316.2	304.5	320.3		307.9
	−138.6	−132.6	−139.3		−133.1
	−177.6	−171.9	−180.9		−174.8
HF	355.6	346.8	363.0		354.2
CH4	196.0	190.2	197.6		191.5
HCCH	223.6	217.1	224.2		203.5±10
HCCCN	219.7	213.0	225.4		203.5±1.5
C6H6	198.4	192.1(187.6)e		202.9(192.2)	186.1±1.8f
	−92.5	−89.6(−88.1)e		−95.8(−90.7)	−88.9±2.3f
	−105.9	−102.5(−99.6)e		−107.2(−101.5)	−97.2±2.3f
	η=0.068	η=0.067(0.061)e		η=0.056	η=0.046±0.017

^aB3LYP/6−311++G(2df,2pd)//B3LYP/6−311G**, this work (method/basis set for the property//method/basis set for the geometry).

^bB3LYP/aug+cc-pVTZ//B3LYP/6−311G(2df,2pd), this work.

^cGerber and Huber³⁰. Note that different basis sets were used for H₂O, HF and CH₄ and the other two molecules.

^dBailey³¹, B3LYP/6−31G(df,3p)//experiment. The numbers in parentheses are the scaled values.

^eValues in parentheses have been corrected for zero-point vibrational effects; see Results and discussion.

^fJans-Bürli et al.³⁷. Our calculations confirm that these authors interchanged the x and y components of the tensor; this table shows the correct assignment. Bürgi et al.³⁸ obtain a value near 180 kHz for the zz component in solid C₆D₆; re-analyzing the data of Pyykkö and Lähteenmäki³⁹ also yields 179.3±2.8 kHz.

The systematic overestimation of quadrupole coupling constants by ab initio calculations was noted by Gerber and Huber³⁰ and Bailey³¹, both of whom achieved predictive accuracy by treating the quadrupole moment of the deuterium nucleus, eQ/h, as a fitting parameter, in effect scaling the calculated values. The adjusted value of eQ/h is close to 636 kHz/au in both references30,31, corresponding to a scale factor of 0.946. The deviation is strongest for π systems such as acetylene and benzene. Gerber and Huber³⁰ and Bailey³¹ attribute this deviation to the combined effects of basis set truncation, limited treatment of electron correlation, and neglect of vibrational averaging. Our results confirm that larger, more flexible basis sets indeed lead to somewhat smaller absolute electric field gradients. Nevertheless, even very large basis sets overestimate the quadrupole coupling for unsaturated systems; indeed calculations with still larger basis sets than the extended aug+cc-pVTZ (not shown) prove that the latter basis set reaches the basis set limit. It is unlikely that the incomplete treatment of electron correlation is responsible, as correlation has only a minor effect on the calculated electric field gradients³⁰, and it generally increases the magnitude of the quadrupole coupling. The overestimation of the quadrupole coupling constants for acetylenes has been noticed earlier by Gerber and Huber³⁰, who excluded these molecules from their scale factor refinement.

In our opinion, the residual discrepancy is clearly a zero-point vibrational effect. C-H bending vibrations, in particular the out-of-plane ones, have low frequencies and consequently high mean-square amplitudes in unsaturated systems. The field gradient tensor is essentially aligned with the C-²H bond, even at distorted geometries, and thus the perpendicular bending vibrations uniformly lower the absolute magnitudes of the principal components. The role of vibrations is also indicated by the fact that Bailey's scaled values for benzene (which are almost the same as our large basis set results without scaling) still show significant discrepancy compared to experiment; cf. Table 2. We have calculated the bending force constants of benzene at the B3LYP/6−311++G(3df,3pd) level, and from this the ²H perpendicular mean-square amplitudes in deuterobenzene. A simple model was used that assumed that the masses of the C atoms are infinite; i.e. the benzene skeleton was frozen. The root-mean-square amplitudes were 0.098 Å in the molecular plane and 0.120 Å perpendicular to the plane. Combined with the calculated dependence of the space-fixed field gradient tensor elements on the mean-square amplitudes, the following corrections to the quadrupole couplings were obtained (in kHz): for the zz (axial) component, −4.46; for the xx (in-plane) component 1.53; for the yy (out-of-plane) component, 2.93. When the vibrational corrections are applied to our best calculation, the corrected calculation of η agrees with experiment for benzene within the rather large error limits of the latter. After applying the vibrational correction, the calculated quadrupole coupling constants of benzene agree with experiment within the error bounds of the latter (± 2 %), as shown in Table 2. The vibrational correction should be quite similar in all aromatic systems, and therefore we have no reason to question the experimental quadrupolar coupling constant of ∼180 kHz for aromatic systems. Nevertheless, more accurate experiments would be a welcome challenge to theoretical calculations.

The data in Table 2 show that both basis set truncation and vibrational corrections manifest themselves mainly as a uniform scaling of the quadrupole coupling constants, justifying the empirical method used by Gerber and Huber³⁰ and Bailey³¹, although it appears that vibrational effects may lower the asymmetry parameter slightly. The uniform scaling also means that we can use the calculated asymmetry parameters directly, without going through the tedious correction procedure for vibrational effects.

It is of interest to compare the asymmetry parameters for the para C4 and C7 deuterons. In the refined indole ring¹, the angle between the C4-H and C7-H bonds is 179.5°. Thus, with their principal V_zz elements nearly (anti)parallel, one would expect almost identical quadrupolar splittings for deuterons at these two ring positions. Yet, in the spectra for some Trp indole rings, one observes often a “twinning” of the C4/C7-²H resonances into slightly different signals¹³. Most likely, this is caused by the notable difference in the asymmetry parameters, namely η = 0.069 at C4 and η = 0.082 at C7 (Table 1). Including the different asymmetry parameters in the model is consistent with the observed spectra.

Figure 2 shows one of the characteristic ²H-NMR spectra, this one representing d5-Trp¹⁵, as reported earlier¹³, in gA channels that are oriented within hydrated bilayers of DMPC. The signals from the C4 and C7 deuterons are closely similar, both having quadrupolar splittings in the range from 0−2 kHz.

Figure 2.

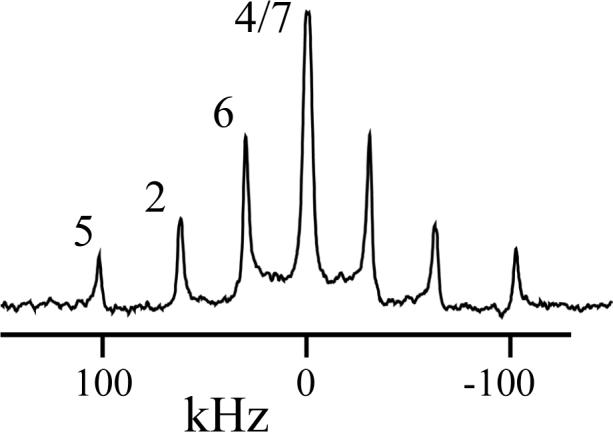
Example ²H NMR spectrum, with resonance assignments, for d₅-Trp¹⁵ gramicidin A in hydrated liquid crystalline bilayers of DMPC at 40 °C; peptide/lipid, 1/20.

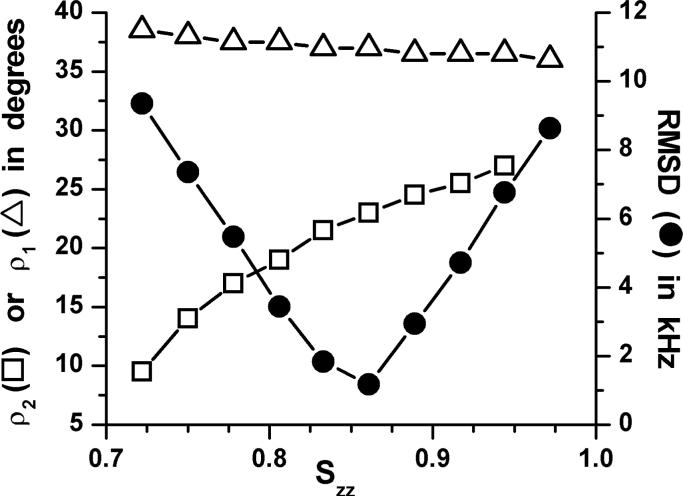
We incorporated the asymmetry parameters from Table 1 into our previous analysis¹. In Figure 3 we show results for the Trp⁹ indole ring. The best fit occurs when S_zz = 0.86, an increase from S_zz of 0.80 in the previous analysis without the asymmetry parameter¹. When S_zz is optimum (giving the minimum rmsd), the effect of a non-zero η on ρ₁ is negligible, representing only a change from 37.5° to 37.0° for Trp⁹. The effect on ρ₂ is larger, a change from 18°, when η is zero, to 23° when the calculated non-zero values of η are used.

Figure 3.

Graph to show the variation of the best-fit ring orientation angles ρ₁ and ρ₂, and the value of the corresponding rmsd-minimum, as functions of S_zz for the Trp⁹ indole ring.

The trends observed for Trp⁹ hold true also for the other tryptophans that anchor membrane-spanning gramicidin channels. The best-fit values of ρ₁, ρ₂ and S_zz when using non-zero η parameters for all of the tryptophans are shown in Table 3. The differences in each parameter, compared to the previous best fits when η was uniformly set to zero¹, are listed in Table 4. One notes again that the changes in ρ₁ are small, and that ρ₂ and S_zz increase for each of the rings when the non-zero η's are included.

Table 3.

Principal order parameters and revised average orientations with respect to the bilayer membrane normal when using non-zero η parameters from Table 1 for Trp 9, 11, 13 and 15 indole rings of gA channels^a.

Trp	ρ1	ρ2	Szz	Minimum rmsd (kHz)
9	37.0°	23.0°	0.86 ± 0.03	1.14
11	46.0°	23.5°	0.86 ± 0.04	0.66
13	46.5°	27.0°	0.93 ± 0.03	1.87
15	50.5°	30.5°	0.91 ± 0.03	2.00

^aThe angles ρ₁ and ρ₂ (Figure 1) were searched in 0.5° increments, while S_zz was searched in increments of 0.006. The rmsd values correspond to the global minima (comparing observed and calculated quadrupolar splittings). The listed tolerance for S_zz represents the range of S_zz yielding rmsd less than 3.0 kHz.

Table 4.

Influence of non-zero asymmetry parameters upon indole ring orientations and principal order parameters for tryptophans in gA channels^a.

Trp	Δρ1	Δρ2	ΔSzz
9	−0.5°	+5.0°	+0.06
11	+1.0°	+7.5°	+0.06
13	−1.5°	+8.5°	+0.05
15	−1.0°	+5.0°	+0.05

^aThe changes were determined by comparing the values of ρ₁, ρ₂ and S_zz in Table 3, obtained using the calculated values of η (Table 1; above), with those previously obtained assuming η = zero (Table 4 of ref #¹). The main insights from the nonzero η values are that the rings are somewhat more tilted in ρ₂ than would otherwise be determined, and the rings exhibit even less 'wobble' motion with respect to the bilayer normal (higher S_zz) than would be deduced if η were zero.

Figure 4 provides a comparison of the revised values of S_zz for two of the rings, Trp¹³ and Trp⁹, with the known S_zz of 0.93 for backbone carbon and nitrogen atoms in the gramicidin channel²³, illustrated by the dashed line. In Figure 4, it is evident that the best-fit S_zz for each ring increases when using the non-zero values of η (closed circles), compared to the fits when all η's are set to zero (open triangles). Indeed, the revised values of S_zz for Trp¹³ (Figure 4) and Trp¹⁵ (Table 3), are remarkably similar to S_zz of the peptide backbone itself. For Trp⁹ and Trp¹¹ , the ring S_zz of ∼0.86 (Figure 4 and Table 3) is slightly lower than the backbone value of 0.93 (yet higher than the earlier estimate¹ of 0.80).

Figure 4.

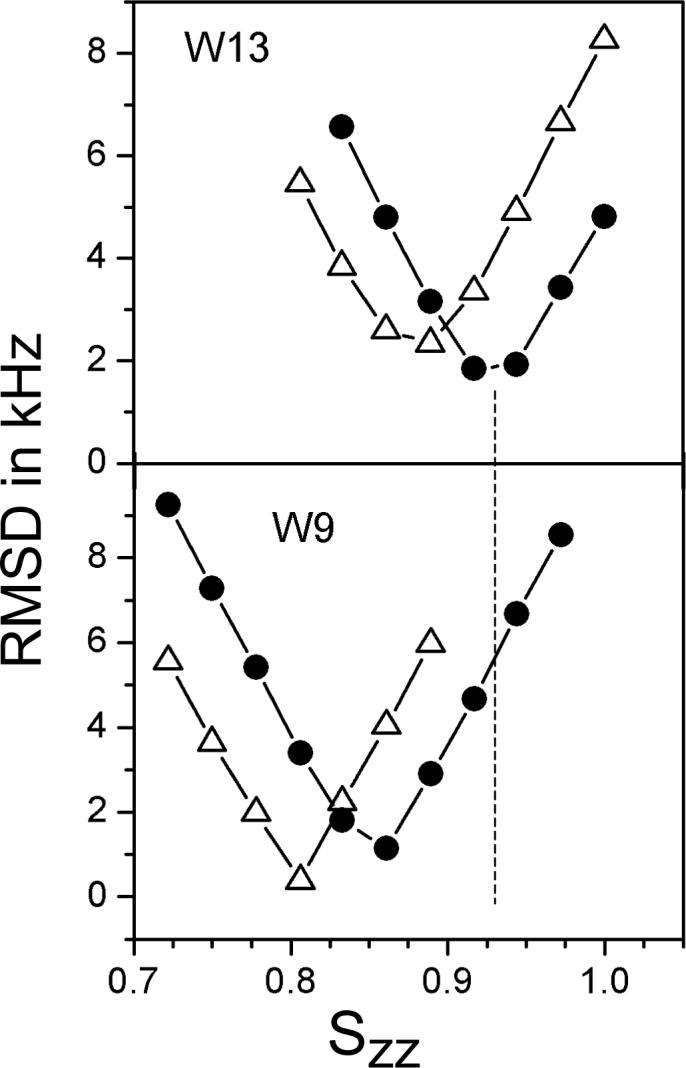
Graph to show the global minimum rmsd for Trp⁹ (W9) and for Trp¹³ (W13) of gA channels as functions of S_zz when each asymmetry parameter η is set to zero ( Δ ); and when using the calculated η values from Table 1 ( • ). The dashed line indicates the value of S_zz = 0.93 for backbone atoms²³.

Each subunit of a membrane-spanning gramicidin channel is anchored by four Trp indole rings, which seek energetically favorable interactions at the membrane/water interface¹⁰. Successive replacements³² of individual Trps with Phe, or dispersing the subunits in very thick lipid bilayers (having acyl chains longer than 20 carbons)³³, serve to destabilize the canonical single-stranded channel conformation³⁴ in favor of other double-stranded conformations^32,33. In the channel conformation, the average orientations of these four Trp indole rings with respect to the membrane normal are all quite similar and can now be defined with increased precision. The inclusion of non-zero η values, calculated independently at each ring position (Table 1), leads to the deduction that each of the rings is more tilted than previously calculated, namely by an additional 5−8° in ρ₂ (Tables 3-4). In Figure 5, we show the relative tilt of each of the membrane-anchoring Trp indole rings of the gA channel with respect to the membrane normal.

Figure 5.

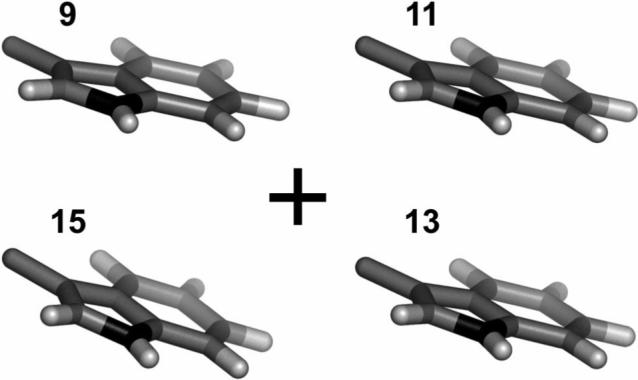
End view showing the revised average orientations, with respect to a membrane surface, for the Trp indole rings 9, 11, 13 and 15 of the gramicidin A channel, looking down a lipid bilayer membrane normal (denoted by “+”). The revised ring orientations are more tilted than the earlier estimated orientations (figure 7 from ref. 1), which did not account for the asymmetry of the off-bond tensor elements.

In addition to being somewhat more tilted, each ring also fluctuates less from its average orientation with respect to the bilayer normal than was deduced previously. Indeed the rings of Trp¹³ and Trp¹⁵ exhibit the same principal order parameter as does the peptide backbone itself (Table 3). In addition to interactions at the interface, the motions of this “outer pair” of Trp indole rings could be constrained by the β-helical peptide backbone conformation and by packing interactions with one (Trp¹⁵) or two (Trp¹³) adjacent D-Leu side chains. It is therefore plausible that Trp indole rings on an α-helical backbone could be less contrained. Nevertheless, it seems that the interface itself places distinct constraints upon the ring motions, because the “inner pair” of Trp⁹ and Trp¹¹ rings exhibit slightly greater motional freedom, with S_zz values of 0.86 (Table 3). These “inner” rings are also bounded by bulky side chains of D-Leu and D-Val, yet are marginally more distant from the interface than are Trp¹³ and Trp¹⁵. Trp⁹ also populates a different rotameric state than do the other tryptophans^35,36.

A “wobble” of the entire transmembrane channel about the membrane normal influences S_zz for the backbone and side chains similarly. The “outer” Trp¹³ and Trp¹⁵ indole rings are essentially devoid of additional local motions, while the “inner” Trp⁹ and Trp¹¹ rings exhibit relatively minor additional motions. This pattern represents a small yet discernible difference in ring dynamics. Given that the neighboring lipid molecules are highly dynamic, the manner in which interfacial anchoring interactions “should” influence the ring dynamics is not immediately apparent. (It is also conceivable that the “inner” residue 9 and 11 peptide planes could be less ordered than are the “outer” 13 and 15 peptide planes, and that such a difference would propagate to the side chains. Against this idea, however, are the findings of nearly identical backbone order at a large number of sequence positions^22-26. In this analysis of the side-chain dynamics, we have focused on the principal S_zz values for each tryptophan. The limited amount of experimental data prevented a complete analysis of (S_xx – S_yy).)

In summary, we have calculated the tensor elements of the electric field gradient for each carbon-deuterium bond in the ring of deuterated 3-methyl-indole, with particular attention to the off-bond tensor elements. Considerations of the asymmetry parameters (η values) for each of the ring C-²H bonds have modest yet important implications for understanding the motions and average orientations of the Trp indole rings that anchor membrane-spanning gramicidin channels.

Abbreviations

DMPC

dimyristoylphosphatidylcholine

gA

gramicidin A.