Sulfur K-edge XAS and DFT calculations on superoxide reductase: Role of the axial thiolate in reactivity

Abstract

Superoxide reductase (SOR) is a non-heme iron enzyme which reduces superoxide to peroxide at a diffusion-controlled rate. Sulfur K-edge x-ray absorption spectroscopy (XAS) is used to investigate the ground state electronic structure of the resting high-spin and CN⁻ bound low-spin Fe^III forms of the 1Fe SOR from Pyrococcus furiosus. A computational model with constrained Imidazole rings (necessary for reproducing spin states), H-bonding interaction to the thiolate (necessary for reproducing Fe-S bond covalency of the high-spin and low-spin forms) and H-bonding to axial ligand (necessary to reproduce the ground state of the low-spin form) was developed and then used to investigate the enzymatic reaction mechanism. Reaction of the resting ferrous site with superoxide and protonation leading to a high-spin Fe^III-OOH species and its subsequent protonation resulting in H₂O₂ release is calculated to be the most energetically favorable reaction pathway. Our results suggest that the thiolate acts as a covalent anionic ligand. Replacing the thiolate with a neutral non-covalent ligand makes protonation very endothermic and greatly raises the reduction potential. The covalent nature of the thiolate weakens the Fe^III bond to the proximal Oxygen of this hydroperoxo species, which raises its pK_a by an additional 5 log units relative to a primarily anionic ligand facilitating its protonation. A comparison with Cytochrome P450 indicates that the stronger equatorial ligand field from the porphyrin results in a low-spin Fe^III-OOH species which would not be capable of efficient H₂O₂ release due to a spin-crossing barrier associated with formation of a high spin 5C Fe^III product. Additionally, the presence of the di-anionic porphyrin π ring in Cytochrome P450 allows O-O heterolysis forming a Fe^IV-oxo porphyrin radical species, which is calculated to be extremely unfavorable for the non-heme SOR ligand environment. Finally the 5C Fe^III site which results from the product release at the end of the O₂⁻ reduction cycle is calculated to be capable of reacting with a second O₂⁻ resulting in superoxide dismutase (SOD) activity. However in contrast to FeSOD the 5C Fe^III site of SOR which is more positive is calculated to have a high affinity for the binding a 6^th anionic ligand which would inhibit its SOD activity.

INTRODUCTION

The enzyme superoxide reductase (SOR) is found in microaerophilic and strictly anaerobic microorganisms and is capable of reducing superoxide to peroxide.^{1, 2, 3, 4,5} Though its in vivo function is not completely understood, it is thought to provide a mechanism for combating oxidative stress in anaerobes, which typically lack the classical superoxide dismutases (SOD), by depleting superoxide concentration via direct reduction to hydrogen peroxide, rather than by a dismutation reaction which produces H₂O and O₂. ⁶ Thus, unlike SOD, SOR does not accumulate dioxygen in these high anoxic microorganisms. The crystal structure of the resting oxidized form of the 1Fe-SOR from Pyrococcus furiosus (Fig. 1) shows that the ferric active site has a non-heme iron coordinated to four histidines in the equatorial plane and a cysteine and glutamate in the trans-axial positions.⁷ There are two peptide N–H---SCys H-bonds to the axial cysteine ligand. Both 1Fe and 2Fe SOR’s have been characterized and found to have similar active site structures and reactivities.^{8, 9} The second Fe in the 2Fe SOR is in a rubredoxin-like Fe(SCys)₄ site for which the function is unknown as eliminating it by mutation does not affect the reactivity of this enzyme.⁹

Fig. 1.

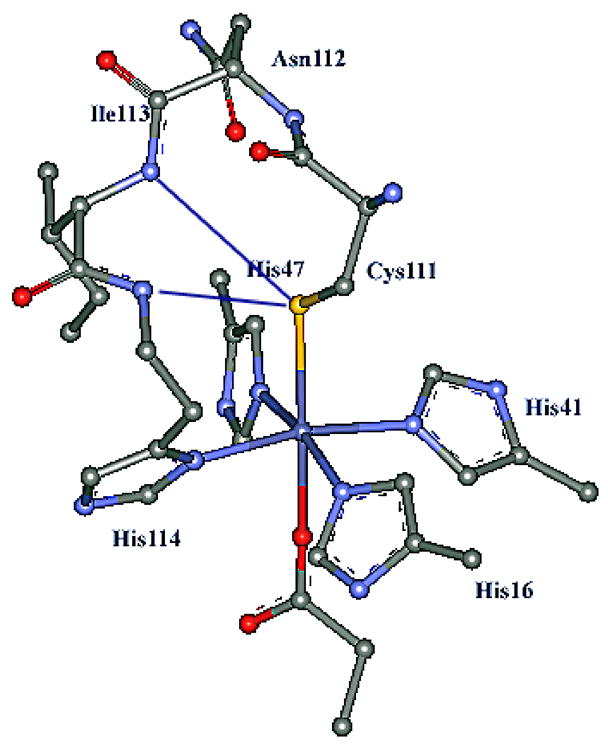
Active site of SOR from P. furiosus at 1.7 Å resolution (pdb:1DQI).⁷ Residues Ile113 and Asn112 are in the vicinity of the active site and proposed to H-bond to the Cys111 thiolate.

The resting oxidized form of 1Fe P. furiosus SOR has been spectroscopically characterized in detail by Clay et. al.^{10, 11} It has a high-spin ground state and an intense CysS⁻ → Fe^III charge transfer (CT) band at 15100 cm⁻¹ (ε ~2500 M⁻¹cm⁻¹) which gives it its characteristic blue color. The EPR spectrum of the high-spin resting state indicated that it is quite axial (E/D = 0.06) and VTVH MCD indicated that a trans N_His-Fe-N_His axis defined the unique direction of the ZFS tensor and not the trans S_Cys-Fe-O_Glu axis.¹⁰ This site is solvent exposed and binds exogenous ligands such as N₃⁻ and OH⁻ in place of the glutamate. Binding CN⁻ converts it to a low-spin site with an intense CysS⁻ → Fe^III CT at 14600 cm⁻¹ (ε ~2700 M⁻¹cm⁻¹).¹⁰

The reaction mechanism of SOR, involving transfer of an electron and two protons to superoxide to form hydrogen peroxide, has been studied in detail using kinetic and spectroscopic techniques.^{12, 13, 14, 15, 16, 17,18} Using kinetic data, Nivière et al. and Kurtz et al. have proposed the presence of at least one Fe^III intermediate (henceforth referred to as intermediate I, characterized by a CT band at 600 nm) in the reaction. The formation of the intermediate was diffusion controlled and had no pH dependence or deuterium isotope effect and thus was proposed to be an Fe^III-μ₂-O₂²⁻ species. The decay of this intermediate involved a diffusion controlled protonation from its pH dependence and a deuterium isotope effect of 2. Lys 14 has been identified as a participating 2^nd sphere residue (mutation of this residue decreases the turnover rate by a factor of 20–30) and has been proposed to assist superoxide binding to the active site.^{19, 20} Though no intermediate has been trapped with the physiological substrate superoxide, Olivier et. al. have trapped and characterized (using EPR, resonance Raman, Mössbauer spectroscopy and DFT calculations) a high-spin (S=5/2) side-on η²-O₂²⁻-Fe^III species by addition of H₂O₂ to the resting Fe^II form of the enzyme.^{21, 22} The relevance of such species in the turnover cycle of SOR is still an issue.²³

A computational study has used DFT to investigate the ground state and has considered possible intermediates along the reaction pathway.¹⁷ The study successfully reproduced most of the geometric parameters and spin state of the experimentally observed high spin ferrous and ferric ground state and concluded that a low-spin Fe^III-OOH is the best candidate for the Intermediate I. A subsequent protonation driven H₂O₂ release from this low-spin Fe^III-OOH was proposed, though the energetic feasibility of such steps were not evaluated.¹⁷ Kovacs et. al. ²⁴ reported a high-spin and Kovacs et. al. ²⁵ and Goldberg et. al. ²⁶ reported low-spin Fe^III-OOH(R) intermediates upon reacting Fe^II SOR model complexes with superoxide or alkyl peroxide in protic solvents. The former study reported weak Fe-O and high O-O stretches in the rRaman spectrum which correlated with the facile rate of dissociation of H₂O₂ from the Fe^III-OOH intermediate in presence of weak acids e.g. methanol.²⁴

The presence of an axial cysteine ligand distinguishes the SOR active site from all other catalytic non-heme Fe enzymes. The role of this thiolate ligand is currently an open issue. The weak Fe-O bond in the high-spin Fe^III-OOH model by Kovacs et. al. requires a strong trans effect of the axial thiolate.²⁴ The trans effect of the thiolate has also been proposed to affect NO binding to this active site.²⁷ The thiolate may also play a major role in controlling the reduction potential of the active site.²³ Alternatively, there is some similarity between the SOR active site and the active site of cytochrome P450 where the four porphyrin Nitrogens are in the equatorial plane and there is an axial cysteine ligand.²⁸ However, these sites differ drastically in reactivity. SOR releases hydrogen peroxide via proton assisted heterolytic cleavage of the Fe-O bond and P450 activates O₂ to oxidize substrates via a low-spin Fe^III-OOH intermediate which protonates at the distal Oxygen to heterolytically cleave the O-O bond to form Compound I.^{29, 30} Also, in spite of having a favorable redox potential (+250 mV), the SOR active site is incapable of performing SOD activity.³¹ The reduced SOR (Fe^II form) will reduce O₂⁻ to H₂O₂, but the oxidized SOR (Fe^III form) will not oxidize O₂⁻ to O₂.²³ This is crucial in maintaining low oxidative stress in anaerobes that are proposed to use SOR to deplete the superoxide concentration in vivo. However FeSOD with Nitrogen and Oxygen based ligands can perform both reactions. The lack of an open co-ordination site has been suggested to be a possible reason for this²³ although the origin of the affinity for this 6^th ligand binding or the feasibility of a SOD reaction in a SOR active site has not been evaluated. Thus it is important to understand the role of the axial thiolate ligand and the lack of heme in determining the reactivity of SOR.

Sulfur K-edge X-Ray Absorption Spectroscopy (S K-edge XAS) is a relatively new spectroscopic method that has been used to study metal-Sulfur (M-S) bonding and how it is affected by the protein in various Cu-S and Fe-S electron transfer (ET) active sites.^32,33,34 The S K edge refers to the ionization of Sulfur 1s (S_1s) orbital. This is a ligand based transition and thus this technique does not suffer from the complications that arise from the interaction of the core hole with the metal 3d manifold in the final state.³⁵ The, lower-energy pre-edge transitions (pre-edge) to unoccupied metal 3d (M_3d) orbitals gain intensity through Sulfur 3p (S_3p) mixing due to covalency and because the Sulfur 1s→3p transition is electric dipole allowed. Thus the S K pre-edge intensity is a direct experimental probe of M-S bond covalency. Recently, we have used this method to investigate the active site structure and bonding in a series of P450 model complexes to quantitatively understand the effect of H-bonding on Fe-thiolate bond covalency and redox potential.³⁶

In the present study we use S K-edge XAS to quantitatively define the Fe-S bond covalency in the resting high-spin and CN⁻ bound low-spin ferric forms of SOR from P. furiosus. We use the S K-edge results in addition to other well defined experimental parameters, e.g. geometry, spin states and Fe-S bond covalency etc., to develop a computational model for the resting ferric SOR active site that required inclusion of H-bonding to the axial thiolate ligand. The S K-edge XAS data on the low-spin CN⁻ bound form are then used to evaluate computational models for this spin state change and further expand the model to include H-bonding to the exchangeable axial ligand. The model that best fits these experimental data is then used to computationally investigate the proposed mechanism of SOR and evaluate possible intermediates. The role of the trans axial thiolate and H-bonding to it in the SOR reaction are computationally evaluated. The Fe^III-OOH species in the SOR site is compared to that in P450 (compound 0). The role of the non-heme vs heme ligand in difference in their reactivity is evaluated. A hypothetical SOD reaction cycle is constructed for the SOR active site and compared to that for the Fe-SOD active site to obtain insight into the lack of SOD reactivity of SOR.

EXPERIMENTAL DETAILS

Sample Preparation

The recombinant form of P. furiosus SOR was obtained from E. coli as described in ref. 10. Absorption at 660nm (ε = 2500 M⁻¹cm⁻¹)¹⁰ indicated that 85% of the protein was loaded with Fe. The protein solutions (in 100 mM phosphate buffer having pH 7.2–7.3) were pre-equilibrated in a water-saturated He atmosphere for ~1 h to minimize bubble formation in the sample cell. The protein samples was oxidized or reduced before experiments by using a ~3–4-fold excess of sodium hexachloroiridate or ascorbic acid solution in the same buffer as the protein solution. The CN⁻ bound form was generated by adding 40 equivalent of CN⁻ to a pre-oxidized sample at pH 9.0. The complete conversion to the low-spin form was confirmed by room temperature absorption and EPR spectroscopy at 8K (Fig. S1, supplementary information). Samples were loaded via a syringe into a Pt-plated Al block sample holder sealed in front using a 6.3 μm polypropylene window and maintained at a constant temperature of 4°C during data collection using a controlled flow of N₂ gas pre-cooled by liq. N₂ passing through an internal channel in the Al block.

Data Collection and Reduction

XAS data were measured at the Stanford Synchrotron Radiation Laboratory using the 54-pole wiggler beam line 6–2. Details of the experimental configuration for low energy studies have been described previously.³⁷ The energy calibration, data reduction and error analysis follow the same approach described previously.³⁸

Fitting Procedures

Pre-edge features were fit using pseudo-Voigt line shapes (sums of Lorentzian and Gaussian functions) using the program PEAKFIT. This line shape is appropriate as the experimental features are expected to be a convolution of a Lorentzian transition envelope³⁹ and a Gaussian line shape imposed by the beam line optics.⁴⁰ A fixed 1:1 ratio of Lorentzian to Gaussian contribution successfully reproduced the pre-edge features. The rising edges were also fit with pseudo-Voigt line shapes. Fitting requirements included reproducing the data and its second derivative, using a minimum number of peaks. Fits were performed using single peaks to simulate the pre-edge feature of each component with a half-width of ~0.9 eV. The intensity of a pre-edge feature (peak area) represents the sum of the intensity of all the pseudo-Voigt peaks which were needed to fit the feature in a given fit. The fitted intensities were converted to %S_3p character using the pre-edge feature of plastocyanin as a reference (where 1.27 units of intensity, obtained using this program, corresponded to 38% S_3p character).⁴¹ Note that the 85% loading of the active site was accounted for by renormalization of the data. This is because the free cysteines that are not bound to iron will contribute to the rising edge but not to the pre-edge.

DFT Calculations

All calculations were performed on dual Intel Xeon workstations using the ADF 2004.01 and the Gaussian 03 package.⁴² The different computational models used in this study are described and evaluated in the results section. The geometries were optimized using either a) the meta GGA BP86 functional available in the ADF package using a TZP basis set on all atoms or b) with B3LYP method using 6-311G* basis sets on Fe, S, N, O atoms and 6-31G* basis set on C and H atoms using the Gaussian 03 program.⁴³ The default convergence criteria in both software were used during optimization. For the Gaussian optimized geometries the energies were obtained from single point calculations using 6-311G* basis-set on all atoms. The stability of the ground states was tested using the “stable” command in the Gaussian program. Frequency calculations were performed on the optimized geometries to ensure that they had no imaginary mode. Only the larger H-bonded models having 7 frozen coordinates had 4–5 <30 cm⁻¹ imaginary modes involving these frozen co-ordinates. For calculating the SOD reaction, the co-ordinates from the X-tal structure of Fe-SOD from P. shermanii (pdbid:1BSM) were used for the starting structure.⁴⁴ The α carbons of the histidine and the glutamate residues were frozen during optimization. All other geometric parameters were optimized. Mulliken⁴⁵ population analyses were performed using PYMOLYZE⁴⁶ program and the molecular orbitals were plotted using Molden ver. 4.1 with a contour value of 0.05. For solvent corrections, experimental free energies of solvation were used for all small ions (since the site is solvent exposed) and a PCM model⁴⁷ with an epsilon of 4.0 was applied to the active site models.⁴⁸ The fragment dissociation energies (bond energies) were computed by comparing the energies of the full molecule to the sum of the energies of the fragments. To check for basis set supposition error we have estimated the energies of the two weakly endothermic key protonation steps with a larger 6-311+g** basis set and found less than 2 Kcal difference in the calculated energies.

RESULTS

A. S K-edge XAS

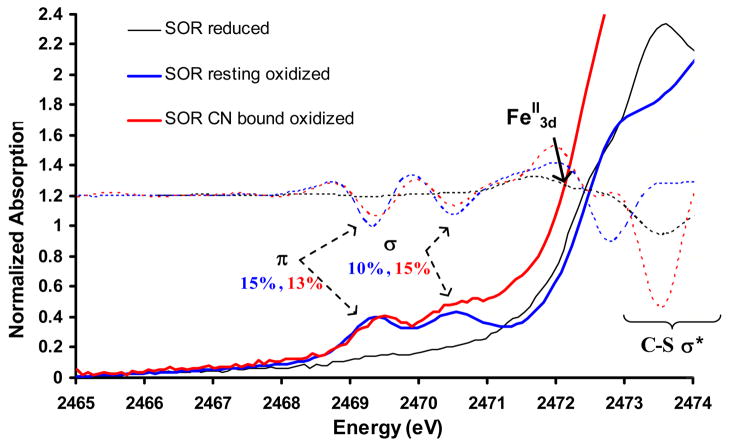
The S K-edge XAS data for the resting oxidized (blue), CN⁻ bound oxidized (red) and reduced (black) forms of SOR enzymes are shown in Fig. 2. The XAS data of the resting oxidized species show two distinct pre-edge features at 2469.3 eV and 2470.5 eV and a rising edge transition at 2472.8 eV. The two pre-edge features correspond to S_1s transitions to the t₂ and e half occupied molecular orbitals of the resting high spin ferric ground state. These features can be quantified by fits to the experimental data to have 0.49 and 0.33 units of normalized intensity. These correspond to 15±2% and 10±2% S_3p character in the singly occupied d-π (t₂) and the d-σ (e) orbitals in the d⁵ resting oxidized high-spin ground state. The CN⁻ bound low-spin form (Fig. 2, red) also exhibits t₂ and e transitions at 2469.5 eV and 2470.7 eV with 0.50 and 0.48 units of intensity, respectively.⁴⁹ These correspond to 13±2% and 15±3% S_3p character mixed into the singly occupied t₂ π and unoccupied e σ orbitals, respectively, of the low-spin d⁵ ferric state. The significant intensity in the low-energy peak indicates that the single d-π t₂ hole is oriented along the Fe-S bond. Although one may have expected the e intensity to go up in the low-spin form (as both α and β Fe-S d-σ orbitals are unoccupied in the low spin state relative to one β d-σ orbital in the high spin state and the Fe-S bond length is shorter) the intensity actually goes down. However for low-spin Fe^III the assignment of the pre-edge features is complicated by multiplet effects in the final state. The S_1s→Fe_3d transition produces an L¹t₂⁵e¹ excited state configuration (where L = ligand hole) which produces two ²A excited states (the t₂⁵e¹ configuration produces a singlet and triplet state which couple to the ligand hole). These wavefunctions were obtained as linear combinations of the parent microstates using lowering operators.^{50, 51} The ²A state originating from the parent dⁿ⁺¹ triplet configuration has three times the intensity of the ²A originating from the dⁿ⁺¹ singlet parent configuration. The observed pre-edge feature at 2470.5 eV can be assigned as the transition to the lower ²A state (originating from the triplet dⁿ⁺¹ parent) with 3/4^th of the intensity while the higher energy multiplet should be shifted up in energy (estimated ~1 eV from DFT)⁵² and obscured by overlap with the C-S σ* transition.⁵³ Corrected for this multiplet shift of intensity the total intensity for the e transition in the low-spin state is 20%.

Figure 2.

S K-edge XAS of superoxide reductase in its reduced (black), resting oxidized (blue) and CN⁻ bound oxidized (red) forms. The 2^nd derivatives of the data are shown in dotted lines. The Fe^II pre-edge feature is indicated by the black arrow.

The data for the resting reduced form show an intense S_1s→ S_{C-S σ}* transition at 2473.6 eV. The S_1s→ Fe^II_3d pre-edge transition appears as a weak feature in the 2^nd derivative of the data⁵⁴ at 2472.1 eV (Fig. 2, arrow on dotted black line) overlapping with the stronger feature at 2473.6 eV.

B. DFT Modeling

a. High-Spin resting

The active site was modeled using the crystal structure of 1Fe SOR (pdb: 1DQI)⁷ with four neutral imidazole rings (representing the coordinated histidines), an axial methyl thiolate (representing cysteine) and an axial acetate (representing glutamate) (fig. 3A). Geometry optimized DFT calculations were performed using BP86 and B3LYP methods on four sets of models (B, C, D and E) presented in figure 3. The relevant optimized parameters are given in Table 1. Full optimization of the active site using BP86 with no constraints led to structure B (Fig. 3) where the metal-ligand bond lengths were in good agreement with the published solution EXAFS results (Fig. 3A), and the 1.7 Å resolution crystal structure.^{10, 7} However, the optimized low-spin state was found to be more stable by 11.2 Kcal/mol (Table 1, row 1). This indicates that the full optimization, which does not include the constraints imposed by protein environment, does not correctly describe the ground state at the BP86 level. This could be either a result of the simplified model that does not account for the constraints imposed on an active site by the protein backbone or an artifact of using a pure density functional, which generally stabilizes a low-spin state.⁵⁵

Figure 3.

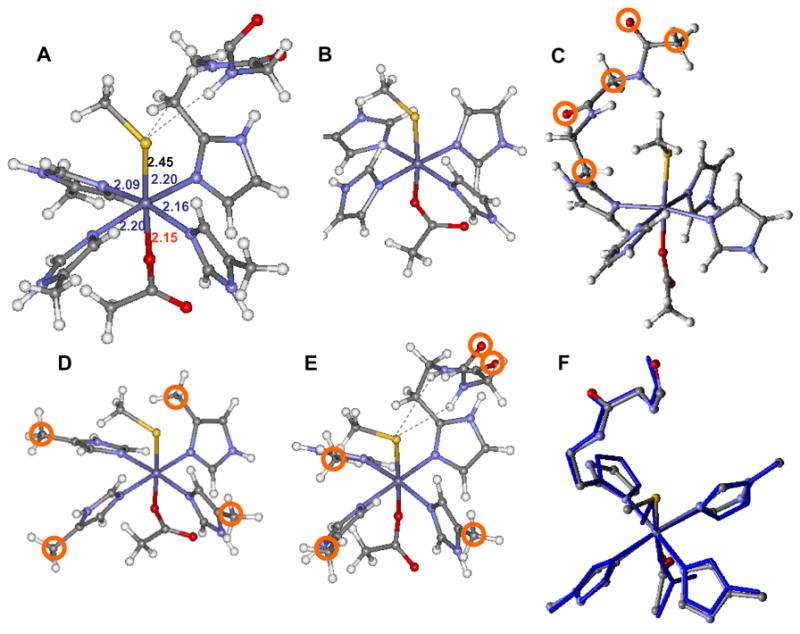
The crystal structure of the active site of resting oxidized SOR (A), the unconstrained model (B), H-bonded only model (C)⁶⁰, α carbon constrained model (D), H-bonded and α-carbon constrained model (E) and overlay between the optimized model E (in blue) and X-tal structure (atom colored) from 1DQI (F). The constrained atoms are circled in the respective structures. Bond lengths of the protein crystal structure are given in Å and are color coded as Fe-S, Fe-N and Fe-O.

Table 1.

Calculated geometric parameters and energy difference of models B, C, D and E using BP86 and B3LYP methods.

Method	Model	Fe-Sa	Fe-N1a,b	Fe-N2a,b	Fe-Oa	C-S-Fec	N-Sa	S- -H-Nc	dΔEHS-LS
X-Ray	1DQI	2.46	2.12	2.20	2.15	117.0	3.50, 3.72	131.7, 165.1
EXAFS		2.36	2.17	2.07	2.15
BP86	B-HS	2.39	2.18	2.22	2.03	111.5			+11.2
	B-LS	2.21	2.00	2.03	2.03	113.0
	C-HS	2.42	2.20	2.22	1.97	121.4	3.62, 3.82	112.8, 140.9	+9.0
	C-LS	2.20	2.01	2.02	1.98	114.7	3.69, 3.97	107.2, 137.1
	D-HS	2.39	2.15	2.20	2.03	120.1			+4.5
	D-LS	2.23	2.05	2.06	2.00	124.4
B3LYP	D-HS	2.43	2.18	2.18	2.01	109.9			−20.0
	D-LS	2.31	2.02	2.03	1.98	109.6
	E-HS	2.43	2.15	2.20	1.95	111.4	3.65, 3.90	126.0, 144.5	−6.8
	E-LS	2.28	2.07	2.04	1.97	113.0	3.81, 4.03	121.8, 143.6

^aUnits Å

^bT he Fe-N distances are grouped together representing long and short Fe-N bonds.

^cUnits degrees

^dUnits Kcal/mol

Two conserved H-bonds to the axial CysS⁻ (see Fig. 1) from the amide N-H’s of His114 and the Ile113 residues are present in the active site of SOR that are absent in model B. These H-bonds can affect the covalency of the axial Fe-S bond and may be an important determinant of the spin state. Thus the two H-bonds were also included in the model and optimized (the carbonyl Oxygen of the H-bonding amides were frozen in space during optimization as these are strongly H-bonded to 2^nd sphere residues, see Fig. 3C). The optimized bond-lengths and bond angles of the high-spin and low-spin states are give in Table 1, Column 3 and 4, respectively. The H-bonding to CysS causes ~0.03 Å elongation of the Fe-S bond length in the optimized structures for both spin sates. Also the H-bonding interaction is weaker in the low-spin state as indicated by the longer N-S heteroatom distances and less linear N-H---S angles (Table 1). This is because the Fe-S bond is more covalent in the low-spin state which shifts electron density away from the thiolate and weakens the H-bonding interaction. Note that even in this model the optimized structure of the low-spin state shows significant shortening of the Fe-N_His bond length relative to the high-spin state (like in model B) and this results in a 9 Kcal/mol more stable low-spin state. This implies that though the H-bonding weakens the Fe-S bond, it does not result in a high-spin ground state for this model of SOR.

In the crystal structure of the enzyme the co-ordinated Histidine residues are involved in direct or indirect (via bridging water molecules) H-bonds from peptide residues (e.g. pro42). These H-bonding interactions will oppose the shortening of Fe-N_His bond lengths observed in these unconstrained calculations that lead to a low-spin ground state. To simulate this tethering of the Histidine residues the active site model was expanded to include the α carbon of the four histidine rings that were frozen during optimization (Fig. 3D). Though the resulting geometry is generally in good agreement with the solution EXAFS results (Table 1, row 3), the low-spin ground state is still more stable; albeit, the energy difference between the spin states in this model is only 5 Kcal/mol relative to 11.2 Kcal/mol in the unconstrained model without the H-bond (Fig. 3B).^{56, 57}

DFT calculations were performed on the model C using the hybrid B3LYP method, which is reportedly less covalent than a pure functional and thus favors the high-spin state.⁵⁸ In this α carbon constrained model (Fig. 3C) the optimized high-spin ground state is more stable than the optimized low-spin ground state by 20 Kcal/mol, thus reproducing the experimentally observed high-spin ground state of resting six-coordinate SOR active site.⁵⁹ The optimized Fe-S distances in B3LYP are ~0.04Å longer than those obtained from BP86 calculations. This is a consequence of over estimation of Fe-S bond covalency by a pure functional.⁵⁸ However, this model does not reproduce one short N-Fe-N (Fe-N_His 2.09 Å, 2.16 Å) and one long N-Fe-N (Fe-N_His 2.20 Å and 2.20 Å) axis as observed in the active site structure. Though this geometric feature may not contribute to reactivity, it serves as another parameter to test the accuracy of these calculations.¹⁰ As a final step we included the H-bonding (which affected the Fe-S bond length) and the α carbon constraints on the histidines (which affected the spin state) in the same model (Fig. 3 E). This B3LYP optimized structure reproduces the experimental Fe-S bond length and has one short N₁-Fe-N₁ axis ((Fe-N₁ 2.17Å and 2.14 Å) and one long N₂-Fe-N₂ axis ((Fe-N₂ 2.20 Å and 2.19 Å) and the high spin state is 6.8 Kcal/mol more stable. Note that the H-bonding residue is covalently linked to one of the histidine ligands with the longer Fe-N_His bond (Fig. 3E). This suggests that this Fe-N_His bond elongation may be a result of steric interaction between the H-bonding arm and the histidine imidazole ring. We considered the possibility of a H₂O molecule H-bonded to the Glu residue since the active site is solvent exposed (Table 1, F) and there is direct Raman evidence for a solvent interaction in the low-spin CN⁻ form (vide infra). However, no significant change in geometry was observed other than a ~ 0.04 Å elongation of the Fe-O Glu bond upon H-bonding.

Electronic structure

The MO diagrams (spin unrestricted unoccupied β orbitals from the B3LYP calculations) of the resting six-coordinate ferric site without (left) and with (right) H-bonding show a pseudo-octahedral ligand field (Fig. 4, left). In both models there are two Fe-S bonding interactions. The lowest energy t₂ orbital forms a π bond with the out of C-S-Fe plane CysS_3p orbital while the highest energy e orbital has a pseudo-σ interaction with the in plane S_3p orbital (Fig. 4, Fe-S π and Fe-S σ). ⁶¹ In the non-H-bonded models these %S_3p covalencies are calculated to be 28% (π) and 15% (σ). These are much higher than the experimental values (15% and 10%, respectively), which suggests the H-bonding interaction in the SOR active site might have a significant effect on the S-Fe bond covalency. Indeed in the H-bonding model, the calculated %S_3p character in these orbitals are 17% and 12%, in reasonable agreement with the experimental values.^{62, 63} The decrease in Fe-S bond covalency is mainly in the π bonding orbital consistent with the orientation of the H-bonds (Fig. 3 A). It is also worth noting that the total calculated %S_3p using the BP86 method on the high-spin H-bonded model (Fig. 3 C) are ~39–40% which are again much higher than the experimental value of 25% (15% π + 10% σ). This reflects the over estimation of Fe-S bonding by a pure functional and further indicates that B3LYP is better for describing the exchange in this system.

Figure 4.

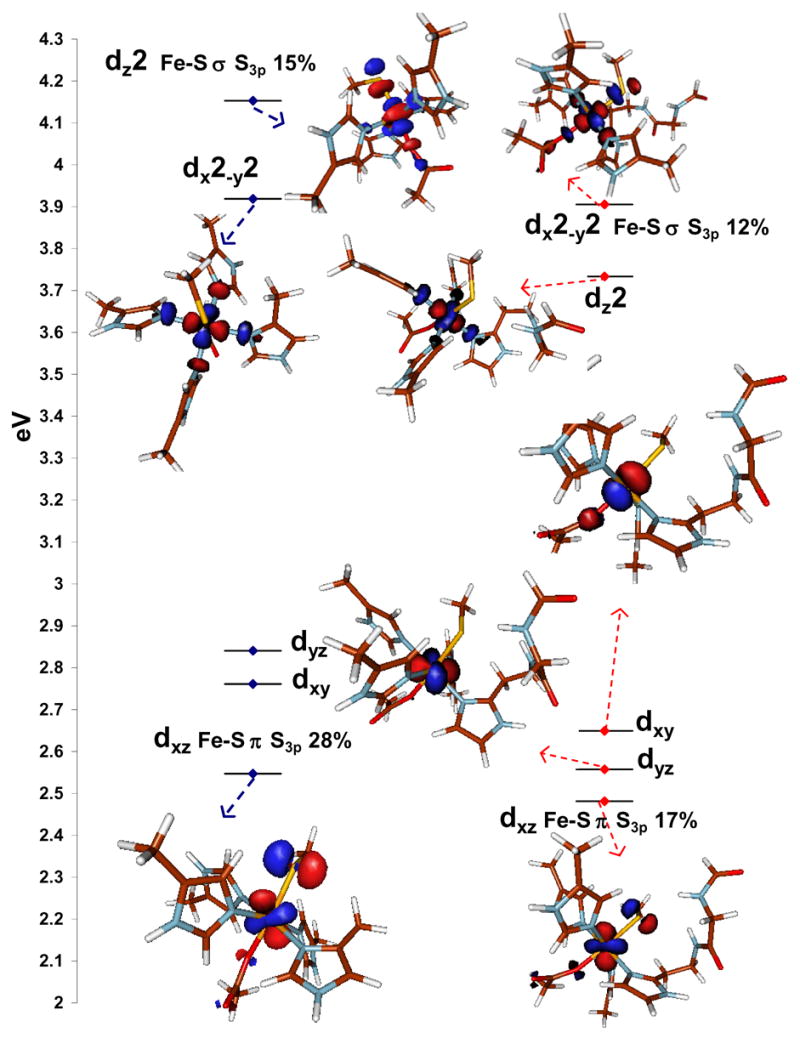
The MO diagrams of the resting six-coordinate high-spin Fe^III active site without, (left) and with (right) H-bonding interactions. The S_3p co-efficients are indicated in text. Only the β contours are shown. The dyz and dxy contours of the model without H-bonding are not shown to avoid crowding.

b. Low-spin CN⁻ adduct

The CN⁻ bound low-spin ferric active site was modeled with the α carbon constraint that proved important to reproduce the correct ground state for the resting Fe^III site (Fig. 3D). The geometry optimized calculations on the CN⁻ bound form of model 3D indicates than the low-spin form is more stable by 90 Kcal/mol consistent with experiments. Thus these α carbon constraints were successful in reproducing the experimentally observed spin states of both the resting and the CN⁻ bound forms. Further the H-bonds to the thiolate were included (model E) as they were crucial in reproducing the experimental covalency of the resting oxidized form.

A recent study using vibrational spectroscopy and pulsed EPR techniques by Clay et. al. has indicated the presence of at least three CN⁻ bound forms in solution; One linear and two bent conformations having Fe-C-N angles of 175°, 131° and 125°, respectively.²⁰ From ²H₂O isotope effect observed on one set of C-N vibrations, it was proposed that the linear conformation is H-bonded to a solvent molecule.²⁰ Thus in addition to the α-carbon constraints and H-bonding interactions that were necessary to reproduce the ground state spin and Fe-S covalency of the high-spin model, an H-bond to the axial CN⁻ ligand from a H₂O molecule was also included in the LS model. Both the optimized geometries (E and E+H₂O, Table 2) have a linear Fe-CN unit and have shorter Fe-S and Fe-N bond lengths relative to the resting form consistent with the low-spin state of the CN⁻ form. The optimized geometries with and without the H₂O H-bonded to the CN⁻ shows that H-bonding leads to an elongation of the Fe-CN bond by 0.02 Å, which is compensated by 0.05 Å shortening of the Fe-S bond (Table 2, E and E + H₂O). This suggests that H-bonding to CN⁻ weakens the Fe-CN bond which is compensated by strengthening of the trans Fe-S bond. These interactions determine the orientation of the single d-π hole in this low-spin Fe^III center (vide infra).

Table 2.

Optimized bond distance and angles of linear, bent and H-bonded CN⁻ models using B3LYP

	Fe- S	Fe-N1	Fe-N2	Fe-C	C-N	Fe-S-C	Fe-C-N	N-S	S- -H-N
E	2.42	2.03	2.06	1.95	1.17	113.1	171.6	3.72, 3.97	126.5, 146.1
E + H2O	2.37	2.03	2.06	1.97	1.17	115.3	174.6	3.74, 4.02	125.6, 145.9

The MO diagrams of CN⁻ bound L.S. models E and E + H₂O (H-bonded to thiolate and H-bonded to thiolate and CN⁻, Fig. 5 left and right, respectively) show a normal low-spin t₂5 configuration with one singly occupied β t₂ hole and two pairs (α+β) of un-occupied e orbitals (only three β orbitals shown in Fig. 5). However, there is a very significant difference in their electronic structure. The t₂ hole of the low-spin Fe^III center is localized in the in-plane d_xy orbital in the H-bonded to thiolate model E, while it is in the d_xz (which is the Fe-S d-π antibonding) orbital in model E + H₂O. The description of model E is in contrast to the experimentally observed low-lying S→ Fe CT, the low energy t₂ pre-edge feature in the S K-edge XAS and recently published ENDOR data all of which indicate that the t₂ hole in the CN⁻ bound state is in the Fe-S d-π orbital.²⁰ The nature of the t₂ hole is determined by an interplay between the stabilization of the d_xz, d_yz orbitals by back bonding to the CN π* orbitals and the destabilization of the d_yz orbital by the donation of the S_3p π orbital. In the case of the linear CN⁻ model with H-bonding to the thiolate (E), the back bonding from the d_xz, d_yz orbitals along the Fe-CN axis into the two CN⁻ π* orbitals dominates which results in localization of the t₂ hole on the d_xy orbital in the Fe-N₄ equatorial plane. H-bonding from the solvent molecule to the CN⁻ (Fig. 5, E + H₂O) weakens this π backbonding interaction with one of the two d-π orbitals (evident from the decreased Fe_3d mixing in one of the two π* orbital from 3.2% to 1%) and the t₂ hole is now localized in the antibonding Fe-S d-π d_xz orbital. Note that of the two possible d-π orbitals along the Fe-CN bond, the Fe-S d-π orbital is higher in energy due to its π* nature which localizes the t₂ hole in this orbital. Note that single point calculations on bent Fe-CN models (as indicated by the Raman data) also show weakening of Fe-CN backbonding and similar localization of the t₂ hole in the d-π d_xz orbital (the effect of bending and H-bonding has an orientation dependence, supplemental information page S1).

Figure 5.

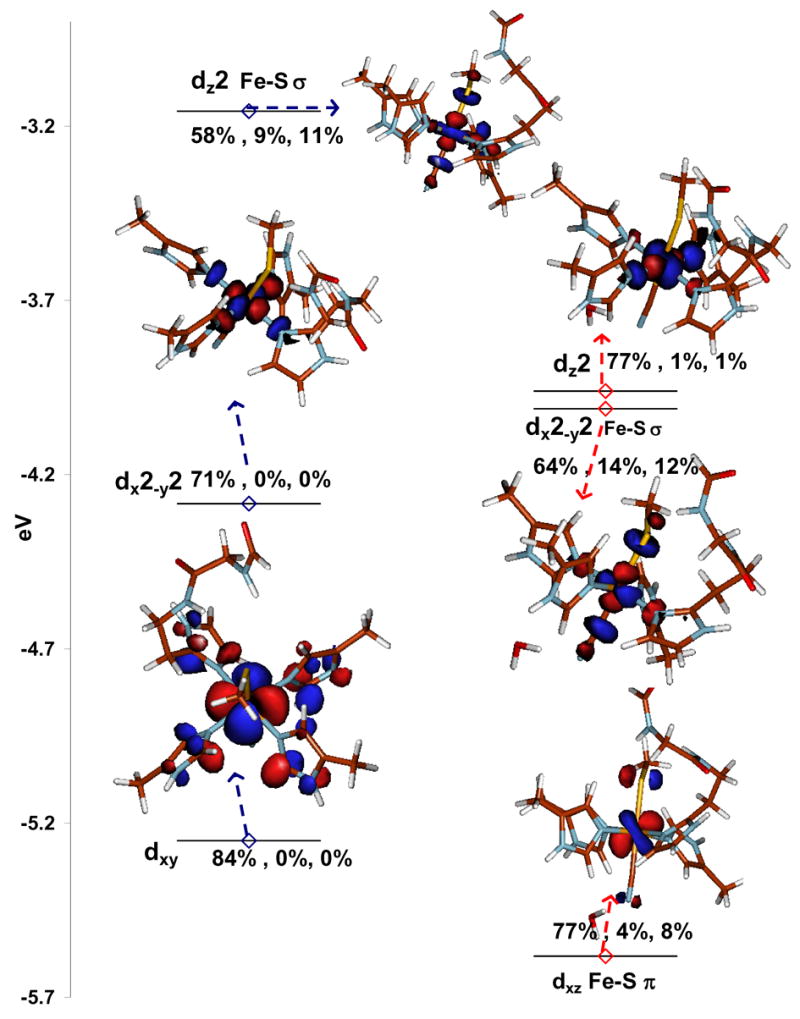
β contours of the E (left) and E +H₂O (right) models of the linear Fe-CN bound LS forms. The two α unoccupied contours are not shown for clarity. The designations of the orbitals are written next to them and the %Fe_3d, CN_2p, S_3p are given as well.

A net result of these interactions is that the t₂ hole in the low-spin CN⁻ bound form has S_3p mixing consistent with the low-energy feature in S K-edge XAS and the presence of a low-energy CT at 14000 cm⁻¹.¹⁰ The %S_3p mixing in the t₂ hole in the E + H₂O and the bent Fe-CN models are calculated to be 8% and 11%, respectively, which are lower than the experimentally observed 13% intensity in the 2469.5 eV feature in Fig. 2. The total %S_3p in the unoccupied d orbitals is calculated to be 35% (11% d-π+24% d-σ (α+β)) for both the linear and bent models which is distributed over one d-π and two dⁿ⁺¹ d-σ final states as presented in Section A. The experimental total S_3p is estimated to be 33% (13% d-π and 20% d-σ).⁶⁴ Note that the Fe-S bond may be expected to get more covalent in its low-spin state relative to high-spin state but the very strong trans CN⁻ ligand in the low-spin state weakens it. This is provides an explanation for the result that the S_3p co-efficient in the d-σ orbital remains the same (12%) between the high (Fig. 4 and Fig. 5 right hand side) and the low-spin states. However the total covalency of the Fe-S bond in the low-spin form is 35% (11% d-π + 2×12% d-σ) which is more than that of the high-spin form (25%) because the d-σ orbital is unoccupied in the low-spin state while it is half-occupied in the high-spin state. While this computational model provides a good qualitative description of the t₂ hole, the Fe-S d-π covalency is under-estimated. Note that the nature of this t₂ hole is strongly dependent on the modeling of the CN⁻ fragment (as described above) and the estimation of the π Fe-S covalency may be improved by expanding the model. However this is not essential for the properties investigated in the following sections.

The pre-edge of the resting Fe^II form could not be resolved due to its overlap with the rising edge. However, the geometric parameters of the calculated model (Fe-S =2.35 Å, Fe-N=2.20 Å) agrees reasonably well with the published EXAFS (Fe-S =2.37 Å, Fe-N =2.16 Å) data. The Fe-S bond covalency is calculated to be 14% which is similar to the Fe-S bond covalency reported for a Fe^II(SR)₄²⁻ model complex.⁶⁵

Overall the computational results indicate that the α-carbon constrained and H-bonded (to both thiolate and the trans axial ligand) model using the B3LYP hybrid functional reproduces the experimentally observed electronic and geometric parameters for the resting high-spin and its conversion to the CN⁻ bound low-spin state. A different modeling approach was used in Ref. 17. Though neither the α carbon constraints nor the H-bonding interactions were included, this model reproduced the high-spin resting state using BP86 functional and a DN** basis set.⁶⁶ In another study the BP86 functional and 6-311g* basis set was used to describe the low-spin CN⁻ bound form.⁶⁷ Though this model gave the correct spin state and localization of the single t₂ hole, it predicts a low-spin ground state for the high-spin resting form and over estimates the Fe-S bond covalency in both high-spin and low-spin forms (which we find is significantly reduced upon inclusion of H-bonding and HF exchange in the computational models) that are both well reproduced by the model used here.

C. Reaction mechanism

In this section we use the experimentally calibrated computational model developed above to evaluate the reaction mechanism commonly invoked for SOR²³ which involves reduction by one-electron and double protonation of superoxide anion to release H₂O₂. Fig. 6 presents the results of the H-bonded thiolate model which also includes H-bonding to the exchangeable axial ligand from a solvent H₂O molecule i.e. the E+H₂O model in section B (the non- H-bonded model is given in Scheme S1, Supplementary Information). One intermediate (intermediate I) has been unambiguously reported in literature by several groups which has the characteristics of a ferric species.^13,23 The possible intermediates involved in the reaction mechanism were calculated in Ref. 17 using a non H-bonded model although the energies of individual steps were not evaluated and a low spin Fe^III-OOH was assigned as intermediate I. Evaluating the energies of the individual steps of the mechanism and identifying possible intermediates (including spin states) will be the main focus of this section. The relevant geometric and ground state parameters are listed in Table 3.

Figure 6.

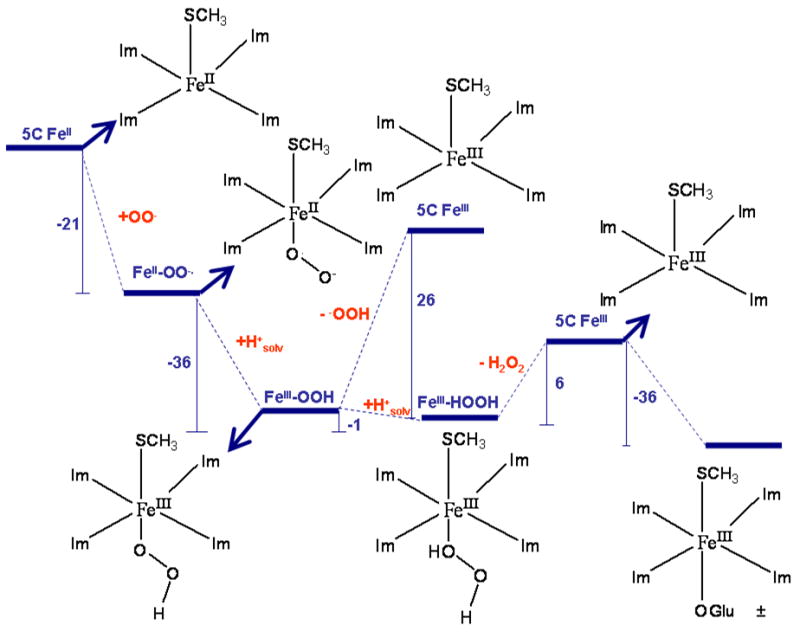
Reaction mechanism of SOR with H-bonding to the CysS⁻ included. The numbers represent ΔE of individual steps (ΔE calculated as E_products - E_reactants) and were calculated using a PCM model (ε = 4.0) and are given in Kcal/mol. Solvation energy of 260 Kcal/mole was used for a proton (H⁺_solv) in this scheme.⁶⁸ The computational model used for this calculation is described in Figure 3E. The H-bonds to thiolate and the axial ligand are not shown for clarity. ± In the E47A mutant where the Glu is replaced by Ala, the axial ligand has been shown to be OH⁻ using rR.⁷² The binding of a OH⁻ from water is calculated to be exothermic by −17 Kcal/mole.

Table 3.

Results of DFT calculations on H-bonded models relevant to the mechanism

	Spin	Fe-S (Å)	Fe- O (Å)	O-O (Å)	Fe-N (Å)		Fe-O-O (0)	SS1	S Fe1	SO1	qS1	qFe1
Resting FeII	S=2	2.35			2.21	2.21		0.14	3.71		−0.66	1.36
FeIII 5C	S=5/2	2.26			2.14	2.13		0.53	4.08		−0.37	1.61
FeII-O2−	S=5/2	2.63	2.16	1.33	2.24	2.18	123	0.03	3.78	0.5,0.5	−0.79	1.54
FeIII-OOH	S=5/2	2.45	1.95	1.44	2.19	2.17	123	0.24	4.15	0.27	−0.59	1.73
FeIII-OOH	S=1/2	2.41	1.81	1.45	2.07	2.00	118	−0.05	0.99	0.11	−0.50	1.47
FeIII-H2O2	S=5/2	2.29	2.75	1.45	2.15	2.15	125	0.53	4.10		−0.38	1.71
Resting FeIII	S=5/2	2.43	1.95		2.2	2.16		0.31	4.19		−0.53	1.76

¹Mulliken spin densities and charges.

The first step involves attack by the superoxide anion at the open co-ordination position of the resting Fe^II to form an inner-sphere complex. The Δ E of the reaction is −21 Kcal/mol. This species is best described as a Fe^II-superoxide complex as the O-O distance is 1.33Å and the spin density on the O₂ fragment is 1.0. Thus it is important to note that this step does not involve electron transfer from the Fe^II center to the bound superoxide ion and hence this species is not likely to be the experimental intermediate I which has spectroscopic characteristics of a Fe^III species.^{23, 13}

The next step involves protonation of the bound superoxide to generate a η¹-HOO-Fe complex.⁶⁹ This species is best described as a Fe^III-OOH species based on the optimized Fe-O, O-O bond distances and the resultant spin densities on Fe and OOH (Table 3, row 4). The calculated energies of the geometry optimized high-spin and the low-spin states of this model indicate that the former is more stable by 4 Kcal/mol. This is in contrast to the results in Ref. 17 where a low-spin ground state was calculated to be more stable. Thus this computational model that predicts the correct ground state and thiolate covalency of both the resting high-spin and the CN⁻ bound low-spin form of SOR predicts a high-spin ground state of an Fe^III-OOH intermediate. The high energy of this protonation step is −35 Kcal/mol (using 260 Kcal/mol for solvated H⁺) will help overcome any barrier that may be involved in protonating the distal Oxygen of this solvent exposed Fe^II-O₂⁻ adduct. The H⁺ may be donated by Lys48 or abstracted from bulk solvent as this site is very solvent exposed. Thus the above results favor a high-spin Fe^III-OOH as the first stable ferric species formed in the reaction cycle. Note that the large driving force for the formation of this species is consistent with its diffusion controlled rate of formation. Further the favorable protonation energy will help drive the process and explain the lack of a ²H isotope effect in its formation.¹⁴

At this point, heterolytic cleavage of the Fe-O bond to generate a five-coordinate high-spin Fe^III center and an ⁻OOH ion may be possible. In fact, a potential energy scan of Fe-O bond in the non H-bonded model of this active site results in a heterolytic Fe-O cleavage (with a barrier of +26 Kcal/mol) in contrast to homolytic Fe-O cleavage generating Fe^II and an ^•OOH radical found in DFT calculations of high-spin non-heme iron hydroperoxide intermediates with neutral ligands.⁷⁰ However this step is calculated to be endothermic (for the computational model used here) and will introduce a 26 Kcal/mol energy barrier (ΔE) in the reaction pathway. An alternative energetically favored path involves protonation of the proximal Oxygen of the Fe^III-OOH species resulting in a Fe^III-O₂H₂ species. This process is enthalpically favorable (ΔE= −1 Kcal/mol, using a solvated proton) as the resulting high-spin Fe^III-O₂H₂ species is stabilized by strong interaction with the axial H-bonded thiolate (the Fe-S bond shortens from 2.45 Å in Fe^III-OOH to 2.29 Å in Fe^III-O₂H₂, Table 3, rows 4 and 6). Note that the favorable enthalpy of protonation does not reflect a greater stability of the Fe^III-O₂H₂ species relative to the Fe^III-OOH species (see calculated ΔG’s below). The ΔE for this step is +6.6 Kcal/mol for a model that does not include the H-bonding interaction with the exchangeable axial ligand from the solvent molecule. This interaction had to be included in the model to get reasonable agreement with the S Kedge XAS data on the low-spin CN⁻ bound form and is observed in the crystal structure of this Fe^III-OOH species. This additional interaction from a solvent molecule makes the reaction more favorable by ~8 Kcal/mol (6.6 Kcal/mol + 1 Kcal/mol from Fig. 6) by stabilizing the weakly bound H₂O₂ by H-bonding. The resulting Fe-O₂H₂ species has a long Fe-O bond (2.7 Å) which facilitates the release of the final H₂O₂ product. Thus the anionic thiolate ligand weakens the Fe-OOH bond favoring its protonation and cleavage. Note that in Compound 0 of peroxidases the protonation of a proximal Oxygen of a Fe^III-OOH species is calculated to have a barrier of 9 Kcal/mol (including ZPE correction).⁷¹ However this is still less than the ΔG^± of diffusion of a small ion in solution (11–12 Kcal/mol) involved in the formation of the Fe^II-O₂⁻ adduct. The following step is cleavage of the weak Fe-(O₂H₂) bond which is endothermic by only E = 8 Kcal/mol and this process is associated with a further 0.03 Å decrease in the Fe-S bond length. The small dissociation energy of the H₂O₂ implies that the axial thiolate also helps avoid product inhibition. It is also possible that the axial glutamate residue displaces this weakly bound H₂O₂ as its binding is exothermic by −36 Kcal/mol. In the E47A mutant the Glu is replaced by a H₂O which binds as HO⁻ from rR studies⁷² and is also calculated to be exothermic by −17 Kcal/mol. This results in the formation of the 6C Fe^III resting form of the enzyme which would be re-reduced in turnover. Note that the presence of the axial glutamate residue competes with superoxide binding to the Fe^III site and has been proposed to be an important factor in avoiding superoxide dismutase activity (vide infra).²

Along the calculated reaction pathway, three species could be identified as possible candidates for the observed intermediate I namely the Fe^II-O₂⁻, the Fe^III-OOH and the Fe^III-O₂H₂ species. Though the calculated ΔE’s provide some insight into the favored pathway, the ΔG’s are more useful in evaluating the feasibility of a possible intermediate. The ΔG for the formation of the Fe^III-OOH upon protonation of the Fe^II-O₂⁻ is calculated to be −25 Kcal/mol. The large driving force for protonation along with the observation that the deprotonated species is Fe^II in nature disfavors the Fe^II-O₂⁻ species as the ferric intermediate I. The heterolytic dissociation of the Fe-OOH to Fe^III and HOO⁻ has a ΔG of +14 Kcal/mol that will result in an estimated rate constant of 400 s⁻¹ (using the Eyring equation and assuming ΔG^± =ΔG for an endothermic process without any additional barrier) which is significantly lower than the experimentally observed rate. Thus this step can not be involved in the reaction pathway. Alternatively, the protonation of this Fe^III-OOH species has a ΔG of +5.4 Kcal/mol and the further dissociation of the Fe-O₂H₂ species have a ΔG of −10 Kcal/mol. The lack of a significant barrier (ΔG^± = 9 Kcal/mol)⁷¹ and requirement of a H⁺ for decay of the Fe^III-OOH are consistent with the pH dependent diffusion controlled decay of intermediate I.⁷³ Also the observed intermediate has a S→ Fe CT band that is blue shifted to 600nm from 647 nm in the resting enzyme. ^14,15 This blue shift of the S→ Fe CT is indicative of a stronger ligand field around the Fe^III in the intermediate which is only present in the Fe^III-OOH species.⁷⁴ Thus the high-spin Fe^III-OOH species is the likely candidate for intermediate I.

The above mechanism is in general agreement with the mechanisms proposed by Kurtz et. al. and Nivere et. al. but with some differences.^{14, 15} While Nivière et. al. suggest that the intermediate I is a high-spin side-on Fe^III deprotonated peroxide our results here suggest that the deprotonated Fe-O₂ adduct is Fe^II-superoxide in nature. In the DFT calculations a side-on Fe^III-μ₂-O₂ species is only formed in the absence of H-bonding to the thiolate (supporting information Scheme S1). Based on DFT calculated energies Kurtz et. al. favor a low-spin Fe^III-OOH as intermediate I¹⁷ but we find the high-spin Fe^III-OOH species to be more stable by 4 Kcal/mol. Also protonation of a low-spin Fe^III-OOH will result in the formation of a high-spin Fe^III-O₂H₂ species and will involve a spin-crossing which will have a barrier. Also the possibility of a 2^nd intermediate has been proposed by Nivere et. al. At this point the calculated mechanism in Fig. 6 does not provide sufficient support for the presence of another intermediate.

D. Perturbations to the model: Contributions to reactivity

The presence of a H-bonded thiolate ligand is a unique feature of the SOR active site. The following sections address the effect of the axial ligand on the two key reaction steps; the protonation of the Fe^III-OOH species and the reduction of the ferric site generated at the end of the reaction in Fig. 6 for further turnover. The following perturbations will be computationally evaluated: Effect of the axial ligand (H-bonded MeS⁻ to H₂O to and F⁻), and the effect of H-bonding (H-bonded MeS⁻ to MeS⁻). These calculations use a model which includes only H-bonding to the thiolate and not to the exchangeable axial ligand i.e. model 3E, Fig. 3.

i. Protonation of Fe^III-OOH

The calculated Fe-O bond length and the energy required to protonate the proximal Oxygen of the Fe^III-OOH species for the different models listed above are given in table 4. Replacing the negatively charged thiolate with a neutral H₂O results in a shorter optimized Fe-O bond length (1.89 Å with H₂O vs 1.95 Å with a thiolate). The stronger Fe-OOH bond with the trans H₂O ligand makes the subsequent protonation of this species to form H₂O₂ energetically uphill by 43 Kcal/mol (also the heterolytic cleavage into 5C Fe^III and ⁻OOH fragments is calculated to be uphill by > 100 Kcal/mol). This is in agreement with the lack of Fe-O bond heterolysis in the 6C high-spin Fe^III-OO^tBu complex with neutral ligands and facile Fe-O heterolysis observed in the 6C high-spin Fe^III-OOH species with an anionic ligand.^70,24 Interestingly, substitution of the axial ligand with another anionic ligand like F⁻ results in a 7 Kcal/mol increase in the protonation energy relative to a trans thiolate ligand. This suggests that although the anionic nature of the thiolate ligand plays a dominant role in lowering the protonation energy (by 29 Kcal/mol) relative to a neutral ligand, its covalent nature further assists the protonation by 7 Kcal/mol. H-bonding to the thiolate makes it a weaker donor and results in a process which is 4.2 Kcal/mol more endothermic relative to a non H-bonded thiolate.

Table 4.

Optimized Fe-O bond length and calculated Fe^III-OOH protonation enthalpy

Model	Fe-O (Å)	ΔE (Kcal/mol)
(MeS)FeIII(His)4OOH H-bonded	1.95	+ 6.7
(F)FeIII(His)4OOH	1.95	+ 14.1
(H2O)FeIII(His)4OOH	1.89	+ 43.0
(MeS)FeIII (His)4OOH	1.95	+2.5

ii. Redox potential

The SOR active site has a redox potential ~250–300 mV. This process involves a 6C ferric and a 5C ferrous species (i.e. Fe^III-Glu + e⁻ → Fe^II + Glu⁻) and is essential for the re-reduction of the Fe^III during turnover.

The effects of the above perturbations of the axial thiolate ligand on the energy of this redox process are tabulated in Table 5. Note that these are shifts in ionization energies (IE) calculated using a PCM model and not reduction potentials. However these shifts in IE are reasonable approximations for the shifts in reduction potentials as the contributions from entropy, zero point energy and solvation of the axial ligand should be similar between these models. Changing the axial thiolate to a neutral H₂O shifts the redox potential by more than +3 V. This is expected as this substitution changes the charge of the model. On substituting the thiolate with an F⁻ the potential shifts more negative by 516 mV which could imply greater stabilization of the Fe^III state by F⁻ or a greater stabilization of the Fe^II state by CysS⁻ ligand. Note that the SOR redox couple includes an increase in co-ordination number upon oxidation. Thus the oxidation process can be divided into two steps; oxidation of a reduced 5C site, and the subsequent co-ordination of the glutamate ligand to the oxidized 5C site. The calculations on a 5C site show that replacing the CysS⁻ with F⁻ shifts this reduction potential only by +44 mV indicating that this ligand change has negligible effect on the relative stabilities of the 5C Fe^II and the 5C Fe^III states. However the F⁻ donates less charge to the Fe and increases its Lewis acidity. This results in an increased 6^th ligand binding energy (~13 Kcal/mole = ~560 mV) for the F⁻ bound oxidized site. Thus F⁻ binding results in additional stabilization of the 6C Fe^III state, which shifts the reduction potential of the coupled redox process by −516 mV. The H-bonded thiolate has a redox potential which shifted by −137 mV relative to a non H-bonded thiolate ligand. This is in contrast to several past studies where H-bonding has been found to shift the redox potential more “positive” as it stabilizes the increased charge density in the reduced form.³⁶ H-bonding affects the oxidation of a reduced 5C site, and the subsequent coordination of the glutamate ligand to the oxidized 5C site differently. The calculations on a 5C site show that the H-bonding interaction with the thiolate shifts the reduction potential by +250 mV as observed in past studies.³⁶ However the H-bonded thiolate donates less charge to the Fe and increases its Lewis acidity. This results in an increased 6^th ligand binding energy (~9 Kcal/mole = ~387 mV) for the H-bonded oxidized site. The net result is that H-bonding shifts the coupled redox process by −137 mV.

Table 5.

Calculated shift of reduction potential upon axial ligand perturbation.

Model	ΔIEo (mV)
(MeS)FeIII(His)4Glu	+137
(MeS)FeIII(His)4Glu H-bonded	0
(F)FeIII(His)4Glu	−516
(H2O)FeIII(His)4Glu	+3000

In summary the anionic nature of the thiolate ligand is necessary to raise the pKa of Fe^III-OOH species while keeping its E_o (tuned by the H-bond to the cysteine) in the range required for SOR reduction. Its covalent character of the thiolate Fe bond helps to further weaken the Fe-OOH bond by +7.4 Kcal/mol relative to a non-covalent anionic ligand like F⁻. This decrease in protonation affinity due to a covalent thiolate corresponds to a ~5 log unit increase in pKa of the Fe^III-OOH species.

E. SOR vs SOD

Interestingly, the SOR active site shows very limited SOD activity (0.5–1% of native Fe type SODs) in spite of having a redox potential (+250 mV) comparable to that of the Fe-SOD active site, which is in between those of the O₂⁻ → + e⁻ and O₂⁻ + 2H⁺ + e⁻ → H₂O₂ employed to investigate the oxidation of superoxide by the H-bonded SOR in comparison to a model of the Fe-SOD active site (Fig. 7).⁷⁶ Elaborate spectroscopic characterization and DFT calculations of Fe-SOD have been reported where the importance of the 2^nd sphere residues has been demonstrated.^{77, 78} We employ a simpler model here consisting of three imidazoles, one acetate and one hydroxide/water and focus mainly on the energies for the individual steps (which are not evaluated elsewhere) as a reference for the SOD activity of the SOR active site. Inner-sphere superoxide binding to Fe^III was assumed. The relevant bondlengths and spin densities are given in Table 6. The superoxide binding is exothermic for both SOR and SOD site leading to the formation of a Fe^III-OO⁻ complex. The binding energy is higher for SOR (−57 Kcal/mol) than SOD (−29 Kcal/mol) active site. This is largely the result of the two anionic donors present at the SOD active site (⁻OH and CH₃COO⁻) which makes a third anionic ligand binding less favorable relative to the one anionic donor in SOR (⁻SMe). The higher shift of electron density from O₂⁻ to Fe^III in SOR leads to an Fe^II-O₂ like species having a O-O bondlength of 1.28 Å and a spin density of 1.5 on the O₂ fragment (Table 6, row 2). Thus facile O₂ dissociation is calculated for this species which is only 1 Kcal/mol uphill. Note that this represents the ΔE for the process. The ΔG will be ~12 Kcal/mol down hill as this step involves O₂ dissociation. In SOD this step is H⁺ driven (as Fe^III-OH is converted to Fe^II-OH₂ in the product) and very exothermic (−35 Kcal/mol).⁷⁹ It is important to note that these results indicate that a five coordinate SOR active site is capable of SOD activity.

Figure 7.

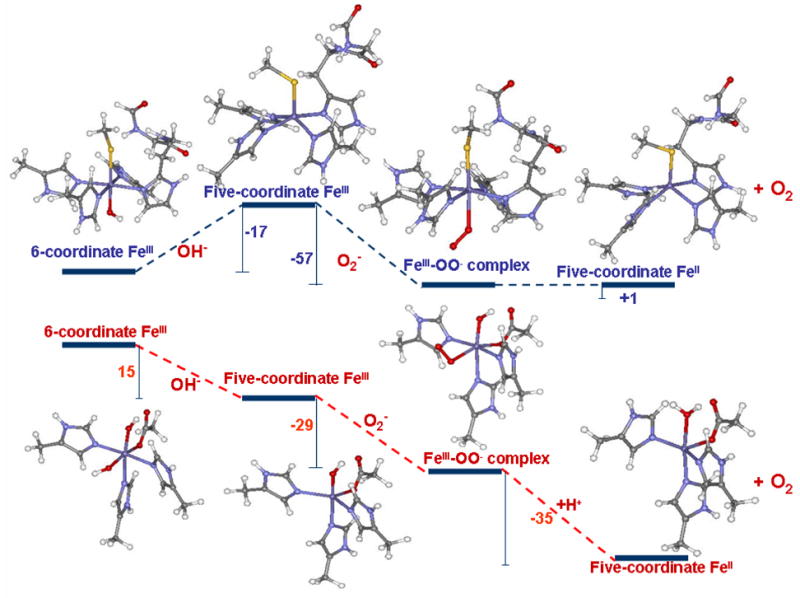
Comparison of energies of superoxide oxidation by SOR (upper panel) and SOD (lower panel) active sites (energies (ΔE) were calculated using a PCM model (ε = 4.0) and are given in Kcal/mol); Solvation energy of 260 Kcal/mol was used for an H⁺.

Table 6.

Relevant Bond Lengths and Mulliken Spin Densities for Species Involved in SOD cycle.

Model		Fe-Ltransa	Fe-Oa	O-Oa	SpinFe	SpinO-O
5C FeIII	SOR	2.26			4.08
	SOD	1.90			4.20
FeIII+O2−	SOR	2.43	2.24	1.28	4.03	1.51
	SOD	2.05	2.09	1.30	4.15	1.28
FeII	SOR	2.35			3.71
	SOD	2.07			3.79
FeIII-OH	SOR	2.47	1.89		4.21
	SOD	2.06	1.88		4.24

^aUnits Å

However while the resting ferric SOD active site is five coordinate, resting SOR is six co-ordinate and the reaction with O₂⁻ would require dissociation of the axial glutamate ligand. This dissociation energy (ΔE) for the glutamate residue in the resting SOR active site is calculated to be +36 Kcal/mol. Although a 5C active site is generated during turnover (Fig. 6) one also needs to consider the possibility of H₂O binding to form an Fe^III-OH species which is kinetically favored over reaction with superoxide ([O₂⁻]=10⁻⁶–10⁻⁹ M under turnover conditions) as proposed by Kurtz et. al.²³ From Fig. 7 the ΔE for Fe^III + 2H₂O → Fe^III-OH + H₃O⁺ for the open five-coordinate Fe^III active site in SOR is favorable by −17 Kcal/mol. Alternatively this process is uphill, ΔE = +15 Kcal/mol, for the five-coordinate Fe^III site in SOD. This is consistent with the SOD active site remaining five-coordinate in solution⁸⁰ while the E47A mutant of SOR (this mutant lacks the axial carboxylate ligand) has a bound ⁻OH at physiological pH.⁷² Thus for SOR but not SOD, O₂⁻ binding to the Fe^III site requires dissociation of an anionic ligand which is endothermic by at least ~15 Kcal/mol (for OH⁻, 36 Kcal/mol for Glu), along the reaction co-ordinate (Fig. 7, left). This will effectively inhibit the SOD activity of the SOR active site.

DISCUSSION

The resting high-spin Fe^III site of SOR has an axial Fe-SCys bond with two peptide NH---S H-bonding interactions. It’s S K-edge XAS exhibits a large t₂-e splitting (1.2 eV) such that the σ and π covalency of this Cysteine thiolate-Fe^III can be directly measured (Fig. 2). The %S_3p characters (i.e. covalency) in the t₂ and e Fe_3d orbitals are obtained experimentally to be 15% and 10%, respectively (total 25%). The total Fe-S bond covalency of SOR is comparable to H-bonded heme thiolate models (30%).³⁶ Comparison of the H-bonded thiolate ligand with a neutral (H₂O) and an anionic ligand (F⁻) reveals that the thiolate plays the role of a covalent anionic ligand. The anionic character of the thiolate ligand increases the pKa of the Fe^III-OOH intermediate facilitating its protonation by 29 Kcal/mol and tuning down its potential to a physiological range. The covalent character of the thiolate facilitates the reaction by further lowering the protonation energy of the high-spin Fe^III-OOH intermediate by 7.5 Kcal/mol relative to a non-covalent anionic donor like F⁻. The high π covalency of the resting ferric SOR site can also facilitate electron transfer into the active site by providing efficient ligand super-exchange coupling into the protein.⁸¹

The mechanism of superoxide reduction by SOR has been found to involve one or more intermediates.^23,16 One is proposed to be a high-spin side-on peroxide based on resonance Raman studies.²² We could computationally stabilize a side-on η2-Fe^III-peroxo species only in the absence of H-bonding to the thiolate and its protonation (leading to an Fe^III-OOH species) was energetically very favorable (Scheme S1). On including the conserved H-bonding residues to the thiolate ligand, which are necessary to reproduce the experimental Fe-S bond covalency, a peroxide level intermediate could be generated only upon protonation. This high spin Fe^III-OOH species is consistent with the experimentally observed stronger ligand field in the intermediate (S→ Fe^III CT blue shifted by ~1100 cm⁻¹) relative to the resting ground state (HOO⁻ is a stronger donor ligand that GluO⁻). The formation of this O₂⁻ adduct and its further protonation, with a large driving force (which helps overcome barriers), and the decay requiring a H⁺ (with ΔG^± = 9 kcals/mol) are consistent with the diffusion controlled pH independent rate of formation and diffusion controlled pH dependent rate of decay observed experimentally.¹⁴ The above mechanism is consistent with recent results from Kitagawa et. al. where a high-spin Fe^III-OOH species has been identified as an intermediate in a functional model of SOR.²⁴ It is important to note that with a non-covalent anionic axial ligand like F⁻ in place of the thiolate this step is +14 Kcal/mol uphill which would be detrimental towards the fast kinetics required for this enzyme.

The active site of SOR is similar to the active site of Cytochrome P450 which also has an axial cysteine co-ordination and a equatorial N₄ co-ordination. However, the porphyrinato di-anion in the active site of P450 provides a strong equatorial ligand field and an aromatic macro-cycle with an additional 2− charge.²³ This produces dramatic differences in the reactivities of the Fe^III-OOH intermediate involved in both active sites. The additional negative charge favors the protonation of the Fe^III-OOH (Compound 0) species in P450 is more favorable than protonation of SOR. Protonation of the distal Oxygen of compound 0 in P450 leads to an energetically favorable O-O bond heterolysis (ΔE = −40 Kcal/mol) forming Compound I where the Fe^III gets oxidized to Fe^IV and the porphyrin ring gets oxidized to a ligand radical. An analogous O-O bond heterolysis of the Fe^III-OOH species in SOR active site results in a Fe^IV and histidine cation radical species and is calculated to be ~+250 Kcal/mol uphill in energy, clearly demonstrating the necessity of the porphyrin dianion in stabilizing the Fe^IV-oxo ligand radical species. Protonation of the proximal Oxygen in Compound 0 in P450 leads to the formation of a Fe^III-O₂H₂ species analogous to SOR. However, due to the strong equatorial ligand field of the porphyrin ring, Compound 0 in P450 is low-spin. Thus protonation and elimination of H₂O₂ from the low-spin Compound 0 which will form the 5C high-spin Fe^III state will involve a barrier associated with the forbidden two-electron spin flip. Indeed the elimination of H₂O₂ in P450 active site is experimentally determined to be <1%.^{82, 83} However, the high-spin nature of the Fe^III-OOH intermediate in SOR enables facile H ₂O₂ release forming a high-spin product.

An important feature of the SOR active site is the presence of the H-bonded thiolate in the first coordination sphere of Fe trans to the O₂⁻ binding site. The H-bonding to the active site causes a significant decrease of the Fe-S bond covalency (decrease in covalency of 11% π and 3% σ in model 3D) which shifts the reduction potential by −137 mV. This negative shift in E^o is opposite to the results in previous studies where positive shifts are observed upon H-bonding. It reflects the net effect of two opposing factors: a) increased stabilization of the 5C Fe^II site (+250 mV, consistent with previous results)³⁶, and b) increased 6^th axial ligand binding affinity (due to increased Lewis acidity) of the 5C Fe^III site (−387 mV). A further effect of the H-bonding to the thiolate is in the nature of the Fe^II + O₂⁻ adduct. It can be described as an η1-O₂⁻-Fe^II species in the presence and an η2-O₂²⁻-Fe^III species in the absence of H-bonding. The Fe^II-η1-O₂⁻ species has higher net charge on the distal Oxygen and a higher energy HOMO donor orbital that activates it for protonation relative to an Fe^III-η2-O₂²⁻ species where the charge on the peroxide moiety is reduced because of its very covalent charge donation to the Fe^III.⁸⁴ Finally the five-coordinate SOR active site is calculated to be able to perform superoxide oxidation to dioxygen. The lack of SOD activity in SOR enzymes then appears to result from a favorable 6^th ligand binding energy of the solvent exposed SOR active site as has been proposed previously by Kurtz et. al..²³ The Lewis acidity of the SOR active site, having only one anionic ligand, is such that the Fe^III state generated during turnover binds a glutamate ligand or an ⁻OH ligand. Superoxide binding to the 6C Fe^III SOR site would entail a dissociative mechanism which is calculated to be endothermic by at least ~15 Kcal/mol that will preclude SOD activity. In contrast, the Fe-SOD active site which has two strong anionic ligands (hydroxide and aspartate) has an unfavorable energy for binding an additional anionic ⁻OH ligand and thus remains five-coordinate at physiological pH’s allowing facile SOD activity.

Supplementary Material

SI1. SUPPORTING INFORMATION.

All optimized geometries, MO diagram of the H-bonded CN⁻ bound form and the reaction scheme without H-bonding is available free of charge via the web at http://pucs.acs.org.