The Electronic Structure, Ionization Potential and Electron Affinity of the Enzyme Cofactor (6R)-5,6,7,8-Tetrahydrobiopterin in Gas Phase, Solution and Protein Environment

Abstract

(6R)-5,6,7,8-tetrahydrobiopterin (BH₄) is a key cofactor involved in the electron transfer to P₄₅₀ heme of nitric oxide synthase. We calculated the electronic structure of the neutral, cation and anion forms of BH₄ in gas phase, solution (both dielectric and explicit water), and in the protein environment using the density functional theory method (B3LYP/6-31+G(d,p)). Subsequently, we derived the ionization potential (IP) and electron affinity (EA) of the cofactor in these chemical environments. We found that the electronic structure of BH₄ is susceptible to the presence of an external electric field, and that conformational changes in the structure of BH₄ alone do not affect its electronic structure significantly. In gas phase, water, and protein environment the neutral BH₄ is the most stable species, while, in dielectric, the anion becomes the most stable species. The IP of BH₄ in the protein environment is about half of that in gas phase and its EA isabout five times smaller than in gas phase. Our results indicate that changes in the external electric field created by moving charged amino acid residues around BH₄ may lead to configurations that have the BH₄ ion as stable as, or more stable than the neutral form, thus facilitating the electron transfer.

Introduction

(6R)-5,6,7,8-Tetrahydrobiopterin (BH₄) is a cofactor for several enzymes and can generate or scavenge reactive oxygen species¹. Molecules that are related to biopterin include pterins, lumazines, alloxazines, folates, and riboflavins. The common structural feature of this group of molecules is a core of two or three fused heterocyclic six-member rings. Pterins are very reactive, they form chelates (five-membered rings) with metals through the O⁴ and N⁵ atoms (see Scheme 1 for atom labeling). In BH₄ the pyrazine ring is hydrogenated, thus adding four more hydrogen atoms, two of which are bound to the two nitrogen atoms of this ring. The pK_a of N⁵ is 5.6². In solution, BH₄ can react with O₂³, hydrogen peroxide^2,4, and peroxynitrite⁵. Glutathione, ascorbic acid, and dihydropteridine reductase (DHPR) reduce the quininoid form of BH₄ ^6,7 and dihydrofolate reductase (DHFR) reduces the dihydro form (BH₂)⁸. It has been suggested that the auto-oxidation proceeds through a radical species, which involves the N⁵ atom². The substitution of the hydrogen atom bound to N⁵ with methyl⁹, or the replacement of N⁵ with a methylene bridge¹⁰, in BH₄, decrease the susceptibility to auto-oxidation. Electronic structure calculations on BH₄ in gas phase show that C^4a has maximum electron density, and that the adjacent N⁵ enhances the reactivity of C^4a1. The reduced susceptibility to oxidation of N⁵-alkylated BH₄ was postulated to originate from the capability of the 5-methyl substituent to block the access of O₂ to the C^4a atom¹⁰.

Scheme 1.

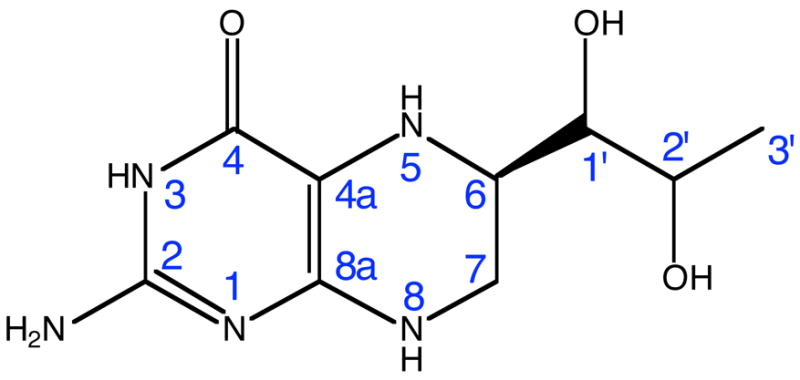
Tetrahydrobiopterin has redox functions in aromatic amino acid hydroxylase (AAH)^11–13 and nitric oxide synthase (NOS)^14,15. In the latter it binds close to P₄₅₀ heme of NOS and is implicated in the timely transfer of one electron to heme in the first step of arginine oxidation to N-hydroxyarginine by NOS. This paper presents such electronic properties of BH₄ such as the ionization potential (IP) and electron affinity (EA) calculated in gas phase, solution, and protein environment, casting light on the possible scenarios of electron transfer from BH₄ to P₄₅₀ heme of NOS.

Theoretical Calculations

Quantum mechanical calculations

The optimized geometry and vibrational frequencies of neutral, cation and anion forms of BH₄have been calculated by quantum mechanics using the density functional theory method (B3LYP Hamiltonian: Becke3 exchange¹⁶ and Lee-Yang-Parr correlation¹⁷ functionals) with the 6-31+G(d,p) basis set. Single point calculations have also been performed with Møller-Plesset second order perturbation theory^18–23 with the 6-31+G(d,p) basis set and B3LYP hybrid method using the 6-311+G(d,p) and 6-311++G(d,p) basis sets. The electrostatic potential-derived (ESP) charges for atoms in neutral BH₄ (used in deriving OPLS parameters²⁴) were obtained from the wave function of the optimized-geometry using the Merz-Kollman²⁵ method as implemented in the Gaussian98 program²⁶. The IP and EA of BH₄ in gas phase, dielectric²⁷, explicit water (TIP4P²⁸) and protein environment (NOS) were calculated at B3LYP/6-31+G(d,p) level. Graphical representations of the highest occupied molecular orbital (HOMO), singly occupied molecular orbital (SOMO), and lowest unoccupied molecular orbital (LUMO) data in CUBE files, in addition to spin densities, were created using the VMD program²⁹ and the POV-Ray visualization program³⁰.

Force field parametrization

In order to perform energy minimization of BH₄ in water and protein environment (NOS) we have developed OPLS parameters²⁴ for the following species: neutral BH₄, P₄₅₀ heme and [Zn(Cysteine)₄] ^2-complex species. The molecular mechanics optimized geometry and vibrational frequencies of neutral BH₄, methylthiolate dioxy-iron (Fe²⁺) porphyrin complex and the tetramethylthiolate-zinc complex [Zn(MeS)₄]^2- were calculated using the OPLS force field²⁴ as implemented in the molecular dynamics simulation program Gromacs³¹. The OPLS force field parameters used for atom types of BH₄, P₄₅₀ heme, and [Zn(Cysteine)₄]^2- complex have been derived in the following way: (a) OPLS atom types similar to those found in these species were first identified and assigned guess parameters; (b) the geometrical parameters (equilibrium bond lengths, bond angles, Ryckaert-Bellemans coefficients³², and improper dihedral angles) were adjusted using a genetic algorithm (GA) optimization program³³ such that the root mean square deviation (RMSD) in the internal coordinates of the quantum and molecular mechanics calculated structures is minimum; (c) the OPLS force constants for bond stretching and angle bending were adjusted (using the GA) such that the RMSDs between the vibrational frequencies of BH₄, methylthiolate dioxy-iron (Fe²⁺) porphyrin and the tetramethyltiolate-zinc complexes calculated by quantum mechanics and molecular mechanics methods were less than the RMSDs calculated for a few amino acids with OPLS parameters (defined in the OPLS force field implemented in the Gromacs program³¹).

Molecular mechanics calculations

The Protein Data Bank structure 1NSI³⁴ was used to obtain an energy-minimized structure of the solvated iNOSoxy dimer. The structure was prepared as follows: (a) one oxygen molecule was bound to Fe²⁺ of heme of each monomer by modifying the PDB file (the first electron transfer reduces Fe³⁺ to Fe²⁺, which allows oxygen to bind to the iron ion, and the second electron transfer is facilitated by BH₄); (b) hydrogen atoms were added and protonation states were assigned (corresponding to pH=7) using the Gromacs utility pdb2gmx. In this particular configuration of 1NSI, there are 3 charged amino acids within 0.5 nm of BH₄ (chain A): Arg^199A, Arg^381A and Glu^479B. It seems that among these charged amino acid residues only Arg^381A interacts significantly with BH₄ (Arg^381A makes a H-bond (0.205 nm) with O⁴ of BH₄, which is 0.242 nm in the crystal structure). Because the crystal structure (1NSI) indicates that the C-NH₂ bonds of the guanidinium moiety of Arg^381A are equal, we considered Arg³⁸¹ (in both monomers) to be protonated (charge +1 e.u.). Following the same argument we also considered Arg¹⁹⁹ to be protonated. Note that this residue together with Trp⁴⁶³ and BH₄ stack on top of each other like a sandwich (with Trp⁴⁶³ in between) and it is reasonable to believe that the positive charge of Arg¹⁹⁹, which is delocalized on the guanidinium moiety, involves this residue in the π-stacking interaction between Trp⁴⁶³ and BH₄. The residue Glu^479B, which is 0.466 nm (0.545 nm in the crystal structure) far from the hydroxy tail of BH₄ (docked in chain A), does not interact with the cofactor and was considered to be deprotonated. There is no experimental evidence that these residues should have a different protonation state than the one assigned in this study. (c) The iNOSoxy structure was solvated in a box of 19529 water molecules (TIP4P); (d) eight Na⁺ ions were added at random positions in the solvent to neutralize the negative charge of the dimer. The potential energy of the solvated iNOSoxy was minimized using the OPLS force field²⁴ implemented in Gromacs³¹.

Results and Discussion

The geometry and the electronic structure of neutral, cation and anion BH₄ Geometry

Figure 1 shows the quantum mechanically optimized geometry of BH₄. This figure also displays a comparison between the bond lengths of the neutral (black), cation (red) and anion (blue) forms of BH₄ in the pyrimidine (aromatic) and tetrahydropyrazine rings. One interesting structural detail of neutral BH₄ is the non-equivalence of the N⁵ and N⁸ nitrogen atoms (Scheme 1). The atom N⁵ is hybridized sp³ (C^4A-N⁵ bond length is .1417 nm, C^4A-N⁵-H bond angle is 108.9º and C⁴-C^4A-N⁵-H dihedral angle is −25.3º), while atom N⁸ is hybridized sp² (C^8A-N⁸ bond length is .1365 nm, C^8A-N⁸-H bond angle is 116.5º and N¹-C^8A-N⁸-H dihedral angle is −7.3º). This structural aspect is important because it was hypothesized that in the BH₄ cation the spin density of the unpaired electron is mainly localized at N⁵.³⁵ Table 1 shows that the geometry of neutral BH₄ calculated at B3LYP/6-31+G(d,p) level is in good agreement with the structure of BH₄ (without H atoms) bound to chain A of the iNOSoxy (PDB id: 1NSI) dimer. The root mean square deviation of the bond lengths given in Table 1 is 0.0026 nm and the RMSDs for bond and dihedral angles are 2.4º and 3.9º, respectively. Figure 1 shows one noticeable aspect of the difference in structure between the neutral, cation and anion forms of BH₄.The alternation of bond lengths involving C^4A, C^8A, N⁵ atoms is reversed in the cation as compared with the neutral and anion BH₄: C^4A-N⁵ is .1417 in neutral and .1425 in anion versus .1340 nm in cation, while C^4A-C^8A is .1386 in neutral and .1387 in anion versus .1431 nm in cation. Table 2 shows a comparison of a subset of bond and dihedral angles (mostly defining the pyrimidine and tetrahydropyrazine rings). As in the case of bond lengths, a substantial change in bond angle (8.2º) is observed between the cation and neutral BH₄ and involves the N⁵ atom (e.g. the C^4A-N⁵-C⁶ angle is 113.8º (neutral), 115.0º (anion), and122.0º (cation)). Overall, the anion geometry is closer to the geometry of neutral BH₄ than the cation geometry is. This may be one of the reasons that the electron affinity (EA) of BH₄ in gas phase is less than 1 eV, while the ionization potential is around 6 eV (vide infra).

Figure 1.

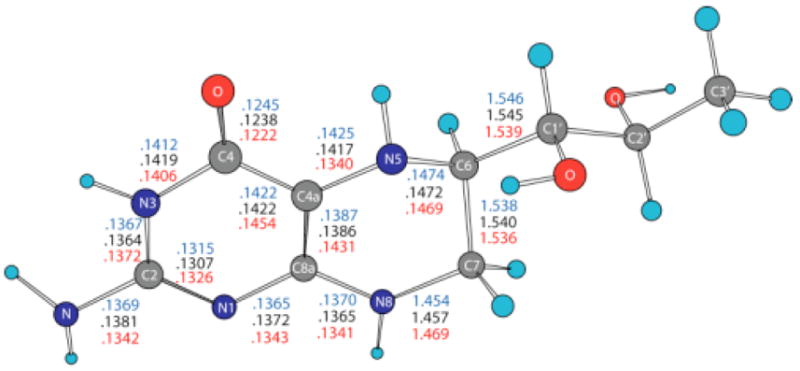
Bond lengths (nm) in BH₄ neutral (black), cation (red) and anion (blue). The geometries have been optimized in gas phase using density functional theory (B3LYP/6-31+G(d)).

Table 1.

Comparison between the X-Ray Crystal Structure of Tetrahydrobiopterin bound to Nitric Oxide Synthase, and the Structure Calculated by Density Functional Theory and Molecular Mechanics (using the OPLS Force Field).

Internal coordinate	Geometry
	QMa	Crystalb	DQM-Cc	M Md	DQM-MMe
Bond lengthf
N1-C2	.1307	.1346	−.0039	.1322	−.0015
N1-C8A	.1372	.1371	.0001	.1389	−.0017
C2-N3	.1364	.1352	.0012	.1349	.0015
N3-C4	.1419	.1402	.0017	.1403	.0016
C4-C4A	.1422	.1417	.0005	.1420	.0002
C4A-N5	.1417	.1448	−.0031	.1408	.0009
C8A-N8	.1365	.1333	.0032	.1382	−.0017
N5-H	.1019	-	-	.1023	−.0004
N5-C6	.1472	.1514	−.0042	.1480	−.0008
C6-C7	.1540	.1509	.0031	.1556	−.0016
C7-N8	.1457	.1455	.0002	.1468	−.0011
N8-H	.1009	-	-	.1013	−.0004
RMSDg			.0026		.0012
MAXh			.0042		.0017
Bond anglei
C4-C4A-N5	119.4	117.6	1.8	118.5	.9
C4A-N5-C6	115.5	111.0	4.5	116.0	−.5
C4A-N5-H	108.9	-	-	110.1	−1.2
C6-N5-H	113.9	-	-	113.6	.3
N5-C6-C7	108.6	108.9	−.3	107.7	.9
C6-C7-N8	110.5	111.7	−1.2	109.9	.6
C8A-N8-C7	120.7	119.9	.8	119.8	.9
C8A-N8-H	116.5	-	-	117.2	−.7
C7-N8-H	120.9	-	-	120.3	.6
RMSD			2.4		.9
MAX			4.5		1.2
Dihedral anglei
C4-C4A-N5-H	−25.3	-	-	−22.4	−2.9
N1-C8A-N8-H	−7.3	-	-	−9.7	2.4
N5-C4A-C8A-N8	−3.4	−1.9	1.3	−1.1	2.2
C8A-C4A-N5-C6	24.9	29.0	−4.1	23.1	1.8
C4A-C8A-N8-C7	10.7	1.6	9.1	9.7	1.0
C4A-C8A-N8-H	175.1	-	-	171.4	3.7
C4A-N5-C6-C7	−49.0	−53.8	4.8	−48.8	−.2
C4A-N5-C6-H	70.7	-	-	69.5	1.2
N5-C6-C7-N8	53.6	53.8	−.2	54.5	−.9
C6-C7-N8-C8A	−36.1	−28.6	−7.5	−37.1	1.0
C6-C7-N8-H	160.0	-	-	161.9	−1.9
RMSD			3.9		4.3 3.2j
MAX			9.1		10.2 6.4j

^aThe structure of BH₄ obtained by calculation using the density functional theory (B3LYP/6-31+G(d,p)) with the Gaussian98 program ²⁶.

^bThe structure of BH₄ used in this comparison was extracted from the crystal structure of iNOSoxy dimer (1NSI)³⁴.

^cDifference between the same internal coordinate measured in the quantum mechanically calculated (DFT) structure and the crystal structure of BH₄.

^dThe structure of BH₄ calculated with the molecular mechanics program Gromacs ³¹ using the OPLS force field ⁴¹ derived by the GA method.

^eDifference between the same internal coordinate measured in the DFT structure and the molecular mechanics optimized structure of BH₄.

^fin nm.

^gRoot-mean square deviation for all bond lengths in BH₄.

^hMaximum difference.

ⁱin degree.

^jCalculated without considering the dihedral angles that contain at least one hydrogen atom.

Table 2.

Bond and Dihedral Angles in the Optimized Gas Phase Geometries^a of the Neutral, Cation and Anion Forms of Tertrahydrobiopterin.

	Neutral	Cation	N-Cb	Anion	N-Ac
Bond angle c
N1-C8a-C4a	123.7	122.6	1.1	124.2	−0.5
C4-C4a-C8a	119.3	119.4	0.1	119.2	0.1
C4a-C8a-N8	119.6	117.8	1.8	119.4	0.2
N5-C4a-C8a	120.8	121.3	−0.5	121.6	−0.8
C4a-N5-C6	113.8	122.0	−8.2	115.0	−1.2
N5-C6-C7	108.4	108.7	−0.3	108.6	−0.2
N5-C6-C1′	106.6	109.2	−2.6	106.4	0.2
C6-C7-N8	110.8	110.4	0.4	110.4	0.4
C7-N8-C8a	122.3	121.8	0.5	121.0	1.3
Dihedral angled
C4-C4a-N5-C6	−148.4	−170.8	22.4	−153.6	5.2
C4a-N5-C6-C7	−53.9	−34.7	−19.2	−48.6	−5.3
C4a-C8a-N8-C7	0.3	12.9	−12.6	10.8	−10.5
C4a-N5-C6-C1′	−175.8	−159.0	−16.8	−170.3	−5.5
N5-C6-C7-N8	50.6	47.0	3.6	53.5	−2.9
C6-C7-N8-C8a	−25.7	−39.8	14.1	−36.4	10.7

^acalculated at B3LYP/6-31+G(d,p) level of density functional theory

^bneutral – cation

^cneutral – anion

^dIn degree (°).

Charges and spin density

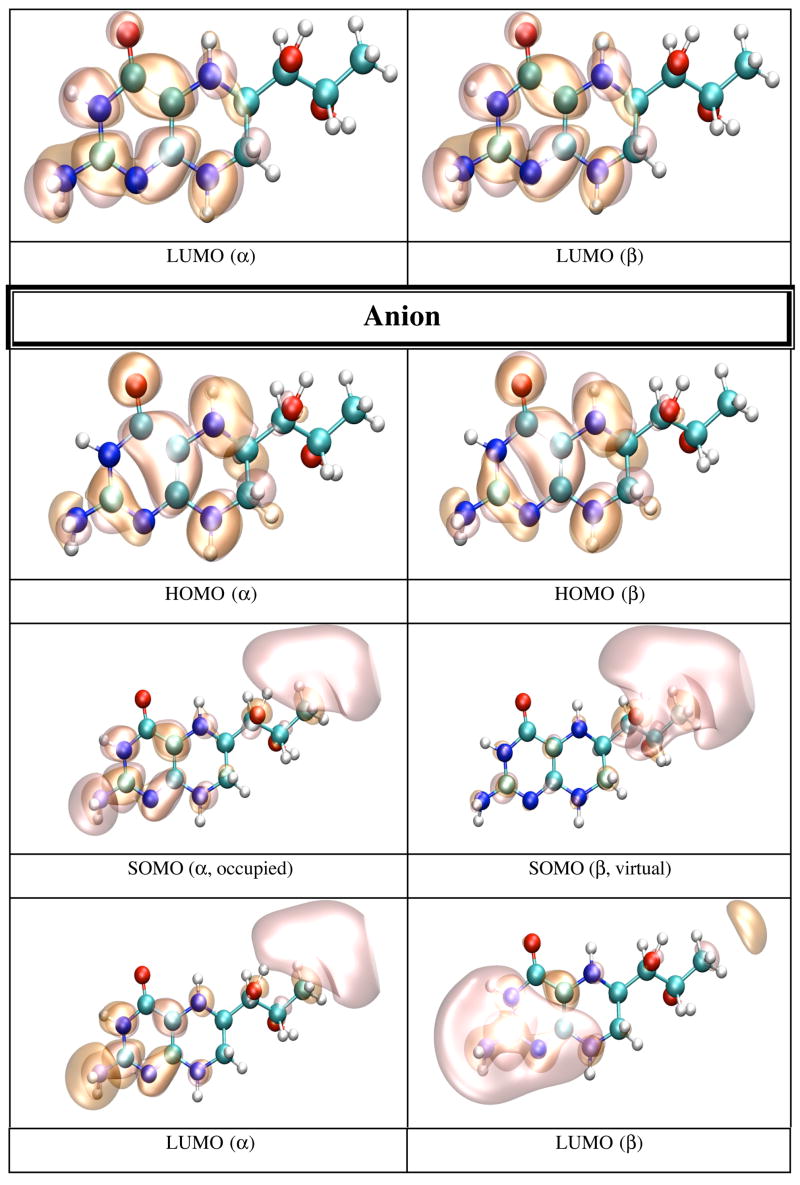
Electrostatic potential-derived (ESP) charges have been calculated using the ChelpG³⁶ and Merz-Kollman (MK)²⁵ methods as implemented in the Gaussian98 program²⁶. The ChelpG-derived charges (not shown) are slightly smaller than the MK-derived charges in the pyrimidine ring of BH₄, but are larger in the tetrahydropyrazine ring of BH₄. The partial charge of N ⁵ (ChelpG: - 0.4974 e.u.; MK: −0.4958 e.u.) is about half the partial charge of N⁸ (ChelpG: −0.8119 e.u.; MK: −0.8089 e.u.). Figure 2 shows MK charges for the neutral (black), cation (red), and anion (blue) forms of BH₄. The C^4A, N⁵ and N⁸ atoms are negatively charged (-.3213, -.4974 and -.8119 e.u., respectively) in neutral BH₄. Removing one electron from BH₄ makes these atoms less negative (-.1622, -.2462 and -.5854 e.u., respectively), but adding one electron causes a small change in the partial charges of these atoms (-.3645, -.4835 and -.8947 e.u., respectively). On the other hand, the partial charges on the C⁶ and C⁷ atoms (in neutral BH₄: .1300 and .3712 e.u., respectively) affect the anion more (.5432 and .8039 e.u., respectively) than in the cation (.1395 and .1335 e.u., respectively). It should be noted that the charge of N³ atom is less negative in the anion (-.4850 e.u.) compared to the neutral and cation forms (-.7400 and -.7226 e.u., respectively). The semi-occupied molecular orbital (SOMO) of the anion is mostly localized on the side of the pyrimidine ring containing the N³ atom and NH₂ group (vide infra), whereas the virtual SOMO is mostly localized near the hydroxy tail of BH₄. Figure 3 gives the spin densities for the cation (red) and anion (blue). In the case of the cation, more than half of the spin density is localized on the C^4A and N⁵ atoms, which supports an earlier suggestion that much of the spin density is localized on atom N⁵. The results for the anion are more difficult to rationalize since the spin densities oscillate from positive to negative values. However, a graphical representation of the spin density for the anion (vide infra) indicates that it is mostly localized on the side of the pyrimidine ring containing the N³ atom andthe NH₂ group.

Figure 2.

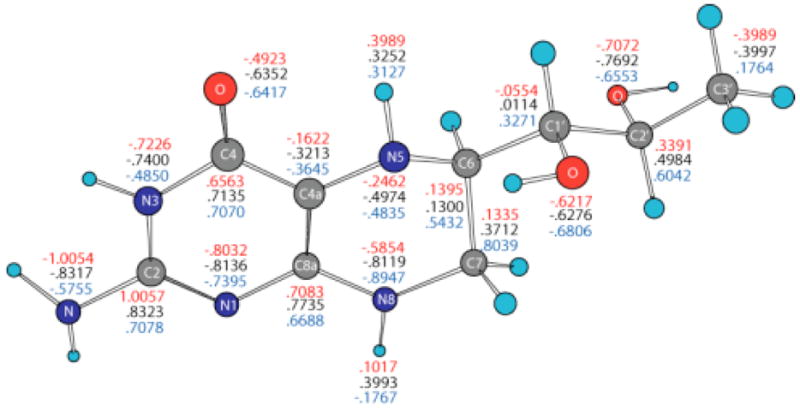
Merz-Kollman electrostatic potential-derived partial atomic charges for atoms in BH₄ neutral (black), cation (red) and anion (blue) calculated by density functional theory (B3LYP/6-31+G(d)) in gas phase.

Figure 3.

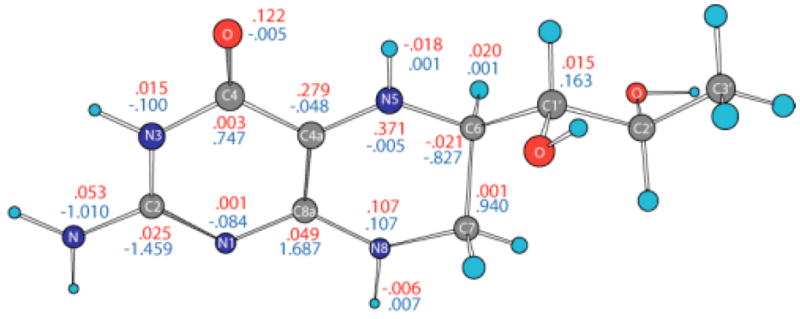
Spin densities for BH₄ cation (red) and anion (blue) calculated by density functional theory (B3LYP/6-31+G(d)) in gas phase.

OPLS force field for BH₄, P₄₅₀ Heme, and Zn(Cys)₄complex

The quality of the OPLS force field parameters (for BH₄ atom types) was assessed by comparing the optimized geometry of BH₄ calculated by quantum mechanics and molecular mechanics methods, and the geometry of BH₄, extracted from the crystal structure of the oxygenase domain from inducible nitric oxide synthase (iNOSoxy, PDB id: 1NSI). The discussion here will be focused on the geometry of the pyrimidine and tetrahydropyrazine rings of BH₄. Table 1 shows the comparison of the quantum mechanical, molecular mechanical and crystal structures using a subset of the internal coordinates of the atoms that compose these two rings. The difference between the quantum mechanical structure, on the one hand, and the crystal and molecular mechanical structures, on the other hand, are expressed as RMSDs for bond lengths, bond angles and dihedral angles, respectively. The root mean square deviation between the QM and MM structures (QM-MM) for bond lengths is 0.0012 nm. For bond angles the QM-MM is 0.9º, and for dihedral angles the QM-MM RMSD is 4.3º. The QM-MM RMSD decreases to 3.2º when the dihedral angles that include hydrogen atoms are excluded (the crystal structure has no hydrogen atoms). Table 1 shows that the MM optimized geometry is very close to the QM optimized and crystal structure geometries.

To produce realistic molecular dynamics (MD) simulations it is essential that the derived force field parameters correctly reproduce not only the equilibrium geometry, but also the dynamics of the molecule (i.e. the normal modes of vibration). The OPLS parameters that modulate the MM-calculated vibrational frequencies are the force constants for bond stretching, angle bending and dihedral angle torsion. By comparing the QM- and MM-derived vibrational frequencies we assess the quality of theseforce constants. The root mean square deviation of 90 normal modes of vibration for BH₄ is 38 cm⁻¹ withthe largest difference being 131 cm⁻¹ for normal mode 75 (see table in the Supporting Information). Table 3 gives a comparison between the QM-MM RMSD of vibrational frequencies calculated for BH₄, glycine (94 cm⁻¹) and tyrosine. (65 cm⁻¹). Table 3 shows that the force field derived in this work for BH₄ is of better quality than the average OPLS parameters used for amino acids. In addition to the BH₄ cofactor, iNOSoxy dimer contains a P₄₅₀ heme cofactor and a Zn-cysteine bridge between the two monomers³⁷. In order to perform an energy minimization of the iNOSoxy dimer in water we derived OPLS parameters for P₄₅₀ heme cofactor³³ and a [Zn(Cys)₄]^2- complex³⁸. Table 3 and 4 list the RMSDs for geometrical parameters (Table 4) as well as for vibrational frequencies (Table 3) for these two moieties.

Table 3.

Root mean square deviation (RMSD) of Vibrational Frequencies for Tetrahydrobiopterin, Dioxy-Iron Porphirin Methylthiolate Complex, Tetramethylthiolate Zn Complex, Glycine and Tyrosine.

Compounda	RMSDb
BH4	38
O2-Fe-PP-SMe c	43
[Zn(MeS)4] 2- d	50
Glycine	94
Tyrosine	65

^aThe vibrational modes were calculated with the OPLS force field obtained by the GA method and implemented in Gromacs program³¹.

^bRoot mean square deviation in cm⁻

^cDioxy-iron porphyrin methylthiolate complex.

^dTetramethylthiolate Zn complex.

Table 4.

Root mean square deviation (RMSD) between the Quantum Mechanical and the Molecular Mechanical Optimized Structures of Tetrahydrobiopterin, Dioxy-Iron Porphirin Methylthiolate Complex, and Tetramethylthiolate Zn Complex.

Compound	RMSD a
	Bond length [nm]	Bond angle [º]	Dihedral angle [°]
BH4	0.0013 0.0012	0.89 1.57	20.6 15.0
O2-Fe-PP-SMe b	0.0010 0.0010	0.98 0.98	2.15 2.15
[Zn(MeS)4] 2- c	0.0036 0.0036	4.62 4.62	23.20 23.20

^aFirst row: RMSD for parameterized bond lengths, bond angles and dihedral angles; second row: total RMSD.

^bDioxy-iron porphyrin methylthiolate complex.

^cTetramethylthiolate Zn complex.

The IP and EA of BH₄ in gas phase, solution and protein environment

The IP and EA of BH₄ in different chemical environments (e.g. vacuum, solution, protein environment) are probably the most relevant electronic properties for understanding the involvement of BH₄ in the electron transfer in NOS because, unlike in other enzymes, the cofactor in NOS is oxidized/reduced without changing protonation states¹. Calculations show that the wave function of BH₄ is highly polarizable and an external electric field shifts the frontier molecular orbitals (i.e. HOMO, LUMO, and SOMO for the cation and anion) and thus changes the IP and EA of BH₄. We calculated the IP and EA of BH₄ in gas phase, dielectric²⁷ (dielectric constant 80.0), explicit water (TIP4P²⁸) and protein environment (iNOSoxy) using the density functional theory at B3LYP/6-31+G(d,p) level.

Gas phase

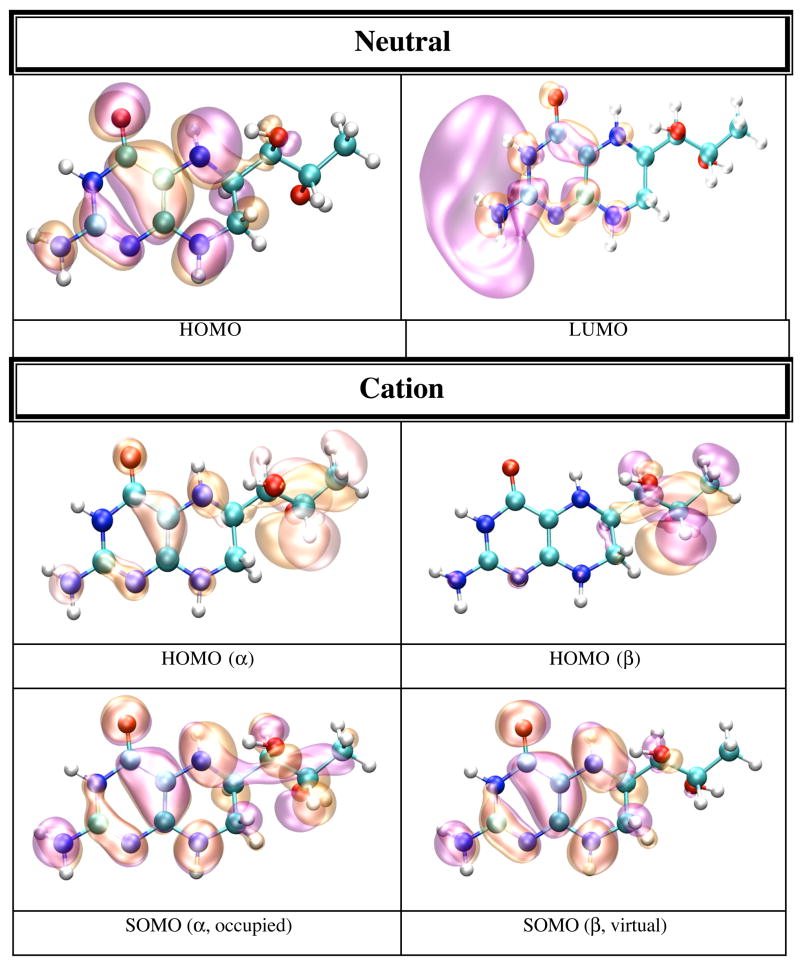
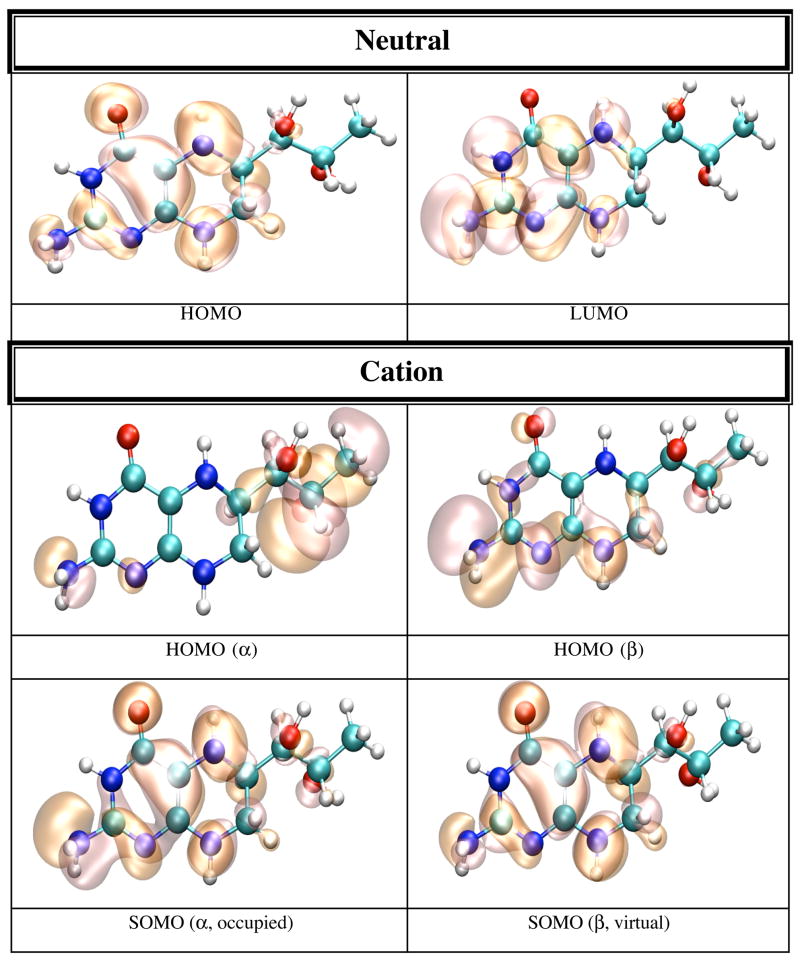
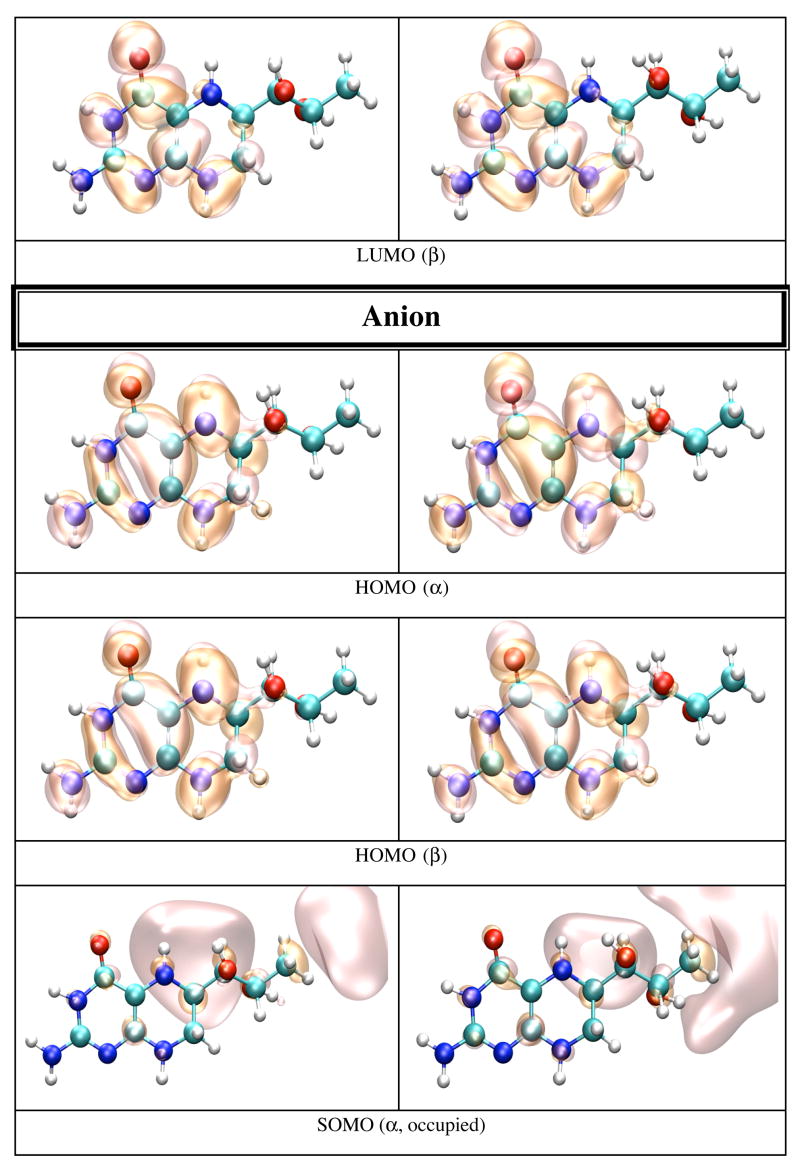
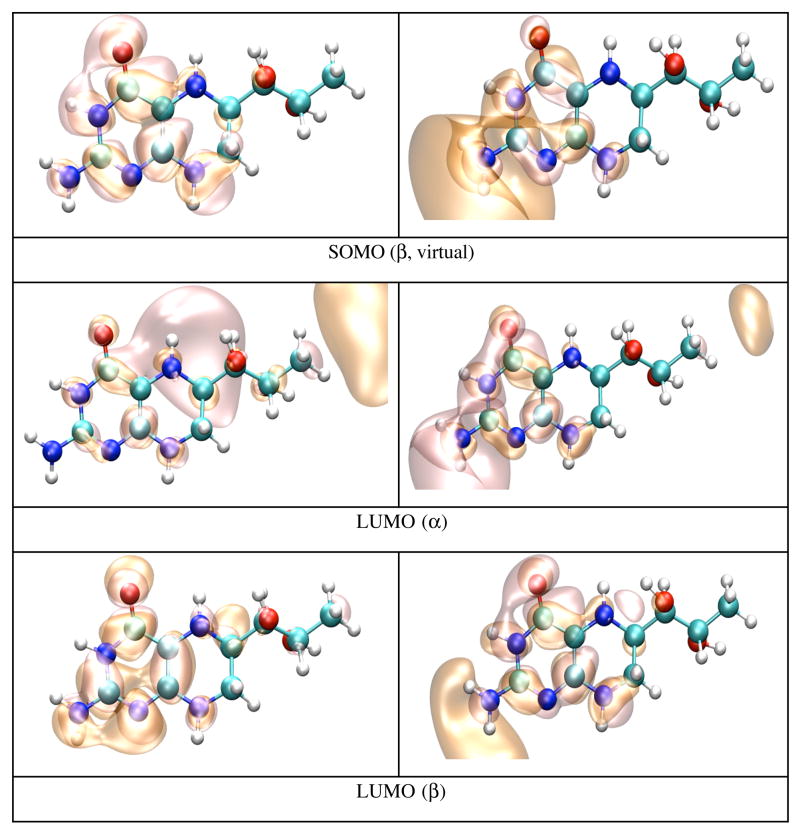
In gas phase the neutral BH₄ is more stable than both its cation and anion. Because there are less geometrical differences between the anion and neutral BH₄ than between the cation and neutral BH₄ (vide supra), one expects that the difference in energy between the anion and neutral BH₄ to be smaller than the difference between the cation and neutral BH₄. Table 5 lists the IP and EA of BH₄ calculated in different chemical environments. The IP increases with the use of more sophisticated basis sets, e.g. from 6.09 eV (6-31+G(d,p)) to 6.77 eV (6-311+G(d,p) and 6-311++G(d,p)). The electron affinity, however, does not show a definite trend; e.g. −0.39 eV (6-31+G(d,p)), −0.44 eV (6-311+G(d,p)), −0.11 eV (6-311++G(d,p)). MP2 calculations performed on BH₄ using the 6-31+G(d,p) basis set yield 7.09 eV for the IP and −1.96 eV for EA of BH₄. It is worthy of note that the IP and EA change only slightly with the change in the conformation of BH₄ and that they are mostly susceptible to the action of an external electric field. Thus, when the calculation is performed on the geometry of BH₄ in solution, or on the geometry of BH₄ in protein environment without the external electric field due to point charges, the IP and EA change from 6.09 and −0.39 eV in gas phase, to 6.60 and −0.42 eV in water, to 6.37 and −0.43 eV for BH₄ bound to chain A, and 6.47 and −0.44 eV for BH₄ bound to chain B of iNOSoxy dimer. Figure 4 shows graphical representations of the HOMO and LUMO orbitals for the neutral BH₄ and of HOMO, SOMO and LUMO orbitals of the BH₄ cation and anion. The pictures were obtained by visualizing CUBE files (obtained with Gaussian98²⁶) with the VMD²⁹ and POV-Ray³⁰ programs. Figure 4 shows that the HOMO of neutral BH₄ is localized on the two rings, while the LUMO is mostly localized near the pyrimidine ring (close to the N³ atom and NH₂ group). The SOMO (occupied) of the anion is similar to the LUMO of the neutral BH₄ (localized mostly in the same region), though the virtual SOMO is mainly localized near the hydroxy tail of BH₄. The localization of the occupied SOMO of the anion confirms that the unpaired electron is basically unbound in gas phase (the EA is negative). On the other hand, the occupied SOMO of the cation spreads over the entire molecule, whereas the virtual SOMO is mostly localized on the two rings of BH₄ and is very similar to the HOMO of the neutral BH₄. Another distinctive feature of these frontier orbitals is that the LUMO (for α and β electrons) of the cation are very different from the LUMO of the neutral species and SOMO of the anion (Figure 4). This observation is valid for all chemical environments of BH₄ used in this study (vide infra).

Table 5.

Ionization Potential and Electron Affinity^a of (6R)-5,6,7,8-Tetrahydrobiopterin in Gas Phase, Dielectric, Water and Protein Environment.

Environment	Energyb			IPc	EAc
	Neutral	Cation	Anion
Gas phase	−851.509486	−851.285676	−851.495086	6.09	−0.39
	−851.7029332d	−851.4540438	−851.6868365	6.77	−0.44
	−851.7033758e	−851.4545306	−851.6993969	6.77	−0.11
	−849.083620f	−848.825127	−849.011603	7.09	−1.96
	−851.467803g	−851.225248	−851.452508	6.60	−0.42
	−851.475396h	−851.241385	−851.459583	6.37	−0.43
	−851.478942i	−851.241096	−851.4626326	6.47	−0.44
Waterj	−1195.536599	−1195.2724002	−1195.523429	7.19	−0.36
Dielectrick	−851.556900	−851.379800	−851.587815	4.82	0.84
Proteinl	−12441.231311	−12441.072356	−12441.139355	4.33	−2.50
	−12441.221713	−12441.096451	−12441.099584	3.41	−3.32

^aCalculations performed by density functional theory at B3LYP/6-31+G(d,p) level unless otherwise specified. All calculations were performed with Gaussian98 program ²⁶.

^bIn Hartree.

^cIn eV.

^dB3LYP/6-311+G(d,p) level.

^eB3LYP/6-311++G(d,p) level.

^fMP2/6-31+G(d,p) level.

^gCalculation on the optimized geometry of BH₄ in solution without the external electric field generated by the surrounding water.

^hCalculation on the optimized geometry of BH₄ in protein environment (chain A of iNOSoxy dimer) without the external electric field generated by the surrounding amino acids, water molecules and P₄₅₀ heme.

ⁱCalculation on the optimized geometry of BH₄ in protein environment (chain B of iNOSoxy dimer) without the external electric field generated by the surrounding amino acids, water molecules and P₄₅₀ heme.

^jCalculation on the optimized solution geometry of BH₄ with external electric field generated by point charges representing TIP4P water molecules. The cofactor’s molecular mechanics force field is described by OPLS parameters ²⁴ obtained as described in the Methodology section. The optimization was performed on BH₄ immersed in a box of 603 water (TIP4P) molecules.

^kCalculation on the gas phase optimized geometry of BH₄ with the external electric field generated by a polarizable dielectric (dielectric constant = 80).

^lCalculation on the optimized geometry of BH₄ in protein environment (iNOSoxy) with external electric field generated by the point charges representing surrounding amino acids, water molecules and P₄₅₀ heme. The molecular mechanics force fields for BH₄, P₄₅₀ heme and [Zn(Cys)₄]²⁻ complex are described by OPLS parameters ²⁴ obtained as described in the Methodology section. The optimization was performed on the iNOSoxy dimer immersed in a box of 19529 water molecules (TIP4P) and 8 counter ions (Na⁺). First row: data for BH₄ bound at chain A of the iNoxy dimer; second raw: data for BH₄ bound to chain B.

Figure 4.

HOMO and LUMO orbitals for BH₄ neutral (N), HOMO SOMO, and LUMO orbitals for the BH₄ cation (C) and anion (A) calculated by density functional theory (B3LYP/6-31+G(d)) in gas phase with Gaussian 98. The MO pictures have been obtained from CUBE Gaussian98 files and displayed with the VMD and POV-Ray programs.

Solution

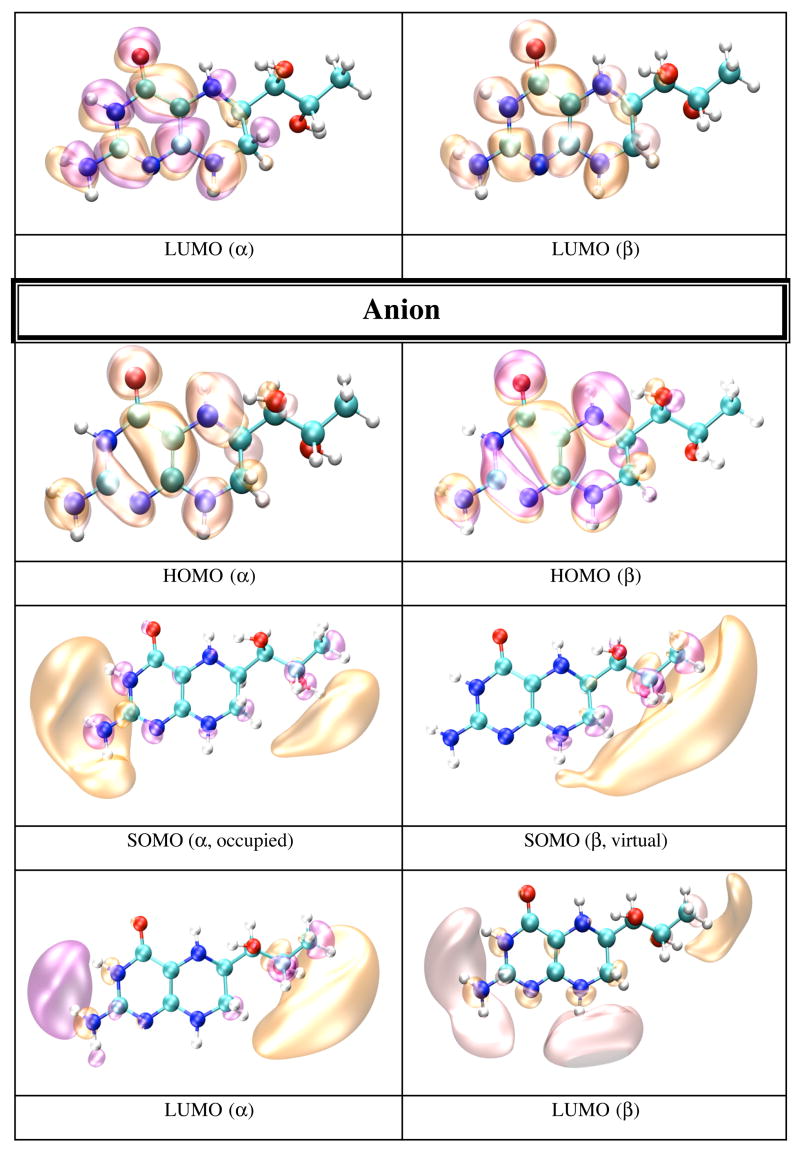
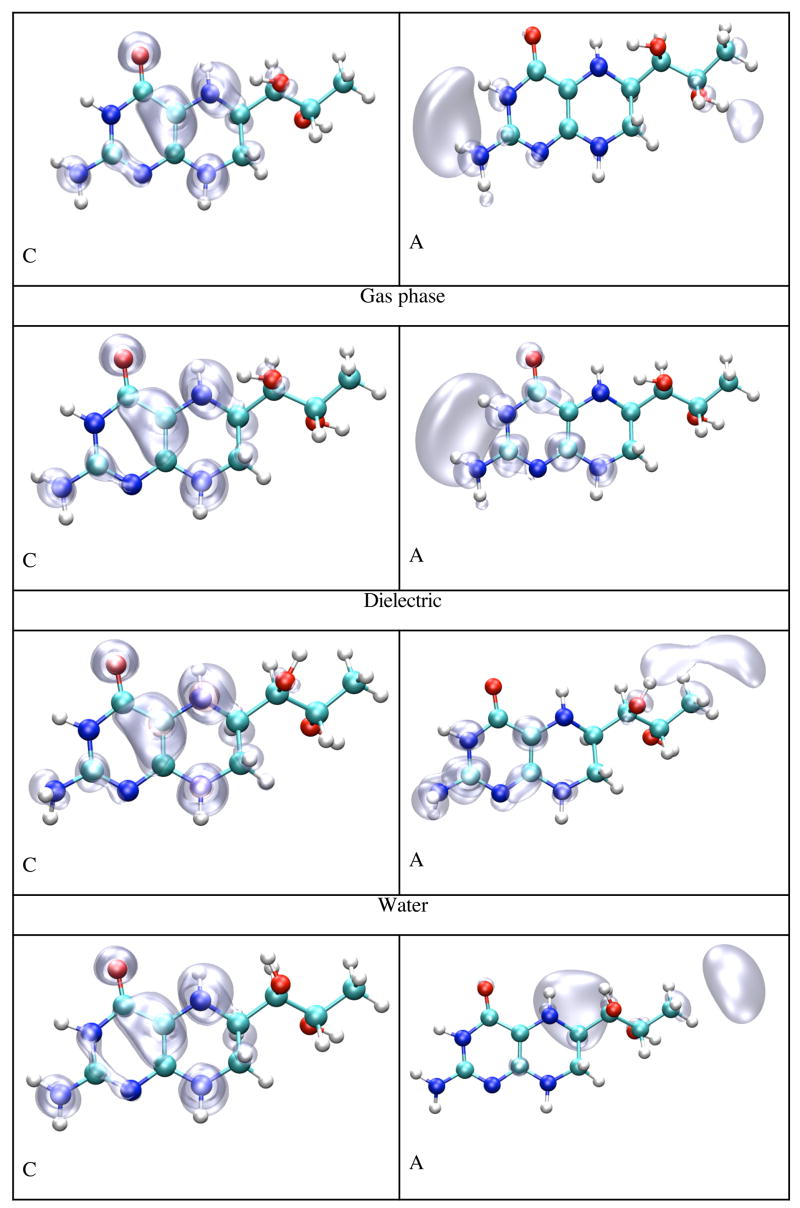
The IP and EA of BH₄ have been calculated both in dielectric and explicit water (TIP4P). The calculation in dielectric (dielectric constant 80.0) gives the effect of an average electric field on the IP and EA due to water polarization, and the calculation in explicit water introduces anisotropy in the electric field due to specific positions of water molecules and the presence of hydrogen bonds. The calculations on BH₄ in dielectric and explicit water show a substantial effect from the external electric field on the IP and EA of BH₄. Calculation in dielectric gives the average effect of water polarization on the electronic structure of BH₄. Thus the IP decreases to 4.82 eV, while the EA becomes positive (0.84 eV), which makes the anion more stable than neutral BH₄ in dielectric. This result suggests that one electron reduction of BH₄ in water should be easy, while one electron oxidation may not^39,40. The calculation in explicit water (Table 5) shows that the IP (7.19 eV) and EA (−0.36 eV) values are closer to the vacuum values rather than the dielectric values. Figure 5 shows that neutral BH₄ makes nine H-bonds with surrounding water molecules (in this particular energy minimized configuration). Five of these H-bonds are made with the BH₄ tail, while the remaining four H-bonds are made with the NH₂ group, N¹, O⁴, H⁵ and H⁸ (Scheme 1). Figures 6 and 7 show pictures of HOMO and LUMO orbitals for the neutral, and HOMO, SOMO, and LUMO for the cation and anion in dielectric (Figure 6) and explicit water (Figure 7). One distinctive feature of the LUMO of neutral BH₄ calculated in either dielectric or water is that it resembles the LUMO of the gas phase cation rather than the LUMO of the gas phase neutral BH₄. There is little difference between the HOMO of neutral BH₄ and the SOMO of the cation (dielectric and water), and the same holds for LUMO. However, the HOMO of the cation (explicit water) show different polarization of α and β electrons: the α electron is localized mainly in the hydroxy tail of BH₄, while the β electron is localized on parts of the two rings of BH₄ containing N¹ and N⁸ atoms. In contrast, the SOMO of the anion in dielectric are very similar to the SOMO of gas phase BH₄ anion (i.e. localized near/on the pyrimidine ring), while the SOMO in water are mostly localized in the tail of BH₄, probably due to specific interactions with water molecules. The α and β electrons in LUMO of the anion have different polarization in water and similar polarization in dielectric. This result demonstrates the limitation on using dielectric calculations as a substitute for explicit solvent environment.

Figure 5.

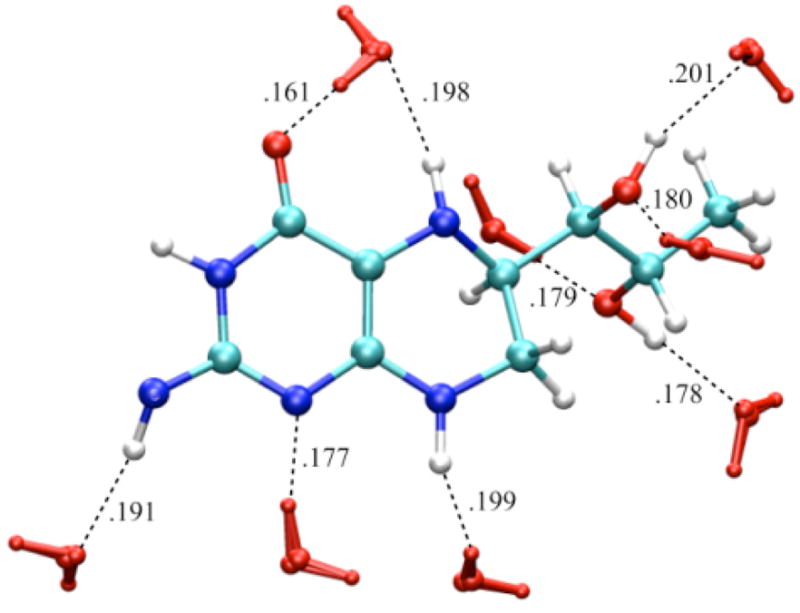
Water configuration (red) around neutral BH₄ neutral: the water (TIP4P) box containing one molecule of BH₄ (OPLS) was energy minimized using Gromacs program. There are nine H-bonds (black dashed lines) between BH₄ and water within 0.2 nm.

Figure 6.

HOMO and LUMO orbitals for BH₄ neutral (N); HOMO SOMO, and LUMO orbitals for the BH₄ cation (C) and anion (A) calculated by density functional theory (B3LYP/6-31+G(d)) in dielectric (dielectric constant 80.0) with Gaussian 98. The MO pictures were obtained from CUBE Gaussian98 files and displayed with the VMD and POV-Ray programs.

Figure 7.

HOMO and LUMO orbitals for BH₄ neutral (N), HOMO SOMO, and LUMO orbitals for the BH₄ cation (C) and anion (A) calculated by density functional theory (B3LYP/6-31+G(d)) in water (TIP4P) with Gaussian 98. The MO pictures were obtained from CUBE Gaussian98 files and displayed with the VMD and POV-Ray programs.

Protein environment

We finally calculated the IP and EA of BH₄ docked in the active site of chains A and B of iNOSoxy dimer. Figure 8 shows that in this particular configuration of the enzyme, there are slightly different chemical environments for BH₄ docked to chain A (top pane) and chain B (bottom pane). One important feature of cofactor docking to NOS is that the carboxylic oxygen of one propionate group of heme makes bifurcated H-bonds (Figure 8) with H³ (0.192 nm in chain A and 0.188 nm in chain B) and one hydrogen atom of the NH₂ group of BH₄ (0.178 nm in chain A and 0.189 nm in chain B). Another distinctive feature is the sandwich arrangement (π-stacking) that BH₄, Trp⁴⁶³, and Arg¹⁹⁹ make together (vide supra). The distance between BH₄ and Trp⁴⁶³ is 0.375 nm in chain A and 0.381 nm in chain B. The interactions of BH₄ with heme, the π-stacking residues (Trp⁴⁶³ and Arg¹⁹⁹), and Arg³⁸¹ seem to be critical for the function of the cofactor. Tetrahydrobiopterin bound to chain A makes nine H-bonds (Figure 8, top pane): four H-bonds are made with water molecules, while the other five H-bonds are made with P₄₅₀ heme_A, Ile^462A, Trp^463A and Ser^118A. Tetrahydrobiopterin bound to chain B makes seven H-bonds (Figure 8, bottom pane); three H-bonds are made with water molecules and the remaining four H-bonds are made with P₄₅₀ heme_B, Ile^462B, Arg^381B and Ser^118B.

Figure 8.

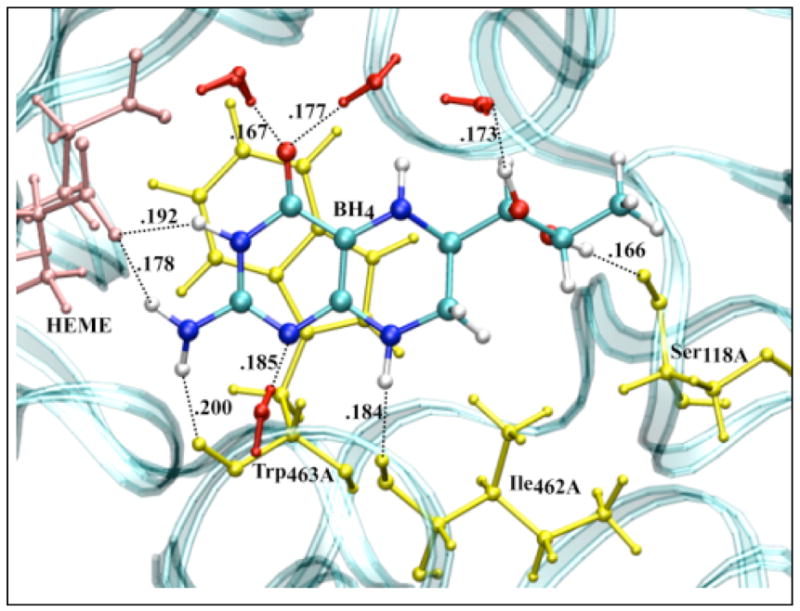
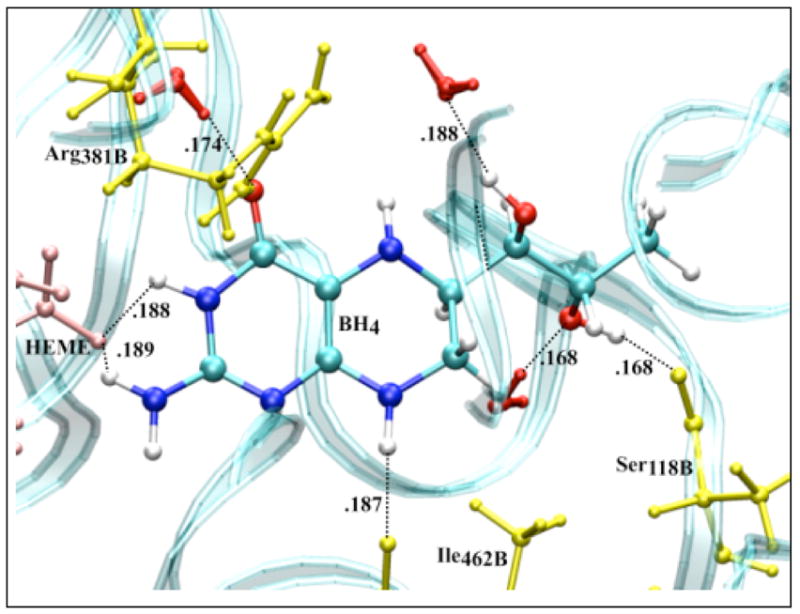
Amino acid residues (yellow), P₄₅₀ heme (pink) and solvent (red) configuration around neutral BH₄ bound to chain A (top) and chain B (bottom) of iNOSoxy dimer. The water (TIP4P) box containing a iNOSoxy dimer (OPLS) was energy minimized using Gromacs program. There are nine H-bonds (black dashed lines) between BH₄ (chain A) and amino acid residues, heme and water within 0.2 nm, and seven H-bonds for BH₄ bound to chain B.

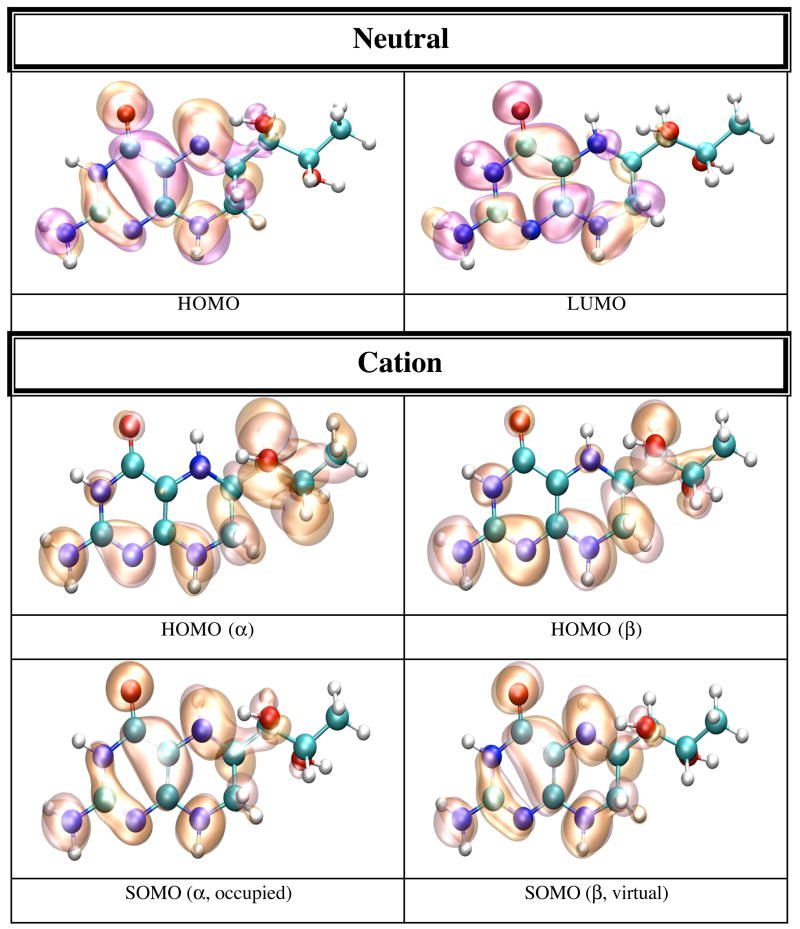
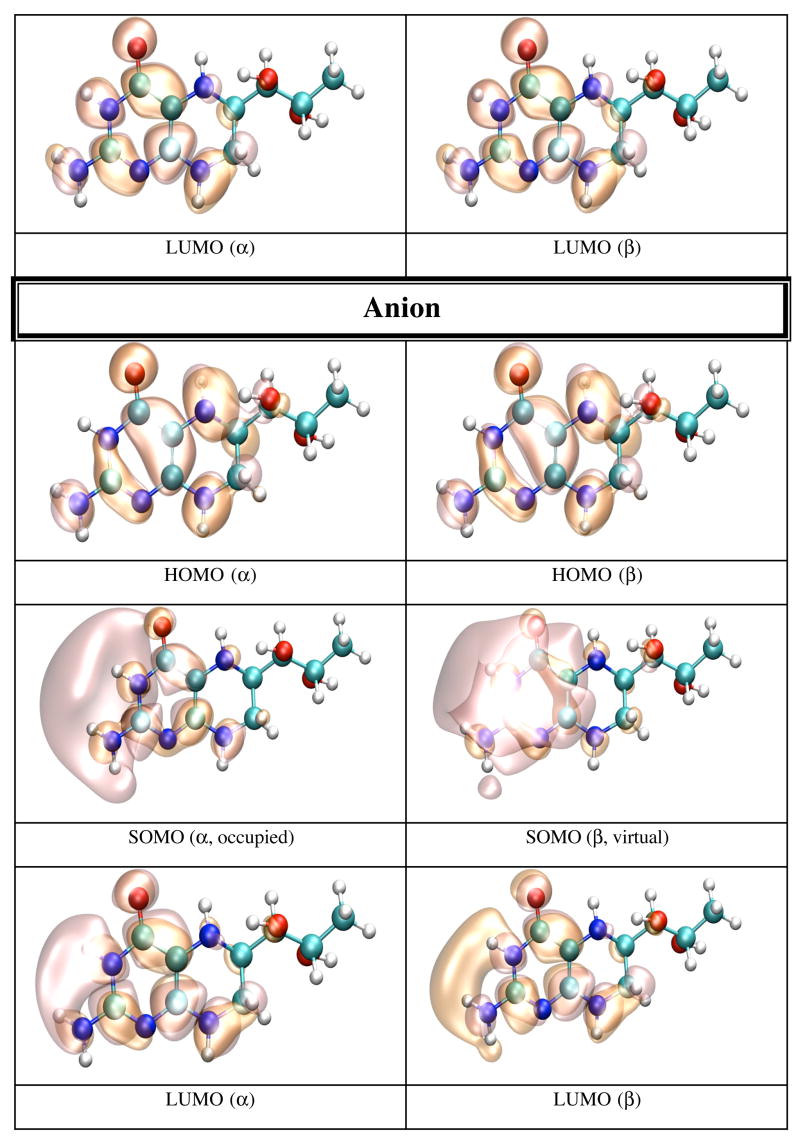
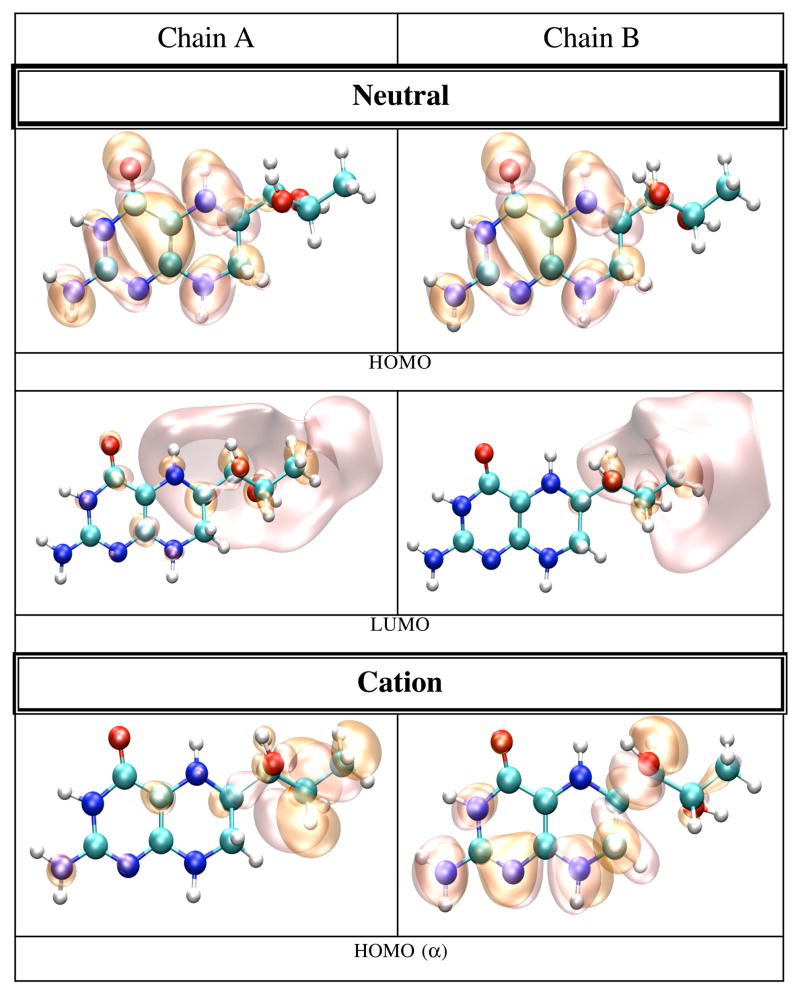
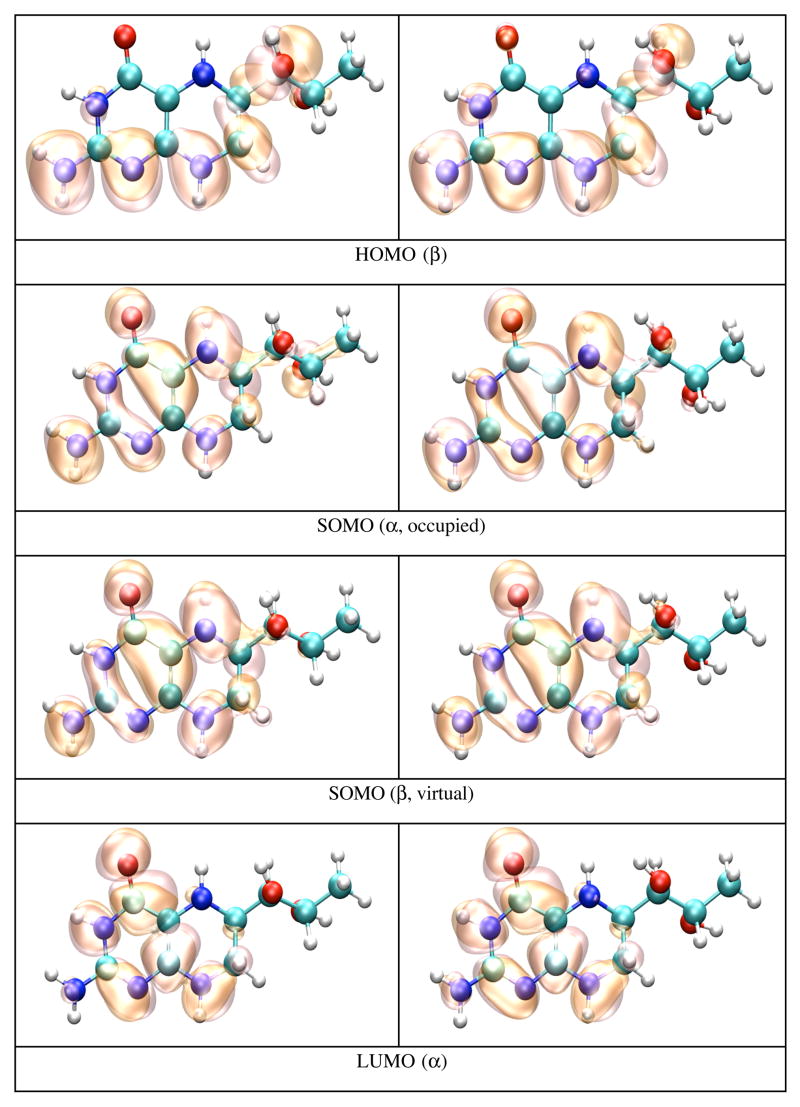
Figure 9 shows pictures of the HOMO and LUMO orbitals of the neutral, and HOMO, SOMO, and LUMO orbitals of the cation and anion BH₄ bound to chain A (left panes) and chain B (right panes). As in the case of BH₄ solvated in water, the HOMO of the neutral BH₄ and the SOMO of the cation are similar and spread over the two rings of BH₄. In contrast, the occupied SOMO of the anion (slightly different for chains A and B, but similar with the LUMO of neutral BH₄) are localized near the BH₄ hydroxy tail, probably because of the presence of the heme propionate group in the vicinity of the pyrimidine ring of BH₄. This should increase the electron repulsion if the unpaired electron is localized in this region; this interaction makes the anion even more unstable. On the other hand, the virtual SOMO (which are slightly different for chains A and B) are mainly localized on the pyrimidine ring. The α and β electrons in the LUMO of the anion have different polarization, as is the case of BH₄ solvated in water.

Figure 9.

HOMO and LUMO orbitals for BH₄ neutral (N), HOMO, SOMO and LUMO orbitals for the BH₄ cation (C) and anion (A) from both iNOSoxy monomers (chains A and B), calculated by density functional theory (B3LYP/6-31+G(d)) in protein environment with Gaussian 98. The MO pictures have been obtained from CUBE Gaussian98 files and displayed with the VMD and POV-Ray programs.

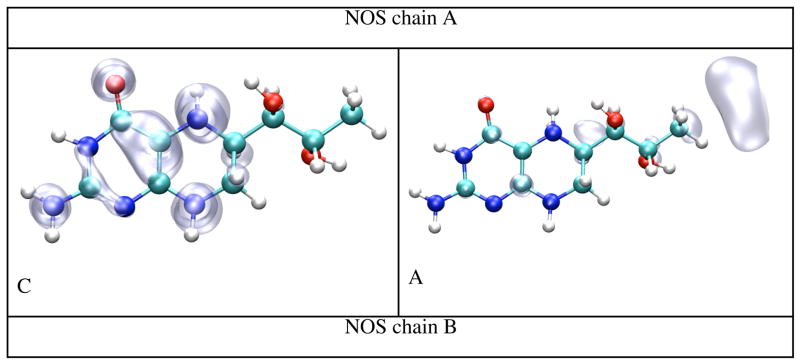
Figure 10 shows the spin densities of the cation (left panes) and the anion (right panes) species of BH₄ in gas phase, solvated in dielectric and explicit water, and bound to chain A and chain B of iNOSoxy dimer. While the cation’s spin densities are very similar in all environments, being mostly localized at the junction between the pyrimidine and tetrahydropyrazine rings (including atoms N⁵ and N⁸), the spin densities found for the anion are much different. For gas phase and dielectric the spin density is mostly localized on the side of the pyrimidine ring, whereas the spin density is localized in the tail for BH₄ in explicit water and protein environment. Table 5 shows that the IP and EA of both BH₄ cofactors (chains A and B) are about 2 eV (IP) and 2.5 eV (EA) lower, respectively, in protein environment than either in gas phase or explicit water. More importantly, there is a significant difference between the IP and EA of BH₄ bound to chains A and B, even though their values in vacuum (calculated for the geometries in protein environment without the electric field of the point charges) differ little (Table 5). The ionization potential and electron affinity of BH₄ bound to chain B are 0.92 eV and 0.82 eV lower, respectively, than those calculated for BH₄ bound to chain A. Figure 11 (top pane) shows that charged amino acid residues of iNOSoxy dimer make a multipole structure around BH₄ with a total charge (chain A BH₄ magenta curve, chain B BH₄ cyan curve) that varies dramatically as a function of the thickness of the layer. The multipole structure for a particular layer (hypothetical) which can have a net charge, demonstrates a fluctuation in the IP (chain A BH₄ black curve, chain B BH₄ red curve) and EA (chain A BH₄ green curve, chain B BH₄ blue curve) as depicted in the bottom pane of Figure 11. This feature suggests that protein dynamics can dramatically alter the configuration of this multipole structure and thus substantially change the IP and EA of BH₄. Table 5 shows that IP of BH₄ in protein environment is about half of its value in gas phase and its EA is about five times smaller, which indicates that ionization becomes more likely and reduction less likely, in protein environment than in gas phase. We argue that during protein movement the multipole structure made of layers of charged residues around BH₄ can drop the IP further such that BH₄ could donate an electron to heme via the propionate bridge. For the anion to mediate the electron transfer it needs to acquire an electron from the reductase part of NOS before transferring it to heme. If BH₄ has to act as a molecular switch and deliver an electron to heme in a timely manner, it is less likely that the electron transfer would depend on another molecular event (i.e. the delivery of one electron from the reductase part of NOS to BH₄), which should be much slower. It should be also noted that the negatively charged propionate localizes the SOMO of BH₄ anion in its tail, that is, on the opposite side of the cofactor.

Figure 10.

Spin densities for the BH₄ cation and anion calculated by density functional theory (B3LYP/6-31+G(d)) in gas phase, dielectric, water and protein environment. The pictures have been obtained from CUBE Gaussian98 files and displayed with the VMD and POV-Ray programs.

Figure 11.

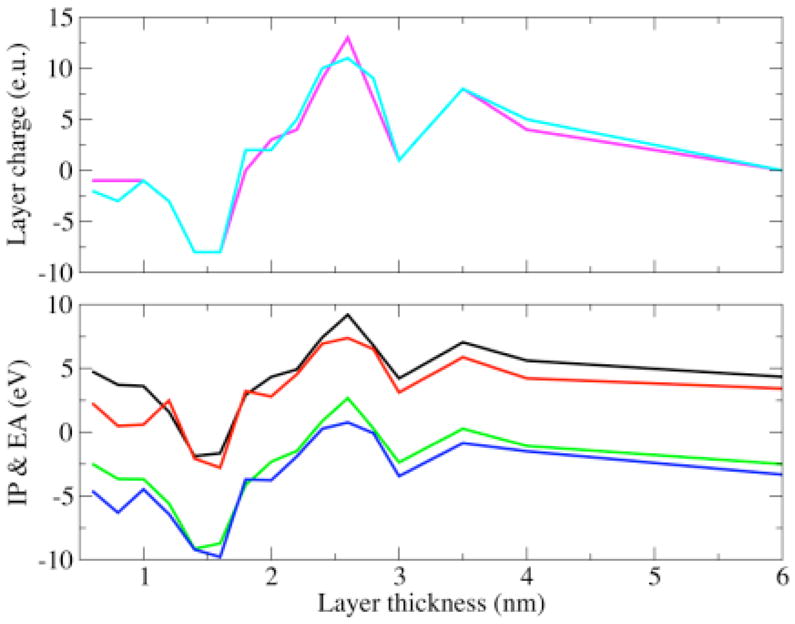
Bottom pane: hypothetical change in the IP and EA of BH₄ due to the charge of a protein layer (of certain thickness) around BH₄: IP of BH₄ bound to chain A (black curve), IP of BH₄ bound to chain B (red curve), EA of BH₄ bound to chain A (green curve), EA of BH₄ bound to chain B (blue curve), Top pane: Variation of the charge on the protein layer (of certain thickness) around BH₄: total charge on the protein layer around BH₄ bound to chain A (magenta curve), total charge on the protein layer around BH₄ bound to chain B (cyan curve).

Conclusions

Our density functional theory calculations show that the electronic properties of BH₄ such as IP and EA are not very sensitive to conformational changes rather they change dramatically in the presence of an external electric field. Calculations of the IP and EA show that, in gas phase, water, and in an energy-minimized protein environment, the neutral BH₄ is the most stable species. The anion is more stable than the cation in all environments. An average polarization of water (provided in the form of a polarizable dielectric) makes the anion the most stable species in solution. The cation, however is still 4.8 eV less stable, making the one electron oxidation of BH₄ in solution difficult. The specific docking of BH₄ in iNOSoxy (i.e., in the vicinity of P₄₅₀ heme with its pyrimidine ring next to a heme propionate group) may favor the cation as electron transfer mediator because the IP of BH₄ is then about half of what it is in gas phase and the EA is about five times smaller. However, the susceptibility of the BH₄ wave function to external electric field fluctuations generated by moving charged residues should allow protein dynamics to produce proper configurations in which the cation (or the anion) becomes nearly as stable as, or even more stable than the neutral BH₄ and thus facilitating the electron transfer to heme. A paramagnetic species is observed during enzyme turnover, but there is no experimental procedure to distinguish whether an anion or a cation is involved in the electron transfer because both are radical species and produce the same electron spin resonance spectrum.

Supplementary Material

si20060926_095. Supporting Information Available.

Table with calculated vibrational frequencies of tetrahydrobiopterin and Complete Reference ²⁶. This material is available free of charge via the Internet at http://pubs.acs.org.