Dynamics of static friction between steel and silicon

Abstract

We conducted experiments in which steel and silicon or quartz are clamped together. Even with the smallest tangential forces we could apply, we always found reproducible sliding motions on the nanometer scale. The velocities we study are thousands of times smaller than in previous investigations. The samples first slide and then lock up even when external forces hold steady. One might call the result “slip-stick” friction. We account for the results with a phenomenological theory that results from considering the rate and state theory of dynamic friction at low velocities. Our measurements lead us to set the instantaneous coefficient of static friction that normally enters rate and state theories to zero.

The understanding of friction has evolved greatly in the last 70 years (1–3). Bowden and Tabor (4) established that friction is due to populations of asperities and that the actual contact area of two solids in frictional sliding is much less than apparent. Dieterich (5–7) showed that the population of frictional contacts evolves during dynamic sliding, and measured changes in force over time and at different steady speeds. Rice and Ruina (8, 9) developed a standard theory for this phenomenon, known as “rate and state friction” in which a single state variable accounts for the population of asperities and its evolution in time. Baumberger and collaborators (10–12) showed that the rate and state equations extend to low velocities, on the order of 1 μm/s, as a sliding object comes to a halt. During stick-slip motion, samples of Plexiglas and paper continue to creep during the “stick” phase.

Here, we describe experiments where silicon and quartz are clamped on steel, motion is measured down to the nanometer scale, and velocities are measured down to 10⁻⁵ μm/s. We see that static friction is not really static. Under conditions where objects are pressed into each other and are not normally expected to slide, the asperity population gives way a little bit and evolves before the contacts lock up and become motionless. The characteristic sliding distance is a fraction of a micrometer, which is the characteristic scale of asperities, and the motion remains regular down to the scale of nanometers. We show that the observations are described quantitatively by modifications of the standard equations of rate and state friction.

Results

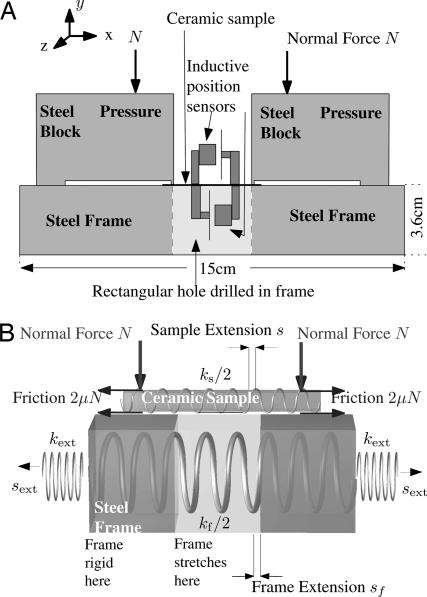
Our apparatus is displayed in Fig. 1. It allows us to press samples of silicon and quartz to a metal frame with normal force N, stretch the frame, and watch how much the samples extend in response. If there were no slipping, the sample extensions s would equal the frame extensions s_f, but because of slipping, the sample extensions s are less. The stretching of the frame s_f is controlled by a stepper motor attached to the frame by means of springs. The extension of the motor s_ext is much larger than the stretch of the frame s_f, but s_f can reliably be deduced from s_ext.

Fig. 1.

Experimental apparatus for friction studies. (A) Side view of experiment, not to scale. Inductive sensors are placed above and below silicon or quartz sample to measure sample extension s. The sample straddles a rectangular hole drilled into the frame, and the lower inductive sensor is within the hole. The average of the two measurements compensates for bending. (B) Schematic geometry of experiment, showing compliant elements in series and parallel with sample. The variables s, s_f,, and s_ext all describe the difference between the location of a portion of the apparatus when it is under tension and its location when the system is completely relaxed. The sample has effective spring constant k_s and extension s; thus, it is under mechanical tension F = k_ss. The apparatus to which it is attached has stretched by amount s_f, so the sample has slipped by amount x ≡ s_f − s. The sample is in parallel with mechanical elements with spring constant k_f, and in series with elements of constant k_ext.

We display the results of two sorts of experiments. In the first, we pull with horizontal forces F that are less than the forces that should cause slipping at Coulomb's threshold μ_sN. We see the sample slip and then stick. In Fig. 2A, we increase the external extension s_ext by 30 μm over 16 s and then hold the stepper motor fixed for 284 s under a normal force of 467 N. The process is repeated several times. One sees the relaxation of the silicon after a perturbation. If the silicon were gripped rigidly by the frame, one would expect it to extend by ≈0.5 μm after the 30-μm rise in s_ext. However, the silicon extends only ≈0.1 μm, meaning that in each step 4/5 of the expected displacement is immediately lost to slipping. Furthermore one can watch the silicon slip backwards while the exterior of the frame is held fixed. The backward slip is logarithmic in time (Fig. 2B). There is slow sliding throughout a range of forces that is supposed to lock solids together in static friction. The sliding is on submicrometer scales that normally escape notice for macroscopic samples.

Fig. 2.

Experiments involving repeated step-like increases of loading on sample. (A) Experiments with machine-ground steel in contact with doubly polished silicon sample, Si/Steel 1 in Table 2. In four separate steps, the stepper motor advances by 30 μm for 16 sec and then is held fixed for 284 sec. The silicon creeps backwards, and the stepper motor is held fixed. The normal force is 467 N. The four steps are compared with calculations of Eq. 14 by using parameters given in Tables 1 and 2. (B) Closer examination of relaxation in the final step. The experiment is compared both with the solution of Eq. 14 and with the best possible fit of the form s = s₀ − s₀ ln(t − t₀).

In a second type of experiment, shown in Fig. 3, we plot sample extension s as a function of the extension applied by the external motor s_ext for six values of the normal force N. In each experiment, the stepper motor produces a steady increase in s_ext from 0 to 127 μm over 370 seconds and thus probes the slipping that accompanies a slow and steady increase in tension. Each experimental curve is an average over five separate realizations of the experiment. The response of the silicon that would be observed if slipping were impossible below the threshold of static friction is depicted by dotted lines in Fig. 3. Once the horizontal force on the sample reaches the threshold μ_sN, it begins to slide freely, just as in elementary accounts of static friction. Below this threshold, however, the elementary theory of friction says samples should be static, whereas experiment shows that they first slip and then stick.

Fig. 3.

Sequence of experiments in which the stepper motor continuously increases the external extension s_ext from 0 to 127 μm. The materials in this experiment are described by Si/Steel 2 of Table 5. We plot silicon extension s versus the extension of the external motor s_ext for six values of the normal force N produced by gas pressure in the bellows pressing down on the sample. The dotted curves show how the silicon would extend if it stretched without slipping to the point where static friction gave way. The gray theoretical curves are obtained from Eq. 14. Better theoretical fits can be obtained if the characteristic length D_c is allowed to depend linearly on the normal force N, but we have not used that freedom for the comparisons in this paper.

Discussion

Phenomenology.

Experiments by Dieterich (5–7) led in the 1970s to a new picture of friction, called rate and state friction. Two surfaces in contact are described not only by their relative velocity v but also by a state variable θ that evolves as the surfaces slide. An expression for the ratio of horizontal force F to normal force N for a sliding object is

Here A, B, θ*, and v* are constants. v = d(s_f − s)/dt is the velocity of frictional sliding, and θ is a state variable that carries information about a population of asperities. This expression differs slightly from what is conventional because if the state variable θ and velocity v vanish, the friction force vanishes as well. Static friction here is due entirely to the state variable θ. This choice is motivated by our inability in experiment to observe any lower threshold of horizontal force below which there is not at first some sliding. Etsion et al. (13) and Lee and Polycarpou (14) have reported the same phenomenon. There is also some variation in the literature on whether to write ln(θ/θ* + 1) or ln(θ/θ*); Dieterich and Kilgore (15) use the former, but the latter form appears more frequently. By including 1 +… inside the logarithm, friction always increases with velocity once v is large enough. Heslot et al. (11) observe this phenomenon directly, and Baumberger and Caroli (1) provide a derivation.

To complete the theory, one must describe the evolution of the state variable θ. There are two common expressions for it (16). A first form is from Dieterich, and is

D_c is a constant that describes a sliding length over which the asperity population reaches a statistical steady state. Another was discussed by Ruina (9) and is

These two expressions behave differently in the static case where v = 0. The first, Eq. 2, predicts aging, which means that when v = 0 the state variable θ increases linearly in time, and the friction coefficient μ increases logarithmically. The second, Eq. 3, predicts that when the sample is not sliding the state variable θ does not evolve.

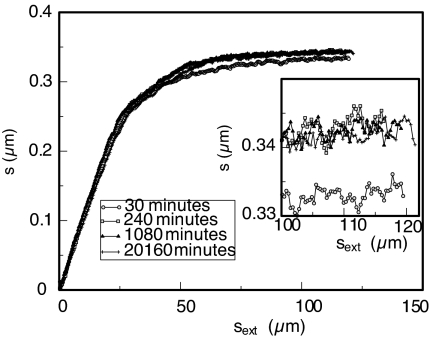
There is compelling experimental evidence dating back to Coulomb that the strength of static frictional contacts increases over time (16). However, this evidence was obtained in specific experimental systems such as wood on wood or rock on rock. Berthoud et al. (17) show that aging rates of polymeric systems drop rapidly as a function of temperature below the glass transition temperature. Thus for a system such as ours, with large yield stresses and far from any melting temperature, one might expect aging effects to be very small. We show in Fig. 4 that the experimental systems of silicon on steel and quartz on steel we have studied give no evidence for aging on a time scale ranging from half an hour to 2 weeks.

Fig. 4.

Sample extension s versus external extension s_ext after four different waiting periods. During the waiting period, the samples sat under a normal load of 200 N, after which horizontal forces were applied. There is no evidence of aging for times >30 min.

Because of the absence of aging in our experiments, we have looked for a generalization of Eqs. 2 and 3 that allows the rate of aging to be controlled. We suppose that there are two state variables θ and φ, where φ is proportional to the aging time of contacts, and θ describes how the contacts evolve during sliding. Equations implementing this idea are

where N is the normal stress, τ is a yield stress, and α is dimensionless. Ruina (9) similarly presents equations for a pair of state variables. To understand the behavior of these equations, it is useful to consider a situation where the horizontal force increases slowly from zero and then holds at a constant final value F. For almost all initial conditions, the sample initially begins to slide with nonzero velocity v and then heads toward solutions where v and θ are time-independent. The time-independent solutions are of two forms. If F is below a critical threshold, the final solution has v = 0 and θ is given by F = B ln(1 + θ/θ*). This solution corresponds to a system gripped by static friction. However, these solutions are only stable so long as θ is less than a critical value of 1 + φ. When F/N is larger than B ln(1 + (1 + φ)/θ*), the steady solutions instead have nonzero v and θ = (1 + φ)/(1 + v/v_s). This situation corresponds to sliding friction. The critical shear force that divides these two regimes is

which we identify with the static coefficient of friction. If instead one waits for a long time T before beginning to ramp the force up from zero, φ increases by αNT/τ, the critical shear force increases by the log of this value, and thus the equations can describe the phenomenon of aging.

We now return to a more detailed analysis of our experiments. In view of the fact that our experiments show no aging, we simplify to

Now the expression Eq. 6 for the static coefficient of friction simplifies to

The transition to sliding at this critical force value can be either subcritical or supercritical depending on the values of A and B.

Realistic Loading Configuration.

We next extend the model to correspond to the experimental geometry shown in Fig. 1B. We assume that the experiment is symmetrical about the horizontal midpoint and focus on the right-hand side. The amount the sample has slipped is x ≡ s_f − s. Denote the force of friction by μN. In our experiments, s > 0, and friction pulls the right-hand side of the sample to the right. Assuming that none of these quantities changes sign, and neglecting inertia, mechanical equilibrium requires

where

Thus one has the following set of equations:

In the limit when one increases s_ext very slowly and measures s, one can solve for s_ext and obtain

This function is zero when s = 0, and diverges when k_ss/n = B ln(1 + 1/θ*), which recovers the result in Eq. 8.

Fig. 3 compares our experiments in which the sample was stretched slowly with the predictions of Eq. 14 using the parameters in Table 1. The best fits to these experiments set the values of D_c and θ* in Table 1, and B is determined from Eq. 8. To obtain the fitting parameters reported in this article, we have relied upon direct integration of Eqs. 14 a–d, although Eq. 15 can be used for a first rapid scan through parameter space. Fig. 2 compares experimental results in which one repeatedly stretches the sample and waits with integrations of Eqs. 14 a–d. The parameters A and v_θ are determined by searching for a fit. When slipping velocities v are much larger than the cutoff velocity v*, Eq. 14b has solutions where the slip x is logarithmic in time. As shown in Fig. 2B), this logarithmic slip is observed until displacements become too small to measure accurately. Thus, we cannot really determine the cutoff velocity v* but only say that it is 10⁻⁵μm/s.

Table 1.

Parameters for phenomenological theory of friction

Parameter	Value, N/μm	Parameter	Value, N/μm
kext	98.1	kf	5.93 × 103
ks (silicon)	279	ks (quartz)	161.5
cext (silicon)	4.60	cext (quartz)	2.56
cx (silicon)	283	cx (quartz)	157

All parameters were obtained by direct mechnaical measurements on the loading apparatus.

Conclusion

We have seen reproducible motion of macroscopic surfaces in frictional contact at velocities down to nanometers per second. As in elementary theories of static friction, our experiments (Fig. 3) show that a friction coefficient sets the point where free sliding begins. However, for forces too small for free sliding, there is dynamical behavior that can be described by modified rate–state friction equations. Static friction is the consequence of a small amount of sliding on a submicrometer scale that causes surfaces to lock together; before the sliding, they do not grip each other at all.

At a microscopic level, the phenomena we observe must be quite complicated. The silicon and steel are in contact through very thin layers of organic molecules or water pressed between micrometer-scale asperities (18–21). The slipping we observe should correspond, in fact, to detachment waves moving among asperities (22–24). But the net result of these complicated phenomena is surprisingly simple, reproducible slip-stick motion. We expect our results to be significant for micromachines that involve frictional contact between some of their parts, and whose tolerances require control below the submicrometer scale, because on these scales, static friction as we normally understand it does not always exist.

Materials and Methods

Our experiments are carried out in an apparatus previously used to induce tensile fracture in rectangular specimens of silicon (25). A frame is made from a machine-ground and polished steel block (15 × 20 × 3.6 cm) with a rectangular hole (3.3 × 16.5 × 3.6 cm) milled out of the center as shown in Fig. 1A. Horizontal tensile forces along x, monitored by a stress gauge, are applied to the frame through rods attached to a stepper motor (Model M; Compumotor). When loaded, the frames act as two rigid bars connected by two extension elements that function as very stiff springs (Fig. 1B). To extend the extension elements by 1 μm requires a loading force of 5,930 N distributed over four loading points on the outer edges of the frame. The extension pulls apart the inside edges of the frame uniformly. Samples of either silicon or quartz sit on top of the frame in the center. The sample is pressed on the frame by two pressure blocks that are driven by four pressurized bellows (not shown in Fig. 1). The pressure block has two steps on the bottom surface that allow the block to be in contact with both the sample and the frame simultaneously. The inner edge of the pressure block is aligned with the inside edge of the frame. All of the frictional contact takes place at the inner edges of the frame where the sample is clamped down by a 2.54-mm-wide step on the pressure block.

We use a pair of inductive sensors (SMU 9000; KAMAN Instrumentation) to obtain precise measurements of the motions of the sample and of the loading apparatus. In one set of measurements, the sensors are mounted on the steel frame in Fig. 1, at opposite ends of the central opening. They measure how far the steel frame opens in response to external forces and thereby determine the frame spring constant k_f. In other sets of experiments, the inductive sensors are placed on the top and bottom of the ceramic samples and measure the sample extension s. Two sensors are needed because, otherwise, bending of the sample cannot be distinguished from stretching. The extension of the outer boundary of the apparatus, s_ext is measured by a standard micrometer capable of resolving displacements down to 10 μm. Because the behavior of so many parts of our apparatus has been measured independently, the only assumption we must make about our stepper motor is that each pulse sent to it produces an equal displacement at the outer boundary, and we have checked this assumption as carefully as our instruments allow.

When tensile forces are applied to the outside of the frame, the frame stretches. Measurements show no relative motion between the pressure blocks and the frame. Frictional forces due to sample-frame and sample-block contacts stretch the sample and are balanced by internal tension. Our analysis treats the center of the apparatus as a stationary point of origin. The variable that describes displacement of the edge of the sample is s, s_f describes motion of the inside edge of the frame, and s_ext describes the displacement generated by a stepper motor on the outside of the whole apparatus. Because the center of the sample is taken to be stationary, its extension from one end to the other is 2s. In the course of an experiment, s_ext is determined from the number of driving pulses sent to the stepper motor, given the knowledge that 74,000 pulses produce an extension s_ext of 127 μm. The effective forces changing the sample displacement s are the elastic restoring force of the silicon k_ss and the frictional forces, which, because of the two surfaces of contact, are represented as 2μN. The frame provides an elastic force in parallel with the sample of magnitude k_fs_f and is stretched by compliant external portions of the loading apparatus, represented by spring constant k_ext and the external displacement s_ext. We have measured all of the spring constants directly, and values appear in Table 1. In view of the very small motions we are measuring, we double checked our measurements of the spring constants of our apparatus by mounting inductive sensors on the frame. We verified directly that extension of the frame was a reproducible linear function of the force applied on it by the stepper motor. We also verified that connecting a silicon sample in parallel with the frame led to the expected small increase in stiffness.

All of the experiments were repeated for three different pairs of material surfaces. In a first set of experiments (Si/Steel 1 in Table 2) the surface of the steel frame was machine ground, and the silicon samples were 7.5 cm in diameter and 0.04 cm in thickness, chemically polished on both surfaces. In a second set of experiments (Si/Steel 2 in Table 2), the silicon samples were the same, but the steel frame was hand sanded with superf̄ine CAMI grit 400 sandpaper. In the third set of experiments, the frame was again machine ground, and the silicon was replaced with quartz crystals 7.5 cm in diameter, 0.035 cm in thickness, and polished on both sides. The experiments were conducted at a temperature of 23 ± 1°C and humidity of 60 ± 5%. Finally, we measure the macroscopic coefficient of static friction μ_s by finding the angle at which samples of silicon or quartz begin to slide over tilted steel blocks.

Table 2.

Surface-dependent parameters for phenomenological theory of friction for three different pairs of surfaces.

Parameter	Si/steel 1	Si/steel 2	Quartz/steel
Dc, μm	1.33	0.5	0.8
μs	0.188	0.16	0.05
θ*	1.15	0.2	1.15
A	7.5 × 10−4	5.0 × 10−4	5.0 × 10−4
vθ, μm/s	0.0295	0.2	1.5
v*, μm/s	10−6	10−6	10−6

The first three parameters refer to static properties of friction. The static friction coefficient is obtained by measuring the angle at which the sample slides off a tilted frame while loaded with weights. The parameter B appearing in Eq. 1 is then determined from Eq. 8. The parameters D_c and θ* are obtained by fitting to the data in Fig. 3. The final three parameters are linked to dynamical phenomena and are obtained from the data of Fig. 2. The parameter v* is uncertain, but one can conclude from Fig. 2B that it must be <10⁻⁵ μ/s, and the ability to match our experiments does not depend on its value so long as this condition is met; thus, we have somewhat arbitrarily settled on a value of 10⁻⁶ μ/s in comparing with the experiments.