Abstract
Quantum mechanical/molecular mechanical molecular dynamics and free energy simulations are performed to study the acylation reaction catalyzed by kumamolisin-As, a serine-carboxyl peptidase, and to elucidate the catalytic mechanism and the origin of substrate specificity. It is demonstrated that the nucleophilic attack by the serine residue on the substrate may not be the rate limiting step for the acylation of the GPH*FF substrate. The present study also confirms the earlier suggestions that Asp 164 acts as a general acid during the catalysis and that the electrostatic oxyanion-hole interactions may not be sufficient to lead a stable tetrahedral intermediate along the reaction pathway. Moreover, Asp 164 is found to act as a general base during the formation of the acyl-enzyme from the tetrahedral intermediate. The role of dynamic substrate assisted catalysis (DSAC) involving His at the P1 site of the substrate is examined for the acylation reaction. It is demonstrated that the bond breaking and making events at each stage of the reaction trigger a change of the position for the His sidechain and lead to the formation of the alternative hydrogen bonds. The back and forth movements of the His sidechain between the C=O group of Pro at P2 and Oδ2 of Asp 164 in a P1ng-pong-like mechanism and the formation of the alternative hydrogen bonds effectively lower the free energy barriers for both the nucleophilic attack and the acyl-enzyme formation and may therefore contribute to the relatively high activity of kumamolisin-As towards to the substrates with His at P1 site.
Kumamolsin-As belongs to the recently characterized family of serine-carboxyl peptidases (sedolisins) that were originally described by Murao, Oda and co-workers about 20 years ago (1–3). Sedolisins are present in a wide variety of organisms, including archaea, bacteria, molds, slime molds (mixomycetes), amoebas, fishes, and mammals, and they are active at low pH and often high temperature. This family of enzymes seems to have been derived through divergent evolution from a common ancestor with classical serine peptidases; the structural studies (4–10) showed that sedolisins have a fold resembling that of subtilisin, although they are significantly larger (the mature catalytic domains contain approximately 375 amino-acid residues). One interesting question is why Nature needs another family of subtilisin-like peptidases. For bacterial sedolisins, one possible explanation is that some organisms might have to utilize such evolved serine-carboxyl peptidases for their survival, presumably under acidic environments and high temperature. The biological importance of sedolisins in mammals has already been demonstrated by the fact that mutations leading to the loss of the human enzyme CLN2 (11–13), another member of the sedolisin family, result in a fatal neurodegenerative disease, classical late-infantile neuronal ceroid lipofuscinosis (14).
The three-dimensional structures are available for three members of the sedolisin family, including sedolisin (also known as pepstatin-insensitive carboxyl proteinase or PSCP) (4–6), kumamolisin (7–8), and kumamolisin-As (9–10). The defining features of these enzymes are a unique catalytic triad, Ser-Glu Asp (Ser278-Glu78-Asp82 for kumamolisin-As; see Figure 1A), as well as the presence of an aspartic acid residue (Asp 164 for kumamolisin-As) that replaces Asnl55 of subtilisin, a residue that creates the oxyanion hole in the classical subtilisin-like serine peptidase. The X-ray crystallographic and mutagenesis studies (4–10) demonstrated that the serine residue is the catalytic nucleophile for sedolisins, while the nearby Glu is likely to act as the general base to accept the proton from Ser and assist in the nucleophilic attack. Recent computational studies (15–17) further suggested that Asp 164 may act as a general-acid catalyst to protonate the substrate and stabilize the tetrahedral intermediate (TI). This mechanism of the TI stabilization is similar to the one proposed for aspartic peptidases (18), but is different from that of serine peptidases, in which the electrostatic oxyanion-hole interactions are used instead (19). Thus, although sedolisins might have evolved from a common precursor of classical serine peptidases, they seemed to have ended up with the use of some of the chemistry of aspartic peptidases for the catalysis. The existence of significant mechanistic similarities between sedolisins and both serine and aspartic peptidases makes the detailed understanding of this newly characterized family of enzymes extremely interesting.
Figure 1.
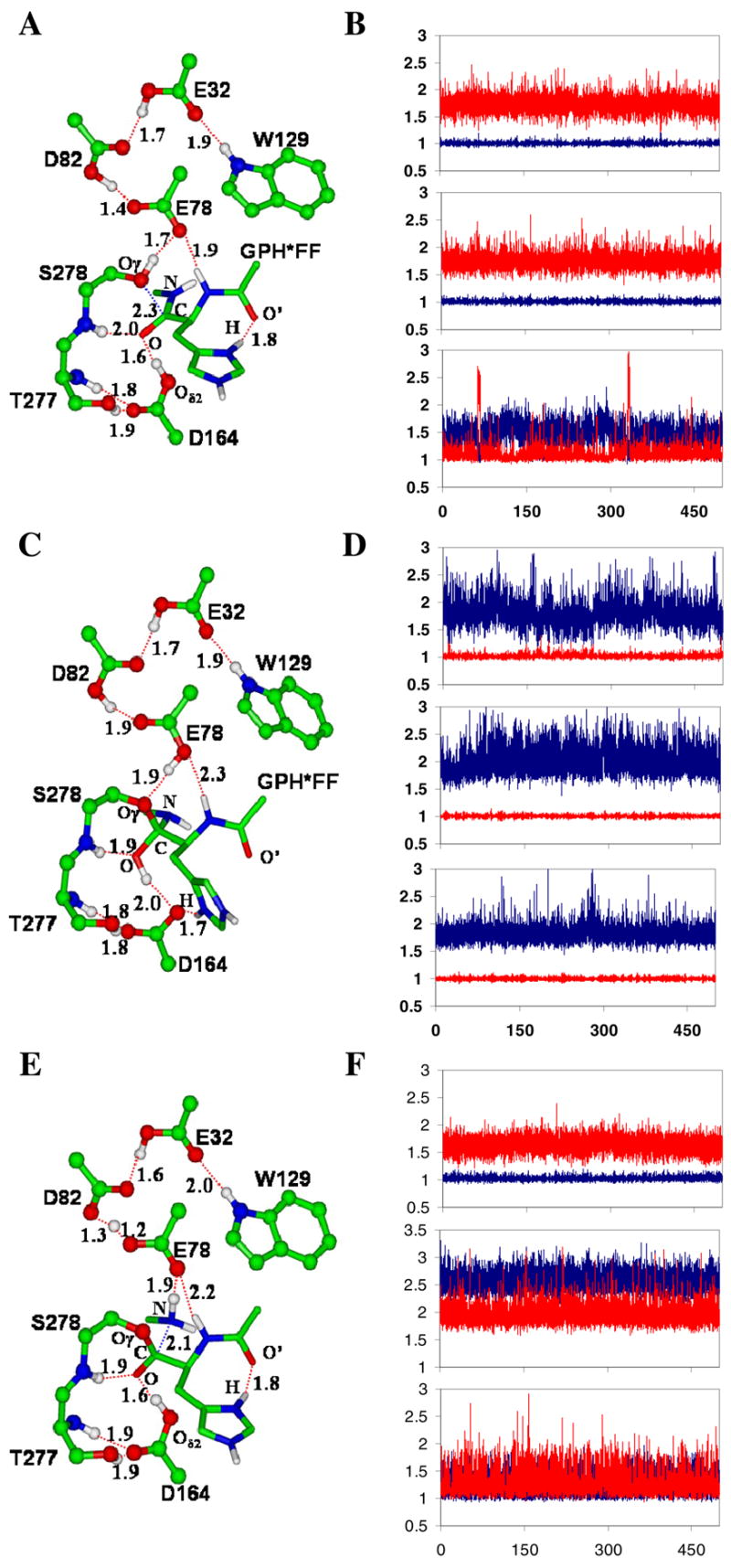
The average active-site structures of the kumamolsin-As-substrate (GPH*FF) complex, tetrahedral intermediate and acyl-enzyme obtained from the QM/MM MD simulations and the motions of the three key protons involved in the catalysis. The initial structures of the simulations for the tetrahedral intermediate and acyl-enzyme were based on the structures from the free energy simulations (see below). (A) The average structure of the substrate complex. The enzyme is plotted in ball and stick and the substrate in stick. Hydrogen bonds (H-bonds) are indicated by red dashed lines. Only the sidechain of the P1 (His) residue of the substrate is shown for clarity. The catalytic triad contains the Ser278, Glu78 and Asp82 residues. The His sidechain at P1 donates an H-bond to the C=O′ group of Pro at P2, in addition to the carboxylate of Asp179 (not shown). The backbone N-H group of the P1 residue donates a hydrogen bond to Glu78. (B) Fluctuations of the distances (in Å) related to proton motions (vibrations) between Asp164 and substrate, Ser278 and Glu78, and Glu78 and Asp82 in the substrate complex. Top panel: fluctuations of the H-O(D164) and H…O(substrate) distances as function of time. Red, r[H…O(substrate)]; blue, r[H-O(D164)]. The proton is on Asp 164 and is involved in an H-bond with the C=O group of the substrate (see also Figure 1A). Middle panel: the fluctuations of the H-O(S278) and H…O(E78) distances as function of time. Red, r[H…O(E78)]; blue, r[H-O(S278)]. The proton is on Ser278 and is involved in an H-bond with Glu78. Bottom panel: the fluctuations of the H…O(E78) and H-O(D82) distances as function of time. Red, r[H-O(D82)]; blue, r[H…O(E78)]. The H-bond formed between Glu78 and Asp82 has a short distance of !1.5 Å, and the proton is mainly located on Asp82. (C) The average structure of the tetrahedral intermediate after the nucleophilic attack by Ser278 on the substrate. The His sidechain at P1 now interacts with Oδ2 of Asp164 and may, therefore, play a role in stabilizing the charge formation on Asp164. The H-bond between the backbone N-H group of the P1 residue and Glu78 becomes significantly weaker due to the protonation of Glu78. (D) Fluctuations of the distances related to proton motions (vibrations) in the tetrahedral intermediate complex. Top panel: the fluctuations of the H…O(D164) and H-O(tetrahedral intermediate) distances as functions of time. Red, r[H-O(tetrahedral intermediate)]; blue, r[H…O(D164)]. The proton is on the tetrahedral intermediate and is involved in an H-bond with Asp164 (see Figure 1C). Middle panel: the fluctuations of the H…O(S278) and H-O(E78) distances as function of time. Red, r[H-O(E78)]; blue, r[H…O(S278)]. The proton is on Glu78 and is involved in an H-bond with Ser278. Bottom panel: the fluctuations of the H…O(E78) and H-O(D82) distances as function of time. Red, r[H-O(D82)]; blue, r[H…O(E78)]. (E) The average structure of the acyl-enzyme with the C-N bond broken. (F) Fluctuations of the distances related to proton motions (vibrations) in the acy-enzyme. Top panel: the fluctuations of the H-O(D164) and H…O distances as function of time. Red, r[H…O]; blue, r[H-O(D164)]. Middle panel: the fluctuations of the H…O(S278) and H…O(E78) distances as function of time. Red, r[H…O(E78)]; blue, r[H…O(S278)]. Bottom panel: the fluctuations of the H…O(E78) and H…O(D82) distances as function of time. Red, r[H…O(D82)]; blue, r[H…O(E78)].
Here we examine the acylation reaction catalyzed by kumamolisin-As of the GPH*FF substrate (* designates the scissile peptide bond), using quantum mechanical/molecular mechanical (QM/MM) molecular dynamics (MD) and free energy (potential of mean force) simulations. Although the enzyme has been a subject of previous computational studies (15–17), the earlier investigations have mainly focused on the inhibitor binding and the nucleophilic attack by Ser278. To the best of our knowledge, a detailed examination of the acylation reaction as well as the corresponding free energy barriers has not been performed for this enzyme, or indeed for any sedolisins. Kumamolisin-As can cleave the -Pro-Xaa*Yaa- sequence (here Xaa and Yaa denote the residues at the P1 and P1′ sites, respectively). One experimental observation that is of considerable interest is the fact that this enzyme generally has higher specificity for the substrates with a positively charged residue at the P1 site than for those they do not carry such charge (3,9). For instance, it was found that the kcat value for a substrate containing the -Pro-Arg*Gly sequence is ~ 65-fold higher than for a substrate containing the -Pro-Gly*Gly sequence and km ~ 6.5-fold higher, leading to 10-fold increase of kcat/KM (3). The higher specificity for the substrates with a positively charged residue at P1 was also confirmed from specificity profile analysis using a peptide library (18–20). It was suggested in our earlier computational study (16) that the dynamics involving His at P1 triggered by the bond breaking and making events may play an important role in the stabilization of the tetrahedral intermediate and therefore contribute to the relatively high specificity for the substrates with His at P1. This type of catalytic processes is normally referred to as substrate-assisted catalysis (SAC) (21), with one or more functional groups from the substrate, in addition to those from the enzyme, contributing to the rate acceleration for the enzyme-catalyzed reaction. However, many of the previous studies of SAC (22) have focused on the catalytic effects resulting from the well-positioned substrate groups that can participate in SAC directly, without undergoing significant conformational changes. A major difference in the case of kumamolisin-As is that His at the P1 site is not located at such an ideal position in the enzyme-substrate complex, but is able to undergo a conformational change for the TI stabilization during the nucleophilic attack. We define this type of SAC involving conformational changes of the substrates as dynamic SAC (DSAC), to distinguish it from the standard SAC for which the conformational changes of the substrate are not required. It is shown here that such DSAC involving His at P1 also plays an important role for the acyl-enzyme formation. The importance of DSAC or similar types of catalytic processes involving the conformational changes of protein groups triggered by the bond breaking and making events might have been overlooked in some other enzymes, due in part to the dynamic nature of the effects that may not be well reflected in the X-ray structures.
Here we demonstrate that the nucleophilic attack by the serine residue on the substrate may not be the rate limiting step for the acylation reaction for kumamolisin-As, which is different from some previous calculations on classical serine peptidases (20). The results support our earlier conclusion that the general acid mechanism involving Asp 164 is crucial for the stabilization of the tetrahedral intermediate during the catalysis and that the electrostatic oxyanion-hole interactions may not be sufficient to generate a stable TI along the reaction pathway (15–17). Moreover, Aspl64 is found to act as a general base during the formation of the acyl-enzyme from the tetrahedral intermediate, and therefore plays multiple roles in the catalysis. The present study also provides important new insights into the role of DSAC. The previous suggestion (16) for the existence of DSAC was based on the results of the nucleophilic attack on a substrate (RPH*FR). Since the nucleophilic attack may not be rate limiting for the acylation (see above), a question remains as to whether the dynamics involving the His residue at P1 would also play a role in stabilizing the transition state for the acyl-enzyme formation (so that an overall rate enhancement for the acylation reaction could be achieved). In this paper, it is shown that the bond breaking and making events at the different stages of the acylation reaction trigger the back and forth movements of the His sidechain at P1 between the C=O group of Pro at P2 and Oδ2 of Aspl64, leading to the formation of the alternative hydrogen bonds and the reduction of the free energy barriers for both the nucleophilic attack and formation of the acyl-enzyme. It is proposed that such motions and the formation of the alternative hydrogen bonds may contribute to the relatively high activity of kumamolisin-As towards the substrates with His at the P1 site and lead to the reduction of the free energy barriers for the de-acylation reaction as well.
Methods
A fast semi-empirical density-functional method (SCC-DFTB) (23) implemented in the CHARMM32b program (24) was used in the present study for the QM/MM molecular dynamics (MD) and free energy (potential of mean force or PMF) simulations. The efficiency of the semi-empirical QM methods (such as SCC-DFTB) makes possible to sample millions of the structures and conformations for enzyme systems and to determine the free energy profiles of the enzyme-catalyzed reactions. These important tasks for understanding enzymes are not feasible with high-level first-principle ab initio methods. Moreover, recent testing studies and comparisons with high-level ab initio QM methods on model systems seem to indicate that the SCC-DFTB method offers certain advantages over some other semi-empirical QM methods (for reviews, see Refs. 25–27). However, it should be pointed out that care must be exercised in using the semi-empirical QM methods for the studies of enzymes. Indeed, while the high-level QM/MM approaches based on energy-minimization may face the intrinsic problem for the lack of sampling sufficient conformational spaces, the accuracy of the semi-empirical QM/MM MD and free energy simulations may be limited by the approximations in their descriptions of the breaking and formation of chemical bonds as well as interactions. Indeed, Jorgensen and his co-workers (28–30) have performed extensive testing of the SCC-DFTB and other semi-empirical methods and provided some very useful data concerning the deficiencies of the SCC-DFTB method. They showed that heats of formation from SCC-DFTB are not improved compared to traditional semiempirical methods (e.g., PM3), even though the conformational and interaction energies seem to be more accurate. For the results reported in this paper, the deficiencies of the SCC-DFTB method could affect some of the conclusions reached from this study (even though the SCC-DFTB energies are not used directly to generate the profiles). Thus, the comparisons of performance of the SCC-DFTB method on certain models as well as on simplified enzyme systems with those from high-level ab intio calculations are of fundamental importance. This would allow us to obtain important insights into the question as to whether the conclusions obtained from the QM/MM MD and free energy simulations could still hold if high-level QM methods would be used.
Although the SCC-DFTB method has been tested on a large number of models and enzyme systems (for reviews, see Refs. 25–27), additional comparisons with the results from high-level ab initio calculations for the systems related to the present study are necessary. In our earlier work (15), we compared the performance of the QM(SCC-DFTB)/MM simulations with the calculations based on the QM(B3LYP/6-31G**)/MM energy minimization for the process of the nucleophilic attack of Ser278 on an inhibitor Af-acetyl-isoleucyl-prolyl-phenylalaninal (AcIPF) in the kumamolisin-As complex. We found that the results from the both methods are consistent with each other concerning the role of Asp164 and Glu78 as the general acid-base catalysts. There are two additional conclusions obtained from the present study that could also be affected by possible deficiencies of SCC-DFTB. One conclusion is that the nucleophilic attack by Ser278 on the substrate may not be rate limiting for the acylation reaction and the other is the existence of dynamic substrate assisted catalysis (DSAC). The first conclusion could be affected if the SCC-DFTB method underestimates (overestimates) the activation barrier for the nucleophilic attack more (less) significantly than the activation barrier for the acyl-enzyme formation (i.e., the breaking of the peptide bond). In this case, the relatively low barrier for the nucleophilic attack might be simply due to the deficiencies of SCC-DFTB. We have compared the performance of SCC-DFTB with B3LYP/6-31G** on a small model system and on selected snapshots of the enzyme complex. It was found that the SCC-DFTB method may in fact underestimate the activation barrier for the acyl-enzyme formation more significantly than that for the nucleophilic attack. Thus, the first conclusion mentioned above is likely to be true even with the high level ab initio method. For the conclusion concerning the existence of DSAC, the high-level ab initio MD simulations could not be performed due to the reason that these simulations are extremely expensive. In order to confirm this conclusion, we changed the treatment of His at P1 from SCC-DFTB to MM (31). The same conformational transition involving His at P1 was also observed, confirming our conclusion of the existence of DSAC.
There are additional questions that need to be mentioned for the model building processes. The family of sedolisins is only active at low pH, and the models used in the present study (e.g., the information concerning the protonation states of Asp and Glu residues) were based on the computer models of the tetrahedral adduct complex obtained in the earlier studies (15–17), in which the models were manually modified by adding protons on some ionizable residues (e.g., Asp and Glu), based on their local environments. In other words, the models were built to mimic the structures determined at low pH and to represent the active enzyme at low pH (i.e., not at neutral pH at which the enzyme is inactive). The average structure from the 1.2 QM/MM MD simulations for the tetrahedral adduct complex was then performed to test whether the experimental X-structure could be well reflected from the models that we built. If the interactions in the experimental structure could not be well represented by a model, the structure would be expected to deviate significantly from the experimental structure during the simulations. After several tests, we were able to generate the model for which the average structure from the MD simulations was rather close to the experimental structure obtained at low pH, suggesting that the interactions in the tetrahedral adduct complex are well represented and that the model should be reasonable. For instance, the distances between the non-hydrogen atoms for the key hydrogen bonds in the active site from the simulations are very close to those in the experimental structure, with an average deviation of only about 0.1 Å. We also tested other cases and noticed that we could not reproduce the X-structures from the simulations if we used different (presumably incorrect) protonation states for certain residues.
The initial coordinates for the enzyme were taken from the crystal structure (PDB ID: 1SIO, resolution 1.8 Å) of kumamolisin-As complexed with the inhibitor AcIPF (N-acetyl-isoleucyl-prolyl-phenylalaninal) (9–70). The substrate used in the present study, GPH*FF, contains the key residues of the internally quenched fluorogenic (IQF) substrate [NMA-MGPH*FFPK-(DNP)DRDR] used in the earlier experimental study (9–10), although it is considerably smaller. One of the key questions for performing the simulations on kumamolisin-As is how to obtain the coordinates for the substrate (tetrahedral intermediate) in the enzyme complex. Fortunately, an X-ray structure for the S278A mutant of pro-kumamolisin (PDB ID: 1T1E. Resolution 1.18 A) (8) is available that makes generating the enzyme-complex possible. This X-ray structure contains an activation peptide/linker running through the active site cleft. The catalytic domain of the Ser278Ala mutant of pro-kumamolisin has a virtually identical structure compared to the active kumamolisin. Kumamolisin-As and kumamolisin share high sequence identity (92.7%) and their structures superimpose very well. The structures of the kumamolisin-As-AcIPF complex and the catalytic domain of the S278A mutant of pro-kumamolisin were first superposed, and the coordinates of the P3-Arg169p—P2-Pro170p—P1-His171p—P1′-Phe172p—P2′-Arg173p peptide fragment from the linker were used to generate the coordinates of the GPH*FF substrate, with P3-Argl69p replaced by Gly and P2′-Arg173p replaced by Phe. The coordinates of kumamolisin-As and the GPH*FF peptide were then combined to generate the putative kumamolisin-As substrate complex used to initiate the computational studies.
The stochastic boundary MD method (32) was used for the QM(SCC-DFTB)/MM simulations. The system was separated into a reaction zone and a reservoir region; the reaction zone was further divided into the reaction region and the buffer region. The reaction region was a sphere with radius R of 16 Å, and the buffer region had R equal to16 Å ≤ R ≤ 18 Å. The reference center for partitioning the system was chosen to be the carbonyl carbon atom (C) of the His residue at the pi site (see Figure 1). The side chains of Glu32, Asp82, Glu78, Ser278, and Asp164, as well as a part of the substrate [the backbone atoms of P2-Pro (C=O), P1-His, P1′-Phe (Cα-NH) and the sidechain of P1-His] were treated by QM and the rest of the system by MM. The all-hydrogen potential function (PARAM22) (31) was used for MM atoms. The link-atom approach (33) available in the CHARMM program (24) was used to separate the QM and MM regions. A modified TIP3P watermodel(34–35) was employed for the solvent, and explicit water spheres covering the whole region of interest were used to solvate the system using the standard procedure in the CHARMM program. The resulting system contains 3431 atoms (2630 enzyme atoms and 267 water molecules, including 79 crystal water molecules). The initial structure for the entire stochastic boundary system was optimized by adopted basis Newton-Rhaphson (ABNR) method. The system was gradually heated from 50 to 310 K in 20 ps and equilibrated at 300 K for 80 ps. A 1-fs time step was used for integration of the equations of motion, and coordinates were saved every 10 fs for analyses. The LD frictional constants were 250 ps−1 for the protein atoms and 62 ps−1 for the water molecules. The bonds involving hydrogen atoms in the MM region were fixed by the SHAKE algorithm (36). 500 ps QM/MM MD simulations were performed for the substrate, tetrahedral intermediate and acyl-enzyme complexes of the wild-type enzyme; the initial structures of the tetrahedral intermediate and acyl-enzyme complexes were obtained from the free energy simulations (see below). The fluctuations of some important distances related to the proton motions were monitored with the coordinates obtained from the trajectories of the 500 ps simulations.
The umbrella sampling method (37) implemeted in the CHARMM program and Weighted Histogram Analysis method (WHAM) (38) were applied to determine the change of the free energy (PMF) for the acylation reaction in wild-type. The reaction coordinate [ζ = R(C-N) − R(C…Oγ)] used in the study is the difference between the bond distance of the scissile peptide bond [R(C-N)] and the R[Oγ(Ser278)…C] distance of the nucleophilic attack (see Figure 1A), the two key distances for the change of the substrate to the acyl-enzyme. The determination of multi-dimensional free energy maps involving all the coordinates would be too time-consuming. Our previous study (17) indicated that the one-dimensional free energy simulations with the suitable reaction coordinate would be sufficient to determine the key energetic properties for the reaction. The free energy profile for the wild-type enzyme, with the proton fixed on Asp164 using the SHAKE algorithm (36), was also obtained. 18–22 windows along the reaction coordinate were used between the substrate complex and acyl-enzyme. The force constants that were used are in the range of 100-800 kcal·Mol−1·Å−2. Similar free energy profiles and the same conclusions were obtained from different sets of PMF calculations with the MD simulations ranging from 40 ps (20 ps equilibration and 20 ps production run) to 250 ps (50 ps equilibration and 200 ps production run) in each window.
Results and Discussion
Structural and Dynamic Properties of the Substrate Complex, Tetrahedral Intermediate, and Acyl-enzyme
The average active-site structure for the kumamolisin-As-substrate (GPH*FF) complex obtained from the QM/MM MD simulations is given in Figure 1A. Ser278 is the nucleophile that attacks the carbonyl carbon atom (C) of the substrate, while Glu78 and Asp164 act as the general base and acid catalysts, respectively (4–10,15–17). Two additional residues, Glu32 and Trp129, interact with Asp82 of the catalytic triad through hydrogen bonding networks. These two residues may play an important role in maintaining the structural integrity of the active site. Indeed, the previous experimental study (8) on kumamolisin showed that Glu32→Ala and Trp129→Ala mutations affect the active-site conformation, leading to a 95% decrease in the activity. The backbone N-H group and sidechain of Thr277 interact with Asp164, and it was suggested in the earlier computational study (15) that these interactions might play a role in stabilizing negative charge formation on Asp 164 during the nucleophilic attack. The motions of the three protons that may be important for catalysis (i.e., those between Aspl64 and substrate, Ser278 and Glu78, and Glu78 and Asp82) are monitored from the trajectories of the MD simulations of the substrate complex and are plotted in Figure 1B. Figure 1B shows that, for the substrate complex, these protons are located on Asp164, Ser278 and Asp82, respectively, consistent with the average structure shown in Figure 1A. The fluctuation of the H-O(D82) distance is larger than that for a normal H-O bond [e.g., comparing the fluctuations with those of H-O(D164) and H-O(S278)], indicating that the corresponding H-O(D82) covalent bond is weakened as a result of the strong hydrogen bonding interaction with Glu78 (the distance of the hydrogen bond between Glu78 and Asp82 is only 1.5 Å).
The average structure for the tetrahedral intermediate obtained from the simulations is shown in Figure 1C. In this structure, the Ser278 residue has already attacked the substrate and transferred its proton to Glu78. The proton on Asp164 has transferred to the substrate during the formation of the tetrahedral intermediate. Thus, Glu78 and Asp164 played the roles of the general base and acid catalysts, respectively, during the nucleophilic attack. Preventing the proton transfer from Asp 164 to the substrate increases the free energy for the formation of the tetrahedral intermediate significantly (see below), highlighting the importance of the role of Asp164 as the general acid catalyst. A similar discussion can be made for Glu78 (17). It is of interest to note from Figure 1D (bottom panel) that the H-O(D82) bond does not undergo the large fluctuations (as observed in the substrate complex) in the tetrahedral intermediate; the corresponding H-bond distance to Glu78 is also longer (~1.9 Å). The average structure of the acyl-enzyme is given in Figure 1E, and the fluctuations of the distances related to the proton motions are plotted in Figure 1F. Figures 1E and 1F show that Glu78 has given up its proton to the nitrogen atom (N) of Phe at P1′, leading to the breaking of the C-N peptide bond between P1-His and P1′-Phe and the formation of the acyl-enzyme. Asp164 becomes protonated again and therefore acted as a general base during the acyl-enzyme formation. It is interesting to note that a low-barrier hydrogen bond is formed between Glu78 and Asp82 in the acyl-enzyme (Figure 1F, bottom panel); the proton is almost equally distributed on Glu78 and Asp82 during the MD simulations.
Free Energy Profiles of the Acylation
The changes of free energy (potential of mean force) as functions of the reaction coordinate (ζ) for the acylation reaction in kumamolisin-As and D164A mutant are given in Figure 2A. The free energy change in which the proton on Asp 164 is fixed by the Shake algorithm (36) (to prevent Asp164 acting as the general acid and base catalyst for the nucleophilic attack and acyl-enzyme formation, respectively) is also given. It should be pointed out the free energy profiles in Figure 2A were based on the one-dimensional free-energy simulations. For the step-wise bond breaking and making events this may not pose a serious problem. However, for the concerted processes some information that would be contained in multi-dimensional free-energy profiles may be absent in the one-dimensional profiles. Indeed, there are several proton transfers during the acylation reaction, and some of these proton transfers may be coupled to the rearrangement of the system (i.e., the nucleophilic attack and the formation of the acyl-enzyme). For instance, our earlier two dimensional free energy simulations on the nucleophilic attack of Ser-278 on AcIPF in kumamolisin-As showed that there are important free-energy relationships between the nucleophilic attack and the proton transfers. Such free energy relationships between the nucleophilic attack (acyl-enzyme formation) and proton transfers are absent in the one-dimensional free energy profiles (Figure 2A). However, the previous study (17) also indicates that one-dimensional free energy simulations with the suitable reaction coordinate should be sufficient to determine the key energetic properties for the acylation reaction.
Figure 2.
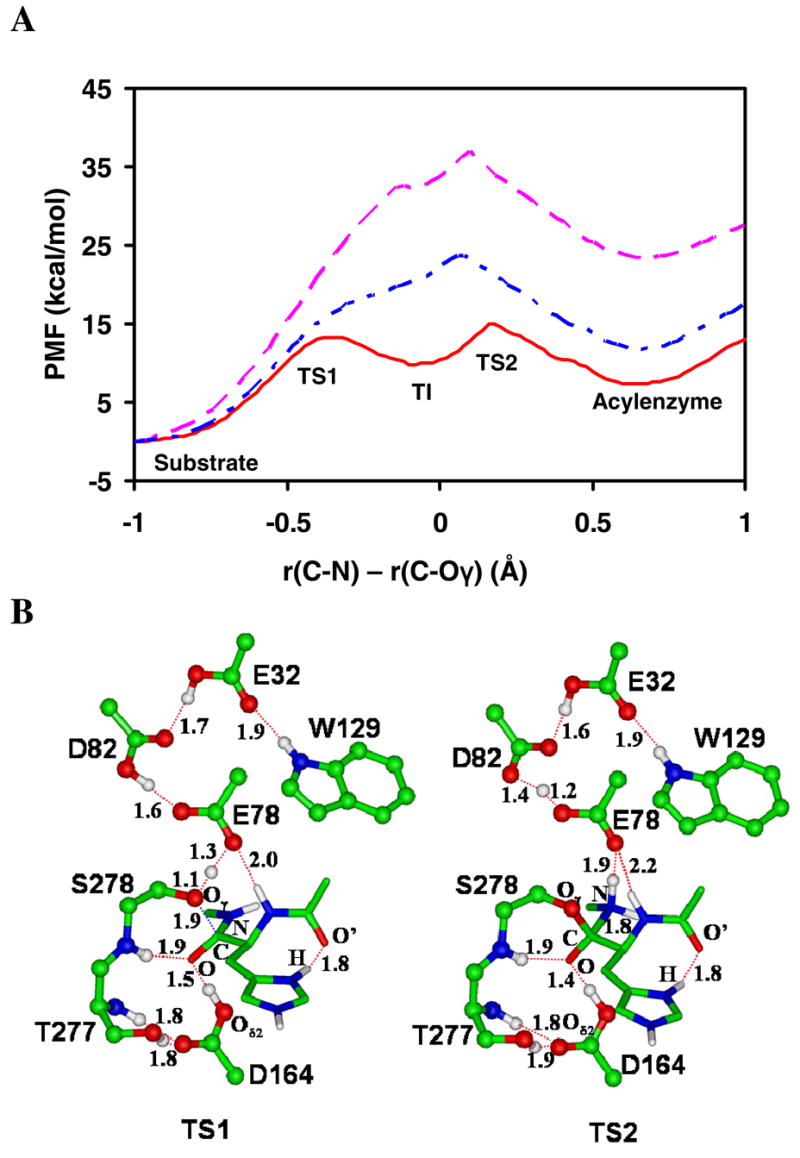
(A) The free energy profiles of the acylation reaction for the wild-type kumamolisin-As and D164A mutant as a function of the reaction coordinate [ζ = R(C-N) - R(C…Oγ)] obtained from the QM/MM free energy (potential of mean force) simulations. Red solid line: wild-type; blue dot-dashed line: wild-type with the proton fixed on Asp164 with the SHAKE algorithm; pink dashed line: D164A. The average structures for the substrate complex, tetrahedral intermediate and acyl-enzyme for wild-type are given in Figure 1A, 1C and 1E, respectively. The average structures of TS1 and TS2 for wild-type are given in Figure 2B. (B)The average active-site structures for wild-type near the transition states for the nucleophilic attack (TS1) and the formation of the acyl-enzyme (TS2), respectively, obtained from the free energy simulations.
Figure 2A shows that the nucleophilic attack by the serine residue on the substrate is not rate limiting for the acylation reaction, although the free energy barriers for the nucleophilic attack (TS1) and formation of the acyl-enzyme (TS2) do not differ significantly, with the barrier at TS2 slightly higher. The result obtained for kumamolisin-As is different from the previous calculations on trypsin (20) which suggested that the nucleophilic attack is rate limiting for the acylation in the serine peptidase. It is of interest to note in Figure 2A that preventing the proton transfer away from Asp164 leads to an increase of the free energy barrier of the acylation reaction by about 10 kcal/mol and the tetrahedral intermediate along the reaction pathway disappeared as a result of fixing the proton on Asp164. Thus, the electrostatic oxyanion-hole interaction involving the protonated Asp164 is unlikely to be sufficient for generating a stable tetrahedral intermediate during catalysis. Figure 2A also shows that the replacement of Asp164 by A1a increases the free energy barrier considerably. The results of the simulations reported here support the earlier proposal (15) for the existence of the general-acid mechanism involving Asp164 in the stabilization of the tetrahedral intermediate and are consistent wth the available mutagenesis studies (7–10). For instance, the D164A mutant of kumamolisin did not show any measurable proteolytic activity (7). For the D164N mutant of kumamolisin-As, a low but appreciable level of catalytic activity (1.3%) was found (10), corresponding to an increase of the activation barrier of about 2.5 kcal/mol. It should be pointed out, however, that care must be exercised in making direct comparisons of the computational results with experimental data. For instance, the acylation reaction has not been proven to be rate-limiting and the processes of the deacylation, substrate binding, and product release may need to be considered as well. Furthermore, structural analyses of the unliganded D164N mutant showed that, although the catalytic triad is intact, the mutated residue (Asn164) unexpectedly makes a hydrogen bond with the side chain of Ser278 (10). The consequence of this structural change and the way by which the sidechain Asn164 stabilizes the transition state in the reaction catalyzed by the D164N mutant are still unknown.
The average active-site structures near the transition states for the nucleophilic attack (TS1) and the formation of the acyl-enzyme (TS2) are given in Figure 2B. Figure 2B (left) shows that there is little progress of the proton transfer from Asp164 to the substrate before the system reaches TS1. The result is consistent with the earlier suggestion that such proton transfer mainly occurs at a later stage of the nucleophilic attack (15,17). The proton transfer from Ser278 to Glu78 seems to be more synchronous with the nucleophilic attack, although two-dimensional free energy maps are required for a detailed understanding of the relationship between the nucleophilic attack and proton transfer (17). Figure 2B (right) shows that the proton transfer from Glu78 to the nitrogen atom (N) of Phe at P1′ has been basically completed at TS2.
Dynamic Substrate Assisted Catalysis (DSAC)
Kumamolisin-As was found to have a higher specificity for the substrates with a positively charged residue (such as His or Arg) at the P1 site than for those they do not (2–3,9). Interestingly, the linkers of pro-kumamolisin-As and pro-kumamolisin (-P3-Arg169p—P2-Pro170p—P1-His171p—P1′-Phe172p—P2′-Arg173p-) also have a positively charged His residue at P1 (7–10); the coordinates of this peptide fragment from pro-kumamolisin have been used to generate the substrate complex used in this study (see above). It was found in our earlier simulations (16) that the His sidechain at P1 rotated significantly during transition from the substrate to the tetrahedral intermediate. This movement was triggered by the deprotonation/protonation events and resulted in the interaction of His at P1 with the unprotonated Asp164 making the tetrahedral intermediate more stable. We suggested that the dynamics involving the His residue at the P1 site may play an important role in the catalysis and contribute to the higher specificty for the substrates with His at P1. These results are confirmed here with a different substrate. Indeed, while His at PI forms a hydrogen bond with the C=O′ group of Pro at P2 in the substrate complex (Figure 1A), it interacts with Asp164 in the tetrahedral intermediate (Figure 1C).
The previous proposal for the existence of DSAC in the kumamolisin-As-catalyzed reaction was based on the results of the nucleophilic attack by Ser278 on a substrate. However, as demonstrated earlier, the nucleophilic attack may not be the rate limiting step for the acylation. Thus, question remains as to whether the His residue at P1 would be able to stabilize the transition state for the acyl-enzyme formation (TS2) as well, and therefore lead to an overall rate enhancement for the acylation reaction. The structure shown in Figure 1E suggests that this may indeed the case, as His at P1 moves back to its original position (i.e., to that found in the substrate complex) to interact with the C=O′ group of Pro at P2 in the acyl-enzyme. Figure 2B (right) showsthat the motion of the His residue from the position in the tetrahedral intermediate to that in the acyl-enzyme is almost completed as the system reaches TS2, the transition state for the acyl-enzyme formation. This is in contrast to the case of the TI formation, where His at P1 undergoes the conformational change mainly after the system passes TS1 (see above).
Figure 3 shows a plot of the free energy profiles for His at P1 moving between the C=O′ group of Pro at P2 and Oδ2 of Asp164 in the substrate complex, tetrahedral intermediate, and acyl-enzyme; the distance between the Hδ1 hydrogen atom of the His sidechain (i.e., H indicated in Figures 1A, 1C and 1E) and Oδ2 of Aspl64 is used as the reaction coordinate (RC). For the substrate complex, the free energy for the conformations for which the His residue forms a hydrogen bond with the C=O′ group (RC ~ 4.2 Å) is considerably lower than the free energy of those with the Oδ2(Asp164)…H(His) hydrogen bond; the conformations in the former case are therefore more stable. This result is consistent with the average structure shown in Figure 1A where the His residue interacts with C=O′. For the TI complex, the conformations with the Oδ2(Asp164)…H(His) hydrogen bond become more stable, as indicated by the relatively low free energy at RC = 1.7 Å. The conformations with the Oδ2(Asp164)…H(His) hydrogen bond become less stable again after the system changes to the acyl-enzyme. Therefore, the His residue at P1 moves between the C=O′ group of Pro at P2 and Oδ2 of Asp164. Each movement is triggered by the bond breaking and making events at a given stage of the reaction, as well as the corresponding changes of the interactions with the His residue. The back and forth movements of the His sidechain between the C=O′ group of Pro at P2 and Oδ2 of Asp164 in a ping-pong-like mechanism and the formation of the alternative hydrogen bonds effectively lower the free energy barriers for the both nucleophilic attack and the acyl-enzyme formation. It is possible that this mechanism also works for the deacylation reaction. In other words, the water attack on the acyl-enzyme and the formation of the product might also be helped by the motions of the His residue in the same ways as what happened for the nucleophilic attack by Ser278 and the formation of the acyl-enzyme, respectively.
Figure 3.
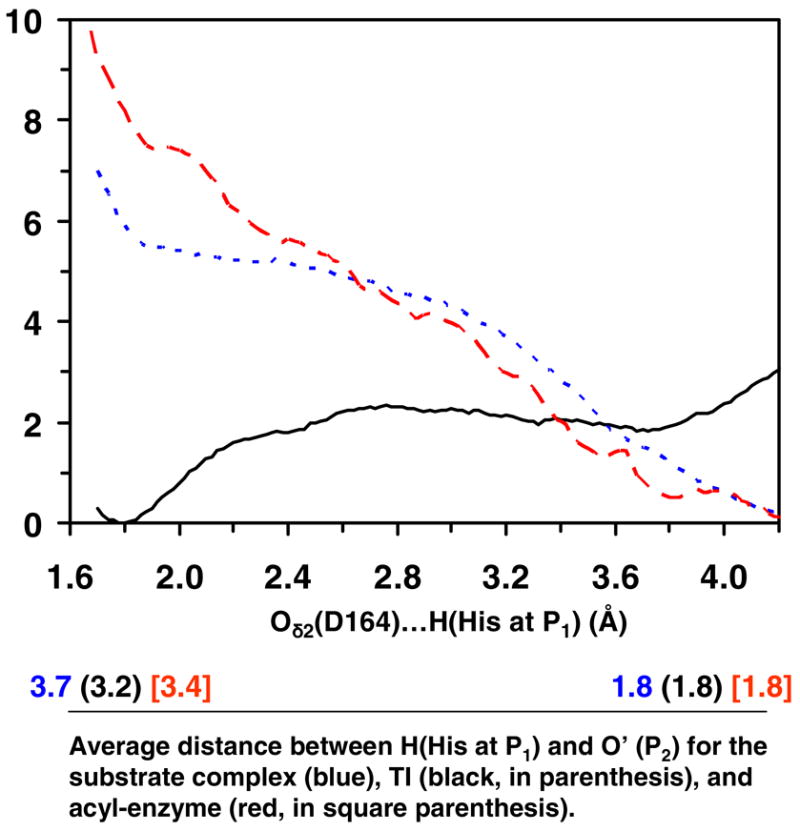
The free energy change as the His residue at P1 moves between Oδ2 of Asp164 and O′ of the C=O′ group of Pro at P2 in the substrate complex, tetrahedral intermediate and acyl-enzyme for kumamolisin-As (see Figures 1A, 1C and 1E). The reaction coordinate is the distance between the hydrogen atom (H) of the His residue at P1 and Oδ2 of Asp164. The corresponding average distances between H and O′ are given below. For instance, when the reaction coordinate is 4.2 Å for the substrate complex, the average distance for R(H…O′) is about 1.8 Å based on the trajectory of the corresponding window (i.e., H forms a hydrogen bond with the C=O′ group of Pro at P2). Blue dotted line: the free energy change in the substrate complex. For the substrate complex, the conformations for which His at PI forms a hydrogen bond with the C=O′ group of Pro at P2 (i.e., the structure shown in Figure 1A) are considerable more stable (by about 5–6 kcal/mol) than the conformations for which the His residue interacts with Oδ2 of Asp164. Black solid line: the free energy change in the tetrahedral intermediate. For the tetrahedral intermediate, the conformations for which the His at P1 forms a hydrogen bond with Oδ2 of Asp164 (i.e., the structure shown in Figure 1C) are more stable (by about 2 kcal/mol) than the conformations for which His interacts with C=O group of Pro at P2. Red dashed line: the free energy change in the acyl-enzyme. The conformations for which the His residue forms a hydrogen bond with the C=O′ group of Pro at P2 (i.e., the structure shown in Figure 1E) are considerable more stable than the conformations for which His at P1 interacts with Oδ2 of Asp164.
Conclusions
The QM/MM MD and free energy simulations demonstrated that the nucleophilic attack by the serine residue on the substrate may not be the rate limiting step for the acylation of the GPH*FF substrate. The results given here confirm the earlier suggestions that Asp164 acts as a general acid during the nucleophilic attack by Ser278. It was also shown that this residue acts as a general base during the formation of the acyl-enzyme from the tetrahedral intermediate. The role of dynamic substrate assisted catalysis (DSAC) involving His at the P1 site was examined, and it was shown that the bond breaking and making events at each stage of the reaction trigger a change of the position for the His sidechain and lead to the formation of alternative hydrogen bonds. The back and forth movements of the His sidechain between the C=O′ group of Pro at P2 and 652 Asp164 and the formation of the corresponding hydrogen bonds effectively lower the free energy barriers for the both nucleophilic attack and the acyl-enzyme formation and leads to a relatively high activity.
Acknowledgments
We thank Professor Martin Karplus for a gift of the CHARMM program.
Abbreviations
- DSAC
Dynamic substrate assisted catalysis
- SAC
substrate-assisted catalysis
- QM/MM
Quantum mechanical/molecular mechanical
- MD
molecular dynamics
- TI
Tetrahedral intermediate
- PMF
potential of mean force
- SCC-DFTB
self consistent charge density-functional tight-binding
- TS
transition state
- WHAM
weighted histogram analysis method
Footnotes
This work was supported in part by the Center of Excellence for Structural Biology and UT-ORNL Science Alliance, the University of Tennessee and the Petroleum Research Fund (HG) and in part by the Intramural Research Program of the NIH, National Cancer Institute, Center for Cancer Research (AW).
References
- 1.Oda K, Sugitani M, Fukuhara K, Murao S. Purification and properties of a pepstatin-insensitive carboxyl proteinase from a gram-negative bacterium. Biophys Acta. 1987;923:463–469. doi: 10.1016/0304-4165(87)90055-9. [DOI] [PubMed] [Google Scholar]
- 2.Wlodawer A, Li M, Gustchina A, Oyama H, Dunn BM, Oda K. Structure and enzymatic properties of the sedolisin family of serine-carboxyl peptidases. Acta Biochim Pol. 2003;50:81–102. [PubMed] [Google Scholar]
- 3.Tsuruoka N, Nakayama T, Ashida M, Hemmi H, Nakao M, Minakata H, Oyama H, Oda K, Nishino T. Collagenolytic serine-carboxyl proteinase form Alicyclbacillus sendaiensis strain NTAP-1: purification, characterization, gene cloning, and heterologous expression. Appl Envioron Microbiol. 2003;69:162–169. doi: 10.1128/AEM.69.1.162-169.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Wlodawer A, Li M, Gustchina A, Uchika K, Oyama H, Dunn BM, Oda K. Carboxyl proteinase from Pseudomonas defines a novel family of subtilisin-like enzymes. Nat Struct Biol. 2001;8:442–446. doi: 10.1038/87610. [DOI] [PubMed] [Google Scholar]
- 5.Wlodawer A, Li M, Gustchina A, Oyama H, Oda K, Beyer BB, Clemente J, Dunn BM. Two inhibior molecules bound in the active site of Pseudomonas sedolisin: a model for the bi-product complex following cleavage of a peptide substrate. Biochem Biophys Res Commun. 2004;314:638–645. doi: 10.1016/j.bbrc.2003.12.130. [DOI] [PubMed] [Google Scholar]
- 6.Wlodawer A, Li M, Gustchina A, Dauter Z, Uchida K, Oyama H, Goldfar NE, Dunn BM, Oda K. Inhibitor complexes of the Pseudomonas serine-carboxyl proteinase. Biochemistry. 2001;40:15602–15611. doi: 10.1021/bi011817n. [DOI] [PubMed] [Google Scholar]
- 7.Commellas-Bigler M, Fuentess-Prior P, Maskos K, Huber R, Oyama H, Uchida K, Dunn BM, Oda K, Bode W. The 1.4 Å crystal structure of kumamolysin: a thermostable serine-carboxyl-type proteinase. Structure. 2002;10:865–876. doi: 10.1016/s0969-2126(02)00772-4. [DOI] [PubMed] [Google Scholar]
- 8.Commellas-Bigler M, Maskos K, Huber R, Oyama H, Oda K, Bode W. 1.2 Å crystal structure of the serine carboxyl proteinase pro-kumamolisin: structure of an intact pro-subtilase. Structure. 2004;12:1313–1323. doi: 10.1016/j.str.2004.04.013. [DOI] [PubMed] [Google Scholar]
- 9.Wlodawer A, Li M, Gustchina A, Tsuruoka N, Ashida M, Minakata H, Oyama H, Oda K, Nishino T, Nakayama T. Crystallographic and biochemical investigations of kumamolisin-As, a serine-carboxyl peptidase with collagenase activity. J Biol Chem. 2004;279:21500–21510. doi: 10.1074/jbc.M401141200. [DOI] [PubMed] [Google Scholar]
- 10.Okubo A, Li M, Ashida M, Oyama H, Gustchina A, Oda K, Dunn BM, Wlodawer A, Nakayama T. Processing, catalytic activity and crystal structures of kumamolisin-As with an engineered active site. FEES J. 2006;273:2563–2576. doi: 10.1111/j.1742-4658.2006.05266.x. [DOI] [PubMed] [Google Scholar]
- 11.Rawlings ND, Barrett AJ. Tripeptidyl-peptidase I is apparently the CLN2 protein absent in classical late-infantile neuronal ceroid lipofuscinosis. Biochim Biophys Acta. 1999;1429:496–500. doi: 10.1016/s0167-4838(98)00238-6. [DOI] [PubMed] [Google Scholar]
- 12.Lin L, Sohar I, Lackland H, Lobel P. The human CLN2 protein/tripeptidyl-peptidase I Is a serine protease that autoactivates at acidic pH. J Biol Chem. 2001;276:2249–2255. doi: 10.1074/jbc.M008562200. [DOI] [PubMed] [Google Scholar]
- 13.Walus M, Kida E, Wisniewski KE, Golabek AA. Ser475, Glu272, Asp276, Asp327, and Asp360 are involved in catalytic activity of human tripeptidyl-peptidase I. FEBS Lett. 2005;579:1383–1388. doi: 10.1016/j.febslet.2005.01.035. [DOI] [PubMed] [Google Scholar]
- 14.Sleat DE, Donnelly RJ, Lackland H, Liu CG, Sohar L, Pullarkat RK, Lobel P. Association of mutations in a lysosomal protein with classical late-infantile neuronal ceroid lipofuscinosis. Science. 1997;277:1802–1805. doi: 10.1126/science.277.5333.1802. [DOI] [PubMed] [Google Scholar]
- 15.Guo HB, Wlodawer A, Guo H. A general acid-base mechanism for the stabilization of a tetrahedral adduct in a serine-carboxyl peptidase: a computational study. J Am Chem Soc. 2005;127:15662–15663. doi: 10.1021/ja0520565. [DOI] [PubMed] [Google Scholar]
- 16.Xu Q, Guo HB, Wlodawer A, Guo H. The importance of dynamics in substrate-assisted catalysis and specificity. J Am Chem Soc. 2006;128:5994–5995. doi: 10.1021/ja058831y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Guo HB, Wlodawer A, Nakayama T, Xu Q, Guo H. Catalytic role of proton transfers in the formation of a tetrahedral adduct in a serine carboxyl peptidase. Biochemistry. 2006;45:9129–9137. doi: 10.1021/bi060461i. [DOI] [PubMed] [Google Scholar]
- 18.Dunn BM. Structure and mechanism of the pepsin-like family of aspartic peptidases. Chem Rev. 2002;702:4431–4458. doi: 10.1021/cr010167q. [DOI] [PubMed] [Google Scholar]
- 19.Hedstrom L. Serine protease mechanism and specificity. Chem Rev. 2002;102:4501–4523. doi: 10.1021/cr000033x. [DOI] [PubMed] [Google Scholar]
- 20.Ishida T, Kato S. Theoretical perspectives on the reaction mechanism of serine proteases: the reaction free energy profiles of the acylation process. J Am Chem Soc. 2003;125:12035–12048. doi: 10.1021/ja021369m. [DOI] [PubMed] [Google Scholar]
- 21.Carter P, Wells JA. Engineering enzyme specificity by “substrate-assisted catalysis”. Science. 1987;237:394–399. doi: 10.1126/science.3299704. [DOI] [PubMed] [Google Scholar]
- 22.For a review of SAC, see Dall’Acqua W, Carter P. Substrate-assisted catalysis: Molecular basis and biological significance. Protein Sci. 2000;9:1–9. doi: 10.1110/ps.9.1.1.
- 23.Cui Q, Elstner M, Kaxiras E, Frauenheim T, Karplus M. A QM/MM implementation of the self-consistent charge density functional tight binding (SCC-DFTB) method. J Phys Chem B. 2001;110:6458–6469. [Google Scholar]
- 24.Brooks BR, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J Comput Chem. 1983;4:187–217. [Google Scholar]
- 25.Riccardi D, Schaefer P, Yang Y, Yu HB, Ghosh N, Prat-Resina X, Konig P, Li GH, Xu DG, Guo H, Elstner M, Cui Q. Development of effective quantum mechanical/molecular mechanical (QM/MM) methods for complex biological processes. J Phys Chem B. 2006;110:6458–6469. doi: 10.1021/jp056361o. [DOI] [PubMed] [Google Scholar]
- 26.Elstner M, Cui Q, Munih P, Kaxiras E, Frauenheim T, Karplus M. Modeling zinc in biomolecules with the self consistent charge-density functional tight binding (SCC-DFTB) method: Applications to structural and energetic analysis. J Comput Chem. 2003;24:565–581. doi: 10.1002/jcc.10201. [DOI] [PubMed] [Google Scholar]
- 27.Konig PH, Hoffmann M, Frauenheim T, Cui Q. A critical evaluation of different QM/MM frontier treatments with SCC-DFTB as the QM method. J Phys Chem B. 2005;109:9082–9095. doi: 10.1021/jp0442347. [DOI] [PubMed] [Google Scholar]
- 28.Sattelmeyer KW, Tirado-Rivers J, Jorgensen WL. J Phys Chem A. 2006;110:13551–13559. doi: 10.1021/jp064544k. [DOI] [PubMed] [Google Scholar]
- 29.Sattelmeyer KW, Tubert-Brohman L, Jorgensen WL. J Chem Theo Comp. 2006;2:413–419. doi: 10.1021/ct050174c. [DOI] [PubMed] [Google Scholar]
- 30.Tubert-Brohman I, Guimaraes CRW, Jorgensen WL. J Chem Theo Comp. 2006;1:817–823. doi: 10.1021/ct0500287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.MacKerell AD, Jr, Bashford D, Bellott M, Bunbrack RL, Jr, Evanseck JD, Field MJ, Fischer S, Gao J, Guo H, Ha S, Joseph-McCarthy D, Kuchnir L, Kuczera K, Lau FTK, Mattos C, Michnick S, Ngo T, Nguyen DT, Prodhom B, Reiher WE, III, Roux B, Schlenkrich M, Smith JC, Stote R, Straub J, Watanabe M, Wiorkiewicz-Kuczera J, Yin D, Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 32.Brooks CL, III, Brunger A, Karplus M. Active site dynamics in protein molecules: A stochastic boundary molecular-dynamics approach. Biopolymers. 1985;24:843–865. doi: 10.1002/bip.360240509. [DOI] [PubMed] [Google Scholar]
- 33.Field MJ, Bash PA, Karplus M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J Comput Chem. 1990;11:700–733. [Google Scholar]
- 34.Jorgensen WL, Chandrasckhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 35.Neria E, Fisher S, Karplus M. Simulation of activation free energies in molecular systems. J Chem Phys. 1996;105:1902–1921. [Google Scholar]
- 36.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J Comp Phys. 1977;23:327–341. [Google Scholar]
- 37.Torrie GM, Valleau JP. Monte Carlo free energy estimates using non-Boltzmann sampling: Application to the sub-critical Lennard-Jones fluid. Chem Phys Lett. 1974;28:578–581. [Google Scholar]
- 38.Kumar S, Bouzida D, Swendsen RH, Kollman PA, Rosenberg JM. The weighted histogram analysis method for free-energy calculations on biomolecules: 1. The method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]


