Abstract
Changes in the subject’s breathing rate or depth, such as a breath-hold challenge, can cause significant MRI signal changes. However, the response function that best models breath-holding induced signal changes, as well as those resulting from a wider range of breathing variations including those occurring during rest, has not yet been determined. Respiration related signal changes appear to be slower than neuronally-induced BOLD signal changes and are not modeled accurately using the typical hemodynamic response functions used in fMRI. In this study, we derive a new response function to model the average MRI signal changes induced by variations in the respiration volume (breath-to-breath changes in the respiration depth and rate). This was done by averaging the response to a series of single deep breaths performed once every 40s amongst otherwise constant breathing. The new “respiration response function” consists of an early overshoot followed by a later undershoot (peaking at approximately 16s), and accurately models the MRI signal changes resulting from breath holding as well as cued depth and rate changes.
Introduction
Time series of MRI signal changes measured in functional MRI (fMRI) can be strongly influenced by many factors, including changes in the subject’s breathing rate and/or depth over time. This can be seen most clearly in studies involving periods of breath-holding, where a breath-hold of even a few seconds can cause signal changes of several percent (Abbott et al., 2005; Kastrup et al., 1999; Kastrup et al., 1999; Kwong et al., 1995; Li et al., 1999; Stillman et al., 1995; Thomason et al., 2005). More recently, studies have shown that even subtle variations in breathing depth and rate that occur naturally during rest can result in significant signal changes (Birn et al., 2006; Wise et al., 2004). These signal changes arise from a number of hypothesized mechanisms. First, a number of brain regions are activated in association with voluntary changes in breathing (McKay et al., 2003). In addition to these neuronally-induced blood oxygenation level dependent (BOLD) signal changes, there are a number of non-neuronal, artifactual, signal changes. One source of these artifactual signal changes is the breathing cycle itself: the motion of the chest during breathing causes changes in the magnetic field, which leads to image distortions (Brosch et al., 2002; Raj et al., 2001). Secondly, changes in the depth and rate of breathing result in variations in the arterial level of CO2, a potent vasodilator (Van den Aardweg et al., 2002). Fluctuations in breathing therefore cause either vasodilation or vasoconstriction, resulting in blood flow and oxygenation changes. These changes typically occur at very low temporal frequencies (<0.1 Hz), and are not removed by typical physiological correction routines (Glover et al., 2000; Josephs et al., 1997). These additional physiologically induced fluctuations can impede the detection of functional activation, or they can result in additional false positives if the breathing changes are correlated with the task. Furthermore, these breathing-related fluctuations are particularly problematic for resting-state connectivity analyses, which rely on the correlation of time-series between brain regions to infer a functional connection. As demonstrated in previous studies, the fluctuations in breathing during rest generally occur at similar frequencies (~0.03 Hz) and in similar brain regions as those implicated in resting-state default-mode network activity (Birn et al., 2006; Modarreszadeh et al., 1994; Van den Aardweg et al., 2002; Wise et al., 2004). Therefore, in order to obtain resting-state activity maps that reflect fluctuations in neuronal activity exclusively, it is vital that these respiration-induced fluctuations are modeled or removed from the data. Finally, respiratory challenges, such as breath-holding, have been suggested as ways to measure relative baseline venous blood volume across the brain, which can be used to calibrate the BOLD signal. All of these analyses – correcting for false positives and negatives, improving functional connectivity analysis, and mapping the relative amplitude of respiration induced signal changes – require that we know precisely how a change in respiration affects the MRI signal.
Previously, respiration changes have been modeled in one of 3 ways – 1) as the timing of breathing changes convolved with a hemodynamic response function derived from BOLD activation dynamics (a gamma-variate function, or the default hemodynamic response function included in SPM) (Abbott et al., 2005; Thomason et al., 2005; Thomason et al., 2007); 2) by time-shifting a boxcar waveform representing the cue for breathing changes (e.g. cues for breath-holding) (Kastrup et al., 1999; Kastrup et al., 1999; Li et al., 1999); or 3) by time-shifting an estimate of the respiration volume per unit time (Birn et al., 2006). It is not apparent whether the use of a relatively rapid activation-derived BOLD signal change response function is necessarily the best model for the slower respiration-induced changes. First, the flow and BOLD changes induced by variations in breathing are mediated in part by levels of arterial oxygen saturation, intra-thoracic pressure changes, and variations in arterial CO2 (Thomason et al., 2005). These changes in arterial CO2 do not occur immediately after a change in the breathing volume or rate, but may take several seconds to develop (Van den Aardweg et al., 2002). Additionally, signal changes induced by an administration of CO2 have been observed to result in relatively slow signal changes, with a time constant of approximately 45 seconds and a delay of approximately 6 seconds (Corfield et al., 2001; Poulin et al., 1996). Since the time constants of these signal changes are not the same as neuronal-activation induced BOLD changes, it is unlikely that a gamma-variate impulse response, with time constants originally derived from the BOLD fMRI signal change to a 1s visual stimulus, accurately models the MR signal response to respiration changes. Finally, the MR signal response to breath-holding has often shown a strong bimodal response, with an early signal decrease followed by a later overshoot, particularly when the breath hold is performed after inspiration. The correlation of the MRI time course with an estimate of the respiration volume per time changes during rest has also suggested a bi-modal response to breathing changes, with a positive correlation at short latencies, and an even larger negative correlation at longer latencies (Birn et al., 2006). In other words, a decrease in the breathing depth or rate results in an initial decrease in signal followed by a strong overshoot, while an increase in the breathing depth or rate results in an initial overshoot with a later decrease. All of these findings and observations suggest that the MRI signal response to variations in respiration has a longer time constant and is potentially more complex than the BOLD fMRI response to activation, and should therefore be modeled with a different response function.
In a previous study we showed that a time-shifted estimate of the temporal changes in respiration volume per time (RVT) is significantly correlated with MRI signal variations (Birn et al., 2006). However, fully removing the variance in the MRI signal induced by respiration changes requires a function that is not only roughly correlated with the response, but one that matches the precise temporal shape of the induced signal change. A sudden change in breathing rate or depth, for example, results in a relatively slow flow and oxygenation change. Regressing a shifted estimate of the respiration volume per time out of the MRI signal time series therefore leaves a significant amount of residual variation, which can still cause problems in resting-state connectivity analyses (Birn et al., 2006). In addition, this approach is problematic if the respiration changes are correlated with a task being investigated in a study. Allowing for a variable time-shift of the RVT time course would result in true task-related BOLD responses as being falsely classified as artifact, and a resultant decreased ability to detect true activation. If, however, the respiration changes result in CO2 mediated responses that are slower than activation induced BOLD responses, separating respiration-induced from activation-induced changes more cleanly and completely may be possible, even if breathing changes are correlated with the task.
The goal of this study is to determine the transfer function between respiration changes and MRI signal changes. This transfer function is estimated by having the subject perform a series of single deep breaths, spaced 30–40s apart, during otherwise constant respiration rate and depth. The rationale for this is that a single deep breath will result not only in known magnetic field changes, which occur during the breath, but also in other physiological changes, such as a transient decrease in arterial CO2, evident in a series of breaths and their associated rate and depth changes. Three breathing manipulations – depth changes, rate changes, and breath-holding – are studied. In addition, we test whether this “respiration response function” can accurately predict the fluctuations in the MRI signal resulting from RVT fluctuations at rest.
Methods
Subjects and Imaging Parameters
Eleven normal, healthy, right-handed volunteers were scanned under an Institutional Review Board (IRB) approved protocol after obtaining informed consent. (Ages: 23–40y, mean age 31.8y +/− 6.2y, 6F) Time series of T2*-weighted echo-planar MR images were acquired on a 3 T General Electric (GE) MRI scanner (Waukesha, WI, USA) using an 8-channel GE receive coil with whole body RF excitation. A limited coverage of six 5 mm thick axial slices positioned at the level of the visual cortex was acquired. This limited coverage was used in order to obtain a faster temporal resolution. (TR: 500 ms, TE: 30 ms, Flip angle: 90°, FOV: 24 cm, slice thickness: 5 mm, matrix: 64×64, 165 image volumes per time series.) A high resolution anatomical image was acquired using a T1-weighted Magnetization Prepared Rapid Gradient Echo (MP-RAGE) sequence. Subjects' heart beats were recorded using a pulse-oximeter placed on the left index finger. Respiration was measured with a pneumatic belt around the chest. These two physiological monitoring devices are an integrated part of the General Electric MR scanner (Waukesha, WI), and are recorded to a text file with 25ms sampling period by changing a manufacturer supplied control variable on the MR console. The measurement obtained from the respiration belt is linearly related to the expansion of the belt.
Tasks
Subjects were scanned during rest and during the performance of different cued respiration modulations. This cue consisted of a visually presented bar that moved left or right, indicating the timing and depth of the respiration that was to be performed (inspiration reflected by the bar increasing in size, and expiration indicated by the bar decreasing in size). This stimulus was programmed using the Psychophysics Toolbox (Brainard, 1997) implemented in Matlab (MathWorks, Inc.). In the first echo-planar imaging (EPI) run, subjects were scanned at rest, and were instructed to keep their eyes closed. In other runs, subjects were cued to: 1) take one deep breath every 30–40 s (10 breaths), with otherwise constant breathing; 2) increase their breathing depth for periods of 15–20 s (10 breaths), alternated with 30–45s periods (20 breaths) of constant breathing rate and depth; 3) increase their breathing rate for periods of 20 s (10 breaths), alternated with 40 s periods (10 breaths) of constant breathing rate and depth, and 4) hold their breath at the end of their normal expiration for periods of 20s, alternated with normal breathing for periods of 40–60 s. The rate of respiration for the periods of constant breathing rate and depth were set to each subject’s average respiration rate measured from their resting run, typically between 15–20 breaths per minute (3–4s per breath). Runs during rest and cued single deep breaths were repeated in all subjects.
Analysis
All image analysis was performed using AFNI (Cox, 1996). Reconstructed images were first corrected for motion using a rigid-body volume registration. Fluctuations at the respiration and cardiac frequencies and their first harmonics were removed by using RETROICOR (Glover et al., 2000). This technique is similar to those developed earlier by Josephs et al (Josephs et al., 1997) or X. Hu et al (Hu et al., 1995). It does not simply filter out a prescribed range of frequencies, but rather corrects the signal based on the phase of the cardiac and respiratory cycle in which each image was acquired. More specifically, for each image, the phase of the respiratory and cardiac cycles is determined. The sine and cosine of this phase, and 2 times this phase, are then computed, and regressed out of the data. This is equivalent to reshuffling the data based on the phase of the cardiac and respiratory cycle in which each image was acquired, and then fitting a low order Fourier series to this reshuffled data. The advantage of this technique over simple filtering of a prescribed range of frequencies is that it deals with physiological fluctuations (e.g. cardiac) that are of a higher frequency than the rate of image acquisition (determined by the TR), and it allows for a variation in the cardiac and respiration rate. It does not, however, remove the slower (~0.03 Hz) signal changes induced by breath-to-breath variations in the depth and rate of breathing (i.e. the changes in the envelope of the respiration measurement). Signals were then converted to percent signal change by dividing each voxel’s time course by the mean signal across time and multiplying the result by 100.
Changes in the respiration volume per time (RVT), which reflect changes in the envelope of the respiration changes as well as the rate of breathing, were estimated in a manner similar to that described by (Birn et al., 2006). The maxima and minima for each breath were determined from the respiration belt measurement. The series of maxima and minima were then each interpolated to the imaging TR. The respiration period was determined by subtracting the time between successive maxima, and again this series of respiration periods was interpolated to the imaging TR. The time series of RVT changes was then computed by subtracting the minma from the maxima and dividing by the period for each time point. (Birn et al., 2006).
The average response to a single deep breath was determined in each subject by deconvolution. In this case, where the inter-stimulus interval is long and continuous, deconvolution is equivalent to averaging (in time) the response to each deep breath. This estimated response function was then averaged over all voxels with a full F-statistic (of the model fit in the deconvolution) greater than 2 (p<0.0001). Compliance with the cued single deep breath was verified by looking at the respiration belt measurement. Three subjects did not have deep breaths in response to the cues, and the responses were therefore not used in determining the average respiration response function. The deconvolved responses were then averaged across all remaining subjects This average response represents the respiration induced signal change to one deep breath of 3–4 second duration. In order to obtain a respiration response function that can be convolved with respiration volume per time changes, the averaged response was deconvolved using Wiener deconvolution, implemented in Mathcad (Parametric Technology Corp., Needham, MA). The difference of two gamma-variate functions was then non-linearly fit to this deconvolved response. This fit will be referred to as the “respiration response function” (RRF).
The time series of RVT changes, RVT(t), were convolved with three different response functions: 1) a gamma-variate hemodynamic response function (with parameters according to Cohen et al. (Cohen, 1997)) (Eqn 1); 2) a difference of two gamma-variate functions (the canonical HRF used in SPM) with a post-stimulus undershoot (from a 20s duration stimulus) one-fourth the amplitude of the overshoot (Wellcome Department of Cognitive Neurology, http://www.fil.ion.ucl.ac.uk/spm) (Eqn. 2); and 3) with the new RRF (see Egn. 3). For comparison, the three response functions were also convolved with the ideal stimulus timing, rather than the RVT time course. These convolved response time series were then fit to the signal intensity time courses from the other respiration modulations (breath-holding, cued depth changes, cued rate changes, and rest) using a linear regression analysis.
| [1] |
| [2] |
To assess the goodness of fit of the various response functions, convolved with either the RVT(t) or the stimulus timing, to the data, the t-statistic of the fit was averaged over a those voxels in the brain that showed a significant response to breath-holding. More precisely, this region of interest was determined by those voxels that showed a significant (F>2, p<0.0001) time-locked response to the breath-holding task, computed by deconvolution.
Since the latency of the respiration induced signal change can vary across the brain, an additional analysis was performed where the latency of the response was allowed to vary for each voxel. This was accomplished by repeating the regression analysis 51 times (for shifts from −10s to 40s in 1s increments) and choosing for each voxel the latencies that gave the best positive and the best negative fit.
Results
Repeated single deep breaths, series of cued deep breaths, cued rate increases, and breath holding all resulted in significant signal changes in gray matter and regions that are known from previous studies to contain a higher baseline venous blood volume fraction (see Fig. 1 and Fig. 2). A single deep breath resulted in a bimodal response with an early signal increase, peaking at 3 s, followed by a pronounced undershoot of even greater magnitude, peaking at 16 s. This response was fit well by a difference of two gamma variate functions with the equation,
| [3] |
Figure 1.
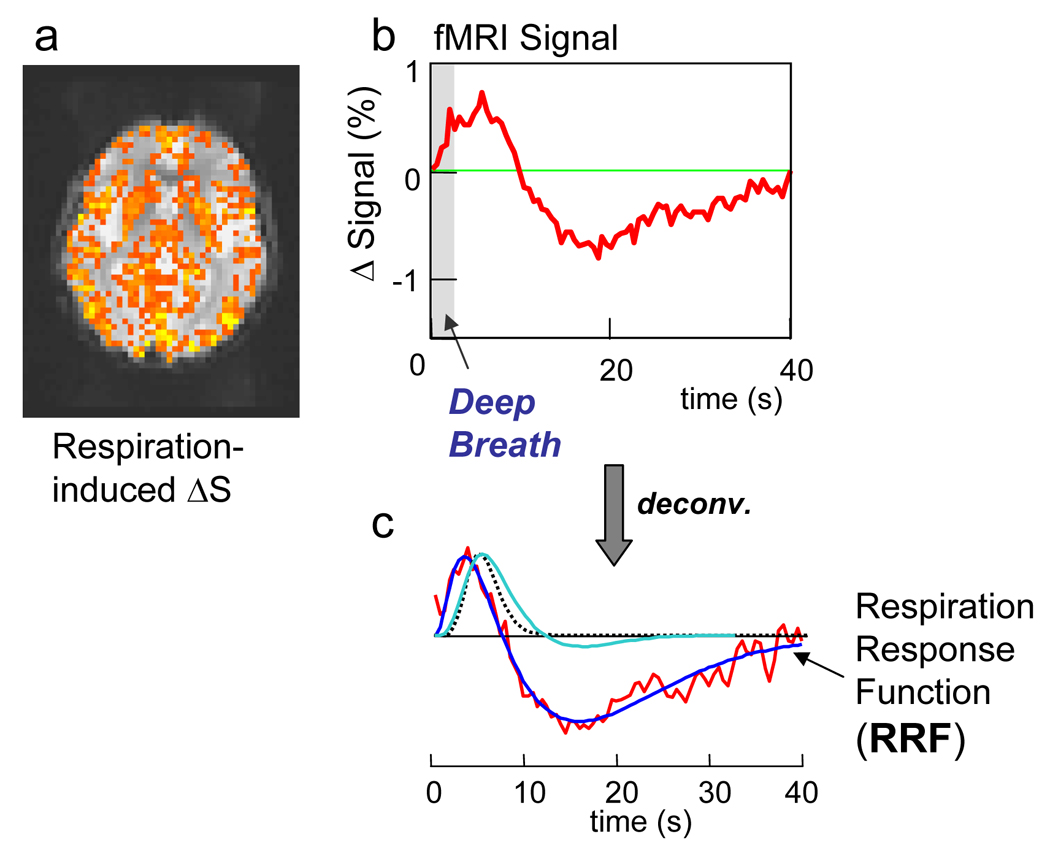
a) Respiration-induced signal changes in one slice from a representative subject in response to a deep breath. Colors show regions significantly time-locked with the cued deep breath (i.e. the F-statistic of the deconvolution analysis). b) averaged signal time course in response to a single deep breath. c) red: impulse response function derived from a Wiener deconvolution of the averages response to a single deep breath. Dark blue: ideal fit representing the Respiration Response Function. Dotted line shows the typical gamma-variate HRF typically used to model activation induced BOLD fMRI signal changes. The light-blue line shows the canonical HRF used on SPM, based on a difference of two gamma-variate functions.
Figure 2.
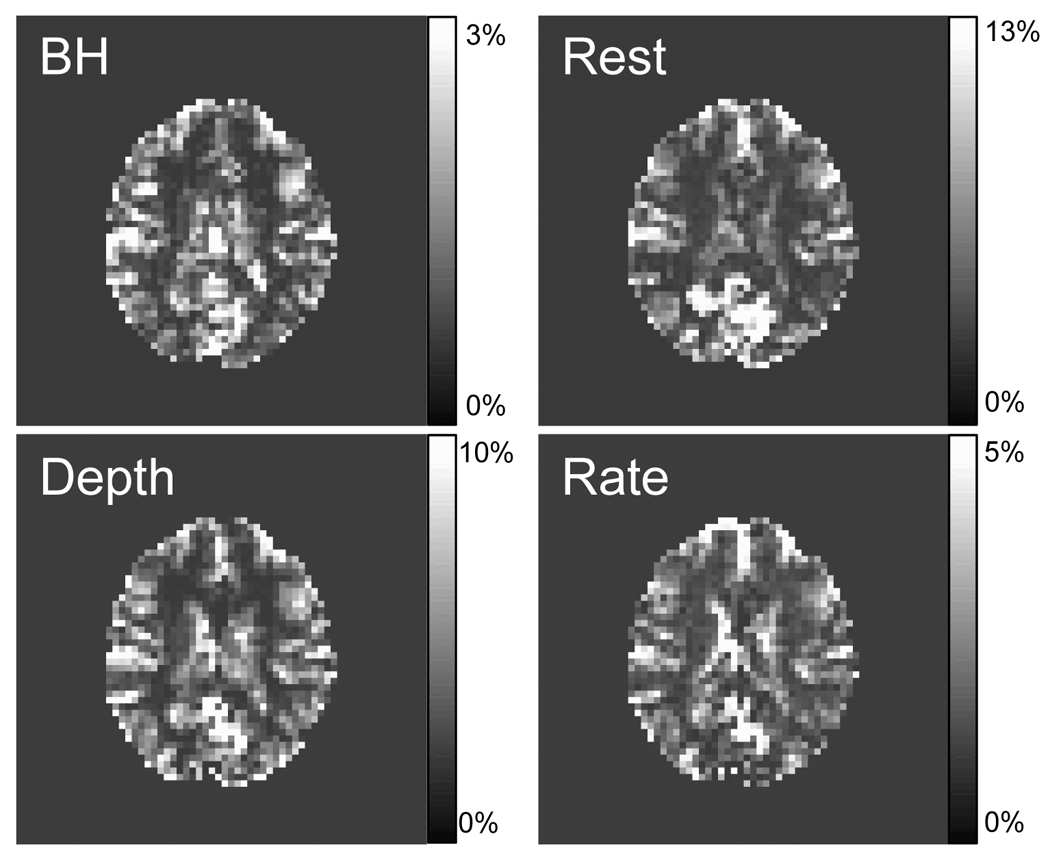
Respiration-induced signal changes in one slice from a representative subject during various cued respiration modulations: Breath-holding (BH), cued Depth changes (Depth), cued Rate changes (Rate); or during Rest. Maps show the fit amplitude of fitting the time series of the respiration volume per time (RVT) convolved with the new respiration response function (RRF) (i.e. RVT(t) * RRF(t)) to the data.
The correlation coefficient between the idealized RRF and the averaged and deconvolved response to a single deep breath was 0.935 (corresponding to a p-value of 3×10−18). In all subjects, the RVT(t) changes during breath-holding, cued depth changes, and cued rate changes, convolved with this new “respiration response function” (RRF) accurately modeled the respiration induced signal changes (mean t-statistics = 7.1 (Breath-holding), 4.1 (Cued depth change), 3.0 (Cued rate change)) (see Fig. 3 and Fig. 4). The majority of the signal change resulted from the undershoot in the RRF, leading to the pronounced signal overshoot in response to breath-holding, and the signal decrease in response to increases in respiration depth or rate. These respiration-induced changes were generally slower than neuronally-induced BOLD fMRI signal changes, and were therefore not as accurately modeled with the gamma-variate or canonical SPM hemodynamic response function (mean t-statistics = 0.4 (Breath-holding), −0.1 (Cued depth change), −0.8 (Cued rate change)). Interestingly, signal changes induced by variations in breathing during rest appeared to be slightly faster, and were not modeled as well using either the new response function or the hemodynamic response functions typically used to analyze neuronally-induced BOLD changes. Allowing a variation in the latency of the respiration response resulted in a significantly better fit, particularly for the gamma-variate response function, canonical SPM response function, and delta function IRF (i.e. simply a shifted RVT or ideal stimulus timing).
Figure 3.
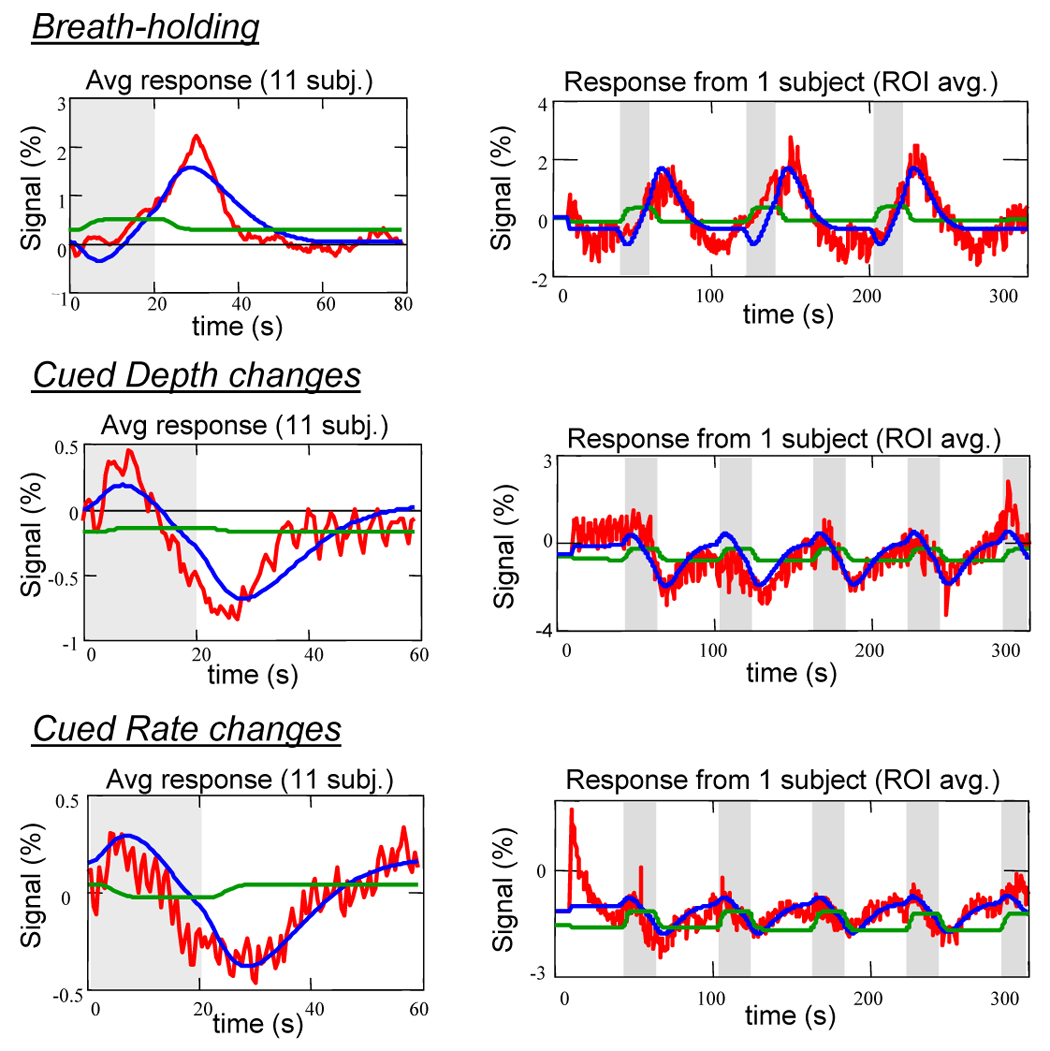
Red: Averaged MRI time courses in response to various respiration modulations: Breath-holding, cued Depth changes, and cued Rate changes. Blue curves: fit of RVT convolved with respiration response function. Green curve: fit of RVT time course convolved with typical Gamma-variate used for activation-induce BOLD responses. Figures on left are averaged across 11 subejcts. Figures on right show the entire time course (averaged over the brain) for one representative subject.
Figure 4.
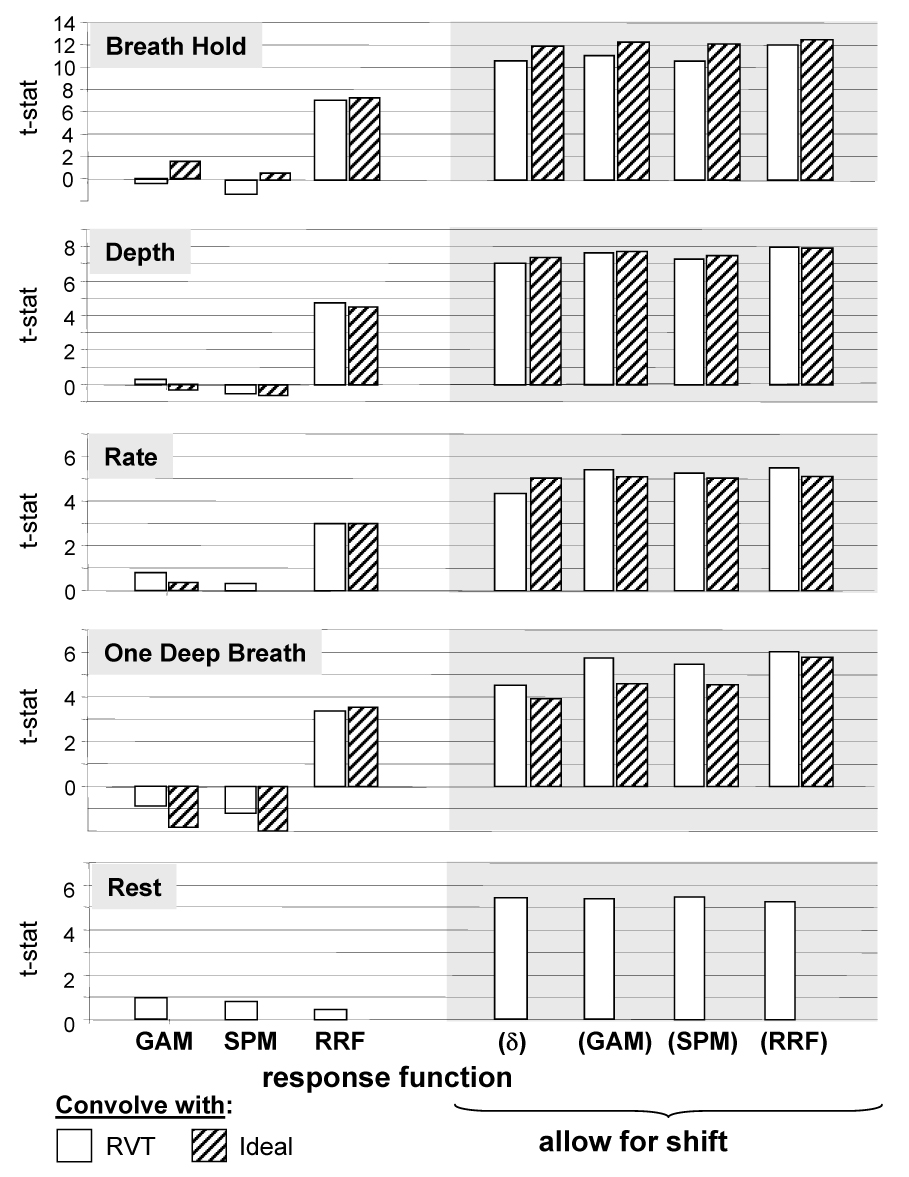
T-statistics of fitting either the respiration volume per time (RVT) time course or Ideal stimulus timing convolved with either a gamma-variate (GAM) or the respiration response function to the data from the breath-holding challenge (B.H.), cued depth changes (Depth), cued rate changes (Rate), or Rest. Bars on right allow for a shift between −10s to +40s. For each voxel, the latency that resulted in the best fit was used. (δ) refers to a fit of the RVT time course or ideal response convolved with a delta function – i.e. the RVT time course or ideal response by itself, allowing for a shift.
Figure 2 shows a map of the fit amplitude of fitting the RVT time course convolved with the new respiration response function (RRF) to the cued breathing changes and to rest in one representative subject. The latency of the response was allowed to vary for each voxel.
Figure 5 shows a histogram of the optimal latencies for voxels that showed significant respiration related signal changes, across all subjects. For all cued respiration conditions and for rest, there is a large range of optimal latencies across voxels, approximately +/− 5 s relative to the average latency. When either the RVT(t) changes or the ideal stimulus timing alone are used to predict respiration-induced signal changes, they have to be shifted by approximately 15 seconds. When convolved with the gamma-variate function, the resulting waveform must still be shifted by over 10s in order to accurately fit the respiration induced signal changes. Similar shifts were required for the canonical SPM response function. The optimal latency for the new RRF is closer to zero. The peak of this histogram is slightly less than zero for the new RRF, indicating that the estimated RRF may be too slow for several voxels.
Figure 5.
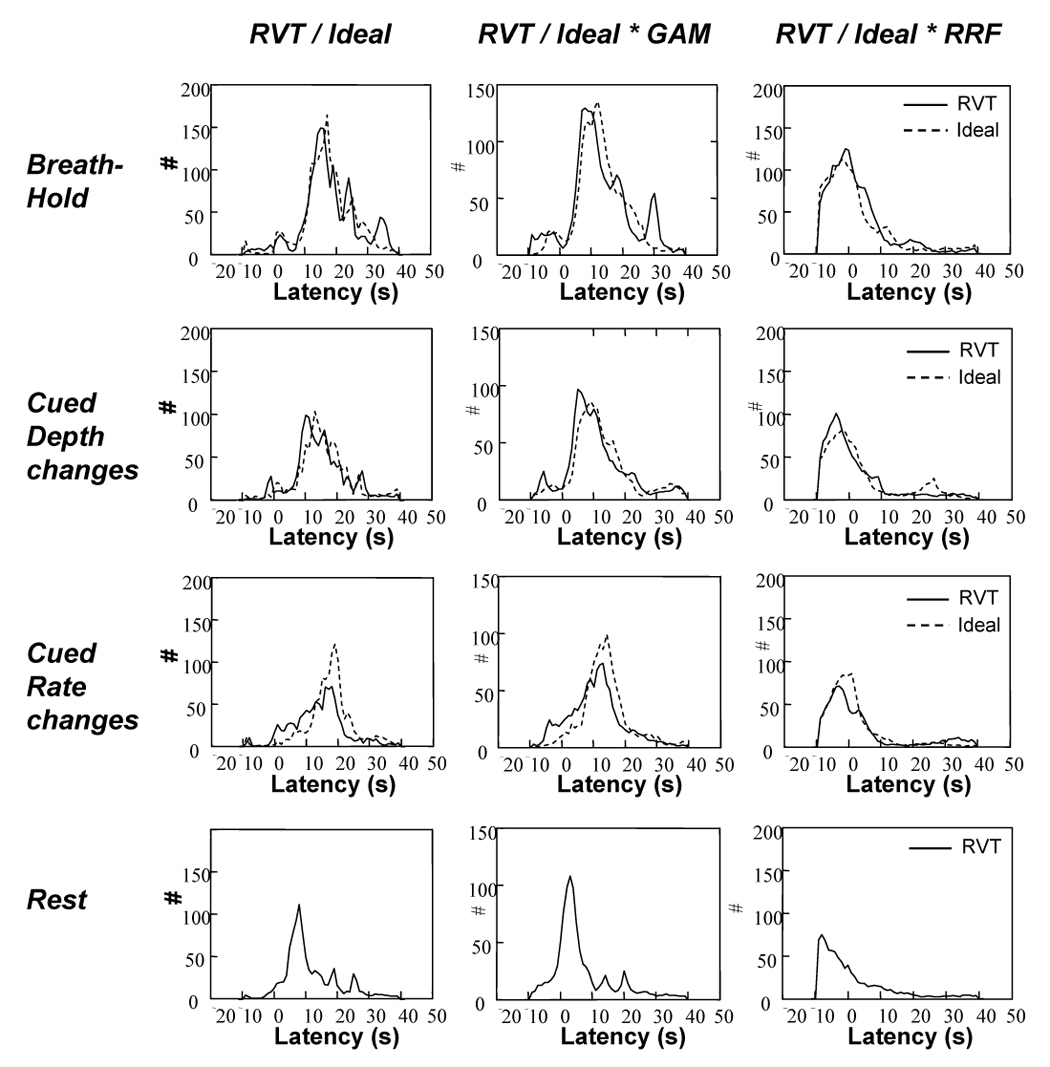
Histograms of latency values across the brain that resulted in the best voxel-wise fit to the various respiration induced responses. Histograms were computed for each subject, then averaged across subjects.
There was a considerable range of optimal latencies across the brain for the modeled respiration induced signal changes fit to the data, approximately +/− 8 s around the average value. This variability results primarily from the variability in latency within each subject, rather than a different average latency across subjects (see Figure 7). Figure 6 shows a map of the optimal latencies in one representative subject, and the corresponding time series for voxels with the optimal latency (of the ideal response fit to the data) within four ranges: −10s to −5s, −5s to 0s, 0s to 5s, and 5s to 10s.
Figure 7.
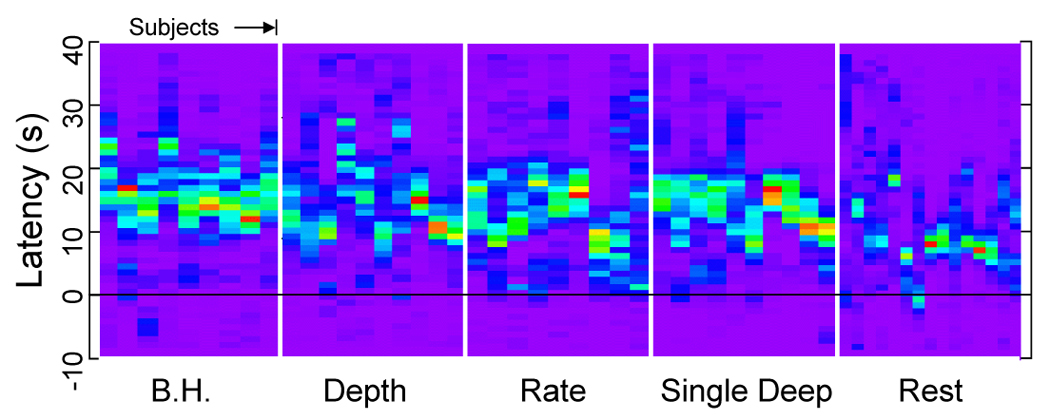
Histograms of the latency of fitting the respiration volume per time (RVT) time course to each voxel ranging from −10s to +40s (vertical axis), for different tasks and for different runs across subjects (horizontal axis). Each subject has a spread of latency of several seconds in the cued breathing variation runs (B.H. = Breath Hold, Depth = Cued Depth changes, Rate = Cued Rate changes, Single Deep = Cued single deep breath, Rest = Resting run.)
Figure 6.
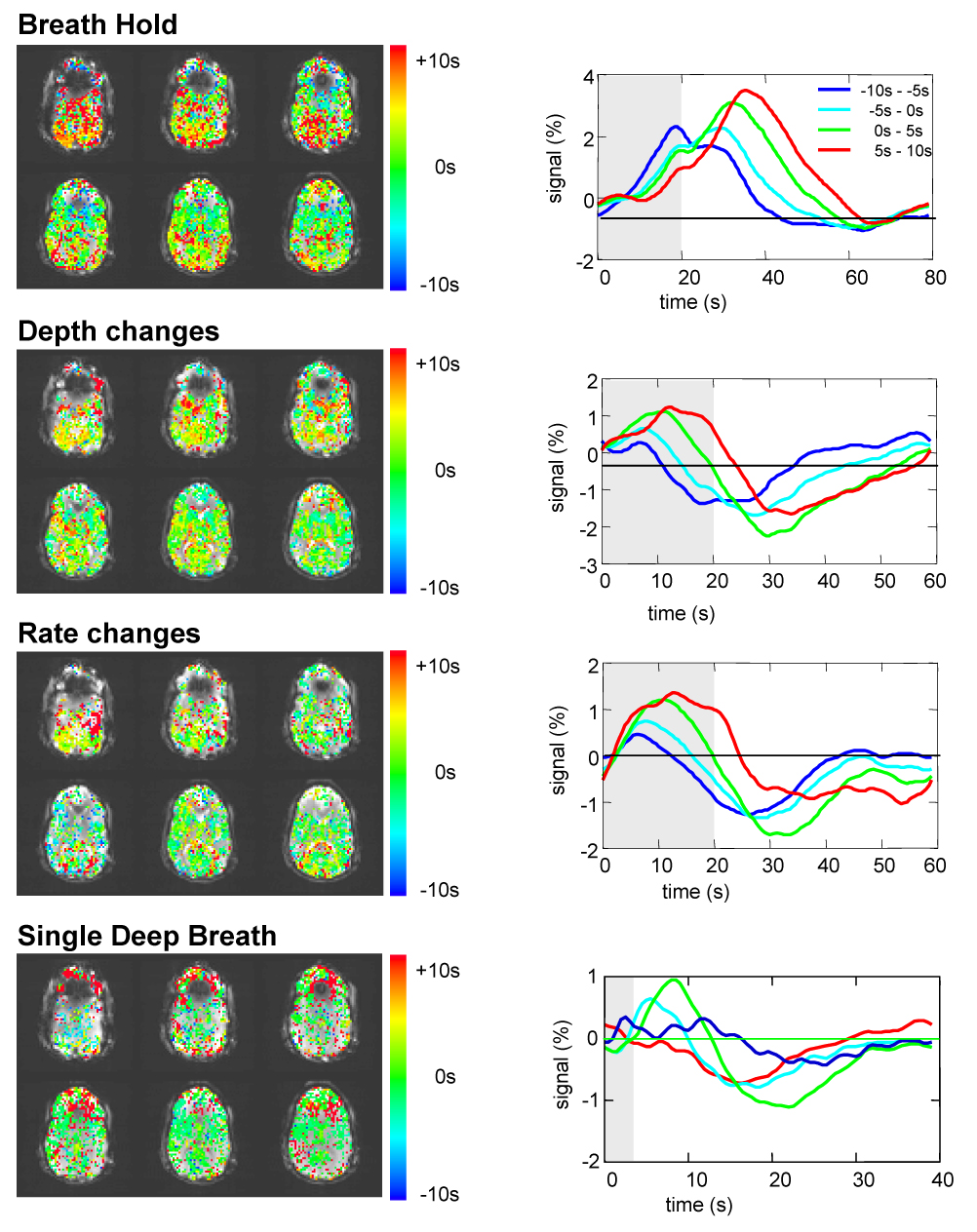
Left: Maps showing the optimal latency for each voxel in fitting the RVT time course (RVT(t)) convolved with RRF to the different cued respiration changes (breath-hold, cued rate changes, cued depth changes). These values reflect the amount that the RVT(t)*RRF had to be shifted in order to result in the optimal fit. Right: average signal intensity time courses for voxels with the optimal latency within four ranges: (−10s to −5s, −5s to 0s, 0s to 5s, and 5s to 10s).
Discussion
The goal of this study was to find a respiration response function that can best describe the average respiration induced response function across the brain, in a similar way that the typical hemodynamic response functions used in fMRI data analysis were derived to model the average hemodynamic BOLD fMRI response.
In this study, we derived an estimate of the “impulse response function” for respiration-induced MRI signal changes by using what could approximately be considered to be an impulse (or brief) breathing change – a single deep breath. The response to this single deep breath was found to capture sufficient temporal characteristics to allow modeling of longer durations of breathing depth changes, breathing rate changes, and even breath-holding. The single deep breath resulted in an early increase in signal, slightly faster than an activation induced BOLD response, followed by a later post-undershoot, peaking at 16 s. In taking this to be an estimate of the “impulse response”, we make no explicit assumptions about what causes these signal increases and decreases. We only assume that all of the mechanisms resulting in MRI signal changes due to variations in breathing rate and depth, including breath-holding, are present in the MRI signal response to a single deep breath.
Conceptually the most straightforward approach to obtaining the transfer function (or impulse response function) would have been to deconvolve the response given the respiration volume per time estimate. In fact, we attempted this initially, but failed to obtain a physiologically plausible impulse response. The difficulty with this approach is that the RVT time course is dominated by low frequency changes. Deconvolution therefore amplifies the high frequencies, resulting in an extremely noisy estimate of the impulse response. This is analogous to estimating an impulse response function from blocked-design data.
The estimation of an “impulse response function” does make the implicit assumption that relationship between respiration changes and MRI signal changes is linear. While this may not necessarily be the case with the full range of breathing perturbations, investigating respiration-induced MRI signal changes as a linear system is an important first step (and similar to what researchers have assumed in previous studies that have convolved a gamma-variate response with the respiration timing (Thomason et al., 2007)). As shown in this study, using even a perhaps overly simplistic linear system model, the average response to one deep breath can accurately predict the responses to a series of deep breaths, rate changes, breath-holding.
The statistics reported in Figure 4 reflect the average goodness of fit (as assessed by a t-statistic) over all voxels that showed a significant time-locked response to the breath-holding task. The purpose of this figure is to compare the effectiveness of the various response functions in fitting the average signal changes in the different cued breathing runs, and to show that all of the cued breathing variations resulted in significant signal changes. An average over the whole brain would result in a smaller average t-statistic, since not all brain regions are significantly affected by respiration changes (cf. (Birn et al., 2006) and Figure 2). This could then be falsely interpreted as reflecting a nonsignificant effect of breathing variations on MRI signal intensity time courses. The breath-holding task was used to determine this region of interest (ROI), since it is the most commonly studied respiration variation, it is known to induce robust signal changes, and it produced the strongest and most reliable signal changes in our study. The values in Figure 4 therefore reflect the average t-statistic of fitting each response function over those regions that show a strong breath-holding induced response, regardless of the shape of that response. Note that this ROI is determined purely by the significance of the signal changes time locked to the cued breath-holding (as measured by the full F-statistic in the deconvolution), not by the significance of a particular response function.
In general, using the ideal stimulus timing was similar to using the time series of RVT changes in the convolution (Fig 4), but there was some variability between subjects and between tasks. This is likely a reflection of how well the subject performed the task, and how accurately the time series of RVT changes, estimated from only one respiration belt, model arterial CO2 changes and resulting blood flow and blood oxygenation changes. The time series of RVT changes are admittedly a simplistic estimate of the arterial CO2. A more accurate estimate might be obtained with two respiration belts, one around the abdomen and one around the chest, or by monitoring end-tidal CO2. The use of only one belt, however, is considerably easier, as the device and the procedure for acquiring this data are often supplied by the scanner manufacturer. An additional source of variability is that the MRI signal can be influenced by other respiration related mechanisms (e.g. intrathoracic pressure changes), which are not fully reflected in the RVT time course measurement. In addition, the finding that the ideal (cued) stimulus timing can be convolved with the RRF to obtain a good fit to the MRI signal changes induced by cued respiration changes suggests that this response function can also be used in studies where the cued respiration changes are not explicitly measured.
The data in this study were acquired at a relatively short TR (500ms) and large flip angle (90 degrees). This can enhance the signal changes from blood flowing into the slice, and thereby increase the amplitude, and possibly the dynamics, of physiologically induced fluctuations. It is possible that the spatial variation of this inflow effect could explain some of the spatial variability of the respiration related signal change. The dynamics of the average breath-holding induced change, however, appears similar to that measured in previous studies which used a 2s TR. It is therefore expected that the respiration response function derived in this study will also apply to studies with longer TRs.
Previous studies have implicated several brain regions that are involved in the conscious control of breathing. These include the primary sensory and motor cortexes, supplementary motor area, cerebellum, thalamus, caudate nucleus, globus pallidum, and medulla (McKay et al., 2003). It is therefore possible that some of the MR signal changes time-locked to the cued respiration changes, such as the single deep breath, may be neuronal in origin. The volume imaged in this study, however, consisted of only six axial slices positioned at the level of the visual cortex, and did not extend into the primary motor cortex. Furthermore, the respiration response was averaged over all voxels that showed a significant time-locked response to a breath-holding challenge. This included most of the gray matter and are typically believed to reflect more general blood flow and oxygenation changes. A neuronally-induced BOLD response is therefore likely to be only a small contribution to the overall respiration modulation induced signal change.
The relatively poor fit of the new respiration response function to resting fluctuations in breathing was at first puzzling. After all, in a previous publication, we showed that RVT changes were significantly correlated with MR signal changes during rest (Birn et al., 2006). In this previous study, however, the RVT time course was shifted in time by several seconds (on average 5.4 s) in order to obtain a good fit. Furthermore, this latency varied in different regions of the brain. In order to compare the current results with the results of the previous study, we again allowed the latency to vary in each voxel. When this was done, all of the ideal response functions (the gamma-variate, the canonical SPM response function, the new respiration response function, and a delta function) convolved with the RVT time course or the stimulus timing resulted in a significant fit to the MRI data in similar regions of the brain. It is important to note, however, that the RVT time course convolved with the typical neuronal-induced BOLD gamma-variate function only resulted in a significant fit when shifted on average by about 10 s. Such a large temporal shift cannot be accomplished by simply including the derivative of the ideal response as another regressor (Henson et al., 2002). This large latency also offers hope that respiration induced signal changes can be separated from task-induced BOLD signal changes in the event that respiration changes are synchronized with the task.
This latency analysis showed that the signal changes induced by variations in breathing during rest appeared to be slightly faster (see Fig. 4). For most of the voxels, the best fit occurred when the RVT time course was shifted by 8 s, when the RVT time course convolved with the gamma-variate was shifted by 3 s, or when the RVT time course convolved with the RRF was shifted by −8 s. In other words, the respiration induced signal changes during rest were slower than the typical hemodynamic response to neuronal activation, but faster than the signal changes in response to cued respiration changes. It is unclear what the source of this difference between cued and resting breathing responses is, but it may reflect different physiological processes governing cued versus natural breathing changes.
The latency and temporal evolution of the average respiration induced signal change was found to vary across the brain by several seconds. This could reflect different underlying blood vasculature (e.g. vessel size, type, blood volume fraction). Alternatively, the spatial variation in latency may reflect different mechanisms of respiration induced MR signal changes. The signal changes in some areas may in fact be a BOLD fMRI response to neuronal activation associated with breathing variations, which have a different latency. A closer look at the averaged responses to the different respiration challenges (Figure 6) shows that the variation in latency is driven by a difference in the width of the response, rather than a large difference in the onset time. For example, in response to a 20s breath hold, the MRI signal in some areas returns to baseline within 20s of resuming normal breathing, while in other areas the signal continues to increase for another 20s, and only then slowly returns to baseline. The spatial variation in the latency of the respiration-induced response also raises the interesting possibility that the average response to the single deep breath could be used as the RRF for each voxel. In the current study, however, the averaged responses to only 14–20 deep breaths (spaced apart by 30–40 s) were too noisy to be used as a response function to accurately predict respiration induced signal changes. An additional consequence of this latency variability is a potential broadening of the averaged respiration response, when the signal changes are averaged over the brain. The variation of this latency across the brain also suggests that when modeling the respiration induced changes, a variable latency must be taken into account. While a slight improvement can be obtained by using a single regressor with a variable latency (but which is kept constant across space), a better fit can be obtained by allowing the latency to vary for each voxel (see Fig. 4).
If the spatial variation in the shape and latency of the response is consistent across subjects, then a region-specific response function could be derived and applied to each voxel. This, however, would require more extensive whole-brain studies on multiple subjects, and the reliability of this voxel-specific response function would have to be assessed. The focus of the current experiment was the first step in modeling the MR signal changes induced by changes in respiration – deriving a single response function that could be used to model the average response across the brain. This single response function provided a much better fit to respiration-induced signal changes compared to other response functions more commonly used to model activation-induced BOLD fMRI signal changes.
The average response to single deep breath could potentially reveal interesting and important physiological information – the vascular response to a brief stress. It is easy for the subject to perform, and several time constants can be derived from the response (e.g. the onset latency, time to peak, and duration of the undershoot). Additionally, the variability of the these time constants across space may reflect variations in the underlying blood vessels. For this to be clinically relevant, it will, of course, necessitate a more complete physiological understanding of the mechanisms leading to the signal increases and decreases.
Conclusion
Using the average response to a single deep breath, we have determined a new “respiration response function” that can be used to model respiration induced signal changes across a range of cued breathing manipulations. This response function provides a significantly better fit, on average, to the signal changes induced by cued breathing variations than hemodynamic response functions typically used to model BOLD fMRI signal changes. When latency is allowed to vary, the fit is improved, which may result from a spatial variability of the respiration induced response. Future studies should therefore be designed to more closely examine the spatial variations of this response function.
Accurately modeling respiration induced signal changes is important and practically useful for several reasons. First, changes in breathing rate and depth can cause significant signal changes that can lead to both false positives (when correlated with a functional task) or false negatives. Removing these artifactual fluctuations can lead to an improved detection of true BOLD fMRI signal changes and a reduction of false positives. Filtering these slower respiration induced signal changes is also a crucial step before performing functional connectivity analysis. Additionally, the use of these response functions, at the appropriate latencies, will result in a more accurate determination of respiration induced signal change amplitudes across the brain and across the subjects. This will be particularly important when respiration-induced signal changes, such as breath-holding, are used in order to calibrate the spatial and inter-subject variability of the BOLD response (Bandettini et al., 1997; Cohen et al., 2004; Davis et al., 1998; Hoge et al., 1999; Thomason et al., 2007)
Acknowledgements
This research was funded by the National Institutes of Mental Health Intramural Research Program.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Abbott DF, Opdam HI, Briellmann RS, Jackson GD. Brief breath holding may confound functional magnetic resonance imaging studies. Hum Brain Mapp. 2005;24(4):284–290. doi: 10.1002/hbm.20086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bandettini PA, Wong EC. A hypercapnia-based normalization method for improved spatial localization of human brain activation with fMRI. NMR Biomed. 1997;10(4–5):197–203. doi: 10.1002/(sici)1099-1492(199706/08)10:4/5<197::aid-nbm466>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- Birn RM, Diamond JB, Smith MA, Bandettini PA. Separating respiratory-variation-related fluctuations from neuronal-activity-related fluctuations in fMRI. Neuroimage. 2006;31(4):1536–1548. doi: 10.1016/j.neuroimage.2006.02.048. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spat Vis. 1997;10(4):433–436. [PubMed] [Google Scholar]
- Brosch JR, Talavage TM, Ulmer JL, Nyenhuis JA. Simulation of human respiration in fMRI with a mechanical model. IEEE Trans Biomed Eng. 2002;49(7):700–707. doi: 10.1109/TBME.2002.1010854. [DOI] [PubMed] [Google Scholar]
- Cohen ER, Rostrup E, Sidaros K, Lund TE, Paulson OB, Ugurbil K, Kim SG. Hypercapnic normalization of BOLD fMRI: comparison across field strengths and pulse sequences. Neuroimage. 2004;23(2):613–624. doi: 10.1016/j.neuroimage.2004.06.021. [DOI] [PubMed] [Google Scholar]
- Cohen MS. Parametric analysis of fMRI data using linear systems methods. Neuroimage. 1997;6(2):93–103. doi: 10.1006/nimg.1997.0278. [DOI] [PubMed] [Google Scholar]
- Corfield DR, Murphy K, Josephs O, Adams L, Turner R. Does hypercapnia-induced cerebral vasodilation modulate the hemodynamic response to neural activation? Neuroimage. 2001;13(6 Pt 1):1207–1211. doi: 10.1006/nimg.2001.0760. [DOI] [PubMed] [Google Scholar]
- Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Computers & Biomedical Research. 1996;29(3):162–173. doi: 10.1006/cbmr.1996.0014. [DOI] [PubMed] [Google Scholar]
- Davis TL, Kwong KK, Weisskoff RM, Rosen BR. Calibrated functional MRI: mapping the dynamics of oxidative metabolism. Proceedings of the National Academy of Sciences of the United States of America. 1998;95(4):1834–1839. doi: 10.1073/pnas.95.4.1834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glover GH, Li TQ, Ress D. Image-based method for retrospective correction of physiological motion effects in fMRI: RETROICOR. Magn Reson Med. 2000;44(1):162–167. doi: 10.1002/1522-2594(200007)44:1<162::aid-mrm23>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Henson RN, Price CJ, Rugg MD, Turner R, Friston KJ. Detecting latency differences in event-related BOLD responses: application to words versus nonwords and initial versus repeated face presentations. Neuroimage. 2002;15(1):83–97. doi: 10.1006/nimg.2001.0940. [DOI] [PubMed] [Google Scholar]
- Hoge RD, Atkinson J, Gill B, Crelier GR, Marrett S, Pike GB. Linear coupling between cerebral blood flow and oxygen consumption in activated human cortex. Proc Natl Acad Sci U S A. 1999;96(16):9403–9408. doi: 10.1073/pnas.96.16.9403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu X, Le TH, Parrish T, Erhard P. Retrospective Estimation and Correction of Physiological Fluctuation in Functional MRI. Magnetic Resonance in Medicine. 1995;34:201–212. doi: 10.1002/mrm.1910340211. [DOI] [PubMed] [Google Scholar]
- Josephs O, Howseman AM, Friston KJ, Turner R. Proceedings of the International Society for Magnetic Resonance in Medicine. Canada: Vancouver, B.C.; 1997. Physiological Noise Modelling For Multi-Slice EPI FMRI Using SPM. [Google Scholar]
- Kastrup A, Kruger G, Glover GH, Neumann-Haefelin T, Moseley ME. Regional variability of cerebral blood oxygenation response to hypercapnia. Neuroimage. 1999;10(6):675–681. doi: 10.1006/nimg.1999.0505. [DOI] [PubMed] [Google Scholar]
- Kastrup A, Li TQ, Glover GH, Moseley ME. Cerebral blood flow-related signal changes during breath-holding. AJNR Am J Neuroradiol. 1999;20(7):1233–1238. [PMC free article] [PubMed] [Google Scholar]
- Kastrup A, Li TQ, Moseley ME. Functional MRI and Hypercapnia. In: Moonen CTW, Bandettini PA, editors. Functional MRI. Berlin: Springer Verlag; pp. 433–439. [Google Scholar]
- Kwong KK, Wanke I, Donahue KM, Davis TL, Rosen BR. EPI imaging of global increase of brain MR signal with breath-hold preceded by breathing O2. Magn Reson Med. 1995;33(3):448–452. doi: 10.1002/mrm.1910330322. [DOI] [PubMed] [Google Scholar]
- Li TQ, Kastrup A, Takahashi AM, Moseley ME. Functional MRI of human brain during breath holding by BOLD and FAIR techniques. Neuroimage. 1999;9(2):243–249. doi: 10.1006/nimg.1998.0399. [DOI] [PubMed] [Google Scholar]
- McKay LC, Evans KC, Frackowiak RS, Corfield DR. Neural correlates of voluntary breathing in humans. J Appl Physiol. 2003;95(3):1170–1178. doi: 10.1152/japplphysiol.00641.2002. [DOI] [PubMed] [Google Scholar]
- Modarreszadeh M, Bruce EN. Ventilatory variability induced by spontaneous variations of PaCO2 in humans. J Appl Physiol. 1994;76(6):2765–2775. doi: 10.1152/jappl.1994.76.6.2765. [DOI] [PubMed] [Google Scholar]
- Poulin MJ, Liang PJ, Robbins PA. Dynamics of the cerebral blood flow response to step changes in end-tidal PCO2 and PO2 in humans. J Appl Physiol. 1996;81(3):1084–1095. doi: 10.1152/jappl.1996.81.3.1084. [DOI] [PubMed] [Google Scholar]
- Raj D, Anderson AW, Gore JC. Respiratory effects in human functional magnetic resonance imaging due to bulk susceptibility changes. Phys Med Biol. 2001;46(12):3331–3340. doi: 10.1088/0031-9155/46/12/318. [DOI] [PubMed] [Google Scholar]
- Stillman AE, Hu X, Jerosch-Herold M. Functional MRI of brain during breath holding at 4 T. Magnetic Resonance Imaging. 1995;13(6):893–897. doi: 10.1016/0730-725x(95)00037-h. [DOI] [PubMed] [Google Scholar]
- Thomason ME, Burrows BE, Gabrieli JD, Glover GH. Breath holding reveals differences in fMRI BOLD signal in children and adults. Neuroimage. 2005;25(3):824–837. doi: 10.1016/j.neuroimage.2004.12.026. [DOI] [PubMed] [Google Scholar]
- Thomason ME, Foland LC, Glover GH. Calibration of BOLD fMRI using breath holding reduces group variance during a cognitive task. Hum Brain Mapp. 2007;28(1):59–68. doi: 10.1002/hbm.20241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van den Aardweg JG, Karemaker JM. Influence of chemoreflexes on respiratory variability in healthy subjects. Am J Respir Crit Care Med. 2002;165(8):1041–1047. doi: 10.1164/ajrccm.165.8.2104100. [DOI] [PubMed] [Google Scholar]
- Wise RG, Ide K, Poulin MJ, Tracey I. Resting fluctuations in arterial carbon dioxide induce significant low frequency variations in BOLD signal. Neuroimage. 2004;21(4):1652–1664. doi: 10.1016/j.neuroimage.2003.11.025. [DOI] [PubMed] [Google Scholar]


