Prediction Models for the Pleasantness of Binary Mixtures in Olfaction

Abstract

Whereas the rules underlying the perceived intensity of binary mixtures have been investigated, minimal efforts have been directed at elucidating the rules underlying the perceived pleasantness of such mixtures. To address this, 84 subjects ranked the pleasantness and intensity of 5 distinct binary mixtures (15 pairs, inter-stimulus interval = 4 s, inter-trial interval = 30 s, flow = 6 l/min, pulse = 2 s) constructed from different ratios (0:100%, 25:75%, 50:50%, 75:25%, and 100:0%, olfactometer-generated vapor phase). We found that in the majority of cases, the pleasantness of the mixture fell between the pleasantness values of its separated constituents and that it was strongly influenced by the relative intensities of the constituents. Based on these results, we proposed a prediction paradigm for the pleasantness of binary mixtures from the pleasantness of their separated constituents weighted by their respective perceived intensities. The uniqueness of the proposed paradigm is that it neither requires presetting an interaction constant between the mixture components nor require any factorization of the pleasantness weights. It does, nonetheless, require solid psychophysical data on the separated components at their different concentrations, and currently it can only explain the behavior of intermediate pleasantness of mixtures.

Introduction

A key to the rules underlying the link between the physical structure of stimuli and their eventual percept may lie in the dynamics of stimulus mixture perception. The classic example of this was in vision where the psychophysical study of color mixtures provided significant insight into the neurobiology of color vision. Here we aim to use a similar approach in the study of olfaction. In the case of vision, mixing stimuli that varied along the key perceptual axis of color may have been an intuitively obvious choice, but what perceptual axis should one concentrate on in olfaction? One possibility is to address the categorical identification of an odorant mixture based on the categorical identification of its constituents, independent of any axis on which they may lie (Olsson 1994, 1998; Deisig et al. 2002; Cometto-Muniz et al. 2005). This, however, amounts to mixing multidimensional objects rather than mixing a particular trait. Unsurprisingly, when 2 multidimensional objects are mixed, the result is an object that is an impoverished version of either one or the other of the original objects (Spence and Guilford 1933; Moskowitz and Barbe 1977). This is true in vision and audition and is evident in olfaction where binary mixtures typically (although not always) smell like poor versions of one of their constituents. Which constituent will dominate the percept of the eventual mixture can indeed be predicted based on the perceived intensity of each (Lawless 1977; Laing et al. 1984; Olsson 1994, 1998).

With this in mind, an alternative to mixing odor objects is mixing odorants that vary along a selected olfactory trait or axis. The olfactory perceptual axis with the clearest link between physical stimulus attributes and ensuing percept is perceived intensity, which is a reflection of stimulus concentration (Cain 1969). Indeed, several experiments and models have detailed the expected perceived intensity of a binary mixture based on the intensities of its constituents (Laffort and Dravnieks 1982). Among these models is the vector model (Berglund et al. 1973), in which the perceived intensity of the mixture, R_AB, is a vector sum of the perceived intensities of the unmixed components (R_A and R_B). That is, 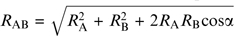, where α is an interaction coefficient between the mixture constituents. The Euclidean additivity model, which is the special case where cos(α) = 0. The U model (Patte and Laffort 1979), followed by the equation: 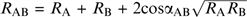, with 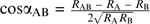as an estimate for the interaction coefficient α and others (Berglund et al. 1973; Berglund 1974; Laffort et al. 2002).

An additional key perceptual axis in olfaction is odorant pleasantness. Pleasantness is the primary perceptual aspect humans use in order to discriminate odorants (Schiffman 1974; Godinot and Sicard 1995) or in order to combine them into groups (Berglund et al. 1973; Schiffman et al. 1977). Also, pleasantness emerges as the primary dimension in multidimensional analyses of perceptual odor space (Moskowitz and Barbe 1977; Khan et al. 2007). Finally, studies with newborns suggest that at least some aspects of olfactory pleasantness may be innate (Steiner 1979; Soussignan et al. 1997). In other words, several lines of research converge to suggest that pleasantness is a primary perceptual dimension of olfaction. Efforts to elucidate the principles underlying mixture pleasantness have so far met with limited success. Spence and Guilford (1933) reported intermediacy between the pleasantness scores of the components, that is, the pleasantness estimates of the mixture were lower than the values of the pleasant component and higher than the values of the less pleasant one. Nonetheless, they could not evaluate an exact rule for predicting the mixture's pleasantness.

Moskowitz and Barbe (1977) also observed intermediacy in the pleasantness estimates of mixtures in the majority of cases, but not in all. They reported modestly successful attempts at finding a quantitative model for pleasantness additivity in binary mixtures. However, their regression analysis was applied to a limited set of odorants, required experimental factorization of the model for each mixture, and did not account for the contribution of the intensities of the components, which is known to contribute to the quality of the olfactory percept.

Because the psychophysical attributes of pleasantness and intensity are interrelated (Henion 1971; Doty 1975), a good predictive approach to mixture pleasantness is to account for the causal effects of shifts in intensity on the pleasantness of the mixture. Lawless proposed a prediction model for the pleasantness of binary mixtures from the pleasantness of their constituents, based on their pleasantness intensity dependency (Lawless 1977). He tested 2 examples of binary mixtures, each composed of a pleasant odorant mixed with an unpleasant one at various mixture concentrations. He then suggested a linear regression model for the pleasantness of the mixture from the pleasantness of its constituents. That is, for a given mixture of odorants A and B, $P_{\text{AB}}=C_{\text{A}}{P}_{\text{A}}+C_{\text{B}}{P}_{\text{B}},$ with P_AB as the pleasantness of the mixture, P_A and P_B as the pleasantness of the separated constituents, and C_A and C_B as their respective weights. The pleasantness of the constituents (P_A and P_B) was in turn a second-order polynomial function of their intensity. For example, for substance A, $P_{\text{A}}=\hspace{0.17em}{C}_0+C_1{I}_{\text{A}}+C_2{I}_{\text{A}}^2$, with I_A as the intensity of substance A at a certain concentration and C₀ through C₂ as the polynomial weights, which were fitted experimentally. These pleasantness intensity polynomial functions developed in Lawless (1977) for the mixture's constituents required odorant-specific adjustment of the weights, and the linear model describing the pleasantness of the mixture (P_AB) required experimental adjustment of the weights of the mixture constituents (C_A and C_B).

Here we propose a new prediction paradigm for the pleasantness of binary mixtures from the pleasantness and intensities of their separated constituents at different mixing ratios. This paradigm neither requires presetting an interaction constant between the mixture components nor require factorization of the pleasantness weights. It does, nonetheless, require solid psychophysical data of the separated components at their different concentrations, and currently it can only explain the behavior of intermediate pleasantness of the mixture.

Materials and methods

Subjects

Eighty-four healthy normosmic subjects (50 females) ranging in age from 23 to 36 years participated in the study after providing informed consent to procedure approved by Helsinki committee. Subjects were paid for participation.

Olfactometer

Experiments were conducted in a stainless steel–coated room subserved by high efficiency particulate air filter (HEPA) and carbon filtration. A 7-channel air dilution olfactometer of a type previously described in detail (Johnson and Sobel 2007) was used for the delivery of binary mixtures and of unmixed odorants (Figure 1). Undiluted liquid odorants, 98%, supplied by Sigma–Aldrich (Sigma–Aldrich, Rehovot, Israel) were sited in stainless steel vessels generating the odor vapors in closed channels. Two separate mass flow controllers (MFCs) determined the airflow of each of the mixture's components, followed by the opening of the respective channels with 2-way valves. Another MFC determined the dilution of the mixture with clean air. Comfortably seated subjects situated their head on a chin rest where stimuli were delivered through a stainless steel filter situated in front of the nose.

Figure 1.

Experimental setup: Left is the user panel for rating the absolute and relative pleasantness. Right is the automated olfactometer introducing the subject the odorized stimuli.

Odorants

Six different odorants were chosen for composing the various mixtures. The odorants were selected based on their locations within previously published olfactory perceptual and chemical spaces, where the primary perceptual axis reflected odorant pleasantness (Khan et al. 2007).

Specifically, 3 odorants had positive pleasantness values (L-carvone, linalool, and phenylethyl alcohol), and the other 3 had negative pleasantness values (valeric acid, isovaleric acid, and butanoic acid). Three types of mixtures were tested: 1) pleasant odorant mixed with a pleasant odorant (L-carvone and linalool); 2) unpleasant odorant mixed with an unpleasant odorant (valeric acid and isovaleric acid); and, finally, 3) pleasant odorant mixed with an unpleasant odorant (L-carvone mixed with valeric acid, linalool mixed with isovaleric acid, and phenylethyl alcohol mixed with Butaoinc acid). See Table 1.

Table 1.

Mixture composition

Inclusive pleasantness	Odorant name (abbreviation)	CAS #	Flow rate of mixture components (l/min)
			1) 0%	1) 25%	1) 50%	1) 75%	1) 100%
			2) 100 %	2) 75%	2) 50%	2) 25%	2) 0%
Unpleasant	Valeric acid (VA)	109-52-4	A1) 0	B1) 1.4	C1) 2.9	D1) 4.4	E1) 5.9
Pleasant	Linalool (LIN)	78-70-6	A2) 6	B2) 4.5	C2) 3	D2) 1.5	E2) 0
Unpleasant	Isovaleric acid (IVA)	504-74-2	A1) 0	B1) 1.3	C1) 2.8	D1) 4.25	E1) 5.7
Pleasant	L-Carvone (LC)	6485-40-1	A2) 6	B2) 4.5	C2) 3	D2) 1.5	E2) 0
Unpleasant	Butanoic acid (BA)	107-92-6	A1) 0	B1) 1	C1) 2.6	D1) 4.2	E1) 5.7
Pleasant	Phenylethyl alcohol (PEA)	60-12-8	A2) 6	B2) 4.5	C2) 3	D2) 1.5	E2) 0
Unpleasant	Valeric acid (VA)	109-52-4	A1) 0	B1) 1.35	C1) 2.75	D1) 4.2	E1) 5.7
Unpleasant	Isovaleric acid (IVA)	504-74-2	A2) 6	B2) 4.5	C2) 3	D2) 1.5	E2) 0
Pleasant	L-Carvone (LC)	6485-40-1	A1) 0	B1) 1.4	C1) 3	D1) 4.5	E1) 5.9
Pleasant	Linalool (LIN)	78-70-6	A2) 6	B2) 4.5	C2) 3	D2) 1.5	E2) 0

Composition of the 5 mixtures. Columns from left to right: mixture type, odorant names, odorant CAS numbers, mixture composition at 5 concentration ratios (denoted by the approximated percentages of the components in the mixture, numbered as 1 or 2). For each mixture, the separated constituents were diluted with clean air to the overall flow of the mixture and tested for their pleasantness and intensity, as detailed in the text.

Procedure

Selecting concentrations of mixture constituents

A critical decision when setting out to predict the interaction of components in a mixture is whether the components will be selected based on their relative concentrations or their relative perceived intensities. Because the perceived intensities of the mixture constituents play a pivotal role in determining the mixture's perceived quality (Laing et al. 1984), we opted for equating perceived intensity. In order to generate a good first approximation of equated perceived intensity, the components of each mixture were determined using a group of 10 subjects independent from those tested later. The procedure for equation was as follows: for a mixture of A and B, we aimed at generating 5 mixture versions: 1) 100% A – 0% B, 2) 75% A – 25% B, 3) 50% A – 50% B, 4) 25% A – 75% B, and 5) 0% A – 100% B, where 100% A would be equated for intensity with 100% B, 75% A would be equated for intensity with 75% B, 50% A would be equated for intensity with 50% B, and 25% A would be equated for intensity with 25% B. To this end, taking the case of equating the intensities of 25% A and 25% B, subjects smelled a stimulus of 25% A/75% clean air and a stimulus of 25% B/75% clean air (repeated and counterbalanced for order) and determined which of the stimuli was of higher perceived intensity. This stronger component, 25% A or 25% B, was diluted by replacing quanta of 100 ml/min of the odorized air with equivalent quanta of clean air. For example, if trial 1 consisted of 1.5 l/min A + 4.5 l/min clean air (total 6 l/min) versus 1.5 l/min B + 4.5 l/min clean air and odor A was rated as more intense, then trial 2 would consist of 1.4 l/min A + 4.6 l/min clean air (total 6 l/min) versus 1.5 l/min B + 4.5 l/min clean air. This procedure was repeated (inter-stimulus interval [ISI] = 4 s, inter-trial interval [ITI] = 30 s, total flow = 6 l/min, and pulse duration = 2 s) and counterbalanced for order, until the 2 stimuli were equated for perceived intensity (note that total flow denoted as 100% ranged between 5.7 and 6 l/min across experiments but was always exactly equal within experiments). Thus, by definition, one of the 2 components was at exactly 25% air dilution and the other was at some lower dilution concentration (e.g., 22%) where they were matched for perceived intensity. This was repeated for the 50%, 75%, and 100% dilutions. The actual concentrations used for each component are detailed in Table 1.

Obtaining pleasantness estimates

Following the preset of the odorants' concentrations, a minimum of 20 subjects ranked the pleasantness of each of the 5 mixtures and their separated constituents diluted with clean air. On a given trial, the subject first received one stimulus (first odor) and ranked its pleasantness on a visual analogue scale (VAS). Then, he/she received a second stimulus (second odor) and ranked its pleasantness on a second VAS, with the previous one still visible (Figure 1). This provided us with both an absolute measure of pleasantness for each stimulus (i.e., the rating between −5 and 5 on each VAS) as well as a relative measure of pleasantness for one stimulus versus the other (model building was eventually based on the absolute, not relative, values). Table 2 shows all randomized pairs of stimuli presented in an experimental session. In this table, each adjacent pair of rows of the same column (namely “First odor” and “Second odor”) represents a single trial, in which the two stimuli presented to the subject were denoted by “first” and “second” odor. Note that each trial was repeated twice with odor order counterbalanced. For example, the trial A1 preceding C1 (Table 2, first column, rows 3 and 4) was repeated in the reverse order—C1 preceding A1 (Table 2, second column, rows 3 and 4). In all cases, ISI = 4 s, ITI = 30 s, and pulse duration = 2 s. Following the pleasantness scoring, in 10 additional trials, subjects ranked the intensity of the mixture's constituents diluted with clean air, that is, 0%, 25%, 50%, 75%, and 100% of each of the separated components. Due to machine precision error inherent to MFCs, the minimal flow of an odorant, here described as 0% odor, in fact ranged up to 0.3 l/min.

Table 2.

Stimuli pairs presented in an experiment session

First odor	A1 + A2	C1 + C2	C1 + C2	E1 + E2	B1 + B2	D1 + D2	A1 + A2	D1 + D2	B1 + B2	E1 + E2
Second odor	C1 + C2	A1 + A2	E1 + E2	C1 + C2	D1 + D2	B1 + B2	D1 + D2	A1 + A2	E1 + E2	B1 + B2
First odor	A1	C1	C1	E1	B1	D1	A1	D1	B1	E1
Second odor	C1	A1	E1	C1	D1	B1	D1	A1	E1	B1
First odor	A2	C2	C2	E2	B2	D2	A2	D2	B2	E2
Second odor	C2	A2	E2	C2	D2	B2	D2	A2	E2	B2

Thirty randomized trials given in one experiment session are specified. Each adjacent pair of rows of the same column represents a pair of stimuli presented in successive order in a single trial, denoted as “first” and “second” odor. These pairs were ranked for their relative and absolute pleasantness as described in the text. Rows 3 through 6 represent the separated constituents of the mixtures diluted with clean air to the overall flow of their respective mixtures. Following the 30 trials of pleasantness ratings, the separated mixture constituents were also ranked for their intensities (i.e., 10 randomized stimuli: A1 through E1 and A2 through E2).

Results

Intensity ratings

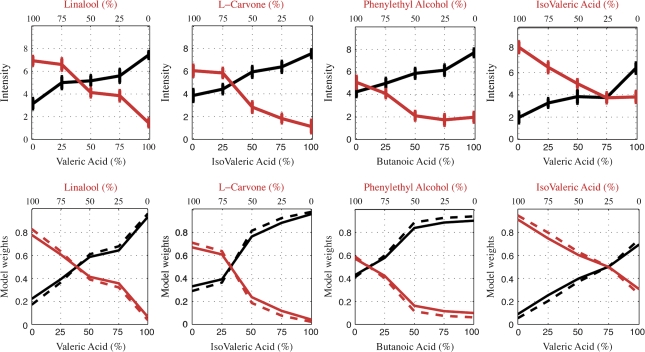
In most cases, the intensity values of the mixture components diluted with clean air decreased gradually as a function of their dilution, as shown clearly in the top panel of Figure 2. The only exceptions were the cases of 0% and 25% dilutions in isovaleric acid and the 50% and 75% dilutions in valeric acid, where no significant change was observed with the change in dilution (Figure 2, top right panel). Also, the linalool–L-carvone mixture showed only mild change in intensity as a function of concentration with significantly large variances across subjects and almost no dynamic range within subjects (Figure 4, right panel).

Figure 2.

Top: Intensity estimates of the separated constituents diluted with clean air to the overall flow rate of their corresponding mixtures. In each experiment session, these 10 randomized stimuli were estimated for their intensity on a number-free VAS scale ranging between “extremely mild” (0) and “extremely intense” (10). X axis is the approximated percentage of the neat odorants (see Table 1). Y is the median of the intensity estimates of all subjects with corresponding standard errors of the mean. VA – LIN: n = 21, IVA – LC: n = 20, BA – PEA: n = 22, VA – IVA: n = 21. Bottom: Model weights constructed from the constituents’ intensities (top panel) for the 2 models that performed best: dashed, weights implemented from the “interaction model” (Olsson 1994, eq. 5); continuous, weights of the sin model (eq. 2). These weights were substituted as the linear summation coefficients (W_A, W_B), composing the mixture's pleasantness (eq. 1).

Figure 4.

Left: Mean Z scores of pleasantness ratings of LC – LIN mixtures (blue) and their separated constituents diluted with clean air to the overall flow of the mixture. black, LC; red, LIN. Right: Intensity estimates of the LC – LIN mixture separated constituents, with corresponding standard errors of the means. black, LC; red, LIN. In spite of the increased sample size (n = 34), significantly large intersubject variances were observed and only moderate gradients of the intensity as a function of the constituents' concentrations.

Intensity estimates obtained during the pleasantness experiments differed slightly, but significantly from those obtained with the independent group of 10 subjects. Specifically, there were consistent differences in the perceived intensity of butanoic acid and phenylethyl alcohol in all dilution steps. In isovaleric acid and L-carvone mixture, there were differences in all but the 75% dilution step. In valeric acid and linalool mixture, we observed a difference only in the 0% case, and in the case of valeric acid and isovaleric acid, we observed differences in all but the 25% dilution step. The intensity ratings of all substances exceeded 0 at their 0% concentration. This presumably reflected a combination of subject bias (subjects rarely perceive “no odor”) and the aforementioned olfactometer machine precision error.

Because the probability distributions of the intensity scores were not always normal, we used the median values of the subjects’ ratings rather than their means. These intensity scores were then used for the calculation of the weights in the prediction models detailed later (eqs 1 through 5).

Pleasantness ratings

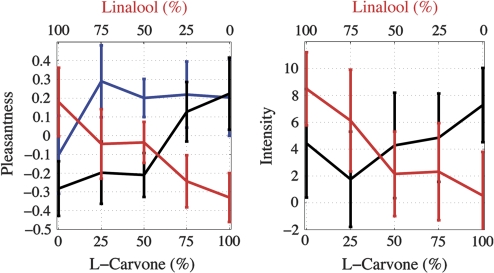
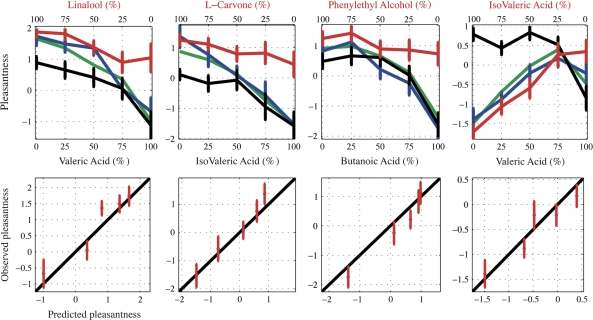
In most cases, the pleasantness ratings of the mixtures (Figure 3, blue curves) fell between the pleasantness ratings of their separated constituents (Figure 3, red and black curves), that is, intermediacy of the mixture's pleasantness was observed. Significant hyperadditivity in the Z scores of the mixture's pleasantness was observed in the mixture of L-carvone and linalool, that is, the pleasantness of the mixture (Figure 4 left panel, blue curve) was higher than the pleasantness of the constituents (Figure 4 left panel, red and black curves) in more than one standard error of the mean Z score value in the 50–50% case.

Figure 3.

Top: Medians of pleasantness ratings of the mixtures (blue) and their separated constituents (black and red). Green curves are the predicted pleasantness values of the mixtures calculated with the sin model (eqs 1 and 2). An important distinction regarding this graph is that the percent values of the X axis for each component reflect the ratios after equating the components’ perceived intensity. Thus, for example, the point of 50% L-carvone mixed with 50% isovaleric acid in fact reflects a mixture of 3 l/min L-carvone mixed with 2.8 l/min isovaleric acid = 5.8 l/min (blue) and the corresponding mixture constituents: 3 l/min L-carvone + 2.8 l/min clean air = 5.8 l/min (red) and 2.8 l/min isovaleric acid + 3 l/min clean air = 5.8 l/min (black). Bottom: Observed versus predicted pleasantness of the mixtures with corresponding standard errors of the observed means. Linear black curve represents the identity diagonal of the observed data (Y = X). Red dots are the predicted pleasantness values at the locations of the observed ones using the sin model (eqs 1 and 2). In majority of cases, the predicted estimates fell within the standard errors of the observations. VA – LIN: n = 21, IVA – LC: n = 20, BA – PEA: n = 22, VA – IVA: n = 21.

An insignificant trend toward subadditivity was observed in the case of butanoic acid and phenylethyl alcohol (Figure 3, second panel from the right), that is, the pleasantness of the mixture (Figure 3, blue curve) was lower than that of the less pleasant component (Figure 3, black curve).

In accordance with previous observations (Doty 1975), the pleasantness of substances varied as a function of their intensity, which was in turn a function of their concentration. For example, an odorant that was unpleasant at suprathreshold concentration could be pleasant at near-threshold concentrations. This phenomenon was evident here in the cases of valeric acid and butanoic acid. As noted above, the intensity ratings often exceeded 0 at the 0% concentration. In accordance with the nonzero intensities at 0% concentration, the pleasantness scores of valeric acid and butanoic acid at this concentration were not neutral, but in fact slightly pleasant.

The pleasantness estimates of the pleasant–pleasant pair (L-carvone–linalool) were exceptional in their large variances across subjects and their moderate increase as a function of concentration (Figure 4). For this reason, we chose to show here the Z score values of the pleasantness rather than the medians or means.

Prediction models

The proposed scheme aims at predicting the pleasantness of binary mixtures mixed in gas phase from the pleasantness of their separated constituents diluted with clean air to the same mixture volume, given the perceived intensities of the constituents.

In other words, given pleasantness values of the mixture constituents, P_A and P_B, and their respective intensities, I_A and I_B, we suggest a prediction paradigm for the pleasantness of the mixture, P_AB, using a linear combination (eq. 1) of the components pleasantness, weighted by W_A and W_B that are computed in different ways.

(1)

In the “sin model”, the weights of the mixture's constituents, W_A and W_B, depend on the normalized intensities of the separated constituents (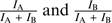) in a squared sinusoidal manner (eq. 2):

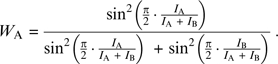(2a)

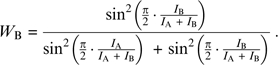(2b)

In the “arithmetic mean,” the pleasantness of the mixture is simply an arithmetic average of the pleasantness of the constituents:

(3)

In the “intensity weights,” the weighted intensities of the mixture's constituents serve as the pleasantness summation coefficients (eq. 1):

(4)

And in the “squared weighted intensities,” the weighted intensities in equation 4 were raised by the power of 2, resulting in the vector coefficients used in the interaction model of odor quality and intensity (Olsson 1994):

(5)

The performance of the models was summarized in Table 3. The choice of a linear model (eq. 1) that does not include mixing terms of P_a and P_b (e.g., P_a·P_b) stems from the limitations of our system and the given results.

Table 3.

Performance levels of the 4 prediction models expressed by their R² values for each of the tested binary mixtures

Mixture type	VA + LIN	IVA + LC	BA + PEA	VA + IVA
R2 (sin model)	0.8848	0.9406	0.9042	0.8711
R2 (squared intensities)	0.8769	0.9463	0.9209	0.8585
R2 (intensity weights)	0.8969	0.9163	0.8395	0.8293
R2 (arithmetic mean)	0.7748	0.6409	0.5146	0.1415

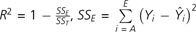, and 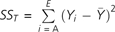. (VA, valeric acid; LIN, linalool; IVA, isovaleric acid; LC, L-carvone; BA, butanoic acid; PEA, phenylethyl alcohol). First row is the sin model (eqs 1 and 2). Second row is the squared weighted intensities model (eqs 1 and 5) followed by the integrated model for odor quality (Olsson 1994). Third row is the weighted intensities model (eqs 1 and 4), and fourth row is a simple arithmetic mean (eqs 1 and 3).

The problem in using sine or cosine elements in a prediction model for the pleasantness of mixtures is that pleasantness, unlike probability of identification of an odor, or its intensity is a bidirectional psychophysical attribute. That is, it can be assigned with both positive and negative values (e.g., a VAS that ranges between −1 and 1), whereas intensity and probability of identification of an odor are always positive (e.g., a VAS that ranges between 0 and 1).

For example, if one wishes to assign the pleasantness of the separated constituents (P_A, P_B) into a cosine function (e.g., 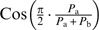), the result of both negative and positive elements might end up having the same sign.

Alternatively, using a sine function on the pleasantness of the constituents (e.g., 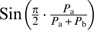) might again lead to loss of directionality in cases where both P_a and P_b are negative. Then, the weighted expression 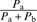turns positive, and the whole expression (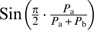) changes its sign.

This adds to the fact that assigning the pleasantness values (P_a and P_b) into a sinusoidal term requires prior radian normalization, as demonstrated above, and causes masking of the actual amplitudes because these functions are bounded by their nature. One way of compensating for this disadvantage is to add a correction factor as a multiplier, which we tried to avoid.

For all these reasons, we chose a linear combination as our initial working paradigm and used only the intensities for the calculation of the vector weights, avoiding any mixing terms or more complex functions.

The psychophysical rational behind the choice of a squared sine function for the constituents’ coefficients in eq. 1 was that the stronger constituents were consistently more influential on the mixture's pleasantness than the weaker ones and the squared sine function elicited best this perceptual notion. An equivalent psychophysical rational stood behind the composition of the coefficients in the “squared intensities model” (Olsson 1994), only that this model gives even more power to the stronger component in the mixture, as illustrated in the bottom panel of Figure 2. Therefore, the sin model (eq. 2) and the squared weighted intensities (eq. 5) performed significantly better than the “weighted intensities” (eq. 4) and the arithmetic mean (eq. 3), as shown in Table 3.

Comparison between models

Table 3 shows the performance level of the 4 prediction models detailed above (eqs 1 through 5). The performance was quantified by the R² values of the prediction curves. R² equations are specified in the caption of Table 3. Although the prediction curves were not linear by definition, the closer the R² to 1 the smaller the mean squared error of the prediction from the experimental values, that is, the better the performance.

Because the L-carvone and linalool (L>C – LIN) mixture generated only minimal variance across dilutions but significant variances across subjects, we did not include this mixture in our model testing.

The sin model and the squared weighted intensities model performed equivalently better than the intensity weights and the arithmetic mean. However, a closer look at Table 3 reveals that the sin model performed slightly better than the squared weighted intensities in 2 cases: VA – LIN and VA – IVA. In these mixtures, the less intense components contributed more than expected to the pleasantness of the mixtures. For this reason, both the sin model and the squared weighted intensities, that give significant power to the intense components over the less intense ones, performed below 0.9. As the slope of the weights in the sin model is slightly more moderate than the slope of the weights assigned by squared weighted intensities, it performed slightly better in these cases (Figure 2, bottom panel).

The only case where both the sin model and the squared weighted intensities underperformed the intensity weights was the case of VA – LIN mixture (R²_{sin model} = 0.8848, R²_{squared intensities} = 0. 8769, R²_{intensity weights} = 0.8969). Specifically, differences in the performance were observed at the 100% VA – 0% LIN mixture. In this case, the intensity weights model gave less power to the intense unpleasant component (100% VA) and slightly more power to the less intense pleasant one (0% LIN) in comparison to the weights assigned by the other models.

Pleasantness prediction

As shown by the large R² values (Table 3) and by the fits between the predicted and the observed pleasantness in all mixtures (Figure 3), both the sin model and the squared weighted intensities were capable of predicting the pleasantness of a binary mixture from the pleasantness and intensities of its constituents (with R² value above 0.87). Specifically, in the sin model, all predicted values but 3 outliers fell within the standard errors of the mean observed pleasantness of the mixtures at their various concentrations. No directional bias was observed (Figure 3, bottom panel).

The large R² values obtained for all cases, regardless the chemical similarity or dissimilarity of the mixture's constituents, further convinced us that this prediction paradigm is sufficiently reliable as an initial working model for solving this complicated task.

Discussion

We set out to predict binary mixture pleasantness from the pleasantness of the separated constituents of the mixture. We found that in the majority of cases, the pleasantness value of the mixture fell between the values of its separated constituents and that it was influenced by the relative intensities of the constituents. Based on these observations, we tested several linear models that predict the pleasantness of a mixture from the pleasantness of its constituents weighted by their partial intensities in various ways. We found that the sin model and the squared weighted intensities model outperformed the other coefficient models. Both these models assign significantly more power to the relatively intense component in the mixture over the power assigned to the less intense one. They differ in that the sin model is slightly more moderate in the power it assigns to the intense constituent over the power assigned to the less intense constituent, and so it performs better in cases where the relative contribution of the less intense constituent is larger than expected.

The only presumption required for our prediction paradigm is intermediacy of the mixture pleasantness with respect to the pleasantness of its constituents.

Choice of odorants for the mixtures

Our choice of odorants was made intentionally such that 3 types of extreme cases were examined. In the first 2 cases, we mixed the far ends of the pleasantness axis within themselves, that is, pleasant with pleasant and unpleasant with unpleasant. In these cases, we chose odorants that were as close to each other chemically and perceptually as possible. Specifically, isovaleric acid and valeric acid for the unpleasant case and L-Carove and linalool for the pleasant case. In the third case, we mixed the far ends of the axis across each other, that is, unpleasant odorants were mixed with pleasant ones. Because this type of mixture spans the pleasantness axis, we double checked it with 2 mixtures that were as similar to each other as possible. This was done by choosing again the 2 similar unpleasant odorants and the 2 similar pleasant ones and mixing them across each other.

The only mixture we opted not to use for testing our prediction model was the one that did not show a significant gradient of pleasantness as a function of concentration (and as a function of intensity, in turn). Also, the variances of both the intensities and the pleasantness estimates of this type of mixture were so large that one could not distinguish between the attributes of the mixture and its separated constituents in almost all concentrations. Thus, for proof of principle, the actual pleasantness of the mixture was not significantly different from the pleasantness of its constituents. Or, under the notation of our model, $P_{\text{A}}\approx P_{\text{B}}\approx P_{\text{AB}}$ and $I_{\text{A}}\approx I_{\text{B}}\approx I_{\text{AB}}$. If we were to use the model, we would get the same result as this hand-waving approximation.

Hyper and subadditivity in mixture pleasantness

As mentioned above, we observed an insignificant subadditivity in the mixture of butanoic acid and phenylethyl alcohol. We speculate that, as a rule, subadditivity of mixture's pleasantness occurs in cases where at least one of the components shows steep decline in pleasantness as a function of its intensity.

A possible reason for subadditivity in the pleasantness of mixtures is an increase in the intensity of the mixture above the intensity of its constituents, which, in turn, induces reduction in the pleasantness even below the values of the less pleasant constituent. Because we were primarily interested in predicting the pleasantness of the mixture, we did not check for the intensities of the mixtures and therefore can only speculate that this was the case here too.

Clear hyperadditivity in the mixture's pleasantness was observed in the case of 2 pleasant substances (LC – LIN, Figure 4). This effect can also be accounted for by an additive effect in intensity of the mixture in cases where both constituents show gradual increase in pleasantness as a function of their intensity.

As mentioned, this case did not serve us for building the prediction model because variances in both the pleasantness and the intensity attributes of the mixture and its constituents were too large. We speculate that the reason for these large variances was the small change in the intensity at this range of concentrations in both of the mixture's constituents, that is, because pleasantness and intensity are interrelated attributes, the insignificant change in intensity associated with large variances induced an insignificant change in pleasantness with corresponding variances. Subjects reported difficulty in rating the pleasantness as well as the intensity of the stimuli of this mixture; they reported that they were all mild and pleasant, as expressed by the large variances in the psychophysical attributes.

Pleasantness intensity dependence in binary mixtures

Our results support the observation made by Laing et al. (1984) that the perceptual interaction between the components in a mixture is strongly influenced by their intensities. They also concur with the integrated model of intensity and quality by Olsson (1994, 1998), which predicted the categorical identification probabilities of the components in mixtures based on their intensities. For example, in three cases out of four (Figure 3: valeric acid/linalool, isovaleric acid/L-carvone, and butanoic acid/phenylethyl alcohol), the pleasantness of the 25:75% mixture was significantly closer to the 75% diluted component than to the 25% one, which was also in accordance with their perceived intensities. The only mixture that deviated from this behavior was the isovaleric acid/valeric acid, which showed equal intensities of the components in the 25:75% mixture and equal pleasantness values of both the separated constituents and their mixture. This, of course, does not contradict the above claim regarding the strong influence of intensity on the quality of the mixture.

Predicting the pleasantness of binary mixtures

Our results emphasize the notion that relative intensities influence the resultant pleasantness of binary mixtures (Lawless 1977; Moskowitz and Barbe 1977). All models but the arithmetic mean build on this observation. Specifically, the weights in the linear summation of the pleasantness (eq. 1) depend on the intensities of the separated constituents in various ways.

The weighting coefficients of the sin model (eq. 2) and of the squared weighted intensities (eq. 5) outperformed the simple arithmetic mean (eq. 3) and the direct substitution of the constituent's weighted intensities (eq. 4).

As observed in the bottom panel of Figure 2, the weights assigned by the squared weighted intensities were very close to the weights assigned by the sin model. This was also emphasized by their similar levels of performance as shown in Table 3. Whereas the reason for this was simply the mathematical definition of the coefficients, the psychophysical implication of the weights gives rise to the fine tuning of the constituents’ contribution to the pleasantness of the mixture in each of the models.

Specifically, both these models give rise to a sigmoid curve as a function of the normalized intensity. However, the squared weighted intensities exerts a steeper slope resembling a step function, in comparison to the sin model that gives rise to a slightly smoother sigmoid.

The outcome of this feature is that the sin model performs slightly better in cases where the relatively mild constituent in the mixture had more influence on the mixture's pleasantness than expected. Or, in other words, it assigns greater power to the more intense constituent in the mixture over the power assigned to the less intense constituent, but not in an exaggerated manner that will diminish the influence of the mild one.

This character is pivotal in mixture's pleasantness especially in cases where an addition of small quanta of a substance to a mixture increases its pleasantness in a nonlinear manner.

Unlike former prediction models aiming at predicting mixture pleasantness, our prediction scheme does neither require prescaling of an interaction constant between the components of the mixture nor require experimental parameterization of the prediction equation, which is specific for each chemical substance. Its only requirement is that we have solid estimates of the pleasantness and intensity attributes of the mixture's constituents, regardless of their chemistry.

The main drawback of our model lies in its presumption of pleasantness intermediacy. In other words, it cannot predict pleasantness values of mixtures that exceed in either direction (above or below) of the pleasantness of their unmixed constituents.

Two approaches may offer future solutions to this drawback. The first is to introduce interaction elements into the equation, in the form of P_A·P_B with suitable weights, $W_{AB}^A\text{\hspace{0.17em}and\hspace{0.17em}}{W}_{AB}^B$, that will rely on the expectation values of the mixture's intensity. Such elements should correct the mixture's pleasantness primarily in cases where the intensity of the mixture is significantly larger than the intensities of its separated components. Several efforts in this direction have been made with no reported success. We think that with given solid estimates of the mixture's intensity, this problem might be solved.

The other approach, which might capture the behavior of odd outliers, is a piecewise gradient approach. This approach relies on the observation that the pleasantness of different odorants behaves differently as a function of their intensity. For example, many unpleasant odorants tend to decrease in pleasantness sharply with increasing intensity, whereas as observed here, many pleasant odorants tend to have only a moderate increase in pleasantness until they reach a plateau (Doty 1975).

With this in mind, one could calculate the local gradient of the pleasantness as a function of the intensity of each component, (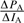, 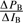), and then introduce these derivatives into the weights of pleasantness of each component in the correction terms, W_A(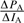) , W_B(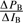). In other words, the pleasantness of the mixture will remain a linear combination of the pleasantness scores of the constituents, but the weights of the constituents, W_A and W_B, will be added as a differential term.

Outliers in prediction

Two outliers were of significant interest. The first was the case of 50:50% linalool and valeric acid (Figures 2 and 3). In this case, the observed pleasantness of the mixture was nearly the same as the pleasantness of linalool. However, the predicted pleasantness of the mixture was in the midway between that of linalool and valeric acid. This means that the weight the model assigned to valeric acid was too high and that, unexpectedly, the slightly weaker component had a far greater contribution to the pleasantness of the mixture. This could be explained by an increase in intensity of the mixture above the intensity of the components, which, in turn, caused the unexpected increase in pleasantness. We speculate that an additive interaction of binary mixture's pleasantness occurs only when the intensities of the constituents are nearly the same and both pleasantness attributes of the constituents are positive.

The other outlier was the case of 50:50% phenylethyl alcohol and butanoic acid (Figures 2 and 3). Here, the intensity of the unpleasant component, butanoic acid, was nearly 3 times higher than the intensity of the pleasant one, phenylethyl alcohol. The pleasantness of butanoic acid was nearly zero, whereas the pleasantness of phenylethyl alcohol was high and positive. Surprisingly, the pleasantness of the mixture went below the pleasantness of butanoic acid but was not significantly different from it. As butanoic acid was the stronger component, our prediction value for the pleasantness of the mixture was almost equal to the pleasantness of this component. In this case, our prediction “missed” because it cannot exceed the pleasantness of the unmixed components. Furthermore, phenylethyl alcohol did not have any positive contribution to the pleasantness of the mixture in the experimental values, in spite of its positive scores in the unmixed state. This negative interaction is also of unique character.

To conclude, we proposed a working paradigm for the prediction of binary mixtures’ pleasantness from the pleasantness of the mixture's constituents. Although this paradigm generated accurate predictions, it fell short of a universal predictive framework. That said, we provided data collected under strict conditions, which, combined with future data, may make it possible to construct a model that will also account for mixture outcomes of the type currently unaccounted for.

Funding

This work was supported by ERC-STG-200850 Odor Space grant and by The Center for Complexity Science fellowship.