Prediction of Protein Loop Conformations using the AGBNP Implicit Solvent Model and Torsion Angle Sampling

Abstract

The OPLS-AA all-atom force field and the Analytical Generalized Born plus Non-Polar (AGBNP) implicit solvent model, in conjunction with torsion angle conformational search protocols based on the Protein Local Optimization Program (PLOP), are shown to be effective in predicting the native conformations of 57 9-residue and 35 13-residue loops of a diverse series of proteins with low sequence identity. The novel nonpolar solvation free energy estimator implemented in AGBNP augmented by correction terms aimed at reducing the occurrence of ion pairing are important to achieve the best prediction accuracy. Extended versions of the previously developed PLOP-based conformational search schemes based on calculations in the crystal environment are reported that are suitable for application to loop homology modeling without the crystal environment. Our results suggest that in general the loop backbone conformation is not strongly influenced by crystal packing. The application of the temperature Replica Exchange Molecular Dynamics (T-REMD) sampling method for a few examples where PLOP sampling is insufficient are also reported. The results reported indicate that the OPLS-AA/AGBNP effective potential is suitable for high-resolution modeling of proteins in the final stages of homology modeling and/or protein crystallographic refinement.

1 Introduction

A necessary component for an effective computational approach to the homology modeling problem¹ for protein structure prediction² and crystallographic and NMR structure refinement^{3, 4} is a scoring function that scores more favorably the native conformation over other possible conformations.^{5, 6} Scoring functions aimed at fold recognition and secondary structure assignment have been evaluated on the basis of their ability to recognize the known native protein conformation among a set of plausible misfolded decoy structures.^7–12 Both physics-based^13–19 and empirical knowledge-based scoring functions,^20–23 have performed reasonably well in this kind of evaluation tests.

Recent development efforts have been focused on the refinement stages of the homology modeling problem; such as the conformational prediction of protein loops^24–26 and surface side chains,²⁷ as well as the modeling of ligand/receptor induced fit effects,²⁸ which are essential steps to make the model useful as a drug discovery and optimization target. These kinds of high-resolution protein structure prediction applications have generally been performed using atomistic physics-based free energy estimators.

Protein decoy scoring exercises have been useful to determine the key global features of physics-based energy functions (such as the inclusion of solvation effects¹⁹) necessary for recognizing the broad characteristics of native protein structures. The decoy evaluation technique, however, is in general too blunt an instrument for discriminating the ability of energy functions to recognize small structural variations within the native ensemble. For thorough testing, it is necessary to challenge the energy function by performing extensive local conformational searches to actively look for minima of the energy functions and measure the degree of correspondence of these with the known native conformation.

Determining the correct conformation of a loop on a protein is one of the final steps in homology model building. After secondary structures have been assigned and placed, model construction often proceeds by conformational prediction of connecting loops. In loop prediction tests, we assume that the rest of the protein frame has been folded accurately and the conformation of the loop of interest remains to be determined. Effectively, the loop is a tethered peptide whose conformations can be sampled extensively while in the presence of the energy field generated by the rest of the protein. Many different conformations of the loop can be generated and tested for false global minima which exist in the presence of the effective potential field of the protein framework. This makes the protein loop prediction problem a powerful benchmarking tool to test the accuracy of energy functions.

An accurate molecular mechanics model suitable for protein structure prediction and refinement requires a representation of the aqueous solvent environment. The polarization of the solvent favors the hydration of polar and especially charged groups that, in the absence of solvation forces, tend to form non-native intramolecular interactions. Explicit solvent models provide the most detailed and complete description of hydration phenomena.²⁹ However, computer simulations using explicit solvent models are computationally intensive, not just because of the much larger number of atomic interactions that need to be considered, but also, and perhaps more importantly, because of the need to average the fuctuating effects of the solvent reaction field to obtain a meaningful estimate of the solvation free energy of each protein conformation. For protein structure prediction applications effective potential models that treat the solvent implicitly have much to offer. The modeling community has developed a strong interest in a class of implicit solvent models based on the Generalized Born framework;^30–32 an approximation of the Poisson equation of continuum electrostatics.^33–34 Much of the popularity of Generalized Born (GB) models stems from their computational efficiency and ease of integration in molecular simulation computer programs.^31,35–38 Generalized Born models have been shown to be able to reproduce with good accuracy Poisson^32,39–41 and explicit solvent^42,43 results at a fraction of the computational expense.

In this work we evaluate the accuracy of the Analytical Generalized Born plus Non-Polar (AGBNP) implicit solvent model,⁴⁴ in predicting the native conformation of protein loops using the Protein Local Optimization Program (PLOP).²⁶ The PLOP program²⁶ performs loop and sidechain conformational predictions based on an efficient hierarchical conformational sampling algorithm in torsional angle space, combined with a recent parametrization of the OPLS-AA force field^45,46 and a Generalized Born implicit solvation model. The AGBNP implicit solvent model is based on an analytical pairwise descreening⁴⁷ implementation of the Generalized Born model,³⁰ and a novel non-polar hydration free energy model which combines separate estimators for the solute-solvent van der Waals dispersion energy and the work of cavity formation.^48–50

We previously showed⁴⁴ that the OPLS-AA/AGBNP effective potential was able to consistently score native loop conformations more favorably than non-native decoy loop conformations generated by PLOP using the OPLS-AA/SGB/NP effective potential.²⁶ The present work extends that work by including a larger set of loops as well as longer loops targets, and by employing the OPLS-AA/AGBNP model directly in the conformational search and optimization procedure implemented in PLOP. We also evaluate various parameterizations of the AGBNP model to determine the role of the non-polar model and of the correction terms we developed aimed at reducing the occurrence of intramolecular ion pairing, and we compare them to the distance dependent dielectric and the Surface Generalized Born (SGB/NP)^51,52 solvation models as implemented in the PLOP program.

As part of this work we have also evaluated the efficiency of the recently proposed loop conformational search schemes based on PLOP^26,53 which improves on earlier torsion angle based sampling methods.^24,25 These PLOP-based conformational search schemes have been optimized for loop conformational prediction in the crystal environment. We evaluate enhanced versions of these schemes more suitable for loop prediction calculations in the solution environment (the biologically relevant environment for most homology modeling applications). We also tested the applicability of temperature Replica Exchange Molecular Dynamics (T-REMD) to the problem of protein loop prediction, which, given its favorable scaling with respect to the number of degrees of freedom, offers an alternative route for conformational prediction of long loops, and for simultaneous refinement of interacting protein elements.

2 Methods

2.1 Loop Prediction Algorithms

The loop prediction algorithm implemented in the Protein Local Optimization Program (PLOP) is described in detail in Ref. 26. During loop build-up, a series of filters of increasing complexity is applied to eliminate unreasonable conformations as early as possible. Some of these filters detect clashes between backbone atoms and the atoms of the rest of the protein (referred to as the "frame"), and check that enough space is available to place the sidechain of each residue. On the order of hundreds to thousands of loop conformations are generated in the loop build-up stage. To reduce the number of conformations passed to the next stages, loop conformations are clustered based on backbone RMSD using the K-means algorithm,⁵⁴ a clustering method that requires a predetermined number of clusters. The two most important parameters that control the trade-off between accuracy and efficiency of PLOP’s loop prediction algorithm are the overlap factor parameter (ofac), defined as the minimum permitted ratio of the interatomic distance over the sum of the Lennard-Jones radii of the atoms of interest, which controls the amount of overlap tolerated between any two atoms, and the number of clusters N_clust. A smaller ofac allows more overlap between atoms which in effect allows for more loop conformations to be sampled which otherwise would have been eliminated due to steric clashes. The efficiency of the loop-prediction procedure is partially determined by the value of ofac. If ofac is too small, a large number of irrelavent loop conformations are generated that have to be processed in subsequent steps. On the other hand with a large ofac native-like loops may be rejected due to steric clashes caused by the discreteness of the torsion library used to generate the loops. Based on the oberved value of ofac found in the PDB, Jacobson et al. set ofac to between 0.70 to 0.75.²⁶ The number of clusters N_clust needs to be sufficiently large to account for each non-redundant loop conformation. If N_clust is set too small, conformationally different structures could potentially be clustered together. The number of non-redundant loop conformations will depend upon how large is the conformational space available to the loop. Based on empirical evidence, Jacobson et al. set the number of clusters to four times the number of residues in the loop.²⁶

The PLOP program allows sampling of loop conformations in the crystalline phase with the SGB/NP solvation model.^42,51 We performed SGB/NP prediction calculations with and without crystal symmetry in order to compare with previous literature.²⁶ Loop prediction calculations with all of the other implicit solvent models were conducted without crystal symmetry.

The basic loop prediction algorithm described above is often insufficient for loops with nine or more residues. For these longer loops we have adopted prediction schemes based on multiple executions of PLOP with different parameters.^26,53 These schemes are based on focusing conformational sampling in promising and progressively smaller regions of conformational space. The initial predictions with the most favorable energy scores are subjected to a series of constrained refinement calculations with PLOP in which selected loop backbone atoms are not allowed to move or move only within a given range.

The standard 9-residue loop prediction scheme is based on the procedure described in detail by Jacobson et al.²⁶ For loops which the standard version of loop prediction fails to find low-energy, native-like conformations, we attempted to predict these loops with an extended version of the loop prediction algorithm. An extended version of this scheme involves using twice the number of clusters (from 36 to 72) and reduced ofac (overlap factor) coefficients (0.5 instead of 0.75) during the initial prediction stage. All other stages as described by Jacobson et al.²⁶ remain the same.

For the 13-residue loops we have adopted an alternative long loops prediction scheme developed previously for longer loops.⁵³ This scheme is based on the idea of refining the loop structure by sampling increasingly shorter loop segments which can be handled by PLOP’s conformational search procedure. Briefly, initial predictions are produced with 3 different overlap factors (0.65, 0.70, and 0.75) and subjected to constrained refinement. The five lowest energy non-redundant structures so obtained are passed to a series of loop prediction stages which sample progressively shorter segments obtained by fixing any possible combination up to five residues at either terminal end of the loop. The standard sampling and extended sampling variations of this sampling method differ in the number of non-redundant lowest energy models that are processed at each stage. With extended sampling five lowest energy models are passed from one stage to the next. With standard sampling the number of PLOP iterations is reduced by half by progressively reducing the number of models passed to later stages.

We also investigated if a technique based on replica exchange molecular dynamics importance sampling could predict loop conformations. We selected 9-residue loops which were not successfully predicted by the standard sampling algorithm built around PLOP to see if importance sampling would succeed. This subset of the 9-residue loops (Table 3) was investigated with the temperature replica exchange sampling method (T-REMD)^55–57 as implemented in the IMPACT software package.⁵⁷ The lowest energy loop configuration obtained in the third stage of PLOP optimization was chosen as a starting point for the corresponding T-REMD run. Each loop was minimized in the field of the surrounding immobilized protein frame. T-REMD was based on constant temperature MD and exchanges between replicas were attempted every 500 steps. During T-REMD simulations, the protein frame conformation was fixed. The OPLS-AA force field was employed to model the intra-molecular potential while the solvent was treated implicitly by the AGBNP+ effective potential model (see below). We used twelve replicas at 270, 298, 329, 363, 401, 442, 488, 539, 595, 657, 725 and 800K. The T-REMD simulation length varied from 15 ns to 35 ns, the data collected over the last 5 ns of the T-REMD trajectories were used for final analysis.

Table 3.

Summary of the loop conformational predictions results with the OPLS-AA/AGBNP+ force field and T-REMD conformational sampling, compared to the corresponding predictions with the PLOP-based standard sampling procedure.

PDB (Rfirst–Rlast)	PLOP RMSD (Å)	T-REMD RMSD (Å)
1npk (102–110)	3.60	4.30
1one (70–78)	7.43	2.06
1fus (31–39)	6.03	1.78
1byb (246–254)	4.00	4.95
1noa (99–107)	5.67	3.94
1wer (942–950)	4.29	1.34

2.2 The Energy Functions

The energy functions we used to score the predicted loops are composed of the all-atom force field, OPLS-AA,^45,46 and an implicit solvent model. The particular version of OPLS-AA⁴⁶ we used has improved torsional parameters based on fits to high-level LMP2 quantum chemical calculations of the torsion interactions of small peptides. These fits led to improvements in the accuracy of the φ, ψ, and side chain χ torsion energies for amino acids.²⁷

The implicit solvent models we investigated in this study are the simple distance--dependent dielectric and two generalized Born solvation models, the Surface Generalized Born (SGB)^42,51 and Analytical Generalized Born (AGB).⁴⁴ It is assumed in the distance-dependent dielectric model that the interaction energy between partial charges in a heterogeneous dielectric environment follows a simple Coulomb law. The Coulomb energy term is given by,

$$E_{\text{Coul}}=\frac{q_i{q}_j}{\epsilon r_{ij}},$$ (1)

where r_ij is the interatomic distance between atoms i and j, and ε is the dielectric constant. In the distance-dependent dielectric model, ε is no longer constant, but proportional to the interatomic distance as such

$$\epsilon =r_{ij}.$$ (2)

While the distance-dependent dielectric is known to be a poor model for solvation, we use the results generated with it to benchmark the improvements in loop prediction that can be obtained with more accurate physical models.

2.2.1 SGB/NP Implicit Solvent Model

The SGB model is the surface implementation^42,51 of the generalized Born model.³⁰ The generalized Born equation

$$G_{\text{GB}}=-\frac{1}{2}\left(\frac{1}{{\epsilon }_{\text{in}}}-\frac{1}{{\epsilon }_{\text{w}}}\right)\sum _{ij}\frac{q_i{q}_j}{f_{ij}(r_{ij})},$$ (3)

where q_i is the charge of atom i and r_ij is the distance between atoms i and j, gives the electrostatic component of the free energy of transfer of a molecule with interior dielectric ε_in from vacuum to a continuum medium of dielectric constant ε_w, by interpolating between the two extreme cases that can be solved analytically: the one in which the atoms are infinitely separated and the other in which the atoms are completely overlapped. The interpolation function f_ij in Eq. (3) is defined as

$$f_{ij}={[r_{ij}^2+B_i{B}_{j}exp(-r_{ij}^2/4B_i{B}_j)]}^{\frac{1}{2}},$$ (4)

where B_i is the Born radius of atom i defined as the effective radius that reproduces through the Born equation

$$G_{\text{single}}^i=-\frac{1}{2}\left(\frac{1}{{\epsilon }_{\text{in}}}-\frac{1}{{\epsilon }_{\text{w}}}\right)\frac{q_i^2}{B_i},$$ (5)

the electrostatic free energy of the molecule when only the charge of atom i is present in the molecular cavity. The $G_{\text{single}}^i$ are evaluated numerically by integrating the interaction between atom i and the charge induced on the solute-solvent boundary surface, S, by the Coulomb field of this atom

$$G_{\text{single}}^i=-\frac{1}{8\pi }\left(\frac{1}{{\epsilon }_{\text{in}}}-\frac{1}{{\epsilon }_{\text{w}}}\right){\int }_S\frac{q_i^2}{\mid \mathbf{r}-{\mathbf{r}}_i{\mid }^4}(\mathbf{r}-{\mathbf{r}}_i)\cdot \mathbf{n}(\mathbf{r})d^2\mathbf{r},$$ (6)

where n(r) is the normal to the surface, S, at r. The atomic radii that define the solute-solvent dielectric boundary are set to the van der Waals radii based on the Lennard-Jones σ parameters. The Born radii for Eq. 4 are calculated using Eqs. (5) and (6). In this work, we set ε_in = 1 and ε_w = 80. The SGB implementation used in this work includes further correction terms that bring the SGB reaction field energy into closer agreement with exact PB results.⁵¹ Coupled with the SGB model is a function describing the nonpolar interactions between the solute and solvent which is based on two terms: the van der Waals interaction between solute and solvent and the work to form the cavity in the solvent. The full solvation model is referred to as SGB/NP. Exact details of the nonpolar function in SGB/NP can be found in Ref. 52.

2.2.2 AGBNP Implicit Solvent Model

The analytical generalized Born (AGB) implicit solvent model differs from SGB in the way that the Born radii are calculated. AGB is based on a novel pairwise descreening implementation⁴⁴ of the generalized Born model.⁵⁸ The combination of AGB with a recently proposed nonpolar hydration free energy estimator described below is referred to as AGBNP.⁴⁴ AGB employs a parameter-free and conformation-dependent analytical scheme to obtain the pair-wise descreening scaling coefficients used in the computation of the Born radii used in the generalized Born equation, Eq. 3. The agreement between the AGB Born radii and exact numerical calculations was found to be excellent.⁴⁴ The AGBNP nonpolar model consists of an estimator for the solute–solvent van der Waals interaction energy in addition to an analytical surface area component corresponding to the work of cavity formation.⁴⁴ Because AGBNP is fully analytical with first derivatives it is well suited for energy minimization as well as MD sampling. A detailed description of the AGBNP model and its implementation is provided in Ref. 44.

The nonpolar solvation free energy is given by the sum of two terms: the free energy to form the cavity in solvent filled by the solute and the dispersion attraction between solute and solvent.^49,59 The nonpolar free energy is written as⁴⁴

$$\mathrm{\Delta }{G}_{\text{np}}=\sum _i({\gamma }_i{A}_i+\mathrm{\Delta }{G}_{\text{vdW}}^{(i)}),$$ (7)

where the first term is the cavity term, γ_i is the surface tension proportionality constant for atom i, and A_i is the solvent exposed surface area of atom i. The second term is the dispersion interaction term which is given by⁴⁴

$$\mathrm{\Delta }{G}_{\text{vdW}}^{(i)}={\alpha }_i\frac{-16\pi {\rho }_w{\epsilon }_{i,w}{\sigma }_{i,w}^6}{3{(B_i+R_w)}^3},$$ (8)

where α_i is an adjustable solute–solvent van der Waals dispersion parameter for atom i. The parameter ρ_w is the number density of water at standard conditions (0.033428/ų). ε_iw and σ_iw are the pairwise Lennard-Jones (LJ) well-depth and diameter parameters for atom i and the TIP4P water oxygen as given by the OPLS-AA force field.^45,46 ( ${\epsilon }_{i,w}=\sqrt{{\epsilon }_i{\epsilon }_w}$, where ε_i is the LJ well-depth for atom i and ε_w is similarly for the TIP4P water oxygen. The ε for water hydrogens is set to zero. σ_iw is defined in a similar manner.) R_w, is the radius of a water molecule (1.4 Å). By not incorporating the Lennard-Jones parameters into the dispersion parameter, αi, atoms with different though similar ∊_i;’s and σ_i’s are assigned the same α so as to minimize the number of adjustable parameters. B_i is the Born radius of atom i. The Born radius in this equation provides a measure of how buried atom i is in the solute. The deeper the atom is in the solute, the smaller will be its contribution to the total solute-solvent dispersion interaction energy. The functional form of ΔG_vdW in both SGB/NP and AGBNP depend upon the Born radius since it is a measure of the degree of burial of the atom. In SGB/NP, the dependence of ΔG_vdW on the Born radius was chosen on an ad hoc basis. The form of Eq. 8 for the solute-solvent van der Waals interaction energy component has been derived on the basis of simple physical arguments.⁴⁴

In this work we use two sets of parameterizations of α and γ to test the full nonpolar function described above relative to a simpler nonpolar function. In past implementations,¹⁹ the total nonpolar solvation free energy is given by a term proportional to the solvent-accessible surface area, or in terms of Eq. 7, setting all values of α_i to zero,

$$\mathrm{\Delta }{G}_{\text{np}}=\sum _i({\gamma }_i{A}_i),$$ (9)

where γ_i is set for all atoms to 0.015 kcal/mol/Ų. This implicit solvent model with the less-detailed nonpolar function is referred to as “AGB-γ”. When we use the full nonpolar function including the dispersion term (Eq. 8) using the parameters set forth in the work of Gallicchio and Levy,⁴⁴ the implicit solvent model is referred to as “AGBNP”.

A third parameterization aimed at implementing a correction for salt bridge interactions (which are generally overestimated by generalized Born solvent models)^56,60 is also investigated. To correct for the overstabilization of salt bridges by the generalized Born model, we used modified radii and γ_i, for carboxylate oxygens. The radius of the carboxylate oxygen is decreased from 1.48 Å, as in the original AGBNP, to 1.30 Å; γ_i of the carboxylate oxygen is set to −0.313 kcal/mol/Ų. These have the combined effect of increasing the solubility of carboxylate oxygens and decreasing the likelihood of ion pairing between the carboxylate groups on glutamate and aspartate, and positively charged groups found on lysine and arginine. We have parameterized this radius and γ_i, to experimental data for small molecules and to provide results which matched those generated with explicit solvent (unpublished results). The implicit solvent model that has additional descreening of ion pairing is referred to as “AGBNP+”.

2.3 The Protein Loop Datasets

We have tested the loop prediction algorithms on two sets of protein loops of known structure of nine and thirteen residues in length. The first set is composed of the 57 9-residue loops listed in Table 1. This set was originally compiled by Fiser et al.²⁴ and by Xiang et al.²⁵ The 35 13-residue loop set is the same as the one investigated by Zhu et al.⁵³ These loops were culled from the PISCES⁶¹ database. The proteins in these databases have been filtered using the following selection criteria: (i) low sequence identity (60% for Fiser et al.,²⁴ 20% for Xiang et al.,²⁵ and <40% for Zhu et al.⁵³), (ii) complete X-ray structure available with resolution < 2 Å, R < 0.25, and average temperature factor within the loop < 35, (iii) 6.5 < pH < 7.5, (iv) overlap factor for any loop atom > 0.7, (v) no significant loop secondary structure, (vi) no more than 4 additional loop residues on either side of the selected loop, (vii) distance between any loop atom and any ligand atom > 4 Å (6.5 Å for a metal ion).^26,53 While some of the loops contain very small amounts of secondary structure, in general, they are representative of longer loops found in globular proteins. All crystallographic water molecules are removed prior to loop prediction. Hydrogen atoms are added to each structure.²⁶

Table 1.

9-residue and 13-residue loops indicated by their the Protein Databank (PDB) designation for the protein and R_first and R_last are, respectively, the first and last residue of the loop (a letter indicates the chain on which the loop is found).

PDB(Rfirst–R1ast)	PDB(Rfirst–R1ast)	PDB(Rfirst–Rlast)
1aac(58–66)	1pda(108–116)	1cnv(110–122)
1aba(69–77)	1pgs(117–125)	1d0c(A:280–292)
1amp(57–65)	1php(91–99)	1dpg(A:352–364)
1arb(90–98)	1ptf(10–18)	1dys(A:290–302)
1arb(168–176)	1ra9(142–150)	1ed8(A:67–79)
1arp(127–135)	1rhs(216–224)	1eok(A:147–159)
1aru(36–44)	1sgp(E109–E117)	1f46(A:64–76)
1bt1(102–110)	1tca(170–178)	1g8f(A:72–84)
1byb(246–254)	1tca(217–225)	1gpi(A:308–320)
1cse(E95–E103)	1xif(59–67)	1h4a(X:19–31)
1csh(252–260)	1xnb(116–124)	1hnj(A:191–203)
1ede(257–265)	1xyz(A568–A576)	1hxh(A:87–99)
1fus(31–39)	1xyz(A795–A803)	1iir(A:197–209)
1fus(91–99)	1xnb(133–141)	1jp4(A:153–165)
1gpr(63–71)	1wer(942–950)	1kb1(A:793–805)
1isu(A30–A38)	2alp(139–159)	1krh(A:131–143)
1ivd(244–252)	2ayh(169–177)	1l8a(A:691–703)
1lkk(A142–A150)	2cpl(24–32)	1lki(62–74)
1lkk(A193–A201)	2eng(172–180)	1m3s(A:68–80)
1mla(194–202)	2hbg(18–26)	1mo9(A:107–119)
1mrj (92–100)	2sil(183–191)	1nln(A:26–38)
1mrk(53–61)	3pte(78–86)	1o6l(A:386–398)
1mrp(284–292)	3pte(107–115)	1ock(A:43–55)
1nfp(12–20)	3pte(215–223)	1ojq(A:167–179)
1nif(266–274)	3tgl(56–64)	1p1m(A:327–339)
1nls(131–139)	4gcr(94–102)	1qqp(2:161–173)
1noa(9–17)	1a8d(155–167)	1qs1(A:389–401)
1noa(76–84)	1ako(203–215)	1xyz(A:645–657)
1noa(99–107)	1arb(182–194)	2hlc(A:91–103)
1npk(102–110)	1bhe(121–133)	2ptd(136–148)
1onc(70–78)	1bkp(A:51–63)

2.4 Characterization of The Predicted Loop Structures

The predicted loop conformation is the one that has the lowest energy among those found by the conformational search procedures described above. The accuracy of the predicted conformations is analyzed by computing their root mean square deviation (RMSD) with respect to the corresponding crystallographically-determined native structures (the X-ray structure). The native and predicted protein loops are already in a common frame because only the conformation of the loop is varied during loop torsion angle sampling. The RMSD of the backbone atoms (N, C, and C_α) predicted and X-ray conformations are calculated in this common frame. We characterize the accuracy of the predictions based on the average and median backbone RMSD of the predictions, and the number of correct predictions. Correct predictions are defined as those that fall within a chosen RMSD threshold value from the X-ray structure.

An incorrect prediction (one with an RMSD larger than the threshold, see below) is further classified as an energy error when the prediction has an energy significantly lower than native, and otherwise as a sampling error, when the predicted loop has an energy higher than the native. This classification of incorrect predictions is aimed at determining the cause of the failure of the method to produce a native-like conformation. An energy error is indicative of the failure of the energy function to score the native conformation more favorably than non-native conformations; so that, even if the conformational search method had produced them, near-native conformations would not be recognized as good predictions. A sampling error is indicative of the conformational search procedure failing to sample conformations near the native conformation, even though the energy function scores at least some of them more favorably than non-native conformations.

The classification of correct and incorrect predictions requires the specification of a RMSD threshold value. This choice depends on the level of prediction accuracy required by the application. We report our results based on C_α RMSD thresholds of 1.5 and 2.0 Å for the 9-and 13-residue loop sets respectively, which have been used before to analyze the accuracy of loop prediction methods.^26,53 In addition, the classification of incorrect predictions requires the specification of an energy gap threshold value. If the difference in energies of the native and predicted conformations (where the predicted is lower in energy than the native) exceeds the energy gap threshold value, the incorrect prediction is classified as an energy error. In this work the results have been reported using an energy gap threshold value of 5 kcal/mol. The choice of this value absorbs the effects due to configurational entropy missing from our free-energy estimator, as well as the acceptable level of error in the energy function. We have explored a range of RMSD and energy gap threshold parameters and confirmed that the conclusions drawn in this work are not qualitatively affected by the particular choices made here. The energy of the native conformation used in the computation of the energy gap of the predicted conformation is determined in three ways: 1) a minimization of the loop with the frame, 2) a minimization followed by an optimization of the side chains on the loop, and 3) a confined search within 2 Å RMSD from the X-ray conformation similarly as for the second stage of refinement in the loop prediction procedure. We selected the native energy as the lowest energy determined from any of these. In almost all cases this conformation differs from the X-ray structure by no more than 1 Å C_α RMSD.

A minority of incorrect predictions were not classifiable as either energy errors or sampling errors. These were typically cases that do no qualify as clear energy errors because, even though the energy of the predicted non-native conformation is lower than the native conformation, the magnitude of the energy gap is within the 5 kcal/mol margin, and do not qualify as sampling errors because native conformations of reasonable low energy were sampled. In the following we label these cases as marginal errors. Marginal errors are effectively incorrect predictions due to subtle and not easily attributable energetic, entropic, and methodological causes.

In order to be able to compare the T-REMD predictions with those obtained from the PLOP-based prediction schemes and with the native structures, we energy-minimized the loop conformations found at the lowest target temperature of 270K and recomputed the loop backbone RMSDs with respect to the reference crystal structure. The conformation with the lowest energy was selected as the predicted conformation. The predicted conformation was then classified in terms of the energy gap and RMSD from the native conformation using the scheme described above.

3 Results

The results of the loop prediction tests are summarized in Table 2 for the standard and extended conformational sampling procedures (see Methods). Extended sampling was conducted on the loops that resulted in a sampling error with standard sampling; Table 2 includes the combined standard and extended sampling results. For the 57 9-residue loops (see Table 1) loop prediction tests were conducted with OPLS-AA and the following implicit solvent models: distance-dependent dielectric, SGB/NP, AGB-γ, AGBNP, and AGBNP+. It has been stated that the results for loop prediction with PLOP was independent of the presence of crystal symmetry.²⁶ However, we found that crystal symmetry significantly influenced the results with SGB/NP. In order to compare with previous results,²⁶ we performed loop predictions with SGB/NP both in the presence and absence of crystal symmetry. Loop prediction calculations with all of the other implicit solvation models were conducted only in the absence of crystal symmetry. Loop prediction tests for the 35 13-residue loops (see Table 1) were conducted with AGBNP+. As described in the Methods section we characterized each loop prediction as being either correct or incorrect. In turn each incorrect prediction is classified as an energy error, a sampling error, or a marginal error. Table 2 reports the total number of errors and the number of energy and sampling errors, and the mean and median RMSD of the predictions from the X-ray structure.

Table 2.

Summary of the loop conformational predictions results with the standard and enhanced sampling procedures.

	9-residue						13– residue
	SGB/NP-X	SGB/NP	ddd	AGB–γ	AGBNP	AGBNP+	AGBNP+
E	8	11(10)	19	6	4(3)	2	2
S	5(5)	7(14)	4(7)	4(7)	4(9)	5(10)	5(14)
M	2	3(4)	3	1	0	1	1(2)
E+S+M	15	21	26	11	8	8	8
〈RMSD〉	1.44	1.91	2.31	1.10	1.04	1.00	1.87
median RMSD	0.58	0.60	1.27	0.52	0.52	0.58	0.67

SGB/NP-X : SGB/NP with crystal symmetry

ddd : distance-dependent dielectric

E : number of energy errors (results listed for both enhanced and (standard) sampling)

S : number of sampling errors (results listed for both enhanced and (standard) sampling)

M : number of marginal errors (results listed for both enhanced and (standard) sampling)

The values listed were obtained with enhanced sampling; the values in parentheses were obtained with standard sampling.

〈RMSD〉 : average RMSD (in Å) of the lowest energy loops

The results in Table 2 for the 9-residue loops demonstrate that the total number of prediction errors (energy and sampling) is the lowest for the AGB implicit solvent models. The distance-dependent dielectric model (ddd) performs the worst, followed by SGB/NP in the absence of crystal symmetry. The introduction of crystal symmetry results in a significant reduction in the number of sampling errors. (This is discussed further below.) Of the three AGB-based models, AGB-γ which mimics GB/SA is the one with the largest number of prediction errors whereas AGBNP and AGBNP+ are equivalent in this respect. The number of energy errors, a measure of the quality of the energy model, vary greatly from one energy model to another. The fewest energy errors are found with AGBNP+, followed by in order AGBNP, AGB-γ, SGB/NP with crystal symmetry, SGB/NP, and distance-dependent dielectric. The number of sampling errors in general does not vary as greatly from one energy model to another and their occurrence decreases significantly by using the extended sampling procedure (as shown in Table 2). This is particularly noticeable for the 13-residue loops for which two thirds of the sampling errors with standard sampling are avoided (decrease fourteen errors to five) when using extended sampling.

Comparison of the results for SGB/NP with and without crystal symmetry reveals that the inclusion of crystal symmetry has a dramatic effect on the number of sampling errors when using standard sampling; SGB/NP without crystal symmetry produces fourteen sampling errors compared to five sampling errors with crystal symmetry (see Table 2). The effect of crystal symmetry on the number of sampling errors is greatly diminished when using extended sampling (Table 2). With extended sampling the number of SGB/NP sampling errors drops to seven whereas the number of sampling errors (five) with SGB/NP with crystal symmetry is unchanged.

Table 2 also reports the mean and median RMSD of the loop predictions with respect to the X-ray structure. The mean RMSD of the 9-residue loops predictions with the AGB-based energy models is around 1 Å, which is significantly better than all the other solvation models including SGB/NP with the inclusion of crystal symmetry. The worst mean RMSD for the 9-residue loops is 2.31 Å obtained with the distance-dependent dielectric model. The median RMSD’s, which are less affected by outliers corresponding to grossly incorrect predictions, are significantly smaller than the mean RMSD’s. The difference between mean and median RMSD’s is larger for SGB/NP-based and distance-dependent dielectric models than AGB-based solvation models due to the fact that incorrect predictions with the latter are generally closer to the X-ray structures than with the other models. The larger difference between mean and median RMSD for the 13-residue loop predictions with AGBNP+ relative to the 9-residue loop predictions reflects the fact that, expectedly, incorrect predictions with the longer loops tend to be farther away from the X-ray structure in terms of RMSD.

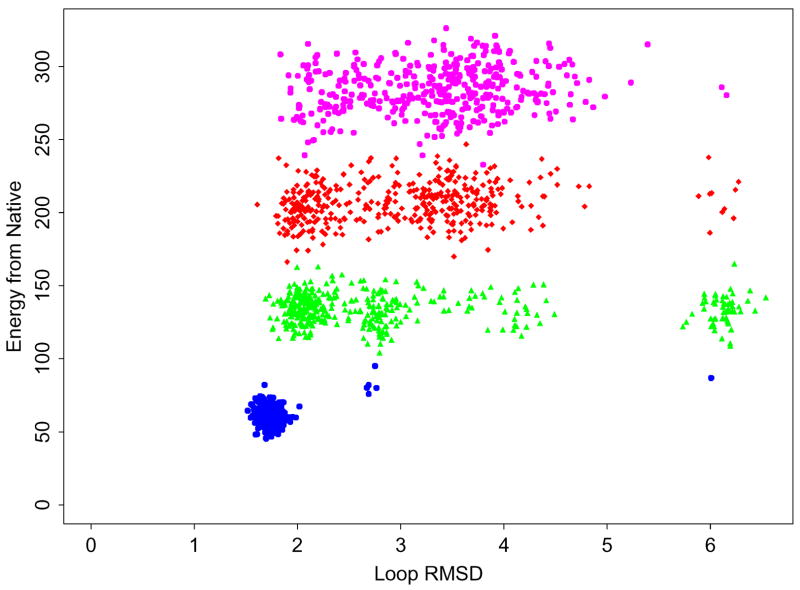
We repeated loop prediction calculations for six of the 9-residue protein loops classified as sampling errors with the loop prediction algorithm and using the AGBNP+ solvation model, using the T-REMD sampling procedure described in the Methods section. These loops are 1npk (residues 102–110), 1one (70–78), 1fus (31–39), 1byb (246–254), 1noa (99–107) and 1wer (942–950) (see Table 1). We sampled these loops using temperature replica exchange molecular dynamics (T-REMD) as implemented in the IMPACT molecular mechanics package. The distribution of conformations in terms of potential energy and RMSD from the X-ray structure from the last 5 ns of the T-REMD trajectories for 1fus (31–39) is shown in Figure 4. The RMSD from the native of the lowest energy conformations extracted from the T-REMD trajectories is reported in Table 3. For comparison, this table also reports the corresponding predictions using the standard conformational search procedure with PLOP. This table shows that in half of the cases examined (1one, 1fus, and 1wer), T-REMD is able to produce predictions significantly closer to the X-ray structure than the the PLOP-based standard sampling procedure. However, only one (1wer) of the six incorrect PLOP-based predictions results in a correct prediction with T-REMD, based on the 1.5 Å RMSD threshold value.

Figure 4.

Energy gaps relative to the optimized native conformation (in kcal/mol) versus the RMSD (in Å) relative to the X-ray crystal conformation for the T-REMD prediction calculation of the Ifus (31–39) loop. The conformationas from the ensembles at 270 K, 400 K, 595 K, and 800 K are shown in blue, green, red, and magenta, respectively. Energies are in kcal/mol and RMSD is in Å.

4 Discussion

4.1 Prediction Accuracy

The loop prediction procedure based on PLOP with the AGBNP+ solvation model and the extended sampling schemes we devised is very successful in predicting the conformations of the 9 and 13-residue loops we have investigated. As Table 2 shows, the successful prediction rate is 86% and 77% for 9 and 13-residue loops, respectively. We obtained a significant reduction in the rates of successful predictions when using the SGB/NP and distance-dependent dielectric solvation models, even when we include crystal symmetry.

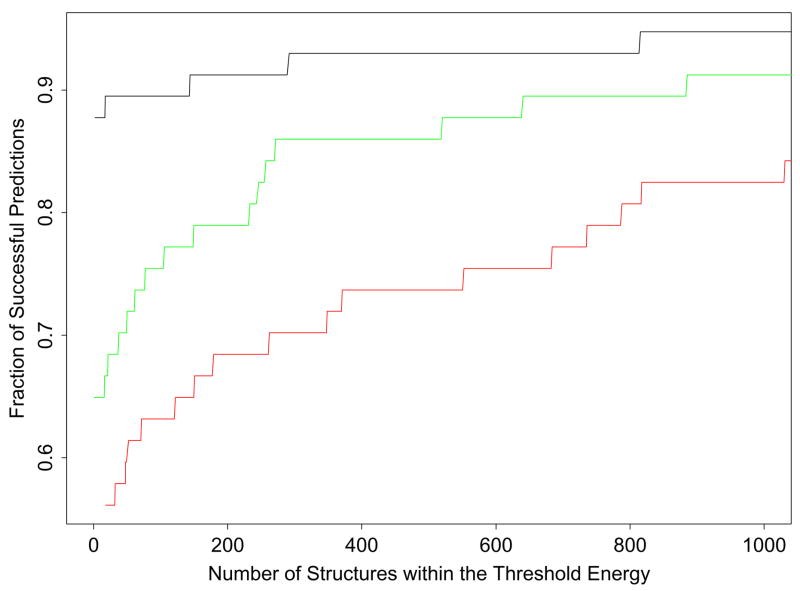
Although in this work we define the predicted conformation as the lowest energy loop conformation, it is interesting to examine also how well the loop prediction procedure captures native-like conformations within a given energy range from the minimum energy conformation found. In homology modeling, the choice of the candidate structures may not be restricted to selecting only the lowest-energy conformation. It may be desirable to investigate structures whose energies lie within some range about the minimum energy structure found in the search. For instance, a modeller may consider all those structures whose energies are within the lowest 5 kcal/mol as possible candidates to represent the native conformation. Under this scenario the prediction calculation can be considered successful if any one of the candidate conformations approximates well the native conformation. While the energy range is increased the probability of including a native-like conformation increases at the expense of the greater cost associated with having to carry over a larger number of candidate conformations. On average there are roughly 150 loop predictions per protein within 5 kcal/mole from the minimum energy. Fig. 1 illustrates this cost/benefit analysis for the 57 9-residue loop prediction calculations (Table 2). Each point on the curves in Fig. 1 was obtained by collecting for each loop target the set of predicted conformations with energies within a given energy range ΔE from the energy of the lowest energy prediction and recording their number N as well as whether at least one native conformation (within 1.5 Å RMSD from the X-ray conformation) is contained in this set, that is whether for this particular loop target and energy range the result is regarded as a successful prediction. We did this over a range of ΔE values for all 9-residue targets and solvation models. We then plotted the ratio between the number of successfully predicted loop targets and the total number (57) of loop targets (the fraction of successful predictions) for a given ΔE versus the average number of low-energy predicted conformations within this value of ΔE for the AGBNP+, SGB/NP, and distance-dependent dielectric solvation models (see Fig. 1). The abscissa in this plot represents the cost, as measured by the number of conformations that one is willing to consider as possible candidates, whereas the ordinate represents the benefit, as measured by the probability of including at least one native conformation within this set of conformations. This plot can be used in two complementary ways. Given the maximum cost one is willing to sustain on the abscissa the corresponding ordinate of the curves yield for each solvation model the expected rate of success. Alternatively, given the desired rate of success in the ordinate, the curves give the required associated cost.

Figure 1.

We plotted the ratio between the number of successfully predicted loop targets and the total number (57) of loop targets (the fraction of successful predictions) for a given threshold energy, ΔE, versus the average number of low-energy predicted conformations within this value of ΔE for the AGBNP+, SGB/NP, and distance-dependent dielectric solvation models. All loop predictions are ordered relative to their energy from the lowest energy prediction. For an average given number of loops from the minimum (the abscissa), the fraction of proteins that have at least one native-like loop among the top number of loops is shown above along the ordinate. The black line presents the results for AGBNP+, the green line for SGB/NP, and the red line for distance-dependent dielectric.

The minimum cost corresponds to retaining only the lowest energy prediction (N = 1). This assumes that the lowest-energy loop prediction from the algorithm is the native conformation without any additional analysis. For this value of N the success rates are 86%, 77%, and 55% for the AGBNP+, SGB/NP, and distance-dependent dielectric models respectively, see Fig. 1. For all values of ΔE examined, the AGBNP+ solvation model provides the best success rate for a given cost level, followed by SGB/NP and the distance-dependent dielectric solvation models. A greater cost level entails retaining more than one low-energy loop conformation which would have to be analyzed in more detail. Conversely, AGBNP+ yields a higher success rate with less cost than the other solvation models; for example, to obtain with the SGB/NP model a success rate of 86% requires considering on average 500 conformations. To obtain a similar success with distance-dependent dielectric would require consideration of over 1000 conformations on average per loop target.

It is useful to compare our results with those obtained by other groups for 9-residue and 13-residue loops. Fiser et al. used MD along with simulated annealing to predict loop conformations with an all-atom force field and a statistical treatment of solvation.²⁴ The percentage of predictions they report within 2 Å RMSD (described as good and medium predictions) is 55%.²⁴ Using a tighter RMSD cutoff of 1.5 Å, we obtain with PLOP and AGBNP+ an 86% success rate in our predictions for 9-residue loops. For a set of 13-residue loops, Fiser et al., using the same 2 Å RMSD cutoff, report a very low 15% success rate,²⁴ compared to the 77% success rate we obtained using the AGBNP+ scoring function. Xiang et al. performed a search over a discrete rotamer library with scoring based on their colony energy. For 9-residue loops, they report an average RMSD of 2.68 Å.²⁵ In comparison the average RMSD we have obtained with PLOP and AGBNP+ is 1.00 Å. De Bakker et al.⁶² generated loop conformations with their program RAPPER⁶³ and scored them with a knowledge-based potential and with a physics-based potential, AMBER/GBSA. For 9-residue loops from the Fiser set,²⁴ the average RMSD of the lowest energy loops was over 2 Å when scored with the AMBER/GBSA potential which produced their best results.⁶²

Jacobson et al.²⁶ performed loop prediction calculations on a large set of 9-residue loops using the SGB/NP model with the crystal symmetry included and using the standard conformational sampling algorithm used here.²⁶ Based on the supplementary material they provided, ²⁶ we were able to determine the number of energy and sampling errors using a 1.5 Å RMSD cutoff and a −5 kcal/mol energy cutoff. Based on our analysis of their data, they had obtained ten energy errors and eight sampling errors.²⁶ In comparison, we find eleven energy and seven sampling errors with SGB/NP without crystal symmetry but we find only eight energy errors and five sampling errors with SGB/NP with crystal symmetry. This might indicate that crystal symmetry is important for prediction accuracy; however, we obtained two energy errors and five sampling errors using AGBNP+ without the presence of the crystal environment. A recent study based on the comparison of X-ray and NMR structures of identical proteins suggests that in most cases the impact of the crystal environment on protein structures is relatively small and not strongly correlated with crystal packing.⁶⁴ Recently, Zhu et al.^{53, 65} have reported loop prediction results for the same 35 13-residue loops investigated here using the SGB/NP potential with crystal symmetry supplemented by hydrophobic correction terms and a variable dielectric model. Zhu et al. show that these promising models lower the average backbone RMSD’s of the 13-residue predictions substantially, from 2.73Å to 1.08Å. In comparison, we obtain for the 13-residue loop set with AGBNP+ without crystal symmetry an average RMSD of 1.87Å which is intermediate between the range of RMSD measures reported by Zhu et al.^{53, 65} The best performing model reported by Zhu et al. produces according to our definition five energy errors on the 13-residue loop set (see supplementary material of reference ⁶⁵) compared with the two energy errors obtained here.

4.2 Accuracy of Scoring Functions

The ability of the effective potential model to consistently score native conformations more favorably than non-native conformations is essential for successful loop prediction. The results in Table 2 for the 9-residue loops indicate that significant differences, in terms of the number of energy errors, exist between the different solvation models we investigated. We observed that the occurrence of energy errors for each solvation model only depends weakly on the choice of conformational sampling as shown in Table 2. This is further confirmation that the energy errors are incorrect predictions mainly attributable to deficiencies of the energy functions, and as such they provide a means to analyze solvation models and suggest possible routes for improving them.

A more direct test of the potential energy functions used in loop prediction is to look at the relative percentage of energy errors rather than the relative percentage of correct predictions discussed previously which includes the effects of sampling errors. For the 9-residue loops in the absence of crystal symmetry, the largest percentage of energy errors (33.3%) was obtained for the distance-dependent dielectric. For the other implicit solvent models we tested in the absence of crystal symmetry, the percentage of energy errors decreases with, in order, SGB/NP (19.3%), AGB-γ (10.5%), AGBNP (7.0%), and AGBNP+ (3.5%).

The distance-dependent solvation model is clearly the worst in terms of accuracy, with nearly two thirds of the incorrect predictions with extended sampling caused by energy errors (Table 2). Distance-dependent solvation models lack hydration free energy terms which provide the driving force toward solvent exposure of polar groups and vice versa the burial of hydrophobic groups. We have observed that a major structural problem with distance-dependent dielectric predictions is the occurrence of non-native salt bridges. Indeed after rescoring the distance-dependent dielectric predictions with AGBNP+, all are found to have energies greater than the native conformation due to the fact that Coulomb interaction energies of non-native ion pairs are countered by unfavorable electrostatic and non-polar desolvation self energy terms.

We observe about half as many energy errors with the SGB/NP solvation model as with the distance-dependent dielectric. However the occurrence of energy errors remains high; about half of the 21 incorrect predictions of 9-residue loops with SGB/NP in solution with extended sampling are attributed to the energy function. The reduction in the number of energy errors (eleven to eight) with the inclusion of crystal symmetry can in principle be rationalized by the stabilization of the experimental structure due to crystal contacts not considered when evaluating the energy in solution but we found very few examples (see below). In general the influence of the crystal environment appears to be secondary at this resolution in light of the fact that the occurrence of energy errors is significantly more pronounced with SGB/NP with crystal symmetry than with AGB-based solvation models without crystal symmetry (see Table 2). The reduction of SGB/NP energy errors with crystal symmetry is mainly due to crystal packing steric interactions preventing the formation of non-native low-energy conformations that occur in the absence of crystal contacts. Some examples illustrating the influence of the crystal environment on the loop conformation are discussed below.

Most SGB/NP predictions classified as energy errors were found to have electrostatic interaction energies significantly more negative than native conformations (results not shown), suggesting that SGB/NP overestimates the occurrence of salt bridges and intramolecular hydrogen bonds. When SGB/NP predictions are rescored with AGBNP+, all but two of the SGB/NP’s energy errors are removed. Zhu et al.^53,65 recently obtained results indicating that the occurrence of energy errors with SGB/NP can be further reduced by including an empirical hydrophobic potential and a variable dielectric model designed to favor conformations with packed hydrophobic cores and to disfavor the occurence of salt bridges.

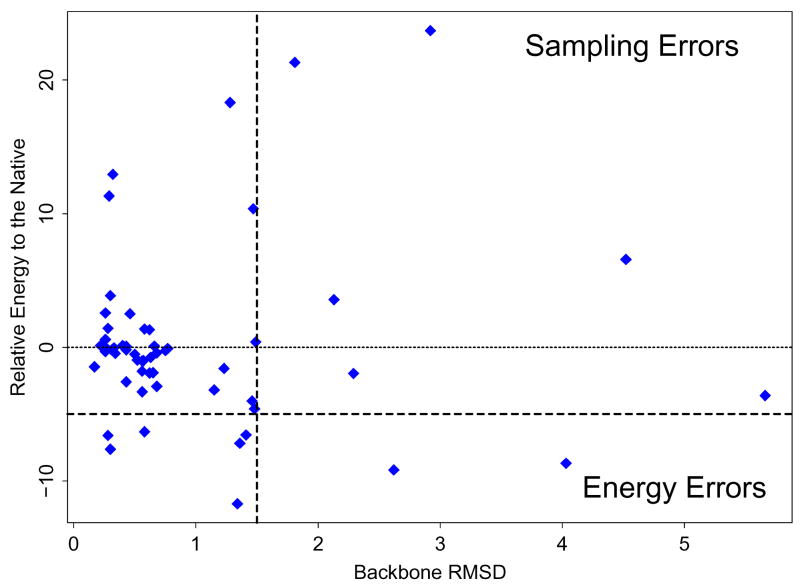
The AGBNP+ implicit solvent model with OPLS-AA yields only two energy errors for the 57 9-residue loops, the fewest among the solvation models tested (Table 2). The distribution of AGBNP+ results for 9-residue loops are plotted in Fig. 3, where the energy errors are shown in the lower right of the plot. Only two of the 35 13-residue loop predictions with AGBNP+ are classified as energy errors. By analyzing the energy errors obtained with the various AGB-based models we are able to establish which features of the model aid in loop prediction. The number of energy errors for the 9-residue loops decreases consistently from six with the AGB-γ model, which is based on the simple surface area-only non-polar model, to four with the AGBNP model, ⁴⁴ which implements a non-polar model that takes into account dispersive solute-solvent van der Waals interactions, to only two with the AGBNP+ model, which additionally adopts a parametrization designed to reduce the occurrence of salt bridges (See Methods).

Figure 3.

The results of the OPLS-AA/AGBNP+ loop predictions on the 57 9-residue loops in Table 1. The energies (in kcal/mol) relative to the native are plotted with respect to the backbone RMSD (in Å) to the native. The vertical dashed line is the RMSD cutoff, 1.5 Å. The bold, horizontal dotted-dashed line is the energy cutoff, −5 kcal/mol. Cases corresponding to the points to the left of the RMSD cutoff line are successful predictions, those in the top-right quadrant are sampling errors, and those in the bottom-right quadrant are energy errors.

These results indicate that the AGBNP model performs well for loop prediction applications regardless of the specific parameterization. Fine-tuning of the non-polar model and salt bridge correction can yield, nevertheless, additional improvements. Two of the six energy errors with AGB-γ are removed when considering the AGBNP model and of the remaining 4 energy errors, two are removed when adopting ion pairing corrections in AGBNP+. One of these is the 1ivd (244–252) AGBNP prediction, which has an energy −12.10 kcal/mol and an RMSD of 1.91 Å relative to the native. This incorrect prediction is stabilized by electrostatic interactions between Asp251 and Arg253. This interaction is absent in the 1.36 Å RMSD predicted conformation with AGBNP+, consistent with the fact that the energy of the incorrect prediction is raised above that of the correct prediction when rescored with AGBNP+. Similarly, the AGBNP incorrect prediction for 1sgp(109–117) is stabilized by a non-native ion-pair between residue Lys115 on the loop and the C-terminal carboxyl group of residue 242 which is avoided when using AGBNP+.

With AGBNP+ only two of the 13-residue loop predictions are classified as energy errors, moreover, as discussed below, the native conformations of these two loops are likely affected by intermolecular interactions present in the crystal that were not taken into account in the present calculations. In comparison, thirteen of the 35 loops in this set were found to produce energy errors with the OPLS-AA/SGB/NP potential, and six of the loops are energy errors with the OPLS-AA/SGB/NP potential augmented by a hydrophobic contact correction term, ⁵³ even though these calculations took into account crystallographic intermolecular interactions. The OPLS-AA/AGBNP+ potential function is in general able to identify the native conformation without the additional aid of knowledge-based empirical corrections, suggesting that the AGBNP solvation model captures the appropriate balance between polar and hydrophobic solvation and intramolecular interactions.

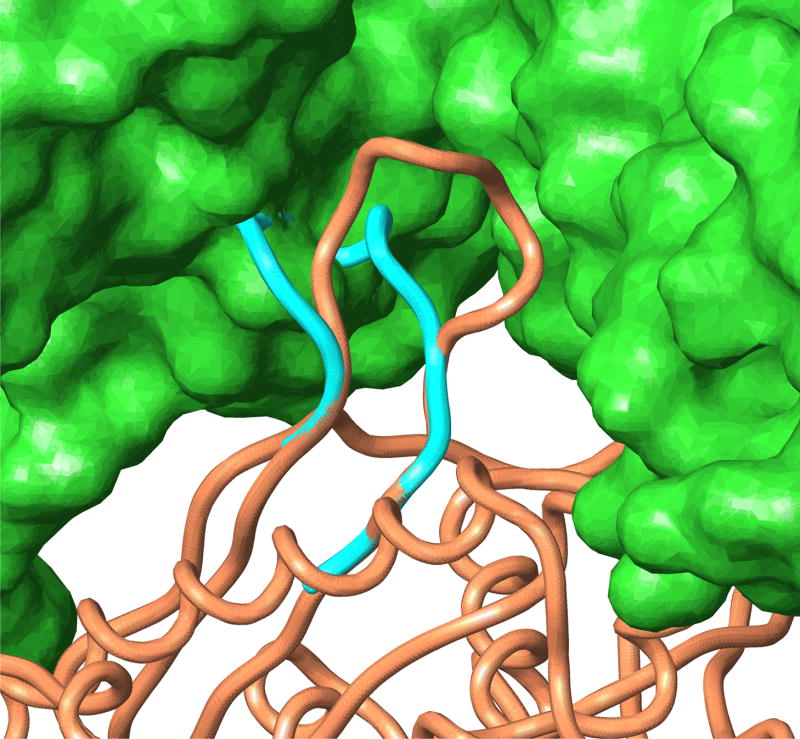
The small number of energy errors with the OPLS-AA/AGBNP+ force field are generally not very informative in terms of how to modify the potential in order to avoid them. The energy errors correspond to the 1xif(59–67) and 3pte(215–223) 9-residue loops and the 1hnj(A:191–203) and 1jp4(A:153–165) 13-residue loops. In all of these cases the native conformation is influenced by crystal contacts. Although we modeled 1xif as a monomer as did Fiser et al.²⁴ and Jacobson et al.,²⁶ the asymmetric unit of 1xif is a tetramer. However our attempt to model 1xif as a tetramer still resulted in an energy error possibly due to a native salt bridge not correctly modeled by AGBNP+. The native conformations of 3pte(215–223), 1hnj(A:191–203) and 1jp4(A:153–165) are clearly influenced by crystal packing forces. As for example shown in Fig. 5 for 1jp4, these loops extend away from the body of the protein, assuming a conformation unlikely to occur in solution. These loops make however extensive contacts with surrounding protein molecules in the crystal. The AGBNP+ predicted conformations without crystal symmetry instead pack closely against the protein body in a way which would not occur in the crystal due to steric repulsion. Moreover in the case of 1hnj and 1jp4, PLOP rejects backbone conformations that stray more than a certain distance from the protein body and prevents the evaluation of conformations near the native conformations. It should also be noted that, whereas we modeled only the monomer, the biological unit of 1hnj is a dimer and the loop in question (A191–A203) of one of the monomers makes contact with the same loop in the other monomer.

Figure 5.

The X-ray (gold) and predicted (blue) conformations of the 13-residue loop 1jp4 (A:153–165). The surfaces of the crystallographically symmetric protein molecules are shown in green.

Apart from these cases, it appears that, within the resolution threshold we considered, the loop conformations predicted without using crystal symmetry are very close to the conformations seen in the crystal environment. This suggests that instead of crystal packing influencing loop conformations, in most cases it is the conformational propensity of the loop in solution which determines the packing arrangement in the crystal. This observation rationalizes the use of X-ray crystallographically determined structures as training sets in the development of homology modelling techniques for modeling protein loops in the solution environment.

4.3 Sampling Efficiency

Although they are indirectly influenced by properties of the energy function, such as its roughness and the level of degeneracy of native and non-native conformations, incorrect predictions classified as sampling errors primarily reflect limitations of the loop prediction algorithm. These are cases in which an incorrect prediction was made even though the energy of the native conformation is lower than that of the predicted conformation. It is important to reduce as much as possible the occurrence of sampling errors in order to decrease the overall number of mispredictions.

With the standard loop sampling procedure (Table 2) sampling errors generally represent a large fraction of incorrect predictions. This is in contrast to our results with the inclusion of crystal symmetry with the SGB/NP model in which only one third of the incorrect predictions are classified as sampling errors. We conclude therefore that, although the parameters of the standard sampling algorithm (the value of the ofac parameter, the number of clusters, and the number of conformations that are passed from one stage of refinement to the next) work well when including crystallographically symmetry-related molecules,^26,53 the performance using standard sampling is significantly degraded when preforming loop prediction in the absence of the crystal environment. Evidently, the larger conformational space available to the loops in the absence of the crystal environment requires more extensive conformational search strategies. This has serious implications for loop prediction calculations as part of homology modeling projects which are typically carried out in the solution environment. Including the crystal environment is required to achieve high accuracy with the current sampling schemes. But in the majority of homology modeling applications, only the sequence and a related template protein is known. In most cases when the crystal parameters are known, so is the structure of the protein.

Sampling errors result from the sampling algorithm failing to produce near-native conformations of low enough energy or from failing to consider near-native conformations altogether. We refer to the first as a local sampling error and the latter as to a global sampling error. Global sampling errors typically occur when at the initial prediction stage the loop build-up procedure cannot find, within the resolution of the backbone and sidechain rotamer library and the value of the ofac threshold parameter, any conformation free of clashes in the neighborhood of the native conformation. We also found that several of the global sampling errors with 9-residue loops are due to an insufficient preset number of clusters (36 for 9-residue loops), causing near-native conformations to sometimes be included in largely non-native conformational clusters. Local sampling errors are cases in which a near-native conformation produced by the initial prediction stage is abandoned prematurely and is not carried over to the subsequent refinement stages, which are responsible for adjusting the structure to lower the energy to a value closer to that of the native conformation. We found that the majority of 13-residue mispredictions are caused by local sampling errors.

Based on these observations we have modified the standard loop sampling procedure for 9-residue loops by decreasing one of the values of ofac tried at the initial prediction stage (from 0.75 to 0.5), and doubling the number of clusters (from 36 to 72) employed in the initial prediction stage. The standard loop sampling procedure for 13-residue loops was modified by increasing the number of candidate conformations carried over from one stage of refinement to the next (see Methods). These extended sampling schemes were then evaluated by applying them to the loops that resulted in sampling errors with the standard loop procedure. As Table 2 shows, the number of sampling errors was substantially reduced for both the 13-residue and the 9-residue loops by using the extended sampling scheme. Interestingly, none of the sampling errors obtained with SGB/NP including crystal symmetry using the standard sampling scheme improved with the extended sampling scheme, confirming the results of earlier studies^26,53 that concluded that the standard sampling procedures were sufficient for loop predictions in the crystal environment.

4.4 Loop Prediction with Replica Exchange Molecular Dynamics

To better understand the origin of the observed sampling errors we investigated with T-REMD the six 9-residue loops that resulted in global sampling errors with the standard loop sampling procedure. As has been demonstrated,^26,53 the conformational search algorithms based on PLOP perform well for predicting the conformation of protein loops of up to thirteen residues in length; however, because of the exponential explosion in the number of possible loop configurations that need to be examined, the application of this method to longer loops and situations which involve several interacting loops, as well as simultaneous refinement of the protein region surrounding the loops, is problematic. In contrast, importance sampling schemes concentrate sampling in the most thermodynamically relevant regions of the conformational space and scale linearly with the increase of the number of degrees of freedom.

The all-atom potential energy landscapes of proteins are rugged, containing many local minima separated from each other by high barriers. Because of this there are long dwell times in local minima which slows sampling rates making application of conventional room temperature MC or MD methods impractical for loop structure determination. New simulation strategies, called collectively generalized ensemble methods,⁶⁶ have been developed which overcome this sampling bottleneck. One of the most popular methods in this class is the temperature Replica Exchange Method (REM),^66,67 which can be paired with a constant temperature molecular dynamics engine (T-REMD).^{55,56,68–70} The REM technique has been used to improve sampling of rough energy landscapes. The REM methodology has been used to predict the hypervariable regions of a llama VHH antibody domain⁷¹ and has shown promise in other protein structure determination applications.^72–74

Prior to applying the T-REMD procedure to the group of protein loops classified as sampling errors by the standard loop prediction routine, we tested the T-REMD protocol on a less challenging set of five 9-residue loops for which the PLOP conformational search scheme was able to locate near native conformations. The T-REMD approach produced matching results within reasonable simulation times, indicating that the T-REMD protocol can also easily provide good predictions in these cases. However, as the results summarized in Table 3 show, the more challenging cases of conformational sampling, although improved over the PLOP predictions, remain problematic. The T-REMD scheme was able to substantially improve within the allocated simulation time half of the PLOP sampling errors, resulting in much higher quality structures. The RMSD’s of the predictions for the 1onc, 1fus, and 1wer, improved from the range between 4Å to 7.5Å to ~2 Å or less. Only one case, however, (1wer) resulted in a correct prediction based on the 1.5 Å RMSD threshold.

The T-REMD trajectory for the 1fus (31–39) loop is illustrated in Fig. 4, where the energies of conformations sampled in the last 5 ns of simulation at various temperatures are plotted. The patchy pattern of the lowest temperature ensemble of loop configurations signifies the presence of high energy barriers which separate loop configurations into different conformational states. The absence of a direct path between these structurally distinct macrostates clearly shows that efficient sampling of the conformational space would not be possible with standard molecular dynamics conducted at room temperature. Transitions between the macrostates are accomplished by acquiring enough thermal energy (moving up the temperature ladder) to surmount the separating barrier. Afterwards, there is a subsequent gradual annealing of the structure and temperature leading to the native conformation at low temperature. The numbers of transitions between macrostates during 5 ns is small.

5 Conclusion

We have conducted loop conformation prediction tests on challenging benchmark sets consisting of nine and thirteen residue loops using the conformational search schemes built into PLOP to investigate the accuracy of the AGBNP implicit solvation model in conjuction with the OPLS-AA intramolecular force field. For a set of 57 9-residue loops investigated previously^24–26 we accurately predicted 88% of the loops using the OPLS-AA/AGBNP+ potential. This is a substantial improvement over the use of a distance-dependent dielectric model (63%) or SGB/NP, with (77%) or without (67%) the inclusion of crystal symmetry, as the implicit solvent model. A more substantial difference between implicit solvent models is apparent when examining the relative percentage of energy errors. AGBNP+ has the lowest percentage of energy errors at 3.5%, which is less than one fifth as many as for SGB/NP (19.3%) and one ninth as many as for distance-dependent dielectric (33.3%).

The fact that we have obtained high accuracy without crystal symmetry when using AGBNP+ suggests that the presence of crystal symmetry in the model is not crucial for reproducing the loop structures which have been experimentally determined via X-ray crystallography. In general, although the side chain positions have been reported to be strongly influenced by the neighboring crystallographically symmetry-related molecules,²⁷ the backbone conformation does not appear to be as strongly influenced by crystal packing interactions at the resolution of the current study. A recent comparison between structures determined by X-ray crystallography and NMR of identical proteins showed little correlation between structural differences and crystal contacts.⁶⁴ We found, however, the conformation sampling schemes previously developed for loop predictions in the crystal environment needed to be extended in order to avoid sampling errors when crystal symmetry is not included in the model. We recommend the use of these updated extended sampling protocols for homology modelling applications in the solution environment.

We expect importance sampling conformational search methods such as T-REMD to become an important complement to traditional discrete conformational search methods in cases when the number of degrees of freedom is large such as interacting loops, imperfect frameworks for loop prediction, etc. We note that development of better implementations of REM ideas which will offer faster sampling in the context of structure prediction of protein loops is the subject of intensive ongoing research. This will go beyond simple temperature exchanges in REM and will involve modifying the system Hamiltonians and swapping replicas with different energy potentials, constructed to effectively increase the range of conformational motion.⁷¹ Another avenue of improvement is to consider more rational ways of selecting pairs of replicas for exchanges of temperatures or Hamiltonian parameters,⁷⁵ with the goal being to examine how sampling can be enhanced through maximizing mixing among replicas. Such a multidimensional replica exchange procedure appears to be promising for exploring the conformational space of protein loops.

It should be noted that the success rates we obtained likely overestimate the success rate obtainable in actual homology modeling applications because these tests were performed in the idealized case in which the frame of the protein surrounding the loop is known. Successfull prediction in this idealized situation is a necessary but not sufficient requirement for the ability to predict the correct native-like loop conformation with partial knowledge of the protein framework. We have begun to investigate cases in which the conformations of the protein sidechains surrounding the loop are predicted at the same time as the loop conformation. We find that the successfull prediction rate for these cases is significantly reduced relative to the tests reported here with the conformations of the sidechains of the protein frame fixed in their native conformations. Clearly more work is still needed to develop fast and accurate loop prediction protocols for “real life” homology modeling applications.

Figure 2.

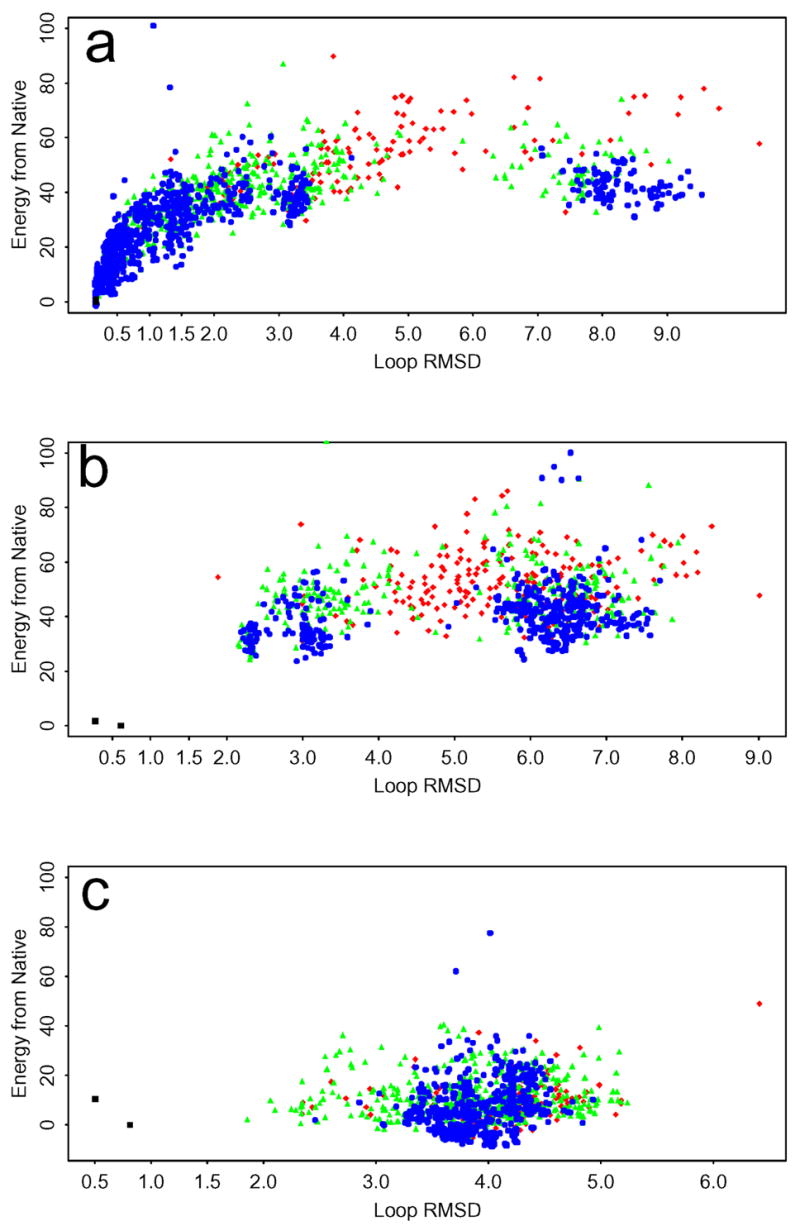
Energy gaps relative to the optimized native conformation (in kcal/mol) versus the RMSD (in Å) relative to the X-ray crystal conformation for three representative 9-residue loop prediction cases with the OPLS-AA/AGBNP+ potential and the standard conformational sampling algorithm: (a) lphp(91–99) (a successful prediction), (b) lfus(31–39) (a sampling error), and (c) 3pte(215–223) (an energy error). The initial prediction results are in red, the first stage of refinement is in green, and the second stage of refinement is in blue. The native (minimized and optimized) are in black.