Ab initio folding of proteins using all-atom discrete molecular dynamics

Summary

Discrete molecular dynamics (DMD) is a rapid sampling method used in protein folding and aggregation studies. Until now, DMD was used to perform simulations of simplified protein models in conjunction with structure-based force fields. Here, we develop an all-atom protein model and a transferable force field featuring packing, solvation, and environment-dependent hydrogen bond interactions. Using the replica exchange method, we perform folding simulations of six small proteins (20–60 residues) with distinct native structures. In all cases, native or near-native states are reached in simulations. For three small proteins, multiple folding transitions are observed and the computationally-characterized thermodynamics are in quantitative agreement with experiments. The predictive power of all-atom DMD highlights the importance of environment-dependent hydrogen bond interactions in modeling protein folding. The developed approach can be used for accurate and rapid sampling of conformational spaces of proteins and protein-protein complexes, and applied to protein engineering and design of protein-protein interactions.

Introduction

Computer simulations, from simple lattice Monte Carlo to all-atom molecular dynamics methods, have proven to be essential in our understanding of proteins (Chen et al., 2007). Among these simulation techniques is discrete molecular dynamics (DMD; see Methods), in which the interaction potentials are approximated by discontinuous step functions, and the simulations are driven by collisions (Rapaport, 1997). The discrete nature of the collision-driven DMD simulations is akin the distinct move set in Monte Carlo simulations; thus, the DMD algorithm features the fast sampling efficiency (Ding et al., 2005b) characteristic of Monte Carlo algorithms. DMD has been used in studies of protein folding thermodynamics and kinetics, protein evolution, protein domain-swapping, and amyloid fibril formation (Hall et al., 2006;Urbanc et al., 2006;Dokholyan et al., 2000).

DMD simulations of simplified protein models with structure-based force fields have been used in previous studies of protein folding and aggregation (Dokholyan et al., 2000). Despite the simplicity of the utilized protein models, the DMD simulations show strikingly predictive power in uncovering the underlying molecular mechanisms of various biological processes (Ding et al., 2005b;Dokholyan, 2006). With continued advances in our understanding of proteins, there is an ever growing interest in the application of our knowledge toward medically relevant studies (Chen et al., 2007), such as designing novel protein-protein interactions and drug discovery. Such a shift of research focus requires higher resolution protein models and transferable force fields (Shimada et al., 2001). Borreguero et al. devised an all-atom DMD model to study the thermodynamic structure of a short ten-residue peptide from an amyloid β polypeptide (Borreguero et al., 2005). The interactions were assigned according to the experimentally-determined hydrophobicity. Additional examination of the hydrophobicity-based force field with additional systems is necessary to assess the transferability. Zhou et al. have developed an all-atom DMD model to study the folding dynamics of proteins using a structure-based interaction function (Luo et al., 2007;Zhou et al., 2003). The built-in structural information hinders broader applications due to the lack of transferability. Here, we develop an all-atom DMD model with a transferable interaction function.

In the all-atom DMD force field, we use the van der Waals potential to model packing, and Lazaridis-Karplus effective energy (Lazaridis et al., 1999) to model solvation. We also explicitly model hydrogen bond interactions (Ding et al., 2003). Hydrogen bonds play a pivotal role in protein folding (Baldwin, 2007b;Rose et al., 2006b). It has been experimentally shown that hydrogen bonds stabilize globular proteins (Myers et al., 1996). Recent experimental evidence (Deechongkit et al., 2004a) suggests that stability contribution of a backbone hydrogen bond depends on its solvent-exposure in the native structure. Mutating backbone amides with esters in the WW domain, Deechongkit et al. (Deechongkit et al., 2004b) illustrated that a solvent-exposed hydrogen bond has a stability contribution of 1.0 to 2.0 kcal/mol while a buried hydrogen bond contributes as much as 3.1±1.0 kcal/mol to the stability. To model the environment-dependent hydrogen bond interaction, we assume that a hydrogen-bonded backbone peptide has a weaker desolvation energy (approximately 2 kcal/mol) than that of the non-hydrogen bonded one. As a result, the buried hydrogen bond will be effectively stronger than the solvent-exposed one, therefore, mimicking the environment-dependent effect.

Given the vast conformational space available to proteins, the ability to capture protein native states (Dinner et al., 2000) provides an important benchmark test for a computational sampling method. Using all-atom DMD method, we perform ab initio folding simulations (Yang et al., 2007) of six structurally diverse proteins: Trp-cage (20 residues; a mini α/β protein; PDB code: 1L2Y), WW domain (26 residues; the central three-strand β-sheet (GLY5-GLU30) of the all-β protein; PDB code: 1I6C), villin headpiece (35 residues; an all-α protein; PDB code: 1WY3), GB1 domain (56 residues; an α/β protein; PDB code: 1GB1), bacterial ribosomal protein L20 (60 residues; an all-α protein; PDB code: 1GYZ), and the engrailed homeodomain (54 residues; an all-α protein; PDB code: 1ENH). We demonstrate that our method enables proteins to reach the native or near-native states in all cases. For three small proteins: Trp-cage, WW domain, and villin headpiece, multiple folding transitions are observed and the computationally-characterized thermodynamics are in quantitative agreement with experiments. Due to the complex nature of protein folding and the fact that tested proteins are all small in size with relatively simple topology, we do not expect our method to fully resolve the protein folding problem. We do posit that our new all-atom DMD method can be used for the accurate sampling of conformational spaces of proteins and protein-protein complexes, which is crucial for protein engineering and design of protein-protein and protein-ligand interactions.

Results

The all-atom DMD method employs a united atom protein model, where heavy atoms and polar hydrogen atoms are explicitly modeled (Methods). We include van der Waals, solvation, and environment-dependent hydrogen bond interactions. We adopt the Lazaridis-Karplus solvation model and use the fully-solvated conformation as the reference state. The desolvation energy of each atom is decomposed into pair-wise interactions with its surrounding atoms. For example, unfavorable to be buried, a hydrophilic atom has repulsive Lazaridis-Karplus interactions with other atoms. For simplicity, we do not include the long-range charge-charge interactions in the current model. Due to the strong screening effect of solvent, charges far away have weak polar interactions. For salt-bridges, we expect the hydrogen bonds to partially account for their polar interactions. Similar neutralization of charged residues were also employed in the implicit solvent model of the effective energy function of CHARMM19 (Lazaridis et al., 1999). In DMD, the interaction potential between two atoms is a step function of their distance. We adapt the continuous energy functions of Medusa into step functions by mimicking the attractions and repulsions (Methods). The Medusa force field has been used to recapitulate the sequence diversity of protein folding families (Ding et al., 2006) and to predict protein stability changes upon mutation (Yin et al., 2007).

In modern molecular dynamics force fields, the hydrogen bond interaction is often modeled implicitly by the electrostatic interaction between dipoles. In contrast, our method explicitly models hydrogen bond formation (Ding et al., 2003) by effectively considering the distance and angular dependence of a hydrogen bond (Methods). To account for the environment-dependent effect of hydrogen bonds, we assign weaker solvation energy to a hydrogen-bonded backbone carbonyl oxygen atom compared to that of a non-hydrogen-bonded atom (Methods)

To efficiently explore the conformational space, we utilize replica exchange DMD (REXDMD) simulations (Methods). In REXDMD simulations, replicas perform DMD simulations at a given set of temperatures in parallel. The temperatures range from low to high. Periodically, replicas with neighboring temperature values exchange their temperatures in a Metropolis-based stochastic manner. Thus, each replica effectively follows a random walk in temperature space (Supplementary Figure S2). A temporarily trapped state in a replica can be rescued by simulating at a higher temperature, thereby enhancing the sampling efficiency of DMD simulations.

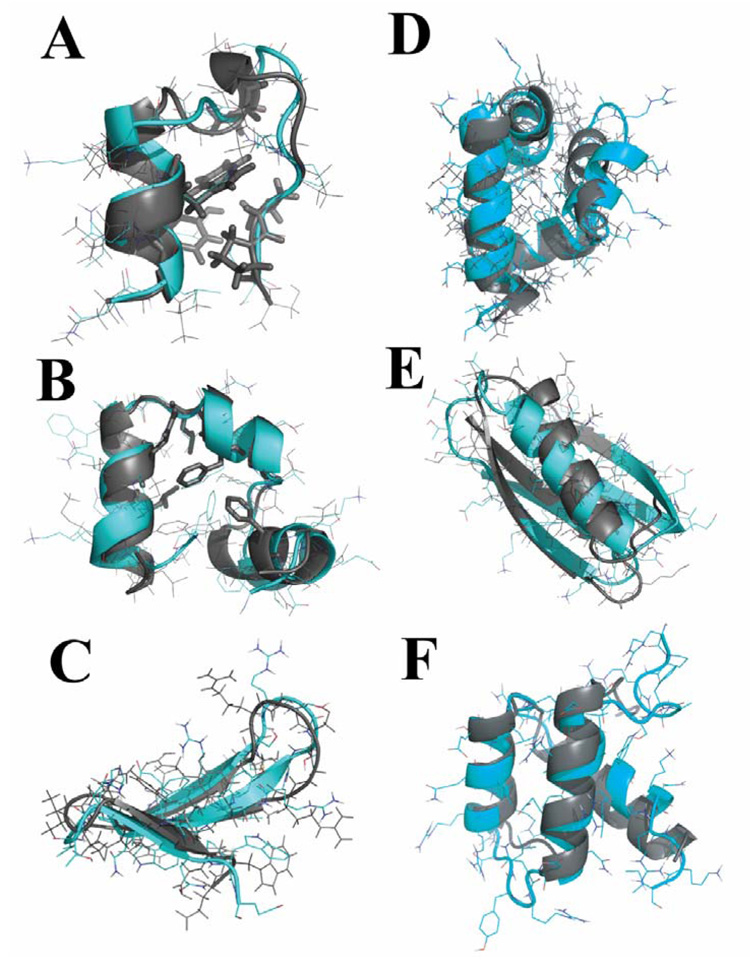
For each of the six proteins, we start from fully extended conformations and perform REXDMD simulations (Methods). Native or near-native conformations are observed for all six proteins in at least one replica of REXDMD simulations. In Fig. 1, the computational structures with the lowest root-mean-square deviation (RMSD) for the native states are aligned with corresponding experimentally-determined structures. For three small proteins (Trp-cage, WW domain, and villin headpiece), we observe multiple folding transitions in different replicas (e.g., the trajectories of Trp-cage folding in the Supplementary Fig. S2A), suggesting an equilibrium sampling of conformational space during DMD simulations. The remaining three larger proteins (GB1 domain, bacterial ribosomal protein L20, and engrailed homeodomain) take a long simulation time to reach the native or near-native states (Supplementary Fig. S1) and lack multiple folding/unfolding transitions. The folding transition into lowest-RMSD structures only occurs in one or two replicas, where temperatures remain low for the rest of the simulations. However, the ability of the all-atom DMD model to capture the native or near-native states in simulations for all six proteins highlights its predictive power.

Figure 1. Ab initio folding of six small proteins in all-atom DMD simulations.

(A) In the lowest-RMSD Trp-cage structure from simulations, the protein core is well packed and the sidechain rotamers of core residues (in stick representation) are also consistent with the NMR structure. The structure from simulations is in cyan and the one determined by experiments is colored in gray. The same color code is used in the following panels. (B) In simulations of villin headpiece, we find that the protein consistently folds to its native state with an average RMSD of 2–3Å. The core residues Phe₆, Phe₁₇, Leu₂₀, Gln₂₅, and Leu₂₈ are as closely packed against each other as they are observed in the crystal structure. For the WW domain (C) and engrailed homeodomain (D), the secondary structures from simulations align well with respect to the experimentally determined structures except that loops have larger deviations. In the simulations of GB1 (E) and bacterial ribosomal protein L20 (F), the near native states are observed in DMD simulations.

We use the weighted histogram analysis method (WHAM; see Methods) to compute the folding thermodynamics from REXDMD simulation trajectories. The WHAM method computes the density of states in a self-consistent manner (Kumar et al., 1992). An accurate estimation of the density of states requires sufficient data points along the reaction coordinates. Therefore, we do not attempt to determine the folding thermodynamics of GB1 domain, bacterial ribosomal protein L20, and engrailed homeodomain due to insufficient sampling in simulations. However, the achievement of equilibrium sampling of the three small proteins in REXDMD simulations enables us to study the folding thermodynamics of these three proteins and compare the results with experimental studies.

Trp-Cage

Trp-cage is a thermodynamically stable 20 residue mini-protein (Neidigh et al., 2001). Due to its simple topology and fast folding nature, Trp-cage has been successfully folded in computer simulations using different computational methods (Ding et al., 2005a;Pitera et al., 2003;Schug et al., 2005;Snow et al., 2002;Zhou, 2004), including DMD simulations of a simplified protein model (Ding et al., 2005a).

Starting from the fully extended conformation, the mini-protein is able to reach its native state (Fig. 1a). In the lowest-RMSD structure of the folded state in simulations (Fig. 1a), we find that the protein core is well packed and the sidechain rotamers of core residues are also consistent with the NMR structure. The protein folds consistently in all replicas (Supplementary Fig. S2A). For each replica, we observe multiple folding events during the simulations and the protein is able to fold early in the simulation (within 20,000 time units, Supplementary Fig. S2A), indicating that the Trp-cage is a fast folding protein (Neidigh et al., 2001).

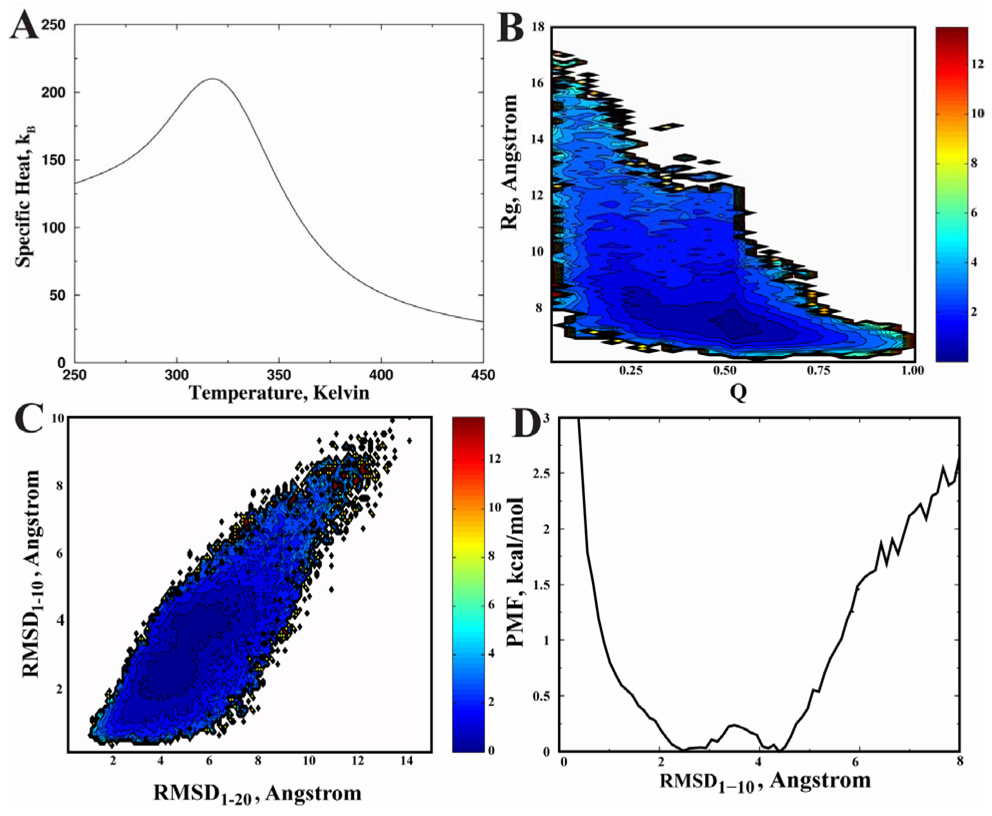
We use WHAM to analyze the folding thermodynamics (Fig. 2) from all the replica exchange simulation trajectories. We find that the specific heat of the protein features a broad peak at the temperature T_peak~320K (Fig. 2A). To closely examine the folding thermodynamics, we compute the two-dimensional potential mean force (2D-PMF) with respect to the fraction of native contacts (Q) and radius of gyration (Rg) at T=320K (Fig. 2B). Here, the contacts are defined by positions of C_β atoms and a cutoff distance of 7.5 Å is used. We find that the PMF features a broad peak with a wide range of Q values but compact dimensions. We also compute the PMF as a function of the RMSD of the N-terminal α-helix (1–10) and the whole structure at T=320K (Fig. 2C). Here, we choose the RMSD of the N-terminal α-helix as one of the reaction coordinates since we observe independent folding of the α-helix at high temperatures. At temperature T_peak (Fig. 2C), we find that the 2D-PMF has two basins that correspond to the folding/unfolding of the N-terminal α-helix. Interestingly, these two basins are almost interconnected. The 1D-PMF with respect to the N-terminal RMSD at T_peak shows that there is a small barrier (< 1 k_BT) for the N-terminal α-helix formation (Fig. 2D). At a lower temperature T=300K (Supplementary Fig. 2B), the 2D-PMF has only one basin, which features a wide spread of the RMSD (from 1.5 Å to 6 Å), corresponding to the non-cooperative docking of the C-terminal coil to the N-terminal α-helix. Therefore, our simulations of Trp-cage suggest that the protein features a small folding barrier, and thus, fast folding rate.

Figure 2. All-atom DMD simulation of the Trp-cage.

(A) The specific heat computed from simulations is shown as the function of temperatures. (B) The contour plot of the 2D-PMF at T=320K is plotted as the function of Q and R_g. The free energy difference between two consecutive contours is 0.6 kcal/mol in all contour plots. (C) The 2D-PMF at T=320K as a function of RMSD of the N-terminal a-helix (RMSD_1–10) and the whole structure (RMSD_1–20). (D) The 1D-PMF as a function of the RMSD_1–10 at T=320K.

Villin Headpiece

The villin headpiece is a 35-residue α-helical protein. It has been heavily studied experimentally (Buscaglia et al., 2005;Kubelka et al., 2003;Wang et al., 2003) and through computational simulations (Pitera et al., 2003;Schug et al., 2005;Snow et al., 2002;Steinbach, 2004;Zhou, 2004;Duan et al., 1998) since it is perhaps one of the smallest, fastest folding, and naturally occurring proteins. Folding-kinetics studies of villin headpiece in experiments indicated the existence of a biphasic folding kinetics (Kubelka et al., 2003). Further solid-state NMR studies suggests a two-step folding mechanism (Havlin et al., 2005). Several computational groups have been investigating the folding of villin headpiece using all-atom molecular dynamics simulations. Many of these computational studies were able to fold the protein with a RMSD from the native state of 3–4 Å. Notably, a recent MD simulation of villin headpiece (Lei et al., 2007) using a replica exchange sampling technique is able to reach the native state with sub-angstrom accuracy. Hence, this small protein serves an excellent benchmark for the test of all-atom DMD methods.

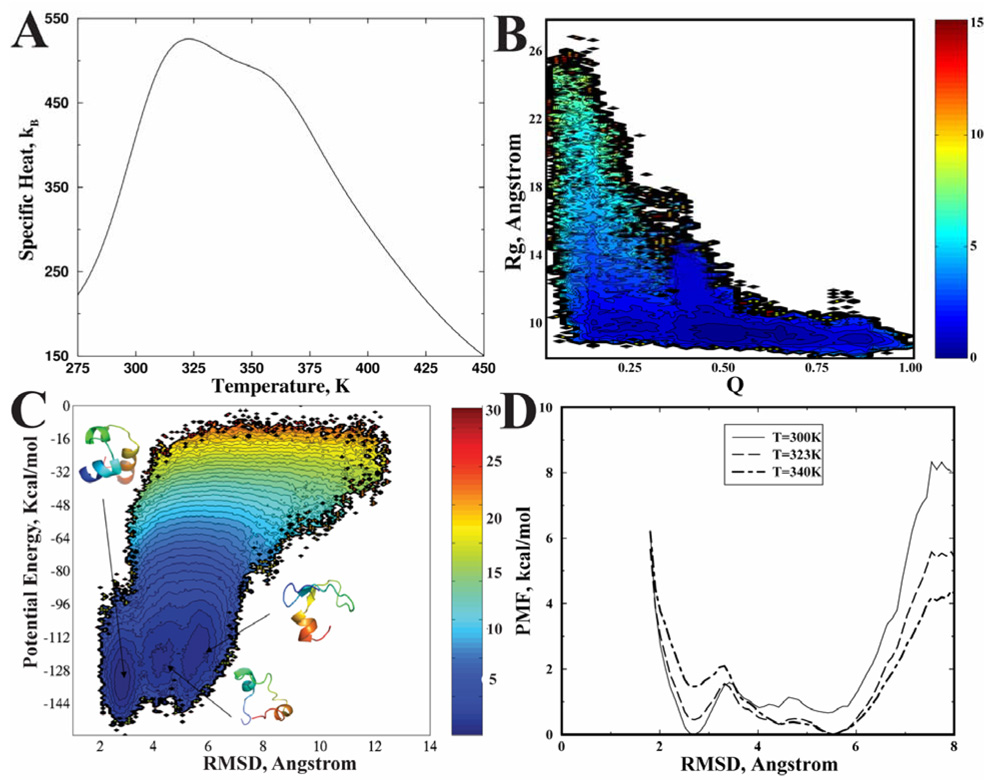
In the simulations, we find that the protein consistently folds to its native state with an average RMSD of 2–3 Å (Fig. 1b). The core residues Phe₆, Phe₁₇, Leu₂₀, Gln₂₅, and Leu₂₈ are as closely packed against each other as they are observed in the crystal structure. We perform WHAM calculations to analyze folding thermodynamics using the replica exchange simulation data. We calculate the specific heat as the function of temperature (Fig. 3A). Interestingly, we find that there is a shoulder near T=358K beside the major peak at T=323K, suggesting non-two state folding dynamics of the villin headpiece. We calculate the potential mean force as a function of RMSD at T=300K, T=323K, and T=340K (Fig. 3D). We find that at T=300K, the folded state is the dominate specie with the lowest free energy. At higher temperatures (T=323K, T=340K), the protein is mainly present in the denatured state (RMSD~5–6 Å), and there is a weak population of an intermediate state (RMSD~4–5Å). To better visualize the folding free energy landscape, we compute the 2D-PMF at T=323K as a function of Q and Rg (Fig. 3B). We find that there are three basins with high, medium, and low Q-values corresponding to folded, intermediate, and unfolded states, respectively. These states all feature a compact dimension with similar R_g values. Similarly, a 2D-PMF as a function of potential energy and RMSD at T=300K (Fig. 3C) also features the folding intermediate state. The typical conformations for the folded (F), denatured (D) and intermediate (I) states from the replica exchange trajectories are illustrated as inserts in Fig. 3C. The intermediate state features a compact conformation with partially folded helices. Therefore, the all-atom DMD simulations are able to recapitulate the folding dynamics of villin headpiece.

Figure 3. The all-atom DMD simulation of villin headpiece.

(A) The specific heat computed from simulations is shown as the function of temperatures. The contour plot of the 2D-PMF at T=323K is presented as the function of (B) Q and R_g, and (C) of potential energy and RMSD. The typical structures corresponding to the three basins are shown in cartoon representation. (D) The 1D-PMF at different temperatures (300K, 323K, and 340K) are shown as the function of RMSD.

WW domain

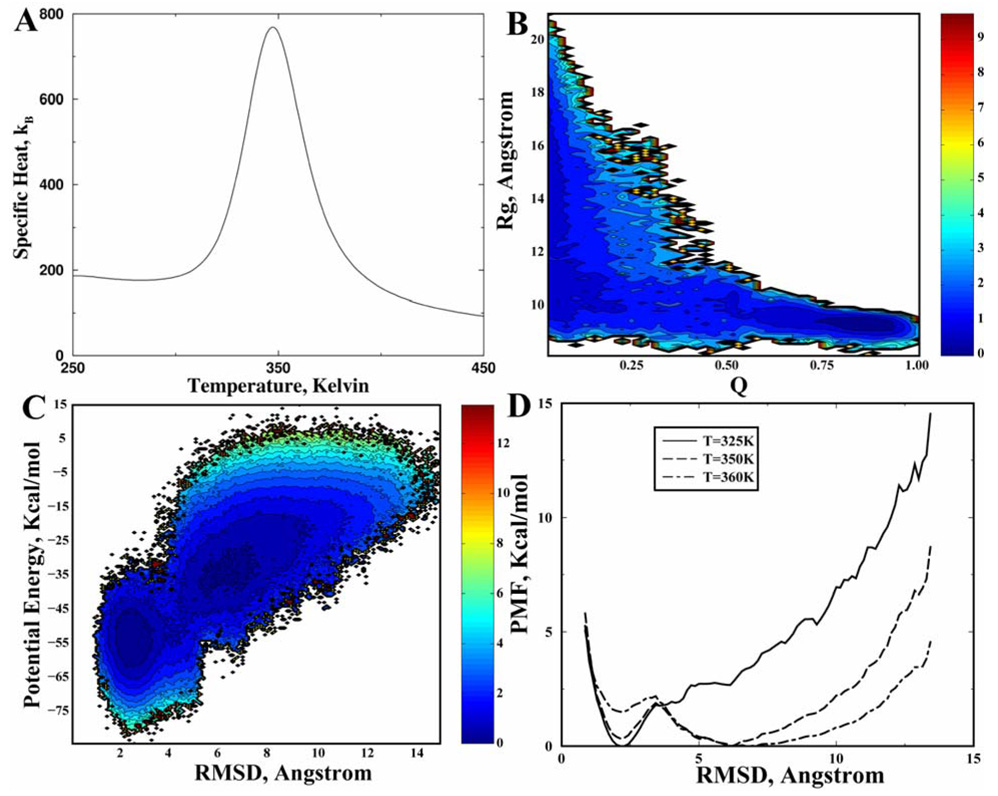
The full length WW domain is a three-stranded, all-beta protein with 39 residues. The termini of WW domains feature unstructured and flexible loops. In this study, we use the central three-stranded β-sheet with only 26 amino acids (GLY5-GLU30) as the reference structure. Starting from the extended conformation, we perform replica exchange DMD simulations. We find the specific heat of the WW domain (Fig. 4A) features a single sharp peak at T_f~350K, suggesting a two-state folding behavior. The folded state from the simulations is in agreement with the NMR structure (PDB code: 1I6C; Fig. 1c). We also compute the 2D-PMF at T=350K with respect to Q and R_g (Fig. 4B) and with respect to the potential energy and backbone RMSD (Fig. 4C). The 2D-PMF features two basins: a folded state with low energies, low RMSD, low R_g, and high Q along with an unfolded state with high energies, high RMSD, high R_g, and low Q. The inter-conversion between these two states results in a high specific heat. The 1D-PMF as the function of RMSD at temperatures near T_f also confirms two-state folding thermodynamics (Fig. 4D). Therefore, our simulations suggest that the WW domain folds in a highly cooperative two-state manner as observed in experiments (Ferguson et al., 2001;Ferguson et al., 2003).

Figure 4. The all-atom DMD simulation of the WW domain.

(A) The specific heat computed from simulations exhibits a sharp peak at T~350K. The contour plot of the 2D-PMF at T=348K is plotted as the function of (B) Q and R_g, and of (C) potential energy and RMSD. (D) The 1D-PMF at different temperatures (325K, 350K, and 360K) are shown as the function of RMSD.

We provide the movies of a folding event of WW domain as well as movies of villin headpiece and GB1 domain (http://dokhlab.unc.edu/research/Abinitio/). It is interesting that although the folding thermodynamics of WW-domain is two-state, a particular folding event features the initial formation of the first two β-strands. This is consistent with the experimentally observed kinetics where the first two strands are more ordered in the folding transition state than the rest (Deechongkit et al., 2004c). However, detailed comparison of folding kinetics between simulations and experiments requires systematic kinetic studies in the future.

Discussion

The contribution of backbone hydrogen bonds to protein stability has been controversial. Some believe that the peptide hydrogen bond is destabilizing since formation of intra-peptide hydrogen bonds break peptide-water hydrogen bonds despite desolvation of the backbone peptide (Honig et al., 1995;Yang et al., 1995). Others propose that backbone hydrogen bonds stabilize proteins given the experimentally observed α-helix propensity of short poly-alanine peptides at low temperatures (Baldwin, 2007a;Rose et al., 2006a). Kelly and co-workers (Deechongkit et al., 2004d) designed elegant experiments to target specific backbone-hydrogen bond donors or acceptors by mutating the backbone amides to esters. They found that indeed the disruption of a buried hydrogen bond destabilizes the proteins more than a solvent exposed hydrogen bond does, and the difference of ΔΔG can be as large as 2–3 kcal/mol. Such a difference can be explained by the redistribution of partial charges in the hydrogen bonded peptides, which in turn, affects their solvation energies. Such an environment-dependence effect of the hydrogen bond interaction can be readily modeled using the “reaction” algorithm for hydrogen bonds in DMD (Ding et al., 2003), where donors and acceptors change their types upon hydrogen bond formation (see Methods). With the environment-dependent hydrogen bond model, we are able to reach native or near-native conformations in DMD simulations of six proteins. As a control, we also perform DMD simulations without the solvent-dependent effect: With weak hydrogen bond strength (1–2 kcal/mol), proteins neither fold into specific structures nor form regular secondary structures. In contrast, a strong hydrogen (>3 kcal/mol) bond strength tends to fold proteins into all-α helices, including the natively all-β proteins (data not shown). Therefore, our study suggests that the environment-dependent hydrogen bond is important for protein folding.

Since multiple folding/unfolding transitions are observed for three small proteins, we are able to analyze the folding thermodynamics from simulations. We found qualitative agreement between the simulation-derived thermodynamics and experimental observations. In our simulations, we discover that native states always correspond to the lowest free energy state at room temperature (300K; Fig. 2–Fig 4). Although these native states often have low potential energies, there are still individual conformations with low potential energies but high RMSD values. This observation suggests that potential energy alone is not an appropriate reaction coordinate for protein folding. Hence, ensemble analysis of the protein conformations, such as clustering, is necessary for structure determination applications (Bradley et al., 2005b).

We attribute the success of the all-atom DMD method to its ability to rapidly sample protein conformational space. Proteins usually fold in the milliseconds to seconds range: the fast-folding Trp-cage protein was experimentally shown to fold within microseconds (~µs). During our simulations we find that this mini protein folds very rapidly, where the folding time is on the order of 10⁴ time units (10⁴ × 50 fs = 0.5 ns; see Methods), and multiple folding events are observed in all replicas (Fig. 2a). The observation of multiple folding events during Trp-cage DMD simulations is mainly due to faster protein dynamics in the absence of explicit solvent. The speed-up in this case is over 1,000-fold. Additionally, the application of replica exchange increases the conformational sampling efficiency (Okamoto, 2004). As a result, we are able to observe the folding of all six proteins to their native or near-native states within an accumulative 1.6×10⁷ time units in REXDMD simulations.

We believe that the success of the current model is also due to the fact that these six proteins are fast folders and their topologies are relatively simple. As the protein size increases and the topology becomes more sophisticated, longer simulations will be required and the folding of these proteins may become practically intractable, even in all-atom DMD simulations. For example, we do not observe multiple folding events of the relatively larger proteins (GB1 domain, bacterial ribosomal protein L20, and the engrailed homeodomain) in the DMD simulations due to the insufficient sampling. Therefore, a multi-scale folding method may be required where simplified protein models are used to sample the large scale conformational changes and the all-atom protein model is used to sample the conformational spaces at smaller time scales (Bradley et al., 2005a). The applicability of the current approach to folding of larger proteins requires further investigation.

Protein flexibility modeling with accurate sampling of the protein conformations near its native states is essential in protein design (Kuhlman et al., 2003), protein stability estimation (Yin et al., 2007), and protein-protein, protein-ligand designs (Kortemme et al., 2004). Due to the fast conformational sampling efficiency of DMD and the ability to capture the folding free energy landscape of proteins under study, we believe that the current all-atom model is able to rapidly and accurately sample the available conformations near the target states of proteins. We expect applications of the all-atom DMD method in protein engineering, protein-protein interface design, and protein-ligand design by combining the dynamics sampling method with protein design methods.

Methods

Discrete molecular dynamics

A detailed description of the DMD algorithm can be found elsewhere (Dokholyan et al., 1998;Rapaport, 1997;Zhou et al., 1997). Briefly, inter-atomic interactions in DMD are governed by square-well potential functions. Neighboring interactions (such as bonds, bond angles, and dihedrals) are modeled by infinitely high square well potentials. During a simulation, an atom’s velocity remains constant until a potential step is encountered, where it changes instantaneously according to the conservations of energy, momentum and angular momentum. Simulations proceed as a series of such collisions, with a rapid sorting algorithm employed at each step to determine the following collision.

The difference between discrete molecular dynamics and traditional molecular dynamics is in the interaction potential functions. Approximating the continuous potential functions with step-functions of pair-wise distances, DMD simulations are reduced to event-driven (collision) molecular dynamics simulation. The sampling efficiency of DMD over traditional MD is mainly due to rapid processing of collision events and localized updates of collisions (only collided atoms are required to update at each collision). At an adequately small step size, the discrete step-function approaches the continuous potential function and DMD simulations become equivalent to traditional molecular dynamics.

All-atom protein model

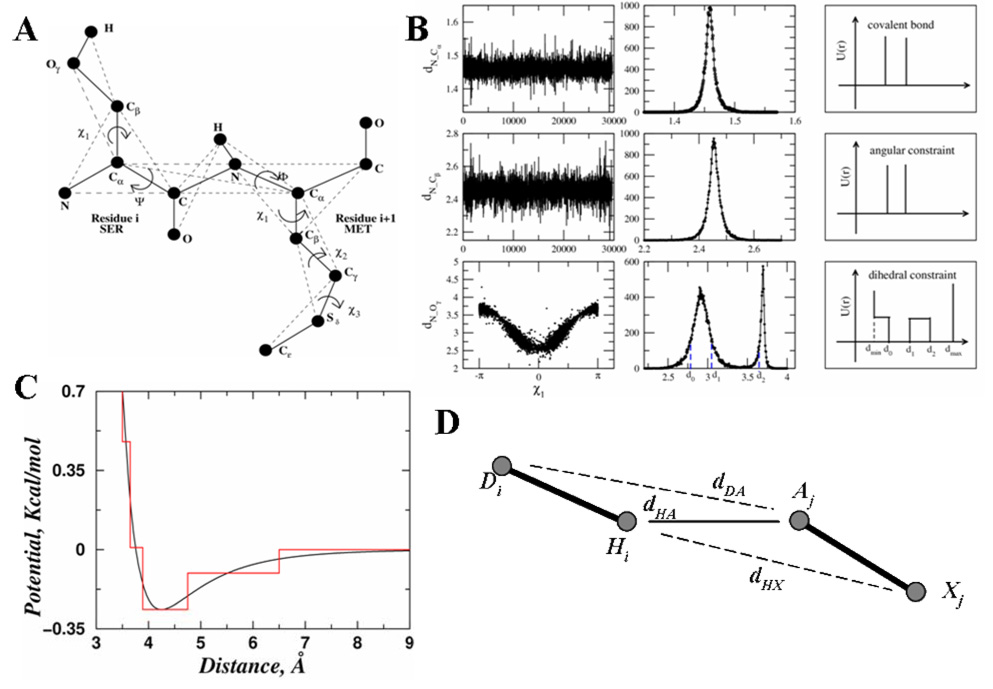
We use a united-atom representation to model proteins, in which all heavy atoms and polar hydrogen atoms of each amino acid are included (Fig. 5a). In order to maintain the protein backbone and sidechain geometries, we introduce three types of bonded constraints between neighboring atoms: (a) consecutive atoms (i, i+1) covalently bonded, (b) next-nearest neighbors (i, i+2) under angular constraints, and (c) atom pairs (i, i+3) linked by dihedral interactions. For covalent bonds and bond angles, we use a single-well potential (Fig. 5b) with two parameters: effective bond length d_AB, and its variance, σ_AB. The dihedral interactions are modeled by multi-step potential functions of pair-wise distance as introduced in Ref. (Ding et al., 2005a), which is characterized by a set of distance parameters, {d_min, d₀, d₁, d₂, d_max} (Fig. 5b). We obtain these parameters by sampling the corresponding distance distribution in a non-redundant database of high-resolution protein structures. These bonded interaction parameters are listed in the Supplementary Table S1. For the non-bonded interactions, we include the van der Waals (VDW), solvation, and hydrogen bond interactions (Ding et al., 2003):

Figure 5. The all-atom protein model.

(A) Schematic diagram for the all-atom protein model. Only two consecutive residues are shown. The solid thick lines represent the covalent and the peptide bonds. The thin dash lines denote the effective bonds which are needed either to fix the bond angles, model the sidechain dihedral angles or to maintain the planarity of the peptide bonds. (B) Parameterization of the bonded interactions for representative atom pairs. The first column shows the distribution of the distances in serine, between N-C_α, N-C_β and N-O_γ respectively. The second column shows the corresponding histogram for the distribution of each atom pair. The third column shows the resulting constraint potentials schematically. For bonds (e.g., N-C_α) and bond angles (e.g., N-C_β), the left and right boundaries of the constraint potential corresponds to d−σ and d+σ, respectively. Here, d is the average length and σ is the standard deviation of the distance distribution. (C) Parameterization of non-bonded interactions in all-atom DMD. The continuous red line corresponds to the van der Waals and solvation interaction between two carbon atoms. The black step function is the discretized potential for DMD. (D) A schematic for the hydrogen bonding interaction between hydrogen H_i and acceptor A_j. Atom D_i is the donor and X_j is the heavy atoms directly bonded to A_j. Besides the distance between hydrogen and acceptor d_HA, we also assess the auxiliary distances of d_DA (distance between atoms D_i and A_j) and d_HX (distance between atoms H_i and X_j).

VDW and solvation interactions

The VDW and solvation interactions are pair-wise functions of distances, while the hydrogen bond interactions are angular- and distance-dependent, making them multi-body interactions. Therefore, we combine the VDW and solvation together as the pair-wise interactions. We use a standard 12-6 Lennard-Jones potential to model the Van der Waals interactions: $E^{VDW}={\displaystyle \sum _{i,j>i}4{\epsilon }_{ij}[{({\sigma }_{ij}/r_{ij})}^{12}-{({\sigma }_{ij}/r_{ij})}^6]}.$ Here, the van der Waals radii σ_ij and interaction strengths ε_ij betweem atoms i and j are taken from CHARMM19 force field: ${\epsilon }_{ij}=\sqrt{{\epsilon }_i{\epsilon }_j};{\sigma }_{ij}={\sigma }_i+{\sigma }_j.$ We use the Lazaridis-Karplus (Lazaridis et al., 1999) solvation model:

$$\begin{array}{l}{E}^{LK}={\displaystyle \sum _{i,j>i}[-\frac{2\mathrm{\Delta }{G}_i^{\mathit{\text{free}}}}{4\pi \sqrt{\pi }{\lambda }_i{r}_{ij}^2}\text{exp}(-x_{ij}^2)V_i-\frac{2\mathrm{\Delta }{G}_j^{\mathit{\text{free}}}}{4\pi \sqrt{\pi }{\lambda }_j{r}_{ij}^2}\text{exp}(-x_{ij}^2)V_j]}.\\ x_{ij}=(r_{ij}-1.12{\sigma }_i)/{\lambda }_i;x_{ji}=(r_{ij}-1.12{\sigma }_j)/{\lambda }_j\end{array}$$

Here, parameters of reference solvation energy (ΔG^free), volume of atoms (V), correlation length (λ) and atomic radius (σ). are taken from Lazaridis and Karplus (Lazaridis et al., 1999). The discrete potential functions mimic the continuous potential $E_{ij}(d_{ij})=E_{ij}^{VDW}(d_{ij})+E_{ij}^{LK}(d_{ij})$ by capturing the attractions and repulsions (Fig. 5c). We keep the number of steps minimal since increasing the amount of steps reduces the computational efficiency of DMD. The discrete potential function is characterized by the hardcore distance d_hc and a series of potential steps {d_i, e_i}. Here, d_i is the distance where potential energy E has a step E(d_i−1,d_i)-E(d_i,d_i+1)=ei (d_hc<d₁<d₂<⋯<d_n). We use a cutoff of 6.5 Å as the interaction range between all atom pairs. Details of the discrete potential function are provided in the Supplementary Table S2.

Hydrogen bonds

We use the reaction algorithm to model the hydrogen bond interaction as described in Ref. (Ding et al., 2003). Briefly, after the formation of a hydrogen bond, the acceptor (A) and hydrogen (H) change their types to A' and H', respectively. The interaction potential between an atom and A(H) can be different from its interaction potential with respect to A'(H'). Thus, the formation of a hydrogen bond depends on its neighbors. To mimic the orientation-dependent hydrogen bond interaction, we introduce auxiliary interactions in addition to the distance-dependent interaction between the hydrogen and the acceptor (Fig. 5d). The auxiliary interactions are between the acceptor (A') and the donor (D), and between the hydrogen (H') and the nearest heavy atoms bonded to the acceptor (X). For example, once the hydrogen H_i and the acceptor A_j (Fig. 5d) reach the interaction range, we evaluate the distances between H_iX_j and D_iA_j which define the orientations of the hydrogen bond. The total potential energy change, ΔE, between H_i/A_j and other surrounding atoms are also evaluated before and after the putative hydrogen bond formation: $\mathrm{\Delta }E={\displaystyle \sum _{k\ne i,j}[E(A_i^{\text{'}},{\sigma }_k)-E(A_i,{\sigma }_k)+E(H_j^{\text{'}},{\sigma }_k)-E(H_j,{\sigma }_k)]+E_{HB}.}$ Here, σ_k is the other atoms. If these distances satisfy the pre-determined range and the total kinetic energy is enough to overcome the potential energy change ΔE, we allow the hydrogen bond to be formed, and forbid its formation otherwise. We include all possible interactions between backbone-backbone, backbone-sidechain, and sidechain-sidechain. The donors include backbone amide hydrogen atoms and sidechain polar hydrogen atoms of His, Trp, Tyr, Asn, Gln, Arg, and Lys. The acceptors include backbone carbonyl oxygens; sidechain oxygens of Asp, Glu, Ser, Thr, and Tyr; and the sidechain nitrogen of His. The interaction parameters of both donor-acceptor and auxiliary interactions are described in the Supplementary Table S3A.

Environment-dependence of hydrogen bonds

To model the environment-dependent effect, we assume that the hydrogen bonded peptide has weaker solvation energy than the non-hydrogen bonded backbone peptide. For simplicity, we use the carbonyl oxygen as the solvation center of a peptide. We assign a weaker reference solvation energy ΔG^free value (3.85 kcal/mol) to a hydrogen-bonded backbone carbonyl oxygen atom than that of a non-hydrogen-bonded atom (5.85 kcal/mol). In the Lazaridis-Karplus solvation model, it is unfavorable to bury a backbone carbonyl oxygen atom. The desolvation energy depends on its environment: the more it is buried, the higher the total desolvation energy. The formation of a buried hydrogen bond leads to a less unfavorable desolvation of the carbonyl oxygen, and thus, results in a higher potential energy gain ΔE than a solvent-exposed hydrogen bond. The environment-dependent hydrogen bond model features the multiple body interaction, which is akin to the polarizable force field. Therefore, this approach effectively models the environment-dependent effect of a hydrogen bond. The discontinuous potentials between a hydrogen bonded carbonyl oxygen atom and other atoms are listed in the Supplementary Table S3B.

Units in all-atom DMD

In the all-atom DMD simulations, the units of mass, length, and energy are dalton (1.66×10⁻²⁴ gram), angstrom (10⁻¹⁰ meter), and kcal/mol (6.9×10⁻²² joule), respectively. Given the units of mass [M], length [L], and energy [E], the time unit can be obtain as $[L]·\sqrt{\raisebox{1ex}{$[M]$}\!\left/ \!\raisebox{-1ex}{$[E]$}\right.},$ which is approximately 50 femtoseconds. The temperature unit is kcal/mol·k_B or 5.03×10² Kelvin, where k_B is the Boltzmann constant.

Replica exchange DMD

Efficient exploration of the potential energy landscape of molecular systems is the central theme of most molecular modeling applications. The ruggedness and the slope toward the energy minimum in the landscape govern sampling efficiency at a given temperature. Although escape out of local minima is accelerated at higher temperatures, the free energy landscape is altered due to larger entropic contributions. To efficiently overcome energy barriers while maintaining conformational sampling corresponding to a relevant free energy surface, we utilize the replica exchange sampling scheme (Okamoto, 2004;Zhou et al., 2001). In replica exchange computing, multiple simulations or replicas of the same system are performed in parallel at different temperatures. Individual simulations are coupled through Monte Carlobased exchanges of simulation temperatures between replicas at periodic time intervals. Temperatures are exchanged between two replicas, i and j, maintained at temperatures T_i and T_j and with energies E_i and E_j according to the canonical Metropolis criterion with the exchange probability p, where p=1 if Δ=(1/k_BT_i−1/k_BT_j)(E_j − E_i) ≤ 0,and p=exp(−Δ), if Δ > 0. In DMD simulations, we use an Anderson thermostat to maintain constant temperature in simulations (Andersen, 1980).

For each protein, we start from a fully extended conformation. We perform eight replicas with temperatures ranging from 0.50 (~250 Kelvin) to 0.75 (~375 Kelvin) with an increment of 0.035 (~17.5 Kelvin). Here, the temperature unit is kcal/mol·k_B or 5.03×10² Kelvin. The exchange takes place every 1×10³ time units. The length of each simulation is 2×10⁶ time units.

Weighted Histogram Analysis Method

We use the MMTSB tool (Feig et al., 2004) to perform WHAM analysis using replica-exchange trajectories. In short, the WHAM method utilizes multiple simulation trajectories with overlapping sampling along the reaction coordinates. The density of states ρ(E) is self-consistently computed by combining histograms from different simulation trajectories (Kumar et al., 1992). Given the density of states, the folding specific heat (C_v) can be computed at different temperatures according to the partition function, Z = ∫ρ(E)exp(−E/K_BT)dE. To compute the potential of mean force (PMF) as the function of reaction coordinate A, we compute the conditional probability P(A | E)of observing A at given energy E, which is evaluated from all the simulation trajectories. The PMF is computed as PMF(A) = −ln(∫P(A | E)ρ(E)exp(−E/K_BT)dE) + C. Here, C is the reference constant and we set it in such a way that the lowest PMF always corresponds to zero. Since our simulations start from fully extended conformations, we exclude the trajectories from the first 5×10⁵ time units and use those of the last 1.5×10⁶ time units for WHAM analysis. We use the trajectories from all replicas to compute the histograms.