Identification of repeat structure in large genomes using repeat probability clouds

Abstract

The identification of repeat structure in eukaryotic genomes can be time-consuming and difficult because of the large amount of information (~3×10⁹ bp) that needs to be processed and compared. We introduce a new approach based on exact word counts to evaluate, de novo, the repeat structure present within large eukaryotic genomes. This approach avoids sequence alignment and similarity search, two of the most time-consuming components of traditional methods for repeat identification. Algorithms were implemented to efficiently calculate exact counts for any length oligonucleotide in large genomes. Based on these oligonucleotide counts, oligonucleotide excess probability clouds, or “P-clouds”, were constructed. P-clouds are composed of clusters of related oligonucleotides that occur, as a group, more often than expected by chance. After construction, P-clouds were mapped back onto the genome, and regions of high P-cloud density were identified as repetitive regions based on a sliding window approach. This efficient method is capable of analyzing the repeat content of the entire human genome on a single desktop computer in less than half a day, at least 10-fold faster than current approaches. The predicted repetitive regions strongly overlap with known repeat elements, as well as other repetitive regions such as gene families, pseudogenes and segmental duplicons. This method should be extremely useful as a tool for use in de novo identification of repeat structure in large newly sequenced genomes.

1 INTRODUCTION

Eukaryotic genomes contain many repetitive sequence, and understanding genome structure depends crucially on their identification [1–3]. The predominant repeat annotation approach, implemented in RepeatMasker [4], focuses on the identification of repeat element sequences based on their alignment with consensus sequences, and relies on a curated library of known repeat families provided by Repbase [5]. This approach is presumably most effective for the human genome, which has attracted the greatest interest and the longest curation history, whereas the necessary libraries for more recently sequenced genomes may be substantially less complete or non-existent. It is unknown how effective this common approach is overall, however, as there is no “gold standard” to determine the proportion of true repeats that have been identified, and this approach has simply been implemented on an ad hoc basis.

Methods for the de novo analysis of repeat structure have also been developed to annotate repeat elements in newly sequenced genomes independent of an a priori established repeat library. Such approaches have been implemented in RepeatFinder [6], RECON [7], RepeatScout [8] and PILER [9]. These methods essentially construct a repeat library by assembling genome alignments, and use sequence similarity searches to annotate repeat elements in the genome (analogous to RepeatMasker). All require extensive computational effort and/or capability that limit the ability of individual genomic researchers to extensively investigate repeat structure, particularly for mammalian and other large genomes [10].

Repeat structure in large genomes has been analyzed without first constructing consensus repeat family sequences [11, 12], including the use of oligonucleotide (hereafter “oligo”) or l-mer similarity, rather than sequence similarity [13, 14], and analytical counting methods, such as RAP [15] and the method of Healy and colleagues [16]. There has been some statistical evaluation of oligo-based repeat region identification using these methods [15, 16], but no comprehensive genomic annotation approaches have been developed for oligo-based repeat analysis.

Here, we describe the implementation of a new approach for the identification of repetitive regions of large genomes using oligo frequencies. Our goal was to develop a fast algorithm for de novo identification of repeated structures applicable to entire eukaryotic genomes that could be reasonably implemented using existing desktop computers. The resulting approach is computationally efficient for analyzing large genomes and is effective at identifying repeat elements. The principle novelty behind our approach arises from the realization that repetitive elements are likely to have given rise to clusters of similar oligos, and that it may be statistically easier to detect clusters of related oligos than to determine whether each oligo is individually repeated more often than expected by chance.

To elaborate, duplicated sequences are identical at first, but will tend to diverge over time. Given this simple fact, it is clear that many duplicated sequences will be more closely related to each other than are random sequences, but perhaps not identical. Thus, it occurred to us that clusters of related sequences may be observed more often than expected by chance, and might be more easily detected than searching only for over-abundant identical sequences. Furthermore, it is not necessary to identify repetitive elements prior to assessing these clusters, or clouds, of related sequences observed at higher than expected frequencies. By tuning parameters of the process for assembling these clouds of related sequences, the stringency of the identification process can be controlled. If the oligos are long enough, individual oligo sequences belonging to over-represented clusters should have a high probability of originating from a duplication event.

There are three main steps to our approach: counting oligo occurrences in a genome, creating clusters of similar repeated oligos, and demarcating boundaries of predicted repeat structure in the genome based on the relative density of occurrence of repeated oligos. The algorithm that classifies repetitive oligos into clusters of related similar sequences that are observed more often than expected by chance is heuristic (ad hoc), and requires about as much computational time as the oligo counting method. We will refer to these clusters as “P-clouds”, or “probability clouds”, because we view them as loose clouds of potentially related sequences that probably would not have formed by chance. Once constructed, the P-clouds are mapped back onto the genome, and regions of high P-cloud density are demarcated (mapped) as repeat regions. The method is adjustable, with a controllable number of expected false positives, and annotations overlap with a diversity of repeated genomic regions based on empirical observations. The speed, accuracy and sensitivity of this new method were also evaluated.

2 METHODS AND ALGORITHM DESIGN

2.1 Counting the observance of oligo words

The first step in our method entails calculation of the number of occurrences of each specific oligo in a large genome, which is a moderate computational challenge. To determine a reasonable oligo length (W) for analyses of different length genomes (n), we used W = log₄ (n) + 1, which has reasonable sensitivity and specificity, assuming that oligo sequences are sampled approximately randomly [8, 15]. This rough approximation predicts that individual oligo words of length W are expected to occur less than 1 time in the genome by random chance. For example, mammalian genomes are typically around 3 billion base pairs (Gbps), and the expected oligo count for an oligo of length 16 is 0.7, assuming equal base frequencies. Note that this approximation is used only to choose an oligo length, and that later statistical assessments are based on observed dinucleotide frequencies.

A rapid approach for counting oligos in genomes is to use an integer counting array for every possible oligo “word”, and then increment the appropriate site in the array by one each time a particular word is encountered; we refer to this as the “direct count” method. This requires prohibitively large amounts of physical memory for long words. Modern computers commonly have 1 Gbyte (Gb) of physical memory (random access memory, or RAM), which limits oligo lengths to 13 (13mers) with this direct count method, regardless of the genome size. To analyze 16mers with this method would require over 16 Gb of RAM, well beyond the capacity of most current desktop computers.

We reduced RAM requirements for oligo counting in two ways, both of which capitalize on the fact that we were not interested in oligos observed less than twice. In the first method, the “mixed” approach, an array of bits corresponded to each oligo word. Since a single bit array can only count up to 1, a hash index was also included to count words that occur more than once. Under the assumption of equal nucleotide frequencies, fewer than 16% of oligos (0.155) are expected to be observed twice or more, and for unequal frequencies the number is even smaller. Nevertheless, for large genomes the memory size required for the hash plus the bit array exceeded 1 Gb in practice. Thus, when physical memory was full, the hash was copied to the hard disc and emptied. For analyses of human chromosomes 1 and X no memory dumps were required, and this mixed method was only slightly slower than the direct count method (see Results).

The size of the bit array limits the mixed method to 16mers or less if a 1Gbyte of RAM memory limit is imposed, so we also tested what we call the “overlap” method for longer oligos. This method relies on the fact that for a particular 17mer to have more than one copy in the genome, the 16mer corresponding to the first 16 nucleotides of the 17mer must also have more than one copy. If a hash of all 16mers with more than one copy is created, then it is necessary to create hash entries only for those 17mers that have a multi-copy 16mer beginning. The overlap method, therefore, requires successive passes through the genome, but can be extended to any length oligo. It requires many hash comparisons, however, and the second pass is much slower than the direct count method. Although we did not require the overlap method in the analyses presented here, it might be useful for some implementations (e.g., unassembled whole eukaryotic genomes). More extensive rationale and details of implementation for the counting methods (“direct count”, “mixed method”, and “overlap method”) are described in the Supplementary Materials.

The mixed method was used for all analyses other than the initial evaluation and comparison of the three methods. All speed calculations were assessed on human chromosome 1 using an affordable modern desktop computer (a single 3.0 Ghz Pentium processor, 1 Gb RAM, running RedHat Enterprise Linux 3.0 with kernel 2.4.21-20.ELsmp), unless otherwise noted.

2.2 P-cloud Construction

Prior to genome annotation, groups of similar oligos that occurred more often than expected by simple chance were clustered. For example, based on the assumptions of equal base frequencies and the Poisson distribution, the probability that any 16mer would occur by chance 10 times or more in a 3 Gbp genome is only 4 × 10⁻⁹, and the probability that any oligo will occur more than 10 times is only about 50%. The oligos that are high frequency by chance are unlikely to cluster, whereas in contrast oligos arising from the biological processes of duplication and divergence are likely to cluster. Thus, our basic presumption is that we might be able to use the tendency of biologically-related sequences to cluster as a means of predicting whether medium-frequency oligos arose from a duplication process. We refer to these oligo clusters as “P-clouds” because they involve cloud-like clusters of oligos that are not expected from simple probability calculations, and also because an approximation to this concept was suggested by Price and colleagues [8]. This step requires only the oligo counts, not the original genome sequence.

P-clouds were constructed using the highest-frequency oligo to initiate a cloud, then expanding the cloud by adding similar high-frequency oligos to form a P-cloud “core”. Here, “similar” was defined to mean differences of up to three nucleotides from a previously-identified core oligo (depending on the magnitude of the highest-frequency oligo), but the definition of “similar” and the definition of “high-frequency” were free parameters or adjustable “cutoffs” (see below). It is worth pointing out that our choices of parameters are ad hoc, in that there is no theory to establish the “optimal” parameter settings, and a good theory may not even be possible given that the best parameter choices will probably depend primarily on the unknown phylogenetic relationships of all the (mostly unknown) repetitive elements that make up a newly-sequenced genome. Preferred parameter settings for P-cloud construction were determined based on analyses of the sensitivity and accuracy estimated for each set of parameters (see below).

Multiple P-clouds were created by removing the oligos that belong to an identified P-cloud and repeating the core identification and core expansion process with the remainder until no oligos remained with counts greater than the “core cutoff”. The core cutoff (which was set at between 5 and 200 observations in different runs), and the numbers of repeats required for inclusion of oligos in a P-cloud were also separately adjustable parameters.

Following expansion of the P-cloud cores, the “outer” layer of each P-cloud was created by attaching any medium-copy oligos that were similar to an oligo in the core set. The “lower cutoff”, which ranged from 20 down to 2 copies, determined the definition of “medium-copy”, and thus which oligos were potentially included in the outer layer. Furthermore, the definition of “similar” varied among P-clouds, depending on the highest copy oligo in the core. For most P-clouds, a candidate oligo for the outer layer had to have only a single difference from a core oligo, but if a core oligo in the P-cloud had more than e.g., 200 copies (the secondary cutoff), a difference of two nucleotides was sufficient for inclusion. We also sometimes included an even higher tertiary cutoff (e.g., there must be an oligo with 2000 copies in the core layer) which would allow oligos with up to three nucleotides difference to be included. In the process of P-cloud construction, when a given oligo might have belonged to two or more different P-clouds, it was assigned to the P-cloud with the highest frequency oligo in its core.

The appropriate setting for the cutoffs depends predominantly on oligo length and the length of the genome segment under consideration, but also on how much divergence has occurred between the core oligos and related elements (i.e., how old the duplication events were that were responsible for the cloud). Most clusters of related oligos presumably arose from the duplication of repetitive elements, and thus will reflect the evolutionary history of those elements, but even within the same repetitive element family different regions of the repetitive element may have evolved differently. The core cutoff was chosen to conservatively identify repetitive clusters, while outer layer extension cutoffs were chosen to limit the size of the outer cloud, only extending it broadly in cases where the core sequences were particularly frequent, and thus likely to have spawned more copies of divergent nucleotides. Note, however, that since the method is designed to detect repetitive sequences in the absence of knowledge about repetitive element structure, and in the face of an unknown mixture of repetitive element phylogenetic histories, the choice of parameter settings is a purely empirical decision at present.

The parameter settings defining various cutoff values used in P-cloud construction are the lower and core cutoffs, and the three core sizes (primary, secondary and tertiary cutoffs) used to define outer layer extension distances. Suites of parameter settings are abbreviated by their core cutoff values: C⁵ (2, 5, 10, 100, 1000), C⁸ (2, 8, 16, 160, 1600), C¹⁰ (2, 10, 20, 200, 2000), C²⁰ (2, 20, 40, 400, 4000), C⁴⁰ (4, 40, 80, 800, 8000), C¹⁰⁰ (10, 100, 200, 2000, 20000), and C²⁰⁰ (20, 200, 400, 4000, 40000), with the numbers in parentheses referring to lower, core, primary, secondary and tertiary cutoffs, respectively.

Since we were not certain if simple sequence repeats (SSRs) would confound the construction of the P-clouds, low complexity oligos, such as one-, two-, three- and four-nucleotide tandem repeats, were excluded prior to P-cloud construction.

2.3 Repeat region annotation

Given an alignment of repeat elements in a repeat family, each consecutive oligo in the alignment would be ideally included in one P-cloud, and each repetitive element would be covered by consecutive P-clouds. In practice, we have found that related oligos from different repetitive elements often overlap each other, and that P-clouds contain oligos arising from multiple repetitive elements. Nevertheless, contiguous stretches of the genome containing many oligos that belong to P-clouds are more likely to have arisen from repetitive elements (or other repeated regions). Hence, high-density P-cloud regions are obvious targets for stronger prediction of repetitive element membership.

To identify high-density P-cloud regions, oligos that were members of P-clouds were mapped back to the original genome sequence, and segments of the genome with high P-cloud oligo density were demarcated as “repeated regions”. A smoothing algorithm was used to eliminate very short P-cloud stretches and merge short P-cloud gaps into otherwise dense P-cloud regions. Our criterion was that 80% of every ten consecutive oligos (using a sliding window) be comprised of P-clouds oligos, thus yielding a minimum demarcated region length of 25 bp if 16mer oligos are used. We chose the 80% P-cloud annotation criterion to prevent excessive false positives, but this criterion is fully adjustable in the program.

2.4 Comparison of annotation speed across programs

To compare the speed of repeat structure identification of the P-cloud method with other (non-word counting) de novo repeat identification tools [7, 8], we analyzed human chromosome X (123.8 Mbps). P-clouds were built from 14mer counts and then mapped to the chromosome according to the P-cloud assignment of each oligo to identify genomic repeat structure. Based on preliminary experimentation, parameter set C¹⁰ was used.

2.5 Sensitivity and accuracy estimation

For a range of P-cloud parameters, the relationship between sensitivity (the fraction of known repetitive elements detected) and accuracy (the presumed true-positive rate) was evaluated. The purpose was to identify the parameter settings that optimally balanced these two measures of performance, since preferred parameter settings are otherwise uncertain. Here, “detection” of a repetitive element was defined as overlap of an demarcated P-cloud region with a RepeatMasker-annotated region. While we note that there is no known exhaustive or comprehensive standard set of all segments of a genome that are derived from repetitive elements, RepeatMasker-annotated regions at least represent a minimal (i.e., conservative) set of likely repeat elements. To estimate the sensitivity of the P-cloud method, we calculated the proportion of known RepeatMasker-annotated repeat elements that were identified by the P-cloud method. To estimate the probability of false positive identification of repeat regions in human chromosomes 1 and X, we simulated a random genome sequence that was the same size as these two human chromosomes. This simulated dataset was constrained to have the same dinucleotide frequencies within 1Mbp windows as the original chromosomes. Repeat regions demarcated in this simulated data provide an estimate of the false positive rate of the P-cloud method. The “accuracy” of the P-cloud method is the proportion of estimated true repeat regions in the repeat demarcated regions (i.e., 1 − [false-positive rate] = accuracy).

2.6 P-cloud performance on known repeat sequences

To evaluate the fine-scale repeat mapping performance of the P-cloud method on real genomic data, we tested the identification success of the method on Alu elements. 100 known Alu elements were randomly chosen from human chromosomes 1 and X, and analyzed with the P-cloud method under various settings. The genomic location and classification of each Alu are listed in Supplementary Table S1. To visualize the results, a multiple sequence alignment of these Alu elements (and the flanking 15 bp segments) was assembled using ClustalX [17], and P-cloud density and demarcation were mapped along this alignment.

3 RESULTS

3.1 Computational efficiency of the P-cloud method

Because the P-cloud method begins with oligo counting, it appeared worthwhile to consider different possibilities for this simple initial task. A “direct count” method of memorizing counts for all possible 16-mers (the preferred size for mammalian genomes; see Methods) requires 4 Gb of RAM. Methods for counting and storing counts of oligos were therefore developed to facilitate analyses on standard desktop computers with only 1 Gb of RAM: these are the “mixed method”, and the “overlap method” (see Methods and Supplementary Materials).

The counting methods were applied to human chromosome 1 (245.5 Mbp), and the speed and memory requirements were compared with published results for other counting methods [8, 15]. The direct count method was the fastest (as expected) but limited to words of length 13 or less under the 1Gb memory constraint (Table 1). The RAP method uses a similar algorithm as our direct count method, and as expected achieves similar speeds (after compensating for different computer speeds and their use of dual processors) for words up to length 16, but requires 8 Gb of memory [15].

Table 1.

Comparison of computation required to count oligos in human chromosome 1.

Program	Algorithm	Oligo length	Speed (min/100 Mbp)	Hardware configuration
P-clouds1	direct count method	≤13	1.4	3GHz Processor, 1Gb RAM
	mixed method	14 ~ 16	6.0
	overlap method	≥17	+ 7.0 per additional nucleotide
RAP2	direct pattern index array	≤ 16	0.7	1U Dual Opteron 146 workstation, 8Gb RAM
Healy3	suffix tree and Burrows-Wheeler transform compression	any size	100	1GHz Dual Processor, 4Gb RAM

¹Algorithm descriptions for P-clouds methods are provided in the Supplementary Materials.

²RAP Method [15] (applied to the whole Caenorhabditis elegans genome and to mammalian genomes).

³Method of Healy and colleagues [16].

The mixed method (combining bit array and hash storage) worked well for oligos of length 16bp or less, but was about four-times slower than the direct count method (Table 1). Compared to the mixed method for oligos of length 16, the overlap method was half as fast for oligos of length 17bp, with linearly increasing computational time as oligo-word length increases (Table 1). In comparison, the suffix tree compression method of Healy and colleagues [16] should theoretically maintain similar speeds for oligos of any size, but our overlap method (compensating for differences in processor speeds) would be >10-fold faster for oligos of length 20, >2-fold faster for oligos of length 30, and of comparable speed for oligos of length 45. The memory required for the suffix tree method is also much larger than our 1Gb target memory size.

Based on these computation speed results, we subsequently used the mixed method for all analyses (oligos were length 15 or 16 bp). P-cloud construction and repeat annotation were performed on human chromosome X (123.8 Mbps) using 15 bp oligos to allow comparison with published results from the fastest current method, RepeatScout [8]. The time required to complete P-cloud analysis was 46 minutes; this includes the entire P-cloud process: constructing P-clouds, mapping P-clouds to the chromosome, and annotating repeated regions based on P-cloud density. This is relatively rapid compared to other methods, especially standard methods that do not employ word counting. There is no comparable report on the time required for RECON implementation on human chromosome X, but RECON required 39 hours to analyze a 9 Mbp segment of the human genome (less than 7.3% the size of the X chromosome; [7]). RepeatScout [8] is orders of magnitude faster than RECON, but required eight hours to analyze human chromosome X (P-clouds can be constructed for the entire human genome in that time). Thus, even including the ten minutes required to obtain repeat counts, the P-cloud method is about 10 times faster than the fastest existing approach.

3.2 Sensitivity and accuracy under varying P-cloud parameter settings

Human chromosomes 1 and X were analyzed based on 15mer P-clouds. Parameter settings were varied to identify the best set of parameters for further analyses. In total, 66,449,854 15mers were observed two or more times, and P-clouds were constructed after the exclusion of 154 oligos containing tandem repeated nucleotide patterns. The higher values assessed for the core and lower cutoffs appear overly strict, with relatively few oligos included in the P-clouds (Fig. 1). For lower cutoffs, the percentage of oligos included in P-clouds was far greater, up to almost 60% of all observed 15mers (Fig. 1).

Fig. 1. Percentage of multiple copy 15mers included in P-clouds under different parameter settings.

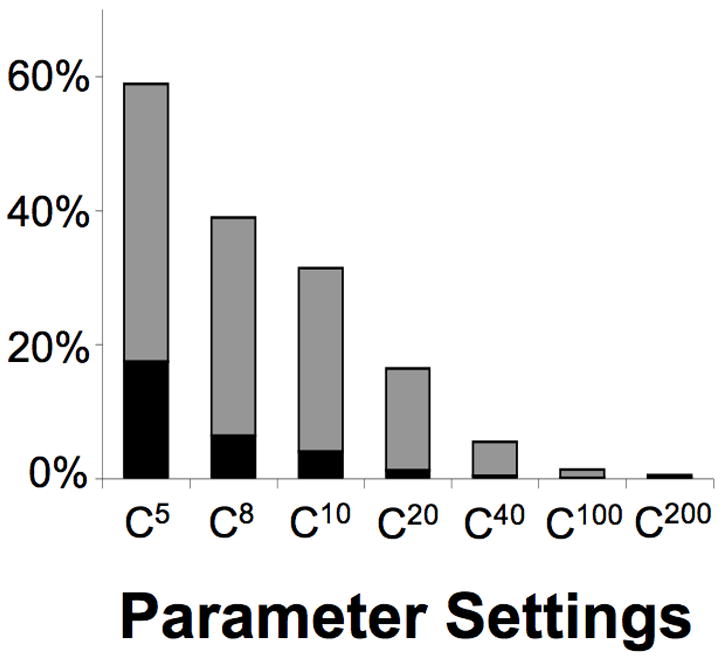
The percentage in the core layer is in black, and the outer layer in gray. Suites of parameter settings are abbreviated by their core cutoff values, as C⁵ (2, 5, 10, 100, 1000), C⁸ (2, 8, 16, 160, 1600), C¹⁰ (2, 10, 20, 200, 2000), C²⁰ (2, 20, 40, 400, 4000), C⁴⁰ (4, 40, 80, 800, 8000), C¹⁰⁰ (10, 100, 200, 2000, 20000), and C²⁰⁰ (20, 200, 400, 4000, 40000), with the numbers in parentheses referring to lower, core, primary, secondary and tertiary cutoffs respectively.

Based on detection rates in simulated sequences with the same dinucleotide structure as the human 1 and X chromosomes, the false positive rate for the P-cloud method is low (and thus the accuracy is high) under a broad range of parameter settings (Fig. 2). Even when the core cutoff was set as low as eight (C⁸), P-clouds maintained a false-positive rate < 4%. The sensitivity of the method for detecting RepeatMasker-annotated regions decreases substantially, however, when the core cutoff is set to larger values (Fig. 2). The relationship between accuracy and sensitivity suggests that different parameter settings may ideally suit different applications of the P-cloud method depending on the relative importance of exhaustive repeat annotation versus a minimal rate of false-positive annotations. The C⁸ parameter conditions appear reasonably conservative for basic analyses, and the simulated false-positive rate can be used for corrections.

Fig. 2. Accuracy and sensitivity of the P-cloud annotation under different parameter settings.

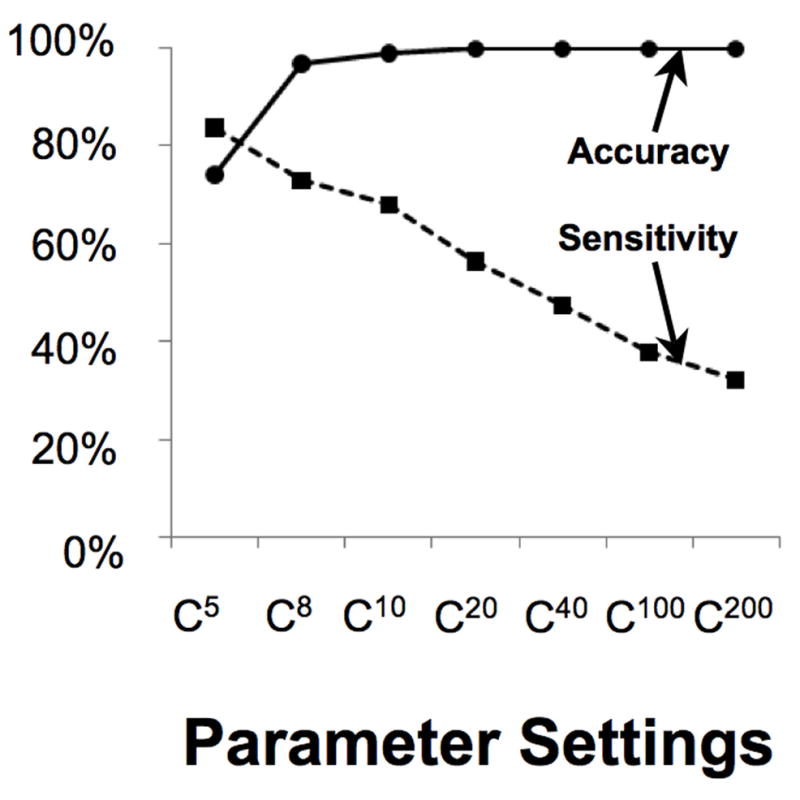
Accuracy is labeled with circles and a solid line, and sensitivity with squares and a dotted line. The parameter settings of each point are the same as in Fig. 1. Accuracy is one minus the estimated false-positive rate (based on whole genome simulation), and sensitivity is defined as the percentage of RepeatMasker repeat elements that were annotated by the P-cloud method.

3.3 Evaluation of P-cloud annotations on Alu elements

To more thoroughly evaluate the ability of P-cloud annotations to identify known repetitive elements, 100 random Alu elements were aligned and their average P-cloud coverage was assessed. Despite discontinuous initial P-cloud coverage of some regions (Fig. 3A), the secondary sliding window identification step substantially increases the continuity and consistency of the P-cloud repeat element mapping (Fig. 3B). Nearly 100% of all Alu element regions were identified as repetitive regions, even under the most stringent parameter settings (Fig. 3B). Based on these results, the P-cloud mapping and demarcation process appears effective, and known boundaries of Alu repeat elements are well-defined by the P-cloud predictions (Fig. 3B).

Fig. 3. P-cloud coverage of Alu elements.

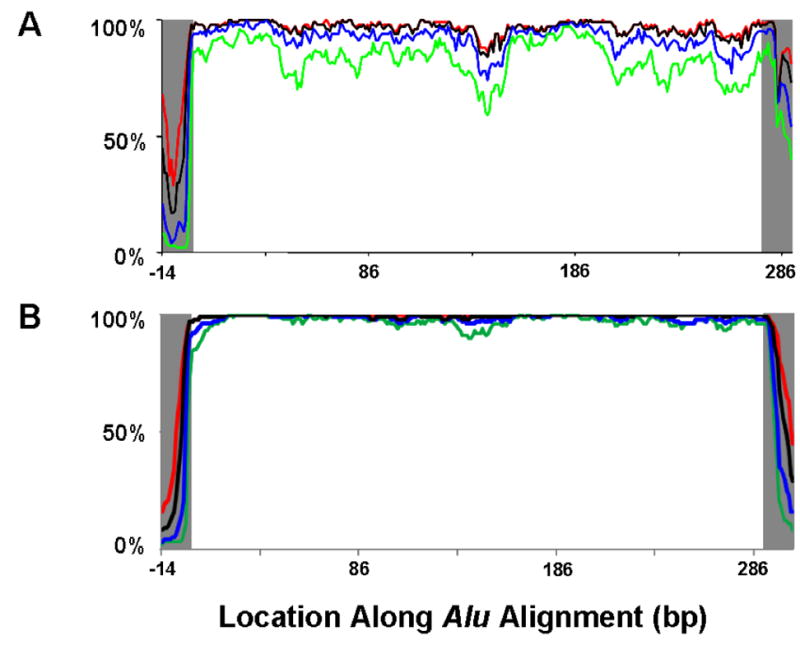
The percentage of 100 randomly chosen and aligned Alu elements (A) that belonged to P-clouds, and (B) that were annotated based on sliding window detection of contiguous P-cloud segments. These are shown for various P-cloud parameter settings: C⁵ (red), C¹⁰ (black), C⁴⁰ (blue), and C²⁰⁰ (green). The 15 bp flanking each Alu region were not re-aligned, and are shown in gray. Gray shading indicates the boundaries of Alu elements. Note that while the Alu alignment upon which these annotations were visualized was 292bp, the end of the white unshaded region in (A) marks the last 15mer that is pure Alu, at alignment site 292bp alignment - 15bp oligo length = 277bp, and the alignment ends at 292bp alignment + 15bp flank − 15bp oligo length = 292bp. In (B), each nucleotide is either annotated or not based on whether it is located in a contiguous region of P-clouds, so the grey region begins after the end of the alignment, at 293bp.

3.4 Overlap between P-cloud demarcations and RepeatMasker annotations on human chromosomes

P-cloud mapping of all repeat elements in human chromosomes 1 and X under C⁸ parameter conditions was compared to RepeatMasker annotations. Examples of strong overlap between P-cloud demarcations and RepeatMasker annotation of repetitive elements were numerous and clearly observable (Fig. 4). 38% of the genome was identified by both the P-cloud method and RepeatMasker (Fig. 5). 13.3% of the genome was identified by RepeatMasker but not P-clouds (Fig. 5), partly because the selected parameter settings may have been overly conservative. P-clouds usually identified at least part of each whole repeat elements, but occasionally missed parts of the more divergent regions (Fig. 4). Only 3.4% (22,547 of 663,879) of known repeat elements in human chromosomes 1 and X were completely missed by the P-cloud method.

Fig. 4. P-cloud and RepeatMasker annotation.

Two example regions are shown to compare P-cloud annotation of repeated regions (green) with RepeatMasker annotation of repetitive elements (black). The human genome browser views are based on the May-2004 version. Visualizations are from the UCSC genome browser.

Fig. 5. Overlap of P-cloud and RepeatMasker annotation in human chromosomes 1 and X.

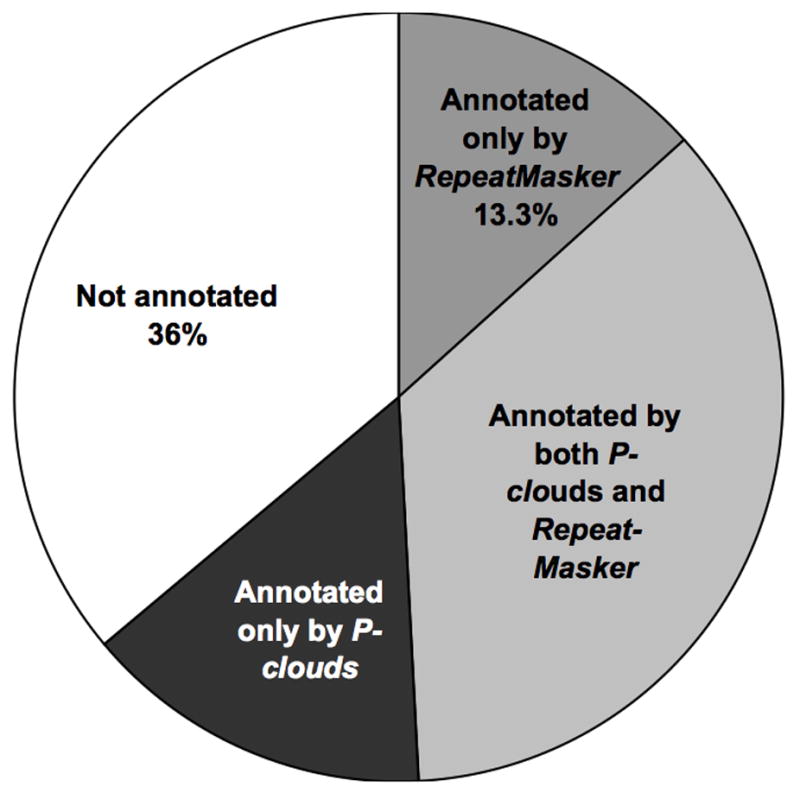
The percentages of the nucleotides in the genome annotated by either, both or neither method are shown.

Notably, 14.7% (58.74 Mbps) of human chromosomes 1 and X was mapped by the P-cloud method but not annotated by RepeatMasker. The P-cloud method was designed to identify repetitive regions that originate from any duplication events, not necessarily constrained to identifying only traditional repetitive or transposable elements (e.g., Alu), as is RepeatMasker. Thus, a portion of these regions identified by P-clouds but not by RepeatMasker may represent other duplicated sequences, such as tandem duplications, multi-gene families, and segmental duplications, and this is verified by empirical observations. There are many examples of strong overlap between P-cloud demarcated regions and multi-gene family members (Supplementary Fig. S1A), pseudogenes (Supplementary Fig. S1B), or segmental duplications (Supplementary Fig. S1C). Such regions represent, however, only a small fraction of the regions identified only by the P-cloud method.

It is an interesting question whether a substantial fraction of regions uniquely identified by P-clouds are repetitive elements that were previously unidentified. If so, it is possible that they may represent new repeat families not included in RepBase, but it is more likely that a notable fraction represent known repeat elements that the RepeatMasker procedure failed to annotate. While this is primarily a methods paper, and this question will be addressed in detail later, it is worth noting that the P-cloud method identified repeat structure in regions that have not been previously characterized as either known repeat families, gene families, pseudogenes or segmental duplications (Supplementary Fig. S1D). The hypothesis that P-clouds can help identify undiscovered repetitive elements is consistent with the observation that the region shown in Supplementary Fig. S1D was not annotated by RepeatMasker in the May 2004 human genome annotation that we originally used, but was subsequently annotated as a LTR element in the current release of the RepeatMasker annotation (March 2006). We note that we do not see any particular reason to believe that the RepeatMasker annotation of repetitive elements is itself completely exhaustive.

4 DISCUSSION

The P-cloud approach represents an attractive alternative tool for mapping of genomic repeat structure. It is capable of jointly analyzing two human chromosomes (1 and X) on a standard desktop computer in about two hours, and the entire human genome in less than half a day. It does not require prior assessment of repetitive element families, and is not restricted to identifying transposable elements. The false positive rate and sensitivity can be controlled by adjusting algorithm parameters, and thus may be set to best fit the goals of specific research applications. The P-cloud method is well-suited for de novo analysis of newly sequenced large eukaryotic genomes, and is likely to complement other methods in identification of new repeat families. It may also augment analyses of even well-characterized genomes such as that of humans, since it is possible that repeat libraries in RepBase may not be complete even for the intensively studied human genome [8].

The ability of the P-cloud method to rapidly conduct de novo repeat structure analysis for large complete genomes on a standard desktop computer is unique, providing a significant step towards making computational genomic research more tractable for a broader set of researchers. The method does not require large-scale alignments or a priori knowledge of repeat families, further extending its versatility. Instead, it relies on the observation that many repetitive families are fairly large, and that divergent evolution subsequent to duplication has created large clouds of related oligos. In contrast to consensus sequence matching algorithms used by existing annotation tools, the P-cloud method is effective even for relatively small repeated segments (as short as 25 bp, based on adjustable annotation criteria). The P-cloud approach rapidly identifies a majority of the repeat regions annoated by RepeatMasker, the latter of which required substantially more computation and extensive manual curation of repeat databases. Clearly, further research and empirical study is required to fully optimize the tuning of parameters, understand the false negative and false positive rates of parameter settings, and to more practically interpret the impacts of parameter settings within the P-cloud approach. Limited empirical analyses presented here (and more extensive unpublished empirical research) indicates that the method appears to work remarkably well in accurately predicting repeat structure, especially considering the tremendous (10–100 fold) increase in computational efficiency of the P-cloud method versus comparable repeat annotation methods.

The P-cloud method has clear potential for enabling more detailed dissection of repeat structure in eukaryotic genomes. Putative regions of repeat origin identified by P-clouds can be verified by alignment using standard methods, but the speed of P-clouds to work with newly-sequenced genomes has the potential to dramatically accelerate the repeat discovery and demarcation process. P-clouds may also be applicable for comparative analysis of repeat structure among multiple vertebrate genomes. Furthermore, it could easily be used for analysis of local repetitive structures in more moderately-sized genomic regions even prior to genome assembly, including regions cloned into bacterial artificial chromosomes (BACs), for which it can be important to have an immediate understanding of repeat structure prior to the development of genome-specific repeat libraries [18].

Although we have compared the P-cloud method primarily to other repeat identification tools, the basis of the method is designed to provide a broad perspective on how the process of duplication has shaped the content and structure of large genomes. Given its accuracy, efficiency, and flexibility, we expect that the availability of P-cloud maps will make complete comparative analysis of genomic repeat structure more accessible to a broader diversity of genomic researchers. This new computational feasibility should thus enable a new generation of in-depth genomic analyses contributing to our understanding of the function, diversity, and evolution of eukaryotic genomes.

Abbreviations used

oligo

oligonucleotide

RAM

random access memory

Gb

billion bytes

Gbp

billion base pair

SSR

simple sequence repeat

Mbp

million base pair

BAC

bacterial artificial chromosome