On the Interactions Between Top-Down Anticipation and Bottom-Up Regression

Abstract

This paper discusses the importance of anticipation and regression in modeling cognitive behavior. The meanings of these cognitive functions are explained by describing our proposed neural network model which has been implemented on a set of cognitive robotics experiments. The reviews of these experiments suggest that the essences of embodied cognition may reside in the phenomena of the break-down between the top-down anticipation and the bottom-up regression and in its recovery process.

Introduction

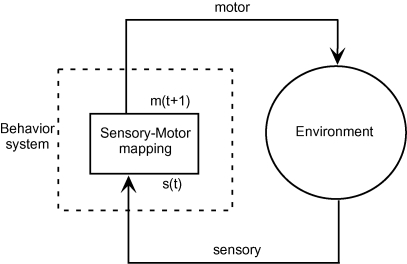
The ideas of embodied cognition (Varela et al., 1991) are now widely accepted after decades of dedicated researches in which the community of the behavior-based robotics (Brooks, 1999) and adaptive behaviors have largely contributed to the success of this trend. The core ideas of embodied cognition can be summarized as illustrated in Figure 1. It is said that cognitive behavior is the result of dense interactions between the internal process and the environmental processes by means of the tight sensory-motor coupling of them (Beer, 1995). In the actual implementations for behavior-based robots, the internal process is often merely a mapping process from sensory inputs to motor outputs where the mapping function might be acquired through evolution or learning processes. It has been argued that cognition of these robots are “situated” when certain stable dynamic structures are generated in the coupling of the internal process and the environmental dynamics. Although this view is straightforward and seems to capture some important aspects in behavior systems especially in the reflex behavior, we may wonder that the overwhelm of this simplified view may underestimate the essential problems of the embodied cognition.

Figure 1.

Sensory-motor coupling between behavior system and environment.

First of all, cognitive behavior is not just the results of iterations of sensory-motor mapping in adopted environments since it does not explain any of mental processes beyond perception and motor generation. It has been considered that behavior systems of mammal levels have anticipatory functions for future with utilizing internal models (Kawato et al., 1987). This anticipation can be either just for direct near future in implicit sensory-motor level or more explicit prediction for event sequences in longer future periods. The anticipation mechanisms enable the behavior systems to mentally simulate or plan for future (Tani, 1996; Ziemke et al., 2005). At the same time, the behavior systems may have regression mechanisms in order to re-interpret their own experiences from the past to the current time. The error between the reality and its anticipation can be utilized for modulating the internal parameter of the behavior systems in order to situate themselves to dynamically changing contexts. Therefore, it is better to consider that cognitive processes are time-extended both in past and future directions rather than limited to just current time sensory-motor reflex.

Although “internal models” have been prohibited words in the behavior-based robotics community (Brooks, 1991), we may argue that behavior systems without internal models are blind. The author and his colleagues have shown through a set of robotics experiments that internal models or representation can be well situated in behavior context if they can be acquired as self-organized dynamic attractors in the internal neuronal dynamics (Tani, 1996; Tani and Nolfi, 1999; Tani et al., 2004). Our thoughts in this point might be parallel to recent discussions by Steels (Steels, 2003) in which he claims that an exploration of adaptive “external” representations in terms of language might lead the research to go beyond physical behavior towards cognition although his approach seems to be much more computational than ours.

It is true that the internal models can never be a complete world model but be an only partial one. However, the errors by the internal models can tell the behavior systems at the least how much they are familiar or fit with the current situation and may, in hope, guide them to re-situate when they are lost in the current situations. In other words, the internal models can tell the boundary of rationality in terms of the predictability. On the other hand, the behavior systems without internal models merely continue to iterate sensory-motor reflex in the same way always without awareness of what are going on in the current situation. Since the rationality of any cognitive systems are bounded at the best in dealing with dynamic environments, certain meta-level cognitive functions of monitoring their own situations and conditions are inevitable. If we agree that the internal models are dispensable for any cognitive behaviors, the problem would be how to acquire them. The internal models should be acquired through direct experiences of the behavior systems and they should be organized in multiple levels from the lower sensory-motor flow level to the higher episode sequences level.

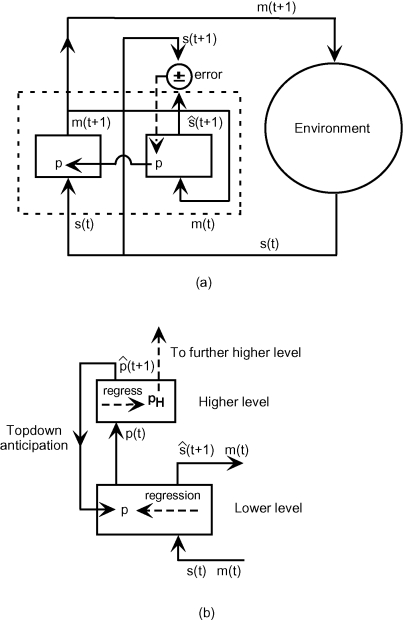
Figure 2a illustrates our ideas. The system has a motor generation part and a sensory anticipation part both of which are modulated by the internal parameters. The motor generation part is just a sensory-motor mapping function with the internal parameter. We can think of generating specific sensory-motor sequence patterns by setting their corresponding values into the internal parameters. This is like as if a specific behavior primitive or motor schema (Arbib, 1981) in repertory were retrieved by using a key of this internal parameter. The anticipation part is realized by a forward model (Demiris and Hayes, 2002; Kawato et al., 1987; Tani, 1996; Werbos, 1990; Wolpert and Kawato, 1998) where the sensory inputs of the next time step are anticipated based on the current motor outputs and the internal parameters. Then, one step after, the gap between the anticipation and the reality comes out as the error. This error is utilized to modulate the internal parameters by means of the inverse dynamics computation of minimizing the error through the forward model. This is the regression which proceeds in real time while the system interacts with the environment. It is assumed that the internal parameters can modulate only slowly compared to the time constant of the system. The modulation of the internal parameters means that the current behavior primitive is switched to others because it does not fit with the current sensation of the environment.

Figure 2.

(a) Behavior system with anticipation and regression mechanism. (b) Extension to multiple levels. m(t) and s(t) represent the current motor and sensory patterns. p represents the internal parameter which corresponds to the PB vector in the later sections.

Furthermore, the internal parameters can be fed into the next higher level (see Figure 2b). The higher level receives this internal parameters as the inputs and attempts to anticipate their future time developments as well as to regress for their past with having additional internal parameters of this higher level. The higher level is operated with much slower time constant and therefore the information processing in the higher level becomes abstracted. The anticipations of the inputs in the higher level are fed back to the lower level as the top-down signal from the higher level. Therefore, the internal parameters in the lower level are determined through dynamic interactions between the top-down anticipation from the higher level and the bottom-up regression from the lower level. This top-down and bottom-up interactions are one of the most essential characteristics in our proposed scheme by which continuous sensory-motor sequences are automatically segmented into a set of reusable behavior primitives, as will be detailed in the later section.

There have been various trials to utilize hierarchy in order to scale learning and generation capability of systems (Dayan and Hinton, 1993; Morimoto and Doya, 1998; Tani and Nolfi, 1999). In studies of reinforcement learning, it is proposed that the upper level decomposes the entire task into easier sub-tasks and that each sub-goal is achieved in the lower level in simulation defined in 2-D maze-like state space (Dayan and Hinton, 1993) and in robotics experiment with high-dimensional continuous motor space (Morimoto and Doya, 1998). The sub-tasks may correspond to behavior primitives and change of sub-goals do for that of the internal parameter in our proposed scheme. However, in these studies sub-tasks have to be learned as separated from whole task. This means that cues to segment whole task into sub-tasks are given by experimenters. On the other hand, (Tani and Nolfi, 1998) showed that hierarchically organized gating networks can segment sensory-motor sequences into behavior primitives through learning process. The segmentation can be achieved in the bottom-up way by introducing autonomous gating mechanism utilizing the prediction error (Wolpert and Kawato, 1998; Tani and Nolfi, 1998). However, the study (Tani and Nolfi, 1998) could not investigate the top-down and bottom-up interactions, which is the main interest in the current paper, because the system lacks the top-down pathway.

It is considered that embodied cognition requires two different aspects which seem to conflict with each other in various contexts. On the one hand, the sensory-motor processes have to deal with detailed interactions with the environment for the purpose of precise control of bodily movements. On the other hand, higher level cognition would require abstractions of those lower level sensory-motor processes, manipulating them compositionally for conducting goal-directed planning, inference, etc. This conflict is well represented by the symbol grounding problem by Harnad (Harnad, 1990), in which it is argued that symbol systems consisting of arbitrary tokens cannot be grounded because they are not constrained by physical interactions with the external world. We have, however, presumed that this gap might be reduced significantly if both share the same metric space of physical dynamical systems, and if dense bi-directional bottom-up and top-down interactions can be achieved there. For the purpose of elucidating the nature of bi-directional interactions by means of physical dynamics, the ideas shown in Figure 2 have been implemented on a specific neuronal dynamic model and its characteristics have been examined under various cognitive robotics experiments. By reviewing these experiments, the current paper will discuss what is required beyond the conventional ideas of the embodied cognition and the behavior-based robotics for the purpose of modeling human cognition including its metaphysical problems.

RNNPB

This section introduces our proposed model, recurrent neural network (RNN) with parametric biases (RNNPB) (Tani, 2003) which implements our ideas discussed in the introduction. The RNNPB is a variance of RNN models (Elman, 1990; Jordan, 1986; Pollack, 1991) which are good at learning temporal patterns by allowing re-entry of the internal activation state with allocating the so-called context units. Jordan (Jordan, 1986) showed that a simple attractor dynamics can be embedded in a RNN with utilizing its context units dynamics. Elman (Elman, 1990) and Pollack (Pollack, 1991) showed that the certain linguistic grammars can be learned by self-organizing fractal-shape attractor in the RNN dynamic structure. As inspired by these prior studies, we investigated the possibility of scaling RNNs with aiming that a set of behavior primitives are learned as embedded in multiple attractor dynamics of a single RNN by sharing the same synaptic weights among them. However, it turned out that multiple attractors of hosting different behavior primitives can hardly self-organize through training in the conventional RNN, as have been indicated by Doya et al. (Doya and Yoshizawa, 1989).

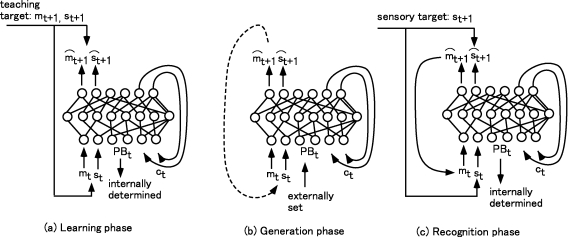
On this account, we proposed a novel scheme of the RNNPB as shown in Figure 3. In this scheme the parametric biases (PB) units are allocated in the input layer of the conventional RNN of the heavyside activation type. The PB works as bifurcation parameter of the network dynamics for switching among different subsequence patterns in a single RNN (Tani, 2003; Tani and Ito, 2003). The PB as bifurcation parameter actually corresponds to the internal parameter p in Figure 2. For a given PB vector, a specific sequence pattern is generated. On the other hand, the PB vector can be inversely computed to account for given input subsequence patterns through the regression by means of the error back-propagation scheme. This is actually the recognition process of the RNNPB. These explain an interesting mechanism of the RNNPB for both recognizing and generating the same subsequence patterns by the same encoding of the PB vector.

Figure 3.

The system flow of RNNPB in learning (a), generation (b) and recognition (c). Note that generation and recognition can be conducted simultaneously. PB_t and c_t denote the PB vector and the context activation state.

In the current implementation the generation and recognition processes are conducted simultaneously in the on-line operation of robots. The PB vector is constrained to modulate only slowly compared to change in the sensory-motor patterns and that in the context activation. By this means, it is aimed that the PB dynamics of slow time constant encode sequential changes of behavior primitives and that the context activation dynamics encode short-range sensory-motor profile of each behavior primitive.

Architecture

This section describes more details of the RNNPB.

The role of learning is to self-organize the mapping between the PB vector and spatio-temporal sensory-motor patterns. It is important to note that the PB vector for each learning pattern is self-determined in a non-supervised manner. In the learning phase, a set of sensory-motor patterns are learned through the forward model of the RNNPB by self-determining both the PB vectors, which are assigned differently for each pattern, and a synaptic weight matrix, which is common for all the patterns. The information flow of the RNNPB in the learning phase is shown in Figure 3a. This learning is conducted using both target patterns of motor pattern m_t and the sensory pattern s_t. When given m_t and s_t in the input layer, the network predicts their values at the next time step in the output layer as ${\widehat{m}}_{t+1}$ and ${\widehat{s}}_{t+1}$. The outputs are compared with their target values m_t+1 and S_t+1 and the error generated is back-propagated (Rumelhart et al., 1986) for the purpose of updating both the synaptic weights and PB vectors. C_t represents the context units where the self-feedback loop is established from C_t+1 in the output layer to C_t in the input layer. The context unit activations represent the internal state of the network.

After the learning is completed, the sensory-motor sequences can be generated by means of the forward dynamics of the RNNPB with the PB vectors of currently obtained as shown in Figure 3b. The PB vectors could be self-determined through the on-going regression processes as well as the top-down anticipation of them if the higher level network is implemented. In the generation process, the RNNPB can be operated in a closed-loop mode where the next step's sensory-motor prediction outputs are fed back to the current step as inputs, as denoted by a dotted line on the left-hand side in Figure 3b. In this way, the RNNPB can look ahead of imaginary sensory-motor sequences in future steps without receiving the actual sensory inputs from the environment.

Figure 3c illustrates how the PB vectors can be inversely computed for the given target sensory sequences in the regression process. The RNNPB, when receiving the current sensory inputs s_t, attempts to predict their next vectors, ${\widehat{s}}_{t+1}$, by utilizing the temporarily obtained PB vectors. In the next step, the error for this prediction outcome is obtained from the target value $s_{t+1}$ and it is back-propagated to the PB units and the current PB vectors are updated in the direction of minimizing the error with employing the steepest descent method. The actual computation of the PB vectors is conducted by using the so-called regression window of the immediate past steps. The error signal in the output layer is back-propagated through time (Rumelhart et al., 1986) to the PB vectors which is averaged over the window steps in order to make the PB vector modulated smoothly over time steps. The regression is iterated for order of 10–50 times for each step shift of the regression window in the forward direction. If pre-learned sensory sequence patterns are perceived, the PB vectors tend to converge to the corresponding values that were obtained in the learning phase.

In the actual implementation in the on-line operation of our robot platforms, the recognition of the past sensory sequences by the regression and the forward sensory-motor anticipation for future steps are conducted simultaneously. By means of this, the forward anticipation for near future is dynamically obtained based on the PB vector which is obtained as situated to the current sensory-motor sequences. Furthermore, the forward anticipation of the PB vector by the higher level allows the system to generate the future anticipation of sensory-motor sequences for longer steps. The introduction of the higher level will be revisited in the later section.

Adapting PB vector

Now, the exact mechanism for adapting the PB vector is described. The PB vectors are determined through regression of the past sequence pattern in both recognition and learning processes. In the recognition process, the regression is applied for the immediate past window steps L, by which the temporal profile of the PB, p_t from L steps before to the current step ct, is updated. The window for the regression shifts as time goes by while p_t is updated through the iterations in the on-line recognition process. In the learning phase the regression is conducted for all steps of the training sequence patterns. (This means that the window contains the whole sequence and it does not shift.)

The temporal profile of p_t in the sequence is computed via the back-propagation through time (BPTT) algorithm (Rumelhart et al., 1986; Werbos, 1990). In this computation ρ_t, the potential of the parametric bias, is obtained first.

The potential ρ_t changes due to the update computed by means of the error back-propagated to this parametric bias unit, which is integrated for a specific step length in the sequence. Then the parametric bias, p_t, is obtained by taking a sigmoid function output of the potential. The utilization of the sigmoid function is just a way of computationally bounding the value of the parametric bias to a range of 0.0–1.0. In this way, the parametric bias is updated to minimize the error between the target and the output sequence.

For each iteration in the regression of the window, L steps of look-ahead prediction, starting from the onset step of the window, are computed by the forward dynamics of the RNN. Once the L steps of the prediction sequence are generated, the errors between the targets and the prediction outputs are computed and then back-propagated through time. The error back-propagation updates both the values of the parametric bias at each step and the synaptic weights. The update equations for the ith unit of the parametric bias at time t in the sequence are:

$$\delta {\rho }_t^i=k_{bp}·{\displaystyle \sum _{\text{step}=t-l/2}^{t+l/2}{\delta }_t^{b{p}^i}}+k_{nb}({\rho }_{t+1}^i-2{\rho }_t^i+{\rho }_{t-1}^i)$$ (1)

$$\Delta {\rho }_t^i=\epsilon \cdot \delta {\rho }_t^i+\eta \cdot \Delta {{\rho }^{\prime }}_t^i$$ (2)

$$p_t^i=\text{\hspace{0.17em}sigmoid}({\rho }_t^i/\zeta )$$ (3)

where t sweeps from the onset of the window L - t_c to the current step t_c in the on-line operation. In Equation (1), δρ_t, the delta component of the potential of the parametric bias unit, is obtained from the summation of two terms. The first term represents the summation of the delta error, ${\delta }_t^{b{p}^i}$, in the parametric bias units for a fixed time duration l which should be much smaller than L. ${\delta }_t^{b{p}^i}$, which is the error back-propagated from the output units to the ith parametric bias unit, is summed over the period from t - l/2 to t + l/2 time steps. By summing the delta error, the local fluctuations of the output errors will not affect the temporal profile of the parametric bias significantly. The parametric bias should vary only with structural changes in the target sequence. Otherwise it should become flat, or constant, over time.

The second term plays the role of a low pass filter through which frequent rapid changes of the parametric bias are inhibited. k_nb is the coefficient for this filtering effect. ρ_t is updated based on δρ_t obtained in Equation (1). The actual update Δ ρ_t is computed by utilizing a momentum term to accelerate convergence as shown in Equation (2), where Δ${\acute{\rho }}_t^i$ denotes the update in the previous iteration. Then, the current parametric bias p_t is obtained by means of the sigmoidal outputs of the potential ρ_t divided by ζ in Equation (3). ζ denotes the steepness parameter of the sigmoid output which is usually set as 1.0 as default.

Although number of the PB units seem to enhance memory capacity of the RNNPB, the detailed relation has not been obtained yet. Our preliminary examination showed that there is a tendency of losing generalization capability in learning if the number is increased. In the later described experiments, 4 PB units are allocated.

Cognitive Robotics Projects

In this section, two different cognitive robotics experiments are reviewed. The first experiment introduces a task of imitative interaction by a humanoid robot in which a single level RNNPB is utilized. This experiment examines how the current interactive situations are recognized and how their corresponding motor sequence patterns are generated simultaneously. The second experiment introduces a task of object handling by an arm robot. In this task, problems of self-organization of behavior primitives and chunking as well as the on-line behavior plan generation and modulations are investigated with utilizing the RNNPB model with the two levels structure.

Imitative interactions

Experimental studies of the imitative interactions (Ito and Tani, 2004) between robots and humans were conducted by using a humanoid robot built by Sony (see Figure 4).

Figure 4.

A user is interacting with the Sony humanoid robot.

In this experiment, the robot learns multiple movement patterns shown by a user's hand movements in the learning phase. The RNNPB shown in Figure 3 learns to anticipate how the positions of both the user's hands change in time in terms of the sensory mapping from s_t to s_t+1 and also it learns how to change the motor outputs correspondingly in supervised ways. The positions of the user's hands are sensed by tracking colored balls in his hands. In the interaction phase, when one of the learned movement patterns is demonstrated by the user, the robot arms are expected to move by following the pattern. When the hand movement patten is switched from one to another, the robot arm movement pattern should switch correspondingly. This sort of on-line adaptation can be done by conducting the generation and the recognition processes simultaneously as a mirror system. When the prediction of the user's hand movement generates error, the PB vector is updated to minimize the error in real time while the motor outputs are generated depending on the current PB values.

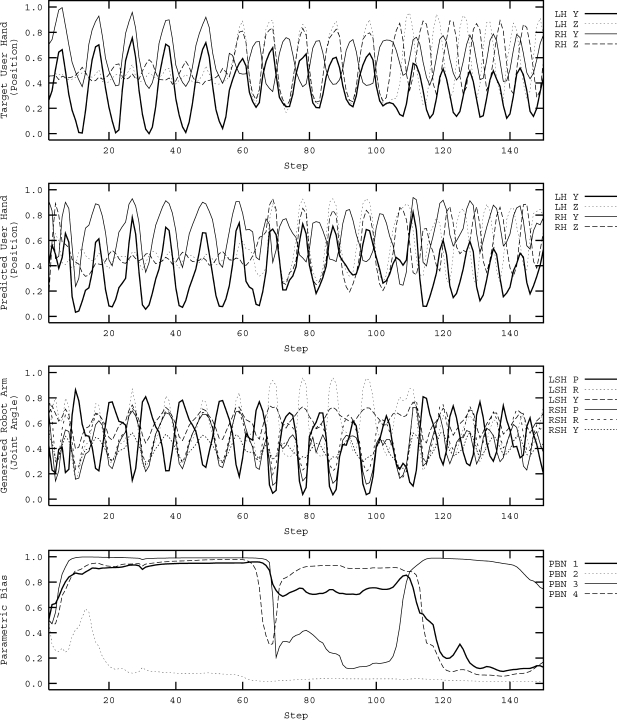
The results of the experiment are plotted in Figure 5. It is observed that when the user hand movement pattern is switched from one of the learned patterns to another, the patterns in the sensory prediction and the motor outputs are also switched correspondingly by accompanying substantial shifts in the PB vector. Although the synchronization between the user hand movement pattern and the robot movement pattern is lost once during the transitions, the robot movement pattern is re-synchronized to the user hand movement pattern within several steps. The experiments also showed that once the patterns were synchronized they were preserved robustly against slight perturbations in the repetitions of the user's hand movements. Our further analysis concluded that the attractor dynamics system, with its bifurcation mechanism via the PB, makes the robot system manipulatable by the users as well as robust to possible perturbations.

Figure 5.

Switching of the robot movement pattern among three learned patterns as initiated by switching of user hand movement.

RNNPB with multiple levels for chunking

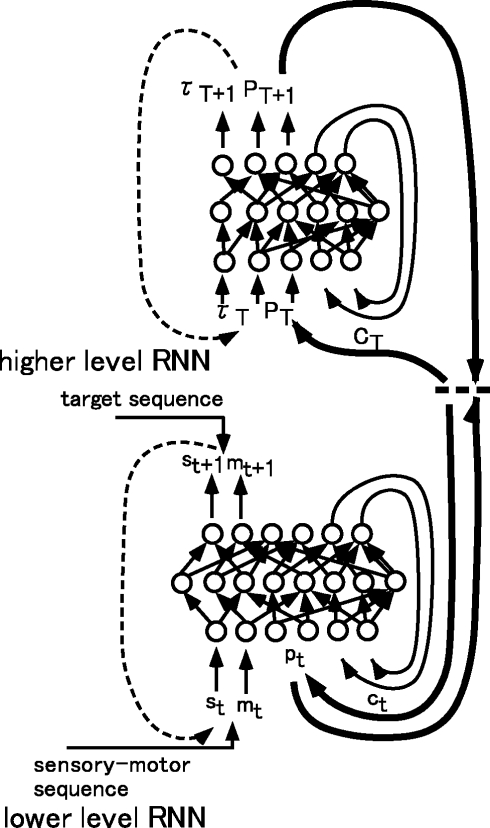
The RNNPB is extended to have multiple levels by which it can deal with generation and recognition of more complex behavior patterns. Figure 6 shows the extended architecture. The higher and lower level RNNs are bi-directionally interfaced using the PB vector. The prediction of the PB vector sequences generates a top-down plan of motor sequences while recognition of the sensory flow generates PB vector feedback corresponding to the actual experience in the environment. The following will describe how we addressed the problems of chunking in sensory-motor flow by learning, the bottom-up and top-down interactions between the levels in behavior generation.

Figure 6.

The complete architecture of hierarchically organized RNNPB. P_T: the PB predicted in the higher level interacts with p_t: the PB inversely computed in the lower level.

Chunking of sensory-motor flow through iterative learning

The experiments were conducted for the task of simple object manipulation using an arm robot of 4-DOF. In this task, the robot perceives the center position of the object and the arm tip position by the robot camera as the sensory inputs. The extended RNNPB with two levels is forced to learn multiple behavior tasks in a supervised manner. Each task consists of a sequence of behavior primitives, such as approaching an object, pushing it, and then returning to the home position. There is no prior knowledge about those primitive in the networks but the experimenter demonstrates them to the robot in terms of their combinational sequences. It is also noted that there are no signs for segmentation of the primitives in the continuous sensory-motor flow which the robot is exposed to learn. The network has to discover how to segment the flow of the on-going task by attempting to decompose the sensory-motor flow into a sequence of segments (behavior primitives) which are reusable in other tasks to be learned. The actual learning of the network are conducted with using seven training task sequences. The connection weights in the both nets are initialized with random values with range from -0.1 to 0.1 in the beginning of the learning.

In the current implementation of the PB regression, one minor modification is made. The PB vector receives the pressure to be modulated toward either extremes of 0.0 or 1.0 by setting ζ as a smaller value than 1.0. This alternated scheme enables the PB values to change stepwisely in the segmentation points. When at the least one element of the PB vector changes its value stepwisely with crossing 0.5, the higher level recognizes this as the moment of segmentation. In the learning process of the lower level, the PB sequences are generated as the results of the segmentation by means of the regression which are used for the training of the higher level. The forward computation of the higher level RNN proceeds along with T of the event step accompanied by the segmentation (the event step in the higher level proceeds to next step in the timing of the segmentation occurrence). The higher level learns to predict the next PB vector to switch as P_T+1 with its timing accompanied by the segmentation denoted as τ_T+1.

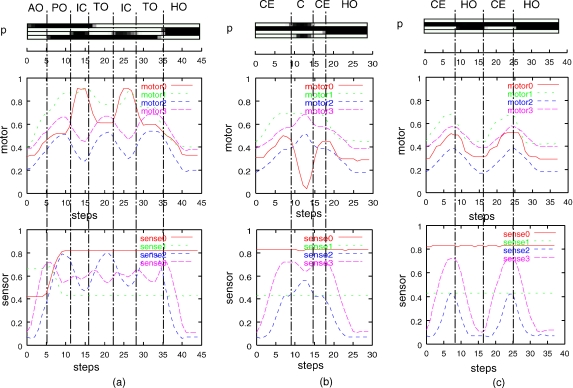
Figure 7 shows how the PB sequences are generated in the learning results, for three of representative training sensory-motor sequences out of seven. The plots in the top row in this figure show the activation of four parametric bias units as a function of the time step; the activation values from 0.0 to 1.0 are represented using the gray scale from white to black, respectively. The plots in the second and the third rows represent the temporal profile of motor and sensor values for each training sequence. The vertical dotted lines indicate the occurrence of segmentation when the behavior sequence switches from one primitive to another in generating the training sequence. The capital letters associated with each segment denote the abbreviation of the corresponding primitive behavior. In this figure, it is observed that the switching of bit patterns in the parametric bias takes place mostly in synchronization with the segmentation points known from the training sequences although it is observed that some segments are fragmented. Our examinations for all the trained sequences showed that the bit patterns in the parametric bias correspond uniquely to primitive behaviors in a one-to-one relationship in most cases. They are shown in Figure 7 with the following abbreviations. AO, approach to object in the center from the right-hand side; PO, push object from the center to the left-hand side; TO, touch object; IC, perform inverse C shape; HO, go back to home position; CE, go to the center from the right-hand side; and C, perform C shape.

Figure 7.

For the three representative training sequences (a)–(c), the temporal profiles of the parametric bias, the motor outputs are plotted in the second row and the sensor inputs are plotted in the third row. The vertical dotted lines denote occurrence of segmentation when the primitive behaviors switched. The capital letters associated with each segment denote the abbreviation of the corresponding primitive behavior.

Dynamic motor plan adaptation through bottom-up and top-down interactions

The actual behavior of the robot is generated through the dynamic interactions between the top-down pathway, based on look-ahead prediction of the PB sequences in the event step, and the bottom-up pathway, based on the regression of the PB for the sensory flow of actually experienced. More specifically, the current PB vector is iteratively updated by summing both signals derived from the PB prediction in the higher level and the error back-propagated in the regression of the actual sensory flow in the lower level.

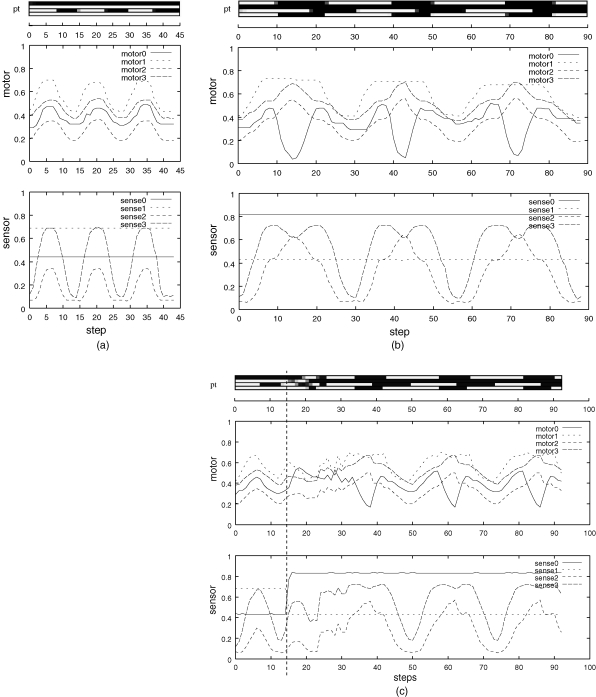
We examined how action plans can be dynamically adapted due to changes in the environment by going through bottom-up and top-down interactions (Tani, 2003). In the new experiment, the robot learns to generate two different behavior sequences depending on the position of the object which is perceived as one of the sensory inputs. When the object is perceived in the center on the task space, the robot has to perform the task-A in which the arm repeatedly approaches the object and returns to the home position periodically, as shown in Figure 8a. When the object is perceived on the left-hand side of the task space, the robot has to perform the task-B in which the arm repeats a sequence of centering, making a C-shape, and then returning home, as shown in Figure 8b.

Figure 8.

Profiles of task-A and task-B are shown in (a) and (b), respectively. (c) shows the profile of the dynamic switching from task-A to task-B, where a dotted line indicates the moment when the object is moved from the center to the left-hand side.

The learning of these two tasks were attempted by training only the higher level with utilizing the behavior primitives learned in the lower level in the previous experiment. The lower level was not re-trained in this new experiment. After the learning was converged, it was shown that the robot can generate either of the behavior sequences correctly depending on the position of the object, center or left-hand side. When the robot starts to move its arm, the PB vector in the initial event step is inversely computed to account for the sensory inputs of representing the current position of the object as well as the current position of the hand tip. The two different situations concerning the object position generate two different PB vector in the initial event step which are followed by the corresponding PB sequences learned in the higher level. However, our current interest is to examine what would happen if the position of the object is switched from the center to the left-hand side in the middle of the task execution. The question is that if the behavior plans as well their executions can be dynamically adapted to the sudden situational changes through the process of the bottom-up and the top-down interactions.

The experiment showed that in the initial period the task-A behavior patten is generated stably by following its mental plan. When the object is moved from the center to the left-hand side, the anticipation of the sensory inputs goes wrong and the behavior pattern becomes unstable as deviated from the task-A. However, this period of unstability is gone afterwhile and the second behavior pattern initiates and it continues stably. Figure 8c shows the temporal profile of the behavior generated. The vertical dotted line denotes the moment when the object is moved from the center to the left-hand side of the task space. Observe that it takes 20 steps until the second behavior pattern is initiated after the object is moved to the left-hand side. Observe also that the PB, the motor outputs, and the sensory inputs fluctuate during this transition period. The fluctuation is initiated because of the gap generated between the top-down prediction of the PB values and their bottom-up estimation through the regression based on the sensory inputs. In the five repeated trials in this parameter setting, the profiles of the transient patterns were diverse. The observed fluctuation seems to play the role of a catalyst in searching for diverse transition paths from the steady attractor, associated with the first behavior pattern, to that for the second behavior pattern. Once the transition is complete, the second behavior pattern proceeds steadily. It was also found that the success of the current task largely depends on the parameter which defines the ratio between the two forces of the top-down anticipation and the bottom-up regression acting on the PB. If the top-down is too strong, just the first behavior sequence continues with neglecting the situational change. On the other hand, if the bottom-up is too strong, the behavior generation becomes unstable by being sensitive to various noise in the physical world. The current task becomes successful with setting the ratio parameter in the middle of these two extremes. The future study will examine the scheme for on-line adaptation of the ratio parameter by extending the idea shown in (Tani, 1998).

It is concluded that the bottom-up and top-down interactions are crucial in resolving conflicts between the levels and thus in adaptively generating behavior sequences.

Discussion and Summary

The current paper discussed that the mechanisms of anticipation and regression are indispensable in modeling cognitive behavior. The anticipation tells the behavior system that how much the system is currently situated in the environment and the regression tells the system how to become re-situated when the anticipation goes wrong with facing dynamic changes in the environment. This idea was implemented in a neural network model of RNNPB with/without levels. The PB vector in the model works as the internal parameter which encodes a set of behavior patterns.

The scheme of the RNNPB with multiple levels can show one possible way to acquire compositionality in behavior generation. The term compositionality comes from philosophy and linguistics (Evans, 1981) saying that whole can be reconstructed by combination of parts. Our scheme shows how compositionality can be acquired without using symbols and their manipulations but with dynamical systems metaphor. More specifically, complex sensory-motor sequences are decomposed into a set of reusable behavior primitives by utilizing the parameter bifurcation characteristics of the non-linear neuronal dynamics.

On the one hand, it might be possible to utilize multiple attractor dynamics to embed different behavior primitives into different basins of attraction. The switching of behavior primitives can be carried out by perturbing the system state to transit from one basin to another from the higher level. However, the problem is that it is quite difficult to generate multiple attractors of the desired through training of the standard RNNs regardless of number of context units and hidden units alllocated. This seems to come from the fact that significantly high correlations are established among context units activities due to full connectivities introduced in the networks, as we have written briefly in the previous section. Instead, it might be possible to use the echo-state machine (Jaeger and Haas, 2004) to embed number of different attractor dynamics because of its inherently rich “reservoir” dynamics in the internal neurons activities due to sparse connectivities among them. This research direction could be for future.

The current paper showed that the behavior patterns of learned can either be generated by the top-down anticipation of the PB or be recognized by the bottom-up regression of the PB. The actual behavior is generated through the interactive process between these two pathways. In the first experiment of the imitative interactions, it was observed that the sensory-motor sequences are segmented into chunks of different patterns as accompanied by stepwise changes of the PB values. The anticipation error during each chunk is low while it becomes larger at the transit from one chunk to another. During the chunk everything goes smoothly and automatically where the perfect coherence are generated between the anticipation by the internal system and the reality from the environment. However, in the transit, this coherence is lost and intensive computational processes of the regression are conducted in order to optimize the PB of the internal parameter. The similar phenomena was observed in the second experiment with the arm robot. The incoherence, in this experiment, appears in the transit from the task-A to the task-B which is triggered by the environmental changes regarding to the position of the object. It might be said that at these moments of “breakdown” the behavior system becomes rather “conscious” about the gap between the its subjective expectation and the reality which results in the intensive regression and adjustments for the “self”. ( Tani, 1998, 2004). On the other hand, in the coherent state, there are nothing to be “conscious” about.

The conventional dynamical systems approaches for behavior systems tend to focus only on the structural stability in the sensory-motor coupling. The current paper has focused rather on the moment of the breakdown and proposed novel mechanisms to deal with it. It is highly speculated that such trials may lead us to further understanding of the problems in embodied cognition including some metaphysical problems.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that should be construed as a potential conflict of interest.