The infinite sites model of genome evolution

Abstract

We formalize the problem of recovering the evolutionary history of a set of genomes that are related to an unseen common ancestor genome by operations of speciation, deletion, insertion, duplication, and rearrangement of segments of bases. The problem is examined in the limit as the number of bases in each genome goes to infinity. In this limit, the chromosomes are represented by continuous circles or line segments. For such an infinite-sites model, we present a polynomial-time algorithm to find the most parsimonious evolutionary history of any set of related present-day genomes.

Chromosomal DNA is a double-stranded polymer consisting of two directed strands of bases denoted A, C, G, and T, each strand running in the opposite direction. The strands are paired such that an A in one is always associated with a T on the other, and G with C. This double-stranded chromosomal DNA polymer can be either linear or circular. Each organism carries a genome consisting of a set of such chromosomes that defines its genetic heritage, part or all of which it passes on to its offspring through the process of reproduction. In a population of organisms of the same species, mutations arise spontaneously during this process. Most of these mutations disappear over the generations, but periodically one of these mutations becomes fixed and present in the genome of all organisms in the population. Major changes such as chromosomal rearrangements happen infrequently enough and fix in the population rapidly enough that when working on a scale of tens of millions of years, we may profitably represent the genetic diversity of the species by a single “reference” genome and represent the evolutionary history of the species as a linear series of major evolutionary changes to this single reference genome.

Through models of this type, one can study the history of changes in which the double-stranded DNA is broken and rearranged in various ways, sometimes with loss or duplication of DNA segments (1–4). These changes can occur through the process of chromosomal breakage and nonhomologous end joining (5). In diploid species, where two copies of every chromosome are present, these changes can also occur as a result of nonhomologous recombination events and other errors in meiosis (6).

Genomes are often quite large, e.g., the human (haploid) genome consists of some three billion base pairs. Mathematically, it is convenient to move from the standard finite representations of the double-stranded DNA polymer to a continuous representation in which continuum many “sites” containing either A-T or G-C base pairs exist in each chromosome. Representations like this are often used in population genetics to examine the statistical properties of the variations due to mutations in individual base pairs, and are known as “infinite sites” models (7, 8). Here we introduce an infinite sites model for the study of genome evolution by large-scale duplication and rearrangement.

Chromosomes are either continuous intervals or continuous circles in the infinite sites model. In an evolutionary operation, a set of k breaks are made in these chromosomes, leaving 2k free ends. These 2k ends are then rejoined in a new manner to form a rearranged set of chromosomes (9, 10). In addition to these basic sorts of rearrangements, a set of chromosomes can be duplicated (11, 12), chromosomes can be lost, and DNA that was never observed before can be inserted into preexisting chromosomes. The latter operation models viral integration and other types of horizontal transfer of DNA from other branches of life. Periodically in evolution a species splits to form two new species, through a process called speciation. This process is also included in the model we study here.

Local changes consisting of substitutions that alter a single base pair are individually invisible in this model of genome evolution. As is standard, we assume that such substitutions occur at a finite rate per site. The substitution rate is the same for all sites in a species, but is allowed to vary between species, i.e., no universal molecular clock is assumed. Thus, since every segment of continuous DNA of nonzero length contains infinitely many sites, it accumulates infinitely many substitutions in any nonzero length of time. We may use a standard continuous time Markov model to convert from the observed fraction of sites that have changed to an evolutionary distance, expressed as the expected number of substitutions per site that have occurred (13–15). By the law of large numbers, the evolutionary distance we measure in the infinite sites model is exact. In this way, rather than explicitly representing substitutions, we represent their effect at each point along the chromosome as a continuous increase in evolutionary distance between the previous version of the genome at that site and, after some time has passed, the next version of the genome at the corresponding site in the descendant.

We refer to two sites that descend from a common ancestral site as homologous. This includes the case where one site descends from the other. When the chromosome is duplicated, either as part of a speciation or within the evolution of a single species, the homologous sites of the two copies begin at evolutionary distance zero, and then they independently accumulate increasing evolutionary distance at the same rate as time goes by. Starting from a single species with a single reference genome, an entire set of new “present day” species evolves through the evolutionary operations of rearrangement (including deletion and insertion), duplication, and speciation. Each of these new species has its own reference genome, and all are derived by evolution from the original reference genome. We assume that parts of the genomes of the present day species are observed, and that the evolutionary distance between any two observed points in any two present day genomes can be measured exactly. We study how one may use the distances between the homologous segments of the observed parts of present day genomes to work out a possible evolutionary history for these genomes with the smallest possible number of rearrangement, duplication, and speciation operations. We call this the simplest history problem.

Corresponding problems in the usual finite sites model of genome rearrangements are nearly all computationally intractable. Even when there are only three present day genomes, each a single chromosome, all parts are observed, no DNA is gained or lost, and apart from the speciations the only operation allowed is the two-breakpoint rearrangement of inversion, the problem, known as the Median Problem, is NP-hard (16). Only heuristic algorithms exist for this and more general cases (17–19). For the infinite sites model, we give an efficient algorithm for the simplest history problem for an arbitrary number of partially observed present day species' genomes and evolution by all of the operations of speciation, duplication, and rearrangement, with gain and loss of DNA, allowing up to k = 3 breakpoints per rearrangement. The key to the difference is that in the infinite-sites model, we can assume that no breakpoint is ever used twice. This assumption is reasonable in the continuous limit, because for any stochastic model of breakpoint choice represented by a continuous density along the chromosome, breakpoint reuse would be an event of measure zero.

To analyze the evolution of actual genomes, some approximations to the infinite-sites model are required. Evolutionary distances are only approximate, and breakpoints are reused, although, as the analysis approaches the level of single-base resolution, reuse of exactly the same breakpoint is expected to become rare. We introduce some heuristics to handle these issues so the model can be applied to actual sequence data. As an illustration, we apply the model to reconstruct the history of chromosome X in human, chimp, macaque, mouse, rat, and dog since their common ancestor. By aligning the chromosome X sequence from each of these species, we identify 1,917 maximal segments that are unbroken by re arrangements. We call these atoms. Each atom consists of a family of segments of DNA that all derive from a common ancestral segment. Each such segment is called an instance of the atom. We estimate the evolutionary distances between these atom instances and use this information to reconstruct a predicted evolutionary history of chromosome X in these species that consists of 110 duplications, 1,660 rearrangements (including 747 deletions and 289 insertions), and five speciation events. At a gross level, our results are consistent with previous reconstructions of the evolution of chromosome X in placental mammals (19–21). However, because previous reconstructions were at much lower resolution and did not model duplications, the results are not strictly comparable. Although considerable additional validation and refinement will still be required, our results suggest that heuristics based on the infinite-sites model may be useful in practice.

Definition of the Model

A genome is a finite set of chromosomes, and a chromosome is a bounded, oriented, continuous interval, either circular (a ring) or linear (a contig). Each point in a chromosome is called a site. The evolutionary process begins with a single genome called the root genome. This genome comes from a species called the original species. The root genome evolves by loss and gain of chromosomes and by the evolutionary operations of duplication and rearrangement, until a speciation event occurs. At this point, an identical copy of the genome is made, each of the two genomes gets a new successor species name, and they each evolve independently thereafter, as did the root genome.

Missing Data.

Only parts of the DNA of a present day species will be observed. There may be whole chromosomes that are there but not observed, and there may be several gaps in the available sequence for a chromosome, making a linear chromosome appear in many contigs as if it were actually several chromosomes or a circular chromosome appear in contigs as if it were one or more linear chromosomes. For mathematical simplicity, we assume that the telomere end of a linear chromosome can never be completely observed, so that all contigs have missing data at the ends, but if desired, knowledge of telomere ends can be represented in this model by adding special atoms to represent them. Further, it is assumed that no ordering or grouping information is available for contigs. Thus, it is not known whether two observed contigs are part of the same underlying chromosome or are part of different chromosomes.

The Evolutionary Tree.

The evolutionary process can be visualized as a directed tree, called the evolutionary tree, with the root genome at the root, each node representing a genome, and each edge representing an evolutionary operation followed possibly by some chromosome gains and losses, as illustrated in Fig. 1. Internal nodes are ancestral genomes and leaf nodes are leaf or present day genomes. If there is a directed edge from node f to node g, then we say that g is the child of f, and f is the parent of g. If node g is reachable by a directed path from node f, we say that the genome g is a descendant of the genome f, and that f is an ancestor of the genome g.

Fig. 1.

An example evolutionary history starting from the root genome r consisting of a single linear chromosome and continuing to its descendants. Breakpoints of each operation are annotated by vertical red bars. The first change after the speciation of r occurs in the genome h₆ when the segment from 6 to 10 is inverted to produce the genome h₅. Meanwhile, on the other lineage descending from r, an inversion also occurs that flips the segment from 5 to 11 in genome e₁ to form genome e. Back in the other lineage, there is a whole-chromosome duplication that forms h₄, followed by a reciprocal translocation that creates h₃. This combination of events models a nonhomologous recombination that creates a tandem duplication of atom 3. The other product of the recombination, a chromosome in which atom 3 is deleted, is lost (shown by shaded box). Then, another tandem segmental duplication occurs that includes the previous one, resulting in genome h₁. Genome h is formed after a deletion of segment (− 9₄, −8₄, −7₄) in h₁, where the deleted portion is a circular product shown shaded by a gray ellipse. After that, a speciation event spawns new species represented by f and g₁. Finally, the genome g₁ has a deletion of the segment from 2₁ to −9₂, creating the genome g.

Each bifurcating node in the genome tree represents a “last snapshot” of the genome of a species just before a speciation event. The nonbranching path leading to the bifurcating node, either from the root or from a previous bifurcating node, including the bifurcating node itself, represents the evolutionary history of the ancestral genomes for that species and is called the species path. Each node along a species path apart from the last denotes a genome f that experiences an evolutionary operation of duplication or rearrangement at that point in the history of that species, plus some number of chromosome gains and losses that may occur after that operation and before the next operation. The outgoing edge (or “branch”) from this parent genome f leads to a child genome g that results from f by application of the operation and the chromosome gains and losses described in the parent node. This branch has positive real-valued length that represents the evolutionary distance between homologous sites in parent and child genomes. The total evolutionary distance from f to any descendant genome g is the sum d of the evolutionary distances on the unique path to g. In this case we say that f derives g in evolutionary distance d. Missing data are allowed in this derivation, as described above and in more detail in Section 1 of supporting information (SI) Appendix.

The evolutionary distance between any two nodes in the tree, even if on different species paths, is the sum of the lengths of the branches leading to them from their last common ancestor, or equivalently, the sum of the distances on the unique shortest undirected path in the tree that connects them.

If we collapse each species path in the genome tree into a single edge of length equal to the total edge length on the path, keeping only the speciation nodes and the leaves of the evolutionary tree, we obtain a tree known as the species tree. This is the usual tree drawn to describe the phylogenetic relationships among the species. The set of all species in the species tree is called the clade of the original species.

Evolutionary Operations.

The evolution of the genome of a single species occurs through two kinds of basic evolutionary operations: rearrangements and duplications.

Two-breakpoint rearrangements.

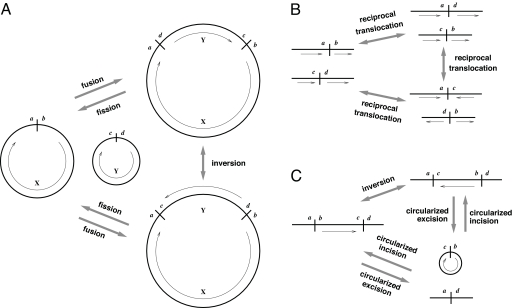
In a two-breakpoint rearrangement, chromosomes are cut at two points, called breakpoints, creating four free ends. These ends are then rejoined in pairs, creating a new genome as illustrated in Fig. 2. Special cases of this operation include the inversion of a segment in a ring, the fission of a single ring into two rings and the fusion of two rings into a single ring (Fig. 2A). For contigs, special cases of two-breakpoint rearrangement include a reciprocal translocation between two contigs (Fig. 2B) and the inversion, circularized excision or circularized incision of a segment in a contig (Fig. 2C).

Fig. 2.

Two-breakpoint rearrangements. (A) Here, we show three genomes, each pair of genomes differing by a single two-breakpoint rearrangement. The genome on the left consists of two rings, and those on the right each have a single ring. The arrows indicate the type of two-breakpoint operation that transforms the one genome into the other. In each operation, four free ends (a, b, c, d) are rejoined in pairs. (B) Reciprocal translocation between two contigs. (C) Inversion, circularized excision, and circularized incision of a segment in a contig.

In any of these cases involving contigs, it is possible that one or both of the breakpoints are at the contig ends. When a breakpoint occurs at the end of a contig, one of the free ends created is a null end. For example, in a reciprocal translocation, if one of the breakpoints lies at the end of its contig, then one of the pieces from this contig being translocated will be empty and the other will be the entire contig. If both breakpoints lie at the end of separate contigs, then the result will be a fusion of these two contigs. If the breakpoints lie at the end of the same contig, then the result will be a circularization of the contig into a ring.

Further special cases occur when one of the two breakpoints falls entirely within a gap. In this case, two of the four free ends are null. If the other breakpoint is in a ring, then the result of the rearrangement is that this ring is linearized. If the other breakpoint is in a contig, then this contig undergoes a fission into two contigs. If the other breakpoint is at the end of a contig or is also in the middle of a gap, nothing apparent happens, so this is not considered to be a distinct operation.

Insertions and deletions.

Topologically, a deletion corresponds to the two-breakpoint operation of chromosome fission or circularized excision, but the excised material is biologically lost on the branch of the derivation tree where the operation occurs. The rearrangement places the excised material into a separate chromosome, which is then subsequently lost as part of the chromosomal gains and losses. Hence, this material is not present in the child genome nor any of its descendants (Fig. 3). The material is said to have been deleted.

Fig. 3.

An insertion operation transforms the genome on the left into the genome on the right. The inserted material, Y, is obtained by horizontal transfer and hence is not present in the parent genome (shaded in the figure). Analogously, in a deletion operation, a two-breakpoint operation of chromosome fission generates two chromosomes on the left, then one of them, Y, is lost.

An insertion corresponds to the two-breakpoint operation of chromosome fusion or circularized incision, except that the material from one of the elements being fused is material previously obtained by horizontal transfer from outside the clade (Fig. 3). This new material is gained on the previous branch. Hence, this new material is only observed in the child genome and its descendants and is not homologous to any other material in the child genome. It is not present in the ancestors of the parent genome nor in any genome that is an outgroup to the subclade rooted at the child genome. The new material is said to have been inserted.

Three-breakpoint rearrangements.

In a three-breakpoint rearrangement, chromosomes are cut in three places, creating six free ends, which are then rejoined with new partners. One important case is the transposition operation, in which a DNA segment is moved to a new location in the genome (Fig. 4). In addition, three-breakpoint operations also include rearrangements such as transpositions with inversion [“transreversals” (22)], and some more exotic operations, e.g., when the three breakpoints are located in three different chromosomes.

Fig. 4.

A transposition operation. The operation breaks adjacencies (a, d), (c, b), and (e, f), and rejoins three pairs of free ends into (a, b), (e, d), and (c, f).

Note that our three-breakpoint rearrangement definition here is slightly different from the “3-breaks” defined in ref. 10, where two-breakpoint rearrangements are special cases of three-breakpoint rearrangements.

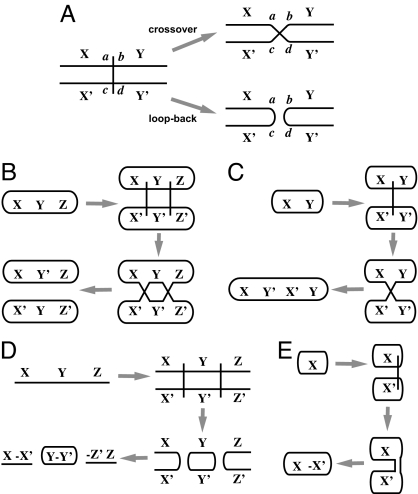
Duplications.

In a duplication operation, each chromosome in the parent genome is copied. Each chromosome is then homologously paired with its copy to form what we will call a bivalent, borrowing a term for a similar structure formed during meiosis (23). A set of k ≥ 0 breaks are created in the bivalents. Each break produces four free ends (Fig. 5A). The four ends at each break are then rejoined among themselves to form a new chromosomal configuration. There are two cases: crossover and loop-back (Fig. 5A). Each of the k breaks may independently be either a crossover or a loop-back. After all crossovers and loop-backs are performed, the homologous DNA from the bivalents is separated to form individual chromosomes (Fig. 5 A–E). Then finally, some of these chromosomes may be lost, and some new chromosomes may be gained.

Fig. 5.

Duplication operations. (A) A bivalent is formed by aligning homologous chromosomes after a duplication. When a break occurs between segments X and Y (denoted X′ and Y′ in the homolog), this creates free ends a, b, c, d, which are then rejoined either by a crossover, creating adjacencies (a, d) and (c, b), or by a loop-back, creating adjacencies (a, c) and (b, d). If this were a duplication of a single contig X Y with a single breakpoint, then because X and X′ are identical and Y and Y′ are identical, the result of the cross-over would be a simple separate duplication of the contig X Y, exactly as if there had been no breakpoint during the duplication at all. However, the loop-back would result in a reverse tandem duplication that creates contigs, X–X′ and −Y′Y. (B) A separate duplication of a circular chromosome results from an even number of cross-overs. The chromosome is duplicated into two identical chromosomes. (C) A tandem duplication of a circular chromosome results from an odd number of cross-overs. The chromosome is duplicated into a single chromosome containing two successive copies of the original chromosome. (D) Multiple loop-backs in a contig create a reverse tandem duplication with two reverse tandemly duplicated contigs at the ends, here X–X′ and −Z′Z, and reverse tandem circular chromosomes derived from the middle pieces, here Y–Y′. (E) In the special case of one loop-back in a circular chromosome, the result is a circular chromosome with a reverse tandem duplication of the original chromosome mirrored around the position of the breakpoint.

The net effect of a duplication is that some chromosomes will be copied, and a restricted kind of rearrangement will occur between chromosomes and their copies. If all of the breaks in a chromosome are crossovers and either (i) there are an even number of these breaks or (ii) the chromosome is a contig, then the net result is two separate, identical copies of the chromosome. We call this a separate duplication of the chromosome [Fig. 5B, also called a duplication of type R⊕R (12)]. In this case, there is no apparent rearrangement after the duplication of the chromosome. On the other hand, if an odd number of crossovers occur in a circular chromosome, the result is a tandem duplication of that chromosome, forming a new ring consisting of two successive copies of the original chromosome [Fig. 5C, also called a duplication of type 2R (12)]. Here, it is apparent that at least one break has occurred in conjunction with the duplication, but there is no way to locate the position of that break. Finally, if there is a mix of crossovers and l ≥ 1 loop-backs within the chromosome, then the loop-backs break the bivalent into separate “bivalent contigs,” and the crossovers within these contigs have no apparent effect. Thus, the result is identical to what would be obtained from just the l loop-backs. The result is that each segment Y of chromosome between a successive pair of loop-backs is formed into a ring chromosome of the form Y -Y, and if the chromosome is a contig, then the left end segment X up until the first loop back forms the contig X–X, and the right end segment Z after the last loop back forms the contig −ZZ (Fig. 5D). One extreme case occurs when the chromosome is a ring X and there is a single loop-back break where X joins back to itself. In this case the result is a single-ring chromosome X–X (Fig. 5E). All of the cases where there are l ≥ 1 loop backs are collectively called reverse tandem duplications of order l.

An extreme case of duplication is a whole-genome duplication, in which every part of the genome is separately duplicated, and both copies are retained. This is distinct from a speciation event, because in a speciation event, two new child genomes are created, each of a new species that thereafter evolved independently, whereas in a whole-genome duplication, one child genome is created, and it is still of the same species. Even though every duplication in the infinite sites model has the potential to be a whole-genome duplication, in practice, we expect that one copy of most chromosomes will be lost after the duplication operation, so the net effect will be that only one or a few chromosomes are actually duplicated. After subsequent rearrangements and further losses, only a duplicated segment of the original chromosome will be retained.

Complex operations derived from basic operations.

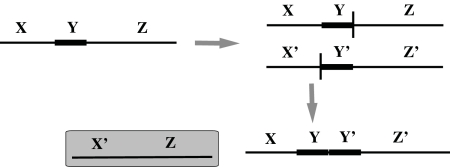
More complex operations occur as combinations of the above basic operations. For example, a tandem segmental duplication is a composite operation in which a segment in one chromosome is copied, and the new copy is inserted after the old copy. In the infinite-sites model, this happens whenever there is a ring chromosome tandem duplication followed by a deletion of less than half of the resulting chromosome, or the duplication of a contig followed by a reciprocal translocation between the two copies and loss of the smaller product (Figs. 1 and 6). This is equivalent to a nonhomologous recombination between the two chromosome copies, with propagation of only the duplication-containing recombinant. Tandem duplications are never created by three-breakpoint transpositions here, and probably also in actual biological processes; this would involve exact breakpoint reuse.

Fig. 6.

Tandem segmental duplication of segment Y in a contig XYZ is achieved by a separate duplication of the contig, followed by a two-breakpoint rearrangement with breakpoints at either ends of the segments Y in the two copies, followed by a deletion of the smaller of the two resulting contigs.

Similarly, a duplicative transposition may be achieved by a duplication, followed by a three-breakpoint rearrangement. The chromosome that contains the segment to be transposed is duplicated, the transposition is then performed from the duplicate chromosome copy back to the original, and then the duplicate chromosome copy is lost. Although most actual biological examples of duplicative transposition do not occur in this manner, the net effect is the same. In each of the above cases, note that only one rearrangement operation is used. Thus, apart from the unavoidable cost of a duplication, the cost model used here treats these operations on a par with other single-rearrangement operations in defining the simplest history.

Properties of Evolutionary Histories

No Complete Turnover.

Even though there is a certain amount of turnover in the content of genomes due to insertion and deletion, normally a pair of leaf genomes will contain at least one segment that traces its common ancestry directly back to a segment in their last common ancestor. By sequencing enough DNA from each species, we will find such a segment. If there is no such segment in the DNA we observe, we say that there is complete turnover between the two leaf genomes. As a technical assumption, here we consider only the case where such complete turnover is not present.

No Breakpoint Reuse.

Finally, and most importantly, we stipulate that the operations satisfy the assumption of no breakpoint reuse. This means that no two homologous sites in the genomes in the evolutionary tree are ever independently used as breakpoints in two different operations. If we view the breakpoints as being chosen at random according to any continuous density function, then there is no breakpoint reuse with probability one. Thus, this is a reasonable assumption in the infinite sites model.

The Simplest-History Problem

We cannot obtain the DNA sequence for ancestral genomes older than a million years (24), but we can obtain the DNA for present-day species. The challenge then is to work out the evolutionary changes that led to the present-day genomes and reconstruct the ancestral genomes. The criterion often applied in solving this problem is to try to find the solution that is consistent with the data from the present-day genomes and implies the fewest evolutionary operations. This is called the parsimony principle (25, 26). In the context of this article, we define a parsimony problem called the simplest-history problem as follows.

The input is a set G of present-day genomes and an evolutionary distance function D that defines a nonnegative distance between every observed pair of sites in them. For nonhomologous sites x and y, we set D(x, y) = ∞. The distance function D between homologous sites is specified by a list of maximal segments of uninterrupted homology between pairs of genomes, which we call local alignments. Each local alignment is a triple consisting of (i) a distance d, (ii) a pair of homologous genome intervals in which corresponding sites are all separated by distance d, and (iii) an orientation “+” or “−” indicating whether these intervals are homologous in the forward direction or if one is reversed relative to the other. These data represent the information that we can obtain from sequencing the genomes of the present-day species and comparing all their genomic segments. The simplest-history problem is to determine whether there exists an evolutionary tree with the observed sequences G from the present-day genomes at the leaves and the given evolutionary distance function D on their sites, and if so, to determine one such tree with the smallest number of operations. The derivation of the leaf genomes must occur with no breakpoint reuse and no complete turnover. Missing data are allowed; in particular, we expect to find missing data in the leaf genomes. We say that an algorithm for the simplest-history problem is efficient if it runs in time that is polynomial in the number of chromosomes plus the number of local alignments in the input. Our main result is the following.

Theorem.

In the infinite-sites model there is an efficient algorithm to solve the simplest-history problem.

The proof of this theorem is given in Section 2 of SI Appendix, which contains the description of an efficient algorithm. The steps of this algorithm are as follows.

1. Make a dot plot that summarizes the local alignments. Use the dot plot to decompose the genomes into atoms.

2. For each atom, build an unrooted atom tree that describes the evolutionary relationships between its instances.

3. Deduce the species tree for the leaf genomes.

4. Reconcile the atom trees with the species tree and from this, produce a duplication tree that identifies the minimum number of duplications needed to derive the leaf genomes and includes a node for each of these duplications.

5. Compute a graph of atom end adjacencies called the master breakpoint graph, check for consistency with the infinite sites model and schedule on the edges of the duplication tree a minimum set of rearrangement operations that will be needed to derive the leaf genomes.

6. Run an a procedure called reverse evolution to work back from the leaves of the duplication tree to the root, determining partial ancestral genomes on the way.

7. Run a fill-in procedure from the root back out to the leaves to complete the ancestral genomes and their evolutionary history.

Most steps are fairly straightforward, except perhaps step 5, where Edmonds matching algorithm (27) is used to obtain a certain optimal matching of some connected components of the master breakpoint graph. The master breakpoint graph constructed in this step is analogous to the breakpoint graph used in the pairwise analysis of the evolution of one genome into another by rearrangements (28). Here, we exploit the fact that breakpoints are never reused, and hence there can be, at most, two different atom ends adjacent to any given atom end throughout the course of the evolutionary history. Thus the master breakpoint graph, which records all such adjacencies that are evident in the leaf genomes, has degree at most two, just as do standard breakpoint graphs for pairwise genome rearrangement analysis. An analogous property has been exploited in the analysis of independent microinversions (29). Steps 2 and 3 rely on the well known result that whenever exact pairwise distances between the leaves of an unrooted evolutionary tree are known, the tree structure and internal branch lengths are easily recovered (30, 31). Finally, we note that as a corollary to the development of the algorithm the standard Fitch definitions of ortholog and paralog for genes (32, 33) are generalized to the notion of orthologous and paralogous atom instances. By using this generalization, once the reconstruction is complete, these definitions can be applied to any pair of homologous genome segments.

Finite Sites Models.

With some simple modifications, we can obtain a “finite sites” variant of the model of genome evolution we have introduced. In the finite sites model, a genome consists of a set of chromosomes, each with only finitely many sites, and each site is labeled with a nucleotide in the set {A, C, G, T}. To obtain this model as a modified special case of the continuous, infinite-sites model, we draw M points independently at random along the length L of the root genome according to some underlying continuous distribution and assign a nucleotide to each of these, where M is the desired number of nucleotides in the initial genome, and R = M/L is the overall nucleotide density. Insertions that occur during evolution are treated analogously as segments containing random nucleotides at the same nucleotide density R. Speciation, duplications, and rearrangements proceed as in the infinite-sites model, with breakpoints chosen from the underlying continuous chromosomes, but we only observe their effects on the sequence of nucleotides. This makes our distance calculations approximate (as discussed below), and when two breakpoints occur between homologs of consecutive nucleotides, we get the phenomenon of apparent breakpoint reuse, which makes the problem of recovering the evolutionary history more difficult. Our heuristic approach to this is to insert “engineered atoms” to represent unobserved segments of continuous genomes where multiple breakpoints have occurred, as discussed in Section 8 of SI Appendix.

In the finite-sites model, we explicitly model base substitution as one of the evolutionary operations, keeping track of the nucleotide label of each site as part of the state of the process. This replaces the evolutionary distance function D with a stochastic quantity. To make the analysis easier, we assume that substitutions at each site occur independently. Even with this assumption, however, the problem is quite difficult. The nucleotide labels essentially provide a very “noisy” version D̃ of the evolutionary distance function D.

The approximate distance function D̃ can be computed by aligning and comparing small segments of the genomes in G and locating those that have statistically significant similarity. We do this using the program BLASTZ (34). These are then be assembled into longer local alignments that are either parallel or antiparallel to the diagonal and used to estimate the set of atom instances and their pairwise evolutionary distances, as is done in the infinite-sites model using the exact D (Section 7 of SI Appendix).

If we assume that all substitutions are equally likely, and that the per-site rate of substitution is λ, we obtain a model for the substitution process known as the Jukes–Cantor model (13). For this model, it is easy to analytically solve for the probability p that the nucleotides will differ at two sites that derive from a common ancestral site in total evolutionary time t along the two branches. It is p = 1 − e^−4λt. It follows that if two segments x and y derive from a common ancestor, and p is the fraction of homologous sites in these two segments that differ, we may estimate the true evolutionary distance λt between these two segments as the expected number of substitutions per site between the two segments, which we may denote D̃ (x, y). Solving the above equation for λt, we obtain $\tilde{D}(x,y)=-\ln (1-\frac{4}{3}p)$(13). The variance in this estimate depends on the rate λ, time t, and the number of pairs of homologous sites between the segments x and y. As the number of homologous sites goes to infinity, the variance goes to 0, and the distance measurement becomes exact, as discussed in the Introduction. Other, more parameterized continuous time Markov models for nucleotide evolution also have this property and could be used in place of the Jukes–Cantor model (14, 15). In practice, we use the distance D̃ in our construction of the simplest history in conjunction with other kinds of information relating to the adjacencies of segments when establishing distances between atom instances (Section 7 in SI Appendix).

Results

Simulations.

We developed a simulation program to evaluate the heuristic extension of the infinite-sites algorithm for finite-sites models discussed above (Section 9 in SI Appendix). The simulator starts with a hypothetical “ancestor” genome consisting of abstract atoms that evolves into the genomes of the extant species through speciation, duplication, and rearrangement operations as described above. We estimated the parameters used in the simulator from reconstructions of the evolutionary history of chromosome X in six mammals (see below), using the phylogenetic tree ((((human, chimp), rhesus), (mouse, rat)), dog), such that 5–10% of the atom instances had observed paralogs in the extant species created by duplications, and the net change in the number of atoms due to insertion, duplication, and deletion was consistent with what we observed in the different lineages, achieved by using an overall deletion/insertion ratio of 3. Fig. 7 shows results from one series of simulations in which the amount of breakpoint reuse is varied. Further results are given in Tables S4—S7 in SI Appendix. We compare the infinite-sites algorithm with the DUPCAR reconstruction program (36), a method purely based on parsimonious inference of ancestral atoms and adjacencies without explicitly modeling operations. The results show that for the accurate reconstruction of ancestral genomes, the infinite-sites algorithm uniformly outperforms the DUPCAR method. Because of its ability to reconstruct ancestral adjacencies that are ambiguously present or not explicitly observed anywhere in the leaf genomes, the infinite-sites algorithm performs dramatically better when there is no outgroup information for the reconstructed ancestral genome (blue lines in Fig. 7). Errors in reconstruction are associated with turnover of atoms due to insertions, duplications, and deletions, which in turn is associated with oversimplified predicted histories (Table 8 in SI Appendix). The more the turnover, the fewer are the operations in the predicted history relative to the true history, and the worse is the accuracy.

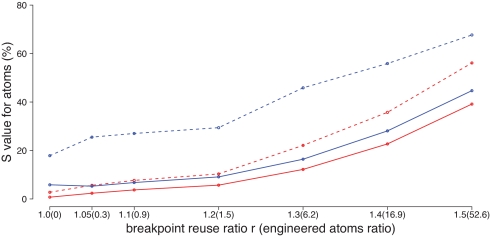
Fig. 7.

Comparison between the infinite-sites algorithm (solid lines) and DUPCAR (dotted lines). Blue lines represent reconstruction of the genome of the Boreoeutherian common ancestor, for which no outgroup is available in this dataset, and the red lines represent the Euarchontoglires ancestor (i.e., the primate–rodent common ancestor). Each data point is the average of 100 simulations, each using ≈2,000 atoms. On the vertical axis, we plot the percentage of atom instances where the true and predicted ancestral genomes disagree, defined as S_atom = ((∣R ∪ P∣ − ∣R ∩ P∣)/(∣R ∪ P∣)) × 100%, where R is the set of atom instances in the true ancestral genome, P is the set of atom instances in the predicted genome, and ∣X∣ denotes the size of the set X. The horizontal axis represents variation in the breakpoint-reuse ratio r (35), defined here as r = (2x + 3y)/(a + m − n) where x is the number of two-breakpoint operations in the whole evolutionary history, y is the number of three-breakpoint operations, a is the total number of atoms, m is the number of uses of contig ends as breakpoints, and n is the number of contigs in the root genome. The justification of this formula is that in the infinite-sites model, if we start with n contigs (counted as initial atoms) and an arbitrary number of circular chromosomes (not counted as atoms) in the root genome, then each two-breakpoint operation adds 2 to the quantity a + m, because each breakpoint it uses that is not a contig end adds another atom. Similarly, each three-breakpoint operation adds 3 to the quantity a + m. Finally, when all of the circular chromosomes are hit by rearrangements at least once, we have a total number of atoms a = 2x + 3y + n − m, and hence the breakpoint-reuse ratio (2x + 3y)/(a + m − n) = 1. Any ratio higher than this represents breakpoint reuse. The number in the parentheses is ((no. of engineered atoms used)/(no. of atoms)) × 10³ (see Section 9 in SI Appendix).

Evolution of Chromosome X in Placental Mammals.

We applied the infinite-sites algorithm to actual genomic sequence on the X chromosome of the six placental mammals above, partitioning the chromosome into 1,917 atoms using BLASTZ pairwise cross-species and self-alignments (Section 7 in SI Appendix) and using the heuristic extensions discussed above to infer and reconcile atom trees and reconstruct an evolutionary history. Out of 3,834 atom ends, 576 were involved in more than two kinds of adjacencies with other atom ends, representing explicit breakpoint reuse. Other breakpoint reuse was implied by large cycles and chains in the master breakpoint graph (Fig. S23 in SI Appendix), resulting in an overall breakpoint-reuse ratio (defined in Fig. 7 legend) of r = 1.39. However, when we reconstructed an intermediate genome, these breakpoint resues were seldom localized to the operations immediately below that genome, and thus the heuristic algorithm introduced only 15 engineered atoms, equivalent to 7.8 × 10⁻³ engineered atoms per atom, roughly comparable with that observed in simulations at breakpoint-reuse ratio ≈1.4. In the resulting predicted evolutionary history of chromosome X in the six species, there were 110 duplications, 1,660 rearrangements, and five speciation events. Of 1,660 rearrangements, 1,462 were two-breakpoint operations, whereas the other 198 were three-breakpoint operations. This bias is partly due to the variant cost function used in this reconstruction, which favors two two-breakpoint operations over one three-breakpoint operation (see below). Among the two-breakpoint operations, 747 were deletions, and 289 were insertions. The results are consistent, at a coarse resolution, with previous reconstructions (19–21). The reconstruction of the evolution of human chromosome X from Boreoeutherian ancestral chromosome X (Fig. S28 in SI Appendix) does not exhibit any megabase-scale rearrangements, as expected (20, 37), and is somewhat more parsimonious than our previous finer-scale reconstruction (19), with only two inversions of size >50 kb instead of four (Fig. S33 in SI Appendix). The reconstruction of the evolution of the mouse chromosome X (Fig. 8) is also similar to that found in other studies done at larger scales, with the exception of a large inversion in the Murinae ancestral chrX corresponding to the first 70 M bases in the mouse chromosome that has been predicted (20, 37) based on MGR (18). In the infinite-sites reconstruction, this change is predicted to result from a combination of operations, including a transposition between what are now mouse chromosome bases 20–70 M and 70–140 M. With just the six genomes used in the present reconstruction, several key ancestral Murinae adjacencies in chromosome X remain ambiguous and are arbitrarily set to agree with those in the mouse genome by our heuristics. Hence, not much stock can be put in this prediction. Further leaf genomes would be needed for our algorithm to be able to resolve this.

Fig. 8.

The evolutionary history of mouse chromosome X. This graph shows the predictions for the order and orientation of atoms on the X chromosome for several mouse ancestral genomes, produced by running the infinite-sites algorithm on the six genomes listed above. The y axis is measured in million-year increments, with the existing mouse genome at the bottom and the root genome labeled “Duplication coalescent ancestor” on top. The root genome is the ancestral genome as reconstructed before the oldest detected duplication. The Boreoeutherian ancestral genome, common ancestor to human, dog, and rodents, lies below the root genome, and is placed at ≈100 million years ago, consistent with estimates from Murphy et al. (38). Between each speciation point (e.g., Murinae ancestor to mouse) the polygons show the rearrangements that are predicted to have occurred on that branch of the species tree colored from dark to light according to the position within the X chromosome of the DNA on the upper branch. Regions that have been inverted are tinted purple. Duplications are shown with red lines for one copy and green lines for the others. Each ellipse represents an atom instance in our reconstruction and is scaled to represent the number of base pairs that are included in that atom instance.

The atom set for the chromosome X experiment was constructed in such a way that extensive breakpoint reuse was to be expected. In forming these atoms, no attempt was made to map endpoints with high resolution so as to minimize breakpoint reuse (see Section 7 of SI Appendix). The number of leaf species used was also quite limited. It remains to be seen whether methods for constructing atoms can be developed that identify breakpoints in actual chromosome data more precisely, which, in combination with additional leaf species to identify intermediate configurations on long branches, substantially reduce effective breakpoint reuse and thereby improve reconstruction accuracy for heuristic extensions of the infinite-sites model.

Discussion

Weighted Parsimony.

The parsimony model we have explored is very simple in that two-breakpoint rearrangements, three-breakpoint rearrangements, and duplications (with arbitrary numbers of bivalent breaks), all “cost” the same. In a slightly more realistic model, each of these three types of operations would have a different positive cost, and the goal would be to find an evolutionary history with minimal total cost for the operations. This is usually called weighted parsimony. It turns out to be easy to generalize the infinite-sites algorithm to solve this weighted-parsimony problem (Section 10 in SI Appendix). In fact, but just skipping the Edmonds optimal matching step, we obtain a variant of the infinite-sites algorithm corresponding to the situation where a three-breakpoint operation costs more than two two-breakpoint operations. This variant is used above in the reconstruction of the evolutionary history of chromosome X. More complex weighted-parsimony problems can be envisioned, where different subtypes of operations have different weights. These remain to be explored.

Fully Stochastic Models.

The infinite sites model of genome evolution that we have introduced treats substitutions as a stochastic process (albeit one of variance 0), but does not provide a stochastic model for the large scale evolutionary operations of speciation, duplication, and rearrangement, including the special cases of insertion and deletion. It is possible to define such a model by assuming that duplications and speciations occur randomly at a particular rate per genome and that rearrangements occur at a particular rate per unit length of chromosome according to some explicit density function, such as the uniform density. This yields a rather complex Poisson-type model for the stochastic process of genome evolution. This is a very interesting area for further research.

Further Generalizations.

We can define a generalized infinite sites model in which the one-breakpoint rearrangement operations of crossover and loop-back on bivalents are viewed not as part of the duplication operation but as distinct one-breakpoint rearrangement operations each associated with a separate cost. Separate two- and three-breakpoint rearrangement operations can be permitted on bivalents after a duplication as well. For example, in a “bivalent” two-breakpoint rearrangement operation, two breaks could be simultaneously made in a bivalent, creating eight free ends and then these rejoined in an arbitrary fashion. It can be shown that in such a model, a segmental reverse tandem duplication, e.g., X Y Z → X Y −Y Z can be achieved in a single two-breakpoint operation, whereas in the standard infinite-sites model, this operation requires breakpoint reuse. For either the standard or the generalized infinite-sites model, we can also further generalize by allowing rearrangements to use up to k breakpoints for some chosen k. These generalized models would be interesting to investigate. It would also be interesting to investigate generalizations where each species is represented by a population of genomes, rather than by a single reference genome. It is also an open problem to extend the theory to the case where partial information is available about the grouping of contigs into chromosomes in the leaf genomes and their relative ordering and orientation. Finally, applied to animal genomes, the model we have defined has the drawback that although it represents the nuclear genomes of the present-day species correctly as containing only linear chromosomes (represented as contigs), it produces a mix of linear and circular chromosomes in the ancestral genomes if this is more parsimonious than a derivation with purely linear chromosomes in the ancestors. In our applications to real data, we have used heuristics to avoid this behavior. It would be interesting to know how the complexity of the problem is affected if we impose the restriction that the ancestors can only contain linear nuclear chromosomes.

Applications to Cytogenetics and Cancer.

Beyond being a possible theoretical foundation for the scientific study of genome evolution, the operations of duplication, deletion, insertion, and rearrangement that are studied in this article create genomic changes in people that are of significant medical importance. Two main areas where they have been studied are the cytogenetic classification of inherited genetic abnormalities leading to birth defects and other diseases, and in the study of somatic cell genetic changes that occur in cancer. One relatively new mechanistic theory of changes in cancer is the theory of the amplisome (39). The additional, transient circular minichromosomes hypothesized by this theory can be modeled quite naturally within the framework discussed here.

New technologies are allowing researchers to map these types of disease-causing changes to the genome with vastly greater accuracy than has been previously possible (40). When multiple changes have occurred to the genome to create a genetic disease state, the theory developed in this article may be useful in better understanding of these changes. By identifying the specific operations that are likely to have occurred and the properties of the DNA sequence near their breakpoints, not only can we better classify a genetic condition, but we can also begin to study specific patterns in recurrent genetic changes associated with specific diseases.