Abstract
Aquaporin 0 (AQP0), the most abundant membrane protein in mammalian lens fiber cells, not only serves as the primary water channel in this tissue but also appears to mediate the formation of thin junctions between fiber cells. AQP0 is remarkably less water permeable than other aquaporins, but the structural basis and biological significance of this low permeability remain uncertain, as does the permeability of the protein in a reported junctional form. To address these issues, we performed molecular dynamics (MD) simulations of water transport through membrane-embedded AQP0 in both its (octameric) junctional and (tetrameric) nonjunctional forms. From our simulations, we measured an osmotic permeability for the nonjunctional form that agrees with experiment and found that the distinct dynamics of the conserved, lumen-protruding side chains of Tyr-23 and Tyr-149 modulate water passage, accounting for the slow permeation. The junctional and nonjunctional forms conducted water equivalently, in contrast to a previous suggestion based on static crystal structures that water conduction is lost on junction formation. Our analysis suggests that the low water permeability of AQP0 may help maintain the mechanical stability of the junction. We hypothesize that the structural features leading to low permeability may have evolved in part to allow AQP0 to form junctions that both conduct water and contribute to the organizational structure of the fiber cell tissue and microcirculation within it, as required to maintain transparency of the lens.
Keywords: membrane, MD simulation, water channel, permeability, cell adhesion
Every tissue has evolved unique adaptations that allow it to perform specialized functions. Such adaptations are especially evident in the lens of the mammalian eye, where many of the usual cellular metabolic pathways have been sacrificed to achieve one overriding goal: transparency. The lens is nonetheless metabolically active, and water balance is critical to lens homeostasis over the lifetime of an animal, as demonstrated by the abundance of the water transporter AQP0, which accounts for >60% of the membrane protein component in lens fiber cells (1–5). Originally designated the major intrinsic protein of the lens, AQP0 is the founding member of the aquaporin family (6); aquaporins have been studied extensively as a result of their central role in ensuring water balance across all kingdoms of life (2, 3, 7, 8). AQP0 is unusual among the aquaporins in two ways. First, AQP0 transports water 10-fold more slowly than other aquaporins (9, 10). Second, AQP0 mediates adhesive contacts between cells (11–16).
For the lens to remain transparent, the spacing between fiber cells must remain smaller than the wavelength of visible light. Transparency also requires that the water content of the fiber cells be carefully regulated, because excess water disrupts the regular structure and organization of the crystallin proteins in the cell interior such that they become opaque (7). AQP0 plays a critical role in maintaining both conditions: it provides the major pathway for water circulation through the nucleus and cortex of the lens (6, 10, 17) and it promotes cell–cell adhesion through formation of thin membrane junctions (11–15), which are believed to maintain intercellular spacing and organization as the lens changes shape while focusing (11, 17). That AQP0 mutations cause congenital cataracts emphasizes the physiological importance of AQP0 (18).
The biological significance of the unusually low permeability of AQP0 remains unclear, as do the structural and dynamic determinants of this low permeability (11, 17, 19–21). Recent x-ray and electron-diffraction structures have shown that AQP0 can exist both as a nonjunctional homotetramer (17), in which each monomer transports water, and as a junctional octamer formed by hydrophobic interactions between two tetramers juxtaposed head-to-head in adjacent membranes (11, 13, 19, 22). The conductance of the junctional form has been debated (11, 17, 19, 20, 22); it has been suggested that AQP0, in its junctional form, is nonconducting (11, 19), but the differences between the structure of this form and that of the conducting, nonjunctional form seem minor (17). Junction formation has been associated with proteolytic cleavage of the C-terminus of AQP0 (11), but experimental evidence suggests that the cleaved form conducts water when not engaged in junction formation (23).
MD simulations have proven highly effective in elucidating water transport by aquaporins (20, 21, 24–29). MD studies of AQP0 are challenging, however, due to the slow dynamics of the protein and the slow kinetics of water permeation (20, 21, 29). Previous simulations have reached timescales up to a few tens of nanoseconds (20, 21, 24, 25, 27–29), but experiments suggest that water permeates AQP0 at a rate of about one water molecule every 10 ns (9), and protein conformational changes that affect water transport may occur over significantly longer timescales.
By using recently developed algorithms for the high-speed, parallel execution of MD simulations (30–33), we have performed all-atom simulations with an aggregate length of ≈500 ns to elucidate the kinetics and control of water transport through both junctional and nonjunctional tetramers of AQP0 as well as the octameric junction. Our simulations allowed us to observe protein conformational changes that open and close the channel on timescales up to 100 ns.
Our results suggest that both tetramers and the octamer each conduct water with similar permeabilities. Our simulations also indicate that in both the junctional and nonjunctional forms, the low permeability of AQP0 is due to a combination of a static barrier and several dynamic gating motions.
Harries et al. (17) pointed out that the low permeability of AQP0 and its high membrane density may ensure a spatially uniform response to osmotic challenge while keeping the overall membrane permeability sufficiently low to prevent excess water from entering the cell. Our results suggest an additional explanation for the low permeability of AQP0 relative to other aquaporins: it may be an adaptation to maintain the mechanical stability of the junction as water flows through in response to pressure differences, thereby permitting AQP0 to maintain both proper hydration and cellular organization.
Results and Discussion
We performed explicit-solvent MD simulations of junctional and nonjunctional AQP0 embedded in hydrated lipid bilayers, as described in Methods and supporting information (SI) Appendix. Beginning with the x-ray structure of Harries et al. (17), we performed a 200-ns simulation of the nonjunctional tetramer (denoted AQP0NJ4) embedded in a single membrane. We also performed a 110-ns simulation of the octameric junction (denoted AQP0J8) embedded in two adjacent membranes (Fig. 1), based on the electron-diffraction structure of Gonen et al. (11). Last, we performed a 170-ns simulation of a single AQP0 tetramer starting from the conformation of the junctional structure (the “junctional tetramer,” denoted AQP0J4) embedded in a single membrane.
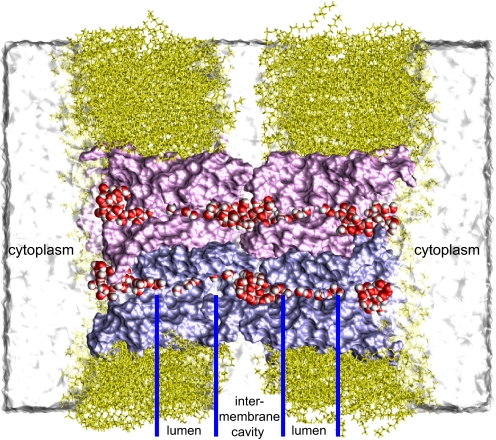
Fig. 1.
An AQP0-mediated membrane junction. Cross-section of an AQP0 octamer (pink and purple) embedded in a double bilayer (yellow). Two pairs of interlocked AQP0 monomers that connect two cells are shown; the other two pairs are omitted for clarity. Permeating water is red and white. Other waters are shown as a white surface.
Osmotic Permeability.
The single-channel osmotic permeability constant, pf, relates water flux (J) to the osmotic pressure difference (ΔP) across the channel as J = pfΔP/RT, where R is the gas constant and T is temperature. We determined pf for the different forms of AQP0 from our equilibrium simulations, as described in SI Appendix and in ref. 34. As shown in Fig. 2, estimation of pf required on the order of 100 ns of simulated time for convergence.
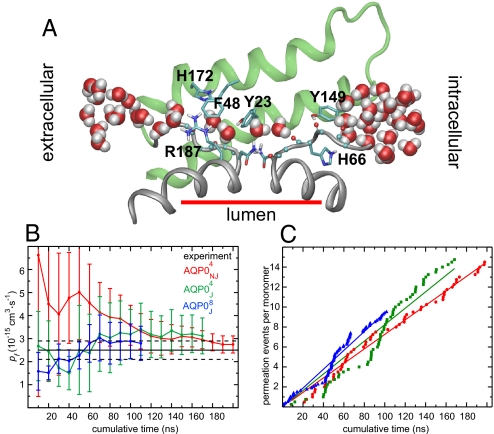
Fig. 2.
Transport kinetics. (A) Snapshot from the AQP0J4 simulation. Only residues 128–179 (helices IV and V and loop D, green), the B and E half helices (gray), and the two nonhelical repeats (gray) are shown. (B) Calculated osmotic permeability constant, pf. Means and standard errors were computed among the monomers in each simulation. The abscissa represents cumulative simulation time included in the pf calculation. The experimental pf value is 2.5 ± 0.4 (9). (C) Cumulative permeation events (per monomer in either direction). Linear regression to these data yielded pd = 1.1 for AQP0NJ4, pd = 1.2 for AQP0J4, and pd = 1.4 for AQP0J8, consistent with the values in Table 1.
AQP0 exhibited water transport in all simulations. For the nonjunctional tetramer we found pf (AQP0NJ4) = 2.8 ± 0.4 (Fig. 2B and Table 1). (Throughout this article, permeability constants are given in units of 10−15 cm3·s−1, and all refer to the permeability of a single monomer.) This value is consistent with results from shorter simulations (21, 29) and is in good agreement with the experimental result of pf = 2.5 ± 0.4 (9), particularly given that the experimental value represents a lower bound on the true permeability (28). For the octameric junction and the junctional tetramer, we calculated per-monomer osmotic permeabilities of pf (AQP0J8) = 2.8 ± 0.7 and pf (AQP0J4) = 3.1 ± 0.8; corresponding experimental results are not available, but our computational results suggest that they are approximately equal not only to one another but also to the permeability of the nonjunctional tetramer. Thus, our results suggest that junctional and nonjunctional AQP0 do not differ significantly in their osmotic permeabilities, while agreeing with experimental findings that the osmotic permeability of AQP0 is an order of magnitude lower than that of other aquaporins (9).
Table 1.
Transport kinetics
| tsim, ns | pf | pd | pf /pd | O | |
|---|---|---|---|---|---|
| AQP0NJ4 | 200 | 2.8 ± 0.4 | 1.1 ± 0.1 | 2.6 ± 0.4 | 5.0 ± 0.3 |
| AQP0J4 | 170 | 3.1 ± 0.8 | 1.3 ± 0.6 | 2.4 ± 1.3 | 4.6 ± 0.3 |
| AQP0J8 | 110 | 2.8 ± 0.7 | 1.4 ± 0.5 | 2.0 ± 0.9 | 5.2 ± 0.3 |
Osmotic (pf) and diffusive (pd) permeabilities are given in 10−15 cm3·s−1. Luminal water occupancy (O) is given as the number of water molecules. Means and standard errors were computed among monomers (see SI).
Diffusive Permeability and Channel Occupancy.
The diffusive permeability constant (pd) of a water channel measures the number of complete permeation events, i.e., the number of water molecules that permeate from one side of the channel to the other (in one direction) per unit time under equilibrium conditions of no net water transport. Although the slow kinetics of AQP0 make it difficult to determine pd accurately by using computational methods (20), our simulation time seems sufficient to reach a steady state. The number of permeation events increased approximately linearly with time (Fig. 2C) All forms of AQP0 exhibited similar diffusive permeabilities: pd (AQP0NJ4) = 1.1 ± 0.1, pd (AQP0J4) = 1.3 ± 0.6, and pd (AQP0J8) = 1.4 ± 0.5. These numbers suggest that, at equilibrium, ≈4 × 107 water molecules permeate each monomer in each direction per second, approximately double an earlier estimate from shorter simulations (20).
In most aquaporins, water molecules form a continuous single file through the lumen. The length of the lumen in the experimental AQP0 structures suggests that ≈10 water molecules would be required to span it (11, 17, 19). In the electron-diffraction structure of junctional AQP0, however, only three luminal waters were identified, leading these authors to suggest that the channel was in a closed, nonconducting state (11). The x-ray structure of nonjunctional AQP0 contained eight luminal waters (17), but only five lie within the region we have defined as the lumen for purposes of our calculations (see SI Appendix). In our simulations, we consistently found that the average number of water molecules in the lumen (the water occupancy) was close to five (Table 1), and that water formed a discontinuous single file. The water file was disrupted by several lumen-protruding side chains (Fig. 2A). Hashido et al. found similar average water occupancy in shorter simulations of the nonjunctional form of AQP0 (29).
For a channel in which water molecules form a single file and translocate simultaneously, one can show that the ratio of pf to pd equals the average water occupancy plus one (35, 36). We found that pf/pd (AQP0NJ4) = 2.6 ± 0.4, pf/pd (AQP0J4) = 2.4 ± 1.3, and pf/pd (AQP0J8) = 2.0 ± 0.9 (see Table 1 and SI Appendix), all significantly lower than the value of ≈11 (10 + 1) expected if the single file were continuous. Experimental measurements of pd and pf/pd are not available for AQP0, but our estimated pf/pd ratios are consistent with structural observations of a relatively low average water occupancy (11) and with our observation that the water file through the AQP0 lumen is not continuous in either the junctional or nonjunctional form.
Gating and Modulation of Water Transport.
The slow kinetics of water transport across AQP0 has been attributed to various structural features, including residues Met-176 of the extracellular vestibule, Arg-187 of the aromatic/arginine (ar/R) region (7, 11, 19, 29), the “phenolic barriers” Tyr-23 and Tyr-149 (7, 11, 17, 19–21, 29), and the extracellular loops A and C (7, 8). Below, we discuss these putative determinants of permeability in light of our simulations. We observed AQP0 in multiple open and closed states, with Tyr-23 and Tyr-149 acting as the major static and dynamic determinants of permeability. We also observed that extracellular loop A undergoes a slow conformational change that gates water transport and may be involved in the pH sensitivity of AQP0 (7, 8).
Met-176.
The side chain of Met-176 assumes a conformation in the junctional form that has been suggested to block water entry into the lumen from the extracellular vestibule, thus preventing water transport (11, 19). AQP0 exhibited water transport in all our simulations, however, implying that Met-176 does not fully occlude water entry in either the junctional or nonjunctional forms. Its side chain underwent similar conformational excursions in all simulations, frequently pointing away from the lumen. Moreover, the channel conducted water even when this side chain pointed toward the lumen. Therefore, Met-176 appears to play a minor role, if any, in explaining the low permeability of AQP0.
ar/R Region.
Like other aquaporins, AQP0 has a conserved luminal arginine, Arg-187, that forms part of the ar/R constriction region. Experiments and simulations have found that the corresponding arginine in Escherichia coli AqpZ can adopt either an “up” conformation, which permits water permeation, or a “down” conformation, which essentially blocks the pore (28, 37, 38). This mechanism has also been suggested to apply to AQP0 (11, 19). In all of our simulations, we found that Arg-187 frequently appeared in the up conformation, permitting permeation across the ar/R region (as represented in Figs. 3 A, B, and D), and occasionally in the down conformation, preventing water passage (Fig. 3C). These results suggest that whereas Arg-187 occasionally blocks water permeation through AQP0, it is not the major cause of low permeability. This residue is also present in faster-conducting aquaporins.
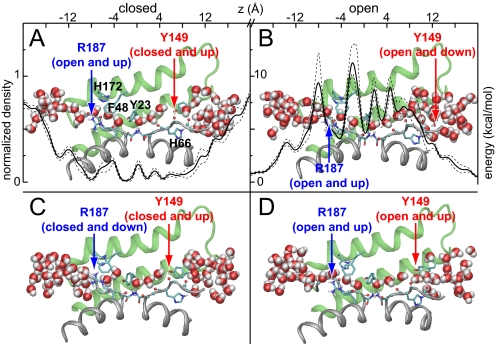
Fig. 3.
Luminal residues modulate transport. Snapshots from the AQP0J4 simulation that represent open and closed states of AQP0, colored as in Fig. 2A. The configurations of Arg-187 and Tyr-149 are classified as “open” or “closed” depending on whether they block water passage, and as “up” or “down” depending on their side-chain dihedral angles. A time-averaged water density profile ρ(z), drawn to scale with the AQP0 lumen, is overlaid in A; dashed lines indicate standard deviations among 13 separate 12-ns windows. A free energy profile, G(z) = −RT ln[ρ(z)], is overlaid in B.
Phenolic Barriers.
Tyr-23 and Tyr-149, which are located at the extracellular and intracellular ends of the lumen, respectively, have been suggested to play a role in limiting water permeation through AQP0 (7, 11, 17, 19–21, 29). The side chains of these residues, referred to as “phenolic barriers” (17, 20, 21), narrow the lumen (Figs. 2A and 3). Both Tyr-23 and Tyr-149 are conserved in all known mammalian and amphibian AQP0s (17). Avian AQP0s conserve only Tyr-23, as does the only other known slow-conducting mammalian aquaporin, AQP6, which is an anomalous aquaporin in that it also conducts chloride (39). Tyr-23 and Tyr-149 are both absent in all faster-conducting aquaporins (see Figure S1 in SI Appendix) (17, 20, 21). Phylogenetic analysis suggests that incorporation of these tyrosine residues is a recent evolutionary event (40); thus, it appears that one or both of these residues serve to reduce the rate of water transport across AQP0.
Recent simulations have found that water passage across Tyr-23 and Tyr-149 is restricted, with low average water occupancy in these regions (20, 21). Our simulations also showed low water occupancy in these regions, as indicated by the water density profile in Fig. 3A and the implied free energy profile in Fig. 3B. Tyr-23, in particular, is responsible for the largest local barrier to water passage.
Whereas the profiles in Figs. 3 A and B describe the thermodynamics of water occupancy along the lumen, they do not capture kinetic effects. However, our simulations were long enough to observe dynamic effects at a variety of timescales, suggesting that both Tyr-23 and Tyr-149 are largely responsible for the low permeability of AQP0. Both residues were able to occlude the lumen and both exerted limiting effects on water permeation through AQP0, but by very different mechanisms.
Tyr-23 predominantly imposed a static barrier to permeation, with its hydroxyl group acting as a hydrogen bond donor/acceptor, thereby allowing it to substitute for a “missing” water molecule in the single file. Tyr-149, on the other hand, acted more as a dynamic gate, with its side chain alternating at random between an “up” state, in which the phenol ring pointed toward the center of the lumen (Fig. 3 A, C, and D), and a “down” state, in which it moved aside (Fig. 3B). When Tyr-149 was down, water was able to flow past the side chain (Fig. 3B), along the lines of a suggestion made by Walz et al. based on the observation of a relatively high temperature factor for this residue (19). When the side chain was up, either the channel remained open (Fig. 3D), or hydrogen bonds formed between the Tyr-149 hydroxyl group and the exposed carbonyl groups of Gly-64, Ala-65, or His-66, under which conditions the channel fully closed (Fig. 3 A and C). To pass Tyr-149 in this closed state, water had to push the phenolic side chain open by breaking those hydrogen bonds.
Whereas transitions between the up and down states of Tyr-149 were relatively rare, occurring every ≈20 ns during our simulations, the lumen remained open for a greater fraction of the time at Tyr-149 than at Tyr-23, which allowed water passage only fleetingly. Movie S1 and Movie S2 illustrate this subtle gating behavior.
pH Regulation.
The water permeability of AQP0 increases 2- to 4-fold at pH 6.5 relative to its minimum at pH ≈8 (7, 8). Experimental evidence suggests that AQP0 exists in an equilibrium between weakly and highly conductive states, with the latter being favored at low pH (7, 8). His-40, located in extracellular loop A (residues 33–40), is believed to function as the pH sensor, but the mechanism of pH regulation is not known (3).
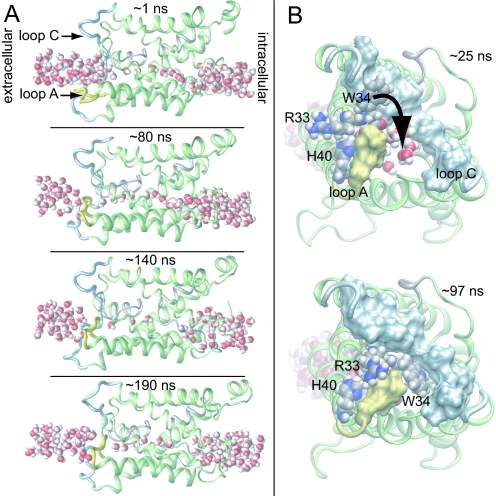
Intriguingly, in our simulations of tetrameric AQP0 at neutral pH with His-40 uncharged, we observed conformational changes indicating that loop A can indeed play a role in regulating water passage through the channel. The loop underwent a slow conformational change with respect to the x-ray structure and partially occluded the extracellular vestibule, as represented by the snapshots from the AQP0NJ4 simulation in Fig. 4. Specifically, over the first 80 ns, loop A gradually pinched off the extracellular vestibule (Fig. 4A Top and Upper Middle), preventing water access to the lumen. The luminal water occupancy decreased gradually over the next ≈60 ns (Fig. 4A Lower Middle), after which the lumen began to refill, predominantly from the intracellular side (Fig. 4A Bottom). Viewed from the extracellular side in Fig. 4B, one sees that tight contact between loop A and loop C (residues 100–127) was established on a ≈100 ns timescale. This contact was formed almost solely by loop A residues Arg-33 and Trp-34; their large side chains moved to pack against the relatively stationary loop C, with the Trp-34 side chain in particular obstructing water entry into the lumen (Fig. 4B). It is tempting to speculate that ionic repulsion at low pH between protonated His-40 and positively charged Arg-33 causes a shift in the equilibrium position of loop A toward the open state (Fig. 4B), thereby explaining the observed pH sensitivity (7, 8).
Fig. 4.
Channel occlusion. (A) Consecutive snapshots from the AQP0NJ4 simulation. The water pathway is pinched off by intrusion of loop A (yellow) while loop C (light blue) remains stationary. The lumen dries out on occlusion, but rehydrates later in the simulation (Lower Middle and Bottom) after loop A reopens. (B) Extracellular view. His-40, Arg-33, and Trp-34 are shown as spheres. Trp-34 slides between loops A and C, thereby occluding the channel.
Biological Relevance of Slow Transport by AQP0 and Implications for Cell Adhesion.
Ultrastructural images of the eye lens indicate that AQP0 exists as isolated tetramers or square arrays of tetramers directly contacting an opposing membrane (14–16, 41, 42). On protein reconstitution, arrays of junctional octamers, proposed to link two cells together, have also been observed (12). Loss of AQP0 leads to disorganized fiber cells and lens opacity (18, 43, 44), raising the question of whether this protein serves primarily as a water channel that functions in water homeostasis and microcirculation of nutrients and waste products (45), or as a cell-adhesion molecule (12, 14–16) that promotes the optically critical close apposition of fiber cells, or both. A related question is the functional significance of the low permeability of AQP0 relative to other aquaporins.
Our simulation results have three direct implications relevant to addressing these questions. First, our results show quantitatively that the junctional and nonjunctional forms of AQP0 conduct water to approximately the same extent. Regardless of any other function AQP0 takes on (e.g., as a junctional or nonjunctional cell-adhesion molecule), AQP0 continues to transport water.
Second, our results suggest that substitution of only two luminal residues, Tyr-23 and Tyr-149, leads to the low permeability of AQP0 relative to other aquaporins, and that these substitutions, conserved throughout most of vertebrate evolution, have similar effects in both the junctional and nonjunctional forms of AQP0.
Third, Harries et al. proposed that large numbers of low-permeability aquaporins can serve to maintain a spatially uniform response to osmotic challenge while limiting overall fiber cell membrane permeability (17). A high channel density would achieve a uniform osmotic response regardless of the single-channel permeability, so one might ask why the low permeability of AQP0 is needed to maintain the lens water content of 60–80%. Notably, intracellular water diffusion in the lens is known experimentally to range from ≈10−6 cm2·s−1 to ≈10−5 cm2·s−1 (46), whereas diffusion through the lumen of AQP0, at ≈10−7 cm2·s−1, is ≈10-fold lower than the bottom of that range, suggesting that AQP0, but not faster-conducting aquaporins, can keep membrane permeability below the lower limit of intracellular water diffusion, thus preventing excessive local hydration of the crystallin proteins.
Our results permit us to propose an additional hypothesis for the functional significance of the low permeability of AQP0. Specifically, we suggest that this low permeability may be an evolutionary adaptation that allows AQP0 to promote intimate cell adhesion by forming mechanically stable junctions. Physical deformation of the lens in the course of visual accommodation leads to pressure differences between adjacent cells and, thus, across the junctions between them. Excessive water flow along this pressure gradient may strain the weak hydrophobic contacts that hold together the two tetramers in a junction (11, 17, 19). Because in dilute solutions the osmotic permeability equals the pressure-driven, hydraulic permeability (47), the decreased osmotic permeability of AQP0 may reduce this strain and thereby the risk of junction breakage, as elaborated below.
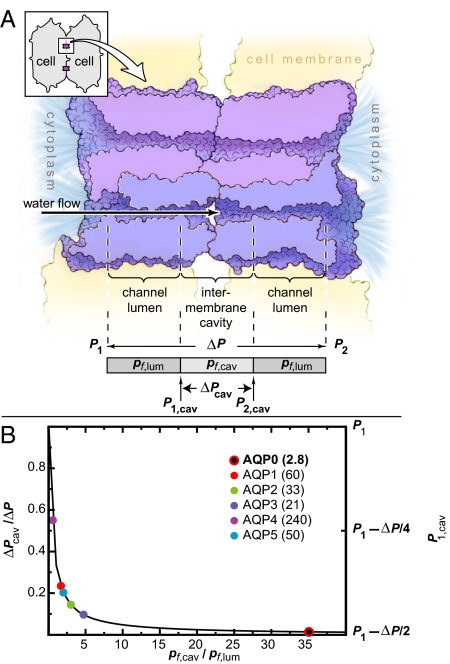
The channel formed by two head-to-head AQP0 monomers can be conceptually decomposed into three water-accessible regions: two lumens, each with permeability pf,lum, and one intermembrane cavity with permeability pf,cav (see Fig. 5A). At steady state, the water flows through the three regions are equal, and the pressure difference across each region is inversely proportional to its permeability. Given a fixed pressure difference ΔP across the entire junction, decreasing pf,lum increases the luminal pressure differences and, therefore, decreases the pressure difference across the intermembrane cavity. Specifically, the intermembrane cavity pressure difference is ΔPcav = ΔP/(1 + 2pf,cav/pf,lum), where ΔP = P1 − P2, and P1 and P2 represent the pressures in the two cells, with P1 ≥ P2 (see SI Appendix). Whereas the pressure at the center of the cavity, (P1 + P2)/2, is independent of the permeabilities, the maximum and minimum pressures, which occur at the ends of the cavity, do depend on the permeabilities. In particular, if pf,lum is much greater than pf,cav, the maximum cavity pressure will be approximately P1. If, however, pf,lum is much less than pf,cav, the pressure throughout the cavity will be approximately (P1 + P2)/2 = P1 − ΔP/2 and thus lower than P1 (see SI Appendix).
Fig. 5.
Luminal permeability may impact junctional stability. (A) Cross-section of an AQP0 junction, showing two monomers per tetramer. (Inset) Two fiber cells with two junctions. The pressure difference across the entire channel is ΔP = P1 − P2 where P1 and P2 are the pressures in the two cells and P1 ≥ P2 (see SI Appendix). The finite cavity permeability causes a pressure difference of ΔPcav = P1,cav − P2,cav within the cavity. (B) Normalized cavity pressure difference ΔPcav/ΔP and the maximum cavity pressure P1,cav plotted as a function of the ratio of cavity to luminal permeabilities. Experimental pf values (in 10−15 cm3·s−1) for aquaporins 0–5 are listed (9).
We estimated the osmotic permeability of the intermembrane cavity from our simulation of AQP0J8 to be pf,cav ≈ 100. The permeability of the AQP0 lumen is much lower, pf,lum ≈ 3 (Table 1). In contrast, the luminal permeabilities of other characterized aquaporins are at least 10 times larger (AQP1, pf ≈ 60; AQP4, pf ≈ 240; ref. 9) and are approximately comparable with the permeability of the intermembrane cavity. As shown in Fig. 5B, the normalized pressure difference across the intermembrane cavity calculated with the above AQP0 permeabilities is <2% of the total pressure difference across the entire junction. The cavity pressure difference would rise by 16- or 37-fold, however, if AQP0 had a permeability equal to that of AQP1 or AQP4, respectively. Only AQP0 has a permeability low enough to approach the ideal case in which the maximum pressure within the intermembrane cavity assumes the lowest possible value, P1 − ΔP/2; a higher maximum cavity pressure might cause the junction to burst.
At least two caveats are in order. First, whereas the cavity pressure difference could increase by more than an order of magnitude due to an increase in luminal permeability, the increase in maximal cavity pressure would be much smaller. If the luminal permeability of AQP0 increased to that of AQP1 or AQP4, for example, the maximal cavity pressure would increase by no more than 52 or 21%, respectively (see SI Appendix). The magnitude of the adhesive forces between fiber cells has not been accurately measured, but a hypothetical volume change of 0.1% during accommodation leads to a force on the junctional contacts on the order of 50 pN, given an approximate cross-sectional cavity area of 2,000 Å2 and a 3-GPa bulk modulus of the lens. The magnitude of this force is comparable with cell-adhesion forces sustained by, for example, integrins (48). However, this estimate does not take into account water release and reabsorption by crystallin proteins or by the lens itself (49, 50), which would lower the bulk modulus and in turn the force on the cavity. Second, in our simulation of the octameric junction, water molecules pass between the intermembrane cavity and the extracellular environment through “portals” in the extracellular domains of AQP0, as suggested by Harries et al. (17). These portals may stabilize the junction by functioning as safety valves, through which water escapes if the cavity pressure becomes too high.
These caveats notwithstanding, although the cell-adhesion strength of a single AQP0 junction is probably low, the high density of AQP0 in each fiber cell suggests that many weak individual interactions might together result in significant adhesion between two adjacent cells. In this regard, it may be worth noting that other intramembrane channels (e.g., transient receptor potential and mechano-sensitive channels in mammalian sensory systems) exhibit sensitivity to even small pressure changes. Low permeability of the AQP0 lumen may also ensure that high water flows due to transiently large pressure differences are avoided.
Aquaporins with high permeability could in principle achieve equally stable junctions by strengthening interactions between the monomers forming a junction, increasing the permeability of the intermembrane cavity, or reducing the luminal permeability through a conformational change on junction formation. We speculate that, from an evolutionary perspective, decreasing monomeric permeability in the nonjunctional as well as junctional forms may be more accessible than any of these alternatives, because it requires only one or two mutations in the channel lumen to introduce the static and dynamic barriers discussed above. Thus, low permeability may represent an evolutionary adaptation that allows AQP0 to play a dual role in water transport and cellular adhesion.
Indeed, AQP0 is the only aquaporin known to form potentially conductive junctions; in the only other known junctional structure of an aquaporin, which involves AQP4, interlocking tetramers are displaced laterally from one another such that no continuous water-conducting channels are formed (51). Intercellular water flow has been proposed by Engel et al. (52) to destabilize such nonconducting AQP4 junctions, but in a manner unrelated to the mechanism proposed here.
Conclusion
Using MD simulations, we determined the kinetics and studied the control of water transport across AQP0, the major membrane protein constituent of eye lens fiber cells. The substantial length of our simulations allowed us to make quantitative estimates of channel permeabilities and to identify the structural factors accounting for these permeabilities. We found that AQP0 conducted water in both junctional and nonjunctional forms; in both cases, the computed osmotic water permeability was comparable to the experimentally derived value for the nonjunctional form of AQP0, which is an order of magnitude lower than that of other aquaporins. Our simulations suggest that this low permeability is due to a static barrier and to several gating motions with timescales up to 100 ns. These observations lead us to speculate that low permeability of AQP0 may have evolved to allow it to form stable junctions by decreasing the risk of junction breakage as water flows through. Low permeability of AQP0 may permit it to simultaneously facilitate water transport and intercellular adhesion in fiber cells and may thus be critical to the maintenance of lens transparency.
Methods
All simulations used the OPLS-AA/L force field for protein (53, 54) and ions (55) and the simple point charge model for water (56). Lipid parameters were generated as described in ref. 54. All MD simulations were performed by using the program Desmond (32), which uses a particular “neutral territory” method (30, 33) called the midpoint method (31) to efficiently exploit a high degree of computational parallelism.
All simulations were performed at constant temperature (310 K) and pressure (1 bar) by using the Berendsen coupling scheme (57) with one temperature group. Electrostatic forces were computed by using the Gaussian Split Ewald method (58). The real-space part of electrostatic and van der Waals interactions were cut off at 10 Å. Bond lengths to hydrogens were constrained. A RESPA integrator (59) was used, with Fourier-space electrostatics computed every 6 fs, and all remaining interactions computed every 2 fs.
Supplementary Material
Acknowledgments.
We thank Ross Lippert, Paul Maragakis, and Kate Stafford for helpful discussions and assistance. Molecular images were produced using Visual Molecular Dynamics (60).
Footnotes
Conflict of interest statement: Desmond, the software used to perform the simulations described in this paper, was developed by D. E. Shaw Research and is currently available free of charge for noncommercial research use from D. E. Shaw Research. D. E. Shaw Research has entered into a licensing agreement with Schrödinger, LLC, which distributes Desmond commercially. D.E.S. has a beneficial ownership interest in D. E. Shaw Research, and R.O.D., M.P.E., and D.E.S. have beneficial ownership interests in Schrödinger, LLC.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0802401105/DCSupplemental.
References
- 1.Agre P, Bonhivers M, Borgnia MJ. The aquaporins, blueprints for cellular plumbing systems. J Biol Chem. 1998;273:14659–14662. doi: 10.1074/jbc.273.24.14659. [DOI] [PubMed] [Google Scholar]
- 2.Agre P. The aquaporin water channels. Proc Am Thorac Soc. 2006;3:5–13. doi: 10.1513/pats.200510-109JH. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Agre P, Kozono D. Aquaporin water channels: Molecular mechanisms for human diseases. FEBS Lett. 2003;555:72–78. doi: 10.1016/s0014-5793(03)01083-4. [DOI] [PubMed] [Google Scholar]
- 4.Hedfalk K, et al. Aquaporin gating. Curr Opin Struct Biol. 2006;16:447–456. doi: 10.1016/j.sbi.2006.06.009. [DOI] [PubMed] [Google Scholar]
- 5.Preston GM, Carroll TP, Guggino WB, Agre P. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 protein. Science. 1992;256:385–387. doi: 10.1126/science.256.5055.385. [DOI] [PubMed] [Google Scholar]
- 6.Gorin MB, Yancey SB, Cline J, Revel JP, Horwitz J. The major intrinsic protein (MIP) of bovine lens fiber membrane: Characterization and structure based on cDNA cloning. Cell. 1984;39:49–59. doi: 10.1016/0092-8674(84)90190-9. [DOI] [PubMed] [Google Scholar]
- 7.Neméth-Cahalan KL, Hall JE. pH and calcium regulate the water permeability of aquaporin 0. J Biol Chem. 2000;275:6777–6782. doi: 10.1074/jbc.275.10.6777. [DOI] [PubMed] [Google Scholar]
- 8.Neméth-Cahalan KL, Kalman K, Hall JE. Molecular Basis of pH and Ca2+ regulation of aquaporin water permeability. J Gen Physiol. 2004;123:573–580. doi: 10.1085/jgp.200308990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yang BX, Verkman AS. Water and glycerol permeabilities of aquaporins 1–5 and MIP determined quantitatively by expression of epitope-tagged constructs in Xenopus oocytes. J Biol Chem. 1997;272:16140–16146. doi: 10.1074/jbc.272.26.16140. [DOI] [PubMed] [Google Scholar]
- 10.Chandy G, Zampighi GA, Kreman M, Hall JE. Comparison of the water transporting properties of MIP and AQP1. J Membr Biol. 1997;159:29–39. doi: 10.1007/s002329900266. [DOI] [PubMed] [Google Scholar]
- 11.Gonen T, et al. Lipid-protein interactions in double-layered two-dimensional AQP0 crystals. Nature. 2005;438:633–638. doi: 10.1038/nature04321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gonen T, Cheng Y, Kistler J, Walz T. Aquaporin-0 membrane junctions form upon proteolytic cleavage. J Mol Biol. 2004;342:1337–1345. doi: 10.1016/j.jmb.2004.07.076. [DOI] [PubMed] [Google Scholar]
- 13.Palanivelu DV, et al. Co-axial association of recombinant eye lens aquaporin-0 observed in loosely packed 3D crystals. J Mol Biol. 2006;355:605–611. doi: 10.1016/j.jmb.2005.10.032. [DOI] [PubMed] [Google Scholar]
- 14.Bok D, Dockstader J, Horwitz J. Immunocytochemical localization of the lens main intrinsic polypeptide (MIP26) in communicating junctions. J Cell Biol. 1982;92:213–220. doi: 10.1083/jcb.92.1.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zampighi G, Simon SA, Robertson JD, McIntosh TJ, Costello MJ. On the structural organization of isolated bovine lens fiber junctions. J Cell Biol. 1982;93:175–189. doi: 10.1083/jcb.93.1.175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zampighi GA, Hall JE, Ehring GR, Simon SA. The structural organization and protein composition of lens fiber junctions. J Cell Biol. 1989;108:2255–2275. doi: 10.1083/jcb.108.6.2255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Harries WEC, Akhavan D, Miercke LJW, Khademi S, Stroud RM. The channel architecture of aquaporin 0 at a 2.2-Å resolution. Proc Natl Acad Sci. 2004;101:14045–14050. doi: 10.1073/pnas.0405274101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Francis P, et al. Functional impairment of lens aquaporin in two families with dominantly inherited cataracts. Hum Mol Genet. 2000;9:2329–2334. doi: 10.1093/oxfordjournals.hmg.a018925. [DOI] [PubMed] [Google Scholar]
- 19.Gonen T, Sliz P, Kistler J, Cheng YF, Walz T. Aquaporin-0 membrane junctions reveal the structure of a closed water pore. Nature. 2004;429:193–197. doi: 10.1038/nature02503. [DOI] [PubMed] [Google Scholar]
- 20.Han BG, Guliaev AB, Walian PJ, Jap BK. Water transport in AQP0 aquaporin: Molecular dynamics studies. J Mol Biol. 2006;360:285–296. doi: 10.1016/j.jmb.2006.04.039. [DOI] [PubMed] [Google Scholar]
- 21.Hashido M, Ikeguchi M, Kidera A. Comparative simulations of aquaporin family: Aqp1, AqpZ, Aqp0, and GlpF. FEBS Lett. 2005;579:5549–5552. doi: 10.1016/j.febslet.2005.09.018. [DOI] [PubMed] [Google Scholar]
- 22.Buzhynskyy N, Hite RK, Walz T, Scheuring S. The supramolecular architecture of junctional microdomains in native lens membranes. EMBO Rep. 2007;8:51–55. doi: 10.1038/sj.embor.7400858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ball LE, et al. Water permeability in C-terminally truncated aquaporin 0 (AQP0 1–243) observed in the aging human lens. Invest Ophthalmol Vis Sci. 2003;44:4820–4828. doi: 10.1167/iovs.02-1317. [DOI] [PubMed] [Google Scholar]
- 24.de Groot BL, Grubmuller H. Water permeation across biological membranes: Mechanism and dynamics of aquaporin-1 and GlpF. Science. 2001;294:2353–2357. doi: 10.1126/science.1066115. [DOI] [PubMed] [Google Scholar]
- 25.de Groot BL, Grubmuller H. The dynamics and energetics of water permeation and proton exclusion in aquaporins. Curr Opin Struct Biol. 2005;15:176–183. doi: 10.1016/j.sbi.2005.02.003. [DOI] [PubMed] [Google Scholar]
- 26.Roux B, Schulten K. Computational studies of membrane channels. Structure. 2004;12:1343–1351. doi: 10.1016/j.str.2004.06.013. [DOI] [PubMed] [Google Scholar]
- 27.Tajkhorshid E, et al. Control of the selectivity of the aquaporin water channel family by global orientational tuning. Science. 2002;296:525–530. doi: 10.1126/science.1067778. [DOI] [PubMed] [Google Scholar]
- 28.Jensen MØ, Mouritsen OG. Single-channel water permeabilities of Escherichia coli aquaporins AqpZ and GlpF. Biophys J. 2006;90:2270–2284. doi: 10.1529/biophysj.105.073965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Hashido M, Kidera A, Ikeguchi M. Water transport in aquaporins: Osmotic permeability matrix analysis of molecular dynamics simulations. Biophys J. 2007;93:373–385. doi: 10.1529/biophysj.106.101170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Shaw DE. A fast, scalable method for the parallel evaluation of distance-limited pairwise particle interactions. J Comput Chem. 2005;26:1318–1328. doi: 10.1002/jcc.20267. [DOI] [PubMed] [Google Scholar]
- 31.Bowers KJ, Dror RO, Shaw DE. The midpoint method for parallelization of particle simulations. J Chem Phys. 2006;124:184109. doi: 10.1063/1.2191489. [DOI] [PubMed] [Google Scholar]
- 32.Bowers KJ, et al. Scalable algorithms for molecular dynamics simulations on commodity clusters. Proceedings of the ACM/IEEE Conference on Supercomputing (SC06); New York: ACM Press; 2006. [Google Scholar]
- 33.Bowers KJ, Dror RO, Shaw DE. Zonal methods for the parallel execution of range-limited N-body simulations. J Comput Phys. 2007;221:303–329. [Google Scholar]
- 34.Zhu FQ, Tajkhorshid E, Schulten K. Collective diffusion model for water permeation through microscopic channels. Phys Rev Lett. 2004;93:224501. doi: 10.1103/PhysRevLett.93.224501. [DOI] [PubMed] [Google Scholar]
- 35.Zhu FQ, Tajkhorshid E, Schulten K. Theory and simulation of water permeation in aquaporin-1. Biophys J. 2004;86:50–57. doi: 10.1016/S0006-3495(04)74082-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hernandez JA, Fischbarg J. Kinetic analysis of water transport through a single-file pore. J Gen Physiol. 1992;99:645–663. doi: 10.1085/jgp.99.4.645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Jiang JS, Daniels BV, Fu D. Crystal structure of AqpZ tetramer reveals two distinct Arg-189 conformations associated with water permeation through the narrowest constriction of the water-conducting channel. J Biol Chem. 2006;281:454–460. doi: 10.1074/jbc.M508926200. [DOI] [PubMed] [Google Scholar]
- 38.Wang Y, Schulten K, Tajkhorshid E. What makes an aquaporin a glycerol channel? A comparative study of AqpZ and GlpF. Structure. 2005;13:1107–1118. doi: 10.1016/j.str.2005.05.005. [DOI] [PubMed] [Google Scholar]
- 39.Yasui M, et al. Rapid gating and anion permeability of an intracellular aquaporin. Nature. 1999;402:184–187. doi: 10.1038/46045. [DOI] [PubMed] [Google Scholar]
- 40.Zardoya R. Phylogeny and evolution of the major intrinsic protein family. Biol Cell. 2005;97:397–414. doi: 10.1042/BC20040134. [DOI] [PubMed] [Google Scholar]
- 41.Bassnett S, Missey H, Vucemilo I. Molecular architecture of the lens fiber cell basal membrane complex. J Cell Sci. 1999;112:2155–2165. doi: 10.1242/jcs.112.13.2155. [DOI] [PubMed] [Google Scholar]
- 42.Costello MJ, McIntosh TJ, Robertson JD. Distribution of gap junctions and square array junctions in the mammalian lens. Invest Ophthalmol Visual Sci. 1989;30:975–989. [PubMed] [Google Scholar]
- 43.Al-Ghoul KJ, et al. Lens structure in MIP-deficient mice. Anat Rec A Discov Mol Cell Evol Biol. 2003;273:714–730. doi: 10.1002/ar.a.10080. [DOI] [PubMed] [Google Scholar]
- 44.Shiels A, et al. Optical dysfunction of the crystalline lens in aquaporin-0-deficient mice. Physiol Genomics. 2001;7:179–186. doi: 10.1152/physiolgenomics.00078.2001. [DOI] [PubMed] [Google Scholar]
- 45.Donaldson P, Kistler J, Mathias RT. Molecular solutions to mammalian lens transparency. News Physiol Sci. 2001;16:118–123. doi: 10.1152/physiologyonline.2001.16.3.118. [DOI] [PubMed] [Google Scholar]
- 46.Moffat BA, Pope MM. Anisotropic water transport in the human eye lens studied by diffusion tensor NMR micro-imaging. Exp Eye Res. 2002;74:677–687. doi: 10.1006/exer.2001.1164. [DOI] [PubMed] [Google Scholar]
- 47.Meinild AK, Klaerke DA, Zeuthen T. Bidirectional water fluxes and specificity for small hydrophilic molecules in aquaporins 0–5. J Biol Chem. 1998;273:32446–32451. doi: 10.1074/jbc.273.49.32446. [DOI] [PubMed] [Google Scholar]
- 48.Evans EA, Calderwood DA. Forces and bond dynamics in cell adhesion. Science. 2007;316:1148–1153. doi: 10.1126/science.1137592. [DOI] [PubMed] [Google Scholar]
- 49.Bettelheim FA, Lizak MJ, Zigler JS., Jr Syneretic response of aging normal human lens pressure. Invest Ophthalmol Visual Sci. 2003;44:258–263. doi: 10.1167/iovs.02-0422. [DOI] [PubMed] [Google Scholar]
- 50.Gerometta R, Zamudio AC, Escobar DP, Candia OA. Volume change of the ocular lens during accommodation. Am J Physiol Cell Physiol. 2007;293:C797–C804. doi: 10.1152/ajpcell.00094.2007. [DOI] [PubMed] [Google Scholar]
- 51.Hiroaki Y, et al. Implications of the aquaporin-4 structure on array formation and cell adhesion. J Mol Biol. 2006;355:628–639. doi: 10.1016/j.jmb.2005.10.081. [DOI] [PubMed] [Google Scholar]
- 52.Engel A, Fujiyoshi Y, Gonen T, Walz T. Junction-forming aquaporins. Curr Opin Struct Biol. 2007;18:1–7. doi: 10.1016/j.sbi.2007.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jorgensen WL, Maxwell DS, Tirado-Rives J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J Am Chem Soc. 1996;118:11225–11236. [Google Scholar]
- 54.Kaminski GA, Friesner RA, Tirado-Rives J, Jorgensen WL. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J Phys Chem B. 2001;105:6474–6487. [Google Scholar]
- 55.Jorgensen WL, Ulmschneider JP, Tirado-Rives J. Free energies of hydration from a generalized born model and an all-atom force field. J Phys Chem B. 2004;108:16264–16270. [Google Scholar]
- 56.Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. In: Intermolecular Forces. Pullman B, editor. Dordrecht, The Netherlands: D Reidel Publishing Company; 1981. pp. 331–342. [Google Scholar]
- 57.Berendsen HJC, Postma JPM, van Gunsteren WF, Dinola A, Haak JR. Molecular dynamics with coupling to an external bath. J Chem Phys. 1984;81:3684–3690. [Google Scholar]
- 58.Shan Y, Klepeis JL, Eastwood MP, Dror RO, Shaw DE. Gaussian split Ewald: A fast Ewald mesh method for molecular simulation. J Chem Phys. 2005;122 doi: 10.1063/1.1839571. 054101. [DOI] [PubMed] [Google Scholar]
- 59.Tuckerman M, Berne BJ, Martyna GJ. Reversible multiple time scale molecular dynamics. J Chem Phys. 1992;97:1990–2001. [Google Scholar]
- 60.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. J Mol Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.