Abstract
During cell volume regulation, intracellular concentration changes occur in both inorganic and organic osmolytes in order to balance the extracellular osmotic stress and maintain cell volume homeostasis. Generally, salt and urea increase the Kms of enzymes and TMAO counteracts these effects by decreasing Kms. The hypothesis to account for these effects is that urea and salt shift the native state ensemble of the enzyme toward conformers that are substrate binding incompetent (BI), while TMAO shifts the ensemble toward binding competent (BC) species. Kms are often complex assemblies of rate constants involving several elementary steps in catalysis, so to better understand osmolyte effects we have focused on a single elementary event, substrate binding. We test the conformational shift hypothesis by evaluating the effects of salt, urea and TMAO on the mechanism of binding glycerol-3-phosphate, a substrate analogue, to yeast triosephosphate isomerase. Temperature-jump kinetic measurements promote a mechanism consistent with osmolyte-induced shifts in the [BI]/[BC] ratio of enzyme conformers. Importantly, salt significantly affects the binding constant through its effect on the activity coefficients of substrate, enzyme and enzyme-substrate complex, and it is likely that TMAO and urea affect activity coefficients as well. Results indicate that the conformational shift hypothesis alone doesn’t account for the effects of osmolytes on Kms.
Keywords: protein-substrate binding, protein dynamics, osmolyte, temperature jump, Kinetics
Cell volume regulation is a trait that is ancient in origin and conserved in all kingdoms of life (1, 2). Extracellular changes resulting in hypo or hyperosmotic conditions frequently occur in living systems, and cells respond to these extracellular changes by importing, exporting or synthesizing osmotically active components so as to balance the extracellular osmotic pressure and maintain volume homeostasis. By way of example, the cellular response in regulating hyperosmotic stress is first to stem the loss of cell water by importing osmotically active extracellular inorganic ions such as Na+ and Cl− (1–4). Such ions exert strong effects on intracellular macromolecule structure and function, and are replaced intracellularly by small organic molecules (organic osmolytes) that are much less perturbing of macromolecule structure and function (1). In contrast to hyperosmotic stress, hypoosmotic stress results generally in rapid loss of intracellular inorganic and organic osmolytes, again to maintain cell volume homeostasis (5). Intracellular osmolyte concentrations can range from tens to hundreds of millimolar, illustrating that the magnitude of osmotic changes can be quite significant (1).
From the importance nature places on cell volume homeostasis in health and disease, and the swings in inorganic and organic osmolyte content in cells, protein function may change markedly during regulatory volume increases and decreases. What effects do salts have on enzyme function and how are the effects modulated by organic osmolytes during osmotic stress? This question is particularly pertinent in the case of kidney collecting duct epithelial cells that must accommodate extraordinary osmotic conditions in antidiuretic animals, with extracellular urea and salt concentrations reaching 1.5 M and 1 M respectively in laboratory rats (6–8). To be sure, kidney collecting duct cells represent an extraordinary example of response to hyperosmotic stress, particularly because urea is not a common osmolyte and it is known to perturb protein function as well as structure (1). In urea-rich cells in mammalian kidney and in sharks and rays, there are osmolytes such as trimethylamine N-oxide (TMAO) or glycerophosphocholine that counteract the effects of urea on protein structure and function (1, 8–10). In such cell types the response of enzymes and other proteins to salt, urea and TMAO are expected to result in the largest effects of osmolytes on protein function.
There are numerous descriptive reports in the literature of osmolyte effects on kcat and Kms of enzymes (1, 11); but because these parameters are composed of multiple rate constants, it is difficult to determine what elementary events are being affected by osmolytes and how. To focus on one elementary event, we undertook investigation of the effects of salt, urea and TMAO on binding of glycerol-3-phosphate (G3P) to yeast triosephosphate isomerase (yTIM). Our goal is to determine how these agents, alone and in combination, affect the elementary event of substrate binding to enzyme.
TIM catalyzes the interconversion of glyceraldehyde 3-phosphate (GAP) and dihydroxyacetone phosphate (DHAP). The enzyme has a well-defined structure. Its active site is close to the surface, and it has been previously shown to bind the inhibitor G3P (12–14). G3P is an analog of the catalytic substrate DHAP, and binds to yTIM like DHAP. However, unlike the natural substrates, G3P is thermally stable with respect to temperature jump experiments and the temperature range studied.
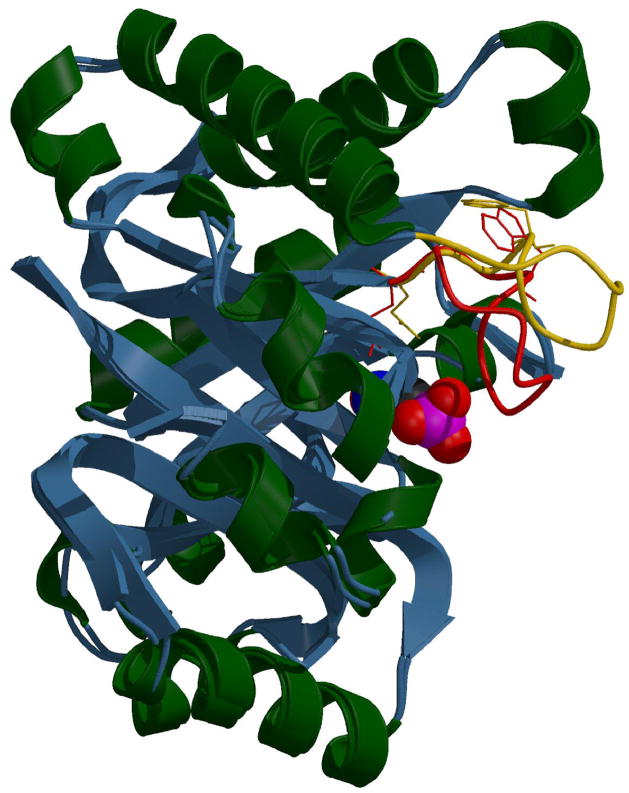
In a previous NMR relaxation studies (12, 13) and fast kinetic studies employing laser induced temperature (T-jump) relaxation spectroscopy methods (14), the binding of ligands to the active site of TIM under physiological solution conditions was shown to proceed via the formation of a TIM·ligand encounter complex in which a protein surface loop, loop 6, that guards the active site crevice is in a presumably open conformation. This loop closes over the protein·ligand complex to form the productive enzyme active Michaelis complex (Figure 1; 12–14). This flexible loop is responsible for shifting the catalytic base, Glu165, by about 2 Å to contact the substrate, and centering it in an optimal position between the substrate’s relevant carbons (15–17). While many of the crucial catalytic contacts, for example the polarizing groups His95 and Lys12, and many of the phosphate hydrogen bond partners, such as the NH groups of Gly233 and Ser211, are involved in a “preformed” substrate pocket, and do not shift substantially upon ligation, others that are attached to loop 6, such as the catalytic base Glu165 and another phosphate ligand, the NH of Gly171, shift into place upon the loop movement.
Figure 1.
Ribbon diagram of yeast triosephosphate isomerase with the overlaid conformations of catalysis controlling loop 6, yellow (open) and red (closed), shown as stick diagrams. The motion of the indole ring of Trp168 and the active site residue Glu165 shown as stick diagrams. The active site loop descends down to engulf the substrate and position some of the catalytic residues. The loop’s tryptophan rotates by about 50° between the two conformations
In laser induced T-jump relaxation spectroscopy, the approach employed in this study, a laser pulse, tuned to a weak water band in the near IR, rapidly heats the volume of water within the laser beam. The heated system subsequently relaxes to an equilibrium set by the new temperature, and the relaxation kinetics can be monitored if a suitable probe of structure is available. For the previous and present studies, this probe is the emission from the indole ring of a Trp residue strategically located in loop 6; the emission from the indole ring is sensitive to the conformation of the loop (closed versus open). Our T-jump spectrometer has a resolution of about 20 ns, which is sufficient to resolve much of the kinetic pathway of G3P binding to TIM.
Materials and Methods
Sample preparation
Wild type yeast triosephosphate isomerase, glycerol 3-phosphate (G3P), glyceraldehyde phosphate (GAP), dihydroxyacetone phosphate (DHAP), urea, and TEA buffer were all purchased from Sigma-Aldrich Co (St. Louis, MO). NADH and α-glycerophosphate dehydrogenase were purchased from Roche Applied Science (Indianapolis, IN). Recrystallized TMAO was prepared as previously reported (9). Enzymatic activity was determined by the conversion of GAP to DHAP in the presence of yTIM and glycerol 3-phosphate dehydrogenase (18). The samples for steady-state fluorescence measurements contained 6 μM yTIM with various concentrations of G3P, different salts, urea, or TMAO, in 55 mM triethanolamine:HCl buffer pH 7.6 at 21°C. The samples for temperature jump measurements were prepared similarly except that the concentration of yTIM was increased to 80 μM to accommodate the smaller pathlength used (0.02 vs 1 cm).
Fluorescence spectroscopy
The fluorescence spectra were measured on a FluoroMax-2 spectrofluorimeter (Instruments S. A. Group, Edison, NJ) with a spectral resolution 1 nm, using 1 cm path length quartz cuvettes. The excitation wavelength was set at 290 nm and the emission spectrum monitored between 300 and 420 nm. The dissociation constant, Kd, was determined by monitoring the change in yTIM tryptophan fluorescence emission, ΔF, as a function of G3P concentration, as described (14).
Temperature jump spectroscopy
The yTIM-G3P binding kinetics in the range of ns-ms were resolved by the laser induced temperature jump spectroscopy as previously described in detail (14, 19, 20).
Results
Kinetics and Mechanisms
The studies reported here are on wild type yeast triosephosphate isomerase from Saccharomyces cerevisiae (yTIM). yTIM contains three tryptophan residues: Trp92, Trp159, and Trp168. The first two tryptophans are buried within the yTIM subunit but Trp168 occurs at the N-terminal hinge of loop 6 (Fig. 1). Studies done on mutant yTIMs (18, 21, 22) show that mutations of Trp90 and Trp157 to tyrosine or phenylalanine do not affect the enzyme kinetics or structure of the enzyme and also that the major effect on the protein’s emission properties from substrate binding arises from Trp168. Although we have chosen to work with the wild type protein, steady state and kinetics control experiments done with yTIM vs. the one Trp mutant with Trp90Tyr and Trp157Phe gave the same results (unpublished control studies). Hence, binding results as well as kinetic emission studies of wild type yTIM report only on Trp168 and directly report on changes in conformation of the catalytically critical loop 6 (14).
In our previous study, we found that a two-step model (Eq.1) accurately describes the kinetics of the binding of G3P to yTIM (low ionic strength and buffer; 14):
| (1) |
The first step in the binding process involves an ‘encounter’ complex between yTIM and G3P with, we conjecture, loop 6 being open to permit entry of the ligand to the binding site. Only a single ‘slow’ (microsecond) step was observed in the T-jump kinetics of the previous study (14). However, the rate saturates with increasing G3P concentration and is not characteristic of encounter complex event. The formation of the encounter complex, which would exhibit bimolecular behavior showing a linear increase in rate with increasing free G3P and TIM, was postulated to occur on the sub-microsecond time scale (14; see also 12, 13). We inferred that this process was too fast to be observed in our previous study, and it may well be the fast relaxation time occasionally detected in experiments discussed below. The second step of the kinetic scheme above is unimolecular involving a protein-ligand isomerization in which it seems reasonable to suppose that the loop closes over the already bound ligand. In agreement with our previous study (14), values determined for the microscopic rate constants in 0.05 M NaCl give a calculated Kd equivalent to the experimental Kd determined in equilibrium binding studies of G3P with yTIM at low salt and absence of osmolyte (see Table 1).
Table 1.
The microscopic rate constants derived from fits to the data.
| Solvents | 0.05 M NaClc | 0.3 M TMAOb | 0.8 M TMAOa | 0.4 M NaCla | 1 M ureaa |
|---|---|---|---|---|---|
| Kd(mM)d | 0.6 ± 0.1 | 0.6 ± 0.1 | 1.3 ± 0.2 | 4.7 ± 0.2 | 6.7 ± 0.8 |
| koff/kon(mM) | 9.9 ± 1.3 | 11 ± 3 | 16 ± 11 | 69 ± 12 | 198 ± 78 |
| kclose(ms−1) | 31.7 ± 0.9 | 16.1 ± 1.1 | 18.6 ± 3.0 | 21.2 ± 1.1 | 23.8 ± 3.6 |
| kopen(ms−1) | 1.5 ± 0.7 | 1.6 ± 0.5 | 2.1 ± 1.8 | 2.8 ± 0.3 | 4.1 ± 0.8 |
| kuopen(ms−1) | --- | --- | 2.0 ± 0.1 | 1.1 ± 0.2 | 0.7 ± 0.1 |
| kuclose(ms−1) | 0.2 ± 0.4 | 0.1 ± 0.3 | 0.5 ± 0.1 | ||
| kd/calc(mM)e | 0.5 ± 0.2 | 0.9 ± 0.4 | 1.6 ± 2.0 | 8.2 ± 1.9 | 20 ± 16 |
Each of these sample solvents contain 0.4 M NaCl and 0.05 M TEA
The sample solvent contains 0.5 M TEA
The sample solvent contains 0.05 M Tris and 0.05 M NaCl
Kd is the dissociation constant determined by fluorescence measurements
Numerous T-jump relaxation studies were conducted to observe the effects of salt, urea, and TMAO on the mechanism of G3P - yTIM binding (Eq. 2):
| (2) |
As in our previous studies (14), the equilibrium of the chemical system was suddenly perturbed by a rapid change in temperature, induced by irradiating the protein solution with a nanosecond pulse of near IR laser light. The system temperature was increased to a final temperature, Tf, within 20 ns (as described in Methods), and relaxation of the system to the new equilibrium temperature Tf, was monitored by the change in tryptophan fluorescence.
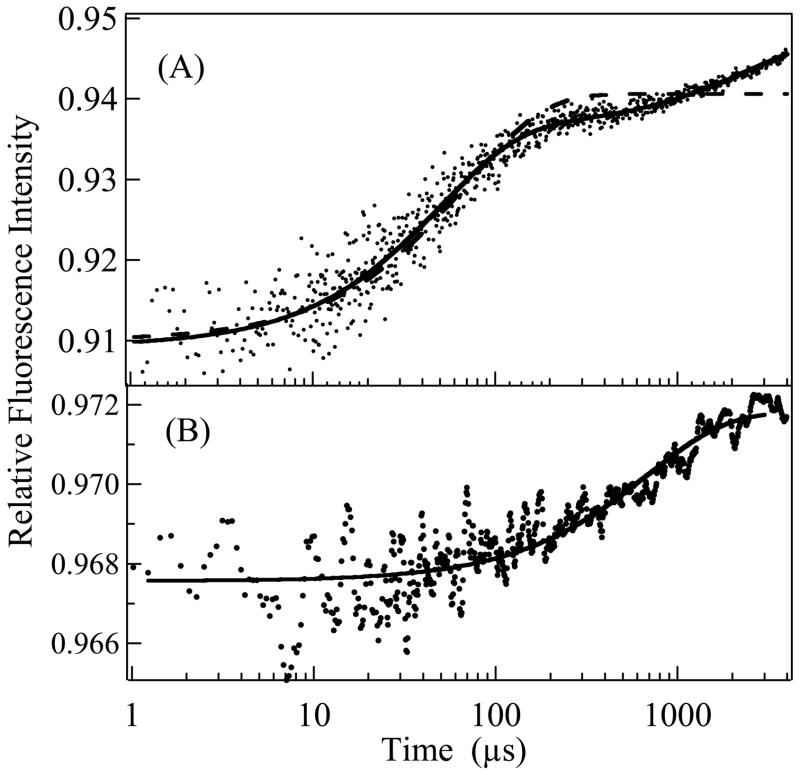
Figure 2A shows T-jump data of the system containing 80 μM yTIM with 320 mM (total) G3P, 400 mM NaCl, and 1 M urea. The data are representative of results obtained in the presence of either high salt or high salt plus urea or TMAO. The kinetic trace is overlaid by both single and double exponential fits to the data. It is obvious that a single exponential function, which sufficed in our yTIM study at low salt concentration (14), is inadequate at these new experimental conditions, and a double exponential function is needed to achieve a proper fit. In addition to the two relaxation times shown in Fig. 2A, there is evidence of a very fast event occurring in the 200–400 ns range (data not shown). The amplitude of this fast signal is quite small and clearly evident only under the most favorable circumstances. This fast relaxation time probably correlates with the initial encounter of G3P with yTIM since the time is close to that predicted for a binding event under diffusion control (see ref. 14). Since we have poor signal/noise in this region and the signal of this fast event is small, we are unable to fully investigate and characterize the underlying process. However, the fast time is well separated from the other observed relaxation times so that the kinetics of the fastest signal does not interfere with a quantitative analysis of the relatively slower and well-resolved relaxation times shown.
Figure 2.
(A) Temperature jump fluorescence intensity profile for G3P complexed with yTIM (λex = 275–302 nm, λem = 340 nm) in response to a 12°C temperature jump to Tf = 21 ± 1.5°C, (individual points shown). Single (dashed line) and double exponential fits to the data are shown (solid line). System conditions: [yTIM] = 0.08 mM, [G3P] = 320 mM in 1.0 M urea, 0.4 M NaCl, 55 mM TEA pH 7.6 buffer. (B) Temperature jump fluorescence emission intensities for unliganded yTIM in response to 9°C temperature jump to Tf = 34 ± 1.5°C. System conditions: 0.08 mM yTIM in 1.0 M urea, 0.4 M NaCl, 55 mM TEA pH 7.6 buffer. Single exponential fit gives kobs = 1.45 (±0.16) ms−1.
The present kinetic results, taken at higher ionic strengths with and without TMAO and/or urea, consistently show double exponential behavior on time scales slower than 10 μs. One is on the microsecond time scale that correlates closely to the signals observed previously at low ionic strength, and the other is nearer to one millisecond. The double exponential requires incorporation of an additional event into our kinetic model, one that occurs on a slower timescale than the two processes evident in low salt (Eq. 1). There is much evidence in the literature that the encounter complex forms too rapidly to suggest that the now observed millisecond process is encounter complex formation (14). Therefore, the new process must be either on-pathway (Eq. 3) or off-pathway (Eq. 4).
| (3) |
| (4) |
The scheme of Eq. 3 can be ruled out for several reasons. The first is that it does not fit well with the physical model of the binding process obtained in our previous study (14). In low salt, we found that Kd determined from equilibrium measurements is in agreement with Kd calculated from the microscopic rate constants (Eq. 1) determined in our earlier study. These results show no evidence of an extra step. Another reason is that for yTIM, substrate unbinding/loop motion is thought to be rate limiting for kcat (18, 22) so that a millisecond on-pathway process slower than the sub-millisecond kcat is unlikely. Finally, as described in detail below, unliganded yTIM in high salt and urea (Fig. 2B) is shown to yield a relaxation time on the millisecond time scale, similar to that observed in presence of G3P. This finding identifies the unbound yTIM as the protein species affected by the inorganic and organic osmolytes.
The kinetic model of Eq. 4 is a minimal model that accounts for experimental observations in presence of high salt, TMAO and/or urea. It seems reasonable that yTIM in solution exists as an ensemble of conformations, a fraction of which is competent to bind G3P and the remainder not. In order to determine if yTIM is in equilibrium between binding competent and incompetent conformations, which is likely to involve loop open and closed conformers that modulate the Trp emission of Trp168 of the loop guarding ligand entry, T-jump studies were performed on unliganded yTIM in high salt. These experiments yielded a relaxation signal in the millisecond time range (Fig. 2B) that does not occur in low salt. Although small, the signal’s amplitude of ~0.6% of total fluorescence is substantially larger than the 0.08% change in the intrinsic fluorescence arising from the 0.5 degree cooling of the system that occurs three milliseconds after excitation with the Nd:YAG pulse. The observed rate of ~1 (ms)−1 is consistent with k3obs in studies described later on G3P binding to yTIM (Fig. 3B; see below). Thus, it seems reasonable to assign the slowest observed rate in our T-jump data to unliganded yTIM loop motion.
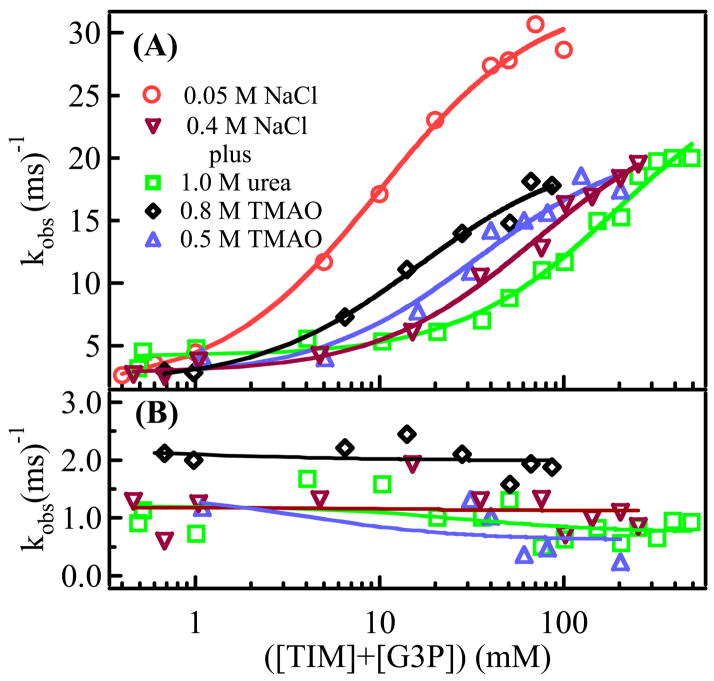
Figure 3.
Observed relaxation rates for G3P complexed to yTIM. The original T-jump data at each concentration were fit to a double exponential. Fits to the kobs vs. ([yTIM] + [G3P])free data gwere performed using the equations 6 (panel A) and 7 (panel B) as described in the text. The symbols used for the graph are: orange, ○, 0.05 M NaCl, 50 mM Tris-HCl; red, ▽, 0.4 M NaCl, 55 mM TEA; blue, △, 0.5 M TMAO, 0.4 M NaCl, 55 mM TEA; black, ◇ 0.8 M TMAO, 0.4 M NaCl; green, □ 1.0 M urea, 0.4 M NaCl, 55 mM TEA. The experiment in 0.05 M NaCl was performed at pH 7.8. All other samples were done at pH 7.6. The final temperature for all runs was 20 – 21 ºC.
The observed relaxation times in our experiments are sufficiently separated in time to be decoupled. Assuming that the formation of the encounter complex is the fastest step, the next fastest is loop closure step in the isomerization of yTIM•G3P, and the slowest step is unliganded yTIM loop motion, the three observed relaxation times depend on the microscopic rate constants for the kinetic model of Eq. 4 in the following manner (23–25):
| (5) |
| (6) |
| (7) |
The individual rate constants can be determined from studies performed as a function of the total concentration of free yTIM plus free G3P in the solution at equilibrium at Tf.
Figure 3 shows the dependence of the observed relaxation times on free [yTIM] and [G3P] for various salt, TMAO, and urea concentrations studied here. Two rate constants are consistently observed at high salt. Table 1 catalogs the calculated microscopic rate constants derived from fits to data shown in Fig. 3. The correlation of these variables is shown in the matrix associated with Table 1, where R2 represents the Pearson correlation coefficient between each set of variables. Pearson’s R2 values quantitatively compare the pairwise correlation of parameters, with R2 = 0 signifying no correlation and R2 = 1 indicating total correlation. Table 1 provides a means of determining how urea and TMAO affect steps in the reaction sequences in low (Eq. 1) and high salt (Eq. 4).
Debye-Hückel limiting law effects on Kd
In determining the dependence of Kd on salt, it is useful to establish whether electrostatic interactions involved in G3P-yTIM binding respond to the effects of ionic strength in accordance with the Debye-Hückel limiting law. For dissociation of a protein-ligand complex bearing a net charge into ionized free protein and ligand, salt will affect the dissociation constant by affecting the activity coefficients of these species as given in Eq. 8a.
| (8a) |
In Debye-Hückel terms, Figure 4 shows that pKd decreases with ionic strength of solution following the relationship (Eq. 8b) (26),
Figure 4.
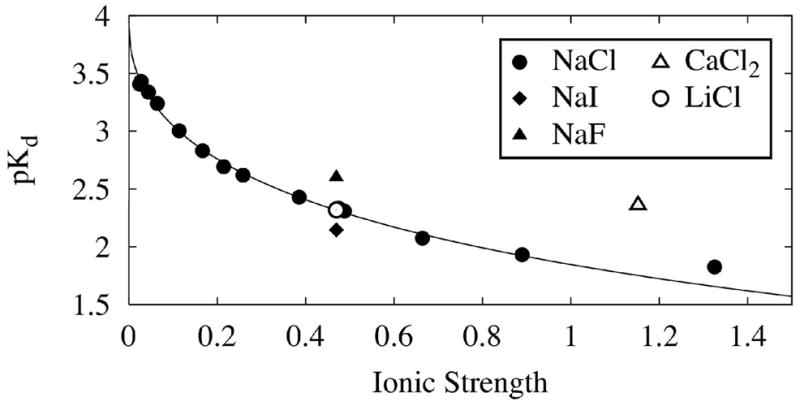
Dependence of pKd on ionic strength. Dissociation constants of G3P-yTIM were determined as a function of ionic strength of solution using NaCl in the presence of 55 mM TEA buffer, pH 7.6. The solid line is the fit to equation 5, with I as the ionic strength of solutions of NaCl (filled circles), and , and represent the square of the charges on protein, ligand and complex, filled triangle (NaF), filled diamond (NaI), open circle (LiCl), open triangle (CaCl2).
| (8b) |
where I is the ionic strength of solution, pKd and are −log of the dissociation constant in presence and absence of salt, and , and are squares of the charges on protein, ligand and complex, and b is an ion specific parameter (0.6 in our case). For small ions, the expression should apply to 0.3 ionic strength or thereabouts (26) and the assumptions and approximations applicable to the system have been discussed (27). The fit gives −6.4 for the term ( ), which at pH 7.5 can be accommodated with protein, G3P and protein-ligand complex having charges of −6, −2, (28) and −6.8 respectively. These numbers could additionally change as a function of salt and osmolyte concentration, especially in the case of G3P, because the second protonation pKa (6.65) is close to the experimental pH (29). Note that the negative protein charges are net charges. The binding site itself is positively charged, but it is primarily the negative net charge of the protein that contributes to the activity coefficient, with secondary effects of the charge distribution that are not explicitly taken into account here. The plot portrays the salt dependence in Debye-Hückel terms with reasonable species charges over a significant ionic strength range. What is unaccounted for in equations 8a & b is the salt-induced change in binding mechanism from low salt (Eq. 1) to high salt (Eq. 4). In addition, we observed effects due to ion type as with the alkali halides and calcium chloride seen in Figure 4. Such effects can arise either from different b values (Eq. 8b) or from Hofmeister effects, but they are not expected to be much of a factor in cell volume regulation. The reason is that inorganic ions principally involved in cell volume regulation are sodium and chloride; the effects seen with NaCl in Figure 4 should be representative of those occurring in cell volume regulation.
Effects of salt, TMAO and/or urea on Kd
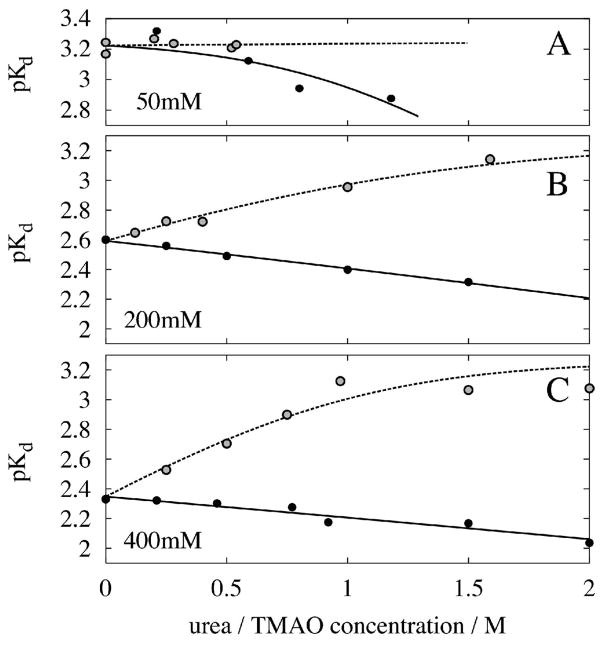
Figure 5 plots pKd as a function of urea and TMAO concentrations at fixed NaCl concentrations of 0.05, 0.2 and 0.4 M. With one exception, the plots show clearly that urea increases while TMAO decreases Kd at all salt concentrations. The exception is in low salt (50 mM) where TMAO appears to have no effect on Kd.
Figure 5.
Dependence of the observed pKd on urea (black circles, continuous lines) and TMAO (grey circles, broken lines) in different salt concentrations. Note that the pKd values saturate at about 3.26, which is assumed to be the intrinsic binding affinity pKL (see eq. 9b). A fit to eq. 9c resulted in mu and mt values that depend on salt concentration. At 50, 200, and 400 mM NaCl mu is −6, −1.3, and −0.9 kJ/molM, respectively. Salt dependence of mt is 3.4 and 5.5 at 200 and 400 mM salt. The value at 50 mM salt could not be determined, because of the small Ko of the pre-equilibrium (see eq. 9c). pKo changes from −1 at 50 mM to +0.56 and +0.86 at 200 and 400 mM salt, respectively. Values are 0.14, 0.2 and 0.02 for Kr in 400 mM salt and in 400 mM salt containing 1M urea and 0.8M TMAO respectively.
To understand these observations it is important to recognize that TMAO and urea generally have opposite effect on the Kms of enzymes, with urea increasing Kms while TMAO decreases them (1, 27, 30). A mechanism to explain the opposing effects of TMAO and urea on ligand and protein binding proposes that the unbound protein consists of two forms, binding competent and binding incompetent, and that urea and TMAO shift the populations of these species in opposite directions (30). As described above, kinetic experiments that involves salt effects on G3P binding to yTIM also provides evidence of a mechanism requiring binding competent and binding incompetent forms of yTIM in high salt. Accordingly, for analysis of the effects of salt, urea and TMAO on equilibrium binding of G3P to TIM we adopt a simplified model of Eq. 4 that involves equilibrium binding of G3P to the binding competent (BC) form of yTIM. The model (Eqs. 9a,b and c) assumes a linear free energy dependence of the equilibrium constant of the conformational change (Kr) on urea and TMAO concentration,
| (9a) |
| (9b) |
| (9c) |
with KL assumed to be independent of osmolyte concentration. Results of the fittings in Figures 5a, b, and c are given in the caption of Fig. 5.
Discussion
The puzzle of how solutes affect protein structure and function is, arguably, the oldest and most elusive question in molecular biophysics, tracing at least as far back as Hofmeister’s work in the 1880s (31). In virtually all organisms, this puzzle is played out to varying degrees in the constantly occurring processes of cell volume regulation, where changing intracellular salt and organic osmolyte concentrations result in functional effects on the impressive array of proteins in the cell. In general, numerous measurements have shown that salts and the organic osmolyte, urea, increase Kms of enzymes while the counteracting osmolyte, TMAO, decreases them (1, 10, 30, 32). The central hypothesis proposed by Mashino and Fridovich to explain these general effects is that urea and salt affect protein function by shifting the ensemble of the enzyme’s native state so as to populate binding incompetent conformers (binding incompetent), thus decreasing substrate binding, while TMAO increases binding by shifting the native state ensemble toward functionally competent conformers (30). The results of the work described here tests this hypothesis of Mashino and Fridovich by evaluating inorganic and organic osmolyte effects on Kd, the substrate dissociation elementary event, instead of Km, a kinetic parameter with units of a dissociation constant that generally contains rate constants of elementary catalytic events in addition to those for substrate dissociation. Osmolyte effects on Kd eliminates ambiguity by being more readily interpretable at the molecular level than effects on Km.
Our T-jump results provide strong evidence that the native state of yTIM consists of binding competent (BC) and binding incompetent (BI) species that interconvert. At low salt, the equilibrium lies so far in favor of BC that no relaxation signal is seen for the BI <-> BC equilibrium and TMAO causes no change in pKd (see Figure 5A) (14). But with addition of salt, T-jump of yTIM in the absence of substrate shows single exponential relaxation kinetics (see Fig. 2B) indicative of interconverting yTIM species. In salt, T-jump kinetics of G3P binding to yTIM reveals a mechanism (Eq. 4) involving interconverting binding competent and binding incompetent conformers of free protein, with a rate constant similar to that in Figure 2B.
In addition to the effect of salt on the [BI]/[BC] ratio, the effects of urea and TMAO at low, intermediate, and high salt concentrations show that Kd increases with urea and decreases with TMAO (Fig. 5). All these observations are in agreement with numerous observations regarding urea, TMAO and salt effects on Kms (1, 10, 30, 32, 33) as well as the molecular mechanism hypothesized by Mashino and Fridovich. A closer look at the T-jump results, however, indicates that a significant part of the observed effects on Kd may arise from sources other than shifting the BI <-> BC equilibrium. A consideration of the kinetic scheme of Eq. 4 and the results of the T-jump experiments in Table 1 reveals that in the presence of high salt (0.4 M NaCl), 0.8 M TMAO decreases and 1M urea increases the dissociation constant (koff kon) by as much or more than the effects of these osmolytes on the [BI]/[BC] ratio ( ). In an effort to determine how much of an effect to expect on the [BI]/[BC] equilibrium constant we analyzed osmolyte effects on pKd values determined by equilibrium methods and assuming TMAO and urea affect the BI <-> BC equilibrium constant Kr, but not the dissociation constant of G3P-yTIM into G3P and yTIM (KL). Results of this analysis (see Fig. 5 and figure legend) gave Kr values of 0.14, 0.2 and 0.02 for 400 mM salt, and 400 mM salt containing 1M urea and 0.8M TMAO respectively. T-jump experiments were also analyzed in terms of kinetically determined [BI]/[BC] equilibrium constants ( ), but the values obtained (0.09, 0.7 and 0.1) under experimental conditions identical to the equilibrium experiments do not compare favorably. From this lack of agreement, we conclude that assuming KL is independent of urea and TMAO effects is too restricting and, as in the T-jump experiments, they also affect the substrate dissociation event.
The question is, how can these results be rationalized at the molecular level? Osmolyte-induced shifts in the [BI]/[BC] ratio can be readily understood from hydrogen-deuterium exchange experiments performed on proteins in the presence and absence of TMAO or urea (34). Exposure of amide protons to solvent during protein structural fluctuations results in HD exchange, and because TMAO has an unfavorable and urea a favorable interaction with the peptide backbone of proteins, TMAO suppresses the native state structural fluctuations while urea increases them (34). These effects occur with all proteins, resulting in TMAO-induced shifts in the native state to a more compact ensemble and urea-induced shifts result in a more flexible and dynamic native ensemble. Provided that binding competent species are associated with more compact and binding incompetent with less compact conformations, their effects on native state fluctuations, and therefore the [BI]/[BC] ratio, are sufficient to explain the generally observed effects of urea and TMAO on Kms and Kd.
While the above rationalizes part of the T-jump results, it does not explain the observation that urea and TMAO shift the G3P-yTIM dissociation (koff kon in Eq. 4) in opposite directions. For this aspect of the mechanism in Eq. 4 we may consider that organic osmolyte-induced conformational shifts might occur in the G3P-yTIM complex, with the complex being structurally less stable in urea than in TMAO. Thermodynamically, this could account for the effects on koff kon, though the degree of destabilization or stabilization by urea or TMAO requires further studies. There are, however, other possible reasons koff kon could change as a function of urea and TMAO concentrations that do not involve protein conformation. In fact, salt has an effect on the conformational ensemble (Figure 3) as well as a significant effect on Kd derived through salt influence on the activity coefficients of G3P, yTIM and G3P-yTIM (Eqs. 8a and 8b). The Debye-Hückel behavior (Figure 4) showing that salt affects Kd by affecting activity coefficients of G3P, TIM and G3P-TIM, suggests that TMAO and urea may also affect Kd by altering substrate activity coefficients, e.g. G3P. In fact, evidence of the effect of urea on the activity coefficient of 3′-CMP was recently presented for 3′-CMP binding to RNase A (35). Seldom are changes in activity coefficients considered in equilibrium constant determinations, but such influences should be considered the norm in thermodynamically non-ideal conditions present in the 0.2 – 0.4 M physiological salt concentration range (1, 11, 27) and at high intracellular osmolyte concentrations.
The present study provides the first detailed study of the effects of inorganic and organic osmolytes on an elementary event in enzyme catalysis as characterized by the substrate dissociation constant, Kd. The results show that increasing salt concentration in the intracellular physiological range shifts the native state ensemble of yTIM toward binding incompetent conformers thereby increasing Kd. Salt also increases Kd by affecting the activity coefficients of G3P, yTIM and the complex G3P-yTIM in accordance with the Debye-Hückel Limiting law. At fixed salt concentrations, urea increases and TMAO decreases Kd. While all of these results are supportive of the reigning hypothesis that counteraction of urea and salt effects on Kms by TMAO is due to the opposite directions these agents shift the [BI]/[BC] ratio that comprises the native state ensemble of an enzyme, the detailed mechanism reveals the inorganic and organic osmolytes affect other aspects of substrate binding as much as they do the [BI]/[BC] ratio. The additional effects beyond shifts in the [BI]/[BC] ratio involve salt effects on activity coefficients of species involved in substrate binding; urea and TMAO may also have effects on substrate activity coefficients and/or osmolyte-induced effects on the stability of the G3P-yTIM closed conformer. In addition, urea and TMAO may affect the thermodynamic stability of the enzyme-substrate complex, with urea decreasing and TMAO increasing stability. Understanding the effects of changing inorganic and organic osmolyte concentrations on protein function in cells undergoing cell volume regulation appears to be more complex and intricate than can be accounted for by shifts in the [BI]/[BC] ratio.
Abbreviations
- TIM
triosephosphateisomerase
- GAP
glyceraldehyde
- 3-DHAP
phosphate;dihydroxyacetone phosphate
- G3P
glycerol-3-phosphate
- TMAO
trimethylamine N-oxide
Footnotes
Work supported by grants from the National Institutes of Health, EB001958 (RHC), GM068036 (RHC), and GM049760 (DWB).
References
- 1.Hochachka PW, Somero GN. Mechanism and Process in Physiological Evolution. Oxford University Press; Oxford: 2002. Biochemical Adaptation. [Google Scholar]
- 2.Pasantes-Morales H, Lezama RA, Ramos-Mandujano G, Tuz KL. Mechanisms of cell volume regulation in hypo-osmolality. Am J Med. 2006;119:S4–S11. doi: 10.1016/j.amjmed.2006.05.002. [DOI] [PubMed] [Google Scholar]
- 3.Chamberlin ME, Strange K. Anisosmotic cell volume regulation: a comparative view. Am J Physiol. 1989;257:C159–C173. doi: 10.1152/ajpcell.1989.257.2.C159. [DOI] [PubMed] [Google Scholar]
- 4.Strange K. Cellular volume homeostasis. Adv Physiol Educ. 2004;28:155–159. doi: 10.1152/advan.00034.2004. [DOI] [PubMed] [Google Scholar]
- 5.Verbalis JG. Whole-body volume regulation and escape from antidiuresis. Am J Med. 2006;119:S21–S29. doi: 10.1016/j.amjmed.2006.05.004. [DOI] [PubMed] [Google Scholar]
- 6.Beck F, Dorge A, Rick R, Thurau K. Intra- and extracellular element concentrations of rat renal papilla in antidiuresis. Kidney Int. 1984;25:397–403. doi: 10.1038/ki.1984.30. [DOI] [PubMed] [Google Scholar]
- 7.Garcia-Perez A, Burg MB. Importance of organic osmolytes for osmoregulation by renal medullary cells. Hypertension. 1990;16:595–602. doi: 10.1161/01.hyp.16.6.595. [DOI] [PubMed] [Google Scholar]
- 8.Garcia-Perez A, Burg MB. Renal medullary organic osmolytes. Physiol Rev. 1991;71:1081–1115. doi: 10.1152/physrev.1991.71.4.1081. [DOI] [PubMed] [Google Scholar]
- 9.Wang A, Bolen DW. A naturally occurring protective system in urea-rich cells: mechanism of osmolyte protection of proteins against urea denaturation. Biochemistry. 1997;36:9101–9108. doi: 10.1021/bi970247h. [DOI] [PubMed] [Google Scholar]
- 10.Yancey PH, Somero GN. Counteraction of urea destabilization of protein structure by methylamine osmoregulatory compounds of elasmobranch fishes. Biochemical Journal. 1979;183:317–323. doi: 10.1042/bj1830317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yancey PH, Clark ME, Hand SC, Bowlus RD, Somero GN. Living with water stress: evolution of osmolyte systems. Science. 1982;217:1214–1222. doi: 10.1126/science.7112124. [DOI] [PubMed] [Google Scholar]
- 12.Rozovsky S, Jogl G, Tong L, McDermott AE. Solution-state NMR investigations of triosephosphate isomerase active site loop motion: Ligand release in relation to active site loop dynamics. J Mol Biol. 2001;310:271–280. doi: 10.1006/jmbi.2001.4673. [DOI] [PubMed] [Google Scholar]
- 13.Rozovsky S, McDermott AE. The time scale of the catalytic loop motion in triosephosphate isomerase. J Mol Biol. 2001;310:259–270. doi: 10.1006/jmbi.2001.4672. [DOI] [PubMed] [Google Scholar]
- 14.Desamero R, Rozovsky S, Zhadin N, McDermott A, Callender R. Active Site loop Motion in Triosephosphate Isormerase: T-Jump relaxation Spectroscopy of Thermal Activation. Biochemistry. 2003;42:2941–2951. doi: 10.1021/bi026994i. [DOI] [PubMed] [Google Scholar]
- 15.Lolis E, Alber T, Davenport RC, Rose D, Hartman FC, Petsko GA. Structure of the Yeast Triosephosphate Isomerase at 1.9 Å Resolution. Biochemistry. 1990;29:6609–6618. doi: 10.1021/bi00480a009. [DOI] [PubMed] [Google Scholar]
- 16.Kursula I, Partamen S, Lambeir A-M, Antonov DM, Augustyns K, Wierenga RK. Structural Determinants for Ligand Binding and Catalysis of Triosephosphate Isomerase. Eur J Biochem. 2001;268:5189–5196. doi: 10.1046/j.0014-2956.2001.02452.x. [DOI] [PubMed] [Google Scholar]
- 17.Kursula I, Wierenga RK. Crystal Structure of Trisoephosphate Isomerase Complexed with 2-Phosphoglycolate at 0.83-Å Resolution. J Biolog Chem. 2003;278:9544–9551. doi: 10.1074/jbc.M211389200. [DOI] [PubMed] [Google Scholar]
- 18.Putman SJ, Coulson AF, Farley IR, Riddleston B, Knowles JR. Specificity and kinetics of triose phosphate isomerase from chicken muscle. Biochemical Journal. 1972;129:301–310. doi: 10.1042/bj1290301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Deng H, Zhadin N, Callender R. The Dynamics of Protein Ligand Binding on Multiple Time Scales: NADH Binding to Lactate Dehydrogenase. Biochemistry. 2001;40:3767–3773. doi: 10.1021/bi0026268. [DOI] [PubMed] [Google Scholar]
- 20.Gulotta M, Gilmanshin R, Callender RH, Dyer RB. Core formation in Apomyoglobin: probing the upper reaches of the folding energy landscape. Biochemistry. 2001;40:5137–5143. doi: 10.1021/bi002256n. [DOI] [PubMed] [Google Scholar]
- 21.Sampson NS, Knowles JR. Segmental movement: definition of the structural requirements for loop closure in catalysis by triosephosphate isomerase. Biochemistry. 1992;31:8482–8487. doi: 10.1021/bi00151a014. [DOI] [PubMed] [Google Scholar]
- 22.Sampson NS, Knowles JR. Segmental motion in catalysis: investigation of a hydrogen bond critical for loop closure in the reaction of triosephosphate isomerase. Biochemistry. 1992;31:8488–8494. doi: 10.1021/bi00151a015. [DOI] [PubMed] [Google Scholar]
- 23.Hammes GG, Schimmel PR. Rapid Reactions and Transient states. In: Boyer PD, editor. The Enzymes. Academic Press; New York: 1970. pp. 67–114. [Google Scholar]
- 24.Bernasconi CF. Relaxation Kinetics. Academic Press; New York: 1976. [Google Scholar]
- 25.Cantor CR, Schimmel PR. Biophysical Chemistry. Vol. 3. W. H. Freeman and Company; San Francisco: 1980. [Google Scholar]
- 26.Edsall JT, Wyman J. Biophysical Chemistry. I. Academic Press Inc.; London: 1958. [Google Scholar]
- 27.Loftfield RB, Eigner EA. Ionic strength effects in the aminoacylation of valine transfer ribonucleic acid. J Biol Chem. 1967;242:5355–5359. [PubMed] [Google Scholar]
- 28.Wade RC, Gabdoulline RR, Ludemann SK, Lounnas V. Electrostatic Sreering and Ionic tethering in Enzyme-Ligand Binding: Insights from Simulations. Proc Natl Acad Sci (USA) 1998;95:5942–5949. doi: 10.1073/pnas.95.11.5942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sober HA. Handbook of Biochemistry. The Chemical Rubber Co.; Cleveland: 1970. [Google Scholar]
- 30.Mashino T, Fridovich I. Effects of urea and trimethylamine-N-oxide on enzyme activity and stability. Archives of Biochemistry & Biophysics. 1987;258:356–360. doi: 10.1016/0003-9861(87)90355-9. [DOI] [PubMed] [Google Scholar]
- 31.Hofmeister F. Zur Lehre von der Wirkung der Salze. Zweite Mittheilung. Archiv für experimentelle Pathologie und Pharmakologie. 1888;24:247–160. [Google Scholar]
- 32.Peterson DP, Murphy KM, Ursino R, Streeter K, Yancey PH. Effects of dietary protein and salt on rat renal osmolytes: covariation in urea and GPC contents. Am J Physiol. 1992;263:F594–5600. doi: 10.1152/ajprenal.1992.263.4.F594. [DOI] [PubMed] [Google Scholar]
- 33.Desmond MK, Siebenaller JF. Non-additive counteraction of KCl-perturbation of lactate dehydrogenase by trimethylamine N-oxide. Protein Pept Lett. 2006;13:555–557. doi: 10.2174/092986606777145733. [DOI] [PubMed] [Google Scholar]
- 34.Qu Y, Bolen DW. Hydrogen Exchange Kinetics of RNase A and the Urea:TMAO Paradigm. Biochemistry. 2003;42:5837–5849. doi: 10.1021/bi0206457. [DOI] [PubMed] [Google Scholar]
- 35.Ferreon AC, Ferreon JC, Bolen DW, Rosgen J. Protein phase diagrams II: nonideal behavior of biochemical reactions in the presence of osmolytes. Biophys J. 2007;92:245–256. doi: 10.1529/biophysj.106.092262. [DOI] [PMC free article] [PubMed] [Google Scholar]