Skip to main content
NCBI home page
Genetics logoLink to Genetics
. 2008 Sep;180(1):1–6. doi: 10.1534/genetics.104.95596

The Phage Mating Theory, With Lessons for Yeast Geneticists

Frank Stahl 1,1
PMCID: PMC2535666  PMID: 18794232

WHEN physicist Max Delbrück undertook the study of phage growth (Ellis and Delbrück 1939), he anticipated that phage would be the best model for elucidating biological reproduction and mutation, uncomplicated by sex (Delbrück 1970). This Perspectives traces Max's attempt to come to grips with realities that threatened that view, and it considers present-day relevance for yeast geneticists of two lessons that remain from his heroic effort.

Readers should understand (or recall) that in 1939 essentially nothing of what we now know about the chemistry of either reproduction or mutation was even imagined—for nucleic acids, it was “known” only that most of the DNA is in the nucleus and most of the RNA is in the cytoplasm and, for proteins, only that some were enzymes and that they were probably the stuff that genes are made of. Furthermore, Max seemed to have little hope that the biochemistry of the day would ask the right questions (Delbrück 1949). (Overheard, one graduate of Max's phage course to another: “Would you want your daughter to marry a biochemist?”) I think Max hoped to solve the secret of life using physics and algebra along with open communication subject to tough criticism.

SOME REALITIES OF PHAGE BIOLOGY

Max ignored the first sign of sexual complexities in phage reproduction when he found that cells co-infected with the related phages T2 and T4 yielded some phage particles that had inherited characteristics from both parents. He titled his article “Induced mutations in bacterial viruses,” evidencing stubborn resistance to the possibility of genetic recombination with its implications of sexual reproduction and the variety of highly evolved stuff that so often goes with it (Delbrück and Bailey 1947).

However, Max's hopes for simplicity were soon challenged again by the results and interpretation of experiments conducted with UV-inactivated phages (Luria 1947; Luria and Dulbecco 1949). The UV experiments showed that phage particles killed by irradiation could cooperate to produce live phage, a trick that was labeled “multiplicity reactivation” (MR) because this cooperation required that a bacterial cell be infected with two or more phage particles. Luria and Dulbecco (1949) collected MR data for a range of UV doses and a variety of multiplicities and found that the data could be fitted to a mathematically expressed theory. The infected cells produced live phage as if the only requirement for success was that each of n identically sensitive, but functionally distinct, subunits be represented in the infecting population by at least one “unhit” subunit of each type (Luria 1947). For T2, n = 25; for T4, n = 15. As long as each type of subunit had a surviving member, reassortment of subunits following their multiplication guaranteed the production of live phages.

The assumption that live, unirradiated phage reproduced in the same manner was the troublesome feature of the MR theory. Hence, when Dulbecco (1952), using T2 phage, demonstrated that the MR theory as mathematically formulated was inadequate, Max asserted with evident relief (Visconti and Delbrück 1953) that the theory was baseless (but see Perspectives by Stahl 1995). On the other hand, the more conventional evidence for genetic recombination was not so easily put down. Hershey and Rotman (1948, 1949), who infected cells jointly with two or more multiply marked strains of T2 (a phage “cross”), had earlier demonstrated that phages do, indeed, swap genetic information with each other in a more-or-less conventional fashion as shown by some (very roughly) additive recombinant frequencies. On that occasion, Max wrote, “This is news that is exciting principally by the blow it deals to our fond hope of analyzing a simple situation” (Delbrück 1949, reprinted in Cairns et al. 1992, p. 14).

Additional studies (Doermann and Hill 1953) strengthened the view that genetic markers in T-even phage could be assigned map positions on the basis of their linkage relations with each other. It began to look as though conventional meiotic concepts of crossing over of linked markers, perhaps concurrent with random assortment of a modest number of chromosomes, might be more-or-less applicable to phage crosses. However, the data from T-even phage crosses (Hershey and Rotman 1948, 1949; Doermann and Hill 1953) indicated that, by several criteria, a phage cross was not the simple equivalent of an act of meiosis. Data collected by Visconti, then working in Hershey's lab at Cold Spring Harbor, supported that view:

  1. Recombinant frequencies among mature phage particles increased with time of sampling of the population (by “premature,” normal, or “delayed” lysis of the infected culture). The genetic exchanges implied by these observations occurred during a noninfectious “vegetative” state, in which the phage multiplied prior to becoming mature virions. Maturation began midway through the infection cycle and continued until the host lysed.

  2. When the infection involved unequal numbers of two parental types, the frequency of recombinants in the progeny of the cross was sometimes greater than the frequency of the minority parent genotype.

  3. The markers available fell into three linkage groups. By two criteria, markers on the three groups appeared to be unlinked: (i) crosses between any two markers from different groups gave about the same frequency of recombinants, and (ii) in three-factor crosses, a marker in one group appeared to assort randomly among progeny preselected for being recombinant within another linkage group. However, crosses between any two of these “unlinked” markers gave <50% recombinants, violating the simple, meiotic expectation for unlinked markers.

  4. In crosses involving three linked factors, double crossovers were found in excess of the “expectation”; i.e., coefficients of coincidence were greater than unity (“negative interference”).

  5. Following infection by three distinguishable genotypes, phage appeared that had inherited markers from all three of the parents.

Max recognized that these distinctive features of a phage cross were properties of a population that was proceeding toward linkage equilibrium. He formalized his views in a Genetics article that included Visconti's data (Visconti and Delbrück 1953). He wrote (p. 6) “… one may attempt to explain the genetic findings … by the idea that mating occurs repeatedly during every intrabacterial cycle of phage growth. The interpretation of mixed infections thus becomes a problem in population genetics.” Max proposed that (i) phages mate pairwise, repeatedly, and at random with respect to genotype; (ii) each mating allows for several break-join exchanges along linear linkage structures, as in meiosis; and (iii) unlinked markers assort at random in individual mating acts. He then incorporated these assumptions into an algebraically formulated model that related frequencies of recombinants in the phage population to the events in the hypothesized individual matings. Because phages are “haploid” and because Max restricted his algebra to crosses with no more than three factors, the derivation, though ponderous, was simpler than the earlier treatment by Geiringer (1944), which he used as a guide. The model would be deemed successful if it proved to be compatible with features 1–5, above. Success would then allow Max to assume that reproduction, although annoyingly contemporaneous with recombination, was not demonstrably dependent on it, so that one could ignore recombination when investigating reproduction.

FORMULATING AND TESTING THE MODEL

Max's first equations for recombinant frequencies were for populations in which the matings were synchronized. Algebraic legerdemain then yielded equations for a more realistic population in which matings were desynchronized and random in time. For a two-factor cross (considered here for simplicity) the elementary, random-in-time equation for the frequency of recombinants was

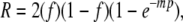graphic file with name M1.gif

where f is the fraction of one of the two parental types in the infecting phage mixture, p is the probability per mating that the two factors will recombine, and m is the average number of matings per phage lineage. In a further development, Max averaged R (from m1 to m2) to account for the view that some of the phages in the “vegetative pool” (known to us now as DNA) become recombinationally inert by being packaged into heads when m = m1, while the last to be packaged have enjoyed an average of m2 rounds of mating. A full-fledged equation contains, in addition, a factor accounting for cell-to-cell variation in f (Lennox et al. 1953).

Testing the theory required that m and p be separately estimated. This was done by setting p = Inline graphic for putatively unlinked markers; m could then be calculated from the observed value of R for those markers. With m in hand, values of R for pairs of linked markers could be transformed to p-values. When these p-values, presumably characteristic of individual matings, were tested, they were found to be free of negative interference. The negative interference that characterized R was thereby attributable to the heterogeneity in pairwise mating experiences embodied in i–iii, above. The theory worked! In fact, it accounted for all the features 1–5 (above) that are peculiar to a phage cross.

The mating theory, as formulated by Max, was discomforted by just one acknowledged fact—complementary recombinants were not generally recovered in equal numbers from individual, infected bacteria. This feature of phage crosses (Hershey and Rotman 1949) had suggested copy-choice recombination to A. H. Sturtevant (cited in Hershey and Rotman 1949), but, with Max-like dismissal, Max stated that classical, reciprocal crossing over, which must be occurring, was simply obscured by subsequent, random variations in reproduction and in removal from the vegetative pool by packaging into virion heads (Visconti and Delbrück 1953).

The manuscript was submitted to Genetics, where it was published after some delay (see Perspective article by Crow 2006). Soon thereafter, Kaiser (1955) tested the model with phage λ. It was striking that the same algebra worked for both phages, even though the sole adjustable parameter, m = average number of matings per phage, was about fivefold different for T-even and λ-phages.

THE MATING THEORY BEGINS TO CRUMBLE

Did the mating theory rescue the process of reproduction from the possible involvement of genetic recombination? As pointed out above, Max's algebra, written with Dale Kaiser's acknowledged help, assumed and embodied break-join recombination, as in the classical view of meiotic crossing over. A more complete, and transparent, theory (Steinberg and Stahl 1959) took account of the possibility of other mechanisms of recombination by adding a parameter for the fraction of phage, emerging from a single mating, that have the possibility of being recombinant. For break-join recombination, this parameter (call it F) is unity; for nonreciprocal copy-choice, for instance, F = 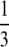Inline graphic. Thus, for a single round of pairwise mating between phages of opposite genotypes, the fraction of recombinants is Fp. For a single hypothetical round of synchronized mating at random with respect to genotype, the frequency of recombinants is 2f(1 − f)Fp. For unlinked markers, p could be taken as Inline graphic and, in principle, F could be evaluated. For successive pairwise matings, random in time and irrespective of genotype, however, the equation becomes

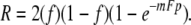graphic file with name M5.gif

Now, with p set at Inline graphic for unlinked markers mF can be evaluated, but there is no way to evaluate m and F separately. Thus, the algebraic conversion to random-in-time mating erased the possibility of determining F and, with that, all traces of the break-join assumption (Steinberg and Stahl 1959). Consequently, the theory in final form was compatible with models (e.g., copy-choice or break-copy) in which recombination was intimately tied to reproduction and was not necessarily reciprocal. It seems likely that the adequacy of the model in its random-in-time format was taken by Max as support of the break-join feature he had consciously written into the synchronized mating algebra but had unconsciously lost with the transition to random-in-time equations. My own recollections support that likelihood—according to Steinberg (C. Steinberg, personal communication), Max insisted that the excess of recombinant over minority parent genotypes in the progeny of the cross (feature 2) implied the destruction of the parental chromosomes by the crossover process. He relented only when faculty from the Caltech Math Department endorsed Charley's crystalline blackboard explanation of our derivation. Thus, whether phage reproduction was, in fact, somehow related to recombination remained an open question.

ACCELERATED DECLINE OF THE MATING THEORY

The mating theory wilted further with the establishment of a circular linkage map for T4 (Foss and Stahl 1963; Streisinger et al. 1964). In the early 1960s, at a Lake Arrowhead meeting, Max temporarily blocked the presentation of George Streisinger's (then unpublished) evidence for circularity.3 Perhaps he realized that linkage circularity posed threats to the mating theory. The immediately apparent threat dealt with the concept of crossover interference (Steinberg and Stahl 1967). On a circular linkage map, the separating of two linked markers requires crossing over in each of the two arcs connecting the loci. This lack of independence will inevitably be manifest as negative interference when interference is assessed by conventional definitions. Could this, rather than randomness of mating, be the origin of the negative interference observed in phage crosses? (Without consequences for our lesson, this discussion dodges the issue of the gene-conversion-like “high negative interference” characteristic of recombination over gene-length distances.)

Circularity also eliminated the possibility of large unexplored regions, making it possible to estimate the number of crossovers per phage per mating (Stahl et al. 1964). A good fit to the linkage data was obtained with a model in which linear chromosomes were circularly permuted and enjoyed exactly one crossover in each pairwise mating, i.e., complete positive interference in the individual matings (Stahl and Steinberg 1964)! Clearly, with one exchange in each mating, the negative interference in T4 could no longer be ascribed to multiple exchanges occurring in randomly distributed matings. Max's concept of pairwise connubial interactions had become superfluous, but was it wrong?

NO MATINGS IN T4

Jan Drake (Drake 1967) devised a simple, powerful test of the pairwise mating concept. He crossed T4 phages that were heteroallelic in the distantly linked e and rII genes. For each of these genes, wild-type recombinants could be selectively plated. The frequencies of e+ and of rII+ recombinants were measured. The cross was then repeated in the presence of an excess number of a third phage that was mutant for both sites in e and was deleted for the entire rII region. If mating involved discrete, pairwise interaction between phage chromosomes, the frequency of e+ and of rII+ recombinants should be depressed to the same extent—for both genes, mating with the third phage is a lost opportunity to produce wild-type recombinants. However, the depression was less for the rII+ recombinants than for the e+ recombinants, indicating that recombination in the rII gene occurred without regard to the presence of the rII-deletion phage. Apparently, segments of the chromosome indulge in exchanges all on their own—no cozy head-to-toe matings.

BREAK-JOIN?

What was left of Max's views? Even though “matings” had been reduced to individual exchanges, might those exchanges be occurring independently of, albeit contemporaneously with, reproduction? The analysis by Steinberg and Stahl (1959) showed that issues of recombination mechanism could not be addressed by measures of recombinant frequencies, which are essentially kinetic in nature. Hence, progress in understanding the mechanism(s) of phage recombination depended on the development of a method that could detect both material and informational exchange in individual progeny phage particles. Meselson and Weigle (1961) developed such a method, and Meselson (1964) applied it in an experiment designed to reveal whether recombinants could be formed without the involvement of detectable amounts of DNA synthesis. Using λ-phages made of heavy isotopes and bearing genetic markers placed symmetrically about the center of its linear linkage map, Meselson showed that some recombinant phage particles were produced that bore fully heavy chromosomes. Thus, replication-related processes such as copy-choice or break-copy (Meselson 1964) could not account for all of λ's recombination. By parsimony, one could believe that all phage recombination was break-join, and such a belief held sway for a while (my recollection; A. D. Kaiser, personal communication). Later, it was shown that Meselson's recombinants arose from the action of the site-specific Int system and that, as predicted by Skalka (1974), “ordinary,” homology-dependent recombination in λ involved extensive DNA replication whenever replication was an allowed option (reviewed in Stahl 1998). In fact, λ-replication occurs poorly in recombination-deficient mutants (Skalka 1974), and late DNA replication in T4 is absolutely dependent on homologous recombination (reviewed by Kreuzer 2000). It is now established that recombination in many circumstances is interrelated to DNA replication in ways that allow each to initiate the other (reviewed by Kuzminov 1999, 2001).

LESSONS FOR YEAST GENETICS

Two lessons remain to be taken from the phage mating theory:

  1. A theory need not be correct to be the right theory. Even though Max's mating theory turned out to be wrong, it was right for the times—it brought order to most of the extant data, it was testable, and it inspired the analyses that brought it down.

  2. Disparate recombination opportunities in a population will confound the analysis of interference, no matter what else may be going on.

The isolation of recombination-related mutants, first in Drosophila and later in yeast, has opened the door to studies on the genetic basis of crossover interference. One hopes that these studies will lead to a molecular understanding of this puzzling aspect of meiotic recombination (Sturtevant 1915; Muller 1916). I briefly discuss some widely cited interference studies in yeast that may have been led astray by heterogeneity in recombination opportunity. Some of these studies echo observations made earlier in Drosophila (reviewed by Sandler and Lindsley 1974).

VARIABILITY IN EFFECTIVE CHROMOSOME PAIRING?

Chua and Roeder (1997) reported a remarkable phenotype for tam1 mutants, which are somewhat deficient in homolog pairing as a result of the loss of a protein that is telomere associated. In their tam1 crosses interference was reduced while map distances were more-or-less unaffected. The reduction in interference could arise from population-based negative interference due to the occasional failure of a pair of homologs to synapse but, nevertheless, to sometimes get distributed properly into viable haploid yeast spores. An a priori expectation for such a pairing defect is that recombination rates would be down, but, in fact, they were not. A separate study (Getz et al. 2008) revealed another phenotype of tam1 (aka ndj1) mutants—these mutants actually increase crossing over but only in a class of crossovers that is interference deficient. Apparently, in the study by Chua and Roeder (1997) the two tam1 phenotypes (reduced crossing over due to poor pairing and increased crossing over among chromosomes that did pair) approximately canceled each other with respect to recombination rate but reinforced each other with respect to the reduction in positive interference. Perhaps the phenotype of tid1 mutants (Shinohara et al. 2003), which are involved in pairing and are similarly reduced for interference while retaining apparently normal crossover rates, will find a similar explanation.

CELL-TO-CELL HETEROGENEITY IN RECOMBINATION RATES?

Shinohara et al. (2003) noted that the recombination deficit of dmc1 mutants could be reversed by expression of a different gene borne on a plasmid. The resulting recombination was devoid of positive interference, suggesting that Dmc1 was a requirement for the interference that is characteristic of wild-type yeast. Dmc1 interacts with Tid1 (above), so could be expected to share a phenotype of reduced interference. In addition, however, the plasmid that was supplying the recombination-restoring gene function is a notoriously unstable one, typically present in widely varying numbers among the cells of a yeast population. Any resulting heterogeneity in suppression of the dmc1 phenotype would further mask any positive interference in the recombination data. For eukaryotes the problem of negative interference resulting from variability in recombination rates has been pointed out previously (Säll and Bengtsson 1989).

At the 1958 Cold Spring Harbor Symposium, Hershey (1959, p. 29), in his last attempt to make sense out of phage cross data, concluded, “In a not quite trivial sense it may be permissible to say that positive interference is not found [in phage] because it is obscured by negative interference.”

A mutation-induced reduction in interference resulting from heterogeneity in recombination opportunity can be recognized by examination of the distance dependence of interference. If the observed reduction in positive interference for neighboring intervals is due either to occasional failure of homologs to pair or to other sources of cell–cell heterogeneity in crossover rates, intervals so distantly linked that they manifest no interference in wild type will manifest negative interference in the mutant. Mutations that introduce unevenness in crossover potential along the length of a chromosome might introduce localized negative interference (Tsubouchi et al. 2006) that will diminish for distantly linked intervals, as illustrated by Amati and Meselson (1965) for phage λ. In contrast, mutations that reduce interference by reducing the ratio of interfering to noninterfering crossovers can be diagnosed by their consequences for the repair of mismatches arising during the repair of meiotic double-strand breaks (Getz et al. 2008).

Acknowledgments

I thank Dale Kaiser, Andrei Kuzminov, Millard Susman, and Jette Foss for their generous help with this manuscript.

This article is dedicated to the memory of Charley Steinberg.2

2

For a fuller appreciation of Charley Steinberg, see the Perspectives by Wu and Lindahl (2001).

3

Max, who answered to his first name only, was a conscientious meetings chairman—conscientious to a fault, according to some. To make sure that every talk in a session that he chaired was worthwhile, he would assemble the scheduled speakers for a rehearsal. George Streisinger was scheduled in Max's session of a Lake Arrowhead meeting in the early 1960s, and since that session was scheduled for the first morning of the meeting, Max assembled the speakers after the dinner that followed registration.

George warned me that he might be late for the meeting and asked me to substitute for him if he failed to arrive for the rehearsal or even for the session. I was willing to do so, since we had shared development of the ideas and experiments regarding linkage circularity of T4. George was absent when the rehearsal started, so Max called on me. At the end of my first sentence, Max interrupted to say “If George does not arrive for the session, we will not have this talk.” I sat, forgetting that, with Max, one was not supposed to give up.

George arrived before the rehearsal was concluded, and Max ordered him to present his talk. George's opening sentence was, almost word for word, the same as mine. Max exploded, “You believe that nonsense, too?” George did not sit—he tried to reason with Max, but Max repeatedly interrupted him. Finally rising to the occasion, I offered a paraphrasing of the point George was trying to make. Max also rose, pointed his finger, and intoned, “THERE BLOWS THE BIG WIND FROM OREGON!”

Max eventually allowed George to present his talk, but he asserted he would not accept circularity of the T4 linkage map until it was demonstrated in a single cross. That was soon accomplished (Foss and Stahl 1963).

Max's unwillingness to put up with nonsense was generally appreciated. His willingness to expound viewpoints contrary to popular opinion was also valuable, as when he challenged the adequacy of the data supporting the one-gene, one-enzyme hypothesis (Delbrück 1947) and when he disdained the Watson–Crick view that DNA unwinding was prerequisite to replication (Delbrück 1954). Both challenges elicited experiments of some interest (Horowitz and Leupold 1951; Meselson and Stahl 1958). This openly expressed skepticism of popular ideas led some to think that Max had poor judgment. Legend has it that a Caltech graduate student was observed leaving Max's office looking glum. “What's wrong?” Jean Weigle asked him. Student replied, “I told Max my idea, and he liked it.”

For a proper appraisal of Max's wisdom in identifying phage as the key to understanding biological reproduction, see Cairns et al. (1992).

References

  1. Amati, P., and M. Meselson, 1965. Localized negative interference in bacteriophage. Genetics 51 369–379. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Cairns, J., G. S. Stent and J. D. Watson, 1992. Phage and the Origins of Molecular Biology, Expanded Edition. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
  3. Chua, P. R., and G. S. Roeder, 1997. Tam1, a telomere-associated meiotic protein, functions in chromosome synapsis and crossover interference. Genes Dev. 11 1786–1800. [DOI] [PubMed] [Google Scholar]
  4. Crow, J. F., 2006. Interesting reviewers. Genetics 173 1833–1834. [Google Scholar]
  5. Delbrück, M., 1947. Discussion. Cold Spring Harbor Symp. Quant. Biol. 11 22–23. [Google Scholar]
  6. Delbrück, M., 1949. A physicist looks at biology. Trans. Conn. Acad. Arts Sci. 38 173–190 (reprinted in Cairns et al. 1992). [Google Scholar]
  7. Delbrück, M., 1954. On the replication of deoxyribonucleic acid (DNA). Proc. Natl. Acad. Sci. USA 40 783–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Delbrück, M., 1970. Preliminary write-up on the topic “Riddle of Life” (Berlin, August 1937). Science 168 1312–1315.5444262 [Google Scholar]
  9. Delbrück, M., and W. T. Bailey, Jr., 1947. Induced mutations in bacterial viruses. Cold Spring Harbor Symp. Quant. Biol. 11 33–37. [Google Scholar]
  10. Doermann, A. H., and M. B. Hill, 1953. Genetic structure of bacteriophage T4 as described by recombination studies of factors influencing plaque morphology. Genetics 38 79–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Drake, J. W., 1967. The length of the homologous pairing region for genetic recombination in bacteriophage T4. Proc. Natl. Acad. Sci. USA 58 962–966. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Dulbecco, R., 1952. A critical test of the recombination theory of multiplicity reactivation. J. Bacteriol. 63 199–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Ellis, E. L., and M. Delbrück, 1939. The growth of bacteriophage. J. Gen. Physiol. 22 365–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Foss, H. M., and F. W. Stahl, 1963. Circularity of the genetic map of bacteriophage T4. Genetics 48 1659–1672. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Geiringer, H., 1944. On the probability theory of linkage in Mendelian heredity. Ann. Math. Stat. 15 25–57. [Google Scholar]
  16. Getz, T. J., S. A. Banse, L. S. Young, A. V. Banse, J. Swanson et al., 2008. Reduced mismatch repair of heteroduplexes reveals “non”-interfering crossing over in wild-type Saccharomyces cerevisiae. Genetics 178 1251–1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hershey, A. D., 1959. The production of recombinants in phage crosses. Cold Spring Harbor Symp. Quant. Biol. 23 19–46. [DOI] [PubMed] [Google Scholar]
  18. Hershey, A. D., and R. Rotman, 1948. Linkage among genes controlling inhibition of lysis in a bacterial virus. Proc. Natl. Acad. Sci. USA 34 89–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Hershey, A. D., and R. Rotman, 1949. Genetic recombination between host-range and plaque-type mutants of bacteriophage in single bacterial cells. Genetics 34 44–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Horowitz, N. H., and U. Leupold, 1951. Some recent studies bearing on the one gene-one enzyme hypothesis. Cold Spring Harbor Symp. Quant. Biol. 16 65–74. [DOI] [PubMed] [Google Scholar]
  21. Kaiser, A. D., 1955. A genetic study of the temperate coliphage. Virology 1 424–443. [DOI] [PubMed] [Google Scholar]
  22. Kreuzer, K. N., 2000. Recombination-dependent DNA replication in phage T4. Trends Biochem. Sci. 25 165–173. [DOI] [PubMed] [Google Scholar]
  23. Kuzminov, A., 1999. Recombinational repair of DNA damage in Escherchia coli and bacteriophage λ. Microbiol. Mol. Biol. Rev. 63 751–813. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kuzminov, A., 2001. DNA replication meets genetic exchange: chromosomal damage and its repair by homologous recombination. Proc. Natl. Acad. Sci. USA 98 8461–8468. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lennox, E., C. Levinthal and F. Smith, 1953. The effect of finite input in reducing recombinant frequency. Genetics 38 508–511. [Google Scholar]
  26. Luria, S. E., 1947. Reactivation of irradiated bacteriophage by transfer of self reproducing units. Proc. Natl. Acad. Sci. USA 33 253–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Luria, S. E., and R. Dulbecco, 1949. Genetic recombination leading to production of active bacteriophage from ultraviolet inactivated bacteriophage particles. Genetics 34 93–125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Meselson, M. S., 1964. On the mechanism of genetic recombination between DNA molecules. J. Mol. Biol. 9 734–745. [DOI] [PubMed] [Google Scholar]
  29. Meselson, M., and F. W. Stahl, 1958. The replication of DNA in Escherichia coli. Proc. Natl. Acad. Sci. USA 44 671–682. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Meselson, M. S., and J. J. Weigle, 1961. Chromosome breakage accompanying genetic recombination in bacteriophage. Proc. Natl. Acad. Sci. USA 47 857–868. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Muller, H. J., 1916. The mechanism of crossing over. Am. Nat. 50 194–221 and ff. [Google Scholar]
  32. Säll, T., and B. O. Bengtsson, 1989. Apparent negative interference due to variation in recombination frequencies. Genetics 122 935–942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Sandler, L., and D. L. Lindsley, 1974. Some observations on the study of the genetic control of meiosis in Drosophila melanogaster. Genetics 78 269–297. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Shinohara, M., K. Sakai, A. Shinohara and D. K. Bishop, 2003. Crossover interference in Saccharomyces cerevisiae requires a TID1/RDH54- and DMC1-dependent pathway. Genetics 163 1273–1286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Skalka, A. M., 1974. A replicator's view of recombination and repair, pp. 421–432 in Mechanisms in Recombination, edited by R. F. Grell. Plenum, New York.
  36. Stahl, F. W., 1967. Circular genetic maps. J. Cell Physiol. 70(Suppl. 1): 1–12. [DOI] [PubMed] [Google Scholar]
  37. Stahl, F. W., 1995. The amber mutants of phage T4. Genetics 141 439–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Stahl, F. W., 1998. Recombination in phage λ: one geneticist's historical perspective. Gene 223 95–102. [DOI] [PubMed] [Google Scholar]
  39. Stahl, F. W., and C. M. Steinberg, 1964. The theory of formal phage genetics for circular maps. Genetics 50 531–538. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Stahl, F. W., R. S. Edgar and J. Steinberg, 1964. The linkage map of bacteriophage T4. Genetics 50 539–552. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Steinberg, C., and F. Stahl, 1959. The theory of formal phage genetics. Cold Spring Harbor Symp. Quant. Biol. 23 42–46 (appendix to Hershey 1959). [Google Scholar]
  42. Steinberg, C. M, and F. W. Stahl, 1967. Interference in circular maps. J. Cell Physiol. 70(Suppl. 1): 4–7 (appendix to Stahl 1967). [PubMed] [Google Scholar]
  43. Streisinger, G., R. S. Edgar and G. H. Denhardt, 1964. Chromosome structure in phage T4. I. Circularity of the linkage map. Proc. Natl. Acad. Sci. USA 51 775–779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Sturtevant, A. H., 1915. The behavior of the chromosomes, as studied through linkage. Z. Indukt. Abstammungs. Vererbungsl. 13 234–287. [Google Scholar]
  45. Tsubouchi, T., H. Zhao and G. S. Roeder, 2006. The meiosis-specific Zip4 protein regulates crossover distribution by promoting synaptonemal complex formation together with Zip2. Dev. Cell 10 809–819. [DOI] [PubMed] [Google Scholar]
  46. Visconti, N., and M. Delbrück, 1953. The mechanism of genetic recombination in phage. Genetics 38 5–33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Wu, G. E., and K. D. Lindahl, 2001. Memories of a mentor: Charlie Steinberg. Genetics 157 927–932. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES