Abstract
The traditional molecular selection index (MSI) employed in marker-assisted selection maximizes the selection response by combining information on molecular markers linked to quantitative trait loci (QTL) and phenotypic values of the traits of the individuals of interest. This study proposes an MSI based on an eigenanalysis method (molecular eigen selection index method, MESIM), where the first eigenvector is used as a selection index criterion, and its elements determine the proportion of the trait's contribution to the selection index. This article develops the theoretical framework of MESIM. Simulation results show that the genotypic means and the expected selection response from MESIM for each trait are equal to or greater than those from the traditional MSI. When several traits are simultaneously selected, MESIM performs well for traits with relatively low heritability. The main advantages of MESIM over the traditional molecular selection index are that its statistical sampling properties are known and that it does not require economic weights and thus can be used in practical applications when all or some of the traits need to be improved simultaneously.
MARKER-ASSISTED selection (MAS) is an important breeding tool in which molecular marker alleles linked to quantitative trait loci (QTL) that control phenotypic variables of important traits are selected. Marker-assisted selection can be more efficient than selecting individuals on the basis of phenotypic trait values. Progeny of specific progenitors can be selected on the basis of molecular markers as long as these are associated with breeding values of the traits under consideration. This is one form of MAS (Dekkers and Dentine 1991; Arus and Moreno-Gonzalez 1993). Another form of MAS is based on the molecular selection index (MSI) proposed by Lande and Thompson (1990). In MSI the selection response is maximized by combining information on molecular markers linked to QTL and the phenotypic values of the traits of interest.
To construct an MSI, it is necessary to identify the linkage between the molecular marker and the QTL, the estimated effect of the QTL linked to the molecular marker (MQTL effect), and the combination of MQTL effects and phenotypic information that allows genotypes to be classified and selected using a selection index. The MQTL effects can be identified and estimated through the linkage disequilibrium that arises when crossing inbred lines or divergent populations (Zhang and Smith 1992, 1993; Xie and Xu 1998). The MSI depends on various factors, such as number and density of molecular markers associated with QTL, population size, trait heritability, additive genetic variances that can be explained by molecular markers, and precision of the estimated effect of gene substitution (Dekkers and Dentine 1991; Moreau et al. 2000).
The MSI is an application of the selection index methodology proposed by Smith (1936), in which MQTL effects are incorporated. As proposed by Lande and Thompson (1990), the MSI performs a linear regression of phenotypic values on the coded values of the molecular markers such that selected molecular markers are those statistically linked to QTL that explain most of the variability in regression models. The coefficient of regression of the molecular marker is the MQTL effect. Statistical models and methods for mapping QTL and estimating their MQTL effects have been developed (Jansen 2003). Several authors have pointed out the effectiveness of the MSI in inbred populations with large population sizes and traits with low heritability values (Zhang and Smith 1992, 1993; Gimelfarb and Lande 1994, 1995; Whittaker 2003) when only one trait (and its associated molecular score) is considered.
The selection index theory was originally developed by Smith (1936) and generalized by Kempthorne and Nordskog (1959) for a restrictive selection index. The standard selection index is defined as a linear combination of the observed phenotypic values of the traits of interest with the traits' previously defined economic weights. Selection indexes are based on improving one trait by incorporating information on related traits (Wei et al. 1996; Falconer and Mackay 1997) or incorporating information on MQTL effects by means of the MSI; other selection indexes are based on improving several traits simultaneously, which requires assigning economic weights to each trait, as proposed by Smith (1936).
Moreau et al. (2000) and Whittaker (2003) found that the MSI is more effective than Smith's selection index only in early generation testing and has the additional disadvantage of increased costs due to molecular marker evaluation. Selection intensity must also be considered because it affects genetic marker means and the ability to detect QTL (Wu et al. 2000). Furthermore, since selection increases the frequency of the QTL's favorable allele, as well as the allele of the molecular marker linked to it, total variability in the selected sample is reduced (Mackinnon and Georges 1992).
The MSI has the same advantages and disadvantages as Smith's selection index; it is simple to use but its sampling statistical properties and selection response are unknown, except in the case of two traits (Hayes and Hill 1980). Even for two traits, the statistical properties of Smith's selection index and its selection response, obtained using the delta method, are difficult to use and evaluate (Harris 1964); furthermore, it is not easy to consistently assign economic weights to the traits.
Recently, Cerón-Rojas et al. (2006) developed a selection index based on eigenanalyses of the phenotypic variance–covariance (or correlation) matrix of the traits of interest (called the eigen selection index method, ESIM). The authors showed that ESIM does not require economic weights or estimates of the genotypic variances–covariances. In ESIM the elements of the first eigenvector determine the proportion each trait contributes to the selection index, and the first eigenvalue is used in the selection response. From a theoretical perspective, Cerón-Rojas et al. (2006) demonstrated that selection responses from Smith's selection index and from ESIM are the same, except for differences in selection index coefficients due to the different estimation methods. In addition, the ESIM of Cerón-Rojas et al. (2006) allows constructing a function to estimate gains (or losses) between selection cycles and predicting the selection response for future selection cycles. Following the restrictive selection index of Kempthorne and Nordskog (1959), Cerón-Rojas et al. (2008) developed a restrictive ESIM (RESIM) that facilitates maximizing the genetic progress of some characters while leaving the others unchanged.
In this article we develop a molecular selection index (molecular eigen selection index method, MESIM) based on the RESIM of Cerón-Rojas et al. (2008) and the molecular selection index developed by Lande and Thompson (1990), using the selection index methodology proposed by Smith (1936), in which MQTL effects are incorporated. Simulated data were generated for comparing the selection response based on various selection indexes: (1) MESIM vs. Lande and Thompson (1990), (2) RESIM vs. the restrictive selection index of Kempthorne and Nordskog (1959), and (3) ESIM vs. the Smith selection index (Smith 1936). Practical and theoretical properties of estimators from  , RESIM, ESIM, the Lande and Thompson molecular selection index, the Smith selection index, and the restrictive selection index of Kempthorne and Nordskog are discussed. The efficiency of MESIM, the Lande and Thompson molecular selection index, ESIM, the Smith selection index, and the restrictive selection index of Kempthorne and Nordskog is evaluated using the genotypic means of the selected individuals. The theory of RESIM is described in Cerón-Rojas et al. (2008).
, RESIM, ESIM, the Lande and Thompson molecular selection index, the Smith selection index, and the restrictive selection index of Kempthorne and Nordskog are discussed. The efficiency of MESIM, the Lande and Thompson molecular selection index, ESIM, the Smith selection index, and the restrictive selection index of Kempthorne and Nordskog is evaluated using the genotypic means of the selected individuals. The theory of RESIM is described in Cerón-Rojas et al. (2008).
THEORY OF SELECTION INDEXES
Smith's selection index:
Details of Smith's selection index (SI) are given in Cerón-Rojas et al. (2006, 2008). A brief description follows. Smith's selection index is based on the linear combinations
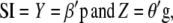 |
(1) |
where 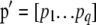 is the vector of the phenotypic values and
is the vector of the phenotypic values and 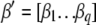 is the vector of coefficients of
is the vector of coefficients of 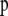 ,
, 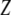 is the breeding value,
is the breeding value, 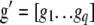 is the vector of genotypic values, and
is the vector of genotypic values, and 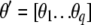 is the vector of economic weights. The phenotypic values
is the vector of economic weights. The phenotypic values 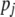 (j = 1, 2, … , q) are modeled as
(j = 1, 2, … , q) are modeled as 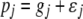 , where
, where 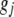 is the genotypic value of the jth trait and
is the genotypic value of the jth trait and 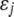 is the environmental component. Assuming that
is the environmental component. Assuming that 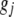 and
and 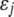 are independent and that
are independent and that 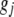 represents only additive effects,
represents only additive effects, 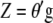 denotes the breeding value (Hazel 1943; Kempthorne and Nordskog 1959). Hence, selection based on
denotes the breeding value (Hazel 1943; Kempthorne and Nordskog 1959). Hence, selection based on 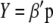 leads to a selection response
leads to a selection response
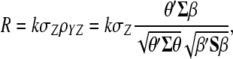 |
(2) |
where 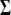 and
and 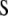 are the variance–covariance matrices of genotypic and phenotypic values, respectively,
are the variance–covariance matrices of genotypic and phenotypic values, respectively, 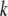 is the standardized selection differential,
is the standardized selection differential, 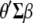 is the covariance between
is the covariance between 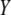 and
and 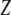 ,
, 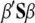 is the variance of
is the variance of 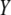 ,
, 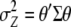 is the variance of
is the variance of 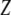 , and
, and 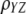 is the correlation between
is the correlation between 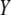 and
and 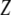 .
.
In Smith's selection index, the vector 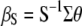 (where the subscript S denotes Smith's method and
(where the subscript S denotes Smith's method and 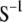 is the inverse of the phenotypic variance–covariance matrix,
is the inverse of the phenotypic variance–covariance matrix, 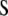 ) allows us to construct the SI,
) allows us to construct the SI, 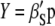 , that maximizes the correlation with the breeding value
, that maximizes the correlation with the breeding value 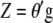 .
.
Molecular selection index:
Lande and Thompson (1990) extended Equation 1 to include the case where information on QTL associated with molecular markers is available and denoted the molecular selection index as
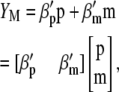 |
(3) |
where 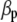 is a vector of phenotypic weights,
is a vector of phenotypic weights, 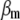 is the vector of weights of the molecular score,
is the vector of weights of the molecular score, 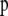 is the vector of phenotypic values, and
is the vector of phenotypic values, and 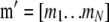 , where each
, where each 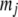 (j = 1, 2, … , N; N = number of molecular scores) is the jth molecular score given by the the sum of the products of the estimated additive effect of the QTL linked to the molecular marker (MQTL effects) multiplied by the coded values of their corresponding molecular markers. The response to this molecular selection index may be written as
(j = 1, 2, … , N; N = number of molecular scores) is the jth molecular score given by the the sum of the products of the estimated additive effect of the QTL linked to the molecular marker (MQTL effects) multiplied by the coded values of their corresponding molecular markers. The response to this molecular selection index may be written as
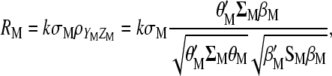 |
(4) |
where
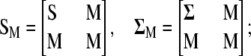 |
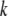 has been defined as in Equation 2,
has been defined as in Equation 2, 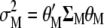 is the variance of the breeding value (
is the variance of the breeding value (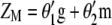 ),
), 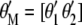 is a vector of economic weights (in the standard molecular selection index,
is a vector of economic weights (in the standard molecular selection index, 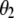 is a vector of zeros),
is a vector of zeros), 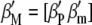 is a vector containing phenotypic (
is a vector containing phenotypic (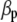 ) and molecular (
) and molecular (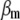 ) weight scores,
) weight scores, 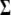 and
and 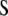 are the variance–covariance matrices defined in Equation 2, and
are the variance–covariance matrices defined in Equation 2, and 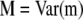 is the variance–covariance matrix of the molecular scores when two or more traits are considered (Lande and Thompson 1990). Only statistically significant additive MQTL effects are included in
is the variance–covariance matrix of the molecular scores when two or more traits are considered (Lande and Thompson 1990). Only statistically significant additive MQTL effects are included in 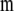 .
.
The vector 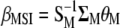 allows constructing the molecular selection index
allows constructing the molecular selection index 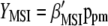 that has maximum correlation (
that has maximum correlation (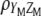 ) with
) with 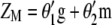 (the subscript MSI in
(the subscript MSI in 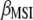 denotes Lande and Thompson's molecular selection index method). In
denotes Lande and Thompson's molecular selection index method). In 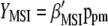 ,
, 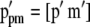 (Equation 3). The variance of
(Equation 3). The variance of 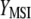 is
is 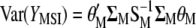 and the maximized selection response can be written as
and the maximized selection response can be written as 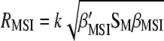 . Estimators of
. Estimators of 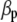 and
and 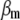 (
(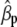 and
and 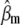 ) for various traits are obtained directly from the estimators of
) for various traits are obtained directly from the estimators of 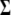 ,
, 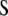 , and
, and 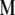 (
(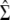 ,
, 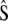 , and
, and 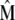 ) and from the vector
) and from the vector 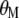 .
.
MESIM
Using a concept similar to that of Kempthorne and Nordskod (1959), which maximizes the selection response (Equation 2) by maximizing the square of the correlation between Y and Z (Equation 1) and utilizing basic concepts from Cerón-Rojas et al. (2008), it can be shown that Equation 4 is maximized by maximizing 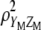 . The key point when maximizing
. The key point when maximizing 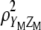 is that the variances (or standard deviations) of
is that the variances (or standard deviations) of 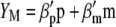 and
and 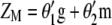 are constants in each selection cycle. Thus, the selection of genotypes can be done using either
are constants in each selection cycle. Thus, the selection of genotypes can be done using either 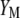 or
or 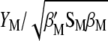 . Because of this fact, when maximizing
. Because of this fact, when maximizing 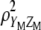 it is possible to impose restrictions
it is possible to impose restrictions 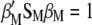 and
and 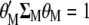 such that, in MESIM, it is required to maximize
such that, in MESIM, it is required to maximize
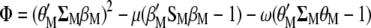 |
with respect to 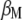 ,
, 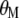 ,
, 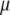 , and
, and 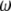 , where
, where 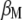 is the vector of
is the vector of 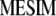 coefficients,
coefficients, 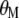 is the vector of economic weights, and
is the vector of economic weights, and 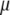 and
and 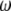 are Lagrange multipliers. In MESIM it is assumed that
are Lagrange multipliers. In MESIM it is assumed that 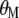 is not a vector of constants.
is not a vector of constants.
When 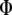 is derived with respect to
is derived with respect to 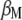 and
and 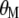 (appendix) and the result is set to the null vector, it follows that
(appendix) and the result is set to the null vector, it follows that
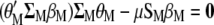 |
(5) |
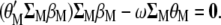 |
(6) |
Because the two restrictions 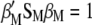 and
and 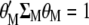 , when Equation 5 is multiplied by
, when Equation 5 is multiplied by 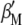 and Equation 6 is multiplied by
and Equation 6 is multiplied by 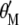 , the result is
, the result is 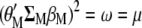 . Hence,
. Hence, 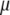 maximizes
maximizes 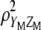 under the restrictions
under the restrictions 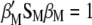 and
and 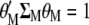 .
.
The following task is to determine the vector 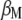 that allows constructing
that allows constructing 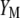 that maximizes its correlation with
that maximizes its correlation with 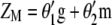 . The appendix shows that the required
. The appendix shows that the required 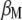 is the solution to the equality
is the solution to the equality
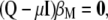 |
(7) |
where 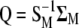 . Thus, for
. Thus, for 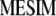 , the value that maximizes
, the value that maximizes 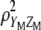 under restrictions
under restrictions 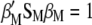 and
and 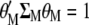 is the first eigenvalue (
is the first eigenvalue (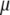 ) of matrix
) of matrix 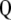 , and the vector that allows constructing
, and the vector that allows constructing 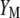 (with maximum correlation with
(with maximum correlation with 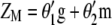 ) is the first eigenvector of matrix
) is the first eigenvector of matrix 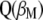 .
.
Let 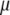 and
and 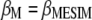 be the first (largest) eigenvalue and its corresponding Q eigenvector, respectively; then, the selection index in the context of
be the first (largest) eigenvalue and its corresponding Q eigenvector, respectively; then, the selection index in the context of 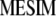 is
is 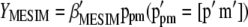 and, because
and, because 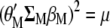 , the maximized selection response can be written as
, the maximized selection response can be written as 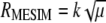 . From
. From 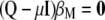 it is possible to determine the
it is possible to determine the 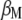 -coefficients of
-coefficients of 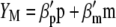 (Equation 3),
(Equation 3), 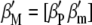 . Although the partial derivatives of
. Although the partial derivatives of 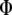 are obtained with respect to
are obtained with respect to 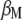 and
and 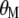 , in estimating
, in estimating 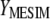 and
and 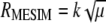 , the vector of economic weights (
, the vector of economic weights (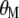 ) is not required because
) is not required because 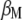 and
and 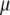 are obtained directly from matrix
are obtained directly from matrix 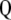 .
.
Note that when information on the QTL linked to the molecular markers is not incorporated into the selection index, i.e., when 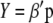 ,
, 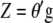 , and
, and 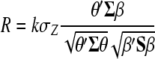 , then Equation 7 can be written as
, then Equation 7 can be written as
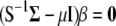 |
(8) |
from which it is evident that 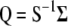 . Equation 8 can be considered a variant of the procedure developed by Cerón-Rojas et al. (2006) for cases where the assumption of ESIM (
. Equation 8 can be considered a variant of the procedure developed by Cerón-Rojas et al. (2006) for cases where the assumption of ESIM (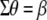 ) is relaxed.
) is relaxed.
As indicated by Ceron-Rojas et. al. (2008), the maximized selection response, 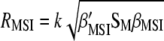 or
or 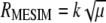 , gives a general theoretical assessment of the gain for all traits considered simultaneously but does not provide genetic gains per trait at each selection cycle. Alternatively, the expected selection response (Baker 1986; Van Vleck 1993) determines the expected genetic gain per trait per selection cycle
, gives a general theoretical assessment of the gain for all traits considered simultaneously but does not provide genetic gains per trait at each selection cycle. Alternatively, the expected selection response (Baker 1986; Van Vleck 1993) determines the expected genetic gain per trait per selection cycle 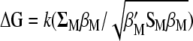 . However,
. However, 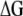 estimates the expected value of the genetic gains with low precision; thus in our simulated data we used the genotypic means of the selected individuals and the regression of the genotypic means of the selected individuals on the selection cycles for evaluating the efficiency of MESIM, RESIM, ESIM, the Lande and Thompson molecular selection index, the restrictive selection index of Kempthorne and Nordskog, and the Smith selection index on the response to selection.
estimates the expected value of the genetic gains with low precision; thus in our simulated data we used the genotypic means of the selected individuals and the regression of the genotypic means of the selected individuals on the selection cycles for evaluating the efficiency of MESIM, RESIM, ESIM, the Lande and Thompson molecular selection index, the restrictive selection index of Kempthorne and Nordskog, and the Smith selection index on the response to selection.
Matrix 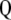 is square and nonsymmetric of order
is square and nonsymmetric of order 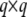 (where
(where 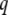 is the total number of variables: phenotypic and molecular scores):
is the total number of variables: phenotypic and molecular scores):
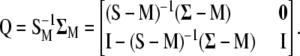 |
(9) |
Therefore, it is not possible to construct a subset of orthogonal vectors from Equation 7. However, orthogonal vectors from Q can be calculated by means of singular value decomposition (SVD) (Mardia et al. 1982). Using SVD, 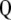 can be written as
can be written as
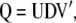 |
(10) |
where the columns of matrix 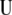 (
(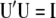 ) are the left singular vector of
) are the left singular vector of 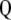 , and the columns of matrix
, and the columns of matrix 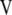 (
(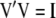 ) are the right singular vector of
) are the right singular vector of 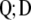 is a diagonal matrix with the square root of the eigenvalues (singular values) of
is a diagonal matrix with the square root of the eigenvalues (singular values) of 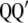 or
or 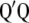 (the eigenvalues of
(the eigenvalues of 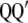 and
and 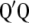 are the same).
are the same).
The problem now is to determine the following: From where should the first singular vector for constructing 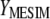 be taken, from
be taken, from 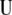 or from
or from 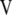 ? Note that Equation 10 can be written as
? Note that Equation 10 can be written as 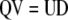 , from which it is evident that if
, from which it is evident that if 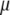 is the first singular value of
is the first singular value of 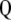 , and
, and 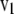 and
and 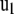 are its associated left and right first singular vectors, respectively, then
are its associated left and right first singular vectors, respectively, then 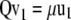 , from which
, from which 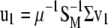 . Let
. Let 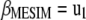 ; then
; then 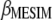 is a linear transformation of
is a linear transformation of 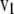 . The estimators of
. The estimators of 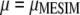 and
and 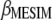 are obtained from
are obtained from 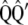 , such that
, such that 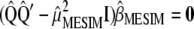 . According to Anderson (2003),
. According to Anderson (2003), 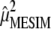 and
and  are the maximum-likelihood estimators of the eigenvector and the eigenvalue of
are the maximum-likelihood estimators of the eigenvector and the eigenvalue of 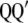 , respectively, and are asymptotically consistent and unbiased. The estimators of
, respectively, and are asymptotically consistent and unbiased. The estimators of 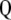 ,
, 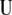 ,
, 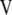 , and
, and 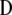 are
are 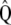 ,
, 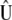 ,
, 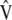 , and
, and 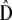 , respectively, so
, respectively, so 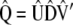 . These results allow estimating
. These results allow estimating 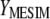 as
as 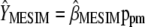 . Asymptotically,
. Asymptotically, 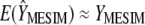 .
.
When only one trait and its molecular scores are considered,
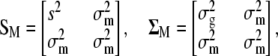 |
and
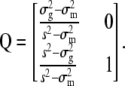 |
When 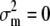 , then
, then
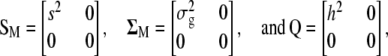 |
where 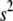 and
and 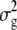 are the phenotypic and genotypic variances of the trait, respectively,
are the phenotypic and genotypic variances of the trait, respectively, 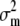 is the variance of the molecular score associated with the trait under selection, and
is the variance of the molecular score associated with the trait under selection, and 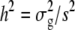 .
.
SIMULATED DATA
We have simulated genotypes from a population with the aim of comparing theoretical and practical results from MESIM, RESIM, ESIM, the restrictive selection index of Kempthorne and Nordskog (1959), the Smith (1936) selection index, and the Lande–Thompson (Lande and Thompson 1990) molecular selection index. The simulator system used in this study, developed by Wang et al. (2004), has two main engines, QU-GENE and QuCim, which require different input data. To simulate a population, the input file for QU-GENE should contain the genetic structure of the genotypes for each specific trait: i.e., number of genes (or QTL); gene effect for each trait including additive, dominance, and epistasis; linkage among the genes in one chromosome; and trait heritability, etc. Component QU-GENE can generate genotypes making up populations of cross-pollinated or self-pollinated species or create different environmental conditions where the simulated genotypes will be evaluated. On the other hand, the input file for QuCim must have the type of crosses and the selection method to be used in each breeding strategy. Selection methods that can be simulated in QuCim include mass selection, pedigree system, bulk population system, backcross breeding, top-cross breeding, doubled-haploid breeding, marker-assisted selection for one trait, and many combinations and modifications of these (Wang et al. 2004). The simulator provides, for each genotype in the population, the true genotypic value as well as the phenotypic value of the traits under study.
Generating a doubled-haploid population for selection:
The original data were taken from an actual doubled-haploid maize mapping population of 236 genotypes with five traits; QTL for all five traits were mapped. The five traits measured were male flowering time (MFL) (days), female flowering time (FFL) (days), plant height (PHT) (centimeters), ear height (EHT) (centimeters), and 100-kernel weight (HKF) (grams). This data file was used to generate 200 doubled-haploid genotypes that form the reference population (cycle 0). Using a selection pressure of 10% (k = 1.755), 20 genotypes were selected under MESIM, the Lande–Thompson selection index, ESIM, RESIM, the Smith selection index, and the restrictive selection index of Kempthorne and Nordskog. These 20 selected doubled haploids were then crossed in diallel fashion, and a new population of 200 doubled haploids was generated. This was repeated during five selection cycles for all five traits. The efficiency of the indexes was compared, using the mean genotypic value and the regression of the mean genotypic value of the selected genotypes on the selection cycles. We used phenotypic, genotypic, and molecular score variance–covariance matrices for estimating the singular vectors and singular values.
We also generated populations on the basis of selection of individual traits with the objective of comparing MESIM and the Lande–Thompson (Lande and Thompson 1990) molecular selection index method for the simultaneous selection of five traits.
Sign of the coefficients, economic weights, and expected genetic gains:
When using MESIM, ESIM, and RESIM, it is often necessary to change the sign of the coefficients of the first singular eigenvector to select the genotypes according to the desired genetic advance; that is, for traits such as MFL, FFL, PHT, and EHT, the signs are always negative (decreasing the mean genotypic value), whereas for HKF the signs are always positive (increasing the mean genotypic value).
Concerning the economic weights for the Lande–Thompson molecular selection index, the restrictive selection index of Kempthorne and Nordskog (1959), and the Smith (1936) selection index, economics weights were assigned following Smith et al. (1981). Then, one set had coefficients of 1 or −1, and the other had the heritability of each trait multiplied by 1 or −1, depending on the trait. Therefore, for MFL, FFL, PHT, EHT, and HKF, the first set of coefficients was −1, −1, −1, −1, and 1, respectively, whereas the second set of coefficients was −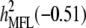 ,
, 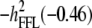 ,
, 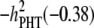 ,
, 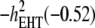 , and
, and 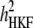 (0.27); all economic weights of the molecular markers associated with the traits were equal to zero. All five traits were simultaneously selected under MESIM, the Lande–Thompson selection index, ESIM, and the Smith selection index, whereas for the restrictive selection index of Kempthorne and Nordskog and RESIM, the traits that were unchanged were MFL and PHT.
(0.27); all economic weights of the molecular markers associated with the traits were equal to zero. All five traits were simultaneously selected under MESIM, the Lande–Thompson selection index, ESIM, and the Smith selection index, whereas for the restrictive selection index of Kempthorne and Nordskog and RESIM, the traits that were unchanged were MFL and PHT.
Furthermore, MESIM and the Lande–Thompson selection index were compared when traits were selected individually. When selection was performed on individual traits, the Lande–Thompson molecular selection index based on heritabilities as economic weights was not applied, and only the index based on coefficients 1 and −1 (depending on the trait of interest), and 0 for the economic weights, was employed.
RESULTS AND DISCUSSION
The genotypic means under MESIM and the Lande–Thompson selection index when selection is practiced on traits individually (not simultaneously on various traits) are shown in Table 1. Because genetic variability became exhausted, only two selection cycles were run. The MESIM-selected genotypes had better genotypic means than those selected under the Lande–Thompson index for all five traits. To clarify the interpretation of the MESIM, consider, for example, the first selection cycle on the individual-trait MFL. The estimated phenotypic, genotypic, and molecular score variances in the original population were 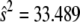 ,
, 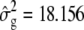 , and
, and 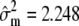 , respectively, from which
, respectively, from which
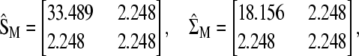 |
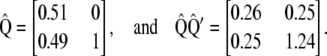 |
The first singular value and its associated singular vector are 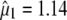 and
and 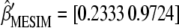 , respectively. However, because MFL decreases, it is necessary to multiply the elements of
, respectively. However, because MFL decreases, it is necessary to multiply the elements of  by −1 such that the selection index in the context of MESIM is
by −1 such that the selection index in the context of MESIM is 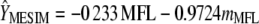 , where MFL denotes the trait of interest, and
, where MFL denotes the trait of interest, and 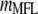 is the molecular score associated with MFL. In this case, the total expected genetic response can be partitioned into two components, the coefficient related to the phenotypic values per se and those related to the molecular scores. Value −0.233 is the phenotypic coefficient, and −0.972 is the molecular score coefficient.
is the molecular score associated with MFL. In this case, the total expected genetic response can be partitioned into two components, the coefficient related to the phenotypic values per se and those related to the molecular scores. Value −0.233 is the phenotypic coefficient, and −0.972 is the molecular score coefficient.
TABLE 1.
Mean genotypic values under MESIM and Lande–Thompson molecular selection indexes when traits are selected individually until genetic variability is exhausted (cycle 2)
| MESIM genotypic means
|
Lande–Thompson genotypic means
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Selection cycles | MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF |
| (−) | (−) | (−) | (−) | (+) | (−1) | (−1) | (−1) | (−1) | (1) | |
| 0 | 98.54 | 98.89 | 139.61 | 88.37 | 20.45 | 98.54 | 98.89 | 139.61 | 88.37 | 20.45 |
| 1 | 93.89 | 97.03 | 124.89 | 75.83 | 22.85 | 93.23 | 96.91 | 132.87 | 72.64 | 20.80 |
| 2 | 91.66 | 93.83 | 120.62 | 63.33 | 92.08 | 94.36 | 127.18 | 66.61 | ||
The traits were male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF) for one and two selection cycles for simulated data using phenotypic, genotypic, and molecular score variance–covariance matrices. The signs and economic weights of the selection indexes for each trait are shown in parentheses.
When selection is practiced on all five traits simultaneously, then economic weights −1, −1, −1, −1, and 1 for each trait are used; the heritability of the traits is also used as weights. The Lande–Thompson molecular selection index is denoted as Lande–Thompson 1 when −1, −1, −1, −1, and 1 are used as economic weights, and when heritabilities are used as economic weights, it is denoted Lande–Thompson 2. Similarly, the standard Smith selection index is denoted as Smith 1 in the first case and Smith 2 in the second case; and the Kempthorne–Nordskog restricted selection indexes are denoted as KN1 and KN2, respectively.
For the trait HKF, the selection gain per cycle for MESIM (0.50 g) was greater than that obtained by Lande–Thompson 1 (0.21 g) and Lande–Thompson 2 (0.31 g) (Table 2). However, for MFL, the opposite was true; that is, Lande–Thompson 1 (−0.91 days) and Lande–Thompson 2 (−0.83 days) under both sets of economic weights were more effective than MESIM (−0.71 days) for maturity (Table 2). Comparing the genotypic means when individual traits are selected (Table 1) with those obtained when five traits are simultaneously selected (Table 2), it is evident that the genotypic means are higher when only one trait is under selection. Correlations between traits play an important role in the correlated response of other traits.
TABLE 2.
Mean genotypic values and gain per cycle of the 20 genotypes selected under MESIM and the Lande–Thompson 1 (economic weights are 1s and −1s) and Lande–Thompson 2 (economic weights are heritability of the traits) molecular selection index for five traits selected simultaneously, male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF) for five selection cycles for simulated data using phenotypic, genotypic, and molecular score variance–covariance matrices
| MESIM
|
Lande–Thompson 1
|
Lande–Thompson 2
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | |
| Selection cycles | (−) | (−) | (−) | (−) | (+) | (−1) | (−1) | (−1) | (−1) | (1) | (−0.5) | (−0.46) | (−0.38) | (−0.5) | (0.27) |
| 0 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 |
| 1 | 97.0 | 98.4 | 123.5 | 74.3 | 21.3 | 98.7 | 99.5 | 130.5 | 80.7 | 20.8 | 98.0 | 98.7 | 127.1 | 76.1 | 21.3 |
| 2 | 96.5 | 99.1 | 118.7 | 70.9 | 21.3 | 97.0 | 98.4 | 123.6 | 71.3 | 20.6 | 96.9 | 98.2 | 129.1 | 74.3 | 19.6 |
| 3 | 96.1 | 96.5 | 119.2 | 64.8 | 21.6 | 96.0 | 97.9 | 122.5 | 66.6 | 21.5 | 95.7 | 97.0 | 121.8 | 68.5 | 20.6 |
| 4 | 95.9 | 95.8 | 117.4 | 60.8 | 22.7 | 95.3 | 98.4 | 119.2 | 64.1 | 21.6 | 95.0 | 97.2 | 120.4 | 70.7 | 21.9 |
| 5 | 94.4 | 95.6 | 114.9 | 59.4 | 23.0 | 94.4 | 96.6 | 117.6 | 59.9 | 21.2 | 94.8 | 96.4 | 119.9 | 67.9 | 22.1 |
| Gain per cycle | −0.71 | −0.78 | −4.04 | −5.48 | 0.50 | −0.91 | −0.44 | −4.15 | −5.62 | 0.21 | −0.83 | −0.51 | −3.59 | −3.55 | 0.31 |
The signs and economic weights of the selection indexes for each trait are shown in parentheses.
Regarding the Smith SI and ESIM, the genotypic means of the selected genotypes are shown in Table 3. In this case, for four of the five traits, MFL, FFL, EHT, and HKF, the selection gain per cycle of ESIM was greater than that obtained with the Smith SI. Concerning KN restricted (R)SI and RESIM (keeping MFL and PHT unchanged), the genotypic means of the selected genotypes are shown in Table 4. For HKF, the selection gain per cycle for RESIM (0.48 g) was greater than that obtained using KN1 RSI (0.27 g) and KN2 RSI (0.19 g). However, for FFL, the opposite was true; that is, KN1 RSI (−1.05 days) and KN2 RSI (−1.10 days) under both sets of economic weights were more effective than RESIM (−0.92 days) for maturity. The effective selection gain per cycle estimated as the linear regression of the mean genotypic trait value on the selection cycle is also shown in the last row of Tables 3 and 4.
TABLE 3.
Mean genotypic values of the 20 genotypes selected under ESIM and Smith SI 1 and 2, for five traits, male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF), during five selection cycles for simulated data using phenotypic and genotypic variance–covariance matrices
| ESIM
|
SMITH SI 1
|
SMITH SI 2
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | |
| Selection cycles | (−) | (−) | (−) | (−) | (+) | (−1) | (−1) | (−1) | (−1) | (+1) | (−0.51) | (−0.46) | (−0.38) | (−0.52) | (0.27) |
| 0 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 |
| 1 | 95.0 | 96.4 | 132.7 | 75.3 | 20.2 | 98.6 | 99.3 | 124.1 | 71.6 | 20.4 | 98.5 | 99.2 | 123.1 | 72.1 | 20.6 |
| 2 | 95.2 | 95.6 | 125.1 | 63.6 | 21.0 | 101.0 | 100.5 | 114.9 | 64.0 | 20.6 | 97.4 | 99.1 | 116.3 | 66.8 | 21.0 |
| 3 | 94.0 | 94.2 | 123.3 | 58.0 | 21.2 | 98.4 | 99.1 | 111.6 | 59.6 | 20.6 | 96.3 | 98.9 | 112.5 | 62.6 | 21.1 |
| 4 | 93.3 | 93.4 | 123.3 | 57.5 | 21.6 | 94.6 | 97.6 | 111.6 | 59.5 | 21.0 | 94.4 | 98.8 | 111.7 | 61.4 | 21.2 |
| 5 | 92.6 | 93.3 | 122.2 | 57.5 | 22.6 | 94.5 | 97.5 | 111.2 | 58.4 | 21.5 | 94.5 | 99.3 | 111.3 | 60.5 | 21.4 |
| Gain per selection cycle | 0.19 | −0.92 | −0.18 | −3.45 | 0.48 | 0.05 | −1.05 | −1.15 | −4.53 | 0.27 | 0.02 | −1.10 | 0.58 | −3.44 | 0.19 |
The gain per cycle is the regression coefficient of the mean genotypic values regressed on the selection cycles. The signs and economic weights of the SIs for each trait are shown in parentheses.
TABLE 4.
Mean genotypic values of the 20 genotypes selected under RESIM, KN1 RSI, and KN2 RSI, for traits female flowering (FFL), ear height (EHT), and 100-kernel weight (HKF) during five selection cycles for simulated data using phenotypic and genotypic variance–covariance matrices
| RESIM
|
KN1 RSI
|
KN2 RSI
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | MFL | FFL | PHT | EHT | HKF | |
| Selection cycles | (−) | (−) | (−) | (−) | (+) | (−1) | (−1) | (−1) | (−1) | (+1) | (−0.51) | (−0.46) | (−0.38) | (−0.52) | (0.27) |
| 0 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 | 98.5 | 98.9 | 139.6 | 88.4 | 20.4 |
| 1 | 97.4 | 96.5 | 141.3 | 84.1 | 20.2 | 97.4 | 96.3 | 141.2 | 84.2 | 20.2 | 97.7 | 96.33 | 140.4 | 82.8 | 20.0 |
| 2 | 97.7 | 94.8 | 143.6 | 80.2 | 20.6 | 99.4 | 95.6 | 143.5 | 80.3 | 20.5 | 98.8 | 95.2 | 145.1 | 81.6 | 20.5 |
| 3 | 97.2 | 94.0 | 141.2 | 76.4 | 21.7 | 98.2 | 94.7 | 139.8 | 74.4 | 21.1 | 97.6 | 94.0 | 143.1 | 75.9 | 20.1 |
| 4 | 98.4 | 94.5 | 140.7 | 76.7 | 22.4 | 97.4 | 93.9 | 137.7 | 70.5 | 21.4 | 97.7 | 93.7 | 145.2 | 75.5 | 21.1 |
| 5 | 99.2 | 93.9 | 139.9 | 71.1 | 22.1 | 98.9 | 93.3 | 135.2 | 67.8 | 21.4 | 98.7 | 93.1 | 141.9 | 71.58 | 21.1 |
| Gain per selection cycle | 0.19 | −0.92 | −0.18 | −3.45 | 0.48 | 0.05 | −1.05 | −1.15 | −4.53 | 0.27 | 0.02 | −1.10 | 0.58 | −3.44 | 0.19 |
The gain per cycle is the regression coefficient of the mean genotypic values regressed on the selection cycles. The signs and economic weights of the SIs for each trait are shown in parentheses. The restrictive traits are male flowering (MFL) and plant height (PHT).
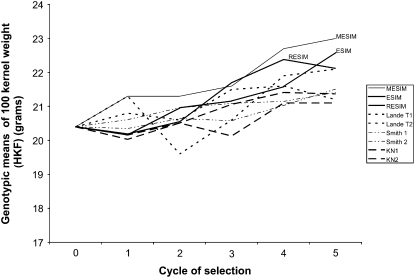
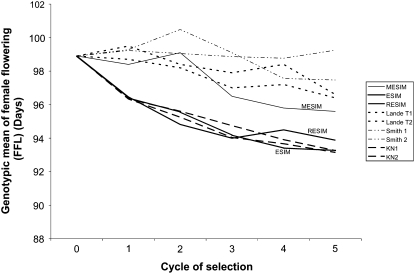
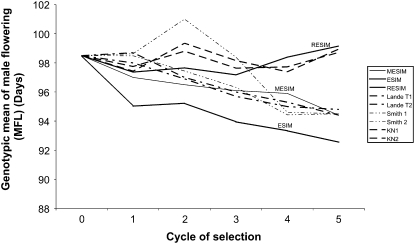
Figures 1–3 show the genotypic means for HKF, FFL, and MFL for five selection cycles when the genotypes are selected under different selection indexes. Increasing trends in the genotypic means of the selected genotypes for the five selection cycles under MESIM, Lande–Thompson 1 and 2, ESIM, Smith 1 and 2, RESIM, and Kempthorne–Nordskog for HKF are shown in Figure 1. Clearly, MESIM selected genotypes with higher HFK in all cycles. For FFL (Figure 2) ESIM was the best in all cycles, whereas MESIM was better than Lande–Thompson 1 and 2 in the last three cycles. For MFL, Figure 3 shows that MESIM results are similar to those of Lande–Thompson 1 and 2. However, ESIM is still the selection index that gave the highest response to selection. Furthermore, note that since MFL was unchanged when applying the restrictive selection indexes (RESIM, KN1, and KN2), their genotypic means did not change over the selection cycles and stayed around the mean of cycle 0 (Figure 3).
Figure 1.—
Mean of the genotypic values of the selected genotypes under under MESIM, Lande–Thompson (Lande T1 and Lande T2) molecular selection indexes, ESIM, Smith selection indexes (Smith 1 and 2), RESIM, and Kempthorne–Nordskog restricted selection indexes (KN1 and KN2) during five selection cycles of traits 100-kernel weight (HKF) (grams) using simulated data. The simultaneously selected traits were male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF). The economic weights used for MFL, FFL, PHT, EHT, and HKF under the Lande–Thompson molecular selection indexes, the Smith selection index, and the Kempthorne–Nordskog restricted selection index were −1, −1, −1, −1, and 1, respectively, and the heritability of the corresponding traits.
Figure 2.—
Mean of the genotypic values of the selected genotypes under MESIM, Lande–Thompson (Lande T1 and Lande T2) molecular selection indexes, ESIM, Smith SIs (Smith 1 and 2), RESIM, and Kempthorne–Nordskog restricted selection indexes (KN1 and KN2) for five selection cycles of the trait female flowering (FFL) (days), using simulated data. The simultaneously selected traits were male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF). The economic weights used for MFL, FFL, PHT, EHT, and HKF under the Lande–Thompson molecular selection indexes, the Smith selection index, and the Kempthorne–Nordskog restricted selection index were −1, −1, −1, −1, and 1, respectively, and the heritability of the corresponding traits.
Figure 3.—
Mean of the genotypic values of the selected genotypes under MESIM, Lande–Thompson (Lande T1 and Lande T2) molecular selection indexes, ESIM, SMITH SIs (Smith 1 and 2), RESIM, and Kempthorne–Nordskog restricted selection indexes (KN1 and KN2) for five selection cycles of the trait female flowering (MFL) (days), using simulated data. The simultaneously selected traits were male flowering (MFL), female flowering (FFL), plant height (PHT), ear height (EHT), and 100-kernel weight (HKF). The economic weights used for MFL, FFL, PHT, EHT, and HKF under the Lande–Thompson molecular selection indexes, the Smith selection index, and the Kempthorne–Nordskog restricted selection index were −1, −1, −1, −1, and 1, respectively, and the heritability of the corresponding traits.
As previously indicated, the molecular selection indexes (MESIM and Lande–Thompson) depend on the heritability of each trait. According to Lande and Thompson (1990), Zhang and Smith (1992, 1993), Gimelfarb and Lande (1994, 1995), and Whittaker (2003), the molecular selection index is expected to be more efficient than the standard selection indexes (i.e., ESIM and Smith's selection index) when the heritability of the trait is low. Figure 1 shows the genotypic means of HKF with a heritability of 0.27, whereas Figures 2 and 3 depict the genotypic means of the selected genotypes for FFL and MFL), with heritabilities of 0.46 and 0.51, respectively. This would explain why MESIM was more efficient than the other indexes for selecting the genotypes with the highest genotypic means. Detailed descriptions of ESIM, RESIM, and the Smith selection index can be found in Cerón- Rojas et al. (2008). For the other traits, the gains of MESIM over Lande–Thompson 1 and 2 are not as clear as for HKF and FFL (Tables 2–4). However, when traits are selected individually, the genotypic mean obtained for MESIM is higher than that achieved by Lande–Thompson for most traits (Table 1).
It is worth noting that when the eigenvectors are obtained from the variance–covariance phenotypic and genotypic matrices, then MESIM, ESIM, and RESIM assign weights proportional to the heritability of the trait; that is, the higher the heritability, the more weight, and vice versa. As mentioned by Cerón-Rojas et al. (2006), a solution would be to use the phenotypic and genotypic correlation matrices. Another solution would be to use the inverse of 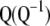 and thus give more weight to traits with low heritability. The latter solution for constructing MESIM comes naturally from Equation 7, since
and thus give more weight to traits with low heritability. The latter solution for constructing MESIM comes naturally from Equation 7, since 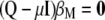 and can be written as
and can be written as 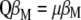 , from which
, from which 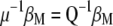 . Then the equation to obtain the eigenvectors is
. Then the equation to obtain the eigenvectors is 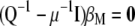 , in which case
, in which case
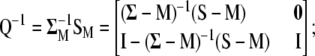 |
when only one trait and its molecular scores are considered, then
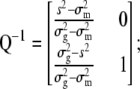 |
and when 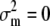 ,
,
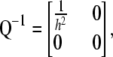 |
from which it is evident that traits with low heritability will have higher weights.
Finally, it is worth noting that although MESIM, ESIM, and RESIM may occasionally not to turn out to be the indexes with the highest selection gains, they have the statistical properties of the principal components. According to Okamoto (1969), these are optimal properties established in terms of maximization and minimization. Thus the first component has the largest variance and the smallest loss of information (Rao 1964). On the other hand, statistical properties of other selection indexes are unknown.
This research found that MESIM has three advantages over Lande–Thompson 1 and 2: first, it can be used to solve practical problems faced by breeders attempting to select plants or animals for the next generation when no estimates of economic weights are available. Even if economic weights are available, in practice it is very unlikely that they would maximize the derivative of 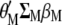 with respect to
with respect to 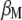 and to
and to 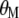 (under the imposed restrictions). Furthermore, if two breeders are interested in improving, say, n traits, it is very unlikely that they would assign the same weights to them. Second, estimates of MESIM have known statistical sampling properties, but estimates for the Lande–Thompson molecular selection index are unknown. Third, results from MESIM using simulated data show that realized genetic gains for various traits simultaneously are similar to, or higher than, those obtained by Lande and Thompson (1990).
(under the imposed restrictions). Furthermore, if two breeders are interested in improving, say, n traits, it is very unlikely that they would assign the same weights to them. Second, estimates of MESIM have known statistical sampling properties, but estimates for the Lande–Thompson molecular selection index are unknown. Third, results from MESIM using simulated data show that realized genetic gains for various traits simultaneously are similar to, or higher than, those obtained by Lande and Thompson (1990).
CONCLUSIONS
This research presents a molecular selection index based on principles developed by Cerón-Rojas et al. (2008). Simulated results show that when genotypes are selected on the basis of individual traits, MESIM increased the response to selection over the Lande–Thompson index. When several traits are selected simultaneously, MESIM outperformed Lande–Thompson for traits with low heritability. For traits with high heritability, ESIM performed very well. One of the most important results of MESIM is that  is the maximum-likelihood estimate of
is the maximum-likelihood estimate of 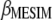 , whereas
, whereas 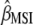 is an estimate of
is an estimate of 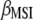 , whose sampling properties are unknown. MESIM can be considered a generalization of ESIM (Cerón-Rojas et al. 2006) when information on QTL is incorporated through molecular markers. The sampling properties of ESIM (and therefore of MESIM) and its selection response are known, and its estimators showed desirable statistical properties such as consistency and asymptotic unbiasedness.
, whose sampling properties are unknown. MESIM can be considered a generalization of ESIM (Cerón-Rojas et al. 2006) when information on QTL is incorporated through molecular markers. The sampling properties of ESIM (and therefore of MESIM) and its selection response are known, and its estimators showed desirable statistical properties such as consistency and asymptotic unbiasedness.
It should be pointed out that MESIM is more general than ESIM (Cerón-Rojas et al. 2006) because the basic underlying assumption made in ESIM, 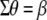 , is relaxed in MESIM. MESIM maximizes the selection response by maximizing the square of the correlation between
, is relaxed in MESIM. MESIM maximizes the selection response by maximizing the square of the correlation between 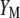 and
and 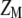 ,
, 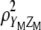 , which is the same as maximizing
, which is the same as maximizing 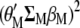 . This basic idea, used for developing a restrictive selection index (Cerón-Rojas et al. 2008), is valid for MESIM when no restrictions are imposed on any of the traits.
. This basic idea, used for developing a restrictive selection index (Cerón-Rojas et al. 2008), is valid for MESIM when no restrictions are imposed on any of the traits.
Some advantages of MESIM over MSI should be pointed out: (1) the sampling properties of MESIM, 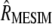 , are known and easy to evaluate; (2) the MESIM eigenvalue and eigenvector are estimated by the maximum-likelihood method; and (3) a restrictive SI can be developed from MESIM when only some markers and/or traits are used. In summary, the results of this study indicate that MESIM is a generalization of ESIM when information on QTL linked to molecular markers is incorporated.
, are known and easy to evaluate; (2) the MESIM eigenvalue and eigenvector are estimated by the maximum-likelihood method; and (3) a restrictive SI can be developed from MESIM when only some markers and/or traits are used. In summary, the results of this study indicate that MESIM is a generalization of ESIM when information on QTL linked to molecular markers is incorporated.
The availability of abundant molecular markers can help to achieve faster breeding progress than with traditional breeding methods or marker-assisted selection by means of genomewide selection (Bernardo and Yu 2007). The MESIM could be a valid option for a genomewide selection method because the serious problem of parameter identification created by the collinearity of the markers is overcome by the singular value decomposition method of MESIM. Furthermore, MESIM naturally performs cross-product between all trait–environment combinations and markers; thus it implicitly introduces estimates of particular epistatic interactions into the seletion index. Further research on the use of MESIM in genomewide selection is required.
Acknowledgments
The authors are grateful to Jiankang Wang for his valuable assistance and help when running the simulation software QU-GENE. The authors thank the associate editor and two anonymous reviewers for their comments and suggestions, which significantly improved the quality of this article. The authors are thankful to BIMBO-Mexico for partially funding this research.
APPENDIX: THEORETICAL DERIVATION OF MESIM
The procedure shown below is a slight modification of that used by Cerón-Rojas et al. (2008) within the context of a restricted selection index method based on eigenanalysis (RESIM). In this case, 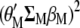 must be maximized under the restrictions
must be maximized under the restrictions 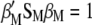 and
and 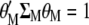 ; i.e., we should maximize
; i.e., we should maximize
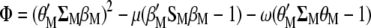 |
with respect to 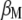 ,
, 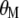 ,
, 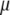 , and
, and 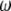 , where
, where 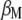 is the vector of
is the vector of  coefficients,
coefficients, 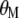 is the vector of economic weights, and
is the vector of economic weights, and 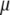 and
and 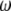 are Lagrange multipliers. In MESIM it is assumed that
are Lagrange multipliers. In MESIM it is assumed that 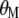 is not a vector of constants.
is not a vector of constants.
When 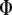 is derived with respect to
is derived with respect to 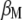 ,
, 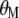 ,
, 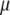 , and
, and 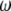 , and the result is set to the null vector, it follows that
, and the result is set to the null vector, it follows that
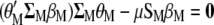 |
(A1) |
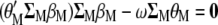 |
(A2) |
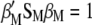 |
(A3) |
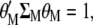 |
(A4) |
where Equations A3 and A4 denote the restrictions imposed for the maximization of 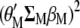 with respect to
with respect to 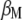 and
and 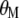 . Because the restrictions
. Because the restrictions 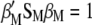 and
and 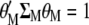 , when Equation A1 is multiplied by
, when Equation A1 is multiplied by 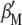 and Equation A2 is multiplied by
and Equation A2 is multiplied by 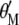 , both equations can be written as
, both equations can be written as
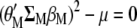 |
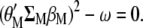 |
Clearly, 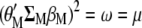 . Therefore,
. Therefore, 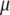 maximizes
maximizes 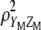 under the restrictions
under the restrictions 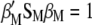 and
and 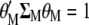 .
.
The following problem is to determine the vector 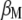 , which allows constructing the selection index
, which allows constructing the selection index 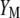 that has maximum correlation with
that has maximum correlation with 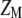 . Because
. Because 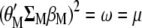 , Equations A1 and A2 can be written as
, Equations A1 and A2 can be written as
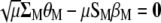 |
(A5) |
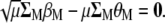 |
(A6) |
Multiplying Equation A5 by 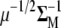 , we obtain that
, we obtain that 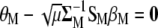 , from which
, from which 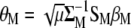 is computed.
is computed.
Substitute, in Equation A6, 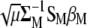 for
for 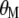 and get
and get  , from which Equation 7 (see the text) is obtained,
, from which Equation 7 (see the text) is obtained,
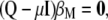 |
where 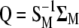 , and
, and 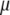 and
and 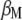 are the eigenvalue and the eigenvector of
are the eigenvalue and the eigenvector of  , respectively. Thus, for
, respectively. Thus, for 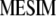 , the values that maximize
, the values that maximize 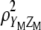 under the restrictions
under the restrictions 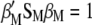 and
and 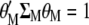 are the eigenvalues (
are the eigenvalues (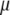 ) of the matrix
) of the matrix 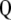 and its eigenvector vector,
and its eigenvector vector, 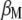 , that allows constructing the index
, that allows constructing the index 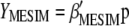 that maximizes its correlation with
that maximizes its correlation with 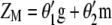 .
.
References
- Anderson, T. W., 2003. An Introduction to Multivariate Statistical Analysis, Ed. 3. John Wiley & Sons, New York.
- Arus, P., and J. Moreno-Gonzalez, 1993. Marker-assisted selection, pp. 315–331 in Plant Breeding: Principles and Prospects, edited by M. D. Hayward, N. O. Bosemark and I. Romagosa. Chapman & Hall/University Press, Cambridge, UK.
- Baker, R. J., 1986. Selection Indices in Plant Breeding. CRC Press, Boca Raton, FL.
- Bernardo, R., and J. Yu, 2007. Prospects for genomewide selection for quantitative traits in maize. Crop Sci. 47 1082–1090. [Google Scholar]
- Cerón-Rojas, J. J., J. Crossa, J. Sahagún-Castellanos, F. Castillo-González and A. Santacruz-Varela, 2006. A selection index method based on eigenanalysis. Crop Sci. 46 1711–1721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cerón-Rojas, J. J., J. Sahagún-Castellanos, F. Castillo-González, A. Santacruz-Varela and J. Crossa, 2008. Arestricted selection index method based on eigenanalysis. J. Agric. Biol. Environ. Stat. (in press). [DOI] [PMC free article] [PubMed]
- Dekkers, J. C. M., and M. R. Dentine, 1991. Quantitative genetic variation associated with chromosomal markers in segregating populations. Theor. Appl. Genet. 81 212–220. [DOI] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1997. Introduction to Quantitative Genetics. Longman, New York.
- Gimelfarb, A., and R. Lande, 1994. Simulation of marker-assisted selection in hybrid populations. Genet. Res. 63 39–47. [DOI] [PubMed] [Google Scholar]
- Gimelfarb, A., and R. Lande, 1995. Marker-assisted selection and marker-QTL associations in hybrid populations. Theor. Appl. Genet. 91 522–528. [DOI] [PubMed] [Google Scholar]
- Harris, D. L., 1964. Expected and predicted progress from index selection involving estimates of population parameters. Biometrics 20 46–72. [Google Scholar]
- Hayes, J. F., and W. G. Hill, 1980. A reparameterization of a genetic selection index to locate its sampling properties. Biometrics 36 237–248. [PubMed] [Google Scholar]
- Hazel, L. N., 1943. The genetic basis for constructing a selection index, pp. 316–330 in Papers on Quantitative Genetics and Related Topics. Department of Genetics, North Carolina State College, Raleigh, NC.
- Jansen, R. C., 2003. Quantitative trait loci in inbred lines, pp. 445–476 in Handbook of Statistical Genetics, Ed. 2, Vol. I, edited by D. J. Balding, M. Bishop and C. Cannings. John Wiley & Sons, Chichester, UK.
- Kempthorne, O., and A. W. Nordskog, 1959. Restricted selection indices. Biometrics 15 10–19. [Google Scholar]
- Lande, R., and R. Thompson, 1990. Efficiency of marker-assisted selection in the improvement of quantitative traits. Genetics 124 743–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackinnon, M. J., and M. A. J. Georges, 1992. The effects of selection on linkage analysis for quantitative traits. Genetics 132 1177–1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardia, K. V., J. T. Kent and J. M. Bibby, 1982. Multivariate Analysis. Academic Press, New York.
- Moreau, L., S. Lemarie, A. Charcosset and A. Gallais, 2000. Economic efficiency of one cycle of marker-assisted selection efficiency. Crop Sci. 40 329–337. [Google Scholar]
- Okamoto, M., 1969. Optimality of principal components, pp. 673–685 in Multivariate Analysis II, edited by P. R. Krishnaiah. Academic Press, New York.
- Rao, C. R., 1964. The use and interpretation of principal component analysis in applied research, pp. 56–85 in Multivariate Statistical Methods: Within-Groups Covariation, edited by E. H. Bryant and W. R. Atchley. Halsted Press, Stroudsburg, PA.
- Smith, H. F., 1936. A discriminant function for plant selection, pp. 466–476 in Papers on Quantitative Genetics and Related Topics. Department of Genetics, North Carolina State College, Raleigh, NC.
- Smith, O. S., A. R. Hallauer and W. A. Russell, 1981. Use of index selection in recurrent selection programs in maize. Euphytica 30 611–618. [Google Scholar]
- Van Vleck, L. D., 1993. Selection Index and Introduction to Mixed Model Methods. CRC Press, Boca Raton, FL.
- Wang, J., M. Van Ginkel, R. Trethowan, G. Ye, I. Delacy et al., 2004. Simulating the effects of dominance and epistasis on selection response in the CIMMYT wheat breeding program using QuCim. Crop Sci. 44 2006–2018. [Google Scholar]
- Wei, M., A. Caballero and W. G. Hill, 1996. Selection response in finite populations. Genetics 144 1961–1974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittaker, J. C., 2003. Marker-assisted selection and introgression, pp. 554–574 in Handbook of Statistical Genetics, Ed. 2, Vol. I, edited by D. J. Balding, M. Bishop and C. Cannings. John Wiley & Sons, Chichester, UK.
- Wu, R., Z. B. Zeng, S. E. Mckeand and D. M. O'Malley, 2000. The case for molecular mapping in forest tree breeding. Plant Breed. Rev. 19 41–68. [Google Scholar]
- Xie, C., and S. Xu, 1998. Efficiency of multistage marker-assisted selection in the improvement of multiple quantitative traits. Heredity 8 489–498. [DOI] [PubMed] [Google Scholar]
- Zhang, W., and C. Smith, 1992. Computer simulation of marker-assisted selection utilizing linkage disequilibrium. Theor. Appl. Genet. 83 813–820. [DOI] [PubMed] [Google Scholar]
- Zhang, W., and C. Smith, 1993. Simulation of marker-assisted selection utilizing linkage disequilibrium: the effects of several additional factors. Theor. Appl. Genet. 86 492–496. [DOI] [PubMed] [Google Scholar]