Selection Mapping of Loci for Quantitative Disease Resistance in a Diverse Maize Population

Abstract

The selection response of a complex maize population improved primarily for quantitative disease resistance to northern leaf blight (NLB) and secondarily for common rust resistance and agronomic phenotypes was investigated at the molecular genetic level. A tiered marker analysis with 151 simple sequence repeat (SSR) markers in 90 individuals of the population indicated that on average six alleles per locus were available for selection. An improved test statistic for selection mapping was developed, in which quantitative trait loci (QTL) are identified through the analysis of allele-frequency shifts at mapped multiallelic loci over generations of selection. After correcting for the multiple tests performed, 25 SSR loci showed evidence of selection. Many of the putatively selected loci were unlinked and dispersed across the genome, which was consistent with the diffuse distribution of previously published QTL for NLB resistance. Compelling evidence for selection was found on maize chromosome 8, where several putatively selected loci colocalized with published NLB QTL and a race-specific resistance gene. Analysis of F₂ populations derived from the selection mapping population suggested that multiple linked loci in this chromosomal segment were, in part, responsible for the selection response for quantitative resistance to NLB.

SELECTION mapping (SM) refers to a range of approaches that identifies alleles, loci, and epistatic interactions using populations that have been subjected to iterative cycles of recombination and selection. The effects of selection can be seen as differences in allele frequency, diversity, and/or patterns of recombination, through comparisons of temporally or spatially defined subpopulations. Several studies have been conducted on the principle that significant phenotypic change can be explained by significant changes in allele frequencies (e.g., Stuber and Moll 1972; Labate et al. 1999; De Koeyer et al. 2001; Coque and Gallais 2006). A fundamental challenge in SM, however, is to differentiate the effects of selection from those of genetic drift. Information on patterns of recombination and sequence variation can be useful for SM in populations that are highly diverged, when genetic drift confounds the identification of significant changes in allele frequency (e.g., Kohn et al. 2000; Pollinger et al. 2005; Wright et al. 2005). A combination of allelic frequency data and functional evidence was used as an alternative to population-genetic evidence in the study of Laurie et al. (2004). In our study, we use temporal shifts in allele frequency to identify putatively selected quantitative trait loci (QTL) for resistance to northern leaf blight (NLB) of maize. Putatively selected QTL are identified with a simulation-based test statistic that compares observed allele-frequency shifts to those expected under genetic drift for the specific maize breeding population under study. We also genetically tested one putatively selected chromosomal region and show that this region does associate with resistance to NLB.

While selection is fundamental to plant breeding and an abundance of selection methodologies have been developed, SM has been a relatively minor element of the rich mapping literature. The authors are aware of only 10 studies that utilized artificially selected plant populations for QTL mapping (Stuber and Moll 1972; Stuber et al. 1980; Sughroue and Rocheford 1994; Labate et al. 1999; De Koeyer et al. 2001; Smalley et al. 2004; Li et al. 2005; Fan et al. 2006; Coque and Gallais 2006; Falke et al. 2007), in contrast to the hundreds of studies that have identified QTL on the basis of trait–marker associations in unselected biparental mapping populations. There thus may be potential to take further advantage of the artificial selection exerted in plant or animal improvement programs to detect useful genetic variation.

Selection mapping has several potential advantages in relation to other QTL mapping approaches. The first is that QTL can be located without the development of dedicated genetic stocks, since the approach can make direct use of the products of the breeding process itself. Hundreds of studies have utilized recombinant inbred populations for QTL mapping; these populations typically consist of hundreds of lines that are inbred for more than five generations, which demands considerable time and resources. A second advantage is that an array of alleles can be assayed simultaneously, and both favorable and unfavorable alleles can be identified through their frequency response. Corollary to this is that even very rare alleles can be identified in SM. In contrast, a typical biparental mapping population allows only two alleles to be tested. Third, and perhaps most important, the most relevant QTL and alleles (or haplotypes) would be identified through the use of populations selected in their target production environments.

SM has several drawbacks as well. There are inherent limitations to the use of populations produced in nature or in a breeding program. The demographic properties of most natural populations are unknown, making it difficult to derive appropriate null models to test. The demographics of selected populations of a breeding program, however, may be adequately documented. The power to detect loci under selection depends on population characteristics, such as random mating, effective population size, and linkage disequilibrium structure. While a range of user-friendly software programs has been developed for identifying QTL through trait–marker associations, none are available for SM. Perhaps the most important drawback to SM of an individual trait arises if selection is exerted for multiple traits, which is typically the case in breeding populations used for production: SM will not distinguish loci responding to a particular selection pressure.

In plants, Stuber and Moll (1972) were among the first to report on the use of recurrently selected plant populations to identify significant allele shifts at marker loci (isozymes, in their case). More recently, larger numbers of markers have been used to monitor allele-frequency changes across the genome over cycles of selection (Sughroue and Rocheford 1994; Labate et al. 1999; De Koeyer et al. 2001; Smalley et al. 2004; Fan et al. 2006; Falke et al. 2007). Selection mapping has also been used in the analysis of noncrop model organisms (e.g., Keightley and Bulfield 1993; Nuzhdin et al. 2005). In all of these studies, significant changes in allele frequencies were associated with chromosomal segments. In some studies, correspondences of loci identified by SM and QTL identified in biparental crosses were examined and often confirmed (Sughroue and Rocheford 1994; De Koeyer et al. 2001; Smalley et al. 2004; Fan et al. 2006). In a study by Coque and Gallais (2006), a recurrently selected population derived from the same recombinant inbred line population in which QTL were initially identified was used to validate those QTL by SM. To date, there is little published evidence validating the function of alleles identified through SM; we are aware of few studies that have corroborated the favorable or unfavorable nature of alleles identified by SM (exceptions: Li et al. 2005; Coque and Gallais 2006; Falke et al. 2007).

This study focused on SM in populations improved primarily for quantitative resistance to NLB of maize, caused by the fungal pathogen Setosphaeria turcica (Luttrell) (anamorph: Exserohilum turcicum; syn. Helminthosporium turcicum). NLB is a constraint to global maize production. It is an endemic disease in the United States, and a resurgence in incidence has been noted over recent years (G. Bergstrom, personal communication). Well-documented maize populations that had undergone recurrent selection for NLB were available from the International Center for Maize and Wheat Improvement (CIMMYT) (Ceballos et al. 1991). Because the founder populations used for selection were reported to be highly diverse and showed strong phenotypic responses to selection (Ceballos et al. 1991), we hypothesized that the materials would be suitable for SM.

Available evidence on the genetic architecture of NLB resistance is ambiguous. Wisser et al. (2006) synthesized 50 published studies on disease resistance in maize, including 7 QTL mapping studies for NLB. While the QTL for some diseases were clustered across studies, the numerous QTL mapped for NLB were scattered over the genome. This pattern was consistent with the hypothesis that a large number of loci contribute to NLB resistance. On the other hand, several studies using recurrent selection to increase NLB resistance have documented strong selection responses, with ∼15–20% reduction in susceptibility per generation (Ceballos et al. 1991; Campaña and Pataky 2005; Carson 2006), which has been interpreted as indicative of an oligogenic mode of inheritance (Ceballos et al. 1991). We hypothesized that SM could reveal the loci that account for the strong selection response and allow the discovery of superior alleles at these loci. In addition, we expected that SM would generate insights that would be of value in the design of future breeding efforts to improve resistance to NLB.

MATERIALS AND METHODS

Plant materials and DNA extractions:

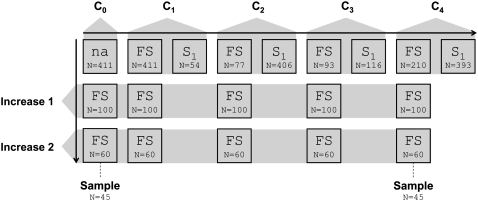
In this study we examined Pool 30, which was one of eight maize populations (referred to by CIMMYT as gene pools) improved by full-sib S₁ recurrent selection by Ceballos et al. (1991). Each cycle of selection was composed of two generations: (1) in one environment individuals were selected from within families and full-sib mated to individuals selected from other families and (2) in a second environment individuals were selected from within full-sib families (produced in step 1) and selfed to produce S₁ families (Figure 1). Primary selection was for quantitative resistance to NLB. Selection for common rust resistance was also practiced, but only in the second environment. In both environments, secondary selection (i.e., after selection for NLB) was practiced for fusarium ear rot resistance and several agronomic traits (for details see Ceballos et al. 1991).

Figure 1.—

Model of genetic drift used for computer simulations of the recurrent selection population under analysis. Each bordered box specifies a population with letter designations indicating the type of mating used (FS, full sib; S₁, selfing) and number of individuals used (N) in establishing each of them. The shaded pentagons relate generations to cycles or stages of the breeding scheme (C₀, cycle 0; C₁, cycle 1; C₂, cycle 2; C₃, cycle 3; C₄, cycle 4; and seed increase 1 and 2). Cycle 0 corresponds to the progenitor population. The arrows indicate the direction of advancing generations and dashed lines indicate which generations were sampled.

The germplasm provided by CIMMYT was derived from the selected populations, by two separate seed increases of ∼100 × 100 and 60 × 60 random plant-to-plant pollinations, whose progeny were bulked in equal quantities. CIMMYT documents the germplasm used for this study with the following identifiers: Pool 30 C0 (N)/TL2001B-6153-176, Pool 30 C1 E.T./TL2001B-6152-29, Pool 30 C2 E.T./TL2001B-6152-30, Pool 30 C3 E.T./TL2001B-6152-31, and Pool 30 C4 E.T./TL2001B-6152-32. Pool 30 was made up of materials from Europe, China, Lebanon, Mexico, South America, and the U.S. corn belt (CIMMYT 1980–81; also see supporting information in Xia et al. 2004). Pool 30 has a yellow-dent grain type, is early in maturity, and has good plant type and yield potential (CIMMYT 1980–81). Prior to the recurrent selection conducted by Ceballos et al. (1991), Pool 30 was improved by 10 cycles of half-sib recurrent selection for tolerance to high plant density and resistance to ear and stalk rots. Pool 30 had not been previously improved for NLB resistance. In general, two guidelines were followed in the improvement of CIMMYT's gene pools: (1) the within-gene pool selection intensity was maintained at a low level and (2) provisions were made for the systematic introgression of additional new promising germplasm (CIMMYT 1980–81; note that systematic introgression was not a component of the improvement made by Ceballos et al.).

Genomic DNA (gDNA) was extracted from a random sample, for which the germination rate was >94%, of 45 individuals from cycle 0 (C₀) and cycle 4 (C₄) (Figure 1). Extractions were performed using either of two methods. In one method, gDNA was extracted from fresh leaf tissue using the FastDNA kit with the FastPrep FP120A instrument according to the manufacturer's protocol (Qbiogene, Morgan Irvine, CA). Alternatively, gDNA was extracted from dried leaf tissue following a standard CTAB extraction protocol (Doyle and Doyle 1987).

Genotypic analysis:

Marker analysis was conducted using simple sequence repeat (SSR) loci in two phases: an initial genomewide survey and a subsequent, more intensive, sampling at four selected genomic regions. For every primer pair assayed, H₂O and gDNA extracts from the maize inbred lines B73 and Mo17 were included in duplicate as controls in the same 96-well plate as the population samples. Initially, 87 SSRs were chosen (supplemental Table S1) and assayed on the basis of their location in different maize “bins” with a bias for tri- and tetranucleotide SSRs. Several of the SSR loci were chosen from SSRs used in other studies for characterizing maize germplasm (Senior et al. 1998; Warburton et al. 2002). Bin locations and primer pair sequences for each locus were obtained from the Maize Genetics/Genomics Database (MaizeGDB) (http://www.maizegdb.org/) and oligonucleotides were purchased from MWG Biotech (High Point, NC) or Applied Biosystems (Foster City, CA). Additional SSR loci (n = 64) were surveyed in certain chromosomal segments (supplemental Table S1).

For most SSR loci, polymerase chain reactions (PCR) were performed using a single-reaction nested PCR method that allows a single labeled primer to be used for an array of different specific primers (Schuelke 2000). The PCR chemistry reported by Schuelke was modified and contained, in a total reaction volume of 20 μl, final concentrations of 1× PCR buffer, 1.5 mm MgCl₂, 1 m betaine, 0.16 μm fluorescently labeled universal primer, 0.04 μm forward-specific primer, 0.16 μm reverse-specific primer, 1 unit Taq polymerase, and 20 ng template DNA. Thermocycling parameters were the same as those described by Schuelke (2000). Four SSR loci (phi116, umc1426, umc1636, and phi022) amplified optimally without betaine.

For 22 loci, 5′-fluorescently labeled forward-specific and unlabeled reverse-specific primers were used (supplemental Table S1). For these loci, the PCR chemistry was identical to the above except a 4-μm final concentration of forward- and reverse-specific primer was used in place of the three primers required for the protocol of Schuelke (2000), and reactions were performed without betaine. Thermocycling parameters for these primers were as follows: 94° (5 min), then 30 cycles of 94° (30 sec)/56° (30 sec)/72° (45 sec), and a final extension at 72° (10 min).

Fluorescently labeled amplicons were separated on an Applied BioSystems 3730xl DNA Analyzer at Cornell University's (Ithaca, NY) Biotechnology Resource Center. Electrophoresis was performed on samples consisting of 9.0 μl formamide, 0.5 μl PCR products, 0.44 μl H₂O, and 0.06 μl size standard (GeneScan-500 LIZ). Amplicon sizes were automatically scored to the nearest 0.1 bp in GeneMapper v. 3.0 or later using the Local Southern algorithm, adjusting the polynomial degree and window size according to the manufacturer's guide when necessary, allowing for resolution of alleles differing by 1 bp. To determine the genotype of each individual at each locus, the automatic scores were manually examined and edited. Allelic bins were calculated from the raw allele sizes with an Excel macro (C. Harjes, personal communication). In short, raw allele sizes were sorted, and each time a gap of 0.3 bp occurred between two sorted alleles, a new bin was defined. When multiple bins were 1 bp apart, when a bin was associated with fewer than three genotypes, or when anomalies were observed, we reexamined the electropherograms to determine whether these were artifacts.

Alleles were sometimes detected in only one cycle (C₀ or C₄). For use of such loci with our test statistic (below) we declared a frequency of 1.0% (i.e., ∼1/90, where 90 is the total number of chromosomes sampled) for each allele not detected in a given cycle. Because this resulted in total allele frequencies greater than one, detectable allele frequencies were adjusted downward by the amount of the introduced allele frequency (e.g., 1% for one allele, 2% for two alleles, etc.) divided by the number of detectable alleles. For instance, if one allele was detected in C₄ but not in C₀, the frequency of each allele detected in C₀ was adjusted downward by 0.01/n, where n = number of alleles detected in C₀, and the undetected allele was considered present at a frequency of 1% in C₀. To prevent this from biasing the test statistic (described below), we set a boundary on allele frequencies for the drift simulations at 0.01 (i.e., alleles that fell below a frequency of 0.01 were reset to 1% and the remaining alleles were adjusted as described).

Genetic diversity:

Summary statistics, including the number of alleles, expected heterozygosity or gene diversity (unbiased estimate, D), observed heterozygosity (H_o), and coefficient of inbreeding (F) were calculated using the software PowerMarker v. 3.25 (Liu and Muse 2005). PowerMarker was also used to compute allele frequencies at the individual and population levels, to compute shared allele distances among individuals, and to test for per-locus deviations from Hardy–Weinberg proportions (HWP). The following advanced settings were used when performing exact tests for HWP in PowerMarker: Method = auto; MaxIterationNo = 1,000,000; ConvergenceBound = 0.01; BatchNo = 1000; PermutationNo = 5000. Errors incurred in multiple testing were controlled using the false discovery rate (FDR) according to the method described by Benjamini and Hochberg (1995). The test results were examined at both q* = 0.05 (i.e., 5.0% FDR) and q* = 0.01. At loci exhibiting significant deviations from HWP, the proportion of excess heterozygotes was measured as .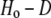

The unweighted pair group method with arithmetic mean (UPGMA) was used to perform hierarchical clustering of individuals on the basis of their shared allele distances. A dendrogram plot was produced using the UPGMA-derived dissimilarities. The extent to which there was agreement between the UPGMA dissimilarities and shared allele distances was measured, using the cophenetic correlation coefficient (Sokal and Rohlf 1962). These analyses were performed in MatLab v. 7.0.1 (Mathworks, Natick, MA).

A statistical test of the null hypothesis of genetic drift:

We developed a statistical test programmed in the R environment (R Development Core Team 2005) on the basis of that of Waples (1989) to test the null hypothesis of genetic drift (see appendix a for details of the test statistic). The test described by Waples requires knowledge of the sample sizes taken from the population, when the samples were taken (i.e., before or after reproduction), the number of generations separating the first and the last generation sampled, and an estimate of the effective population size (N_e). This information was used by Waples to mathematically derive expected variances and covariances of allele frequencies (for further details see Waples 1989). We modified Waples' statistic into a simulation-based framework that included information on the number of individuals selected over the course of selection and the type of mating used in each generation. This allowed genetic drift to be modeled according to the known treatments to the population under study, leading to a more comprehensive model of genetic drift (see below). Consequently, an estimate of N_e was not needed and the mathematically derived variance and covariance expectations were substituted by those determined through 5000 simulations of genetic drift. These simulation-based parameter estimates were then used to calculate expected allele frequencies (referred to by Waples as 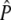) and the test statistic value for each locus as described by Waples (1989).

Waples showed that the test statistic generally follows an expected chi-square distribution with the degrees of freedom n = (number of alleles – 1). It has also been shown that departures from the chi-square distribution may occur in cases where the initial allele frequencies are strongly skewed (e.g., initial allele frequencies <0.05 or >0.95; Waples 1989; Goldringer and Bataillon 2004), which results in inflated error rates. Rather than assume that the test statistic followed a chi-square distribution, we determined the test statistic distribution from 5000 simulations of our model of genetic drift for each locus not exhibiting a significant departure from HWP (q* = 0.01). The value of the test statistic for the observed data was then compared to the empirical distribution derived from those 5000 genetic drift simulations. This allowed for the determination of a P-value for each locus or the probability of a test statistic greater than the value of the test statistic for the observed data. As above, the method of Benjamini and Hochberg (1995) was used to account for errors accumulated in multiple testing.

A model of genetic drift:

We designed a computer simulation of the recurrent selection conducted by Ceballos et al. (1991) under random selection and mating of individuals. For each locus, the allele frequencies estimated from the C₀ sample were used as starting frequencies in performing 5000 repeated simulations of full-sib S₁ recurrent selection. In each repetition, a new group of individuals with C₀ allele frequencies was produced. The choice of starting sample size is expected to have some impact on our test statistic. That is, as the chosen starting sample size decreases, the expected variances of allele frequencies increase, thereby reducing statistical power since the expected variances are used in the test statistic. As we did not know the actual number of individuals used to create C₀, we used the same number of individuals as the first generation of selection (n = 411). We acknowledge that the effect this has on the power of the test is unknown. The subsequent number of individuals selected in each generation of the recurrent selection simulation corresponded to that reported by Ceballos et al. (1991) for Pool 30 (Figure 1). It was noted above that the samples used in this study were derived from multiplication of seed of the original populations. The seed increases and number of individuals sampled were also included in our model of genetic drift. A flow diagram of the model is shown in Figure 1.

Comparisons to previously published QTL:

The locations of markers examined herein were compared to a synthesis of published data on qualitative and quantitative trait loci for resistance to multiple different diseases of maize (Wisser et al. 2006). Specifically, results were considered with respect to the locations of resistance loci for NLB and common rust and to the consensus map summarizing the frequency of QTL for multiple diseases. Integration of the current findings was relatively straightforward because the synthesis map was anchored to a common maize reference map, the IBM2 neighbors map (IBM2n) (Cone et al. 2002). Each additional marker could be compared to the synthesis map using its genetic coordinates on the same map, obtained from MaizeGDB (http://www.maizegdb.org). For SSR loci having unknown genetic coordinates but known bin locations (n = 7), the midpoint coordinate of the bin on the IBM2n map was used. These data were visualized using the software GenomePixelizer (Kozik et al. 2002) and redrawn for publication in QuarXPress v. 5.

Updates were made to the synthesis map produced by Wisser et al. (2006). Two QTL for NLB, one on chromosome 8 from ∼386–404 cM and one on chromosome 9 from ∼425–480 cM were found to be redundant according to their rule set and were therefore removed. A single QTL for common rust from ∼408–532 cM on chromosome 7 was found not to be redundant and was therefore added. The map position for Ht2 in the original synthesis was based on that reported by Zaitlin et al. (1992). A more recent report was found in which the map location for Ht2 was determined using a much larger population (Yin et al. 2003) than the previous study. The Ht2 map location was updated accordingly, to between 329.4 and 369.6 cM on the IBM2n map.

Cosegregation analysis:

Four F₂ populations (POP1–POP4) were used to test for cosegregation of alleles with resistance at a set of linked loci on chromosome 8. The specific loci examined were a subset of those identified through SM (i.e., loci that exhibited significant allele-frequency shifts over cycles of recurrent selection). This region was chosen to examine the validity of the SM results, in part because prior studies had associated this same chromosomal segment with quantitative and qualitative resistance to NLB (see results). The F₂ populations were produced by crossing C₄ individuals to the maize inbred line B73, which is moderately susceptible to NLB. The four F₂ populations inherited three different haplotypes from C₄ defined by a group of linked SSR markers on chromosome 8: (1) umc2356, (2) umc1149, (3) umc1728, (4) umc2395, and (5) umc2357 (see Figure 5 for details). The four F₂ populations consisted of 88, 142, 151, and 172 individuals, respectively.

Figure 5.—

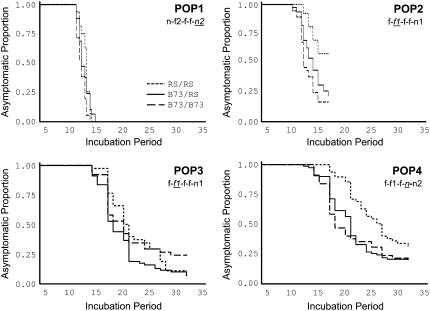
Alleles segregating in the F₂ populations and their frequency response during recurrent selection. The shaded bar represents a segment of chromosome 8. The locations of five linked SEL* SSR loci and previously mapped QTL (solid bars) and a major gene (HtN) are indicated. The centimorgan values shown for each marker were from the IBM2n genetic map. The C₄-derived haplotype segregating in each F₂ population is illustrated as described in the text. The allele-frequency plots show all of the alleles per locus (detected in the recurrent selection population) as dots but only the alleles segregating in the F₂ populations are labeled. The notation (e.g., f1 and f2 for two “favorable” alleles and n for “neutral” or drifting alleles) allows the alleles at each locus to be traced between the allele-frequency plots and F₂ populations. The B73 haplotype was common to each F₂ population. The level of significance determined using the log-rank statistic of survival analysis is indicated by asterisks (*P < 0.05; **P < 0.01; ***P < 0.001). The most significantly associated marker is indicated by white text in a black background (for POP3 the allele indicated was significant at P = 0.09). The “na” superscript indicates that the locus was not tested, either because no genotype data were collected (POP1) or because the locus was monomorphic. The allele-frequency plots for each locus constituting the haplotypes depict alleles as dots and the upper and lower bounds of the 95% confidence interval of genetic drift as shaded lines.

Two of the F₂ populations (POP1 and POP2) were evaluated independently as separate experiments in a growth chamber while the other two populations (POP3 and POP4) were evaluated in a single field experiment. Each population was planted in a completely randomized design. In the growth chamber, each experiment included an F₂ population and the maize inbred lines B73 (moderately susceptible) and Mo17 (moderately resistant) as checks. Plants were grown in a greenhouse and moved to the growth chamber for disease trials 24 hr before inoculations. Inoculations were performed by adding 1000 conidia of a single E. turcicum isolate (NY-001 from the laboratory of R. J. Nelson) suspended in 1.0 ml H₂O with 0.01% Tween 20 to the whorl of ∼1-month-old plants. Resistance to NLB was measured per individual as incubation period (IP) or the number of days after inoculation that the first water-soaked lesion was observed. Incubation period is considered to generally reflect field-based measures of adult quantitative disease resistance for NLB (Carson and Van Dyke 1994).

Field experiments were carried out in the summer of 2007 at the Robert B. Musgrave Research Farm in Aurora, New York. Inoculations were performed by adding 2.5–3.0 ml of dried infected sorghum grains, previously inoculated with the NY-001 isolate of E. turcicum, to the whorl of 6-week-old maize plants. Simultaneously, 0.5 ml of a 4 × 10³ conidia/ml suspension (2000 spores) in H₂O with 0.02% Tween 20 was added to each whorl. Three phenotypes were measured in the field: (1) IP, (2) area under the disease progress curve (AUDPC) (standardized by the total time in which measurements were taken, sAUDPC), and (3) days to pollen shed or anthesis. To estimate sAUDPC, the diseased leaf area for each plant was measured on a 0–100% scale considering the entire leaf area of each plant. Three separate ratings were taken during the epidemic at ∼2-week intervals postanthesis. sAUDPC was calculated for each F₂ individual from the three temporal measurements of diseased leaf area as

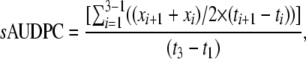where x_i is the score at the ith observation and t_i is the day at the ith observation, with i = 1 to 3 observations.

Two different statistical approaches were conducted to test the significance of trait–marker associations. Considering the unobserved data (i.e., that resulted from experimental truncation, see results) as missing data, we tested the null hypothesis that the IP means among genotypic classes were equal using SAS's PROC GLM (Version 9.1.3 of the SAS system; SAS Institute, Cary, NC). Individuals that did not have IP estimates were not necessarily missing estimates for sAUDPC. When testing sAUDPC, both the complete and the partial data sets were examined. The IP and sAUDPC data from the field-evaluated populations were skewed right and therefore log-transformed to equalize the variances and achieve the normality assumption of the GLM test statistic. Days to anthesis was examined as a covariate for this analysis. As an alternative assessment, we used survival analysis to include the complete data set. The log-rank test statistic of survival analysis is a nonparametric statistic that allows for the analysis of nonnormally distributed and censored data (i.e., we considered missing data due to experimental truncation as censored). This analysis was carried out using SAS's PROC LIFETEST to test the null hypothesis that there was no difference among genotypic classes in their IPs. Kaplan–Meier plots were produced, using the plot function of PROC LIFETEST.

RESULTS

Genetic diversity:

Response to selection is dependent on diversity. Pool 30 was expected to carry a high level of diversity, as it was constructed from ∼125 germplasm sources including land races, population samples, and inbred lines from Europe, China, Lebanon, Mexico, South America, and the U.S. corn belt (CIMMYT 1980–81; also see supporting information in Xia et al. 2004). A priori, however, it was difficult to establish an expectation regarding the allelic diversity of Pool 30 at the time that the recurrent selection program was initiated, because the population had been previously subjected to selection for many generations. Detailed genetic diversity data for each locus can be found in supplemental Table S1. Each of the 151 SSR loci examined was polymorphic among the 45 individuals sampled at each cycle. Gene diversity averaged across all loci (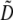) was 0.52 in the progenitor population (C₀) and 0.53 in the full-sibling generation of the last cycle of selection (C₄; sampled generations shown in Figure 1). In C₀, a total of 711 alleles were detected across 151 SSR loci, averaging 4.7 alleles per locus (range: 2–13). In C₄, a total of 667 alleles were detected, with an average of 4.4 alleles per locus (range: 2–14). Across C₀ and C₄, a total of 852 unique alleles were found, with an average of 5.6 alleles per locus (range: 2–20). Among these 852 alleles, 526 (61.7%) were detected in both C₀ and C₄, 185 (21.7%) were detected in C₀ but not in C₄, and 141 (16.6%) were detected in C₄ but not in C₀. Thus, the ∼185 alleles present in C₀ were lost or at very low frequencies in C₄. At the same time, 141 alleles were undetected in C₀ but increased to detectable levels in C₄. Alleles detected in one cycle but not in another could also have been due to estimation inaccuracy as a result of our sample size of 45 individuals per cycle or contamination at any stage of population development. No significant differences in the diversity statistics were observed in an expanded sample of 90 individuals per cycle, genotyped at 3 of the SSR loci (data not shown). In the expanded sample, previously undetected alleles were detected, albeit at very low frequencies (i.e., <0.02; data not shown). No allele was fixed in either generation sampled; the highest-frequency alleles in C₀ were 0.97 and in C₄, 0.98.

The genetic relationships among the 90 individuals sampled from C₀ and C₄ are shown in Figure 2. The cophenetic correlation coefficient between the UPGMA dissimilarities and the shared allele distances was 0.89, suggesting that the dendrogram plot based on dissimilarities was an appropriate representation of the shared allele distances among individuals (Mohammadi and Prasanna 2003). The plot revealed differentiation between individuals from C₀ and C₄. Visual inspection also revealed an apparent reduction in population substructure in C₄ relative to C₀; groups of individuals in C₀ were separated more distinctly or by longer branch lengths compared to those in C₄.

Figure 2.—

UPGMA dendrogram plot of cycle 0 and cycle 4 sampled individuals. The solid circle indicates the split between C₀ and C₄ individuals, which is also demarcated for taxonomic units as a thick line. The bottom axis indicates UPGMA dissimilarity derived from shared allele distances.

HWP:

The test statistic for genetic drift (described in materials and methods and appendix a) assumes random mating, so we tested each locus for deviations from HWP that would invalidate the test. It was expected that loci would be in HWP because the individuals sampled were produced through seed multiplications made by random plant-to-plant pollinations of the recurrent selection population. However, of the 302 tests conducted for HWP, 68 (23%) significant deviations were found (hereafter, loci showing such deviations are designated as HWP*). Of the 151 SSR loci tested, 48 HWP* loci were detected in C₀ and 20 were detected in C₄ (i.e., there were 19% more HWP* loci in C₀ than in C₄ at q* = 0.05). Excess heterozygosity was observed for 35% of these loci in C₀ and 10% in C₄; the majority of HWP* were associated with an excess of homozygotes. The median deviation of H_o from D in C₀ was −3.8% (range: −48.1–28.1%) and in C₄ was −19.0% (range: −58.8–12.8%). At a more conservative FDR of 1.0%, 33 HWP* loci were detected in C₀ and 13 were found in C₄. The median deviation of H_o from D in that case was −10.2 and −19.1% for C₀ and C₄, respectively. Some loci exhibited deviations from HWP in both C₀ and C₄. At a 5% FDR, the two cycles shared 13 HWP* loci, while at a 1% FDR, the two cycles shared seven HWP* loci.

Across the genome, there was no tendency for clustering of HWP* loci. HWP* loci were scattered across the genome and occurred among closely linked, non-HWP* loci. For example, 23 SSR loci were examined in a segment of chromosome 8 spanning ∼35 cM (1 locus per ∼1.6 cM). Of these, 2 HWP* loci were found in C₀ and another 2 in C₄ (q* = 0.05), and none of the HWP* loci were immediate neighbors. [Estimates of the genetic distance are one-fourth the distance of that reported for the IBM2n map from which the centimorgan values were originally obtained. The IBM2n map was derived from an intermated population of maize lines. The centimorgan values were larger, by a factor of approximately fourfold, than those that would have been obtained using an F₂ population (Lee et al. 2002).]

Selection mapping:

From the initial genomewide scan using 87 randomly chosen, uniformly distributed SSR markers, 60 loci did not exhibit significant departures from HWP in either cycle (q* = 0.01). These loci were approximately uniformly distributed across the genome. The null hypothesis of genetic drift was rejected for 17% of the 60 loci tested (n = 10, q* = 0.05). These SSR loci exhibiting significant deviations from drift expectations (hereafter “putatively under selection,” SEL*) were associated with all maize chromosomes except chromosomes 5, 7, and 10.

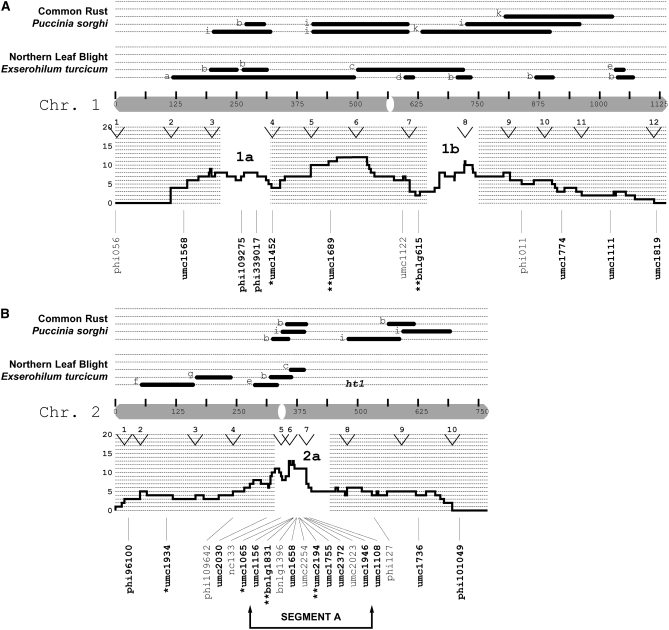
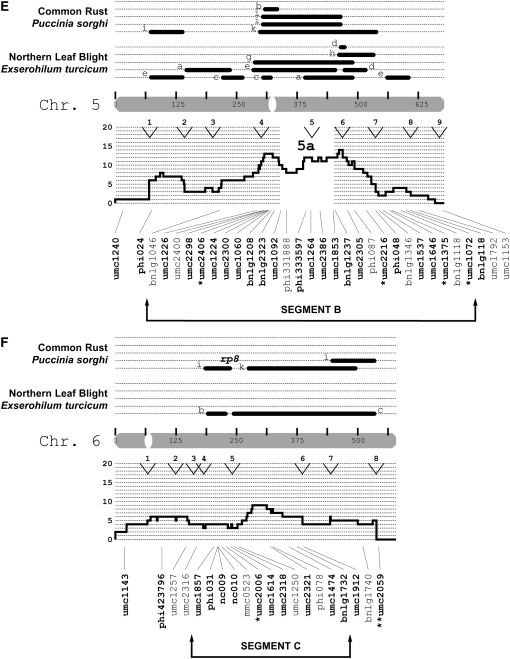
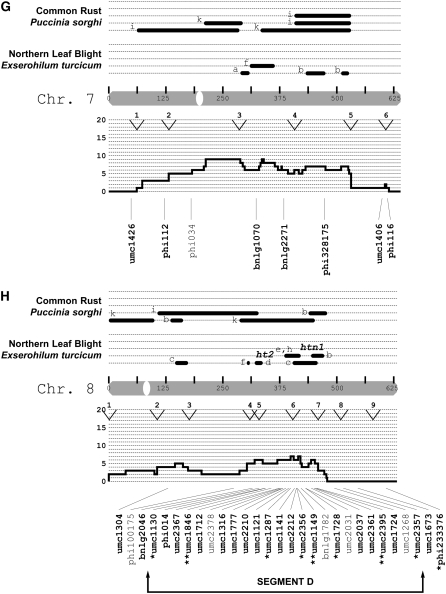
After the genomewide scan, four chromosomal regions were analyzed with an additional 64 SSRs: chromosome 2, from 369 to 395 cM (segment A, n = 10 SSR loci); chromosome 5, from 216 to 600 cM (segment B, n = 21 SSR loci); chromosome 6, from 203 to 374 cM (segment C, n = 11 SSR loci); and chromosome 8, from 330 to 514 cM (segment D, n = 22 SSR loci). (In an F₂ population segment A would correspond to an interval of ∼6.5 cM. To calculate this distance for the remaining segments, the difference of the IBM2n map locations should be reduced by a factor of four.) After excluding HWP* loci from this set of 64 SSRs, 52 could be tested under the null hypothesis of genetic drift. In total, 29% were classified as SEL* (q* = 0.05; note that all loci were included for q* estimation). There was a 9.0% probability that the greater proportion of SEL* loci detected after the genomewide scan occurred by chance alone (Fisher's exact test). Collectively, 22% of the 112 loci were SEL* (q* = 0.05).

Relative to isolated SEL* loci, the identification of clustered SEL* loci would provide stronger evidence for the presence of gene(s) under selection. Clusters can be defined in terms of SEL* density per centimorgan or in terms of contiguous sets of SEL* markers. For chromosomal segments A, B, and D, multiple additional SEL* loci were identified, though the detected “clusters” of SEL* loci were commonly interspersed with non-SEL* loci (Figure 3). In segment A on chromosome 2, three loci spanning ∼3 cM were SEL* (this included one marker from the initial genomewide scan). These were not, however, immediately adjacent to each other according to the reference genetic map. In segment B on chromosome 5, the distribution of SEL* loci was interspersed with non-SEL* loci, with the exception of two neighboring SSRs ∼7 cM apart. In segment C on chromosome 6, only one SSR was SEL*. Segment D on chromosome 8 had the highest number (n = 8) and proportion (42%) of SEL* loci and contained three contiguous SEL* loci. Two of the SSRs (umc2356 and umc1149) were <1 cM apart, while the third SSR (umc1728) was ∼5 cM from them.

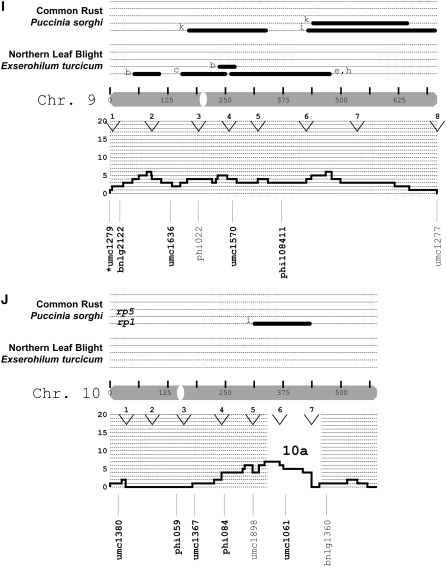
Figure 3.—

Locations of putatively selected loci relative to disease QTL. The markers examined in this study were related to the synthesis map of Wisser et al. (2006). Maize chromosomes are depicted as shaded bars and centromeres as open ovals. The centimorgan scale inside each chromosome corresponds to the IBM2n genetic map. Published QTL (solid bars) or major genes (text) for NLB and common rust are shown above each chromosome. The study in which each QTL was declared is indicated by letters a–i: (a) Freymark et al. (1993), (b) Brown et al. (2001), (c) Welz et al. (1999b), (d) Huang et al. (2002), (e) Schechert et al. (1999), (f) Dingerdissen et al. (1996), (g) Jiang et al. (1999), (h) Welz et al. (1999a), (i) Lübberstedt et al. (1998), and (j) Kerns et al. (1999). A histogram of the frequency for all dQTL (see Wisser et al. 2006) per centimorgan is shown directly below each chromosome. The open and labeled segments (e.g., 1a, 1b, 2a, etc.) within each histogram indicate chromosomal segments where there was an excess of all maize disease QTL relative to that expected on the basis of gene density (for details see Wisser et al. 2006). Maize bin margins are indicated by labeled arrowheads at the top of each histogram. The names of the SSR loci examined in this study are shown with lines depicting their map location. Markers belonging to segments where more intensive SSR genotyping was conducted are indicated. For the marker names, regular type is for loci that exhibited significant departures from Hardy–Weinberg proportions in either C₀ or C₄. Boldface type is for markers that did not exhibit significant deviations from HWP and were used to test for deviations from genetic drift. Asterisks indicate putatively selected loci (*P = 0.05; **P = 0.01).

The characteristics of each SSR at C₀ may result in differential power to detect selection. Factors affecting power include allelic diversity (number and skewness) and factors influencing linkage disequilibrium [including distance between the marker and the gene(s) under selection and the population history of C₀]. We were able to examine the former but not the latter. While there was a tendency for SEL* loci to have more alleles in C₀ than non-SEL* loci, there was no significant difference in their means. Similarly, D in C₀ for SEL* loci was somewhat greater than for non-SEL* loci, but not significantly so. It appeared, however, that relatively rare alleles in C₀ (those at frequencies ≤0.10) were more powerful for detecting selection than were alleles found at higher frequencies. This was visualized when changes in the magnitude of allele frequencies at the 25 SEL* loci and a random sample (n = 25) from the remaining non-SEL* loci were plotted as a function of their starting allele frequencies (Figure 4). SEL* loci were commonly associated with increases in rare allele frequencies and/or decreases in common allele frequencies. Among the SEL* loci, 13 alleles that were rare in C₀ were identified as increasing significantly in frequency relative to the expected change under drift from C₀ to C₄ (Figure 4). In contrast, only 4 alleles that started at frequencies >0.10 were identified as significantly increased in frequency.

Figure 4.—

Comparison of the magnitudes of allele-frequency change for loci exhibiting significant or nonsignificant deviations from genetic drift. The starting allele frequency is shown on the x-axis. The change in allele frequency between C₀ and C₄ (i.e., allele frequency at C₄ minus allele frequency at C₀) is shown on the y-axis. The 95% confidence interval for the magnitude of change in allele frequency conditional on a given starting frequency was determined from 5000 genetic drift simulations.

Four alleles located outside the expected boundaries of drift in Figure 4 are shown as corresponding to non-SEL* loci. This reflects the fact that the test statistic used more information than what is visualized in Figure 4; the figure depicts the single-allele values alone, while the statistic considered the effects of all alleles per locus, accounting for both variances and covariances of allele frequencies. In addition, the correction for multiple tests reduced the number of loci declared as SEL*.

Genetic diversity at SEL* loci:

Loci associated with selection would be expected to be affected differently than unselected or neutral loci. Two types of comparisons were made between selected and unselected loci: the variation at a given cycle and the change in variation from one cycle to the next. There was no significant difference in genetic diversity at C₀ between SEL* and non-SEL* loci (non-SEL* had slightly less diversity; Table 1). Therefore, genetic diversity at C₄ would reflect the change that occurred for the similar standing variation between SEL* and non-SEL* loci at C₀. Compared to C₀, in C₄ an average of one more allele was present at SEL* loci than at non-SEL* loci, and D was 13% greater. Although neither difference was significant (Table 1), the differences arose from a slight increase in diversity at SEL* loci and simultaneous decrease at non-SEL* loci.

TABLE 1.

Genetic diversity at SEL* vs. non-SEL* loci

Cycle	Marker typea	No. locib	Average allele no.	Dc
C0	SEL*	25	4.5 (3.6–5.4)d	0.50 (0.40–0.56)
	Non-SEL*	25	3.8 (2.9–4.6)	0.45 (0.37–0.51)
C4	SEL*	25	4.8 (3.9–5.6)	0.58 (0.49–0.65)
	Non-SEL*	25	3.7 (3.1–4.3)	0.45 (0.37–0.51)

^aSEL* markers exhibited significant deviations from drift expectations and non-SEL* markers did not.

^bSample sizes of SEL* and non-SEL* loci were made comparable by randomly drawing 25 of the 112 non-SEL* loci.

^cUnbiased estimate of gene diversity.

^dNinety-five percent confidence intervals (in parentheses) were calculated using 100 bootstrap resamplings in PowerMarker v. 3.25.

Evidence of selection in relation to mapped QTL:

We supposed that SEL* loci colocalizing with previously published QTL or major genes for resistance to NLB would be more likely to be linked to selected resistance genes, while other loci might be more likely due to linkage with genes for other traits under selection. To allow us to focus our analysis on QTL-rich regions, a synthesis of the available mapping data for quantitative and qualitative disease resistance in maize was produced (Wisser et al. 2006). The QTL summary was produced concurrently with the first half of this study, and the initial marker survey was conducted without reference to the summary QTL map. From the initial genomewide scan, several correspondences between SEL* loci and QTL were found. We assayed more loci in the 46% of the genetic map that was associated with reported NLB QTL (Figure 3). Of the 25 SEL* loci, 19 colocalized with NLB QTL and/or major genes, while 6 did not. There was a 7.2% chance that this association was random (Fisher's exact test). However, all SEL* loci were not necessarily independent—they could be in linkage disequilibrium with the same gene(s) under selection. By visual inspection of the positions of the 25 SEL* loci with respect to the genetic framework map, 13 independent (>50 cM apart) loci appeared to have been associated with selection. For each chromosome, the number of putatively independent loci was as follows: 1 (2), 2 (2), 3 (1), 4 (1), 5 (2), 6 (2), 7 (0), 8 (2), 9 (1), and 10 (0) (Figure 3).

The first segment of the genome chosen for more intensive marker analysis (segment C on chromosome 6; Figure 3) was selected on the basis of the presence of a single SEL* locus. The other three segments (A, B, and D) were chosen subsequent to the completion of the summary QTL map and covered regions where clusters of NLB QTL and/or major genes occurred, in coincidence with high densities of QTL for other diseases. For segment C, to which two nonoverlapping NLB QTL and a major gene (Rp8) and QTL for common rust had been localized, the addition of 11 SSR markers did not reveal any further SEL* loci. The three chromosomal segments selected on the basis of the QTL summary were substantiated by the identification of additional SEL* loci (Figure 3). In segment D, a diffuse set of SEL* loci was associated with a broad peak on the disease QTL synthesis. Five SEL* loci colocalized with a more narrow group of NLB and common rust QTL and a major gene for NLB resistance, HtN.

Cosegregation analysis:

To assess the validity of the SM results, a series of haplotypes from the recurrent selection population at segment D on chromosome 8 were tested against the haplotype of B73, for cosegregation with NLB resistance. Four reference haplotypes were defined by the alleles at the SSR loci umc2356, umc1149, umc1728, umc2395, and umc2357 (Figure 5), but cosegregation analysis was conducted at each locus. We hypothesized that this suite of linked loci would associate with resistance on the basis of the results of SM and correspondences of these SEL* loci with published NLB QTL and a major gene (Figure 3). We denoted the recurrent selection-derived haplotypes in terms of allele-frequency responses in the recurrent selection population at each marker, using the following system: a five-letter string indicated the status of alleles at the five linked loci, and letters were used to indicate their response to selection (f, favorable, positive allele-frequency change greater than that expected from drift during recurrent selection; n, neutral, allele-frequency change expected from drift; u, unfavorable, negative allele-frequency change greater than that expected from drift). The haplotype inherited from the recurrent selection population in POP1 was n-f-f-f-n, in POP2 and POP3 it was f-f-f-f-n, and in POP4 it was f-f-f-n-n.

The growth chamber experiment of POP1 was carried out to completion, while that of POP2 was truncated 7 days after the initial appearance of lesions because of an incident that prevented our entry into the chamber. At the time the experiment was stopped, lesions had not yet been observed on 27% of the individuals. In the field trial of POP3 and POP4, the experiment was truncated at 32 days postinoculation when the proportion of individuals developing lesions on each day became extremely low. On day 32, only 1 (3%) and 2 (6%) of the remaining 30 and 36 asymptomatic plants in POP3 and POP4, respectively, had developed lesions. It is possible that some of the asymptomatic individuals had escaped initial infection.

For each population, two types of test statistics were used to assess whether there were differences in resistance among genotypic classes: (1) a general linear model and (2) survival analysis. Among the two field-evaluated populations, days to anthesis were significantly correlated at a low magnitude with IP in POP4 (r = −0.20, P = 0.025). For all other tests, days to anthesis were not included in the model because they were not a significant covariable. While the magnitude of the test statistics differed among the two types of tests, the trend across loci constituting each haplotype was similar, leading to qualitatively similar results. Significant trait–marker associations were detected in each of the four populations by both tests. At these loci, the average effects of the recurrent selection-derived alleles were always greater than those of the B73-derived alleles.

Not all of the loci constituting each haplotype exhibited significant differences. None of the markers were significant across all of the populations and the most significantly associated marker (i.e., the one with the lowest P-value) was different for three of the populations (Figure 5). Furthermore, the most significantly associated markers were not always segregating for “favorable” SSR alleles (Figure 5). In POP1 and POP4, these loci were segregating for alleles that were classified as neutral during recurrent selection. Based on the general linear model analysis of each population, the amount of phenotypic variation explained by the most significantly associated marker locus was as follows: (1) POP1, umc2357, 7.3%; (2) POP2, umc1149, 7.0%; (3) POP3, umc1728, 10.4%; and (4) POP4, umc2395, 18.2%.

For neither of the field-grown populations was there a significant association with sAUDPC. It should be noted that the disease pressure for these populations was low. sAUDPC (scale: 0–100%) was on average 9.5% (range: 4.9–24.1%) for POP3 and 12.0% (range: 3.0–33.0%) for POP4. Another peculiarity regarding the disease pressure was revealed in the Kaplan–Meier plot of POP3 where an abrupt change in the rate of IP was observed at approximately day 25 among the B73 homozygotes (identified as a crossover in the Kaplan–Meier plot in Figure 6).

Figure 6.—

Kaplan–Meier plots of incubation periods in the three genotypic classes of each F₂ population at a specific SEL* locus. The Kaplan–Meier plots show, for each F₂ population, the proportion of asymptomatic plants belonging to each genotypic class (homozygous for the recurrent selection allele, heterozygous for recurrent selection and B73 alleles, and homozygous for the B73 allele) as a function of time in days postinoculation. Under each population heading, the haplotype of the recurrent selection allele is illustrated as described in the text. The specific locus used to produce each plot is indicated by the italicized and underlined allele and can be related to Figure 5 to obtain the locus name.

DISCUSSION

Selection is generally expected to reduce genetic variation. After four cycles (seven generations; see Figure 1) of selection for NLB resistance, however, little reduction in molecular diversity across the genome was detected in this study. This was apparently because of the relatively large number of individuals selected at each generation. That is, the number of individuals selected consistently exceeded (often substantially) the estimated effective population size (data not shown). Maintenance of gene diversity (D) at putatively unselected loci was concomitant with an overall increase in D at putatively selected loci. The increase in D at selected, but not unselected, loci could be seen as counterintuitive. Inspection revealed that the elevated levels of D at most SEL* loci resulted from a reduction in the initial skewness of allele frequencies; commonly, for a given SEL* locus, low- and high-frequency alleles shifted to intermediate frequencies (i.e., they were generally more balanced in C₄). This suggested that an enrichment of low-frequency alleles was responsible for significant phenotypic changes.

The recurrent selection process is indeed aimed at the enrichment of rare alleles. While our results suggest that rare alleles were effectively selected, a caveat should be noted regarding ascertainment bias: we speculate that loci under selection are more likely to be detected through the increases in frequency of rare alleles at linked marker loci than through frequency shifts of more common alleles. The more frequent alleles at marker loci are more likely to be associated with multiple alleles at the genes under selection, including favorable and unfavorable alleles. As selection acts on favorable alleles and/or against unfavorable ones, the higher-frequency marker alleles would change in both directions, appearing constrained within the boundaries of genetic drift. Conversely, lower-frequency marker alleles may more likely exist in disequilibrium with a specific allele at the gene(s) under selection, in which case changes in marker allele frequencies would more directly reflect the changes in the alleles under selection. The impact of this phenomenon is expected to be reduced as the marker loci tested get nearer to the actual gene(s) under selection. Given the marker density analyzed in this study, most (if not all) of the declared SEL* loci are probably far enough from the genes of interest to be vulnerable to this problem.

Resistance to NLB has been associated with a large number of QTL distributed across the maize genome, as well as a few major genes (e.g., Ht1, Ht2, and HtN; Figure 3). Under this diffuse gene distribution, recurrent selection would be the most appropriate breeding method for improving resistance to NLB. Indeed, several studies have documented strong and significant gains from recurrent selection for NLB resistance (Jenkins et al. 1954; Ceballos et al. 1991; Campaña and Pataky 2005; Carson 2006). The loci identified by SM in this study exhibited a similar distribution, and many of the loci corresponded with previously published QTL or major genes. It may be that a fairly large number of genes were associated with recurrent selection for resistance, though Ceballos et al. (1991) hypothesized that the large gains achieved may have been associated with a small number of genes of major effect. In any case, it seems unlikely that all of the SEL* loci identified would be associated only with improvement for NLB resistance. Primary selection was for resistance to NLB but selection for common rust and some agronomic traits also showed significant gains (Ceballos et al. 1991), and genes associated with adaptation may also have been selected.

Ceballos et al. (1991) performed recurrent selection for quantitative resistance to NLB by distinguishing the type of lesions measured when rating the level of resistance. Chlorotic-type lesions typical of Ht1, Ht2, and Ht3 were not selected (Ceballos et al. 1991). Even so, it is possible that the major gene HtN was selected. Unlike the other major genes for NLB, the lesion phenotype associated with HtN resistance may not be differentiated from necrotic lesions typical of quantitative resistance (Campaña and Pataky 2005). In this light, it is notable that SEL* loci (i.e., umc1728 and umc2395) colocalized with the HtN locus on chromosome 8. However, in our analysis of F₂ populations, the strongest quantitative effect was not detected at umc1728, which corresponds more closely (i.e., more than umc2395) to the HtN map position estimated by Simcox and Bennetzen (1993).

Categorizing the Ht genes of the maize-NLB pathosystem as classically defined R genes can be ambiguous as there appear to be strong genetic-by-environment interactions (Carson and Van Dyke 1994). The qualitative response and race specificity can be overcome under certain lighting conditions, temperatures, or inoculum concentrations (Leonard et al. 1989). The isolate used in our experiment is incompatible with HtN (C. Chung, personal communication) but no major effect was detected in our genetic analysis of four F₂ populations. This further suggests that a QTL was associated with the selection response, but since our experiment did not include a control isolate compatible with HtN, we cannot resolve whether HtN segregated in the F₂ populations.

Haplotypes defined by SEL* loci derived from the recurrent selection population were associated with resistance to NLB, measured as IP (Figures 5 and 6). We attribute the lack of significance of differences in sAUDPC to a low-pressure disease epidemic. On the basis of the analysis of the IP data, it seemed that at least two linked loci on chromosome 8 were associated with resistance (Figure 5). If this is confirmed by further studies, then yet another NLB QTL has been discovered here (i.e., near umc2357, Figure 5). The resolution of this putative multigenic QTL was a consequence of conducting cosegregation analysis on multiple haplotypes. If for each haplotype favorable alleles had been arranged in coupling, it is possible this would have been considered a single locus. This suggests that multiple genes on chromosome 8 were, in part, responsible for the gains from selection. In terms of the genetic basis of selection, it would be interesting to know whether a single haplotype composed of favorable alleles at multiple genes or multiple haplotypes were enriched during selection.

It was encouraging that we were able to identify loci by SM and confirm their role in disease resistance in a separate cosegregation analysis. The trait–locus associations were detected in a different genetic background from the population that underwent selection. Our inoculations were conducted with a single NLB isolate from upstate New York, which was certainly different from the sample of E. turcicum used by CIMMYT some 15 years earlier for recurrent selection. Our experiments were conducted in a growth chamber and field environment, which was obviously different from the environments where selection was practiced. This suggests that the haplotypes identified would be stable under a range of conditions and suitable for introgression into maize germplasm where quantitative resistance to NLB is desired.

Ongoing and future studies will test the associations of additional loci implicated in this study as responding to selection for disease resistance. It may not be possible to validate some SEL* loci given that our experimental conditions are so different from the one in which this population was selected. Some SEL* loci are likely to be associated with traits other than NLB resistance too. A drawback to the SM approach is that one cannot distinguish which loci were important for which trait(s) without further analyses. For instance, significant gains were achieved for common rust and several of the SEL* loci corresponded with published common rust QTL (Figure 3). To obtain a more generalized understanding of the genetic changes responsible for gains from selection, there is a need for the development of systematic approaches to functionally characterize the genes conditioning the selection response (e.g., Laurie et al. 2004).

SM uses multiallelic populations in which phenotypic selection sorts the best alleles from the worst. The trajectory of change in allele frequency allows for the identification of favorable, neutral, or unfavorable alleles. Assuming that the number of SSR alleles in C₀ reflects the number of alleles at the genes that were under selection, then on average approximately six alleles may have been surveyed during recurrent selection of Pool 30. Typically, a single allele per SEL* locus had a significant positive or negative trajectory and the remaining alleles appeared neutral (supplemental Figure S1). This suggests a simple allelic response to selection, where among the approximately six alleles per locus a single allele was selected during recurrent selection. According to a simulation analysis under certain assumptions about the degree of dominance and heritability (data not shown), this type of allelic response is observed when one allele at a locus has a much larger effect than the remaining alleles (e.g., the relative effect is >50% of any other allele). To further examine the effects of each founder allele at a given locus on disease development, an allele series analysis could be conducted by examining more populations derived from the recurrent selection population or by backcrossing recurrent selection alleles into a single genetic background. This analysis would shed light onto the distribution of allele effects and the observed simple selection response at a given locus.

Selection mapping is a relatively underutilized approach to the genetic analysis of quantitative traits. SM can permit the simultaneous discovery and use of linked marker loci and superior alleles for genetic analysis and crop improvement. The validity of SM, however, should be further examined. With current advances in genomic technologies, future studies should utilize larger samples of markers and individuals. This will shed light on interpretations from SM on understanding the genetic basis of the selection response.

APPENDIX A: TEST STATISTIC OF THE NULL HYPOTHESIS OF GENETIC DRIFT: USE OF MEASURED, SIMULATED, AND DERIVED VALUES

Waples (1989) described an adjusted chi-square test statistic for the null hypothesis of genetic drift. The adjusted test includes allele-frequency variances and covariances associated with temporally spaced samples, such that genetic drift parameters are incorporated directly into the test. In our version of the test, we used estimates based on simulation rather than calculation. Here, we describe our use of the test statistic described by Waples.

Consider a single locus with three alleles (a1, a2, and a3) sampled from two generations 0 and t. Because the frequencies of n − 1 alleles are independent, only a1 and a2 would be considered. The test requires the following estimates: (1) the variance in allele frequencies at each time point (Var), (2) the covariance of allele frequencies for the same allele at different time points (Cov 1), (3) the covariance of allele frequencies for different alleles at the same time point (Cov 2), (4) the covariance of allele frequencies for different alleles at different time points (Cov 3), and (5) expected allele frequencies (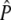). Estimates of 1–4 are derived from simulations of genetic drift (in our case, 5000 simulations) for each locus and the following expected covariance matrix () is constructed:

The expected frequency for each allele (P_0−t,i) is estimated as a weighted mean of sample allele frequencies. As noted by Waples, for a given sample size early generations are better estimates of P; those samples have less variance associated with them because they have not undergone t generations of genetic drift and can be weighted accordingly. Waples suggested the following method to determine weighting terms for each allele:

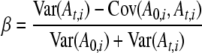(Equation 8 in Waples 1989).

Here, β is the weighting term for A_0,i, while 1 − β is the weighting term for A_t,i. An estimate of the expected allele frequency 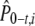is then computed as the weighted mean across time points (0 and t) for the ith allele. In estimating β, we used variances of allele frequencies and their covariance resulting from 5000 simulations of our model of genetic drift.

It should be noted here that there are two methods (or plans) of sampling a population under study. In plan I samples are taken before reproduction, and in plan II samples are taken after. Waples showed that under plan II, sampling Cov(A_0,i, A_t,i) = 0. So long as the simulation is representative of the sampling scheme, the appropriate covariances would be used.

Once variances and covariances of allele frequencies and 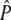are determined the test statistic (TS) is carried out as follows:

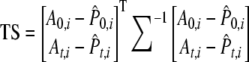(Equation 11 in Waples 1989).

The test statistic is calculated for the observed data and for each replication of genetic drift (i.e., 5001 TS calculations). The probability of a significant test is calculated as the proportion of simulation TS values equal to or greater than the observed TS value to the total number of TS values.