Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2008 Sep;180(1):619–628. doi: 10.1534/genetics.108.090407

A Genomewide Linkage Scan for Quantitative Trait Loci Influencing the Craniofacial Complex in Baboons (Papio hamadryas spp.)

Richard J Sherwood *,†,1, Dana L Duren *,‡, Lorena M Havill §, Jeff Rogers §,**, Laura A Cox §,**, Bradford Towne *, Michael C Mahaney §,**
PMCID: PMC2535711  PMID: 18757921

Abstract

Numerous studies have detected significant contributions of genes to variation in development, size, and shape of craniofacial traits in a number of vertebrate taxa. This study examines 43 quantitative traits derived from lateral cephalographs of 830 baboons (Papio hamadryas) from the pedigreed population housed at the Southwest National Primate Research Center. Quantitative genetic analyses were conducted using the SOLAR analytic platform, a maximum-likelihood variance components method that incorporates all familial information for parameter estimation. Heritability estimates were significant and of moderate to high magnitude for all craniofacial traits. Additionally, 14 significant quantitative trait loci (QTL) were identified for 12 traits from the three developmental components (basicranium, splanchnocranium, and neurocranium) of the craniofacial complex. These QTL were found on baboon chromosomes (and human orthologs) PHA1 (HSA1), PHA 2 (HSA3), PHA4 (HSA6), PHA11 (HSA12), PHA13 (HSA2), PHA16 (HSA17), and PHA17 (HSA13) (PHA, P. hamadryas; HSA, Homo sapiens). This study of the genetic architecture of the craniofacial complex in baboons provides the groundwork needed to establish the baboon as an animal model for the study of genetic and nongenetic influences on craniofacial variation.

CRANIOFACIAL anomalies are among the most common congenital defects. Phenotypic and genotypic characterizations have successfully categorized these disorders, but both approaches are confounded by the heterogeneous nature of the presentation. For example, single mutations may produce different phenotypic syndromes as is found in the craniosynostic disorders Crouzon syndrome and Pfeiffer syndrome, both caused by the same mutation in fibroblast growth factor receptor 2 (Cys278Phe) (Cohen and Kreiborg 1998; Cohen 2002). Alternatively, a specific syndrome, such as holoprosencephaly, may be caused by mutations in different genes. For instance, mutations in different genes such as GLI2, ZIC2, or SHH have been shown to cause holoprosencephaly. Clearly, no simple relationship exists between these genetic errors and their resultant phenotype. Current animal models for the study of the genetic determinants of normal craniofacial form are largely restricted to zebrafish, chick, and mouse or are based on interpretations of human dysmorphic syndromes. While the information gathered from these studies is valuable, the need for an animal model in phylogenetic proximity to humans increases as tissue engineering and gene therapy techniques become more possible.

The primate craniofacial complex is an integrated structure composed of several developmental and functional components. During ontogeny the three primary components, the neurocranium, the splanchnocranium, and the basicranium, are vulnerable to genetic and environmental influences and often show a coordinated response to those influences. Studies of genetic contributions to cranial variation have been conducted in human populations and have generally shown moderately high levels of heritability (e.g., Lundström 1954; Nakata et al. 1974; Byard et al. 1984a,b, 1985a,b; Nakata 1985; Lundström and McWilliam 1987, 1988; Kitahara et al. 1996; Arya et al. 2002; Duren et al. 2003; Sherwood et al. 2003). Although relatively fewer such studies have been conducted in nonhuman primates, the nonhuman primate craniofacial complex also generally exhibits heritable components (Cheverud and Buikstra 1981a,b, 1982; McGrath et al. 1984; e.g., Cheverud et al. 1990a,b; Cheverud 1995; Hlusko et al. 2002). Many of these studies, however, did not include traits from all developmental components; specifically, internal features of the basicranium were frequently absent. This study examines fundamental features of the genetic architecture of phenotypes throughout the craniofacial complex, including the internal cranial base, in a pedigreed colony of baboons (Papio hamadryas), using modern variance components-based statistical genetic methods.

MATERIALS AND METHODS

Data for this study were obtained from 830 animals ranging in age from 1.7 to 28.8 years from the pedigreed baboon colony at the Southwest Foundation for Biomedical Research/Southwest National Primate Research Center (SNPRC), San Antonio, Texas. These animals are a mixture of two subspecies, P. hamadryas anubis and P. hamadryas cynocephalus and their hybrids. The 830 animals with cephalometric data are members of a single, unbroken, extended pedigree containing 2426 individuals. This pedigree is six generations deep, with a majority of the animals (and thereby the genetic information) in generations 0 (founders) through 4.

All nonfounder animals are the results of managed breeding. While most of this large pedigree is noninbred, ∼500 of the youngest baboons in it are inbred progeny obtained in a single generation of matings between selected father–daughter, half-sibling, and avuncular relative pairs. The degree of inbreeding does not approach that of small laboratory animals such as rat and mouse, but it does increase regions of autozygosity throughout the baboon genome, maximizing statistical power to detect, and precision to estimate, genetic and environmental effects on the phenotypes measured in subsets of members of the pedigree.

The majority of animals with cephalometric data come from generations 2–5. Full sibships range in size from 2 (n = 372) to 12 (n = 10), with the median = 5. In addition to parent–offspring and full-sib pairs, the pedigree contains 49 other simple and complex relative pair classes from which genetic information can be extracted in our analyses: e.g., half-siblings (n pairs = 6855), half avuncular (n = 6414), half first cousins (n = 1103), half avuncular and first cousins and double half first cousins (n = 136), etc.

Animal handling:

Animals were anesthetized using Ketamine (some animals also required 5 mg intravenous Valium) and transported for radiography. Each animal was laid on its side and its head positioned for alignment during imaging, and the jaws were held shut with soft tubing. Two right lateral cephalographs per animal were taken according to standard veterinary radiographic procedures. Exposure times varied on the basis of size of the animal. In general, settings of 60–70 kVp and 100–200 mA, for 0.10–0.30 sec, at a tube distance of 37 in. from source to plate, provided excellent images across a wide range of body sizes. Mammography film and screens were used for all images as these provided the highest-quality images. Head width, taken as the maximum width, was measured at the time of radiography using a cephalometric board. The protocol used was approved by both the Institutional Animal Care and Use Committee of the SNPRC and the Laboratory Animal Care and Use Committee of Wright State University.

Phenotyping:

Phenotyping was done using the software package Nemoceph (CDIimaging), a commercially available program designed for rapid and accurate collection of cephalometric data. Although the package is designed for use with human radiographs, it was easily adapted to collect data from the baboon radiographs. Prior to any measurements, available radiographs for each animal were first evaluated visually to assure correct positioning of the animal. Radiographs that demonstrated any condition that may preclude accurate measurement (such as excessive rotation of the skull relative to the plate) were not used. The single best radiograph of each animal was used for measurements.

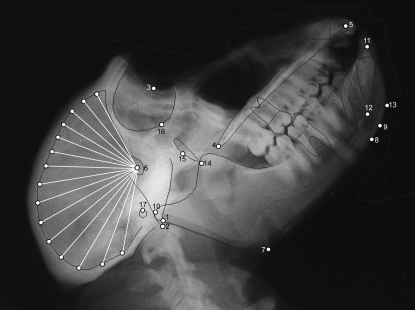
Radiographs were then scanned using an Epson Expression 10000XL scanner equipped with a transparency adapter. Radiographs were scanned directly into Nemoceph, which allows for adjustment of brightness and contrast as necessary, as well as the application of various filters (e.g., false color, inverse image) that may assist in identification of cephalometric points. All radiographs were scanned along with a 10-cm ruler used to calibrate the images prior to measurement. Tracing of the radiograph begins with Nemoceph prompting the user to place markers on predefined cephalometric points (Table 1; Figure 1). Once these points have been placed, Nemoceph provides a rough outline of the external and internal aspects of the skull, central incisors, and first molars. These outlines are fit to the cranial contours and teeth by the user with standard computer drawing tools (e.g., handles and anchors) to provide an exact tracing of the craniofacial features. Once tracing is complete, the user has the option of collecting data on the basis of several standard craniofacial analyses, such as Rickett's or Steiner's analysis (Merow and Broadbent 1990), or defining a unique set of measures. For our purposes, we have identified a data set that incorporates aspects of standard orthodontic analyses in addition to measures associated with other types of cephalometric analyses.

TABLE 1.

Cephalometric points identified on each lateral cephalograph

Trait Abbreviation Description
1. Articulare Ar The intersection of the image of the posterior border of the ramus with the external surface of the basicranium
2. Basion Ba The anterior margin of the foramen magnum
3. Nasion N The intersection of the nasal and frontal bones
4. Posterior nasal spine PNS The posterior point of the hard palate
5. Prosthion Pr The anterior point of the premaxilla between the upper central incisors
6. Sella S The pituitary fossa of the sphenoid bone
7. Gonion Goa The external angle of the mandible
8. Menton Me The most inferior point on the mandibular symphysis
9. Gnathion Gn The lowest, most anterior point on the mandibular symphysis
10. Posterior condylion PCd The point tangent to a perpendicular line extending from the S–N plane
11. Infradentale Id The anterior point of the tip of the alveolar process of the mandible between the lower central incisors
12. Point D D The center of the cross-section of the mandibular symphysis
13. Pogonion Pog The most anterior point of the mandibular symphysis
14. Pterygomaxillary fissure PTMa Teardrop-shaped area between maxilla and pterygoid process of the sphenoid
15. Center of face CFa Posterior-most point of the pterygomaxillary fissure
16. Orbitale Ora Inferior-most point of the orbit
17. Porion Poa Superior margin of external auditory canal
18. Frankfort horizontal FHa Plane defined by right and left porion and left orbitale
19. Facial plane FP Line connecting nasion and pogonion
20. Xnnn Points defined along the endocranial surface of the neurocranium relative to the S–N plane (e.g., X100 is the point at which a line drawn 100° from the S–N plane intersects the endocranium)
Open in a new tab

All points represent midline structures except where noted.

a

Points not on midline of the skull.

Figure 1.—

Figure 1.—

Open in a new tab

Radiograph of female baboon. Cephalometric points used in the analysis are identified (see Table 1 for key).

To describe the crania we used measures taken directly from the radiographs, as well as three variables derived from a principal components analysis of the neurocranial measures described below. Forty measurements were made on the basis of the craniometric points identified (see Table 2). Points and measurements chosen are designed to examine variation both within and between craniofacial components. For example, several measures are contained within their respective component, such as posterior base length (Ba–S), anterior base length (S–N), and angular measures such as basicranial flexion (N–S–Ba), which are all contained within the basicranium. Similarly, there are measures isolated to the splanchnocranium, including facial height (N–Pr) and palate length (Pr–PNS). Other measures are designed to span components, such as Ba–Pr, which incorporates basicranial and splanchnocranial landmarks. Angular measures such as facial hafting (S–N–Pr) or the mandibular plane angle also span multiple cranial components. All linear measurements were corrected for radiographic enlargement using an established correction factor. This correction factor is based on the formula 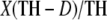Inline graphic, where X is the radiographic measurement, TH is the tube height (a constant 37 in.), and D is the distance from the object (in this case the cranial midline defined as one-half of head width) to the film (Sherwood et al. 2000).

TABLE 2.

Quantitative measures collected from lateral cephalographs

Trait name Definition
Ar–Go Linear distance between Ar and Go
Ba–Ar Linear distance between Ba and Ar
Ba–N Linear distance between Ba and N
Ba–PNS Linear distance between Ba and PNS
Ba–Pr Linear distance between Ba and Pr
Ba–S Linear distance between Ba and S
Facial axis Angular measure between Ba–N plane and the line from foramen rotundum to Gn
Facial taper Angular measure between mandibular plane (Go–Me) and N–Pog plane
Facial depth Angular measure between Frankfort horizontal and facial plane
Go–Me Linear distance between Go and Me
Go–Gn–SN Angular measure between Go–Gn plane and S–N plane
Gonial angle Angular measure from Ar to Go to Me
Interincisal angle Angular measure between axis of upper and lower central incisors
N–PNS Linear distance between N and PNS
N–Pr Linear distance between N and Pr
N–S–Ba Angular measure from N to S to Ba
N–S–PNS Angular measure from N to S to PNS
Neuropc1 Neurocranial principal component 1 score
Neuropc2 Neurocranial principal component 2 score
Neuropc3 Neurocranial principal component 3 score
Occ–S Angular measure between occlusal plane and S–N plane
PNS–Pr Linear distance between PNS and Pr
Posterior condylion Linear distance between S and PCd
Posterior facial height Linear distance from Go to CF
PrNId Angular measure from Pr to N to Id
S–N–Pr Angular measure from S to N to Pr
S–N Linear distance between S and N
S–PNS Linear distance between S and PNS
S–Pr Linear distance between S and Pr
S–X60 Linear distance between S and X60
S–X70 Linear distance between S and X70
S–X80 Linear distance between S and X80
S–X90 Linear distance between S and X90
S–X100 Linear distance between S and X100
S–X110 Linear distance between S and X110
S–X120 Linear distance between S and X120
S–X130 Linear distance between S and X130
S–X140 Linear distance between S and X140
S–X150 Linear distance between S and X150
S–X160 Linear distance between S and X160
S–X180 Linear distance between S and X180
SND Angular measure from S to N to D
SNId Angular measure from S to N to Id
Open in a new tab

Because neurocranial landmarks are difficult to reliably discern on lateral cephalographs, a set of measurements designed to capture the maximal amount of information from the neurocranium was defined as follows. First, a line from sella to nasion is identified. From this reference line, additional lines are placed every 10° up to 180°. For each line, a measurement is taken from sella to the point of intersection with the endocranial surface. As the first five such lines do not always intersect the endocranial surface, these measures are not collected; there are, therefore, 13 measures available to describe the morphology of the neurocranium.

As it could be argued that measurements defined in this manner are not necessarily homologous between individuals (see Gunz et al. 2008 for a discussion of analysis of semilandmark data), we used a principal components analysis to extract latent variables describing the overall morphology of the neurocranium. Three components were extracted using a varimax rotation explaining 38.3, 27.6, and 25.7% of the variance, respectively. Factor patterns describing each component (Table 3) indicate that PC1 is heavily influenced by anterior neurocranial measurements (60°–120° from S–N), PC2 is influenced by intermediate measures (110°–150°), and PC3 is influenced by posterior measures (150°–180°). Thus, in general, individuals loading high on PC1 could be described as anteriorly elongate, individuals loading high on PC2 could be described as possessing taller crania, and individuals loading high on PC3 could be described as posteriorly elongated.

TABLE 3.

Factor loading scores for principal components decomposition of neurocranial measures

Trait Factor 1 Factor 2 Factor 3
S–X60 80a −5 15
S–X70 93a 24 −6
S–X80 92a 29 −18
S–X90 86a 36 −29
S–X100 81a 45 −32
S–X110 74a 59a −26
S–X120 63a 74a −11
S–X130 41 86a 14
S–X140 25 88a 29
S–X150 2 77a 56a
S–X160 −15 31 90a
S–X170 −12 11 94a
S–X180 −9 −1 95a
Open in a new tab

Values are multiplied by 100 and rounded.

a

“Meaningful” factor loadings (loading >55).

Two trained assessors measured all radiographs. To examine interobserver reliability, a set of radiographs was traced and measured by both observers on a regular basis. In total, 121 radiographs were assessed by both individuals. Reliability was assessed using intraclass correlation.

Baboon genotyping and the whole-genome linkage map:

Statistical genetic analyses of these cephalometric measurements took advantage of a baboon whole-genome linkage map based on genotype data at nearly 300 microsatellite marker loci (mean intermarker interval = 8.9 cM) from >2000 pedigreed baboons in this same extended pedigree. The physical locations in the human genome for nearly all marker loci in the baboon map are known, thus facilitating the identification of likely orthologous chromosomal regions in the two species. Construction of the current baboon linkage map is described in detail elsewhere (Rogers et al. 2000; Cox et al. 2006), and additional information can be found at the SNPRC website (http://www.snprc.org/baboon/genome/index.html).

Direct comparison among homologous (orthologous) loci reveals large regions of synteny in which the human marker order is conserved (7 autosomes with no major rearrangement, 15 with one or more rearrangements; see Rogers et al. 2000 and Cox et al. 2006 for further details). Given the degree of similarity, throughout this article we refer to the baboon chromosome number followed by the human number in parentheses to facilitate comprehension of our results and their comparison to humans. For example, “chromosome PHA4 (HSA6)” designates the syntenic grouping of microsatellite marker loci that map to baboon chromosome 4, a syntenic grouping that comprises the loci on chromosome 6 in humans (PHA, P. hamadryas; HSA, Homo sapiens). Using similar logic, “chromosome PHA3 (HSA7/21)” designates baboon chromosome 3, which represents (relative to the humancondition) a fusion of what are two different syntenic groups in humans, i.e., chromosomes 7 and 21.

Statistical genetic analyses:

We used a maximum-likelihood-based variance decomposition approach implemented in sequential oligogenic linkage analysis routines (SOLAR) (Almasy and Blangero 1998) to estimate heritability for each craniofacial variable and to test for evidence of quantitative trait loci (QTL) for cranial traits at 1-cM intervals throughout the genome. This method, described in detail elsewhere (Almasy and Blangero 1998), entails specification of the genetic covariance between arbitrary relatives as a function of the identity-by-descent (IBD) relationships at a given marker locus and models the covariance matrix for a pedigree as the sum of the additive genetic covariance attributable to the QTL, the additive genetic covariance due to the effects of loci other than the QTL, and the variance due to unmeasured environmental factors.

Our linkage analyses incorporate IBD allele sharing estimated from genotype data at the microsatellite markers in the baboon linkage map. We estimated probabilities of IBD among relatives at marker loci in the baboon linkage map, using Markov chain Monte Carlo routines implemented in the computer package Loki (Heath 1997). We tested linkage hypotheses at 1-cM intervals along each chromosome, using likelihood-ratio tests, and converted the resulting likelihood-ratio statistic to the LOD score of classic linkage analysis (Ott 1988).

We tested the hypothesis of linkage by comparing the likelihood of a restricted model in which variance due to the QTL equaled zero (no linkage) to that of a model in which it did not equal zero (i.e., is estimated). The LOD score of classical linkage analysis was obtained as the quotient of the difference between the two ln likelihoods divided by ln 10 (Ott 1988).

To control for the genomewide false positive rate, we calculated genomewide P-values for each LOD score, using our modification of a method suggested by Feingold et al. (1993) that takes into account pedigree complexity and the finite marker density of the linkage map. Accordingly, our threshold for significant evidence of linkage (corresponding to genomewide α = 0.05) was LOD = 2.75, while suggestive evidence of linkage occurred at LOD = 1.50. Respectively, these values correspond to the expected false positive rates of once per 20 (“significant”) and once per 10 (“suggestive”) genomewide linkage screens (Lander and Kruglyak 1995).

Accounting for environmental contributions to the phenotypic variance can improve power to detect genetic effects. Prior to all analyses, we used likelihood-ratio tests to screen each of the following variables for significant mean effects on the cephalographically derived variables: age, sex, age2, age × sex, age2 × sex, and head width. After regressing out the mean effects of all nominally significant (P ≤ 0.10) covariates, we applied an inverse Gaussian transformation to the residuals to correct for departures from multivariate normality that might inflate evidence for linkage (Göring et al. 2001). This transformation produces standardized traits with means and standard deviations approaching 0 and 1, respectively. All reported linkage analyses were conducted using these normalized residual data. The reported h2 is residual heritability (that part of the variance that is attributable to the additive effects of genes after covariate effects, including those of age and sex, are removed).

RESULTS

Baboons are sexually dimorphic animals, and adult male linear measurements in this sample are ∼15–25% greater than those of females, with facial measures tending to show greater sexual dimorphism than basicranial measures; neurocranial size measures are the least sexually dimorphic with males being ∼5–7% larger than females. Angular measures, such as basicranial flexion or facial axis, show minimal sexual dimorphism (∼1–2% difference). Sex differences in cranial dimensions begin to become evident ∼4–5 years of age.

Prior to genetic analyses phenotypic data were examined for reliability, using intraclass correlation. Interobserver reliability of measures was very high, with an average intraclass correlation of 0.96 for all variables. The average intraobserver difference for linear metrics was 1.12 mm, and the average difference for angular measures was 2.9° (complete details are provided in supplemental material). Basic quantitative genetic analyses detected significant (P < 0.001) additive genetic components to the variance (i.e., heritability, h2) for all 43 craniofacial traits measured in this study: Heritability estimates ranged from 0.13 (for Ba-Ar) to 0.71 (for gonial angle) with average h2 = 0.43.

After confirming the measurements were reliable and that we could detect the effects of genes on their variation, we performed whole-genome linkage screens to localize QTL accounting for these genetic effects. Linkage analyses identified several chromosomal regions harboring genes influencing craniofacial variation. Fourteen significant QTL (LOD > 2.75) were identified for 12 craniofacial traits (Figure 2) and these results are presented in Table 4 and Figures 3 and 4. One QTL was found on each of chromosomes PHA1 (HSA1), PHA13 (HSA2), PHA17 (HSA13), and PHA16 (HSA17), three QTL were found on chromosome PHA2 (HSA3), five QTL were found on chromosome PHA4 (HSA6), and two QTL were found on chromosome PHA11 (HSA12).

Figure 2.—

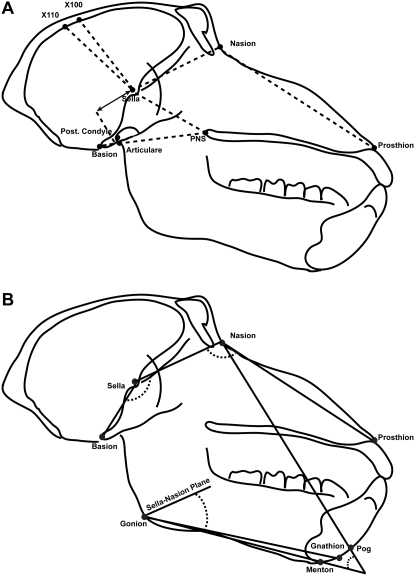
Figure 2.—

Open in a new tab

Angular (A) and linear (B) measures collected from lateral cephalographs. Measurements shown are those for which were detected one or more QTL accounting for a significant proportion of their variance.

TABLE 4.

Quantitative trait loci for craniofacial traits in pedigreed baboons

Baboon (PHA)
Human region orthologous to 1-LOD support interval
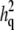Trait N h2a Inline graphica LOD Pb Chromosome cMc Cytogenetic location Width (ntb) No. of known genesd
Posterior condylion 825 0.12 0.156 3.34 0.011 13 51 2p21 13,618,455 104
NeuroPC3 830 0.36 0.119 3.12 0.020 2 69 3q13.13 48,871,949 356
S–N–Pr 822 0.34 0.122 3.17 0.018 2 109 3q11.2 8,191,868 5
Go–Gn–S 815 0.33 0.116 2.94 0.031 2 110 3q11.2 15,687,197 14
S–PNS 811 0.37 0.102 2.93 0.021 4 27 6p21.2 9,392,315 30
Facial taper 811 0.47 0.147 3.32 0.012 4 44 6q12 17,144,062 341
Ba–Ar 819 0.0 0.113 3.96 0.003 4 53 6q15 18,360,803 374
S–X110 830 0.40 0.166 3.01 0.026 4 140 6q27 18,306,109 80
S–X100 830 0.41 0.170 3.01 0.026 4 140 6q27 18,306,109 80
N–S–Ba 822 0.24 0.096 3.45 0.009 11 0 12p13.33 5,296,636 42
Ba–PNS 808 0.28 0.131 3.70 0.005 11 14 12p13.33 9,205,306 114
Facial taper 811 0.53 0.094 2.89 0.035 17 50 13q31.3 16,531,783 82
N–Pr 822 0.25 0.193 2.88 0.036 16 54 17p12 19,688,343 400
Open in a new tab

ntb, nucleotide bases.

a

Maximum-likelihood heritability estimates from linkage models: 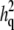Inline graphic is the QTL-specific heritability, i.e., the proportion of the residual phenotypic variance due to the effect of the QTL, and h2 is the residual heritability, i.e., the proportion of the phenotypic variance in the trait due to the effects of genes other than the QTL.

b

Genomewide P-value associated with the LOD score calculated using a modification of a method suggested by Feingold et al. (1993) that takes into account pedigree complexity and the finite marker density of the baboon whole-linkage map used in these analyses.

c

Location in centimorgans from the pter-most marker locus in the baboon genetic linkage map for that chromosome.

d

Within regions of human syntenic groups likely to be orthologous to the region of the baboon genome containing the 1-LOD support interval for the QTL.

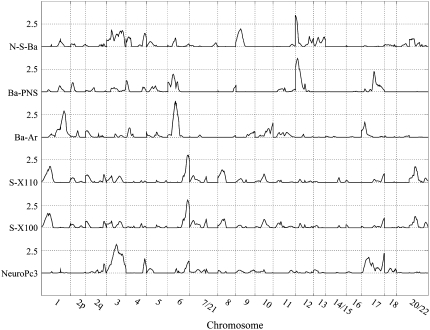
Figure 3.—

Figure 3.—

Open in a new tab

Genomewide linkage results for basicranial and neurocranial traits.

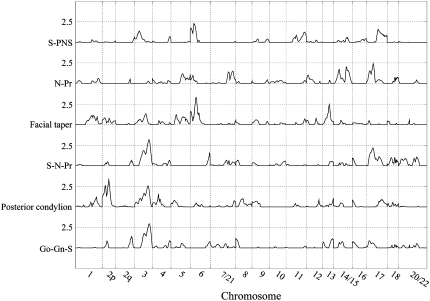
Figure 4.—

Figure 4.—

Open in a new tab

Genomewide linkage results for splanchnocranium and mixed-component traits.

As noted, the cranium is frequently discussed in terms of developmental components, the basicranium (those structures supporting the brain), the splanchnocranium (the face and mandible), and the neurocranium (the bones surrounding the brain). Because these components share similar developmental history and function, we investigated the significant QTL for each component for common patterns. As some traits included aspects of multiple components, we investigated those separately.

The basicranial measurements for which significant QTL were found include three measures, two linear and one angular. One of these measures, Ba–Ar, is a measure of posterior basicranial length and also provides information regarding the relative positioning of the mandible to the basicranium. In the initial whole-genome screen for this trait we detected significant evidence for two QTL: one on PHA4 (HSA6) with LOD = 3.96 and the other on PHA1 (HSA1) with LOD = 2.89. However, when we performed a second, sequential, whole-genome linkage screen conditional on the PHA4 Ba–Ar QTL, the evidence for a second QTL was neither significant nor suggestive (i.e., second pass LOD = 1.10). The significant QTL that was localized to the long (q) arm of PHA4, in an interval orthologous to HSA6q21.2, was estimated to account for between 85 and 100% of the detected additive genetic effects on variation in Ba–Ar; and these effects were responsible for ∼11.3% of the residual phenotypic variance in the trait. Another measure for which we detected a significant QTL, Ba–PNS, describes the position of the hard palate relative to the basicranium. With LOD = 3.70, we localized this QTL to a region of the short (p) arm of PHA11 orthologous to HSA12p13.33. We estimated that this QTL accounted for ∼32% of the detected additive genetic effects and 13% of the residual phenotypic variance, in the measure. The third measure, N–S–Ba (sometimes referred to as the saddle angle), describes basicranial flexion. Basicranial flexion is frequently discussed when comparing nonhuman primates, with a relatively unflexed cranial base, to modern humans who possess a strongly flexed cranial base. Our analyses localized a significant QTL for N–S–Ba to roughly the same chromosomal region in which we also detected the QTL for Ba–PNS—i.e., the p arm of PHA11 (HSA12). Approximately 29% of the additive genetic variance and 10% of the residual phenotypic variance in this trait could be attributed to this QTL.

Our analyses yielded significant evidence for four QTL affecting three splanchnocranial features. We localized one of these, a QTL accounting for 44% of the estimated additive genetic effects, and nearly 20% of the residual phenotypic variance, for a linear measure of facial length, N–Pr, to a region of PHA16 that corresponds to HSA17p12. For S–PNS, a linear measure of facial positioning relative to the basicranium, we localized a second QTL for this craniofacial component to an area of PHA4p that is orthologous to HSA6p21.2. This QTL accounted for ∼22 and 10.2%, respectively, of the additive genetic and residual phenotypic variance in this trait. Our analyses of an angular measure of overall facial positioning, facial taper, returned significant evidence for two QTL: One, accounting for 15% of the additive genetic variance and 9.4% of the residual phenotypic variance in the trait, was localized to PHA17 (HSA13q13.3); and the other, accounting for 24 and 14.7% of these respective variance components, mapped to PHA4q (HSA6q12).

We localized three significant QTL for neurocranial traits. Two of these, influencing variation in the highly correlated S-100 and S-110 variables, mapped to the same location: i.e., 140 cM from the pter-most marker locus (marker locus closest to the terminus, or end, of the p, or short, arm of the chromosome) on PHA4, a region that is orthologous to HSA6q27. The estimated effect of these QTL on these two correlated measures was essentially identical, accounting for ∼30% of the additive genetic variance and 17% of the residual phenotypic variance, in these measures. The third QTL was detected when we analyzed a synthetic variable, PC3, obtained from a principal components analysis of all neurocranial metrics. The QTL for PC3, which (as noted earlier) emphasizes the posterior measures of the neurocranium, is localized to PHA2 (HSA3q13.13) and accounts for ∼25% of the additive genetic effects on variation in this principal component.

Finally, we localized QTL for three mixed-component traits that describe relative positioning of the face (S–N–Pr), mandible (Go–Gn–S), and the mandibular condyle (posterior condylion). The QTL for the former two traits, S–N–Pr and Go–Gn–S, map to identical locations, 110 cM from the pter-most marker locus on PHA2, a region corresponding to HSA3q11.2, and explain roughly the same proportion of the genetic and phenotypic variation in the two traits (i.e., 25 and 12%, respectively). The QTL influencing variation in posterior condylion maps to a region of PHA13 that is orthologous to HSA2p21. Although accounting for only 15.6% of the residual phenotypic variation, the gene(s) at this locus accounted for >50% of the detected genetic effects on this trait.

DISCUSSION

This study is the first to identify QTL influencing variation in craniofacial traits in a nonhuman primate. In addition to substantively augmenting our statistical power to detect and localize genes influencing variation in quantitative traits, the size, configuration, and composition of this pedigreed sample can facilitate the detection of the effects of other factors on these craniofacial traits. As noted, the age range for the >800 baboons in this single, complex pedigree spanned 27 years and included young and adult animals. Our study does not address the question of age-specific genetic contributions to craniofacial variation (i.e., genotype-by-age interactions). However, analytical methods that can do so, while making use of all the genetic and phenotypic information in this large and complex pedigree, are available (Almasy et al. 2001; Diego et al. 2003; Havill and Mahaney 2003) and a comprehensive analysis of age-specific genetic effects is in progress.

Candidate genes:

To investigate potential positional candidate genes under the QTL regions identified in our analyses, the current literature was searched for known genes affecting craniofacial structures in orthologous regions of the human genome. Several reports were found, indicating that mutations in some areas of interest we identified are associated with dysmorphic craniofacial patterns. For instance, the SIX3 gene found on HSA2p21, and linked to the posterior condylion measure in baboons, has been identified as a causative factor in holoprosencephaly, a disorder with severe craniofacial dysmorphology including cyclopia and a midline proboscis situated above the eye (Wallis et al. 1999). Sato et al. (2007) identified a patient with a deletion spanning HSA3q11.2, linked to the trait Go–Gn–S in our study, that presented with the rare condition of congenital arhinia (complete absence of the nose). Additionally, deletions in the HSA17p12 region, linked to N–Pr in this study, have been implicated in cleft palate associated with Smith–Magenis syndrome (Andrieux et al. 2007). Additional disorders such as cleidocranial dysplasia (HSA6p21.2), Opitz trigonocephaly (OTCS; HSA3q13.13), and cat eye syndrome (CECR1; HSA22q11.1) are caused by mutations in regions linked to craniofacial features in our study. Chromosomal regions identified in these linkage analyses, therefore, are identified as containing genes with some effect on cranial features.

Genetics of the craniofacial complex:

Recent advances in developmental biology have led to the discovery of a number of genes and gene products important in the development of the skeleton and, specifically, the skull. However, as is the case with many systems, our primary understanding of the specific genes related to craniofacial morphology comes from animal models phylogenetically distant from humans, such as zebrafish, chick, or mouse (e.g., Alexandre et al. 1996; Helms et al. 1997; Leamy et al. 1999, 2000; Workman et al. 2002; Helms and Schneider 2003; Albertson and Yelick 2004; Eames and Helms 2004), or from genetic disorders associated with human craniofacial anomalies (Slavkin 1983; Olsen 1998; Slavkin 2001; Cohen 2002). Many of these anomalies affect multiple tissue types and are often not restricted to cranial structures (Richtsmeier 1987; Cohen and Kreiborg 1991, 1994a,b). Additionally, these disorders are frequently characterized by high degrees of genetic and phenotypic heterogeneity. While the advances made by studying dysmorphic syndromes are significant, they do not provide an adequate characterization of the genetic background to normal craniofacial development and morphology. This study presents our initial analyses to identify QTL influencing craniofacial traits in a nonhuman primate species.

This study demonstrates that all craniofacial components are characterized by significant heritability of moderate to high magnitude, suggesting that cranial components are relatively similarly influenced by environmental and genetic factors. There is little redundancy in the significant QTL identified for the craniofacial traits from common components or for traits from different components. This lack of patterning with regard to QTL for craniofacial features suggests a level of independence of the craniofacial components and traits. Issues regarding the integration and modularity of morphological characters are particularly important with regard to the craniofacial complex (e.g., Cheverud and Buikstra 1981b; Cheverud 1982, 1995, 1996, 2001; Wagner and Altenberg 1996; Cheverud et al. 1997; Mezey et al. 2000), and future research will further investigate the degree of integration within the baboon cranium.

In conclusion, this study demonstrates that quantitative traits comprising the craniofacial complex in baboons are under significant genetic influence. Several genomic regions have been identified as containing genes responsible for variation in these traits. Future work will interrogate these chromosomal regions to identify specific genes and functional polymorphisms in the baboon and extend our analyses to include humans.

Acknowledgments

The authors are indebted to the Southwest National Primate Research Center (SNPRC), specifically Suzette Tardif and Karen Rice, for facilitating this research. We express our sincere gratitude to the staff of the SNPRC responsible for radiography of the animals—Shannon Theriot, M. J. Bell, Terry Naegelin, and Wade Hodgson. We are also grateful to Kimberly Lever, Rebecca Junker, and Joe Wagner for phenotyping and database assistance. This work was supported in part by the National Institute of Dental and Craniofacial Research (National Institutes of Health, NIH) grants DE016692 and DE016408 to R. J. Sherwood, by NIH grant P51 RR13986 to the SNPRC, and by NIH grant P01HL28972. Development and implementation of the SOLAR statistical genetics analysis package is supported by grant MH059490 from the National Institute of Mental Health. This investigation was conducted in facilities constructed with support from Research Facilities Improvement Program grants C06 RR15456, C06 RR017515, and C06 RR013556 from the National Center for Research Resources, NIH. The supercomputing facilities used in this work at the AT&T Genomics Computing Center were supported by a gift from the SBC Foundation.

References

  1. Albertson, R. C., and P. C. Yelick, 2004. Morphogenesis of the jaw: development beyond the embryo. Methods Cell Biol. 76 437–454. [DOI] [PubMed] [Google Scholar]
  2. Alexandre, D., J. D. Clarke, E. Oxtoby, Y. L. Yan, T. Jowett et al., 1996. Ectopic expression of Hoxa-1 in the zebrafish alters the fate of the mandibular arch neural crest and phenocopies a retinoic acid-induced phenotype. Development 122 735–746. [DOI] [PubMed] [Google Scholar]
  3. Almasy, L., and J. Blangero, 1998. Multipoint quantitative-trait linkage analysis in general pedigrees. Am. J. Hum. Genet. 62 1198–1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Almasy, L., B. Towne, C. Peterson and J. Blangero, 2001. Detecting genotype x age interaction. Genet. Epidemiol. 21(Suppl. 1): S819–S824. [DOI] [PubMed] [Google Scholar]
  5. Andrieux, J., C. Villenet, S. Quief, S. Lignon, S. Geffroy et al., 2007. Genotype phenotype correlation of 30 patients with Smith-Magenis syndrome (SMS) using comparative genome hybridisation array: cleft palate in SMS is associated with larger deletions. J. Med. Genet. 44 537–540. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Arya, R., R. Duggirala, A. G. Comuzzie, S. Puppala, S. Modem et al., 2002. Heritability of anthropometric phenotypes in caste populations of Visakhapatnam, India. Hum. Biol. 74 325–344. [DOI] [PubMed] [Google Scholar]
  7. Byard, P. J., A. B. Lewis, F. Ohtsuki, R. M. Siervogel and A. F. Roche, 1984. a Sibling correlations for cranial measurements from serial radiographs. J. Craniofac. Genet. Dev. Biol. 4 265–269. [PubMed] [Google Scholar]
  8. Byard, P. J., K. Sharma, J. M. Russell and D. C. Rao, 1984. b A family study of anthropometric traits in a Punjabi community: II. An investigation of familial transmission. Am. J. Phys. Anthropol. 64 97–104. [DOI] [PubMed] [Google Scholar]
  9. Byard, P. J., D. V. Poosha, M. Satyanarayana and D. C. Rao, 1985. a Family resemblance for components of craniofacial size and shape. J. Craniofac. Genet. 5 229–238. [PubMed] [Google Scholar]
  10. Byard, P. J., D. V. Poosha, M. Satyanarayana, D. C. Rao and J. M. Russell, 1985. b Path analysis of family resemblance for cranio-facial traits in Andhra Pradesh nuclear families and twins. Ann. Hum. Biol. 12 305–314. [DOI] [PubMed] [Google Scholar]
  11. Cheverud, J. M., 1982. Phenotypic, genetic, and environmental morphological integration in the cranium. Evolution 36 499–516. [DOI] [PubMed] [Google Scholar]
  12. Cheverud, J. M., 1995. Morphological integration in the saddle-back tamarin (Saquinus fuscicollis) cranium. Am. Nat. 145 63–89. [Google Scholar]
  13. Cheverud, J. M., 1996. Developmental integrations and the evolution of pleiotropy. Am. Zool. 36 44–50. [Google Scholar]
  14. Cheverud, J. M., 2001. The genetic architecture of pleiotropic relations and differential epistasis, pp. 411–433 in The Character Concept in Evolutionary Biology, edited by G. P. Wagner. Academic Press, San Diego.
  15. Cheverud, J. M., and J. E. Buikstra, 1981. a Quantitative genetics of skeletal nonmetric traits in the rhesus macaques on Cayo Santiago. I. Single trait heritabilities. Am. J. Phys. Anthropol. 54 43–49. [DOI] [PubMed] [Google Scholar]
  16. Cheverud, J. M., and J. E. Buikstra, 1981. b Quantitative genetics of skeletal nonmetric traits in the rhesus macaques on Cayo Santiago. II. Phenotypic, genetic, and environmental correlations between traits. Am. J. Phys. Anthropol. 54 51–58. [DOI] [PubMed] [Google Scholar]
  17. Cheverud, J. M., and J. E. Buikstra, 1982. Quantitative genetics of skeletal nonmetric traits in the rhesus macaques of Cayo Santiago. III. Relative heritability of skeletal nonmetric and metric traits. Am. J. Phys. Anthropol. 59 151–155. [DOI] [PubMed] [Google Scholar]
  18. Cheverud, J. M., D. Falk, C. Hildebolt, A. J. Moore, R. C. Helmkamp et al., 1990. a Heritability and association of cortical petalias in rhesus macaques (Macaca mulatta). Brain Behav. Evol. 35 368–372. [DOI] [PubMed] [Google Scholar]
  19. Cheverud, J. M., D. Falk, M. Vannier, L. Konigsberg, R. C. Helmkamp et al., 1990. b Heritability of brain size and surface features in rhesus macaques (Macaca mulatta). J. Hered. 81 51–57. [DOI] [PubMed] [Google Scholar]
  20. Cheverud, J. M., E. J. Routman and D. J. Irschick, 1997. Pleiotropic effects of individual gene loci on mandibular morphology. Evolution 51 2006–2016. [DOI] [PubMed] [Google Scholar]
  21. Cohen, M. M., 2002. Malformations of the craniofacial region: evolutionary, embryonic, genetic, and clinical perspectives. Am. J. Med. Genet. 115 245–268. [DOI] [PubMed] [Google Scholar]
  22. Cohen, M. M., and S. Kreiborg, 1991. Genetic and family study of the Apert syndrome. J. Craniofac. Genet. Dev. Biol. 11 7–17. [PubMed] [Google Scholar]
  23. Cohen, M. M., and S. Kreiborg, 1994. a Cranial size and configuration in the Apert syndrome. J. Craniofac. Genet. Dev. Biol. 14 153–162. [PubMed] [Google Scholar]
  24. Cohen, M. M., and S. Kreiborg, 1994. b Unusual cranial aspects of the Apert syndrome. J. Craniofac. Genet. Dev. Biol. 14 48–56. [PubMed] [Google Scholar]
  25. Cohen, M. M., and S. Kreiborg, 1998. Perspectives on craniofacial syndromes. Acta Odontol. Scand. 56 315–320. [DOI] [PubMed] [Google Scholar]
  26. Cox, L. A., M. C. Mahaney, J. L. VandeBerg and J. Rogers, 2006. A second-generation genetic linkage map of the baboon (Papio hamadryas) genome. Genomics 88 274–281. [DOI] [PubMed] [Google Scholar]
  27. Diego, V. P., L. Almasy, T. D. Dyer, J. M. P. Soler and J. Blangero, 2003. Strategy and model building in the fourth dimension: a null model for genotype x age interaction as a Gaussian stationary stochastic process. BMC Genet. 4(Suppl. 1): S34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Duren, D. L., S. A. Czerwinski, R. J. Sherwood, A. F. Roche, R. M. Siervogel et al., 2003. Quantitative genetics of the craniofacial complex in humans. Am. J. Phys. Anthropol. 120(Suppl. 36): 91–92. [Google Scholar]
  29. Eames, B. F., and J. A. Helms, 2004. Conserved molecular program regulating cranial and appendicular skeletogenesis. Dev. Dyn. 231 4–13. [DOI] [PubMed] [Google Scholar]
  30. Feingold, E., P. O. Brown and D. Siegmund, 1993. Gaussian models for genetic linkage analysis using complete high-resolution maps of identity by descent. Am. J. Hum. Genet. 53 234–251. [PMC free article] [PubMed] [Google Scholar]
  31. Göring, H. H., J. D. Terwilliger and J. Blangero, 2001. Large upward bias in estimation of locus-specific effects from genomewide scans. Am. J. Hum. Genet. 69 1357–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Gunz, P., P. Mitteroecker and F. L. Bookstein, 2008. Semilandmarks in three dimensions, pp. 73–98 in Modern Morphometrics in Physical Anthropology, edited by D. E. Slice. Plenum Publishers, New York.
  33. Havill, L. M., and M. C. Mahaney, 2003. Pleiotropic effects on cardiovascular risk factors within and between the fourth and sixth decades of life: implications for genotype x age interactions. BMC Genet. 4(Suppl. 1): S54. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Heath, S. C., 1997. Markov chain Monte Carlo segregation and linkage analysis for oligogenic models. Am. J. Hum. Genet. 61 748–760. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Helms, J. A., and R. A. Schneider, 2003. Cranial skeletal biology. Nature 423 326–331. [DOI] [PubMed] [Google Scholar]
  36. Helms, J. A., C. H. Kim, D. Hu, R. Minkoff, C. Thaller et al., 1997. Sonic hedgehog participates in craniofacial morphogenesis and is down-regulated by teratogenic doses of retinoic acid. Dev. Biol. 187 25–35. [DOI] [PubMed] [Google Scholar]
  37. Hlusko, L. J., K. M. Weiss and M. C. Mahaney, 2002. Statistical genetic comparison of two techniques for assessing molar crown size in pedigreed baboons. Am. J. Phys. Anthropol. 117 182–189. [DOI] [PubMed] [Google Scholar]
  38. Kitahara, T., M. Ichinose and A. Nakasima, 1996. Quantitative evaluation of correlation of skull morphology in families in an attempt to predict growth change. Eur. J. Orthod. 18 181–191. [DOI] [PubMed] [Google Scholar]
  39. Lander, E., and L. Kruglyak, 1995. Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat. Genet. 11 241–247. [DOI] [PubMed] [Google Scholar]
  40. Leamy, L., E. J. Routman and J. M. Cheverud, 1999. Quantitative trait loci for early- and late developing skull characters in mice: a test of the genetic independence model of morphological integration. Am. Nat. 153 201–214. [DOI] [PubMed] [Google Scholar]
  41. Leamy, L. J., D. Pomp, E. J. Eisen and J. M. Cheverud, 2000. Quantitative trait loci for directional but not fluctuating asymmetry of mandible characters in mice. Genet. Res. 76 27–40. [DOI] [PubMed] [Google Scholar]
  42. Lundström, A., 1954. The importance of genetic and non-genetic factors in the facial skeleton studied in 100 pairs of twins. J. Eur. Orthodont. Soc. 30 92–107. [Google Scholar]
  43. Lundström, A., and J. S. McWilliam, 1987. A comparison of vertical and horizontal cephalometric variables with regard to heritability. Eur. J. Orthod. 9 104–108. [DOI] [PubMed] [Google Scholar]
  44. Lundström, A., and J. McWilliam, 1988. Comparison of some cephalometric distances and corresponding facial proportions with regard to heritability. Eur. J. Orthod. 10 27–29. [DOI] [PubMed] [Google Scholar]
  45. McGrath, J. W., J. M. Cheverud and J. E. Buikstra, 1984. Genetic correlations between sides and heritability of asymmetry for nonmetric traits in rhesus macaques on Cayo Santiago. Am. J. Phys. Anthropol. 64 401–411. [DOI] [PubMed] [Google Scholar]
  46. Merow, W. W., and B. H. Broadbent, Jr., 1990. Cephalometrics, pp. 346–395 in Facial Growth, edited by D. H. Enlow. W. B. Saunders, Philadelphia.
  47. Mezey, J. G., J. M. Cheverud and G. P. Wagner, 2000. Is the genotype-phenotype map modular? A statistical approach using mouse quantitative trait loci data. Genetics 156 305–311. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Nakata, M., 1985. Twin studies in craniofacial genetics: a review. Acta Genet. Med. Gemellol. 34 1–14. [DOI] [PubMed] [Google Scholar]
  49. Nakata, M., P. L. Yu and W. E. Nance, 1974. Multivariate analysis of craniofacial measurements in twin and family data. Am. J. Phys. Anthropol. 41 423–429. [DOI] [PubMed] [Google Scholar]
  50. Olsen, B., 1998. The genetic map of craniofacial anomalies. Harv. Dent. Bull. 7 18–19. [PubMed] [Google Scholar]
  51. Ott, J., 1988. Analysis of Human Genetic Linkage. Johns Hopkins University Press, Baltimore/London.
  52. Richtsmeier, J. T., 1987. Comparative study of normal, Crouzon, and Apert craniofacial morphology using finite element scaling analysis. Am. J. Phys. Anthropol. 74 473–493. [DOI] [PubMed] [Google Scholar]
  53. Rogers, J., M. C. Mahaney, S. M. Witte, S. Nair, D. Newman et al., 2000. A genetic linkage map of the baboon (Papio hamadryas) genome based on human microsatellite polymorphisms. Genomics 67 237–247. [DOI] [PubMed] [Google Scholar]
  54. Sato, D., O. Shimokawa, N. Harada, O. E. Olsen, J. W. Hou et al., 2007. Congenital arhinia: molecular-genetic analysis of five patients. Am. J. Med. Genet. A 143 546–552. [DOI] [PubMed] [Google Scholar]
  55. Sherwood, R. J., R. S. Meindl, H. B. Robinson and R. L. May, 2000. Fetal age: methods of estimation and effects of pathology. Am. J. Phys. Anthropol. 113 305–315. [DOI] [PubMed] [Google Scholar]
  56. Sherwood, R. J., D. L. Duren, S. A. Czerwinski, J. Blangero and B. Towne, 2003. Quantitative genetics of modern human craniofacial variation: implications for the interpretation of the hominin fossil record. Am. J. Phys. Anthropol. 120(Suppl. 36): 190. [Google Scholar]
  57. Slavkin, H. C., 1983. Research on craniofacial genetics and developmental biology: implications for the future of academic dentistry. J. Dent. Educ. 47 231–238. [PubMed] [Google Scholar]
  58. Slavkin, H. C., 2001. The human genome, implications for oral health and diseases, and dental education. J. Dent. Educ. 65 463–479. [PubMed] [Google Scholar]
  59. Wagner, G. P., and L. Altenberg, 1996. Complex adaptations and the evolution of evolvability. Evolution 50 967–976. [DOI] [PubMed] [Google Scholar]
  60. Wallis, D. E., E. Roessler, U. Hehr, L. Nanni, T. Wiltshire et al., 1999. Mutations in the homeodomain of the human SIX3 gene cause holoprosencephaly. Nat. Genet. 22 196–198. [DOI] [PubMed] [Google Scholar]
  61. Workman, M. S., L. J. Leamy, E. J. Routman and J. M. Cheverud, 2002. Analysis of quantitative trait locus effects on the size and shape of mandibular molars in mice. Genetics 160 1573–1586. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES