Influence of Brownian Motion on Blood Platelet Flow Behavior and Adhesive Dynamics near a Planar Wall

Abstract

We used the Platelet Adhesive Dynamics computational method to study the influence of Brownian motion of a platelet on its flow characteristics near a surface in the creeping flow regime. Two important characterizations were done in this regard: (1) quantification of the platelet’s ability to contact the surface by virtue of the Brownian forces and torques acting on it, and (2) determination of the relative importance of Brownian motion in promoting surface encounters in the presence of shear flow. We determined the Peclet number for a platelet undergoing Brownian motion in shear flow, which could be expressed as a simple linear function of height of the platelet centroid, H from the surface Pe (platelet) = $\stackrel{.}{\gamma }$ · (1.56H + 0.66) for H > 0.3 μm. Our results demonstrate that at timescales relevant to shear flow in blood, Brownian motion plays an insignificant role in influencing platelet motion or creating further opportunities for platelet-surface contact. The platelet Peclet number at shear rates > 100 s^-1 is large enough (> 200) to neglect platelet Brownian motion in computational modeling of flow in arteries and arterioles for most practical purposes even at very close distances from the surface. We also conducted adhesive dynamics simulations to determine the effects of platelet Brownian motion on GPIbα-vWF-A1 single-bond dissociation dynamics. Brownian motion was found to have little effect on bond lifetime and caused minimal bond stressing as bond rupture forces were calculated to be less than 0.005 pN. We conclude from our results that for the case of platelet-shaped cells, Brownian motion is not expected to play an important role in influencing flow characteristics, platelet-surface contact frequency and dissociative binding phenomena under flow at physiological shear rates (> 50 s^-1).

INTRODUCTION

The distinct size and shape of each of the three blood cell types- erythrocytes, leukocytes and platelets, strongly influence the flow characteristics and adhesive dynamics of these cells within the vasculature. Erythrocytes have a biconcave disc shape with a diameter of 6 - 8 μm and thickness of 2 μm and are highly deformable. The peculiar shape of red blood cells (RBCs) enables the formation of red blood cell aggregates, which flow in the core region of the vessel pushing other blood cells (leukocytes and platelets) to the wall periphery, a phenomenon commonly referred to as margination¹. Radial migration of RBCs away from the vessel wall results in the formation of an RBC-rich core surrounded by a concentric cell-depleted plasma layer². On the other hand, neutrophils, the most abundant class of white blood cells (WBCs) or leukocytes, appear, when unstimulated, as round 8 μm diameter spheres. Leukocytes are observed to deform under moderate-to-high fluid shear rates when tethered to endothelial surfaces. Viscoelastic models are often used to describe the rheological properties of these blood cells. The higher viscosity (or rigidity) and large size of these cells result in their depletion from the smallest microvessels, another well-known observation called plasma skimming. Finally, platelets, the tiniest of the three, are discoid particles approximately 2 μm diameter in size.² In their resting state, these ellipsoidal blood cells are the most viscous of all blood cell types. Platelet cytoplasmic viscosity is two orders of magnitude greater than that of leukocytes,³ and its shape is ten times more resistant to deformation compared to RBCs.⁴ At the time of vascular injury, platelets are recruited from the bloodstream to the exposed subendothelial layer at the lesioned region where they promptly aggregate to seal the wound.

The extent of influence of the platelet shape on (1) duration and frequency of cell-surface contact, (2) magnitude of shear forces exerted on these cells when tethered via receptor-ligand bonds to the subendothelial surface at the site of vascular injury, and (3) platelet collision frequency with other blood cells has not been well characterized to date. One reason for the lack of correlation studies between platelet shape and platelet physiological behavior is that solutions for non-spherical particulate flows are much more difficult to obtain compared to that for suspended spheres because of the complexities in determining the hydrodynamic interactions between non-spherical particles or between a non-spherical particle and a bounding surface. Therefore the number of studies that have addressed unactivated (non-spherical) platelet flow and adhesive characteristics in a bounded space is very few.^5-7

In a previous study⁵, we demonstrated that platelet-shaped particles flowing near a planar wall in linear shear flow exhibit three distinct regimes of flow. Their motion in a fluid near a boundary wall or when tethered to a surface via reversible bonds, is in many aspects different from that of spherical cells⁸. Thus, platelet flow behavior, tethering characteristics and rolling properties on a reactive surface are uniquely different from that of leukocytes. One interesting aspect of blood platelets not yet explored in platelet adhesion/aggregation studies is that these micro-particles fall within the realm of Brownian particles, primarily due to their sub-micron thickness (∼ 0.25 μm)⁹. It is therefore possible that the Brownian motion of a platelet may significantly influence its flow behavior and adhesive dynamics when bound to a surface or to another platelet. Some of the pertinent questions that one would wish to address in this regard are, 1) the characteristics of Brownian motion of a platelet-shaped particle near a bounding wall, 2) the relevance of platelet Brownian motion in the presence of shear flow, and importantly, 3) the influence of Brownian motion on the adhesive dynamics of platelet-surface molecular bonds.

Extensive investigations have been made into the rheological flows of suspensions of spherical and non-spherical Brownian particles, mainly solids of revolution, with ambient flow being either extensional or linear shear.^10-12 A limited number of experimental and theoretical studies have addressed the effects of the presence of a bounding wall on the Brownian motion of immersed particles.^{13, 14} However, none of these studies have considered the specific effects of particle shape on Brownian behavior in proximity of a boundary. Previous investigations of Brownian motion of particles in a bounded region have utilized a single characteristic radius to represent the particle’s size. Thus, the present study is concerned with understanding the influence of the distinctive size and shape of blood platelets and resulting Brownian motion on platelet flow behavior in proximity of a boundary.

In this paper, we address several issues regarding the Brownian motion of a non-spherical particle near a planar wall. First, we determine the average “time until surface-contact”, i.e., the time taken for a platelet undergoing Brownian motion to make contact with the surface as a function of platelet height from the surface in the absence of an external flow field. The results obtained illustrate the role played by Brownian motion in facilitating surface contact as a function of height from the surface. Second, we quantify the relative importance of Brownian motion versus convective motion due to ambient linear shear flow for a range of shear rates and varying heights from the surface. This helps to assess the essentiality of including platelet Brownian motion when modeling platelet flow in various regimes of the vasculature, which are subject to widely different flow conditions. Finally, we describe simulations of platelets having a pre-formed tether bond between the platelet surface glycoprotein receptor GPIbα and surface-bound multimeric plasma glycoprotein von Willebrand factor. Early platelet attachment to the vessel wall involves the platelet glycoprotein receptor GPIbα^15-17. Bond formation of GPIbα with the A1 domain of surface-bound von Willebrand factor (vWF) plays a critical role in initiating platelet surface contact and has been found to occur over a wide range of shear rates up to 6000 s^-1 and higher.¹⁷ In our simulations, the platelet was allowed to undergo translational and rotational Brownian motion, in the absence of any flow (or external shear force) to observe the stressing and resultant rupture of the single platelet-surface tether bond. We studied the dependence of bond lifetime and bond rupture forces on system temperature and initial platelet orientation with respect to the surface. The results obtained from these simulations predict the minimal effects that Brownian motion has on GPIbα-vWF-A1 bond dissociation dynamics.

METHODS

We report on a numerical simulation of a platelet-shaped microscopic particle undergoing translational and rotational Brownian motion near a plane wall in the Stokes regime of flow. The hydrodynamic problem involves the creeping motion of a rigid oblate spheroid in a semi-infinite three-dimensional region bounded by an infinite flat plane at z = 0. Figure 1 depicts the flow geometry of this fluid system. The spheroid is a Brownian particle of dimensions 2 × 2 × 0.5 μm³, with a = 1 μm being the particle major radius. (The blood platelet shape can be approximated as an oblate spheroid of aspect ratio 0.25.⁹) The problem that we solve is the mobility problem, where the Brownian forces and torques acting on the particle are specified, along with the external far-field flow, and the translational and rotational velocities of the particle are to be determined. Since Brownian motion is an unbiased stochastic process with normal distribution, the Brownian forces and torques were calculated using zero mean Gaussian random numbers and a variance equal to $F_{Br}={\mathrm{k}}_{\mathrm{B}}T∕\widehat{a}$,¹⁸ T_Br = k_BT ¹⁹, where k_BT is the product of Boltzmann constant with temperature, and $\widehat{a}$ is defined here as the characteristic radius of the projected area of the platelet cast onto the plane normal to the direction of motion. The Brownian forces and torques were calculated for three directions x, y and z, (see Figure 1) and accordingly a_x, a_y, and a_z, the characteristic radii of the projected area of the platelet on the yz plane, xz plane and xy planes, were determined as needed.

Figure 1.

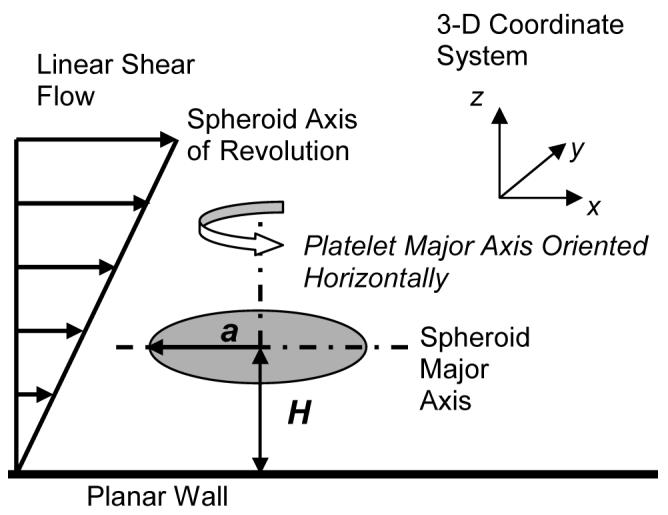
Schematic diagram of the flow geometry in which a single platelet (oblate spheroid of aspect ratio = 0.25) is translating and rotating in linear shear flow near an infinite planar surface. At the instant shown in the figure, the platelet is oriented with its major axis parallel to the surface and its centroid is located at a distance H from the surface.

The Reynolds number of this system is calculated as ${\mathrm{N}}_{\mathrm{RE}}=\stackrel{.}{\gamma }\rho a^2∕\mu =O\left({10}^{-4}\right)⪡1$, where $\stackrel{.}{\gamma }=100{\mathrm{s}}^{-1}$ is the maximum shear rate considered in our simulations, a = 1 μm is the particle radius, μ = 1.0239 g/cm³ is the density of blood plasma, and μ = 1.2 cP is the viscosity of blood plasma. The flow is thus, well within the Stokes regime. When the linear shear flow field is turned off, the Reynolds number is calculated as either

1. N_RE = uρa/ μ = O(10^-7) ≪ 1, where u ∼ 0.62 μm/s is the translational velocity of a platelet oriented horizontally with a centroid height of 0.8 μm from the planar wall, resulting from a Brownian force = k_BT/$\widehat{a}$ (one standard deviation of the zero mean unbiased normal distribution that mathematically defines the platelet’s Brownian motion) acting on the platelet in each of the three x-, y- and z-directions, or

2. N_RE = ωρa² / μ = O(10^-7) ≪ 1, where ω = 0.27 rad/s is the rotational velocity of the platelet situated at a centroid height of 0.8 μm resulting from a Brownian torque = k_BT (one standard deviation of the zero mean unbiased normal distribution that mathematically defines the platelet’s rotational Brownian motion) acting on the platelet about the z-direction.

The Stokes equation is

$$\nabla p=\mu {\nabla }^{2}u,\nabla \cdot v=0,$$ (1)

where, u is the velocity, p is the pressure, μ is the viscosity of the fluid. When the external flow field is turned on, ambient flow is linear shear,

$$u_{\infty }=\stackrel{.}{\gamma }z,$$ (2)

where, $\stackrel{.}{\gamma }$ is the shear rate and z is the distance from the infinite flat wall (Figure 1). There is no slip at the surface of the wall (z = 0) and on the spheroid surface, where the velocity consists only of the rigid body motion of the particle. The computational method employed in our study for calculating the rigid body motion of an oblate spheroid-shaped particle (platelet) is based on the Completed Double Layer - Boundary Integral Equation Method (CDL-BIEM), a boundary elements method proposed by Kim and Karilla¹⁹ to solve the integral representation of the Stokes equation. The derivation and application of this numerical method for particulate flow near a flat wall has been fully described by Phan-Thien et al.²⁰ Below, a brief description of this method is provided; a detailed description is presented elsewhere.²¹

The starting point of the solution technique is the integral representation of the Stokes equation, which when evaluated at the particle surface produces a boundary integral equation (BIE). This BIE when solved for rigid body flow takes the form of a Fredholm integral equation of the first kind, which for a mobility problem is generally ill-posed. ¹⁹ An alternative formulation involves only a compact double layer operator, thus reducing the problem to an integral equation of the second kind. However, this double layer representation is incapable of exerting any force or torque on the fluid and possesses an incomplete range. This is resolved by incorporating into the integral representation, a velocity field arising from a known distribution of point forces and torques placed at the center of the particle, and coupling these forces and torques with the null solutions. Successive convergence of the resulting fixed-point iterative method is ensured however, only after appropriate deflation of the spectral radius of the compact double layer operator.¹⁹ Influence of the proximity of a planar boundary is calculated by incorporating into the imposed velocity field and double layer calculations, the singularity solutions corresponding to reflections (z < 0) of point forces across the plane z = 0.²⁰

Maul et al.²² carried out an experimental and computational study of the sedimentation of “platelets” (hexagonal aluminum flakes) near a wall at low Reynolds numbers to verify the reliability of CDL-BIEM for predicting particle-wall hydrodynamic interactions for the case of a platelet shape, which has two disparate length scales. They showed that this computational method remains efficient and stable and gives good agreement with the experimental results. Further, we extensively validated the flow behavior of a platelet near a wall as predicted by this numerical technique.⁵ We found excellent agreement between (1) the numerical results of Maul et al.²², (2) analytical results of Kim et al²³ and (3) analytical solution of Jeffery²⁴, and our theoretical predictions of platelet 3-D motion near a wall in both quiescent fluid and linear shear flow.⁵

Both particle and wall surfaces were coated with a steric layer of 25 nm to model the glycocalyx layer and surface roughness of biological cell surface membranes.³ It was assumed that the surface roughness layer allowed fluid to easily pass through it and thereby had minimal influence on the nearby flow field. Repulsion between the surfaces results from the interaction of the outer edges of these roughness layers. A very short range repulsive force between the surfaces was included in the model to account for non-specific short-range interactions namely, electrostatic repulsion that strongly dominate when cell membrane roughness layers (glycocalyx) contact one another. This contact force is an empirical relationship of the form

$$F_{\mathit{rep}}=F_0\frac{\tau e^{-\tau \epsilon }}{1-e^{-\tau \epsilon }}$$ (3)

where F₀ =500 N·m, τ = 2000 μm^-1, and ε is the surface-to-surface separation based on the distance between the tips of the opposing surface roughness layers. At distances shorter than 20 nm between the interacting surfaces, the magnitude of repulsive force exerted becomes significant. At 15 nm separation, the repulsive force is 0.0374 pN which is approximately 2 times the Stokes drag force on a 1 μm diameter sphere sedimenting at 1 μm/s in a fluid of viscosity 1 cP. Bell et al. also used an exponential relation, albeit of a different kind, to empirically model the distance-dependent non-specific interaction energy that results in a net repulsion between the cell-cell surfaces.²⁵ Note that except for the calculation of repulsive force acting between two opposing surfaces, the separation distance between the two surfaces was always measured from the edges of the ‘real’ surfaces and not from the outer edge of the steric layers on these surfaces.

Gravitational forces were not included in our calculations although they are of the same order of magnitude as that of platelet Brownian forces since it was desired to explicitly study the effect of Brownian motion on platelet flow behavior in the absence of any other body force. Also, explicitly added lubrication forces to compensate for numerically under-predicted lubrication effects were disregarded in our model since the distances over which the lubrication approximation becomes important are less than the surface roughness layer of thickness 25 nm. Lubrication theory is excluded in many numerical models^{7, 22, 26, 27} that employ the boundary integral technique to obtain solutions for oblate spheroid flow near a wall. A similar numerical model as described above (that did not include Brownian motion calculations) was previously used to study the effects of particle-particle hydrodynamic interactions between flowing and bound leukocytes (spheres) on the adhesive behavior of these cells near the endothelial surface.^{21, 28, 29}

In our platelet numerical model, the particle surface was discretized into 384 QUAD9 elements. Each element has one node at the center and three nodes per edge - totaling 9 nodes per element, giving a total of 1538 nodes on the platelet. Simulations involving breakage of a single pre-assigned bond existing at the start of the simulation between the platelet and the surface were also carried out. The bond between the GPIbα receptor present on the platelet surface and the surface-bound vWF molecule was modeled as a linear spring with endpoints located at the cell periphery and the planar wall. Each bond was initially aligned vertically and positioned in an unstressed state, i.e. the bond length was initially at its equilibrium value. The bond length was approximated as 70 nm, which was calculated by adding the respective sizes of the two participating molecules.^{30, 31} The bond was always placed at the center point of the cell surface facing the wall. The platelet was either given an initial horizontal orientation i.e., its major axis was parallel to the wall or initial vertical orientation i.e., its major axis was normal to the wall. As a result of the particle’s Brownian motion, the platelet-surface bond was pulled and pushed thereby weakening the bond and increasing its probability of dissociation. As the bond length shifts away from its equilibrium (unstressed) length, there is a resulting bond force and torque that is exerted on the cell. The kinetics of bond dissociation of GPIbα and vWF-A1 follow the Bell model characteristics. The Bell model is an expression for the force-dependent dissociation rate of weak noncovalent bonds and is given by

$$k_{\text{off}}\left(F\right)=k_{\text{off}}^o\exp \left[\frac{\gamma F}{k_{B}T}\right]$$ (4)

where, k_off(F) is the bond dissociation (off) rate, k^o_off is the unstressed off-rate, γ is the reactive compliance, F is the applied force on the bond, and k_BT is the product of Boltzmann constant and temperature.³² The reactive compliance represents a transition state position and describes how strongly the dissociation rate changes with force.³² The Bell model parameters (k^o_off = 5.47 s^-1; γ = 0.71 nm) used in this study for GPIbα-vWF dissociation kinetics were obtained from optical tweezer studies conducted by Arya et al.³³

The CDL-BIEM code was written in Fortran 95 and double-precision was used for all calculations. Simulations were executed on dual-core AMD-Opteron SUNFire X2100 (2.4 GHz) processors. Runtime was a function of the time step used and the number of observations required (Brownian motion being a stochastic process, therefore requiring substantial numbers of observations to obtain meaningful average values). Simulations with smaller time steps (microseconds) or when the platelet was placed farther from the surface were computationally expensive requiring large times on the order of weeks for completion. For the case of simple platelet Brownian motion in the absence of external flow a time step of 0.1 s, which allowed translation of not more than 35 nm (1.75% of platelet diameter) in one time step, was found to be suitable in terms of good accuracy and time-constraints. For the case of Brownian motion in shear flow, the time step used depended on the magnitude of shear rate. Finally, time steps used for bond-breakage simulations were reduced to the order of microseconds; the stiffness of the bond spring being responsible for the greater sensitivity of numerical calculations to changes in cell position. For all cases, the time step was appropriately chosen such that the results were convergent, i.e. independent of the time step used. Integration of the double layer during simulations showed reasonably rapid convergence with usually 2-20 iterations necessary to obtain an error of less than 0.0005.

RESULTS

Size, Shape and Proximity of Platelet to Wall Determines Magnitude of Velocity Fluctuations due to Brownian Motion

The platelet disk-like shape is characterized by a much shorter length in one dimension compared to the other two dimensions. This results in asymmetric Brownian motion with the largest cell movement expected along the dimension(s) where the projected (viewable) area of the particle is the smallest. The net Brownian motion of the particle is calculated from the sum of translational motions due to Brownian forces acting in all three directions of the Cartesian coordinate system, and rotational motions due to Brownian torque acting about directions parallel the x-, y- and z-axis passing through the platelet centroid. The presence of a planar boundary in the vicinity of a Brownian particle acts to retard the Brownian motion, albeit unequally in different directions. Figure 2 shows the instantaneous fluctuations at each time step (0.1 s) of the centroid position in all three directions due to Brownian forces acting on a platelet with its major axis initially oriented vertically and with an initial centroid height of 3.0 μm (Fig. 2a) and 1.5 μm (Fig. 2b). During the first 5 seconds of flow the orientation of the platelet does not change much, i.e., it remains more or less vertical and the avg. absolute fluctuations observed are as expected. The motion in the direction of larger projected area (x-direction) is clearly less. Here the initial characteristic radius in the x-direction is twice $(\widehat{a}=1.0\mu m)$ that in the y-direction and z-direction $(\widehat{a}=0.5\mu m)$. When the platelet is brought closer to the wall (Fig. 2b), the avg. velocities in all three directions are affected significantly with the velocity in the z-direction being influenced the greatest (67% change in the z-direction versus 51% change in y-direction and 64% change in the x-direction).

Figure 2.

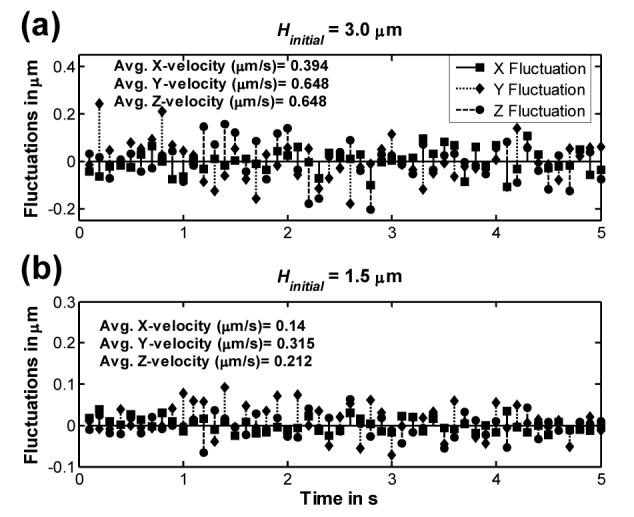
Plot of the distances translated in the x-, y- and z-direction in each timestep of 0.1 s by a platelet undergoing Brownian motion near a surface in a quiescent fluid of viscosity 1 cP in the Stokes regime of flow. Fluctuations in platelet position with respect to its previous position are shown for a period of 5 seconds for (a) an initial platelet centroid height of 3.0 μm and (b) an initial platelet centroid height of 1.5 μm. The average velocities in each direction over the 5 second interval are listed in each plot.

Influence of Brownian Motion on Platelet-Surface Encounters

To study how Brownian motion influences the ability of a platelet to contact the wall, we placed the platelet at various heights from the surface in the absence of an external flow-field and determined the duration of time required for the platelet to contact the surface by virtue of its translational and rotational Brownian motion only. A contact event between the platelet and the surface was deemed to occur when the platelet approached the surface to within a distance sufficiently close for a reaction, i.e., binding of platelet surface receptor GPIbα to bound vWF on the surface, to proceed. Physical contact between the edges of the surfaces is not required for binding between GPIbα and vWF.³⁴ A surface-to-surface separation distance within 120 nm, which is equal to the sum of the glycocalyx roughness layers on both surfaces and the bond length of GPIbα-vWF, was set as the criteria that defined a ‘reactive’ contact event. The platelet was initially positioned at each height with its major axis oriented horizontally, this being the most stable orientation of a platelet during flow⁵ (this orientation will occasionally be referred to as ‘horizontal orientation of the platelet’ in the remainder of this article). Figure 3 shows the average time taken for a platelet at an initial centroid height H_initial to make surface-contact as a consequence of Brownian motion. Due to the randomness of platelet Brownian motion, it was necessary to sample approximately 200 surface-contact observations for each initial platelet centroid height to obtain meaningful H_initial average values. Note that for a particle of this size and shape, it takes an avg. of 57 seconds to achieve surface contact when the platelet centroid is initially situated at a distance of 0.5 μm from the surface, which is greater by three orders of magnitude than the convective timescale $(1∕\stackrel{.}{\gamma })$ for a shear rate of 50 s^-1. For H_initial = 2.0 μm, the average ‘time to contact’ T_c = 21 minutes and for H_initial = 4.0 μm, T_c = 73 minutes, which is much slower than timescales relevant to physiological blood clotting. Based on these large ‘times to contact’, one may expect that convective processes dominate the transport of platelet cells from the peripheral regions of the bloodstream to the subendothelium at the injured vascular wall surface. The time to contact the surface T_c has a quadratic dependence on H_initial, which is expected for a diffusive process. However, very close to the surface, for H_initial < 1.0 microns, this trend disappears since at closer distances there co-exist two important mechanisms for cell-surface contact: translation and rotation of the cell body. At larger initial distances from the surface, translational motion appears to be the dominant mechanism for inducing contact with the wall.

Figure 3.

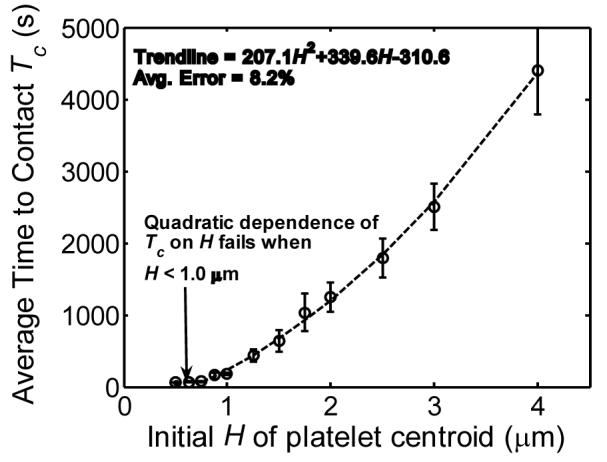
Plot of the average time taken T_c for a platelet at an initial height H to contact the surface when undergoing translational and rotational Brownian motion in a quiescent fluid in the Stokes regime of flow. The dashed trendline does not include data points at initial H = 0.5 μm and 0.625 μm.

For initial platelet centroid heights close to the surface, i.e. H_initial < 1.0 μm, platelet-surface contact was realized for all 200 simulation runs. However, for H_initial ≥ 1.0 μm, a finite number of platelets drift far away from the surface. While these cells may be expected at a later time to return back to their original starting point and therefore encounter the surface as time t → ∞, in order to have a finite end to the simulations, we terminated individual simulations once height of the platelet centroid reached H = 25 μm. This value was chosen considering that the average inner diameter of arterioles is 50 μm.³⁵ Therefore a platelet that went beyond 25 μm from the surface was considered to have crossed the centerline of the vessel. As expected, the probability for platelet encounters with the surface was observed to decrease with increasing H_initial, as the percentage of platelets that drifted away and did not return was 1.5, 5.5 and 12 for H_initial = 1.5, 2.0 and 4.0 respectively. ‘Time until contact’ histograms shown in figure 4 show that T_c for platelets initially placed close to the surface show a log normal distribution about the mean. In contrast, T_c distributions for platelets positioned far from the surface have an extended tail at one end since platelets at greater distances from the surface have increasing freedom to translate and rotate in all directions without contacting the surface.

Figure 4.

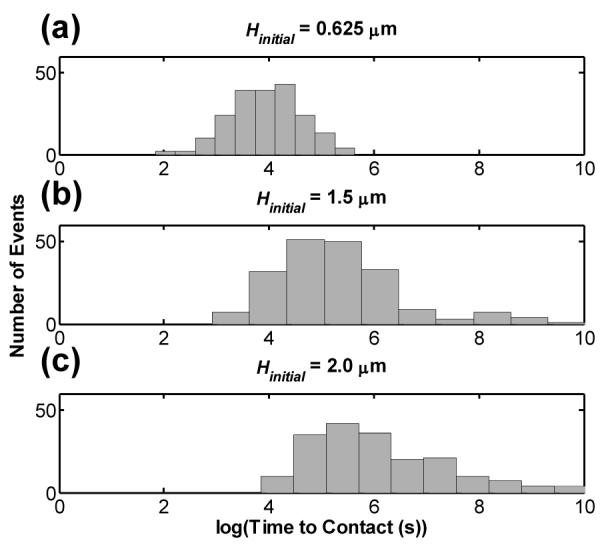
Histograms of the log of time taken T_c for a platelet to contact the surface when undergoing translational and rotational Brownian motion in a quiescent fluid for three different initial heights H: (a) H_initial = 0.625 μm, (b) H_initial = 1.5 μm, and (c) H_initial = 2.0 μm, representing approximately 200 cell-surface contact events for each H_initial.

Importance of Platelet Brownian Motion in the Presence of Shear: Convective versus Diffusive Processes

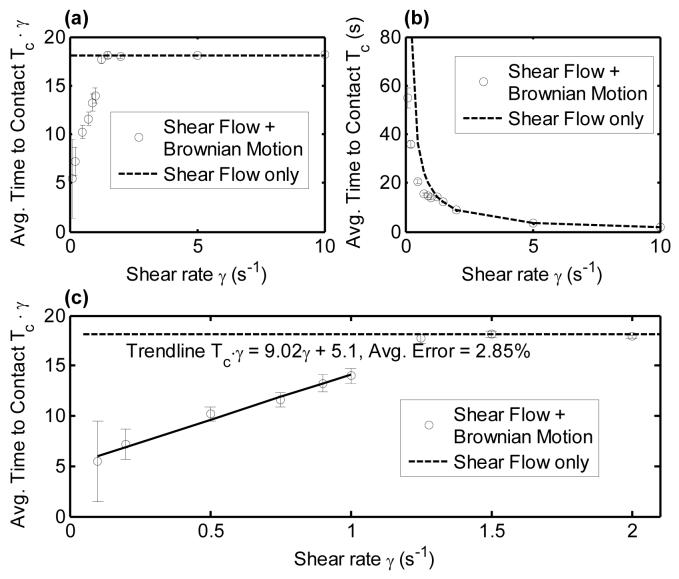
To determine the relative importance of Brownian motion of a platelet in the presence of convective fluid flow, the external flow field was activated in the simulation and a Brownian platelet at H_initial = 0.8 μm and with an initial horizontal orientation was subjected to a range of linear shear flow rates. This initial height was chosen since it lies within the range of platelet centroid distances from the surface (0.75 - 1.1 μm) that result in transient platelet contact with the surface in linear shear flow.⁵ For starting heights below 0.75 μm and an initial horizontal orientation, the platelet flows approximately parallel to the surface and will travel for long distances without making contact with the wall.⁵ The time taken for a platelet to contact the surface was calculated with or without platelet Brownian motion, while shear flow was present. In Figure 5 (a), (b) and (c), the ‘time to surface-contact’ T_c when platelet Brownian motion is absent is shown by the dashed line. Creeping flow streamlines are independent of the shear rate imposed in the system, since the Stokes equation and continuity equation are linear and therefore when T_c (Brownian motion absent) is nondimensionalized with shear rate, we obtain a straight line in Figures 5(a) and 5(c). When platelet Brownian motion was included, 200 data points were collected for each shear rate to determine the average cell-surface contact behavior. As seen from Figure 5, for $\stackrel{.}{\gamma }\le 1{\mathrm{s}}^{-1}$ the effect of Brownian motion is evident, as it leads to substantial reductions in the T_c (compared to shear-only cases). Above $\stackrel{.}{\gamma }=5{\mathrm{s}}^{-1}$, T_c (Shear flow + Brownian motion) is indistinguishable from T_c (Shear flow only). Over the range of shear rates from 1 s^-1 to 5 s^-1 there is a transition from dominance of Brownian (diffusive) motion to dominance of convective motion on the value of T_c. At γ > 5 s^-1, Brownian motion has negligible influence on the platelet’s ability to contact the surface. Note that these shear rate values are extremely low compared to physiological shear rates. For example wall shear rates in the veins, where flow is lowest in the body, ranges from 20 - 200 s^-1, while in large arteries, they range from 300 to 800 s^-1.³⁶ Arteriolar blood flow experiences even higher shear stresses ranging from 500 to 1600 s^-1.³⁶

Figure 5.

Plots of the time until surface contact T_c as a function of shear rate for a Brownian platelet at an initial centroid height of 0.8 μm in linear shear flow. The dashed line indicates ‘time until surface contact’ for platelets undergoing linear shear flow only, i.e. Brownian force and torque were not included in the mobility calculations. In (a) ‘Time to contact’ the surface for a platelet is non-dimensionalized with shear rate, and in (b) ‘Time to contact’ is kept in dimensional form. Plot (c) is a magnified version of 5(a) with a trendline plotted to demonstrate the simple linear dependency of non-dimensionalized ‘time to surface contact’ on shear rate when Brownian motion (diffusion) is the dominant mode of cell transport to the surface.

The Peclet number (Pe = l · u/D_AB = u_convection/u_diffusion), which provides a measure of the relative timescales of convective transport to diffusive transport, is, for this fluid system, a function of distance from the surface. Pe for a platelet undergoing Brownian motion in linear shear flow is given by the following expression showing linear dependence on H as calculated from our computational model:

Platelet $\mathrm{Pe}=\stackrel{.}{\gamma }\cdot (1.56H+0.66)$ for H > 0.3 μm, which estimates Pe with an average error of 0.51%. This expression was obtained with the following considerations: (1) the platelet is oriented horizontally, and (2) translation due to Brownian motion occurring in the x-direction is calculated based on a Brownian force equal to the magnitude of the variance of the normal distribution = k_BT/$\widehat{a}$. The platelet Peclet number for shear rates 0.1 - 100 s^-1 range from 0.19 - 191.42 at H = 0.8 μm. At 100 s^-1 shear rate, the average x-velocities due to Brownian motion are approximately 0.75% that due to shear flow, at the surface, and reduce to 0.25% at 2 μm from the surface, demonstrating the dependence of Peclet number on proximity of the wall.

Influence of Brownian Motion on Bond Lifetimes and Bond Rupture Forces

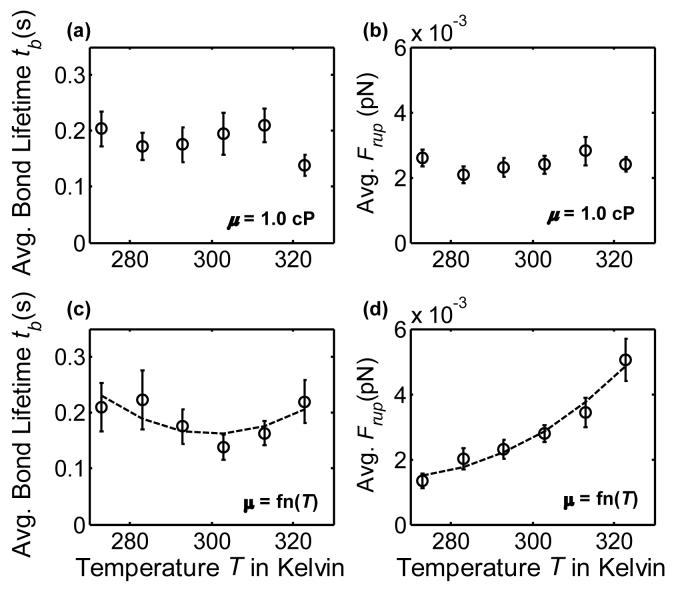
To determine the effects of Brownian motion on the adhesive dynamics of platelet-surface GPIbα-vWF-A1 bonds, the simulation was initiated with the platelet being bound to the surface via a single cell-surface GPIbα-vWF-A1 bond having unstressed bond length (Figure 6). Bond lifetimes and bond rupture forces were obtained for a range of temperatures from 273 K to 323 K. In one set of simulations (Figure 7(a) and 7(b)) the viscosity of the medium was kept constant at 1.0 cP in order to isolate the effects of temperature-dependent Brownian motion on bond dissociation dynamics independent of variation in fluid properties. In a second set of simulations (Figure 7(c) and 7(d)), the viscosity of the fluid was varied as a function of the temperature. The timestep used for these sets of simulations was 1.5 × 10^-5 s, which was found to be the largest time increment that provided consistent and convergent results. Due to the absence of a far-field flow and the miniscule motions of the platelet resulting from Brownian forces and torques, platelet-surface dynamics could be satisfactorily resolved at the chosen time step at all platelet heights without the need to incorporate a dynamic time step into the computational algorithm. These sets of simulations were found to be computationally expensive since Brownian motion produced very small flow velocities within these time increments resulting in minimal bond stressing. A bond breakage event took on average 2-3 days of computational time to occur.

Figure 6.

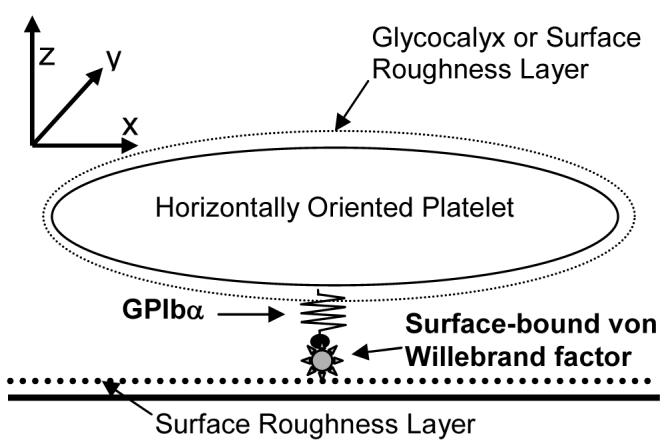
Schematic diagram of a horizontally-oriented platelet bound to the surface via a single GPIbα-vWF bond. Both the surface and platelet are coated with a surface roughness layer of 25 nm.

Figure 7.

Plots of GPIbα-vWF-A1 bond lifetimes and bond rupture forces for a platelet undergoing Brownian motion in a quiescent fluid. (a) Bond lifetimes when the fluid medium has constant viscosity = 1.0 cP. (b) Bond rupture forces when the fluid medium has constant viscosity = 1.0 cP. For both figures 7(a) and 7(b), 41 observations were collected for each temperature. (c) Bond lifetimes for a fluid medium with temperature-dependent viscosity. (d) Bond rupture forces for a fluid medium with temperature-dependent viscosity. For both figures 7(c) and 7(d), 37 observations were collected for each temperature. Quadratic trendlines drawn in figures 7(c) and 7(d) are within 10% and 7.8% average error respectively.

From Figure 7(a) - (b) it is evident that no regular trend of bond lifetime t_b and bond rupture force F_rup with increase in ambient temperature exists. There are several simultaneous non-linear dependencies of bond dissociation on temperature: (1) the Bell model (Equation 4) predicts that the bond half-life increases with temperature, i.e. the dissociation rate constant decreases as the system temperature is raised, while (2) Brownian motion intensifies with temperature increase. Figure 7(d) shows a monotonically increasing trend of F_rup with T, which is expected since lower solution viscosities and higher temperatures lead to more vigorous Brownian motion and therefore greater bond stress. One can easily derive the unstressed bond lifetime = 1/ k^o_off (unstressed off-rate) = 1/5.47 = 0.183 s. It is observed from Figures 7(a) and 7(c) that the lifetimes of the single cell-surface bond with Brownian motion present are similar to the unstressed bond lifetime. Brownian motion, thus appears to have a marginal effect on the force-dependent dissociation rate. Additionally, the bond rupture forces resulting from Brownian motion are all < 0.005 pN, again emphasizing the minimal effect Brownian motion has on bond breakage dynamics. On the other hand, with external flow at a shear rate of 100 s^-1, our simulations predict bond rupture within 0.3 ms and bond rupture forces of 50 - 200 pN (data not shown). The number of bonds that ruptured due to Brownian motion in a compressed state for both sets of simulations: (1) no change in medium viscosity (μ = 1.0 cP) and (2) μ = function(T) were nearly half (49% and 56% respectively). Similar results were also observed for two other sets of simulations where the initial platelet orientation was such that the platelet major axis was normal to the surface (data not shown). In this case the bond was attached at the central point of the platelet edge facing the surface and a smaller timestep of 3 × 10^-6 s was necessary for these simulations. Note that the time-intensive nature of these simulations prevented us from obtaining a larger number of observations of bond rupture events. Perhaps a more distinct trend in bond lifetime or bond rupture force with temperature would be observable if a greater number of observations (e.g. at least 100 - 200) were collected.

CONCLUSIONS

In this paper, the influence of Brownian motion of a blood platelet-shaped particle on its flow behavior close to a planar surface was studied using the Platelet Adhesive Dynamics simulation. We quantified (1) the platelet’s ability to contact the surface when undergoing Brownian motion in the absence of an external flow field, and (2) the relative importance of Brownian motion in promoting surface encounters in the presence of shear flow. Our results demonstrate that at timescales relevant to shear flow in blood, Brownian motion plays a negligible role in influencing platelet motion or creating further opportunities for platelet-surface contact. The platelet Peclet number at shear rates > 100 s^-1 is large enough (platelet Pe > 200) to neglect platelet Brownian motion even at very close distances to the surface for most practical purposes.

These results naturally led to the next important question on the effects of platelet Brownian motion on molecular binding phenomena. It was found through our simulation studies that Brownian forces and torques acting on a platelet resulted in negligible reduction of GPIbα-vWF bond lifetimes and also minimal stressing of the bond. The bond rupture forces plotted in Figures 7(b) and 7(d) average to 0.0034 pN. This magnitude of force, 3.4 fN, is approximately 0.2 times the Stokes drag force on a 1 μm diameter sphere sedimenting at 1 μm/s in a fluid of viscosity 1 cP. On the other hand, bond rupture forces in shear flow at γ = 50 s^-1 are found from calculations based on experimental studies to be approximately 36 pN, ³⁷ - roughly 10,000 times greater than the bond rupture forces stemming from Brownian motion of a platelet. Bell³² calculated that a theoretical critical force of 40 pN/bond was required to detach a cell stuck to a surface with representative antigen-antibody bonds (equilibrium constant in solution = 10⁶ M^-1) having a density of 1000 bond/μm².

Yago and co-workers showed that Brownian motion is one of three transport mechanisms that promote L-selectin binding with P-selectin glycoprotein ligand-1 (PSGL-1) in spherical cell (leukocyte)-surface geometries.³⁸ The flow behavior of spherical particles in shear flow is considerably different from that of platelets. Spheres do not exhibit lateral movement (translation normal to the wall) in creeping flow. Spheroids, on the other hand, not only translate laterally during rotation in shear, but by virtue of their non-sphericity, have different cell-surface clearances (minimum distances of approach) for different angular orientations with respect to the surface. When flowing near a wall, spheroids may be able to contact the surface in certain angular orientations, but not necessarily in other orientations. Freestream platelets rotating near the surface make contact for rather short periods of time, whereas spheres can skim the surface, i.e. flow over the surface at close clearances, for longer periods of time. For spherical cells having sizes of the order of 1 μm and flowing close to the surface, Brownian motion may be expected to be a dominant factor since it may provide greater surface contact opportunities.

For a range of initial platelet centroid heights from the surface, flow at physiological shear rates ensures quick and timely cell-surface contact.⁵ In a previous study, we showed that there is a third regime of flow (wobble flow regime) for platelet-shaped particles, in which, at small initial centroid heights from the surface (H_initial < 0.75 μm), platelets glide over but do not contact the surface.⁵ However, this regime exists only if flow exhibits symmetry about the flow plane (i.e. there is no rotation about the x-axis).⁵ Brownian motion will then have the role of perturbing the symmetry of flow thereby converting symmetric flows of platelets into fully 3-D flows, i.e. Brownian motion will act to destabilize the smooth wobble flow and force a platelet demonstrating wobble flow behavior to eventually contact the surface. Once a surface-contact occurs, full rotational orbits are realized with accompanied repeated transient platelet-wall contacts.⁵ Symmetric flows are idealistic in nature and not physiological considering the myriad of other cells and molecules present in the surrounding blood that will influence the platelet’s three-dimensional flow path. Based on results shown in Figures 3 and 5, one observes that not only is Brownian motion a comparatively slow process, but also at physiological shear rates and higher, it has negligible effect on platelet flow paths and therefore on the platelet’s ability to contact the surface. Very close to the surface, the wall strongly retards translational and rotational motion, as discussed at length by Mody and King⁵ and as evident from Figure 2 in this paper. At close cell-surface clearances and at timescales relevant to blood flow, platelet Brownian motion will have limited effectiveness in redefining the platelet flow path. For example, a platelet initially at 1.3 μm from the surface in linear shear flow of 100 s^-1, undergoes 14 rotations during the first two seconds of flow. Including platelet Brownian motion in the simulations results in a change in the z-position of the centroid by 0.002 μm and in the y-position of the centroid by 0.01 μm at the end of this duration of flow, over a distance of 250 μm translated by the platelet in the x-direction (Figure S1). Here, Brownian motion does not affect the platelet’s trajectories or the rotation frequency in any significant way.

Brownian motion is most relevant in the case of platelet flow when the Peclet number is approximately equal to or less than 1. For linear shear flow, this corresponds to a low shear rate < 5 s^-1. Since shear flow causes complete particle rotation about the y-axis, and Brownian motion causes erratic motion of the particle, a platelet is expected to sample a wide range of orientations with respect to the surface as it translates under these conditions of flow. Platelets are not observed to flow in linear shear with their axis of revolution parallel to the y-direction⁶. This is a highly unstable orientation and this situation is also not relevant to blood cell adhesion since the particle orientation with respect to the surface does not change during rotation in the fluid. This is similar to the case of a translating and rotating sphere in shear flow. The most stable orientation for unactivated platelets, as observed in in vitro parallel-plate flow chamber experiments by us⁶, is when their major axis is oriented parallel to the surface (horizontal orientation). Platelet rotational velocity is highly non-linear with respect to its orientation, and the rotational velocity is large when the axis of revolution of the platelet becomes nearly parallel to the flow direction^{5, 6}. Thus, platelets remain in tilted orientations for rather short periods of time as compared to the time in which they maintain stable horizontal orientations. Quantifications are available in a previous publication⁵; they are not restated here since the physiological relevance of platelet orientation is discussed here only in qualitative manner. In the presence of shear flow, while a platelet can sample all different orientations, the most stable and hence most probable orientation that will be adopted is one in which the tilt about the x-axis is zero. Since Brownian motion is an unbiased stochastic process, and shear flow of platelets near a surface in Stokes flow does not result in a drift towards or away from the wall, we would expect the average drift of the platelet towards or away from the wall to be zero. Brownian motion enhances platelet-surface contact by forcing the platelet to assume an orientation different from the ‘horizontal’ or most stable one faster than the rotation effect caused by shear flow. While the average enhanced platelet-surface encounter frequency for a range of very low shear rates can be determined for long times, Figure 5 gives an estimate of this, albeit for single platelet-surface contact events.

In summary, we found that platelet motion near a surface, frequency of surface contact and bond dissociation dynamics measured by bond lifetimes and bond rupture forces were negligibly affected by including platelet Brownian motion into our numerical computational model. Also at shear rates typical of healthy blood flow, fluid convective motion was found to be the primary dominant mechanism for transporting cells versus diffusive processes due to Brownian motion as evinced from the Peclet numbers calculated for the shear rates of interest. Based on these results, one may conclude that blood platelet studies modeling platelet flows, collisions of platelets with other blood cells and surfaces, platelet-surface adhesion and platelet-platelet aggregation at shear rates typical of the arteries and arterioles may disregard platelet Brownian motion under usual cases. However, Brownian motion could possibly play an important role in influencing platelet flow behavior under certain pathological conditions of flow such as in regions of recirculating flow found proximal or distal to a stenosed region of the artery where flow velocities and shear rates are small. Brownian motion of a platelet may also be important when the cell velocities are close to zero even though flow of the fluid is finite such as in extensional flows (pure straining flows) at a vessel branching site when the platelet is located at the origin where flow is divergent. At pathological shear rates greater than 6000 s^-1, platelet GPIbα binding with surface-bound vWF leads to formation of membrane tethers that sever to produce procoagulant spherical microparticles³⁹ with diameters ranging from 50 to 100 nm. Here, one may need to consider Brownian motion, at both at physiological and pathological shear flow rates, as an important influencing factor in the motion and adhesive binding of these platelet-derived microparticles, which are believed to promote thrombus formation. Future extensions of this work may include the modeling of lateral diffusion of receptors in the cell membrane, which is expected to positively influence platelet-platelet and platelet-surface binding. Finally, while platelet flow behavior may not be affected by Brownian motion to any significant extent in shear flow in blood vessels, multiparticle interactions between cells, and flow characteristics such as pulsatile flow are expected to play important roles in influencing the flow path of platelets and other blood cells; these are subjects of current study in our lab.