Role of Mg²⁺ in Hammerhead Ribozyme Catalysis from Molecular Simulation

Abstract

Molecular dynamics simulations have been performed to investigate the role of Mg²⁺ in the full-length hammerhead ribozyme cleavage reaction. In particular, the aim of this work is to characterize the binding mode and conformational events that give rise to catalytically active conformations and stabilization of the transition state. Toward this end, a series of eight 12 ns molecular dynamics simulations have been performed with different divalent metal binding occupations for the reactant, early and late transition state using recently developed force field parameters for metal ions and reactive intermediates in RNA catalysis. In addition, hybrid QM/MM calculations of the early and late transition state were performed to study the proton-transfer step in general acid catalysis that is facilitated by the catalytic Mg²⁺ ion. The simulations suggest that Mg²⁺ is profoundly involved in the hammerhead ribozyme mechanism both at structural and catalytic levels. Binding of Mg²⁺ in the active site plays a key structural role in the stabilization of stem I and II and to facilitate formation of near attack conformations and interactions between the nucleophile and G12, the implicated general base catalyst. In the transition state, Mg²⁺ binds in a bridging position where it stabilizes the accumulated charge of the leaving group while interacting with the 2′OH of G8, the implicated general acid catalyst. The QM/MM simulations provide support that, in the late transition state, the 2′OH of G8 can transfer a proton to the leaving group while directly coordinating the bridging Mg²⁺ ion. The present study provides evidence for the role of Mg²⁺ in hammerhead ribozyme catalysis. The proposed simulation model reconciles the interpretation of available experimental structural and biochemical data, and provides a starting point for more detailed investigation of the chemical reaction path with combined QM/MM methods.

Introduction

The discovery that molecules of RNA could catalyze complex reactions with efficiency that rivaled many protein enzymes stimulated a new field of research directed toward the understanding of the mechanism of RNA enzymes or ribozymes. This field has attracted a wide range of experimental and theoretical interest owing to the importance of ribozymes in biology,^1–3 their evolutionary implications^4–8 and potential impact on the design of new drugs⁹ and biomedical technology.^{10, 11}

The hammerhead ribozyme¹² is an archetype system to study RNA catalysis.^{1, 3} Despite a tremendous amount of experimental and theoretical effort,^1,3,12,14 the details of the hammerhead ribozyme mechanism have been elusive. In particular, one of the main puzzles involves the apparent inconsistency between the interpretation of thio substitution^{15, 16} and mutational¹⁴ experiments with available crystallographic structural information of the minimal hammerhead sequence.^17–19 Biochemical experiments have been interpreted to suggest that a pH-dependent conformational change must precede or be concomitant with the catalytic chemical step, including a possible metal ion bridge between the A9 and scissile phosphates. This is inconsistent with crystallographic data for the minimal hammerhead motif,^17–19 where A9 and scissile phosphates are found to be ~20 Å apart. Moreover, the function of the 2′OH group of G8 remains unclear from this data.

Very recently, the crystallographic structure of a full-length hammerhead sequence has been determined at 2.2 Å resolution.²⁰ The naturally occurring full-length hammerhead sequence exhibits enhanced catalytic activity and different metal ion requirements relative to the minimal motif.²¹ The crystal structure shows the A9 and scissile phosphates in close proximity,²² (see the stereoview of the active site, Figure S1 of Supporting Information) consistent with the interpretation of thio effect measurements,15 and G8:O_2′and G12:N₁ poised to act as a general acid and base, respectively, consistent with photocrosslinking experiments²³ and mutational data.¹⁴ However, the native divalent Mg²⁺ ions required for catalysis were not resolved in this structure. Very recently, a crystal structure was obtained in the presence of the softer divalent cation Mn²⁺ that allowed the identification of a divalent binding site involving A9 and G10.1 near the active site.²⁴

It remains an open question, however, as to what conformational events and changes in metal binding may occur in proceeding to the transition state from a precatalytic active conformation. Molecular simulation offers a powerful tool to probe the structure and dynamics along the chemical reaction coordinate and the role played by divalent metal ions in stabilizing the transition state. Several fairly short (approximately 1.2 ns or less) molecular dynamics simulations, based on the minimal sequence hammerhead structures, have been reported,^25–28 but to date there has only been communication of preliminary simulation results of the full-length hammerhead sequence with the active site in an in-line conformation, and some speculation as to the divalent metal binding mode.²⁹

The purpose of the present work is to explore in detail the role of Mg²⁺ ions in stabilizing the active conformation and proceeding to the transition state, based on the new crystallographic structure of the full-length hammerhead ribozyme with a divalent metal bound near the active site. Toward this end, we have performed a series of eight 12-ns classical molecular dynamics simulations and two 1-ns combined quantum mechanical/molecular mechanical (QM/MM) simulations with different metal ion occupations at various stages along the chemical reaction coordinate. From these simulations, we present a model for the Mg²⁺ binding in the reactant and transition state and propose a role this cation plays in catalysis that is consistent with available biochemical and structural data. The results of the present work provide insight into the hammerhead ribozyme mechanism and a starting point from further study of the chemical mechanism with QM/MM methods.

The paper is organized as follows. The Methods section describes the computational details of the MD simulations, QM/ MM, and supporting DFT calculations. The Results and Discussion section presents simulation results for the reactant state, activated precursor, early and late transition state mimic simulations, QM/MM simulations of the early and late transition states, and DFT calculations for Mg²⁺ and Mn²⁺ metal ion binding affinities with RNA ligands, and discusses the mechanistic implications of these results with regard to the role of Mg²⁺ ions in hammerhead ribozyme catalysis. The Conclusion section summarizes the main points of the paper and outlines future research directions.

Methods

This section outlines the molecular simulation methods and model construction. A complete description of the technical details is provided in the Supporting Information.

Mg²⁺ Ion Binding Modes in the Active Site

The Mg²⁺ binding sites were not resolved in the original full-length hammerhead RNA structure.²⁰ To explore possible Mg²⁺ binding modes in the active site, two initial positions were selected based on biochemical, theoretical, or crystallographic sources.^15,20,24 The first initial Mg²⁺ binding site, designated the “C-site’’, is an implicated metal-ion binding site based on a very recent hammerhead RNA structure with resolved metal and solvent positions²⁴ in which a Mn²⁺ cation directly coordinates to both A9:O_2P and G10.1:N₇. The second initial Mg²⁺ binding site, designated the “Bridging’’ site, is one in which the Mg²⁺ ion bridges the A9 and scissile phosphates, directly coordinating the two nonbridging O_P2 atoms that are 4.3 Å apart in the crystal structure.²⁰ This type of coordination was inferred both from the O–O distance in the crystal structure and also the thio/rescue effect experiments that suggest a single divalent metal might bridge these positions in the transition state.^15,20,29 No metal ion at this position, however, has yet been observed crystallographically.¹⁵

MD Simulation Setup

A total of eight classical force field MD simulations were performed that involve different points along the catalytic reaction pathway including the reactant state (RS), reactant state activated precursor where the 2′OH nucleophile is deprotonated (RS⁻), early transition state (ETS) and late transition state (LTS) mimics. In addition, the presence and initial position of the Mg²⁺ ion in the active site was also varied so as to include either no bound Mg²⁺ ion (apo-), Mg²⁺ ion bound at the C-site (c-) or in a bridging position (b-) as described above. The parameters for the Mg²⁺ ion and the reactive intermediates in the simulations have been described in detail elsewhere,^29,30 and a summary of the different simulations and their abbreviations are provided in Table 1. All the simulations were performed with CHARMM³¹ (version c32a2) using the all-atom CHARMM27 nucleic acid force field^{32, 33} with extension to reactive intermediate models (e.g., transition state mimics)³⁰ and TIP3P water model.³⁴ Initial structures used in the simulations were based on the crystallographic structure of the full-length hammerhead ribozyme of Martick and Scott.²⁰ The positions of hydrogen atoms were determined using HBUILD facility in the program CHARMM³¹ (version c32a2).

Table 1.

Summary of Simulations Discussed in the Present Work^a

abbreviation	Mg2+ ion	state	time (ns)	potential
apo-RS	absent	reactant	12.0	CHARMM
b-RS	bridging	reactant	12.0	CHARMM
c-RS	C-site	reactant	12.0	CHARMM
c-RS−	C-site	deprotonation reactant	12.0	CHARMM
b-ETS	bridging	early TS mimic	12.0	CHARMM
b-LTS	bridging	late TS mimic	12.0	CHARMM
c-ETS	C-site	early TS mimic	12.0	CHARMM
c-LTS	C-site	late TS mimic	12.0	CHARMM
b-ETSQM	bridging	early TS	1.0	QM/MM
b-LTSQM	bridging	late TS	1.0	QM/MM

^aSimulation for the full-length hammerhead differ by their initial placement of the Mg²⁺, protonation state of the 2′OH of C17, and progression along the reaction coordinate. A total of eight 12-ns simulations were performed with the all-atom CHARMM27 nucleic acid force field³², ³³ with extension to reactive intermediate models,³⁰ and two 1-ns simulations using a QM/MM potential using the AM1/d-PhoT Hamiltonian⁴³ for phosphoryl transfer. Initial Mg²⁺ placement was either in the bridging position²⁹(coordinated to the A9 and scissile phosphates) or the “C-site’’ position²⁴ (coordinating the A9 phosphate and N₇ of G10.1)

With hydrogen atoms built and the Mg²⁺ cation position established, the ribozyme was immersed in a rhombic dodecahedral cell of 10,062 pre-equilibrated TIP3P³⁴ water molecules centered about the active site and pruned such that any water molecule within 2.8 Å from the solute was removed. The ion atmosphere consisted of Na⁺ and Cl⁻ ions that were added at random positions to neutralize the system and reach the physiologic extracellular concentration of 0.14 M. The ions positions were kept initially at least 4.7 Å away from any solute atoms. The resulting system (the reactant state) contained 9053 water molecules, 82 Na⁺ and 23 Cl⁻ ions, and 2021 RNA atoms.

Periodic boundary conditions were used along with the isothermal–isobaric ensemble (NPT) at 1 atm and 298 K using an extended system pressure algorithm³⁵ with effective mass of 500.0 amu and Nosé-Hoover thermostat ^36,37 with effective mass of 1000.0 kcal/mol-ps,² respectively. The smooth particle mesh Ewald (PME) method^{38, 39} was employed with a κ value of 0.35 Å⁻¹, 80 FFT grid points for each of the lattice directions, and a B-spline interpolation order of 6. Nonbonded interactions were treated using an atom-based cutoff of 10 Å with shifted van der Waals potential. Numerical integration was performed using the leapfrog Verlet algorithm with 1 fs time step.⁴⁰ Covalent bond lengths involving hydrogen were constrained using the SHAKE algorithm.⁴¹

The solvent was equilibrated with an annealing procedure (see Supporting Information for details), after which the whole system was energy-optimized, and unconstrained dynamics simulation began from 0 K under constant pressure of 1 atm. The temperature was increased to 298 K at the rate of 1 K/ps and then kept fixed at 298 K. The same equilibration process was applied for each simulation. A total of 12 ns of unconstrained dynamics was performed for each of the eight simulations (reactant with and without Mg²⁺, early TS mimic and late TS mimic), the last 10 ns of which were used for analysis. The motions and relaxation of solvent and counterions are notoriously slow to converge in nucleic acid simulations,⁴² and careful equilibration is critical for reliable simulations. In summary, for each simulation, a total of 3 ns of equilibration (1 ns of solvent relaxation and 2 ns of solvent and structure relaxation) has been carried out before 10 ns of data sampling.

QM/MM Simulation Setup

QM/MM simulations on the early and late transition state mimics were set up as follows. Initial structures were taken from snapshots of the classical molecular dynamics simulations after 2 ns production simulation, and the O_2′-P and P–O_5′ distances of the scissile phosphate were harmonically restrained with a force constant of 1000 kcal/mol/Ų and equilibrium distances of 2.010 and 1.850 Å, respectively, for the early TS mimic and 1.856 and 2.382 Å, respectively, for the late TS mimic. The system is partitioned into a quantum mechanical (QM) region constituting the active site that is represented by the AM1/d-PhoT Hamiltonian⁴³ and the modified AM1 magnesium parameters of Hutter and co-workers.⁴⁴ The total number of solute and solvent atoms and setup of periodic boundary conditions, etc., were identical to the classical simulations. The QM subsystem was defined as the 43 atoms around the active site and included the scissile and A9 phosphates, parts of the nucleophilic and leaving ribose rings, and Mg²⁺ ion and coordinated waters. The generalized hybrid orbital (GHO) method⁴⁵ is used to cut a covalent bond to divide the system into QM and MM region. Full electrostatic interactions were calculated using a recently introduced linear-scaling QM/MM-Ewald method.⁴⁶

Density-Functional Calculations

At the time of initiation of this study, there was no direct structural information from X-ray crystallography about the divalent metal ion binding sites in the full-length hammerhead ribozyme.²⁰ For this reason, we explored plausible divalent metal ion binding in the activated ground state, an early and late transition state mimic simulations, using the native Mg²⁺ ion as a basis for the model.²⁹ Only very recently has a solvent structure of the full-length hammerhead ribozyme become available²⁴ with divalent Mn²⁺ positions unambiguously determined. This was made possible by crystallization of the more electron-rich Mn²⁺ ions that possess a distinct X-ray absorption K edge at 1.896 Å. In the late stages of preparation of the manuscript, we have included comparative analysis with this new structure. The activity in the presence of Mg²⁺ and Mn²⁺ are similar (slightly faster in the presence of Mn²⁺), and there is currently no evidence that suggests the mechanism is significantly altered by interchange of these metal ions. Nonetheless, it should be expected that the specific binding affinities and modes of these ions may be somewhat different.

The molecular mechanical force field model used in the present study lacks explicit polarization and molecular orbital interactions and is likely much too simple to provide quantitative insight into the differences in the metal ion binding affinities. To provide a quantitative characterization of the binding modes of Mg²⁺ and Mn²⁺, we have performed density-functional calculations in the most relevant biological ligand environments of these metals. Calculations were performed using Kohn–Sham density functional theory (DFT) with the hybrid exchange functional of Becke^{47, 48} and the Lee, Yang, and Parr correlation functional⁴⁹ (B3LYP) so as to be consistent with previous work in the QCRNA database.⁵⁰ Frequency calculations were performed to establish the nature of all stationary points and to allow evaluation of thermodynamic quantities. Geometry optimization and frequency calculations were performed using the basis set. Electronic energies were further refined via single point calculations at the optimized geometries using the basis set and the B3LYP hybrid density functional. All single point calculations were run with convergence criteria on the SCF wave function tightened to 10⁻⁸ au to ensure high precision for properties sensitive to the use of diffuse basis functions.⁵¹ The protocol applied to obtain the (refined energy)//(geometry and frequencies) is designated by the abbreviated notation. Aqueous solvation effects were treated using the polarizable continuum model (PCM)^52–54 with UAKS radii.⁵⁵ All density-functional calculations were performed with the Gaussian 03⁵⁶ suite of programs.

Results and Discussion

MD Simulations

The set of molecular dynamics simulations performed in this work comprises four classical (i.e., MM force field) simulations of the reactant state in protonated (RS) or activated/deprotonated (RS⁻) form, two simulations of the early transition state (ETS), two simulations of the late transition state (LTS), and finally two additional QM/MM simulations of the early and late transition state. The various simulations consider different metal ion binding scenarios (see Methods section) including no bound metal (apo-), metal initially bound at the “C-site’’ (c-) to the A9 pro-R_P phosphate oxygen and N₇ of G10.1, or in a bridging (b-) position between the A9 and scissile (C1.1) pro-R_P phosphate oxygens. These simulations and their notation are summarized in Table 1. The heavy-atom root-mean-square deviation (rmsd) for those simulations are shown in Supporting Information.

Structural roles of Mg²⁺ in the Reactant State

Three types of analysis of the four simulations of the reactant state were performed to explore possible structural roles of Mg²⁺: in-line fitness, near in-line attack conformation (NAC), and active site hydrogen bond network analysis.

In-Line Fitness

The in-line fitness index (F) has been used as a measure for the likelihood of activity of a catalytic RNA structure⁵⁷ and is defined by

$$F=\frac{\tau -45}{180-45}\times \frac{3^3}{d_{{{\text{O}}_2}^{\prime }-\text{P}}^3}$$ (1)

where τ is the O_2′–P–O_5′ angle in degrees and dO_2′–P is the O_2′–P distance in Å. A threshold value of F ≥ 0.4 is frequently used to identify catalytically competent in-line fitness.

Table 2 compares the in-line fitness F values for several hammerhead crystal structures with those derived from the molecular dynamics simulations. The two full-length hammerhead structures are considerably in-line, with F values of 0.73 and 0.61 for the 2.2 and 2.0 Å resolution structures (references ²⁰ and ²⁴), respectively. The minimal sequence structures, on the other hand, have considerably lower in-line fitness, with F values that range from 0.06 to 0.25. The reactant simulation results in the absence of Mg²⁺ (apo-RS) have average in-line fitness values of 0.34 ± 0.08. The reactant simulations with Mg²⁺ show higher F values that range from 0.40 to 0.43, just above the threshold value of 0.4 as an index for catalytic activity. Hence, the simulation results suggest that the presence of Mg²⁺ favors slightly larger in-line fitness values, at least for fluctuations that occur in the 10 ns time domain.

Table 2.

Results of the in-Line Attack of the O_2′ Nucleophile to the Scissile Phosphate from Simulation (Top) and Derived from Crystallographic Structures (Bottom) of Hammerhead Ribozyme^a

simulationb	apo-RS		b-RS		c-RS		c-RS−
R(C17:O2′, C1.1:P)	3.83(19)		3.61(23)		3.55(20)		3.57(16)
angle	138(10)		142(11)		134(14)		140(10)
in-line fitness (F)	0.34(8)		0.43(13)		0.40(10)		0.43(9)
NAC%	0.1		5.6		1.8		2.8
X-ray structuresc	2GOZd	2OEUe	1HMH	1MME	299D	300D	301D	359D
R(C17:O2′, C1.1:P)	3.18	3.30	4.36	4.32	3.46	3.51	4.08	3.54
angle	162.0	152.0	127.0	144.9	56.9	60.0	74.9	63.4
in-line fitness (F)	0.73	0.61	0.20	0.25	0.06	0.07	0.09	0.08

^aShown are the O_2′ · · · P distance, “R(C17:O_2′, C1.1:P)’’, in Å, the O_2′-P–O_5′ angle, “angle’’, in degrees, the in-line fitness parameter, “F’’, defined by Soukup and Breaker,⁵⁷ and the percentage of near-attack conformations, “NAC%’’, defined by Torres and Bruice.²⁸

^bSimulation abbreviations and summaries are given in Table 1.

^cX-ray structures are taken from the Protein Data Bank⁷⁹, ⁸⁰ and labeled by PDB ID.

^dThe full-length hammerhead RNA crystallographic structure at 2.2 Å resolution²⁰ that was also used in this paper as the starting structure.

^eThe full-length hammerhead RNA crystallographic structure at 2.0 Å resolution with resolved Mn²⁺ sites and solvent.²⁴

Near in-Line Attack Conformation (NAC)

Figure 1 shows a distribution plot of the in-line angle τ versus attack distance dO_2′–P for each of the reactant simulations and compares with crystallographic values (marked as “X’’ symbols). The regions of the plots that encompass so-called near in-line attack conformation (NAC)²⁸ are enclosed by a blue box. It is evident that two full-length crystal structures and the reactant simulations lie in positions which are in the near-attack conformation region, whereas minimal length structures are considerably far from an ideal attack conformation. The reaction state simulation b-RS shows 5.6% NAC population while the population is reduced to 1.8% for the c-RS simulation, to 2.8% for the c-RS⁻ simulation (in which the C17:O_2′ is deprotonated), and to 0.1% for the simulation lacking the prostetic divalent ion (apo-RS).

Figure 1.

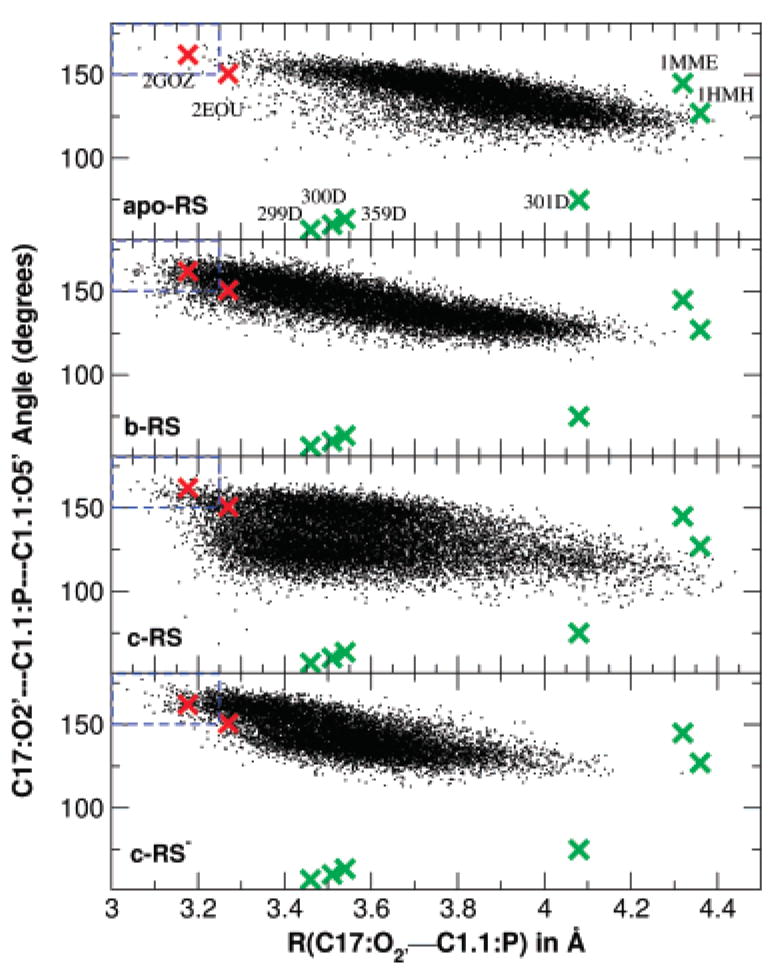
Plot of the O_2′-P-O_5′angle versus O_2′-P distance for the approach of the 2′-hydroxyl of residue C17 to the phosphate of residue C1.1 for reactant state simulations (small black crosses): apo-RS, b-RS, c-RS and c-RS⁻. Also shown are data for previously reported minimal sequence Hammerhead RNA X-ray structures (large green crosses, listed in Table 2), and the two full-length hammerhead structures (large red crosses). Dashed lines at 3.25 Å and 150°are the near in-line attack conformation (NAC) region defined by Torres and Bruice.²⁸

Active-Site Hydrogen-Bond Network

Table 5 lists the hydrogen-bond parameters for key interacting residues in the full-length hammerhead active site. The interactions between G12 and the nucleophilic 2′OH of C17 have implications into the role of G12 as a general base catalyst, whereas the hydrogen bonds between the O_5′ leaving group of C1.1 and the 2′OH of G8 have implications into the role of the G8 hydroxyl as a general acid. Other important interactions include hydrogen bonds involving functional groups on the A9 nucleobase with G12 that maintain the structural integrity of the active site.

Table 5.

Key Hydrogen Bond Parameters Derived from the Simulations^a

	apo-RS			b-RS			c-RS
D–H · · · A	RHA	θDHA	%	RHA	θDHA	%	RHA	θDHA	%
G12:H1 · · · C17:O2′	3.91(79)	129(156)	12	2.08(34)	157(134)	97	4.15(81)	137(144)	12
C17:H2′ · · · G12:O6	4.17(71)	47(326)	5	4.48(67)	34(264)	2	6.27(85)	52(243)	0
G8:H2′ · · · C1.1:O5′	7.48(74)	46(148)	0	4.5(135)	67(470)	20	4.60(106)	81(369)	3
G12:HN2′ · · · A9:N7	2.04(15)	153(108)	100	2.56(102)	147(154)	87	2.10(19)	150(120)	100
A9:HN6 · · · G12:N 3	2.45(40)	157(109)	90	2.40(67)	148(147)	89	2.19(18)	155(93)	100
A9:NH6 · · · G12:O2′	2.46(41)	134(187)	88	2.48(87)	149(145)	87	2.21(25)	146(135)	100
	c-RS−			b-ETS			b-LTS
D–H · · · A	RHA	θDHA	%	RHA	θDHA	%	RHA	θDHA	%
G12:H1 · · · C17:O2′	2.06(20)	154(99)	100	2.22(34)	155(127)	97	1.99(14)	164(83)	100
C17:H2′ · · · G12:O6
G8:H2′ · · · C1.1:O5′	2.80(85)	111(415)	76	5.09(74)	40(90)	0	2.36(42)	118(221)	94
G12:HN2 · · · A9:N7	2.41(48)	130(288)	82	2.99(47)	148(150)	50	2.78(36)	150(135)	73
A9:HN6 · · · G12:N3	2.19(22)	157(105)	99	2.35(27)	139(124)	98	2.32(24)	143(106)	99
A9:NH6 · · · G12:O2′	2.54(43)	141(139)	85	2.09(23)	156(133)	99	2.07(20)	154(128)	100

^aHydrogen bonds are of the form “D–H · · · AXD5”, where D–H and A are the hydrogen-bond donor and acceptor, respectively. Average hydrogen-bond distances (R_HA in Å), angles (θ_DHA in degrees), and hydrogen-bond percentage (%, defined as the percentage of time a hydrogen bond is deemed to exist, i.e., when R_HA < 3.0 Å and θ_DHA > 90°) from different simulations. Standard deviations are shown in parentheses divided by the decimal precision of the average quantity.

In the simulations of the neutral reactant state (RS), there is considerable hydrogen bonding observed between the N₁ amino proton of G12 and the nucleophilic O_2′ of C17, but relatively little hydrogen bonding observed between the O_6′ of G12. This interaction is particularly enhanced in the b-RS simulations with the Mg²⁺ in the bridging position where it is observed 97% of the time during the simulation. It is not yet conclusive that the G12 nucleobase does indeed play the role of a general base, although there is a considerable body of accumulating evidence that suggests that it does.^{58, 59} Nonetheless, the specific details whereby G12 could effect extraction of the nucleophilic 2′OH of C17 remain unclear. Our simulation results hint that it is plausible that G12 might extract the proton from the nucleophile via the N₁ position, either in a deprotonated or tautomeric form. This postulate is consistent with the observed strengthening of the G12:H₁ · · · C17:O_2′ hydrogen bond in the deprotonated reactant state (b-RS⁻) which is locked on over 99% of the time.

Hydrogen bonding between the 2′OH of G8, the proposed general acid catalyst, and the O_5′ leaving group is observed to some degree in all of the simulations. In the protonated reactant simulations, this hydrogen bond becomes successively more evident in the apo-RS, c-RS, and b-RS simulations, being present less than 1%, ~3%, and ~21% of the time, respectively. In the activated precursor (deprotonated) b-RS⁻ simulation, this hydrogen bond is even more pronounced (77% observed) and is strongest in the late transition state simulation (b-LTS) that has negative charge accumulated on the leaving group where the hydrogen bond is maintained 95% of the time. Thus, the interactions between the 2′OH of G8 and the leaving group are facilitated by the presence of a bridging Mg²⁺ ion, and become most prevalent in the late transition state. As will be discussed later, the proton is observed to spontaneously transfer in the QM/MM simulations of the late transition state. These results strongly support the role of the 2′OH of the G8 sugar ring as a general acid, and not directly a functional group of the nucleobase itself.

The other three hydrogen bonds (G12:H_N2 · · · A9:N₇, A9:H_N6 · · · G12:N₃ and A9:N_H6 · · · G12:O_2′) are essentially maintained for all simulations. A possible exception involves the early transition-state mimic simulation where the hydrogen bond of G12:H_N2 · · · A9:N₇ is relatively weak (50% observed).

Mg²⁺ Binding Modes along the Reaction Coordinate

The key heavy-atom distances around the active site are listed in Table 3 for the simulations with Mg²⁺ placed at the bridging position and in Table 4 for the simulations with Mg²⁺ initially placed at the C-site position. In both tables a comparison with the crystallographic values is provided. Several key distances that track the Mg²⁺ migration from the C-site are monitored in Figure 2 for the c-RS, c-RS⁻, c-ETS, and c-LTS simulations. Figure 3 shows a series of snapshots that illustrate the migration of the Mg²⁺. The Mg²⁺ ion clearly migrates from the C-site to the bridging position between the A9 and scissile phosphates (i.e., directly coordinating A9:O_2P and C1.1:O_2P) in both early and late transition-state mimic simulations (c-ETS and c-LTS) and in the reactant state simulation where the nucleophilic O_2′ has been deprotonated (c-RS⁻). However, in the parent reactant state system (c-RS), where C17:O_2′ is protonated, the divalent metal ion stays in the C-site in the course of the 12 ns MD simulation. The Mg²⁺ ion directly coordinates to A9:O_2P with a distance less than 2.5 Å for all simulations (data not shown). The radial distribution of key heavy-atoms around Mg²⁺ are shown in Figure 4 for the simulations with Mg²⁺ at the bridging position and in Figure 5 for the simulations with Mg²⁺ initially placed at the C-site position.

Table 3.

Comparison of Crystallographic and Simulation Data for Selected Heavy-Atom Distances in the Hammerhead Active Site^a

	X-ray		simulationb
	2GOZc	2OEUd	apo-RS	b-RS	b-ETS	b-LTS
C1.1:OP2 · · · 9:OP2	4.33	4.28	7.16(110)	3.36(49)	4.00(60)	4.01(70)
Mg · · · G8:O2′	3.04	3.14		3.97(102)	2.24(13)	3.21(23)
Mg · · · C1.1:O5′	3.84	4.01		4.22(21)	3.68(35)	2.09(50)
G8:O2′ · · · C1.1:O5′	3.19	3.51	6.87(71)	4.29(77)	4.41(65)	2.91(17)
C17:O2′ · · · C1.1:P	3.18	3.30	3.83(19)	3.61(23)	1.89(12)	1.76(40)
G12:N1 · · · C17:O2′	3.54	3.26	4.59(66)	3.02(27)	3.14(28)	2.97(13)
A9:N6 · · · G12:N3	2.63	3.22	3.38(38)	3.27(58)	3.15(21)	3.17(21)
A9:N6 · · · G12:O2′	3.21	2.98	3.19(27)	3.36(86)	3.01(18)	2.99(16)
A9:N7 · · · G12:N2	2.90	2.90	2.95(13)	3.42(93)	3.85(44)	3.66(33)

^aResults are from simulations with Mg²⁺ initially placed at the bridging position. Average values are shown with standard deviations in the parenthesis (divided by the decimal precision).

^bFor simulation summary and abbreviations see Table 1.

^cThe full-length hammerhead RNA crystallographic structure at 2.2 Å resolution²⁰ that was also used in this paper as the starting structure.

^dThe full-length hammerhead RNA crystallographic structure at 2.0 Å resolution with resolved Mn²⁺ sites and solvent.²⁴

Table 4.

Comparison of Crystallographic and Simulation Data for Key Heavy-atom Distances in the Hammerhead Active Site^a

	X-ray		simulationb
	2GOZc	2OEUd	apo-RS	c-RS	c-RS−	c-ETS	c-LTS
C1.1:OP2 · · · 9:OP2	4.33	4.28	7.16(110)	5.06(97)	2.92(26)	4.02(6)	3.78(27)
Mg · · · G8:O2′	3.04	3.14		5.92(28)	4.84(36)	3.66(61)	2.9(85)
Mg · · · C1.1:O5′	3.84	4.01		7.01(79)	4.23(41)	3.59(16)	2.09(6)
G8:O2′ · · · C1.1:O5′	3.19	3.51	6.87(71)	4.54(59)	3.21(35)	5.26(72)	3.66(73)
C17:O2′ · · · C1.1:P	3.18	3.30	3.83(19)	3.55(20)	3.57(16)	1.86(4)	1.76(4)
G12:N1 · · · C17:O2′	3.54	3.26	4.59(66)	4.92(81)	2.99(16)	2.95(14)	3.66(84)
A9:N6 · · · G12:N3	2.63	3.22	3.38(38)	3.11(17)	3.12(21)	3.14(18)	3.14(21)
A9:N6 · · · G12:O2′	3.21	2.98	3.19(27)	3.07(19)	3.36(36)	3.03(18)	3.09(22)
A9:N7 · · · G12:N2	2.90	2.90	2.95(13)	3.00(14)	3.07(20)	3.60(44)	3.06(23)

^aResults are from simulations with Mg²⁺ initially placed at the C-site position. Average values are shown with standard deviations in the parenthesis (divided by the decimal precision).

^bFor simulation summary and abbreviations see Table 1.

^cThe full-length hammerhead RNA crystallographic structure at 2.2 Å resolution²⁰ that was also used in this paper as the starting structure.

^dThe full-length hammerhead RNA crystallographic structure at 2.0 Å resolution with resolved Mn²⁺ sites and solvent.²⁴

Figure 2.

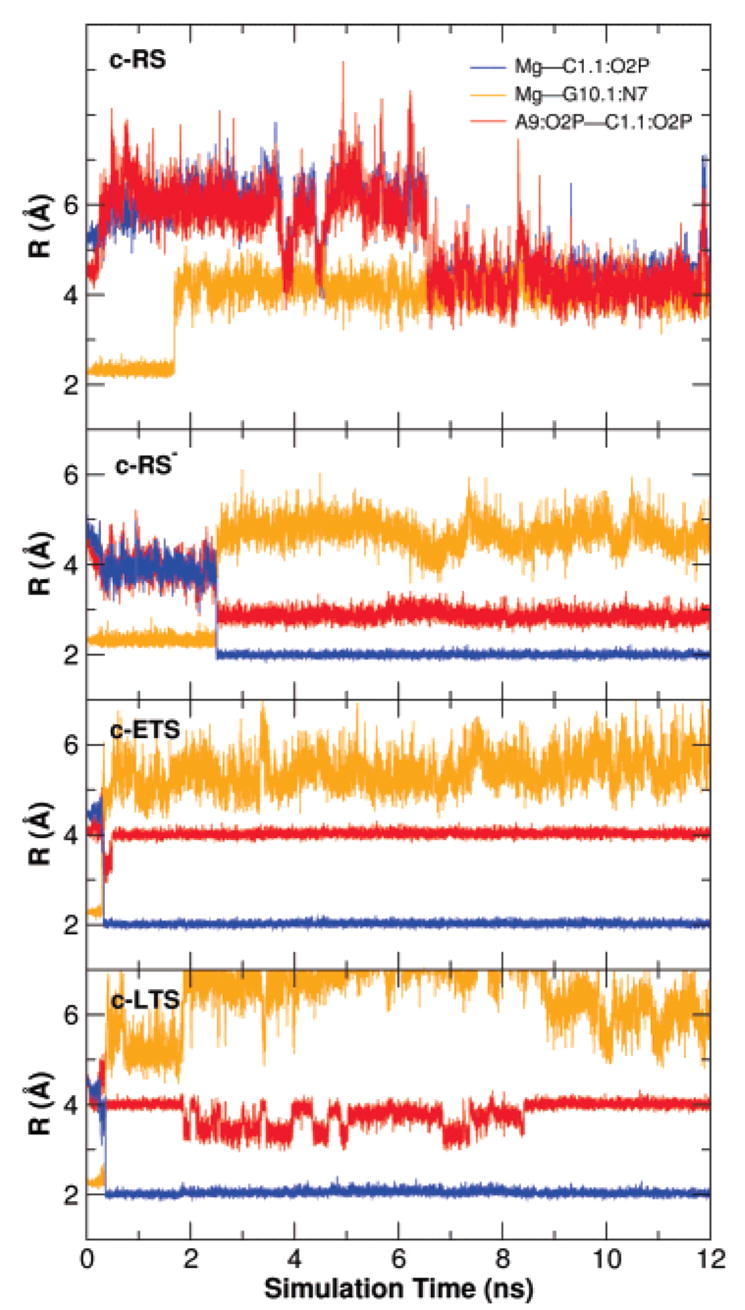
Key distances of the Mg²⁺ ion in the simulations with Mg²⁺ initially placed at the C-site.

Figure 3.

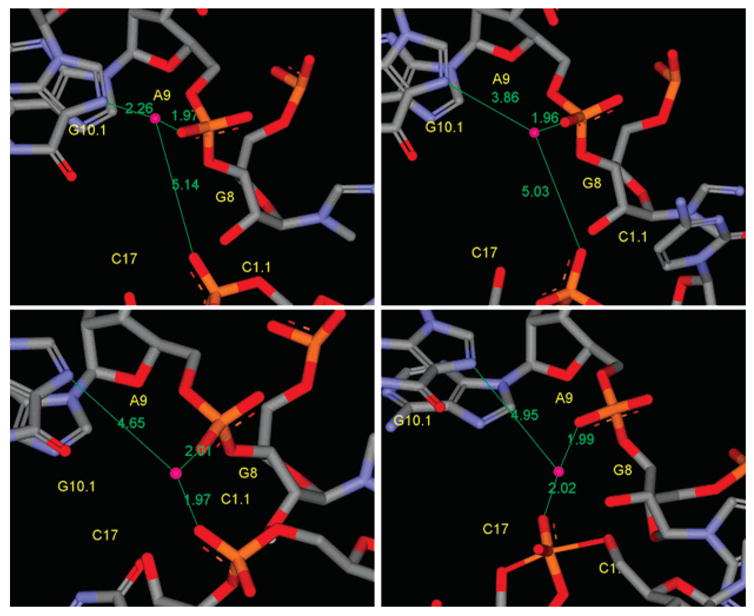
The Mg²⁺ positions from snapshots of simulations with Mg²⁺ initially placed at the C-site position. Snapshots shown are for the initial C-site position (upper left), the reactant state with C17:O_2′ protonated (upper right), the reactant state with C17:O_2′deprotonated (lower left), and the early transition state mimic (lower right). The Mg²⁺ position in the late transition state mimic is similar to the early transition state mimic (not shown). The Mg²⁺ ion migrates from the C-site to the position bridging the A9 and scissile phosphates, i.e., directly coordinated with the A9:O_2P and C1.1:O_2P, in the transition state mimic simulations and in the reactant state simulation with Mg²⁺ initially placed at the C-site position and with C17:O_2′ deprotonated but not in the reactant state simulation with C17:O_2′ protonated. The distances shown are distances to Mg²⁺ from A9:O_2P, C1.1:O_2P, and G10.1:N₇.

Figure 4.

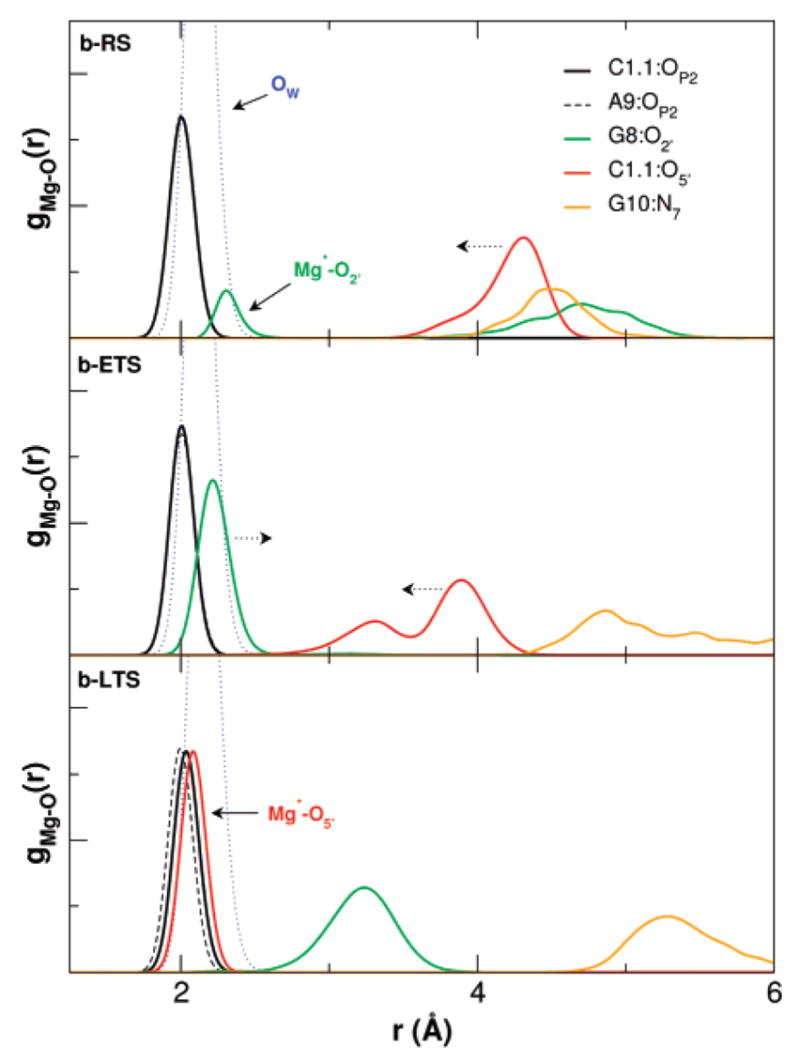
Radial distribution functions of key heavy atoms around Mg²⁺ in the active site for the reactant and early and late TS mimic simulations with the divalent metal ion in the bridging position (b-RS, b-ETS and b-LTS, respectively).

Figure 5.

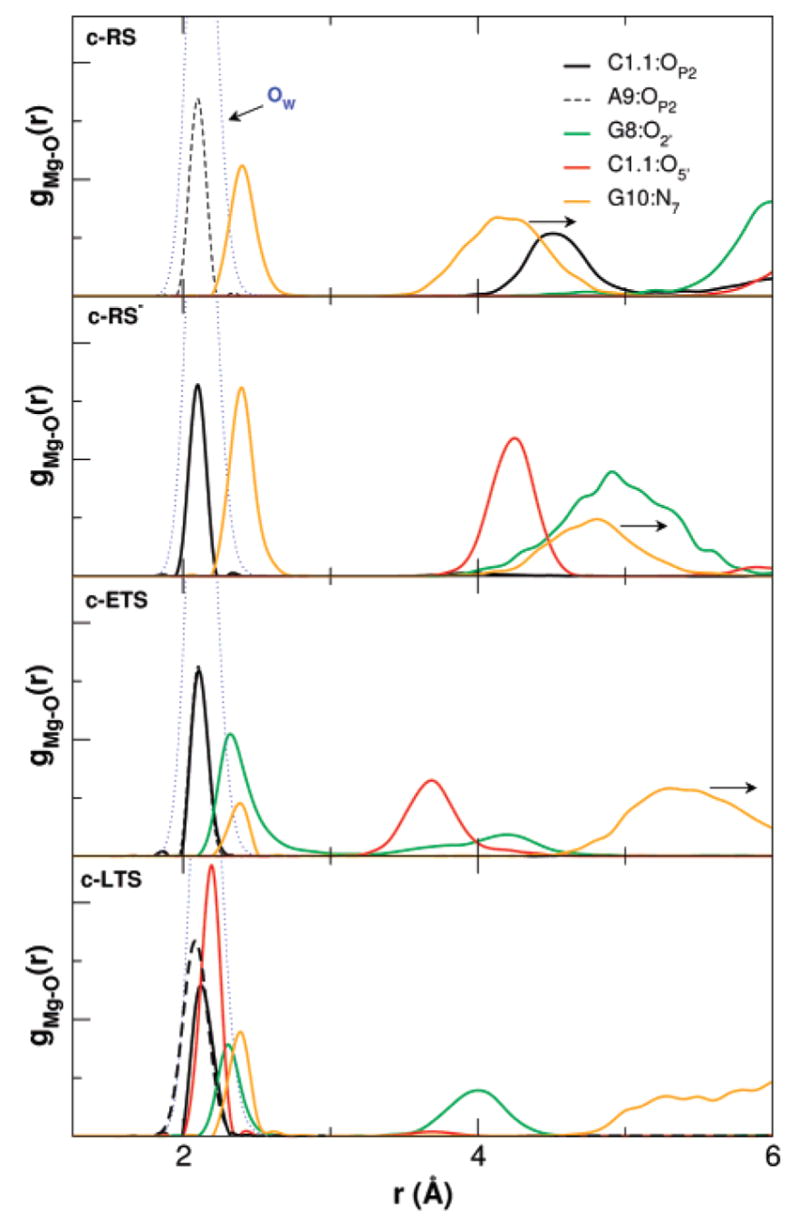
Radial distribution functions of key heavy atoms around Mg²⁺ in the active site for the reactant, the reactant with C17:O_2′ deprotonated, and early and late TS mimic simulations. The Mg²⁺ was initially placed at the C-site position.

Mg²⁺ Binding and Migration In The Reactant State

In the reactant simulations with Mg²⁺ at the bridging position (b-RS), the Mg²⁺ coordination between the C1.1 and A9 phosphate oxygens fluctuates between axial–axial and axial–equatorial modes, resulting in a shorter average oxygen–oxygen distance (3.36 Å) than that observed in the X-ray structure (around 4.3 Å, see Table 3). The reactant simulation with the Mg²⁺ ion initially placed at the C-site (c-RS) shows that, although Mg²⁺ does not move to the bridging position during simulation time (12 ns), its distance to G10.1:N₇ varies from around 2.0 Å to around 5 Å (Figure 2). The distance between the A9 and scissile phosphates jumps to 6 Å at the beginning of the simulation and returns to around 4 Å, resulting in an average of 5.06 Å (Table 4 and Figure 2). In the deprotonated reactant state simulation (c-RS⁻), Mg²⁺ migrates from the C-site to the bridging position after about 2 ns (Figure 2) while maintaining coordination in the axial–equatorial mode. This results in a shorter average in the A9 and scissile phosphate distance of 2.92 Å (Table 4).

In all three reactant simulations with Mg²⁺ ion present, the distances between the A9 and scissile phosphates remain within 1.5 Å of the crystallographic value of 4.3 Å, whereas in the absence of Mg²⁺ this key contact between stems I and II drifts to over 7 Å (Table 3). This suggests that the close proximity of the A9 and scissile phosphates creates an electrostatic requirement for cation occupation in order to maintain structural integrity. This electrostatic requirement may be fulfilled by occupation of a divalent metal ion in either a bridging position or at the C-site, and possibly, in the absence of divalent metal ions, by other monovalent cations at sufficiently high concentrations.

This may suggest that the close proximity of the A9 and scissile phosphates observed in the full-length hammerhead structure²⁰ could be stabilized by a Mg²⁺ ion that brings together stems I and II, either at the bridging or the C-site position. This close proximity is, perhaps, responsible for the formation of near-attack conformations in a way different from previous simulations based on minimal sequence structures.^25–28 The active site conformations of the reactant simulations with Mg²⁺ placed at the bridging position and initially placed at the C-site position are different (Tables 3 and 4; Figures 4 and 5), although in both cases the overall fold is maintained. Of particular interest are the C1.1:O_P2 · · · A9:O_P2, G8:O_2′ · · · C1.1:O_5′ and G12:N₁ · · · C17:O_2′ distances. In the b-RS simulation the Mg²⁺ bridges the A9 and scissile phosphates, effectively tethering them around at a distance of 3–4 Å, whereas in the c-RS simulation the average distance is 5.06 Å. In the deprotonated c-RS⁻ simulation, the negative charge facilitates the migration of the Mg²⁺ into a near-bridging position such that results are quite similar to those of the b-RS simulation. It is also noteworthy that the interaction of the implicated general acid and base become stronger with Mg²⁺ in a bridging position (either in the b-RS simulation or after migration in the c-RS⁻ simulation). These results suggest that in the reactant state the preferred binding mode of Mg²⁺ is at the C-site, which is between A9 and N₇ of G10.1 (through a water molecule),^24,60,61 and that the negatively charged environment near the scissile phosphate, formed after the initial pH-dependent general base reaction, brings the Mg²⁺ into a bridging position between A9 and the scissile phosphate leading to the transition state.¹⁵

Mg²⁺ Binding in the Transition State

In both early and late transition state mimic simulations with Mg²⁺ at the bridging position (b-ETS and b-LTS), the distance between the A9 and scissile phosphates is around 4 Å and the Mg²⁺ coordination between the C1.1 and A9 phosphate oxygens keeps an axial–axial position along the whole simulations (Table 3 and Figure 5). The distance between A9 and scissile phosphates in the crystallographic structure is around 4.3 Å, which is well-suited for Mg²⁺-bridging coordination.³⁰ However, in both early and late transition state mimic simulations with Mg²⁺ initially at the C-site position (c-ETS and c-LTS), the Mg²⁺ ion migrates from the C-site to the bridging position in less than 0.5 ns and remains at the bridging position for the remainder of the simulation. A similar situation was found in the deprotonated c-RS⁻ simulation (see earlier). The migration is also indicated by the broken coordination between the Mg²⁺ ion and G10:N₇, shown in Figure 2. This observation may again suggest that the bridging position is the preferred position for Mg²⁺ when an additional negative charge is accumulated at the scissile phosphate in formation of the transition state.

Role of Mg²⁺ in Catalysis

A possible catalytic role of Mg²⁺ in hammerhead ribozyme catalysis is illustrated in Figure 7. In the reactant state simulation with Mg²⁺ initially placed at the bridging position, the Mg²⁺ spends significant time closely associated with of G8:O_2′ (Figure 4), but remains fairly distant from the leaving group O_5′ position. In the reactant simulations with Mg²⁺ initially placed at the C-site position, the Mg²⁺ is far from both G8:O_2′ and the leaving group C1.1:O_5′ when C17:O_2′ is protonated. In the case when C17:O_2′ is deprotonated, both G8:O_2′ and C1.1:O_5′ move significantly closer to Mg²⁺ and C1.1:O_P2 acquires coordination to the Mg²⁺. The simulations indicate that Mg²⁺ prefers to occupy the bridging position when C17:O_2′ is deprotonated. The result of Mg²⁺ binding at the bridging position is to serve as an epicenter to draw together the A9 and scissile phosphates, the O_2′ of G8 and the O_5′ leaving group.

Figure 7.

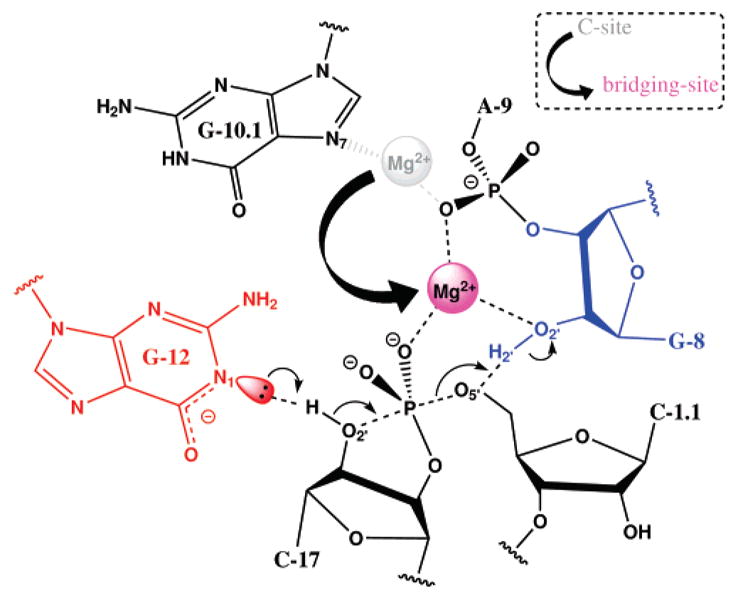
Possible catalytic role of Mg²⁺ in the full-length hammerhead ribozyme. The C-site in the pre-reactive state involves binding at the N₇ of G10.1 and the A9 pro-R phosphate oxygen. Activation of the 2′OH may occur through interactions with G12, the proposed general base. Migration from the C-site to a bridging position between A9 and the scissile phosphate occurs; in proceeding to the transition state the Mg²⁺ acquires additional interaction with the O_5′leaving group and the 2′OH of G8, the implicated general acid.

In the early TS mimic simulations, where the nucleophilic O_2′and leaving group O_5′are equidistant from the phosphorus, the Mg²⁺ ion becomes directly coordinated to the 2′OH of G8 and is positioned closer to the O_5′leaving group (Figures 4 and 5). Both early TS mimic simulations with Mg²⁺ initially placed at the bridging position and the C-site position showed very similar results. The coordination of the Mg²⁺ ion in the early TS mimic simulations is consistent with a role of shifting the pK_a of the 2′OH in G8 so as to act as a general acid.

Late Transition State

In the late TS mimic simulations, both with Mg²⁺ initially placed at the bridging position and the C-site position, a transition occurs whereby the Mg²⁺ coordination with the 2′OH of G8 is replaced by direct coordination with the leaving group O_5′(Figure 4). In this way, the Mg²⁺ may provide electrostatic stabilization of the accumulating charge of the leaving group (i.e., a Lewis acid catalyst).³ At the same time, the 2′OH of G8 forms a hydrogen bond with the leaving group O_5′ and is positioned to act as a general acid catalyst.

QM/MM Transition-State Simulations

The classical MD simulations suggest that in the early TS, the Mg²⁺ ion is positioned to shift the pK_a of the 2′OH of G8 to act as a general acid, and in the late TS, the Mg²⁺ ion can act as a Lewis acid catalyst to stabilize the leaving group and is poised to assist proton transfer from the 2′OH of G8. To lend further support to classical simulation results, QM/MM simulations have been performed for the early and late transition states. The detail QM/MM setup is described in the Methods section.

The possible roles inferred from purely classical MD simulations are supported by the QM/MM results (the key distances near the active site calculated from QM/MM simulations are listed in Supporting Information): The Mg²⁺ ion is bonded to G8:O_2′ in the early transition state mimic and switches to C1.1:O_5′ of the leaving group in the late transition state mimic. In the late transition state mimic, the G8:HO_2′ is strongly hydrogen-bonded to C1.1:O_5′.

Figure 6 shows that, in fact, the proton transfer from G8:O_2′ to C1.1:O_5′ happened in the QM/MM simulation of late transition state mimic and confirms that Mg²⁺ may significantly lower the pK_a of G8:O_2′ such that it may act as a general acid at the catalytic pH. That the proton transfer was observed in the 10 ns time domain suggests that the barrier to proton transfer is quite small. At the very beginning of the simulation, C1.1:O_5′ is tightly bound to Mg²⁺ while G8:O_2′ is around 3 Å away from Mg²⁺. As the simulation proceeds, G8:O_2′ moves closer to Mg²⁺ and eventually binds to Mg²⁺ and gives up its proton to C1.1:O_5′. After being protonated, the binding between C1.1:O_5′ and Mg²⁺ becomes weaker as their distance increases. The observed proton transfer may represent the final chemical step of the reaction.

Figure 6.

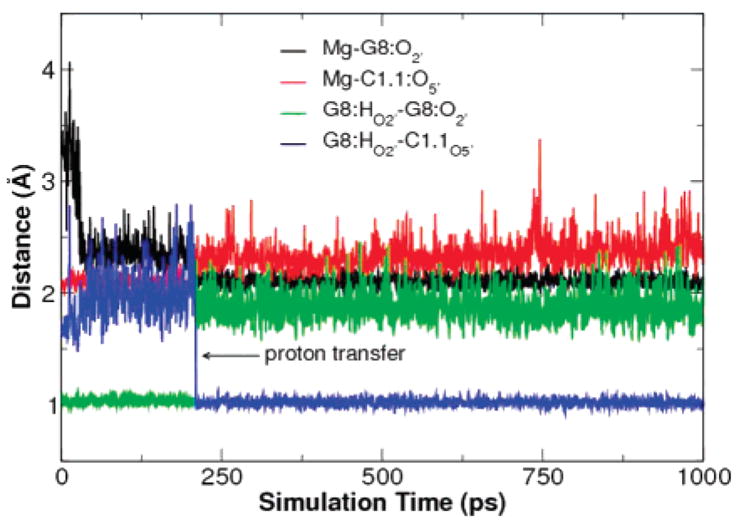
Key distances from QM/MM simulation of the late transition state mimic. The proton transfer from G8:O_2′ to the leaving group, C1.1: O_5′, occurs at around 200 ps.

Mechanistic Interpretation

A thorough understanding of the catalytic mechanism of the hammerhead ribozyme will ultimately rely on a consensus of theory and experiment. Specific mechanistic pathways can be probed using combined QM/MM methods, and the results can be compared with experimental structural and biochemical data. However, the cornerstone on which the study of the chemical steps of the reaction can be built is the determination of the binding mode of Mg²⁺ at the active site and the catalytically active reactant conformation. Once this is achieved the characterization of the nature of the conformational events and the changes in metal binding that accompany formation of the transition state can be undertaken. The presented and future work is aimed at providing answers to these questions.

It is known that Mg²⁺ ions play a fundamental role in RNA folding and are required to maintain the structural integrity of the ground state.^62–65 The results of the present work indicate that the active site forms a region of local negative charge that requires electrostatic stabilization to preserve its structural integrity. This stabilization can be effected by divalent metal ion binding^24,29 or likely by high concentrations of monovalent cations (Li⁺, Na⁺ or NH₄⁺ cations required concentrations 400-fold higher than those used in Mg²⁺ to achieve comparable rates of cleavage).^66–68 In the ground state, a divalent metal ion can occupy the C-site to effect such electrostatic stabilization.²⁴ In the case of Mn²⁺, the C-site formed by A9/G10.1 is a high-affinity binding site, as recently characterized by electron spin–echo envelope modulation spectroscopy.⁶⁹ On the other hand, in the case of Mg²⁺, binding at the C-site does not appear to be strong, as suggested by the molecular simulations and the observed absence of resolved metal cations in that site in the full-length hammerhead crystal obtained in the presence of 1 mM Mg²⁺ and > 1 M NH₄^+.20 However, upon crystallization in the presence of 10 mM Mn²⁺, metal binding was observed in the C-site position,²⁴ likely because the softer Mn²⁺ has higher affinity than Mg²⁺ for binding the N₇ of G10.1, as discussed in the section presenting results of DFT calculations. Our simulations successfully reproduce this weak affinity of Mg²⁺ for the C-site, and suggest that, in the reactant state, a Mg²⁺ ion binds the C-site at solvent separation with the N₇ of G10.1.

Proceeding to the transition state, however, the Mg²⁺ ion migrates to the bridging position as postulated previously.²⁹ Perhaps the most striking result of the current work is the spontaneous migration of the metal ion predicted by the simulation model (Figures 4 and 5). This migration is facilitated by deprotonation of the 2′OH of C17 (the nucleophile), and the accumulation of negative charge that is formed in moving toward the transition state. These results are consistent with thio/ rescue effect experiments and indicate that both the A9 and pro- R_P scissile phosphate oxygen exhibit a stereospecific kinetic thio effect in the presence of Mg²⁺ that can be rescued by Cd²⁺ ions.¹⁵ However, the binding affinity of the metal in the ground state was observed only to be sensitive to phosphorothioate substitution at the A9 phosphate position and not at the cleavage site phosphate. These experiments support a mechanism in which a single metal cation bound at the P9/G10.1 site (the A9 phosphate in the present work) in the ground state acquires an additional interaction with the scissile phosphate in proceeding to the transition state.

From the available crystallographic structures of the minimal sequence hammerhead ribozyme,^17–19 this mechanistic proposal implies a large-scale conformational rearrangement that would bring together the A9 and scissile phosphates that were separated by over 20 Å. The full-length hammerhead exhibits enhanced reactivity and has different metal ion requirements than the minimal sequence hammerhead.^21,70 The structure of the full-length hammerhead, in contrast to the minimal sequence structures, presents the A9 and scissile phosphates 4.3 Å away from each other, ideally positioned for the binding of a bridging divalent metal ion.²⁰ The current results support the formation of such a bridging divalent metal directly coordinating the A9 and scissile phosphates in the forming the transition state.

Kinetic analysis⁵⁸ along with photocrosslinking experiments²³ and mutational data^14,71,72 have implicated the roles of G8 and G12 as a general acid and base, respectively, and have been interpreted to be consistent with a transient conformational change into an active conformation with appropriate architecture for acid–base catalysis.¹⁵ Previous biochemical analyses that identified the G8 nucleobase as a potential candidate as a general acid catalyst (the simplest explanation at that time, in the absence of structural data) suggested that the N₁ position of the base itself could provide the proton to the leaving group. The full-length hammerhead structure revealed that, on the contrary, the 2′OH of G8 was poised to act as general acid catalyst, whereas the G8 base formed a structurally critical base pair with C3. Both G8 and C3 are invariant with respect to single mutations,⁷¹ however, a double G8C/C3G mutation rescues the deleterious effects of the single G8C mutation, suggesting that the base pairing is the essential factor to preserve catalytic activity. The hydrogen-bonding network found for the transition state mimics, outlined in Table 5, is consistent with this interpretation. Moreover, the mechanistic model for metal ion binding proposed here that involves interaction with 2′OH of G8, is consistent with kinetic analysis indicating that the pK_a of the general acid is down-shifted by around 4–7 pK_a units in a metal-dependent manner, correlated with the metal pK_a.⁵⁹ The simulation results suggest that the Mg²⁺ interacts strongly with the 2′OH of G8 in the early TS mimic and could contribute to a significant lowering of the pK_a value, and in the late TS mimic the G8 2′OH is hydrogen bonded to the leaving group and poised to act as a general acid catalyst. The Mg²⁺ ion may additionally play a direct role in stabilizing the negative charge accumulated in the leaving group in the late TS, and when the proton from the G8 2′OH is ultimately transferred, the coordination of Mg²⁺ is positioned to revert back to stabilize the resulting G8 2′-alkoxide.

Recent studies of the RzB hammerhead ribozyme, which is active in the absence of divalent ions (although with efficiency reduced 1000-fold), have suggested that divalent metals have a specific nonstructural role in catalysis that is distinct from an alternate mechanism that occurs in the presence of non-divalent ions such as cobalt hexammine.⁷³ The proposed model derived from the simulations is consistent with the Mg²⁺ having an active role in the chemical steps of catalysis and involving direct coordination to the A9 and scissile phosphates.

Despite the simulation results presented here and an ample experimental precedent being consistent with the direct participation of a single bridging Mg²⁺ ion in hammerhead ribozyme catalysis, the possibility of involvement of a second ion cannot be definitively precluded.^74–76 In the single cation mechanism, the Mg²⁺ preserves the integrity of the active site structure, and may serve as an epicenter in the transition state that coordinates the A9 and scissile phosphates, G8 2′OH general acid and O_5′ leaving group. The present work underscores the need for further investigation of the chemical reaction profile using combined QM/MM models.

DFT Results for Mg²⁺ and Mn²⁺ Binding Modes

The MD simulation results indicate that native Mg²⁺ ions may have a different binding mode at the C-site compared with the crystallographic Mn²⁺ ions (it should be noted that the present simulation study was almost complete when the Mn²⁺ crystal structure was determined). In the new crystal structure²⁴ in presence of Mn²⁺ the metal cation directly binds both A9:O_2P and G10.1:N₇. However, in the present simulations where Mn²⁺ ions are replaced by the native Mg²⁺ ions, the Mg²⁺ ion at the C-site does not directly coordinate G10.1 but instead binds the nucleobase at solvent separation. To quantify the relative binding affinities of Mg²⁺ and Mn²⁺ in the relevant ligand environments in the ribozyme active site, we performed density functional theory calculations in the presence and absence of dielectric continuum solvation corrections, the results for which are summarized in Table 6. The aqueous solvation free-energy corrections are likely not quantitatively accurate but are expected to provide correct qualitative trends with regard to the relative binding and ligand exchange energies between Mg²⁺ and Mn²⁺ ions.

Table 6.

Mg²⁺ and Mn²⁺ Ions in Different Ligand Environments^a

Me(ll)	L1	L2	R1b	R2c	ROwd	ΔE	ΔEZPC	ΔG	ΔΔGsole	ΔGaqf
Mg2+					2.11	−318.13	−303.18	−253.13	200.66	−52.46
Mg2+	DMP− OP		2.00		2.13	−199.99	−200.42	−197.06	190.50	−6.56
Mg2+	GUA N7		2.21		2.12	−44.27	−44.99	−40.81	83.89	43.08
Mg2+	GUA N7	DMP− OP	2.21	2.01	2.13	−223.91	−224.51	−217.52	231.73	14.21
Mn2+					2.21	−301.29	−288.19	−239.59	170.58	−69.01
Mn2+	DMP− OP		2.06		2.24	−199.90	−199.90	−196.23	164.30	−31.93
Mn2+	GUA N7		2.23		2.23	−46.36	−46.77	−42.27	40.76	−1.51
Mn2+	GUA N7	DMP− OP	2.26	2.06	2.26	−225.29	−225.54	−217.04	187.17	−29.87

^aShown are results for the ligand environments. [Me(L 1 · · · Ln)(H₂O)_6–n] for n = 0, 1 or 2. Metal–ligand distances are listed in Å. The energetic and thermodynamic quantities are in kcal/mol at 298.15 K and correspond to the ligand substitution reaction: [Me(L1 · · · Ln)(H₂O)_6–n] + nH₂O→ [Me(H₂O)₆] +L1 + · · · Ln, except for n = 0 (fully hydrated metal) in which case the thermodynamic data refers to the absolute ligand binding energy: [Me(H₂O) ₆] →Me + 6H₂O. Shown are the difference in electronic energy (ΔE), electronic energy with zero-point vibrational correction (ΔE_ZPC), gas-phase free energy (ΔG), solvation free energy (ΔΔG_sol) and free energy in aqueous solution (ΔG_aq).

^bMe(II) · · · L₁ bond length.

^cMe(II) · · · L₂ bond length.

^dMe(II) · · · O_W average bond length.

^eSolution-phase free energy correction (PCM).

^fSolution phase (water) free energy.

The absolute free energy of binding of the first coordination sphere of water in the gas phase is 13.54 kcal/mol more favorable for Mg²⁺ than for Mn²⁺, but when solvation corrections are included, the trend is reversed in favor of Mn²⁺ by 16.55 kcal/mol. To determine the relative binding affinity of the ions in the most relevant coordination environments in the ribozyme active site, comparison of ligand exchange energies with water are considered. The main result is that while the binding of Mg²⁺ to a dimethylphosphate in aqueous solution is favorable relative to a water by −6.56 kcal/mol, the relative binding to a guanine base is highly unfavorable by 43.08 kcal/ mol. Conversely, the binding of Mn²⁺ to both dimethyl phosphate and guanine relative to water are favorable by −31.93 and −1.51 kcal/mol, respectively. With respect to binding at the C-site position, which involves coordination to both a phosphate and a guanine base, the relative binding affinity is unfavorable for Mg²⁺ by 14.21 kcal/mol and favorable for Mn²⁺ by −29.87 kcal/mol. Clearly, the present calculations support stable Mn²⁺ binding at the C-site via direct inner-sphere coordination, and Mg²⁺ binding at the C-site via outer-sphere coordination to guanine (i.e., at solvent separation with guanine). These results are in accord with the MD simulation results that indicate Mg²⁺ does not maintain direct coordination with G10.1: N₇. It should be emphasized that the Mg²⁺ ion parameters were developed specifically to accurately model Mg²⁺ binding to biological phosphates, including reactive intermediates such as those of the present study,³⁰ based on density-functional calculations.⁷⁷

The present results can be rationalized by consideration of the hard–soft acid base (HSAB) principle.⁷⁸ The Mg²⁺ ion is a hard ion and prefers binding to hard ligands such as the nonbridging phosphate anions. The Mn²⁺ ion is a softer ion than Mg^2+, and preferentially binds softer ligands such as the aromatic guanine N₇. It is clear that a primary factor behind the preferential binding is the solvation effect. The ligand coordination distances are slightly larger for Mn²⁺, and consequently the solvation effect, which should vary inversely with the effective ion radius, is smaller for the Mn²⁺ complexes (Table 7). Hence, the larger charge/radius ratio in Mg²⁺ and the longer metal–ligand bond lengths for Mn²⁺ work cooperatively to influence solvation and the relative ligand-binding affinities. Overall, the MD simulation results that native Mg²⁺ ion at the C-site binds stably with the nonbridge phosphate oxygens of A9 (and in the case of metal ion migration to a bridging position, also the scissile phosphate) but does not readily maintain inner-sphere coordination with G10.1:N₇ are consistent with the DFT calculation results.

Table 7.

Key Distances (Å) in the Hammerhead Active Site from Early Transition State and Late Transition State Mimics from Molecular Dynamics (MD) and Combined Quantum Mechanics and Molecular Mechanics (QM/MM) Simulations^a

	b-ETS	b-ETSQM	b-LTS	b-LTSQM
Active site RMSD	1.79(26)	1.32(09)	1.49(22)	1.27(16)
Mg · · · G8:O2′	2.24(13)	2.14(09)	3.21(23)	2.19(22)
Mg · · · C1.1:O5′	3.68(35)	3.95(22)	2.09(05)	2.30(16)
G8:HO2′ · · · C1.1:O5′	5.09(74)	3.19(32)	2.36(42)	1.22(39)
G12:N1 · · · C17:O2′	3.14(28)	4.24(40)	2.97(13)	3.37(31)
A9:N6 · · · G12:N3	3.15(21)	3.08(17)	3.17(21)	3.06(14)
A9:N6 · · · G12:O2′	3.01(18)	3.02(16)	2.99(16)	3.02(16)
A9:N7 · · · G12:N2	3.85(44)	3.00(14)	3.66(33)	3.04(15)

^aThe active site is defined as all residues within 10 Å from the scissile phosphate. The results for MD simulations were calculated over the last 10 ns with data collected every 1 ps. The QM/MM results were calculated over 1 ns with data collected every 0.5 ps. Entries shown are average values and standard deviations are in parenthesis (divided by the decimal precision).

Conclusions

The present work presents a series of molecular dynamics simulations of the full-length hammerhead ribozyme in solution to study the Mg²⁺ binding mode and conformational events at different stages along the catalytic pathway. Results are compared to the recent 2.2 Å crystal structure of the full-length hammerhead in the presence of Mg²⁺ ions,²⁰ and to the 2.0 Å crystal structure with resolved Mn²⁺ binding sites and solvent structure.²⁴ The present simulations results are consistent with a hammerhead ribozyme model whereby the active site forms a region of local negative charge that requires electrostatic stabilization to preserve its structural integrity, and whereby this stabilization can be effected by divalent metal binding at the C-site or in a bridging position in the ground (pre-reactive) state. An Mg²⁺ ion is observed to weakly bind at the C-site position at solvent separation with G10.1, facilitating the formation of near in-line attack conformations, particularly when in the bridging position where there is increased interaction between the nucleophile (C17:O_2′) and the implicated general base (G12). Moreover, the weak binding in the simulations, supported by density functional results, helps explain the absence of a Mg²⁺ ion observed in the original full-length crystal structure.²⁰

Deprotonation of the nucleophile is correlated with the migration of the Mg²⁺ from the C-site into a bridging position, as with the formation of the dianionic transition state, suggesting that the accumulation of negative charge around the scissile phosphate center is sufficient to induce a change in the binding mode of the Mg²⁺. Once in the bridging position in the transition state, the Mg²⁺ ion interacts with the O_5′ leaving group of C1.1 and the 2′OH of G8, the implicated general acid catalyst. The Mg²⁺ ion, in the bridging position, can act both as a Lewis acid catalyst to stabilize directly the accumulating charge on the O_5′ leaving group, and effect a pK_a shift on the 2′OH of G8 to facilitate general acid catalysis. Upon proton transfer from G8:O_2′ to C1.1:O_5′, the Mg²⁺ is poised to directly stabilize the resulting 2′ alkoxide (which could occur synchronously). Combined QM/MM simulations suggest that the barrier for the general acid proton-transfer step may be sufficiently low so as to occur on the nanosecond time scale.

The proposed mechanistic model evinced by these simulations is consistent with a considerable body of experimental work, including (1) thio/rescue effect experiments¹⁵ that support a mechanism in which a single metal cation bound at the C-site in the ground state acquires an additional interaction with the scissile phosphate in proceeding to the transition state, (2) kinetic studies,⁵⁸ photocrosslinking experiments,²³ and mutational data^14,71,72 that implicate G8 and G12 as possible general acid and base, respectively, and (3) recent studies involving metal ion titrations that suggest that the pK_a of the general acid is down-shifted by around 4–7 pK_a units in a metal-dependent manner, correlated with the metal pK_a,⁵⁹ and that divalent metals may play a specific chemical role in catalysis.⁷³

Although our simulation results are consistent with most available experimental evidence, there remain caveats that have not yet been fully resolved. The present work suggests that a bound divalent metal ion at the C-site migrates to a bridging position between the A9 and scissile phosphates in proceeding to the transition state (one metal mechanism). However, at this point one cannot fully discount an alternate mechanism whereby there is no direct participation of a metal at the scissile phosphate in the transition state (no metal mechanism), or a mechanism whereby the metal at the C-site does not migrate, but rather the scissile phosphate acquires an additional metal ion interaction in proceeding to the transition state (two metal mechanism). To fully explore these alternate mechanistic scenarios, full free energy profiles of the chemical reaction steps need to be performed

The present work makes an important first step in the detailed characterization of the structure, dynamics, and free energy profile of the full-length hammerhead reaction: the determination and characterization of plausible Mg²⁺ binding modes and conformational events that occur in the catalytically active reactant state that lead to formation of the transition state. These results open the door to further study of the details of the chemical mechanism using combined QM/MM methods. Together with experiment, it is the hope that a consensus will emerge that explains the detailed molecular mechanisms of hammerhead ribozyme catalysis and in doing so may provide new insight into the guiding principles that govern RNA catalysis.