Removal kinetics of exchange transfusion

Exchange transfusion has just a few elective indications: the therapy of haemolytic disease of the newborn (HDN) and cases in which red cell exchange is appropriate but the child is too small to use a cell separator.

Exchange transfusion has several positive effects in the therapy of HDN: it removes the neonatal red cells, which are destined to be destroyed and hence to generate bilirubin, the already produced bilirubin, and the offending antibody¹. Moreover, exchange transfusion also corrects anaemia, if present¹.

Physiological bases of exchange transfusion in HDN

The offending antibody is an IgG and has a substantial extravascular distribution (about 60%). As the equilibration between the intravascular and extravascular compartments is slow (≈1–3%/hour)², removal of the antibody through the exchange may only be partial and the residual or newly produced neonatal red cells are still exposed to the risk of haemolysis. It is, therefore, justified to remove as many neonatal red cells as possible and to maintain an elevated total haemoglobin concentration with compatible adult red cells, so as to inhibit the autologous production from the bone marrow. The bilirubin in the intravascular space is only a small part of the total and, although equilibration is fast, exchange transfusion is not particularly successful: rebound is immediate¹, so that at the end of an exchange during which 87% of neonatal red cells are removed, the concentration of bilirubin is still 60% of that at the start of the exchange³. It is, therefore, advisable to prevent the production of bilirubin by removing the “doomed” red cells in time¹.

The removal of red cells

Alexander S. Wiener (1907–1976), co-worker of Karl Landsteiner in the discovery of the Rh factor (1940) and pioneer of the therapy of HDN, asserted⁴ that he and Wexler had been the first to derive the formula which describes the removal of red cells during exchange transfusion⁵

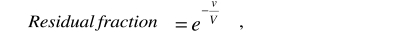where v is the total exchanged volume, V is the patient’s blood volume and e is the transcendental number, base of the natural logarithm. However, he later stated that his formula was not correct because it did not take into consideration the difference between the patient’s haematocrit and that of the transfused blood⁶. Moreover, according to others, even when the two haematocrits happen to be the same, the formula should be modified to account for the difference between venous haematocrit and body haematocrit⁷. Wiener also stated that it was obvious that, for an equal exchanged volume, exchange transfusion would be more efficient, the more the neonate was anaemic⁶. Taken together, these opinions risk misleading the reader seriously.

Wiener’s formula describes a continuous flow exchange. However, during exchange transfusion, neonatal blood is replaced by donor blood, withdrawing and transfusing alternatively 5–20 mL of blood. The exchange is, therefore, intermittent. It can be demonstrated (see Appendix A) that when blood is first withdrawn and then transfused, at each cycle:

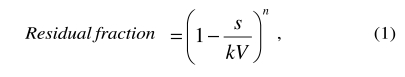where s is the volume exchanged at each cycle (cycle volume), V is the patient’s blood volume, k is the ratio between body and venous haematocrit (= 0.91)⁷ and n is the number of exchange cycles.

Analogously, when blood is first transfused and then withdrawn:

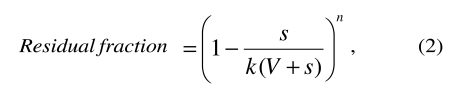In Appendix B, the reader will find instructions for programming a spreadsheet to calculate the residual fraction according to the cycle volume and the neonate’s blood volume. Some exemplary data are shown in table I.

Table I.

Fraction of neonatal red cells remaining after 1, 2, 5, 10, and 20 cycles during the exchange transfusion. It is assumed that the volume exchanged at each cycle is 10% of the total blood volume. Columns “Withdrawal first” and “Transfusion first” show the results when the exchange begins with withdrawal or transfusion, respectively. For the sake of comparison, the column on the far right shows the results of an isovolumetric continuous flow exchange. Its efficiency is intermediate between the other two

		Residual fraction (%) of the neonatal red cells
		Intermittent flow		Continuous flow
Cycle	Total exchanged volume (% of the blood volume)	Withdrawal first	Transfusion first
1	1 0	89.0	90.0	89.5
2	2 0	79.2	81.0	80.1
5	5 0	55.9	59.1	57.4
1 0	100	31.2	34.9	32.9
2 0	200	9.8	12.2	10.8

As can be easily noted, the efficiency of the exchange is greater when blood is first withdrawn. The difference is proportional to the volume exchanged at each cycle. The cycle volume influences the efficiency of the exchange in a peculiar way: when blood is first withdrawn, efficiency is proportional to the cycle volume, whereas when blood is first transfused, efficiency is inversely proportional to the cycle volume. However, as the cycle volume rarely exceeds 10% of the total blood volume, the differences are limited to a few percentage points.

Formulae (1) and (2) do not include references to the patient’s haematocrit, nor to the haematocrit of the transfused blood: contrary to the above cited opinions, the residual fraction only depends on the terms represented in the two formulae.

Absolute amount of neonatal red cells

However, we should be more interested in the absolute amount of the residual neonatal red cells, rather than the fraction. In this case it is clear that, if the neonate is anaemic, during the exchange it is possible to fall under a minimum target level of neonatal red cells earlier.

Incidentally, this was the probable meaning of Wiener’s sentence cited above.

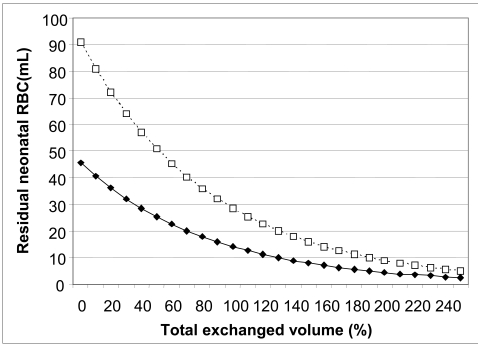
Figure 1 compares the cases of two hypothetical neonates, with the same weight (blood volume) but initial haematocrits of 25% and 50%. If our aim is to leave no more than 9 mL of neonatal red cells (about 10% of the normal initial volume), the target is met in the first case after 14 cycles of exchange and in the second after 20 cycles.

Figure 1.

Effect of the neonate’s initial venous haematocrit on the residual quantity of neonatal red cells during the exchange transfusion. It is assumed that the blood volume of the neonate is 200 mL, the volume of the exchange at each cycle is 20 mL (10%), and blood is first withdrawn and then transfused. The solid curve with closed symbols refers to an initial venous haematocrit of 25%. The dotted curve with open symbols refers to a haematocrit of 50%

The neonate’s venous haematocrit at the end of the procedure

During the exchange transfusion, neonatal red cells are progressively substituted by the transfused cells. The venous haematocrit after n cycles of exchange (H_n) principally depends on the haematocrit of the transfused blood (H_D) and, moreover, the volume exchanged at each cycle (s), the number of cycles (n), and the neonate’s initial venous haematocrit (H_V), according to the following formula (see Appendix A):

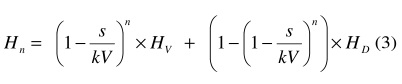The above formula is appropriate when the exchange begins withdrawal of blood. The analogous formula for the opposite case is given in Appendix A.

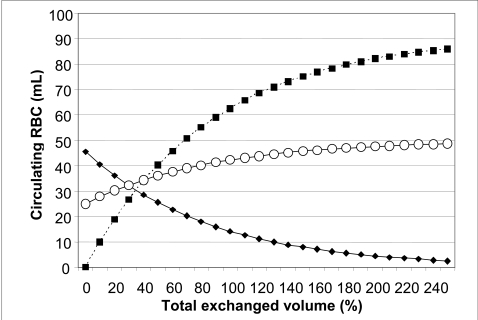
Figure 2 shows the kinetics of the substitution of the transfused blood for the neonatal red cells and the changes of the patient’s venous haematocrit during the exchange transfusion.

Figure 2.

Kinetics of the substitution of donor red cells for the neonatal red cells and of the venous haematocrit during the exchange transfusion. The conditions of the procedure are the same as those imagined in figure 1 (initial venous haematocrit of the neonate: 25%). The haematocrit of the transfused blood is 50%. The solid curve with closed symbols indicates the residual volume of neonatal red cells. The dotted curve with closed symbols indicates the transfused red cells circulating in the patient. The solid curve with open symbols indicates the patient’s venous haematocrit.

Choosing the haematocrit of the blood to be transfused

It has been noted that the haematocrit of the transfused blood does not influence the efficiency of the procedure and, therefore, it may be chosen on the basis of other considerations: the haematocrit should not be too low, in order not to induce a state of anaemia and to correct it, if present; an elevated haematocrit at the end of the procedure exerts an inhibitory effect on autologous marrow production, which is in any case destined to precocious destruction. On the other hand, an excessive haematocrit of the transfused blood limits the total exchanged volume, lest the neonate be made too polycythaemic⁶. This entails the risk of an insufficient exchange⁶. Since the 1950s, it has been customary to concentrate the reconstituted whole blood up to a haematocrit of about 50%⁶. This practice was confirmed by the recent Italian guidelines⁸. Probably, this choice stems from the fact that the normal neonatal haematocrit is about 50%. Such an elevated haematocrit is due to the greater affinity for oxygen by the foetal haemoglobin that, therefore, has a lower oxygen carrying capacity to the tissues. In fact, haematocrit rapidly decreases in the weeks following birth. After about 2 months, even though the substitution by adult haemoglobin is not complete, the haematocrit has fallen to about 35%⁹. Therefore, a haematocrit of 50% is not necessary and it could be decreased to 45% or less, so as to profit from the greater volume of reconstituted whole blood available to increase the removal of neonatal red cells or bilirubin.

Exchange transfusion in the therapy of sickle cell anaemia

Exchange transfusion is used preferentially or as an alternative to simple transfusion in a number of indications in children with sickle cell anaemia¹⁰. In adults or bigger children, automated red cell exchange is the preferred procedure (this topic will be dealt with in the next article of this series), but the manual exchange of whole blood may be necessary for smaller children, given the limitations in the extracorporeal volume. In this case, the removal kinetics is the same as that described above. The difference lies in the target, which is not to remove as many autologous red cells as possible, but to reduce the percentage of haemoglobin S without increasing the haematocrit excessively, in order not to cause a high blood viscosity¹¹.

The relevant parameters are, therefore, the percentage of haemoglobin S and the venous haematocrit. This latter can be calculated from (3). The first part of equation (3) represents the contribution (H_p) of the residual autologous red cells (see Appendix A):

Therefore, the percentage of haemoglobin S after n cycles (HbS_n) will be:

where HbS₀ is the initial percentage of haemoglobin S.

Limitations of the formulae

Most of the terms contained in the formulae can be measured with precision. However, blood volume is, usually, only estimated with the aid of a formula¹² and the value of the correction for the body haematocrit is taken from the literature⁷. In this regard, however, it should be noted that the value may differ from the normal significantly, in case of splenomegaly¹³.

Moreover, the formulae assume that:

• - there is no dead space in the transfusion set used for the exchange;

• - the transfused blood mixes immediately in the circulation;

• - the blood volume does not change during the procedure;

• - all transfused red cells survive in the circulation (at least till the end of the exchange);

• - the patient’s red cells are not destroyed during the procedure.

As regards the first assumption, after the transfusion step, before blood is again withdrawn, it is advisable to aspirate a small volume of blood from the patient and to reinfuse it. The second and third assumptions are plausible. The fourth is also plausible, in the case of HDN, because the neonate’s reticuloendothelial system should preferentially remove the sensitised autologous red cells. Finally, the fifth assumption depends on the duration of the procedure.

Conclusions

The exchange is more efficient if blood is first withdrawn and if the volume exchanged at each cycle is large. However, when the cycle volume does not exceed 10% of the patient’s blood volume, the difference remains within a few percentage points.

The removed fraction of the patient’s red cells only depends on the cycle volume and the number of cycles. However, the absolute amount of residual red cells also depends on the patient’s initial venous haematocrit. The haematocrit of the transfused blood influences the final haematocrit of the patient, but not the removal efficiency.

Appendix A – Derivation of the formulae

The fraction of neonatal red cells removed in the exchange transfusion

If we denote the volume exchanged at each cycle with s and the blood volume of the patient with V, then the fraction removed at each cycle, when blood is first withdrawn, should be $\frac{s}{V}$.

However, the red cells are more concentrated in the venous blood than in the whole vascular system, so that:

$$H_B=k\times H_V$$

where H_B is the body haematocrit, H_V the venous haematocrit and k is the correction factor (= 0.91)⁷.

Let R_B be the total volume of the patient’s red cells:

$$R_B=\frac{H_B}{100}\times V=\frac{H_V}{100}\times k\times V.$$ (1)

Let R_S be the volume of the patient’s red cells in the volume exchanged at each cycle:

$$R_S=\frac{H_V}{100}\times s=\frac{H_B}{100}\times \frac{1}{k}\times s.$$

Then the removed fraction will be equal to $\frac{R_S}{R_B}$, or:

$$Removed\hspace{0.17em}fraction=\frac{s}{kV},$$

and the residual fraction will be:

$$Residual\hspace{0.17em}fraction=1-\frac{s}{kV}$$

At the next cycle, the volumes exchanged will be the same, but the removal will concern the residual amount only $\left(1-\frac{s}{kV}\right)$, therefore the residual fraction after the second cycle will be:

$$\left(1-\frac{s}{kV}\right)\times \left(1-\frac{s}{kV}\right),\text{or}\hspace{0.17em}{\left(1-\frac{s}{kV}\right)}^2.$$

It is easy to see that after n cycles:

$$Residual\hspace{0.17em}fraction={\left(1-\frac{s}{kV}\right)}^n.$$ (2)

When blood is first transfused, on the basis of very similar considerations to those above, it can be derived that:

$$Residual\hspace{0.17em}fraction={\left(1-\frac{s}{k(V+s)}\right)}^n.$$ (3)

In the above formulae, only the correction for the difference between venous and body haematocrit was used. However, a further correction is advisable when the haematocrit is measured by centrifugation because of the small amount of plasma (≈ 2%) that remains entrapped in the red cell column⁸. In this case k = 0.91 x 0.98 = 0.89.

Absolute amount of neonatal red cells remaining after the exchange transfusion

The volume of the neonatal red cells remaining after the exchange cycles (R_R) can be derived from formula (2):

$$R_R=R_B\times {\left(1-\frac{s}{kV}\right)}^n,$$

or formula (3), as appropriate:

$$R_R=R_B\times {\left(1-\frac{s}{k(V+s)}\right)}^n,$$

R_B can be derived from (1). The removed volume can be easily calculated by difference.

Venous haematocrit after the exchange transfusion

Let us consider the case in which blood is first withdrawn. Let $a=\frac{s}{kV}$and b = 1 − a.

At each cycle, a fraction equal to a of the donor’s red cells present in the circulation will be removed, whilst a volume D_S will be added.

Table II shows the situation in the first cycles of an exchange transfusion.

Table II.

Volumes of donor red cells (V_GR) exchanged during the exchange transfusion. At each cycle, blood is first withdrawn and then transfused. In the first cycle, no donor red cells are in the circulation during the withdrawal step. D_S is the volume of donor red cells transfused at each cycle

	Withdrawal step		Transfusion step
CYCLE	Removed VGR	Remaining VGR	Final VGR
1	0	0	DS
2	a × DS	b × DS	DS + b × DS
3	a × (1 + b) × DS	(b + b2) × DS	(1 + b + b2 ) × DS
4	a × (1 + b + b2) × DS	(b + b2 + b3) × DS	(1 + b + b2 + b3) × DS
…	…	…	…
n	a × (1 + b + b2 +…+ bn−2 ) × DS	(b + b2 +…+ bn−1 ) × DS	(1 + b + b2 +…+ bn−1 ) × DS

As can be seen from the far right column, at each cycle, a term to the power n − 1 is added in parentheses.

By definition, we know that:

$$H_D=\frac{D_S}{s}\times 100=\frac{D_s}{(1-b)kV}\times 100$$

where H_D is the haematocrit of the transfused blood, and that:

$$H_d=\left(1+b+b^2+\dots +b^{n-1}\right)\times \frac{D_s}{kV}\times 100,$$

where H_d is the venous haematocrit (in the patient’s circulation) of the transfused red cells after cycle n.

Therefore:

$$H_d=(1-b)\times (1+b+b^2+\dots +b^{n-1})\times H_D=(1-b^n)\times H_D$$

By substitution, the following formula is obtained:

$$H_d=\left(1-{\left(1-\frac{s}{kV}\right)}^n\right)\times H_D.$$

In the same way, we can derive the venous haematocrit of the patient’s red cells after the exchange transfusion (H_p):

$$H_p={\left(1-\frac{s}{kV}\right)}^n\times H_V.$$

Therefore, at the end of n cycles of exchange transfusion, the total venous haematocrit will be the sum of the two partial ones⁷:

$$H_n={\left(1-\frac{s}{kV}\right)}^n\times H_V+\left(1-{\left(1-\frac{s}{kV}\right)}^n\right)\times H_D.$$

This formula allows the calculation of the venous haematocrit of the patient during the exchange transfusion (H_n), starting from the patient’s venous haematocrit before the procedure (H_V) and the haematocrit of the transfused blood (H_D).

Analogously, when blood is first transfused, the following formula can be derived:

$$H_n={\left(1-\frac{s}{k(V+s)}\right)}^n{H}_v\times +\left(1-{\left(1-\frac{s}{k(V+s)}\right)}^n\right)\times H_D.$$

Appendix B – Programming a spreadsheet^*

Spreadsheets are programmes used to perform calculations, especially on large data series.

The most renowned is Excel, which is part of the MS Office (Microsoft) package.

However, the following instructions are equally valid for other similar programmes, such as OpenOffice.org Calc and Gnumeric. As these are less well known, here is a brief description.

OpenOffice.org Calc

This is part of the OpenOffice.org suite. It is freely downloadable from http://www.openoffice.org/ and is available for Windows (98 and later), Mac Os X, Linux and other operating systems. Calc can open, modify, and save files in Excel and other formats, besides its own native one. The available functions are similar to those of Excel.

Gnumeric

Gnumeric is part of the GNU project. It can be freely downloaded from http://www.gnome.org/projects/gnumeric/ and is available in versions for Windows (XP, 2000 or later) and Linux. Gnumeric is able to open, modify and save files in Excel and other formats. Available functions are similar to those of Excel but, in addition, Gnumeric offers a series of statistical tests.

The following instructions only presuppose a basic knowledge of how to use a personal computer.

Instructions

Open the spreadsheet. The programme automatically proposes a new sheet (table), with rows progressively numbered starting from 1 and columns alphabetically labelled starting from A.

Each cell is identified by a couple of column and row identifiers: e.g., the top leftmost cell is A1; the fourth from top in the B column is B4 and so on. Each cell may contain numerical values, formulae or explanatory text. This last is useful for reminding the user of the meaning of the adjacent values or formulae.

Calculation of the residual fraction and absolute quantity of the patient’s red cells

Enter the text listed in Table III into the appropriate cells. Enter the values listed in Table IV.

Table III.

Explanatory text (“labels”) to be entered into the specified cell

Cell	Text to be entered
A1	Kinetics of exchange tansfusion
A3	Patient’s blood volume (mL)
A4	Volume of each exchange cycle (mL)
A5	Patient’s initial venous haematocrit (%)
A6	Haematocrit of the blood to be transfused (%)
A7	Correction factor for the body haematocrit
A9	Cycle
B9	Exchanged volume (% of the blood volume)
C9	Residual fraction (%)
D9	Residual quantity (mL)

Table IV.

Values to be entered into the specified cells. Please enter the numerical values only, not the text

Cell	Value to be entered
B3	Blood volume of the patient (mL), e.g. 200
B4	Volume of each exchange cycle (mL), e.g. 20
B5	Initial haematocrit of the patient, e.g. 25
B6	Haematocrit of the transfused blood, e.g. 50
B7	Correction factor for body haematocrit: 0.91

If the cell seems to be covered by the text of the cell at its left, resize the adjacent cell or begin to write in the desired cell: this will prevent the text in the left cell from exceeding the border.

Enter the numbers from 0 to 25 into the cells from A10 toA35.

These numbers represent the cycles of the exchange transfusion. The number of cycles can be increased further at will. Enter the formulae listed in Table V.

Table V.

Formulae to be entered into the specified cells. Formulae should be entered as plain text, without forgetting the initial “=“ sign

Cell	Formula to be entered
B10	=$B$4/$B$3*A10*100
C10	=100* POWER(1−$B$4/$B$3/$B$7,A10)
D10	=$B$5/100*$B$7*$B$3*C10/100

Right click on cell B10; choose “Copy” from the pop-up menu; paste the cell (“Paste”) on cells B11 to B35 (or further on, if numbering continues past A35).

In the same way, copy the formula in C10 on cells C11 to C35 and that in D10 on cells D11 to D35. The spreadsheet transposes the references to the cells contained in the formulae in an appropriate way. Calculated values appear immediately. Row 10 contains the starting values, before the exchange. Cells B10–B35, C10–C35 and D10–D35 contain the total exchanged volume, expressed as a percentage of the blood volume, the residual fraction (%) and the residual absolute amount (mL) of the patient’s red cells, respectively. If the user changes one or more values in cells B3–B7, the results in the cells B10–B35, C10–C35 and D10–D35 are immediately recalculated by the programme.

When blood is first transfused, the formula to be entered into cell B10 is:

$$=100*\text{POWER}(1-\$\text{B}\$4/(\$\text{B}\$7*(\$\text{B}\$3+\$\text{B}\$4)),\text{A}10).$$

The other instructions are the same.

Calculation of the patient’s venous haematocrit after the exchange transfusion

(The following instructions presuppose that the previous ones have been correctly performed).

Enter text and formulae contained in Table VI.

Table VI.

Instructions to calculate the venous haematocrit of the patient

Cell	Text to be entered
E9	Patient’s venous haematocrit
	Formula to be entered
E10	=$B$5* POWER(1−$B$4/$B$3/$B$7,A10) + $B$6*(1− POWER(1−$B$4/$B$3/$B$7,A10))

Copy cell E10 into cells E11–E35 (or further on, if numbering continues past A35). Cells E10–E35 will show the venous haematocrit of the patient after each exchange cycle.

If blood is first transfused, the formula to be entered into E10 is:

$$\begin{array}{c}=\$\text{B}\$5*\text{POWER}(1-\$\text{B}\$4/(\$\text{B}\$3+\$\text{B}\$4)/\\ \$\text{B}\$7,\text{A}10)+\$\text{B}\$6*(1-\text{POWER}(1-\$\text{B}\$4/(\$\text{B}\$3+\$\text{B}\$4)/\\ \$\text{B}\$7,\text{A}10)).\end{array}$$

Calculation of the percentage of haemoglobin S

(The following instructions presuppose that the previous ones have been correctly performed).

Enter the text, the value, and the formula contained in Table VII.

Table VII.

Instructions to calculate the residual percentage of haemoglobin S

Cell	Text to be entered
A8	Initial percentage of HbS
F9	Residual percentage of HbS
	Value to be entered
B8	Initial percentage of HbS, e.g. 70
	Formula to be entered
F10	=$B$5* POWER(1−$B$4/$B$3/$B$7,A10)/E10*$B$8

Copy cell F10 into cells F11–F35 (or further on, if numbering continues past A35). Cells F10–F35 will show the percentage of haemoglobin S after each exchange cycle.

If blood is first transfused, the formula to be entered into F10 is:

$$=\$\text{B}\$5*\text{POWER}(1-\$\text{B}\$4/(\$\text{B}\$3+\$\text{B}\$4)/\$\text{B}\$7,\text{A}10)/\text{E}10*\$\text{B}\$8.$$