Therapeutic apheresis is aimed at removing a blood constituent, be it a cell or a plasma solute. A partial exception is thrombotic thrombocytopaenic purpura (TTP): in this case the objective of apheresis is to replenish the body's stores of ADAMTS13, a protease that degrades von Willebrand factor multimers1, 2. At any rate, it should be appreciated that removal or replenishment follow exactly the same laws; only, the numerical value should be intended either as a percent decrease or as a percent increase, respectively.
Apheresis can be performed with an intermittent flow cell separator, and in this case the removal kinetics obeys the same laws described in the previous paper of this series3, dedicated to exchange transfusion, or with a continuous flow machine. This paper only concerns continuous flow kinetics.
Rationale of plasma exchange
Plasma exchange has been proposed for a wide array of diseases4. As already stated, it is supposed to exert its effect by removing pathogenic substances. The efficacy of the removal depends on the following factors.
- The distribution space of the substance. Red cells are only present intravascularly; 55%, 58%, and 22% of IgG, IgA, and IgM, respectively, is extravascular5; bilirubin and ammonia also diffuse in the intracellular space. Obviously, plasma exchange only removes the intravascular portion, unless equilibration between the compartments already occurs during the procedure (see below).
- Synthetic and catabolic rates. In a steady state, synthesis and catabolism are balanced. However, when immunoglobulins are acutely removed by plasmapheresis, the catabolic rate decreases, in absolute values, because of the lower plasma concentration. In addition, the fractional catabolic rate of IgG is not constant and is lower at low plasma concentrations6. As a result, the recovery rate seems faster than expected. In any case, the effects of plasma exchange are transitory5, 7 and the recovery rate depends on the catabolic rate and the half-life of the substance. Those values vary widely: e.g., they are 7% and 22 days, respectively, for IgG, and 150% and 0.6 days for FVIII5.
- The equilibration rate between the compartments (intravascular/extravascular space; intracellular/ extracellular space), that constitute the distribution space of a substance. A fast equilibration means a quick rebound. This may also explain why the removal of some substances is lower than expected8: e.g., after an exchange transfusion, where 87% of the red cells were removed, bilirubin was still at 60% of the initial concentration9. The bilirubin mass-transfer coefficient of the cell membrane has been calculated as 0.2 L/min10. In contrast, high molecular weight substances, such as immunoglobulins, equilibrate at a rate of 1-3%/hour5.
Removal kinetics of continuous flow plasma exchange
The following formula was proposed by Wiener and Wexler for the kinetics of exchange transfusion11, although, in fact, it describes the kinetics of continuous flow plasma exchange:
 |
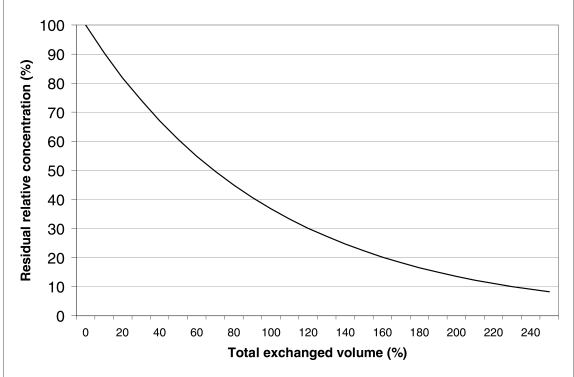
where v is the total exchanged volume, V is the patient's plasma volume and e is the transcendental number, base of the natural logarithms. The derivation of the formula may be found in Appendix A. Figure 1 shows the relative intravascular concentration of a substance during plasma exchange, as predicted by (1). The curve is exponential and the efficiency of the procedure decreases as the exchanged volume increases.
Figure 1.
Removal of a hypothetical substance during a continuous flow plasma exchange. The curve is based on the following assumptions: the patient's plasma volume remains constant; the substance is only intravascular, or there is no equilibration with the extravascular compartment; synthesis and catabolism can be ignored. In these conditions, approximately 63% or 86% of the substance is removed, when one or two plasma volumes, respectively, have been exchanged.
Formula (1) is only valid when a number of assumptions are valid. In particular, the following two assumptions deserve close scrutiny:
- the substance to be removed is only intravascular, or the equilibration is slow;
- the patient's plasma volume remains constant during the procedure.
Effect of the diffusion rate of the substance
High molecular weight molecules, such as immunoglobulins or low density lipoproteins, equilibrate very slowly5, 12. Accordingly, their removal kinetics follows the one-compartment model at the basis of (1). However, the more a substance is diffusible, the less formula (1) is adequate. The faulty part of the formula is V, the patient's plasma volume. In fact, a perfectly diffusible molecule would behave as if the whole distribution space were exchanged12. Therefore, V should be intended as the effective distribution space of the substance, i.e. the intravascular volume plus the portion of the extravascular/intracellular volume that equilibrates during the procedure.
Changes in the patient's plasma volume during the procedure
Generally, the plasma removed during the procedure is replaced with an equal volume of saline, albumin and/or colloids. However, this does not guarantee the constancy of the patient's blood volume. Particularly in cases of hyperviscosity syndrome, plasma volume is greatly increased and undergoes acute changes during the procedure13. The patient's plasma volume can be estimated with sufficient accuracy by means of a nomogram14, but this nomogram is not adequate for patients with splenomegaly or paraproteinemia14. In those cases, it has been suggested14 that the data collected in the first exchange procedure be used to calculate V, rearranging (1) for this purpose:
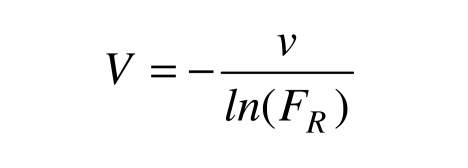 |
where FR is the residual fraction and ln means the natural logarithm. However, the obtained estimate would be reliable only for the same patient and the same v, at the same paraprotein concentration: i.e. in an exactly identical situation. Moreover, there is no empirical confirmation of the validity of this approach.
The patient's plasma volume also varies when the exchange is not isovolumetric. In this case, the appropriate formula is the following (see Appendix A):
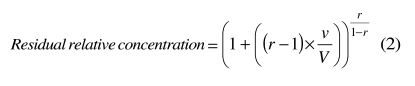 |
where r is the ratio between the volumes infused and withdrawn and v is the volume withdrawn. Formula (2) assumes that r is constant during the procedure and that the patient's plasma volume decreases or increases, accordingly.
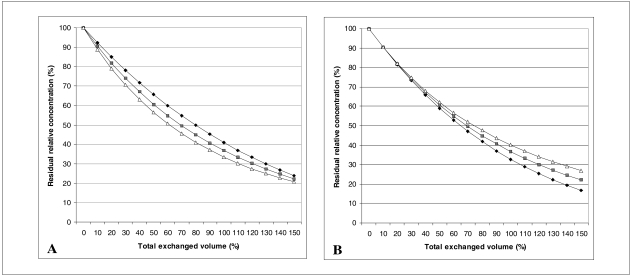
Panel A of figure 2 shows the concentration of a hypothetical substance when r is 0.8 or 1.2, i.e. when the infused volume is 20% less or 20% more than the removed volume. Apparently, the exchange seems more efficient when r >1. However, if the patient's plasma volume rapidly returns to the initial value after the procedure, as it should in most cases, the final results are quite opposite, as illustrated in panel B of figure 2. The formula applied in panel B of figure 2 includes a correction factor equal to the ratio between the final and the initial plasma volumes. After some simplification (see Appendix A), the formula now becomes:
Figure 2.
Residual relative concentration of a hypothetical substance during a plasma exchange. Comparison of an isovolumetric exchange (▪) and a 20% over return (Ä) or a 20% under return (♦). Panel A: results at the end of the procedure. Panel B: results after the the patient’s plasma volume has been restored to normal. Judging from Panel A, over return would seem preferable, but when the effect of the increased plasma volume is subtracted (Panel B), under return emerges as the most effective strategy.
 |
The difference in efficiency between the procedures conducted at different r values progressively increases together with the ratio v/V (Figure 2, panel B). Up to a ratio of 1 (the exchange of one plasma volume), the difference is small and probably not clinically significant. On the other hand, many patients would not tolerate a greater exchange with under return, because of the contraction of the plasma volume. This severely limits the practical applicability of under return.
Other cases in which (1) and (3) are not applicable
Both (1) and (3) assume that the replacement solution mixes immediately and completely with the circulating blood, the anticoagulant does not enter the circulation and its volume is subtracted from the removed volume. In the case of selective removal, there is no replacement solution and the anticoagulant returns to the patient. On the other hand, most immunoadsorption systems use heparin as an anticoagulant, which does not introduce a significant dilution. In fact, the main limitation to the use of (1) in those cases is the efficiency of removal: immunoadsorption systems do not remove 100% of the substance from the processed plasma and the efficiency varies during the procedure15.
A further source of error is the use of double-lumen catheters: in these cases the first assumption is not valid and part of the replacement solution is immediately removed16. In centrally placed catheters, the rate of recirculation is generally no greater than 10%, unless the inflow and outflow lines are reversed16. If the recirculation rate is known, the exchanged volume should be decreased accordingly, before being entered into the formulae.
However, the main limit of the above formulae is that the concentration of the substance to be removed is often not linearly related to the clinical symptoms. Moreover, the formulae do not offer clues to the rebound rate.
Removal of pathogenic substances and clinical symptoms
In many immune diseases, a specific pathogenic antibody has not been identified or the evidence of a causal relationship is lacking17. In the hyperviscosity syndrome of paraproteinemia, the relationship between protein levels and clinical symptoms is not linear and it is different, according to the patient18. In myasthenia gravis, acetylcholine receptor antibody levels correlate poorly with neuromuscular symptoms, but the changes in antibody concentration seem to predict the clinical course19.
Rebound and overshoot
“Rebound” is the return to baseline levels. “Overshoot” occurs when baseline levels are exceeded. The recovery of plasma constituents after plasma exchange has been studied in some detail8, 20, 21. Most coagulation factors and complement components C3 and C4 usually return to pre-exchange values by 72 hours or less8, 20. IgM, fibrinogen and cholesterol have a prolonged recovery of 1-2 weeks8, 20, 21 and it may take IgG more than 2 weeks to return to baseline levels8. Many patients, who underwent three or four exchanges of 50% of the plasma volume in 1-2 weeks, developed hypogammaglobulinaemia20. Plasma exchange was also very effective in removing immune complexes20. In rabbits, overshoot was only observed when the immunoadsorption column released antigen, leading to an increased immune response22-24. However, the behaviour of a particular antibody is unpredictable: in a case of TTP resistant to plasma exchange, ADAMTS13-inhibitor activity increased abruptly more than 3-fold 7 days after beginning the therapy, to decrease under baseline levels after less than 10 days more25. Other cases of overshoot have been documented26 and this led to the concept of synchronisation and pulse therapy26, 27. The idea is that antibody depletion by plasmapheresis induces a proliferation of antibody-producing cells, making them more sensitive to cytotoxic immunosuppression26. However, overshoot is not commonly observed in man28 and a randomised clinical trial failed to show any clinical benefit of pulse/synchronisation in lupus nephritis29.
A comprehensive model of plasma exchange kinetics
Formulae (1) and (3) derive from a one-compartment model and only regard events occurring during the procedure or immediately after. Kellog and Hester12 developed a more ambitious model, including a second (extravascular) compartment and considering also synthesis and catabolism. The aim was to predict post-exchange events and establish the optimal interval between the procedures. Unfortunately, many variables appearing in their equations, such as those representing lymphatic and transmembrane flow rates, synthesis, and catabolism, are both patient-dependent and unknown. The Authors tried to estimate them in the first procedures, but the predictions did not always agree with actual data. This is not surprising: patients are usually treated with plasma exchange in unstable periods of their clinical course and the synthetic rate, in particular, is subject to change (see above).
Automated red cell exchange
Red cell exchange is used in the treatment or the prevention of complications of sickle cell disease30 and for a few other indications4, 13, 31. Formulae (1) and (2) are also suitable for red cell exchange, provided that the meanings of the variables are changed appropriately: in (1), v becomes the volume of pure red cells removed and transfused and V is the patient's red cell volume; in (2), v becomes the volume of pure red cells removed, V is the patient's red cell volume at the beginning of the procedure, and r is the ratio between the volumes of pure red cells transfused and removed. In this context, formula (3) is not suitable, because the red cell mass of the patient at the end of the procedure does not return rapidly to the baseline value.
Both (1) and (2) assume that the haematocrit of the red cells used for replacement is constant. However, the formuale are not influenced by changes in the blood volume or the haematocrit of the patient, because the autologous red cells are centrifuged before being removed.
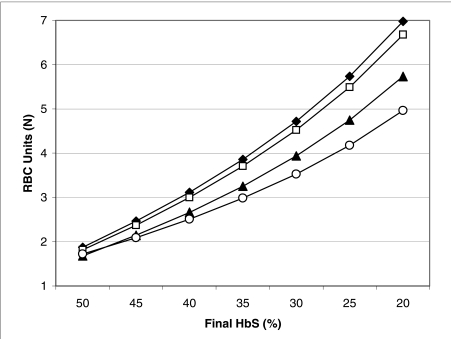
On the other hand, in order to apply (1) or (2), the user must take into account the different haematocrit of the blood withdrawn and transfused. Fortunately, the sophisticated software of modern cell separators facilitates this task, performing most of the calculations automatically. The curious reader can, however, find the relevant formulae in Appendix A. Cell separators can also automatically adjust the inflow and outflow rates so as to balance the volumes of red cells exchanged, or even to reach the desired final haematocrit and haemoglobin S concentration. However, in the case of sickle cell disease, cell separators are not programmed to perform the red cell exchange in the most efficient way automatically: the best technique is a three-step procedure32, 33, including a first phase, in which the removed red cells are replaced with albumin and/or saline; a second phase, during which equal volumes of patient and donor red cells are exchanged; a final phase, in which donor red cells are transfused to reach the desired final haematocrit. Figure 3 also shows that the efficiency of the three-step procedure increases as the minimum allowed haematocrit decreases. Apparently, the patients tolerate well the temporary withdrawal of 300-500 mL of red cell concentrates, even at initial haematocrits as low as 20%33. Particularly in patients with multiple red cell alloantibodies, the possibility to limit the amount of necessary donor blood is invaluable.
Figure 3.
Number of units of red cell concentrates necessary to decrease the haemoglobin S concentration to the desired value, during a red cell exchange. Initial conditions are as follows: haemoglobin S concentration: 70%; blood volume: 3.5L; haematocrit: 30%. The final desired haematocrit is 33%. The average volume and haematocrit of donor red cell concentrates is 300 mL and 65%, respectively. Comparison of a simple exchange (♦), in which donor red cells are transfused in slight excess to reach the desired haematocrit; a two-step exchange (□), in which equal volumes of donor’s and patient’s red cells are initially exchanged, followed by a top-up transfusion to increase the haematocrit; a three-step exchange, in which the patient’s red cells are initially withdrawn without replacement, followed by an isovolumetric exchange and, finally, by a top-up transfusion (▴= minimum allowed haematocrit: 25%; ○ = minimum allowed haematocrit: 20%). The three-step procedure is preferable and its efficiency increases as the minimum allowed haematocrit decreases.
The prediction by computer simulation of the rate of increase of haemoglobin S after the exchange has been attempted with good results in three out of four patients34.
Therapeutic leucapheresis and thrombocytapheresis
Mathematical modelling of therapeutic leucapheresis and thrombocytapheresis is difficult because the efficiency of removal is not 100% and depends on physical properties of the cells (type of white cell; dimension and density of platelets). Moreover, granulocytes have a very rapid turnover in blood and part of them are in a marginated pool35.
Conclusions
When planning the duration and frequency of plasma exchange, it should be considered that the efficiency of plasma exchange decreases as the total exchanged volume increases and that high molecular weight substances require many hours or days to diffuse from the extravascular to the intravascular compartment. Replacing at a lower rate than removing (“under return”) increases the efficiency of the procedure but exposes the patient to hypovolaemia. A similar concept (“three-step exchange”) improves the efficiency of red cell exchange and is clinically safe.
Appendix A – Derivation of the formulae
Removal kinetics of an isovolumetric plasma exchange
If we denote the initial concentration of a substance by C0, the initial quantity (Q0) will be, where V is the plasma volume of the patient. During the exchange, Q will vary according to the equation Q = C× V (1). In an infinitesimal time interval dt, equal volumes of plasma will be removed and replaced by the substitution fluid: , and the removed quantity of the substance will be dQ = − k × dt × C. From (1) we can also derive dQ = C × dV + V × dC, but dV = 0 (the patient’s plasma volume is supposed not to change during the procedure). Therefore − k × dt × C = V × dC (2). Dividing by C (supposed ≠ 0) and integrating both terms of (2): , we obtain , where ln denotes the natural logarithm and A is the integration constant. From the case t = 0, we obtain A = 0.
Denoting by v the exchanged volume (= k× t), we get:
| (3) |
where “relative concentration” means the concentration expressed as a fraction of the initial value .
Removal kinetics of a non-isovolumetric plasma exchange
In this case, dvin ≠ dvout, dvin = k1 × dt, dvout = k2 × dt, and dV = (k1 − k2)×dt. The patient’s plasma volume varies in time according to the equation V = V0 + (k1 − k2)×t (4), where V0 is the plasma volume at the beginning of the procedure. In an infinitesimal time interval dt, the removed quantity of the substance will be dQ = − k2 × dt × C.
Repeating the steps outlined in the previous paragraph, with the appropriate changes, we have − k2 × dt × C = (k1 − k2)× dt × C + V × dC and (5). Substituting the right term of (4) for V and integrating both terms of (5), we get
From the case t = 0, we obtain A = 0. Therefore, we have: .
From (4) we know that k2× t is the volume of plasma removed at time t (vout).
If we denote by r the ratio vin/vout (= k1/k2), by means of a few substitutions we get:
| (7) |
where vout and V0 have the same meaning as v and V in (3), respectively.
Formula (7) gives the final concentration of the hypothetical substance at the end of the exchange, when the patient’s plasma volume is V0 + (k1 − k2)×t = V0 + (r − 1)× vout.
However, in most cases, the plasma volume of the patient will soon return to the initial value.
Therefore, the final concentration of the substance, provided there is no diffusion and no synthesis or catabolism, will be equal to , or .
Substituting the right term of (7) for C we get:
| (8) |
Removal kinetics of automated red cell exchange*
Cell separators separate red cells by centrifugation and remove them at a constant haematocrit, irrespective of the haematocrit of whole blood. Therefore, if we accept the approximation that the red cells used for replacement also have a constant haematocrit, formulae (3) and (7) apply. In (3), v represents the volume of pure red cells removed (equal to the transfused volume) and V is the patient’s red cell volume; in (7), vout is the volume of pure red cells removed, V0 is the patient’s red cell volume at the beginning of the procedure, and r is the ratio between the volumes of pure red cells transfused and removed. When planning a red cell exchange for a patient with sickle cell disease, the aim is to decrease the concentration of haemoglobin S under a threshold level and, generally, to increase the haematocrit moderately. We know the following initial values of the patient: blood volume (V, estimated), venous haematocrit (HV, measured), red cell volume (RB = HV × k × V, where k is the correction for the body haematocrit36), concentration of haemoglobin S (HbS0, measured). We also know the average haematocrit of the red cell concentrates to be used as replacement (HT), the haematocrit of the red cell concentrates removed by the cell separator (HR), the final HbS concentration (HbSF) and haematocrit to be reached (HF). The unknown variables are: the volume of red cell concentrates to be transfused (VT) and removed (VR), and the ratio between them (r). We start with a set of three equations:
| (9) |
| (10) |
| (11) |
where (9) is simply equation (7) in a more explicit form, (10) is just the definition of r, and (11) is also by definition, provided that the blood volume remains constant or returns to the initial value rapidly, and all transfused red cells survive up to the end of the procedure. By a few substitutions, we obtain:
| (12) |
and
| (13) |
If we do not want to change the patient’s haematocrit, (3) applies:
| (14) |
By definition, we know that . Therefore, solving (14), we obtain:
| (15) |
Two-step or three-step red cell exchange
In a two-step exchange, an isovolumetric red cell exchange is followed by a top-up transfusion to increase the patient’s haematocrit. In this case, the first phase follows (14) and the total volume of donor red cells necessary to decrease the haemoglobin S concentration to HbSF and to increase the haematocrit to HF is:
| (16) |
The portion of VT to be used in the top-up transfusion step (VU) is:
| (17) |
In a three-step exchange, a two-step procedure is preceded by the withdrawal of the patient’s red cells, so as to reach a minimum allowed haematocrit (Hm). In this case the total volume of the donor’s red cells is:
| (18) |
The amount of the patient’s red cells to be removed initially (VP) is:
| (19) |
and the portion of VT to be used in the top-up transfusion step (VU) is:
| (20) |
Appendix B – Programming a spreadsheet*
(The reader is referred to the previous article3 of this series for a brief introduction to spreadsheets).
Continuous flow plasma exchange –isovolumetric
Open a new sheet. Enter the text, values and formulae listed in table I.
Table I.
Instructions for calculating the residual concentration (%) after an isovolumetric plasma exchange
| Cell | Text to be entered |
|---|---|
| A1 | Kinetics of continuous flow plasma exchange - isovolumetric |
| A3 | Patient’s blood volume (mL) |
| A4 | Patient’s initial venous haematocrit (%) |
| A5 | Correction factor for the body haematocrit |
| A6 | Exchanged volume (mL) |
| A8 | Patient’s plasma volume (mL) |
| A9 | Exchanged volume (%) |
| A10 | Residual concentration (%) |
| Value to be entered | |
| B3 | Blood volume of the patient (mL), e.g. 4,500 |
| B4 | Initial haematocrit of the patient, e.g. 30 |
| B5 | Correction factor for body haematocrit: 0.91 |
| B6 | Volume of plasma exchanged (mL), e.g. 3,000 |
| Formula to be entered | |
| B8 | =B3*(1−B4/100*B5) |
| B9 | =B6/B8*100 |
| B10 | =EXP(−B6/B8)*100 |
Cell B8 contains the patient’s plasma volume, as calculated from the blood volume and haematocrit; B9 contains the percentage of the plasma volume exchanged, and B10 the residual concentration of a plasma constituent, calculated as a percentage of the initial value.
Continuous flow plasma exchange –non-isovolumetric
Open a new sheet. Enter the text, values and formulae listed in table II. Cells B9–B11 contain the patient’s plasma volume, the percentage of the plasma volume removed, and the residual concentration of a plasma constituent, respectively.
Table II.
Instructions for calculating the residual concentration (%) after a non-isovolumetric plasma exchange
| Cell | Text to be entered |
|---|---|
| A1 | Kinetics of continuous flow plasma exchange – non-isovolumetric |
| A3 | Patient’s blood volume (mL) |
| A4 | Patient’s initial venous haematocrit (%) |
| A5 | Correction factor for the body haematocrit |
| A6 | Removed volume (mL) |
| A7 | Ratio between the infused and the removed volumes |
| A9 | Patient’s plasma volume (mL) |
| A10 | Removed volume (%) |
| A11 | Residual concentration (%) |
| Value to be entered | |
| B3 | Blood volume of the patient (mL), e.g. 4,500 |
| B4 | Initial haematocrit of the patient, e.g. 30 |
| B5 | Correction factor for body haematocrit: 0.91 |
| B6 | Volume of plasma removed (mL), e.g. 3,000 |
| B7 | Ratio between the infused and the removed volumes, e.g. 0.8 |
| Formula to be entered | |
| B9 | =B3*(1−B4/100*B5) |
| B10 | =B6/B9*100 |
| B11 | =POWER(1+((B7−1)*B6/B9), 1/(1−B7))*100 |
Continuous flow red cell exchange –isovolumetric
Open a new sheet. Enter the text, values and formulae listed in table III. Cell B11 contains the patient’s red cell volume; B12 contains the volume of the donor’s red cell concentrate necessary for the exchange.
Table III.
Instructions for calculating the volume of donor red cells necessary to obtain the desired residual concentration of haemoglobin S after an isovolumetric red cell exchange
| Cell | Text to be entered |
|---|---|
| A1 | Kinetics of continuous flow red cell exchange – isovolumetric |
| A3 | Patient’s blood volume (mL) |
| A4 | Patient’s initial venous haematocrit (%) |
| A5 | Correction factor for the body haematocrit |
| A6 | Haematocrit of the removed blood (%) |
| A7 | Haematocrit of the transfused blood (%) |
| A8 | Initial concentration of HbS (%) |
| A9 | Desired final concentration of HbS (%) |
| A11 | Patient’s red cell volume (mL) |
| A12 | Volume of red cell concentrate to be exchanged (ml) |
| Value to be entered | |
| B3 | Blood volume of the patient (mL), e.g. 4,500 |
| B4 | Initial haematocrit of the patient, e.g. 30 |
| B5 | Correction factor for body haematocrit: 0.91 |
| B6 | Haematocrit of the removed blood (%), e.g. 80 |
| B7 | Haematocrit of the transfused blood (%), e.g. 60 |
| B8 | Initial concentration of HbS (%), e.g. 70 |
| B9 | Desired final concentration of HbS (%), e.g. 30 |
| Formula to be entered | |
| B11 | =B3*B4/100*B5 |
| B12 | = − B3*B5*B4/B7*LN(B9/B8) |
Continuous flow red cell exchange –non-isovolumetric
Open a new sheet. Enter the text, values and formulae listed in table IV. Cell B12 contains the patient’s red cell volume; B13 contains the ratio between the transfused and the removed volumes, and B14 contains the volume of the donor’s red cell concentrate necessary for the exchange.
Table IV.
Instructions for calculating the volume of donor red cells necessary to obtain the desired final haematocrit and residual concentration of haemoglobin S after a non-isovolumetric red cell exchange
| Cell | Text to be entered |
|---|---|
| A1 | Kinetics of continuous flow red cell exchange – non-isovolumetric |
| A3 | Patient’s blood volume (mL) |
| A4 | Patient’s initial venous haematocrit (%) |
| A5 | Correction factor for the body haematocrit |
| A6 | Haematocrit of the removed blood (%) |
| A7 | Haematocrit of the transfused blood (%) |
| A8 | Initial concentration of HbS (%) |
| A9 | Desired final concentration of HbS (%) |
| A10 | Desired final haematocrit (%) |
| A12 | Patient’s initial red cell volume (mL) |
| A13 | Ratio between the transfused and the removed volumes |
| A14 | Volume of donor red cell concentrate necessary (mL) |
| Value to be entered | |
| B3 | Blood volume of the patient (mL), e.g. 4,500 |
| B4 | Initial haematocrit of the patient, e.g. 30 |
| B5 | Correction factor for body haematocrit: 0.91 |
| B6 | Haematocrit of the removed blood (%), e.g. 80 |
| B7 | Haematocrit of the transfused blood (%), e.g. 60 |
| B8 | Initial concentration of HbS (%), e.g. 70 |
| B9 | Desired final concentration of HbS (%), e.g. 30 |
| B10 | Desired final haematocrit (%), e.g. 33 |
| Formula to be entered | |
| B12 | =B3*B4/100*B5 |
| B13 | =1/(1+(LN(B10/B4)/LN(B9/B8))) |
| B14 | =B3*B5*(B10/100−B4/100)/(B7/100*(1−1/B13)) |
Continuous flow red cell exchange – three-step procedure
Open a new sheet. Enter the text, values and formulae listed in table V. Cell B13 contains the patient’s red cell volume; B14 the volume of patient’s red cells to be removed in the first phase; B15 the volume of the donor’s red cell concentrate to be exchanged in the second phase; B16 the volume of donor red cell concentrate to be transfused at the end; B17 the total volume of the donor’s red cell concentrate needed for the exchange.
Table V.
Instructions for calculating the volume of donor red cells necessary to obtain the desired final haematocrit and residual concentration of haemoglobin S after a three-step red cell exchange
| Cell | Text to be entered |
|---|---|
| A1 | Kinetics of continuous flow red cell exchange – non-isovolumetric |
| A3 | Patient’s blood volume (mL) |
| A4 | Patient’s initial venous haematocrit (%) |
| A5 | Correction factor for the body haematocrit |
| A6 | Haematocrit of the removed blood (%) |
| A7 | Haematocrit of the transfused blood (%) |
| A8 | Initial concentration of HbS (%) |
| A9 | Desired final concentration of HbS (%) |
| A10 | Desired final haematocrit (%) |
| A11 | Minimum allowed haematocrit (%) |
| A13 | Patient’s initial red cell volume (mL) |
| A14 | Volume of patient’s red cells to be removed in the first phase (mL) |
| A15 | Volume of donor red cell concentrate to be exchanged in the second phase (mL) |
| A16 | Volume of donor red cell concentrate to be transfused at the end (mL) |
| A17 | Total volume of donor red cell concentrate needed for the exchange (mL) |
| Value to be entered | |
| B3 | Blood volume of the patient (mL), e.g. 4,500 |
| B4 | Initial haematocrit of the patient, e.g. 30 |
| B5 | Correction factor for body haematocrit: 0.91 |
| B6 | Haematocrit of the removed blood (%), e.g. 80 |
| B7 | Haematocrit of the transfused blood (%), e.g. 60 |
| B8 | Initial concentration of HbS (%), e.g. 70 |
| B9 | Desired final concentration of HbS (%), e.g. 30 |
| B10 | Desired final haematocrit (%), e.g. 33 |
| B11 | Minimum allowed haematocrit (%), e.g. 25 |
| Formula to be entered | |
| B13 | =B3*B4/100*B5 |
| B14 | =B3*B5/B6*100*(B4/100−B11/100) |
| B15 | = − B3*B5*B11/B7*LN(B10/B11*B9/B8) |
| B16 | =B3*B5/B7*100*(B10/100−B11/100) |
| B17 | =B3*B5/B7*100*(B10/100−B11/100*(1+LN(B10/B11*B9/B8))) |
Footnotes
In order to simplify the appearance of the equations, the haematocrits represented in the formulaE of this section, are intended as fractions: e.g., 0.3 instead of 30%.
Italian readers using the localized (Italian) versions of the spreadsheets should follow the instructions in the Italian translation of this paper, which is available on line at http://www.transfusionmedicine.org/. Briefly, “potenza” should be substituted for “power” and “ ;” should be substituted for “ ,”.
References
- 1.Furlan M, Robles R, Galbusera M, et al. von Willebrand factor-cleaving protease in thrombotic thrombocytopenic purpura and the hemolytic-uremic syndrome. N Engl J Med. 1998;339:1578–84. doi: 10.1056/NEJM199811263392202. [DOI] [PubMed] [Google Scholar]
- 2.Rock GA. Management of thrombotic thrombocytopenic purpura. Br J Haematol. 2000;109:496–507. doi: 10.1046/j.1365-2141.2000.01941.x. [DOI] [PubMed] [Google Scholar]
- 3.Reverberi R, Reverberi L. Removal kinetics of exchange transfusion. Blood Transfusion. 2007;5:93–101. doi: 10.2450/2007.0018-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McLeod BC, editor. Special issue: Clinical applications of therapeutic apheresis. J Clin Apheresis. 2000;15:1–159. doi: 10.1002/(sici)1098-1101(2000)15:1/2<1::aid-jca1>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 5.Kaplan AA. A Practical Guide to Therapeutic Plasma Exchange. Malden, MA: Blackwell Science; 1999. [Google Scholar]
- 6.Waldmann TA, Strober W. In: Metabolism of immunoglobulins. Progress in Allergy. Kallos P, Waksman BH, editors. New York: S. Karger AG; 1969. (Cit. in ref. ) [Google Scholar]
- 7.Volkin RL, Starz TW, Winkelstein A, et al. Changes in coagulation factors, complement, immunoglobulins, and immune complex concentrations with plasma exchange. Transfusion. 1982;22:54–8. doi: 10.1046/j.1537-2995.1982.22182154218.x. [DOI] [PubMed] [Google Scholar]
- 8.Orlin JB, Berkman EM. Partial plasma exchange using albumin replacement: removal and recovery of normal plasma constituents. Blood. 1980;56:1055–9. [PubMed] [Google Scholar]
- 9.Greenough A. Rhesus disease: postnatal management and outcome. Eur J Pediatr. 1999;158:689–93. doi: 10.1007/s004310051180. [DOI] [PubMed] [Google Scholar]
- 10.Magosso E, Ursino M, Colì L, et al. A modeling study of bilirubin kinetics during molecular adsorbent recirculating system sessions. Artif Organs. 2006;30:285–300. doi: 10.1111/j.1525-1594.2006.00216.x. [DOI] [PubMed] [Google Scholar]
- 11.Wiener AS, Wexler IB. The use of heparin when performing exchange blood transfusions in newborn infants. J Lab Clin Med. 1946;31:1016–9. [PubMed] [Google Scholar]
- 12.Kellogg RM, Hester JP. Kinetics modeling of plasma exchange: Intra- and post-plasma exchange. J Clin Apheresis. 1988;4:183–7. doi: 10.1002/jca.2920040409. [DOI] [PubMed] [Google Scholar]
- 13.Klein HG. Principles of apheresis. In: Anderson KC, Ness PM, editors. Scientific Basis of Transfusion Medicine. Philadelphia PA: WB Saunders; 1994. pp. 781–96. [Google Scholar]
- 14.Sprenger KBG, Huber K, Kratz W, et al. Nomograms for the prediction of patient's plasma volume in plasma exchange therapy from height, weight, and hematocrit. J Clin Apheresis. 1987;3:185–90. doi: 10.1002/jca.2920030313. [DOI] [PubMed] [Google Scholar]
- 15.Matic G, Hofmann D, Winkler R, et al. Removal of immunoglobulins by a protein A versus an antihuman immunoglobulin G-based system: evaluation of 602 sessions of extracorporeal immunoadsorption. Artif Organs. 2000;24:103–7. doi: 10.1046/j.1525-1594.2000.06490.x. [DOI] [PubMed] [Google Scholar]
- 16.Depner AT. Catheter performance. Semin Dial. 2001;14:425–31. doi: 10.1046/j.1525-139x.2001.00106.x. [DOI] [PubMed] [Google Scholar]
- 17.Hershko AY, Naparstek Y. Removal of pathogenic autoantibodies by immunoadsorption. Ann N Y Acad Sci. 2005;1051:635–46. doi: 10.1196/annals.1361.108. [DOI] [PubMed] [Google Scholar]
- 18.Beck JR, Quinn BM, Meier FA, et al. Hyperviscosity syndrome in paraproteinemia. Managed by plasma exchange; monitored by serum tests. Transfusion. 1982;22:51–3. doi: 10.1046/j.1537-2995.1982.22182154217.x. [DOI] [PubMed] [Google Scholar]
- 19.Yeh JH, Chen WH, Chiu HC. Predicting the course of myasthenic weakness following double filtration plasmapheresis. Acta Neurol Scand. 2003;108:174–8. doi: 10.1034/j.1600-0404.2003.00107.x. [DOI] [PubMed] [Google Scholar]
- 20.Volkin RL, Starz TW, Winkelstein A, et al. Changes in coagulation factors, complement, immunoglobulins, and immune complex concentrations with plasma exchange. Transfusion. 1982;22:54–8. doi: 10.1046/j.1537-2995.1982.22182154218.x. [DOI] [PubMed] [Google Scholar]
- 21.Filomena CA, Filomena AP, Hudock J, et al. Evaluation of serum immunoglobulins by protein electrophoresis and rate nephelometry before and after therapeutic plasma exchange. Am J Clin Pathol. 1992;98:243–8. doi: 10.1093/ajcp/98.2.243. [DOI] [PubMed] [Google Scholar]
- 22.Schindhelm K, Charlton B, Antony G, et al. Antibody kinetics following extracorporeal removal. In: Smeby LC, Jørstad S, Widerøe T-E, editors. Immune and Metabolic Aspects of Therapeutic Blood Purification Systems. Basel: S Karger; 1986. pp. 329–37. [Google Scholar]
- 23.Harvey GK, Schindhelm K, Antony JH, et al. Membrane plasma exchange in experimental allergic neuritis: effect on antibody levels and clinical course. J Neurol Sci. 1988;88:207–18. doi: 10.1016/0022-510x(88)90218-3. [DOI] [PubMed] [Google Scholar]
- 24.Harvey GK, Schindhelm K, Pollard JD. IgG immunoadsorption in experimental allergic neuritis: effect on antibody levels and clinical course. J Neurol Neurosurg Psychiatry. 1989;52:865–70. doi: 10.1136/jnnp.52.7.865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Knöbl P, Haas M, Laczika K, et al. Immunoadsorption for the treatment of a patient with severe thrombotic thrombocytopenic purpura resistant to plasma exchange: kinetics of an inhibitor of ADAMTS13. J Thromb Haemost. 2003;1:187–9. doi: 10.1046/j.1538-7836.2003.00004.x. letter. [DOI] [PubMed] [Google Scholar]
- 26.Dau PC. Immunologic rebound. J Clin Apheresis. 1995;10:210–7. doi: 10.1002/jca.2920100410. [DOI] [PubMed] [Google Scholar]
- 27.Dau PC. The fundamental basis for therapeutic plasmapheresis in autoimmune diseases. Transfus Sci. 1996;17:235–44. [Google Scholar]
- 28.Derksen RHWM, Schuurman HJ, Gmelig Meyling FHJ. Rebound and overshoot after plasma exchange in humans. J Lab Clin Med. 1984;104:35–43. [PubMed] [Google Scholar]
- 29.Wallace DJ, Goldfinger D, Pepkowitz SH, et al. Randomized controlled trial of pulse/synchronization cyclophosphamide/ apheresis for proliferative lupus nephritis. J Clin Apheresis. 1998;13:163–6. doi: 10.1002/(sici)1098-1101(1998)13:4<163::aid-jca4>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 30.Danielson CFM. The role of red blood cell exchange transfusion in the treatment and prevention of complications of sickle cell disease. Ther Apher. 2002;6:24–31. doi: 10.1046/j.1526-0968.2002.00396.x. [DOI] [PubMed] [Google Scholar]
- 31.Weir EG, King KE, Ness PM, Eshleman SH. Automated RBC exchange transfusion: treatment for cerebral malaria. Transfusion. 2000;40:702–7. doi: 10.1046/j.1537-2995.2000.40060702.x. [DOI] [PubMed] [Google Scholar]
- 32.Kim HC, Dugan NP, Silber JH, et al. Erythrocytapheresis therapy to reduce iron overload in chronically transfused patients with sickle cell disease. Blood. 1994;83:1136–42. [PubMed] [Google Scholar]
- 33.Janes SL, Pocock M, Bishop E, et al. Automated red cell exchange in sickle cell disease. Br J Haematol. 1997;97:256–8. doi: 10.1046/j.1365-2141.1997.322675.x. [DOI] [PubMed] [Google Scholar]
- 34.Nifong TP, Bongiovanni MB, Gerhard GS. Mathematical modelling and computer simulation of erythrocytapheresis for SCD. Transfusion. 2001;41:256–63. doi: 10.1046/j.1537-2995.2001.41020256.x. [DOI] [PubMed] [Google Scholar]
- 35.Greer JP, Foerster J, Lukens JN, et al., editors. Wintrobe's Clinical Hematology. 11. Philadelphia, PA: Lippincott Williams & Wilkins; 2003. [Google Scholar]