Lossless Compression of Chemical Fingerprints Using Integer Entropy Codes Improves Storage and Retrieval

Abstract

Many modern chemoinformatics systems for small molecules rely on large fingerprint vector representations, where the components of the vector record the presence or number of occurrences in the molecular graphs of particular combinatorial features, such as labeled paths or labeled trees. These large fingerprint vectors are often compressed to much shorter fingerprint vectors using a lossy compression scheme based on a simple modulo procedure. Here we combine statistical models of fingerprints with integer entropy codes, such as Golomb and Elias codes, to encode the indices or the run-lengths of the fingerprints. After reordering the fingerprint components by decreasing frequency order, the indices are monotone increasing and the run-lenghts are quasi-monotone increasing, and both exhibit power-law distribution trends. We take advantage of these statistical properties to derive new efficient, lossless, compression algorithms for monotone integer sequences: Monotone Value (MOV) Coding and Monotone Length (MOL) Coding. In contrast with lossy systems that use 1,024 or more bits of storage per molecule, we can achieve lossless compression of long chemical fingerprints based on circular substructures in slightly over 300 bits per molecule, close to the Shannon entropy limit, using a MOL Elias Gamma code for run-lengths. The improvement in storage comes at a modest computational cost. Furthermore, because the compression is lossless, uncompressed similarity (e.g. Tanimoto) between molecules can be computed exactly from their compressed representations, leading to significant improvements in retrival performance, as shown on six benchmark datasets of drug-like molecules.

1 Introduction

In most modern chemoinformatics systems for small organic molecules, molecules are represented by fingerprint vectors^1–6 (and references therein). For a given molecule, the components of this vector record the binary presence/absence or the number of occurrences of particular features, such as functional groups or substructures. It is these fingerprints and the derived similarity measures,^7–10 such as the Tanimoto measure, that are used for efficiently searching large repositories, containing millions of compounds, such as PubChem, ZINC,¹¹ or ChemDB.¹²

In early chemoinformatics systems, these feature vectors were relatively short, with typically a few dozen components associated with a small basis of more or less hand-picked features derived mostly from expert chemical knowledge. In most modern systems, however, the major trend is towards the combinatorial construction of very long feature vectors associated with, for instance, all possible labeled paths up to a certain length (e.g.¹³). The advantage of these much longer representations is twofold: they do not rely on expert knowledge which may be incomplete or unavailable, and they can support extremely large numbers of molecules, such as those that are starting to become available in public repositories and commercial catalogs, as well as the recursively enumerable space of virtual molecules.¹⁴

These long vector representations are in turn compressed to shorter fingerprint vectors, of fixed or variable length. High-compressibility results directly from the sparseness of the long fingerprints. In most modern chemoinformatics systems, this compression is implemented using a simple folding operation described in detail in the next sections. The advantage of the compression is that it yields more compact representations that require less storage space and can be searched faster than the uncompressed version. The drawback of the folding compression, however, is that it is lossy: some information is lost during the compression. As a result, when similarity between molecules is measured by similarity between their compressed representations, retrieval quality deteriorates. And increasingly so, as the length of the compressed fingerprint is reduced.²

To address this problem, in Swamidass and Baldi, 2007¹⁵ we developed a mathematical approach for deriving better estimates of the uncompressed similarity from the lossy compressed-by-folding representations. Here we explore a different direction by deriving lossless fingerprint compression schemes using statistical models of fingerprints and integer entropy coding techniques.

2 Fingerprint Representations, Data, and Statistical Models

2.1 Fingerprint Representations

We use $\mathcal{A}$ to denote a molecule. We assume that molecules are represented by feature vectors, or fingerprints, of fixed-length N_*, denoted by ${\overrightarrow{A}}_{\ast }=\left(A_i\right)$. Because the focus of the algorithms to be presented is the compression of large sparse vectors, the particular set of features and labeling scheme used is not important. But to be specific, in the simulations we illustrate the methods using two different types of chemical features corresponding to two kinds of labeled subgraphs of the molecular graphs: (1) paths; and (2) and circular substructures. Molecular graphs are the familiar 2D representations, used ubiquitously in chemistry, where atoms are associated with labeled vertices and bonds with labeled edges. The details of the features and labeling schemes are given in the next section.

For simplicity, and because they are the most widely used, we present the compression algorithms for the case of binary fingerprints but we then also briefly show how the same principles can be applied immediately to fingerprints based on counts. We define the density of a fingerprint vector as the ratio of the number of non-zero components divided by the total length of the vector.

From binary fingerprints of fixed length N_*, two other equivalent representations that are important for our compression derivations can be obtained: the index representation and the run-length representation. The index representation indexes the fingerprint components that are set to one, whereas the run-length representation indexes the length of the corresponding runs (series of 0-bits followed by a 1-bit). For instance, if we consider the vector (1, 0, 0, 1, 0, 0, 0, 0, 1, 0) with N_* = 10 , the first, fourth, and ninth components are set to one and therefore the index representation is given by (1, 4, 9). The corresponding run-length representation is (0, 2, 4). Thus the index and run-length representations produce a variable-length vector of integers, which is already a form of compressed representation if the initial bit vector is sparse. To further compress the index or run-length representations, one must consider how to encode vectors of integers.

While we use N_* generically to denote the length of the long fingerprint vectors before the compression algorithms are applied, one should be aware of certain distinctions:

• N_tot is the number of all possible features, including some that may not be present in the data.

• N_obs is the total number of features observed across all the molecules in a given database (N_obs ≤ N_tot).

• N_hash is the size of the vector associated with the hash functions that are used to map features to random component locations of a large vector of size N_hash. In some very rare cases, collisions may occur where two different features are be mapped to the same location. This loss of information is very small when N_hash is large and will be ignored; in other words, in practical terms we are interested in lossless compression starting from the vector of size N_hash.

• N_posthash is the length of the fingerprints after a trivial post-processing step which removes all the 0-columns corresponding to components (features) that are absent in all the molecules from a given database.

So, in typical cases: N_hash is larger than N_obs, and N_obs is equal to N_posthash or slightly larger if there are collisions.

2.2 Fingerprint Data

To develop and test the compression algorithms, we use small molecules from the ChemDB database.¹² For illustration purposes, the results reported here are obtained using a large random sample of 50,000 molecules from ChemDB. Retrieval capabilities are also tested using the datasets in Stahl and Rarey.¹⁶ In the simulations we illustrate the methods using fingerprints associated with two schemes: labeled paths of length up to eight (i.e. 9 atoms and 8 bonds), or labeled circular substructures of depth up to two, with Element (E) and Extended Connectivity (EC) labeling.

In the first scheme, referred to as paths throughout the paper, for each chemical we extract all labeled paths of length up to eight (i.e. 9 atoms and 8 bonds) starting from each vertex and using depth-first traversal of the edges in the corresponding molecular graph (Figure 1). Extracting paths in this manner requires approximately O(N D^2.5) steps, where D denotes the maximum path depth and N denotes the number of atoms in the molecule.^10,13 Hence roughly a constant cost per molecule. For this scheme, molecular graphs are labeled as follows; each vertex is labeled by the element (C,N,O, etc) of the corresponding atom and each edge is labeled by the type (single, double, triple, aromatic, and amide) of the corresponding bond. This scheme is closely related to the fingerprints used in many existing chemoinformatics systems, including the Daylight system.³

Figure 1.

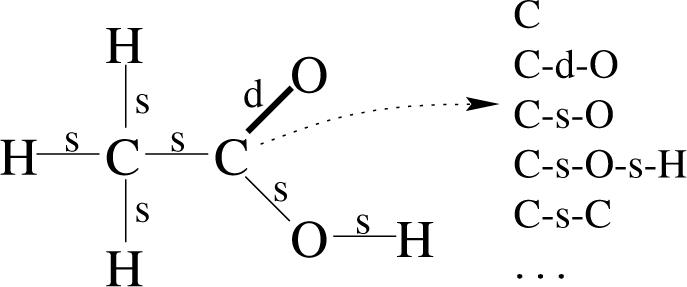
A molecule represented as a labeled graph. The labels on the vertices correspond to atom symbols and those on the edges describe the type of covalent bond between atoms (e.g. ‘s’ for single bond, ‘d’ for double bond). Also shown are examples of labeled paths of length 1 and 2 resulting from a depth-first search exploration of the graph, starting from one of the carbon atoms.

In the second scheme, referred to as circular throughout the paper, for each chemical we extract every circular substructure, of depth up to two, from the corresponding molecular graph. Circular substructures (see Hert et al.,¹⁷ Bender et al.,¹⁸ and Hassan et al.¹⁹) are fully explored labeled trees of a particular depth, rooted at a particular vertex. All the circular substructures of a molecule can be trivially listed using O(N D) steps, where D denotes the maximum tree depth and N denotes the number of atoms in the molecule. For this scheme, molecular graphs are labeled as follows: each vertex is labeled by the element (C,N,O, etc) and degree (1, 2, 3, etc) of the corresponding atom, and each edge is labeled as above. The degree of a vertex is given by the number of edges incident to that vertex or, equivalently, the number of atoms bonded to the corresponding atom. For example, propane would be labeled as C1sC2sC1 and ethene would be labeled as C1dC1. This scheme corresponds to the Extended Connectivity Fingerprints (ECFP) of the literature, which has been shown sometimes to outperform path-based fingerprint schemes in terms of storage size and retrieval.¹⁷

These two schemes are representative of the schemes typically used in chemical informatics systems. Results derived by using reasonable variations of these basic schemes, based on other combinatorial features or other labeling schemes (e.g. SYBYL by Tripos) ought to be robust and consistent with those reported here. All fingerprints are computed using in-house programs written in Python. To give a sense of the ranges, in the experiments we vary N_hash from 2⁵ to 2³². N_obs can vary in the 10⁴ − 10⁶ range, depending on the combinatorial features, the labeling scheme, and so forth. For instance, with N_hash = 2³⁰, we have N_obs = 292, 742 for the E labeling scheme applied to paths of length 0−8, and N_obs = 58, 225 for the EC labeling scheme applied to circular substructure of depth 0−2.

2.3 Fingerprint Statistical Models

Statistical models of fingerprints are important for compression, particularly in entropy coding schemes that match code lengths to symbol probabilities, assigning shorter codes to more probable symbols.^23–25 According to Shannon's source coding theorem, the optimal code length for a symbol is − log_b p, where here b is the size of the coding alphabet and p is the probability of the input symbol.

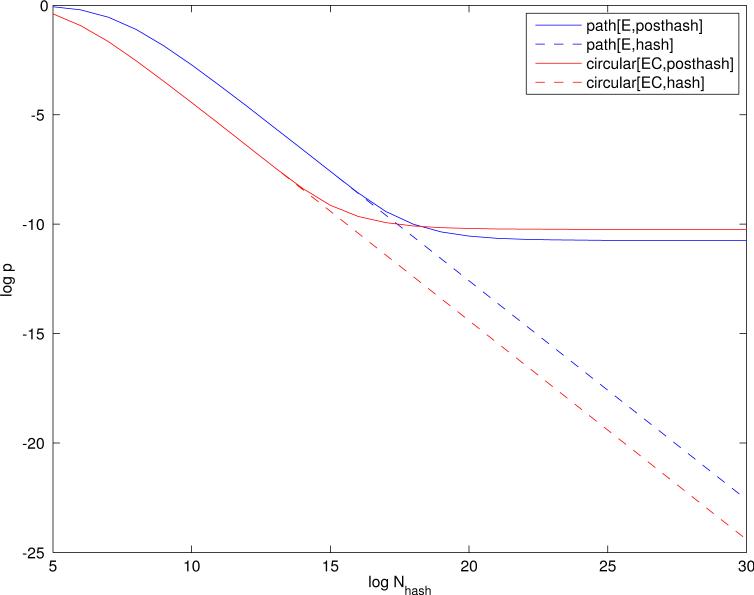
The simplest statistical model for binary fingerprints is a Bernoulli process (coin flip) with probability p of producing a 1-bit, and q = 1 − p of producing a 0-bit. Long fingerprints of length N_* are typically very sparse so the average density p is close to 0 (Figure 2). Under this model, the total number of 1-bits has a binomial distribution $\mathcal{B}(N_{\ast },p)$. Runs, defined by sequences of 0-bits followed by a 1-bit, have a geometric distribution so that the probability of a run of length j (j = 0, 1, 2, . . .) is given by q^jp, and the average run-length is l = q/p. The coin flip model is consistent with fingerprint features that are randomly ordered and statistically exchangeable, in fact even independent.

Figure 2.

Fingerprint density as a function of fingerprint length. Logarithms on both axes are taken to base 2. The average density is captured by p, the probability of a 1-bit in long fingerprint vectors computed across all the molecules. Blue lines correspond to path features with Element labeling. Red lines correspond to circular substructure features, with Extended Connectivity labeling.

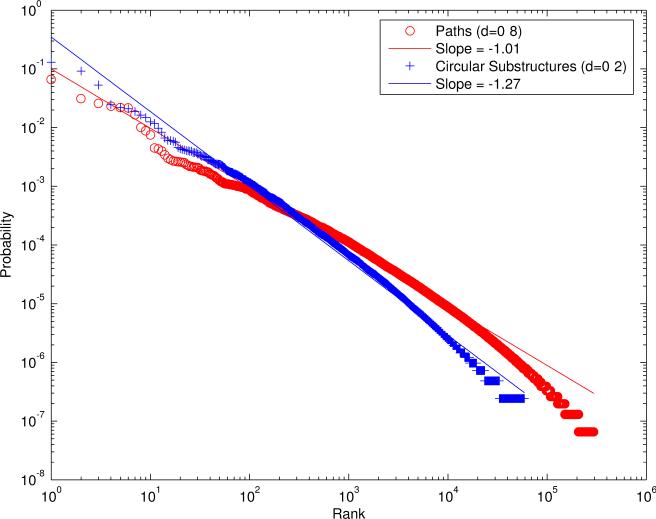
While the coin flip model is useful to derive a number of approximations, it is clear that chemical fingerprints have a more complex structure and their components are not exactly exchangeable since the individual feature probabilities p₁, . . . ,pN_* are not identical and equal to p but vary and, when reordered in decreasing order, follow roughly a power-law distribution. The probability associated with the j-ranked component is given approximately by p_j = Cj^−α, resulting in a line of slope −α in a log-log plot (Figure 3). Thus the statistical model at the next level of approximation is that of a non-stationary coin flip where the probability p_j of each coin flip varies.

Figure 3.

Power law distributions for paths of length 0−8 and circular substructures of depth 0−2. The x axis corresponds to the feature's rank and the y axis to the feature's probability, using logarithmic scales on both axes.

The next level of statistical approximation would have to take into account the correlations between pairs of features. In general and on average, these correlations are close to 0 and will not be considered here.

3 Fingerprint Compression Algorithms

In this section, we first review existing compression algorithms for chemical fingerprints, and then develop new compression algorithms for these fingerprints. Other compression algorithms exist, such as Lempel-Ziv, which have been applied to other molecular representations, such as SMILES strings.²⁰ For fingerprints, however, the most widely used compression algorithm is the modulo compression algorithm, used in many commercial fingerprint systems (e.g. Daylight, Avalon, and Unity).

3.1 Modulo Compression

In the modulo compression algorithm, fingerprints are “folded” using a modulo operator into shorter fingerprints of fixed length N, with N_* = N k. In the binary case, for a given molecule, a bit in position j of the compressed fingerprint is set to one if and only if there is at least one bit set to one in any position k ≡ j modulo N in the full fingerprint of length N_* (Figure 4). Typically, in current chemoinformatics systems, N = 2⁹ = 512 or N = 2¹⁰ = 1024. While in some applications it may be possible to exploit or weigh information associated with specific components, the compression modulo N is most effective only if all the bits are treated equally, so that the specific ordering of the bits is irrelevant. Hence it is most efficient and consistent with an exchangeable statistical model (stationary coin flip). In practice, this requires applying a fixed but random permutation to all the fingerprints of length N_* prior to compression, or using a good hashing function to derive “randomized” fingerprints of length N. The diagram in Figure 4 illustrates the simple process of folding a binary fingerprint vector of size N_* = 16 into a compressed fingerprint vector of size N = 4 using a modulo operator.

Figure 4.

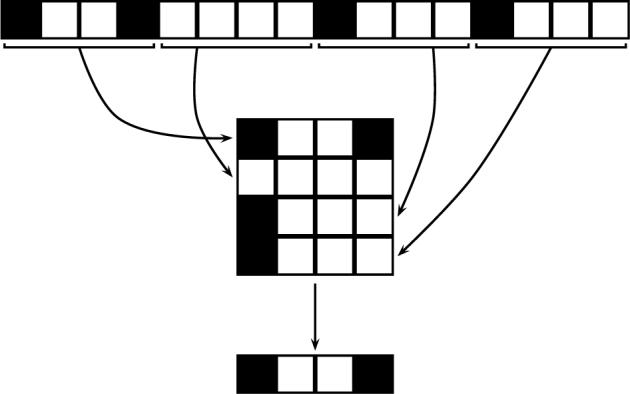
Illustration of the folding process with a binary vector of length N_* = 16 (1 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 ) folded into a binary vector of length N = 4 (1 0 0 1), modulo 4. Note how information in the first position of the compressed vector is lost due to clashes.

Modulo compression is very simple to implement. However it suffers from two drawbacks. First, it is a lossy compression method: when a component of the compressed fingerprint is set to one, there is no way of recovering which corresponding bits were set to one in the unfolded vector. Second, there is no indication that the compression rate may be close to optimal.

3.2 Modulo Compression: Variable Length

For completeness, we also describe a variation on modulo compression which uses variable-length modulo compression,³ where the length of the encoding of a molecule depends on the molecule itself. This is done by setting a threshold α and repeatedly folding the fingerprint vector ${\overrightarrow{A}}_{\ast }$ until the density of the compressed fingerprint exceeds the value α. In this case, ${\overrightarrow{A}}_{\ast }$ is represented by a compressed fingerprint vector ${\overrightarrow{A}}_{N\left({\overrightarrow{A}}_{\ast }\right)}$ of length $N\left({\overrightarrow{A}}_{\ast }\right)$, where $N\left({\overrightarrow{A}}_{\ast }\right)$ varies across molecules, such that $N_{\ast }=N\left({\overrightarrow{A}}_{\ast }\right)k\left({\overrightarrow{A}}_{\ast }\right)$ and ${\overrightarrow{A}}_{N\left({\overrightarrow{A}}_{\ast }\right)}∕N\left({\overrightarrow{A}}_{\ast }\right)\ge \alpha$, the latter inequality being violated if ${\overrightarrow{A}}_{\ast }$ is folded fewer than $k\left({\overrightarrow{A}}_{\ast }\right)$ times. Thus the compressed fingerprint is the longest modulo-compressed vector that satisfies the density inequality. Typically, α = 0.3 which corresponds to a maximum density of approximately 0.5. Variable compression may improve the compression rate but is still a lossy compression scheme. Thus we now turn to lossless compression schemes using integer entropy codes.^21–25

The starting points for these schemes are the lossless integer run-length or index representations of fingerprints. The messages to be compressed are viewed as sequences of integers. Thus the goal of the algorithms considered here is to encode arbitrary integers into variable length (prefix) bit strings in a lossless way. The Shannon entropy of the source distribution provides a theoretical lower bound to the number of bits required on average for lossless transmission (compression) of each symbol (integer) in the limit of very long messages. Thus in entropy coding compression one tries to approach this limit by striving to match the length of the codewords to the distribution over the integers associated with the messages, i.e. the molecules in the database, by assigning shorter codewords to integers that occur more frequently in the messages. Note that encoding by concatenating the binary representations of each integer does not work since the boundaries between the integers are lost. Reserving one binary symbol (e.g. 0) as a delimiter, and using the remaining symbol to unary encode each integer is very inefficient. Thus in the binary encoding of sequences of integers, the differentiation of two successive integers becomes an essential problem to be addressed.

3.3 Golomb and Golomb-Rice Codes

Golomb codes were specifically developed to encode stationary coin flips with p ≠ 0.5.²¹ Thus they can be applied directly to the run-length representation of fingerprints. They are known to be optimal and achieve the Shannon limit if the data is generated by random coin flips or, equivalently, if the distribution over the integers (runs) is geometric. The more skewed the probability p is (towards 0 or 1) the greater the level of compression that can be achieved.

Golomb codes are a family of codes with one integer parameter m. Any positive integer j can be written using its quotient and remainder modulo m as j = ⌊j/m⌋ + (j mod m). To encode j, the Golomb code with parameter m encodes the quotient and remainder by using:

• ⌊j/m⌋ 1-bits for the quotient;

• followed by a 0, as a delimiter (unary encoding of ⌊j/m⌋);

• followed by the phased-in binary code for j mod m for the remainder (described below).

The encoding of integers 0, . . . , m - 1 normally requires B = ⌈log m⌉ bits. If m is not a power of two, then one can sometimes use B - 1 bits. More specifically, in the “phased-in” approach:

• If i < 2^B - m, then encode i in binary, using (B - 1) bits;

• If i ≥ 2^B - m, then encode i by i + 2^B - m in binary, using B bits.

For instance, for m = 5, i = 2 is encoded as “10” using 2 (= B - 1) bits, and i = 4 is encode as “111” using 3 (= B) bits (see Table 1).

Table 1.

Golomb encoding of the integers j = 0 to 8, for different values of the parameter m.

j	m = 2	m = 3	m = 4	m = 5	m = 6
0	00	00	000	000	000
1	01	010	001	001	001
2	100	011	010	010	0100
3	101	100	011	0110	0101
4	1100	1010	1000	0111	0110
5	1101	1011	1001	1000	0111
6	11100	1100	1010	1001	1000
7	11101	11010	1011	1010	1001
8	1111100	11011	11000	10110	10100

Thus the encoding of j requires in total ⌊j/m⌋ + 1 + ⌊log m⌋ or ⌊j/m⌋ + 1 + ⌈log m⌉ bits (Table 1) and the codeword for the integer j + m has one more bit than the codeword for the integer j. Unless otherwise specified, here and everywhere else in the paper all logarithms are taken to base 2. In this section only, we use also “[log m]” to denote “⌊log m⌋ or ⌈log m⌉”.

The entropy of the geometric distribution of run-lengths is given by

$$\mathcal{H}\left(geometric\right)=-\sum _{j=0}^{\infty }{q}^{j}p\log \left(q^{j}p\right)$$ (1)

and provides the optimal Shannon coding lower bound on the expected encoding length per integer

$$E\left(l\right)\approx \sum _{j=0}^{\infty }{q}^{j}p(\lfloor j∕m\rfloor +1+\left[\log m\right])$$ (2)

under the coin flip model. Thus the Golomb code approaches the Shannon limit when q^m = 0.5. In particular, this ensures that for each integer j

$$-\log P\left(j\right)=\log \left(q^{j}p\right)\approx \lfloor j∕m\rfloor +1+\left[\log m\right]$$ (3)

where P(j) is the probability associated with the integer j.

Note that for chemical fingerprints we can use a single value of p = 1 - q (hence m) averaged across all molecules, or we can use a different p (hence different m) for each molecule. In the latter case, for each molecule we must store the value of m at the beginning of the fingerprint. The value of m can be encoded using Elias Gamma codes (see below). Experiments show that this is a small cost to incur compared to the saving achieved by using a value of p that is adapted to the bit density of each molecular fingerprint. Thus the results to be reported are based on an implementation that uses a different value of p for each molecule.

Finally, Golomb-Rice codes are a particularly convenient sub-family of Golomb codes, when m = 2^k. To encode j, we concatenate ⌊j/2^k⌋ 1-bits, one 0-bit, and the k least significant bits of j. The length of the encoding of j is thus ⌈j/2^k⌉ + k + 1. The decoding of Golomb-Rice codes is particularly simple, the position of the 0-bit gives the value of the prefix to be followed by the next k bits. Golomb-Rice codes are used in the simulations.

3.4 Elias Codes

Golomb encoding is optimal for fingerprints generated by a stationary coin-flip model, where each feature is observed with equal probability. As we have seen, however, chemical features are not uniformly distributed across molecules, some features are much more frequent than others and, upon reordering, follow roughly a power law distribution. Elias codes,²² in particular Elias Gamma codes, take advantage of this non-stationarity, observed in real chemical fingerprints.

Elias codes are applied here to the fingerprint integer index representation, although they can also be applied to the run-length representation. In the Elias Gamma coding scheme, one simply concatenates the scale of j with its binary representation. More precisely, to encode the scale and value of j:

• write ⌊log j⌋ 0-bits;

• followed by the binary value of j beginning with its most significant 1-bit.

The length of the encoding of j is 2 ⌊log j⌋ + 1 (Table 3). The decoding is obvious: first read n 0-bits until the first 1-bit is encountered, then read n more bits to get the binary representation of j.

Table 3.

Elias Gamma encoding. Each integer j is encoded by concatenating ⌊logj⌋ 0's with the binary value of j.

Number	Encoding	Implicit Probability	Empirical Probability (Paths)
1	1	0.50	0.65
2−3	01x	0.25	0.27
4−7	001xx	0.125	0.050
8−15	0001xxx	0.0625	0.020
16−31	00001xxxx	0.03125	0.0006

Applying the relationship

$$-\log P\left(j\right)\approx 2\lfloor \log j\rfloor +1$$ (4)

to the integer probabilities, shows that Elias Gamma encoding asymptotically approaches the Shannon limit for P(j) ≈ Cj⁻². This is a power law relationship with exponent −2 and C is a normalizing constant, equal to 6/π² in the case of a perfect power law. Note that for both Golomb (Equation 3) and Elias Gamma codes (Equation 4), several different consecutive integers can be encoded into a bit vector with the same length, hence the relationships - log P(j) ≈ length(j) is only approximate with respect to geometric or power-law distributions over the integers. To be more precise, the optimal distribution associated with the Elias Gamma code can be separated into the product of a probability distribution over the length l given by P(l) = 2^−l and a uniform distribution over the integers having an encoding of length l given by P(j|l) = 2^−l+1.

Golomb codes based on a stationary coin flip model are associated with a random ordering of the fingerprint features. While the Elias Gamma code could be applied to the integer index representation associated with a random ordering of the components, it is most efficient if the components are re-ordered in decreasing order of frequency across the molecules in the database to match the power-law probabilities of the symbols to the codeword lengths. In this way, smaller indices associated with more frequent features are encoded more efficiently using fewer bits. The reordering is an additional preprocessing step but it needs to be carried out only once, or once in a while if the database grows, and can be done entirely off-line.

3.5 Monotone Value Coding (MOV Coding)

Regardless of whether the features are sorted or randomly ordered, it is important to remark that the integers occurring in an index representation are in strictly increasing order. Here we introduce a modification of the codes described above, presented with the Elias Gamma codes, for messages consisting of monotone sequences of integers, such as index representations. When the value of the integers being encoded increases monotonically, additional lossless compression can be obtained by encoding only the scale increases and their location (Figure 5).

Figure 5.

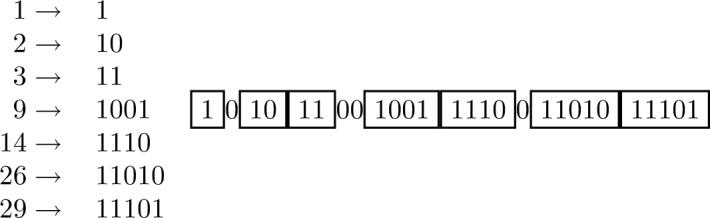
Monotone Value Coding (MOV).The principle is illustrated using the index representation vector (1, 2, 3, 9, 14, 26, 29). Each integer j is converted to a binary representation of length ⌊log j⌋ which begins with a 1-bit. 0-bits are used between two consecutive integers only when the length (scale) increases. The number of 0-bits is equal to the increase in the length.

More precisely, if the index sequence of a fingerprint is given by (j₁, j₂, . . . , j_K) with j₁ < j₂ . . . < j_K:

• encode j₁ using Elias Gamma encoding;

• for i = 2, . . . , K:

  • write ⌊log(j_i)⌋ - ⌊log j_i-1⌋ 0-bits;.
  • followed by the binary value of j_i beginning with its most significant 1-bit.

The MOV-encoded integer index vector can be decoded by a simple algorithm:

• set k = 1;

• decode each integer in succession by repeating the following steps:

  • increment k by the number of 0-bits in the input stream before reaching the first 1-bit;
  • counting this first 1-bit as the first digit of the integer, read the remaining k - 1 bits of the integer from the input stream.

Each of the integers read from the stream corresponds to a single feature observed in the uncompressed feature vector.

3.6 Monotone Length Coding (MOL Coding)

The same idea, with some modifications, can also be applied to the run-lengths. First, we have checked that when the fingerprint components are sorted by decreasing order of frequency, the run-lengths follow approximately a power-law distribution, instead of a geometric distribution in the case of randomly sorted components. Second, when the fingerprint components are sorted by decreasing frequency order, the sequence of run-lengths of a given molecule will be “quasi-monotone”. It will tend to increase, overall, but not in a perfect monotone fashion: occasionally a run-length may be followed by a shorter run-length. Thus one cannot encode only the increases. To address this problem, we use a 1-bit to signal when the scale of a run-length is equal to or smaller than the scale of the previous run-length. Otherwise, we use a number of 0-bits equal to the increase in the scale. Thus, in this case, it is the length of the binary encoding of the integers that varies monotonically, rather than their values. Some care must be taken with the initialization of the variable scale to manage the case when the initial run-length is 0.

More precisely, if the run-length sequence of a fingerprint is given by (j₁, j₂, . . . , j_K):

• initialize scale = 0;

• for i = 1, . . . , K:

  • if ⌊log j_i⌋ + 1 ≤ scale, then write a 1-bit followed by j_i written in binary using scale bits;
  • else write (⌊log j_i⌋ + 1 - scale) 0-bits, set scale = ⌊log j_i⌋ + 1, and write the binary value of j_i using scale bits.

An example of MOL encoding is given in Figure 6.

Figure 6.

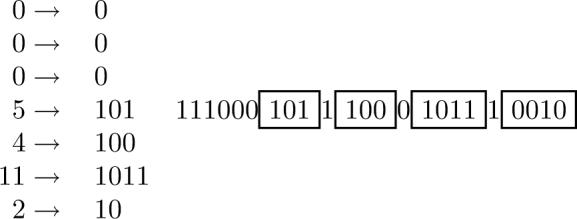
Monotone Length Coding (MOL). The principle is illustrated using the run-length vector (0, 0, 0, 5, 4, 11, 2) associated with the index vector of Figure 5. Each integer j, except for the initial 0's, is converted to a binary representation of length ⌊log j⌋ + 1 which begins with a 1-bit. In addition, a 1-bit is used between two consecutive integers when the scale does not increase. 0-bits are used between two consecutive integers only when the length (scale) increases. The number of 0-bits is equal to the increase in the scale. The three initial 0-bits are associated with a scale of 0 leading to the three initial 1-bits in the encoding, followed by three 0-bits to denote the increase in scale from 0 to 3 bits.

With minor adjustments, the same ideas can be applied to other coding schemes such as Golomb-Rice. However, because after reordering the components both the indices and the run-lengths have power law distribution trends, in the simulations we use primarily MOV/MOL codes with Elias Gamma codes. Slight additional savings could also be obtained by coding the absence of a feature, rather than its presence for the few p_i's satisfying p_i > 0.5. This is an implementation detail which may be effective for some feature sets but not others.

3.7 Byte Arithmetic

Direct implementations of the decoding algorithms process the compressed fingerprints bit-by-bit; however, it is possible to implement faster decoders, which decode the compressed data byte-by-byte. These faster decoders work by looking up information from pre-computed tables. These tables are indexed by: (1) all possible bytes B (ranging from 0 to 255); and (2) a bit-index i (ranging from 0 to 7) which marks the position of the decoder within the byte. These tables may store quantities such as the binary value of byte B starting from bit i, the number of bits turned on in byte B starting from bit i, and the unary value of byte B starting from bit i. The exact quantities stored depend on the details of a particular decoder implementation.

In practice, byte arithmetic considerably increases decoding speed, sometimes approaching as much as an eight-fold improvement (in the case of modulo-compressed fingerprints) over the corresponding bitby-bit implementation. The exact value of the speedup depends on several factors including the dataset of molecules, the compression scheme, and the hardware used. In the simulation benchmarks, we compare the byte-by-byte decoders of various compression schemes operating on compressed representations of identical fingerprints on the same machine.

3.8 Computing Similarity Measures

When searching large databases, one must be able to rapidly compute the similarity between the query molecule and the other molecules in the database from their compressed representations. Most commonly used similarity measures $S(\mathcal{A},\mathcal{B})$ between molecule $\mathcal{A}$ and $\mathcal{B}$ are derived from the intersection $A_{\ast }\cap B_{\ast }=\mid {\overrightarrow{A}}_{\ast }\cap {\overrightarrow{B}}_{\ast }\mid$ and the union $A_{\ast }\cup B_{\ast }=\mid {\overrightarrow{A}}_{\ast }\cup {\overrightarrow{B}}_{\ast }\mid$ of the corresponding uncompressed binary fingerprint vectors. For instance, the widely used Tanimoto measure is given by the ratio $S=(A_{\ast }\cap B_{\ast })∕(A_{\ast }\cup B_{\ast })$. Thus one must be able to rapidly compute or estimate the values of this union and intersection from the compressed fingerprint representations. To achieve this goal, at the beginning of each compressed fingerprint we store in the header the total number (A_*) of 1-bits contained in the corresponding uncompressed fingerprint (${\overrightarrow{A}}_{\ast }$) using Elias Gamma coding. In the case of count fingerprints, we store the same quantity Σ_i A_i. This introduces a very small overhead in the overall compression scheme. Note that the header is also useful to avoid having to define a special terminator symbol to signal the end of the index or run-length sequence. During the decoding phase, bits or counts are progressively added until the total value Σ_i A_i is reached. Alternatively, one can signal the end of an index or run-length sequence by encoding an index or run-length equal to zero.

Since $A_{\ast }\cup B_{\ast }=A_{\ast }+B_{\ast }-(A_{\ast }\cap B_{\ast })$, the union can be computed from the intersection, and so to compute the similarity we need only to compute the intersection. Given a query molecule $\mathcal{A}$, we first uncompress its compressed representation into the corresponding index representation. This is true for both Golomb and Elias coding schemes, with the caveat that Golomb coding requires a small additional processing step whereby the run-length representation is transformed into the index representation. This decompression operation has to be done only once for each query. Then for each molecule $\mathcal{B}$ in the database, we uncompress its compressed representation into its index representation. The intersection $A_{\ast }\cap B_{\ast }$ is then rapidly computed by counting the number of integers in common between the two index representations.

3.9 Count Fingerprints

The described compression methods only compress sparse binary vectors. We can, however, extend Golomb, Elias, or MOV/MOL coding schemes to fingerprint count vectors which also store the number of times a given feature is observed in a given molecule. The basic idea is to interleave two codes together: the code for the positions as described above, and the code for the corresponding counts. The encoding algorithm is as follows: each index with a count greater than zero is encoded using previously derived methods (Golomb, Golomb-Rice, Elias Gamma, MOV/MOL). After encoding each index, but before encoding the next index, we encode the number of times the corresponding feature is observed. Counts can be encoded either with fixed-width bit vectors or, more efficiently, with Elias Gamma encoding. Decoding the interleaved code is trivial. After each index is decoded, the corresponding count is decoded before decoding the next index.

4 Results

Here we compare the lossless integer entropy code algorithms to the lossy modulo-compression algorithms not only in terms of compression rates, but also in terms of time complexity and retrieval accuracy.

4.1 Compression Rates

The main simulation results comparing different compression schemes are illustrated in Figure 7 for paths and Figure 8 for circular substructures. These figures plot the average length of a compressed fingerprint as a function of N_hash for Golomb and MOV/MOL encoding schemes applied to various feature vectors. It must be noted that, although Golomb is most consistent with a random ordering of the uncompressed fingerprint components, it can still be applied to fingerprints where the features have been sorted in decreasing order of frequency. In this case, the run-lengths are increasing on average, but not strictly, as one moves from frequent bits to rare ones.

Figure 7.

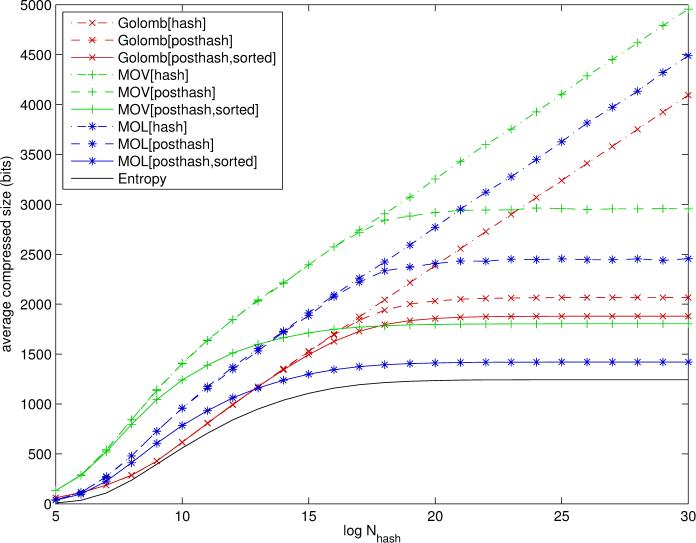
Compression results for Golomb-Rice (red), MOV Elias Gamma for indices (green), and MOL Elias Gamma for run-lengths (blue) encoding schemes applied to binary fingerprints based on paths. Posthash refers to the option where features that are 0 for all the molecules in the database are removed. Sorted refers to the option where features are sorted in decreasing order of frequency across the molecules in the database. Curves represent the average number of bits required per molecule as a function of uncompressed fingerprint size (log N_hash). The entropy curve corresponds to the approximate Shannon entropy limit - Σ_i[p_i log p_i + (1 - p_i) log(1 - p_i)], derived under the independent component approximation. Plots derived using a random subset of 50,000 molecules from the ChemDB.

Figure 8.

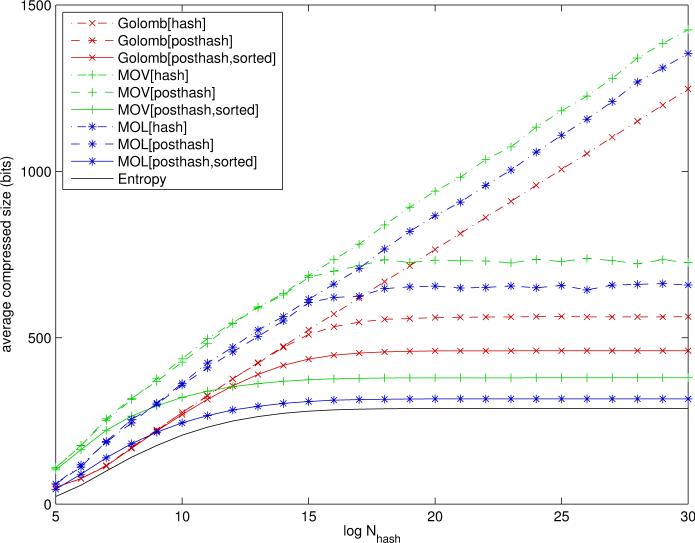
Compression results for Golomb-Rice (red), MOV Elias Gamma for indices (green), and MOL Elias Gamma for run-lengths (blue) encoding schemes applied to binary fingerprints based on circular substructures. Posthash refers to the option where features that are 0 for all the molecules in the database are removed. Sorted refers to the option where features are sorted in decreasing order of frequency across the molecules in the database. Curves represent the average number of bits required per molecule as a function of uncompressed fingerprint size (log N_hash). The entropy curve corresponds to the approximate Shannon entropy limit - Σ_i[p_i log p_i + (1 - p_i) log(1 - p_i)], derived under the independent component approximation. Plots derived using a random subset of 50,000 molecules from the ChemDB.

Likewise, since both sorted and non-sorted fingerprints yield index representations consisting of monotonically increasing lists of integers, MOV/MOL encoding can be applied to indices in both sorted and non-sorted fingerprints. Since MOV/MOL Elias Gamma coding always achieves better compression per- formance than does Elias Gamma coding, here we report only the results of MOV/MOL compression and compare them to Golomb-Rice and modulo compression.

As expected, the results are entirely consistent across feature types or labeling schemes, as can be seen by the relative ordering of the curves associated with different compression schemes, although the magnitude can vary. For small values of log N_hash, less than 14 for paths and 17 for circular substructures, Golomb codes achieve better average compression. However, for larger and more realistic values of N_hash (e.g. above 2²⁰) MOV/MOL encoding achieves the best average compression. MOL is noticeably better than MOV. When columns of zeros are removed (posthash) the average size becomes flat as N_hash is increased, otherwise it grows linearly as N_hash is increased. Sorting the bits by decreasing frequencies improves both Golomb-Rice and Elias-Gamma encodings.

For N_hash = 2³⁰, the average compressed sizes are given in Table 4. Remarkably, lossless compression can be achieved using fewer bits than current lossy systems. With MOL Elias Gamma encoding applied to circular substructures and binary fingerprints after removing columns of zeros (posthash) and sorting the components in decreasing frequency order, the average code size is only 316.2 bits per molecule. This lossless compression performance must be contrasted with current available systems which typically use lossy modulo compression with fingerprints of fixed size 1024. Thus in this case MOL encoding provides more than a three-fold compression improvement without any loss of information. This is to be compared to the sum of entropies - σ_i[p_i log p_i + (1 - p_i) log(1 - p_i)], which in this case is equal to 287.4 bits for N_hash = 2³⁰. This value is a reasonable approximation to the theoretical Shannon limit, although the true limit is likely to be slightly lower due to the correlations between the components. However, it is easy to check that these correlations are typically very small, and zero in average (data not shown). A different theoretical argument given in the concluding section provides a similar lower bound in the range of 250 bits. For comparison, the similar entropy in the case of paths is equal to 1243.5 bits.

Table 4.

Average size in bits of compressed molecular fingerprints for different compression schemes, with path and circular substructure features. These values correspond to the values on the y axis in Figures ?? and ?? when x = log N_hash = 30. Headers are not included.

Encoding	Path	Circular
Golomb-Rice[hash]	4094.8	1247.5
Golomb-Rice[posthash]	2066.1	563.1
Golomb-Rice[posthash,sorted]	1879.6	460.8
MOV[hash]	4955.4	1425.5
MOV[posthash]	2954.9	725.7
MOV[posthash,sorted]	1803.3	379.5
MOL[hash]	4489.3	1354.4
MOL[posthash]	2455.1	658.2
MOL[posthash,sorted]	1420.6	316.2

Headers at the beginning of the compressed fingerprints are relatively short and implementation-dependent, thus a relatively minor issue. In our implementation, headers typically contain one bit for count versus binary fingerprints, the value of A = Σ_i A_i encoded using Elias Gamma, and possibly the value of the parameter m (or k) when using Golomb (or Golomb-Rice) codes with parameter values that are tuned to each individual molecule. The values given in Table 4 are given without including these small headers. The small effect of these headers can be seen in Table 5 where we compare two possible implementations of Golomb-Rice codes using a fixed k for all the molecules, and a variable k adapted to each molecule. Typically the variable k approach costs an additional 5−10 bits to store the value of k in the header, but overall saves 50−100 bits by leveraging the variable fingerprint density to encode the run-lengths.

Table 5.

Average size in bits after Golomb-Rice compression using either a single parameter k for all the molecules, or a different parameter k for each molecule. In the latter case, the value of k is included in the header.

Golomb-Rice	Path		Circular
	fixed k	variable k	fixed k	variable k
hash	4112.4	4103.8	1249.1	1256.5
posthash	2085.4	2073.5	565.5	569.6
posthash,sorted	1993.5	1886.3	544.4	466.8

It is worth noting that with the interleaving encoding algorithm described above, the use of count fingerprints rather than binary fingerprints merely shifts all the curves in Figures 7 and 8 upward by a constant amount, equal to the average number of bits used to encode the counts (Table 6). Therefore the ordering between the curves does not change. For instance, with MOV/MOL encoding applied to circular substructures, an average of 1.89 bits are required to encode each count. On average, this increases the lengths of the fingerprints by 82.49 bits.

Table 6.

Maximum and mean value of the count values across the count fingerprints of the sample of 50,000 molecules from the ChemDB. The logarithm of the maximum value determines the number of bits required to encode the counts using bit vectors of fixed length. Bits/count denotes the average number of bits per count value, using Elias Gamma encoding. Bits/fingerprint denotes the average number of bits per fingerprint required to store all the corresponding counts. It is the amount by which the curves in Figures ?? and ?? are translated upward if count fingerprints are used instead of binary fingerprints.

Statistics	Path	Circular
Max(count)	513	88
Mean(count)	1.78	1.71
Bits/count	1.75	1.89
Bits/fingerprint	303.9	82.49

4.2 Time Complexity

Compression size and accuracy are two important dimensions to consider when deciding on a compression scheme. In this regard, integer entropy codes can achieve better compression rates than modulo compression without any loss of information. However, another important dimension is the complexity and speed of the encoding and decoding operations. In the case of chemical fingerprints, encoding using integer entropy codes is not difficult and can be carried off-line. Thus the only issue left to address is the speed of decoding and computing similarity measures across large numbers of molecules.

Speed benchmarks are given in Table 7 comparing the performance in seconds of various compression algorithms when computing five million Tanimoto similarity measures using binary fingerprints. All compression schemes are implemented using byte-arithmetic and run on the same 2.0 MHz Intel-Dual Core Macintosh laptop computer. As can be expected, plain lossy modulo compression leads to the fastest time of about 2.79 s for the computation of 5M approximate Tanimoto similarity measures using standard compressed fingerprints of fixed length 1,024 bits. Using the mathematical correction described in¹⁵ to derive better estimates of the true (uncompressed) similarity measure, increases this time to 4.04s for circular substructure features. In contrast, the best implementations of the MOV/MOL compression requires 6.34 s. Thus in our implementation the MOV/MOL compression is about 1.5−2 times slower than different variants of modulo compression. This is a relatively modest cost to pay given the considerable improvement in size and accuracy. Finally, it must be noted that all the integer entropy codes discussed here, including MOV/MOL encoding, can be used in combination with the pruning techniques described in²⁶ allowing queries of the entire ChemDB to run typically in less than a second.

Table 7.

Speed benchmarks for various compression algorithms representing approximate time in seconds to perform 100 queries across a random set of 50,000 molecules from the ChemDB (5 million similarity calculations) with N_hash = 2³⁰ using binary fingerprints and Tanimoto similarity measure. The last two lines correspond to modulo compression. Modulo-Uncorrected corresponds to computing the Tanimoto similarity directly on the compressed fingerprints as an estimate of the Tanimoto similarity on the uncompressed fingerprints. Modulo-Corrected refers to a better estimate of the Tanimoto uncompressed similarity derived in.^? These benchmarks were carried on 2.0 MHz Intel-Dual Core Macintosh laptop computer.

Encoding	Path	Circular
Golomb-Rice[hash]	29.7	8.6
Golomb-Rice[posthash,sorted]	20.9	6.5
MOV[hash]	32.1	9.6
MOV[posthash,sorted]	22.0	6.3
MOL[hash]	27.2	9.0
MOL[posthash,sorted]	20.9	6.4
Modulo-Corrected (N=1024)	4.0	4.0
Modulo-Uncorrected (N=1024)	2.8	2.8

4.3 Retrieval Accuracy

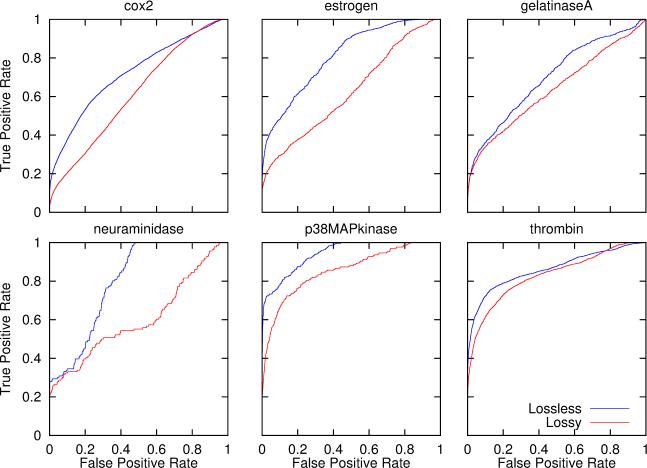
The previous sections establish the effectiveness of the integer entropy code algorithms in terms of compression rate and compression accuracy (lossless) for a relatively small computational cost. However, because the compression is lossless, we can also expect better retrieval accuracy. To test this hypothesis, we use the six benchmark datasets in Stahl and Rarey,¹⁶ corresponding to six groups of diverse small-molecule inhibitors of important pharmaceutical targets. These datasets consist of 128 chemicals which interact with Cox-2, 55 which interact with Estrogen Receptor, 43 which interact with Gelatinase-A, 17 which interact with Neuraminidase, 25 which interact with p38-MAP Kinase, and 67 which interact with Thrombin. These sets are combined with a random subset of 50,000 molecules from the ChemDB. Retrieval of each dataset is tested against this random background using both lossy and lossless compressed fingerprints and Tanimoto similarity measure, using a leave-one-out cross validation procedure. ROC (Receiver Operating Characteristic) curves displaying the tradeoff between true and false positives are computed for each query molecule, and then aggregated within each dataset (Figure 9). The results show that in all six cases, lossless compression leads to better retrieval, for instance in terms of the AUC (Area Under the Curve) measure. On average, in these experiments, the AUC is increased by 18% when lossless representations are used, versus lossy modulo compression to 512 bits. For comparison purposes, the AUC is increased by 11% when the same experiments are done with lossy modulo compression to 1024 bits. Similar improvements are observed with other classification measures.

Figure 9.

ROC retrieval curved based on Tanimoto similarity measures, computed from lossy and lossless compressed fingerprints. Curves are obtained using molecules from six biologically relevant datasets using leave-one-out cross validation. Each ROC curve is constructed by aggregating the ROC curves calculated by using each molecule in the group to search for the rest of the group against the background provided by the random subset of 50,000 molecules from the ChemDB. Lossless compression leads to better retrieval performance corresponding, for instance, to an average increase of 18% for the area under the ROC curves (AUC measure). Lossy fingerprints are derived by modulo compression to 512 bits.

5 Conclusion

In summary, we have shown how by using integer entropy coding techniques, we can achieve efficient lossless compression of large chemical fingerprints. The starting point is first to convert the fingerprint vectors into lists of integers corresponding to indices or run-lengths. Everything else being equal, it is preferable to encode run-lengths because their dynamic range is smaller than the dynamic range of indices. Classical integer coding algorithms, such as Golomb or Elias codes, encode an integer j by the concatenation p(j)m(j) of two bit strings: a preamble p(j) and a mantissa m(j). The preamble encodes the scale of j and sets the stage for the mantissa by providing information about the size of the mantissa or providing additional information about j that is not contained in the mantissa. For instance, in Elias Gamma codes p(m) is a string of zeroes of length ⌊log j⌋, and m(j) is the binary encoding of j. In general, Golomb codes are best suited for geometric distributions over the integers, whereas Elias codes are best suited for power-law distributions over the integers. When the fingerprint components are randomly ordered, the indices tend to have a power-law distribution and the run-lengths tend to have a geometric distribution. When the fingerprint components are ordered by frequency, both the indices and the run-lengths tend to have power-law distributions. Furthermore, within a given fingerprint, the indices are always strictly increasing (by definition). The run-lengths are random and not increasing when the components are randomly ordered. However, when the components are ordered by frequency, the run-lengths are quasi-increasing. The monotonicity or quasi-monotonicity, allows us to gain additional space essentially by using p(m) to encode only the changes in the scale of j, rather than the scale itself.

Combinations of these ideas yield some new compression algorithms and, in short, after comparing many possible combinations and variations, the algorithm we propose has three key ingredients: (1) reordering of the fingerprint components, so that the run-length are approximately power-law distributed and quasi-monotone; (2) encoding the power-law distributed run-lengths using Elias codes; (3) taking advantages of the quasi-monotonicity of the run-lengths to modify the encoding and gain further space by essentially encoding only the changes in the scale of successive integers in the lists. Using large binary fingerprints associated with hash values up to 2³² and circular substructure features, this approach allows us to encode the fingerprints of molecules contained in current large repositories in a lossless fashion using slightly over 300 bits per molecular fingerprint on average. Thus not only is this form of compression lossless, it also produces fingerprints that are approximately 1/3 the size of typical 1024-bit, lossy, modulo-compressed fingerprints.

One obvious question is whether we have reached the limits of compressibility. First we note that the size achieved is close to the approximate Shannon limit of 290 bits, estimated assuming independence among the fingerprint bits. The size difference is more or less within the size of implementation-specific details, such as headers. Since in reality the features are not exactly independent, some relatively small improvements may still be possible. For instance, it may be possible to use a version of Golomb codes where not only each molecule has its own range parameter m, but the parameter m varies within each molecular fingerprint, progressively increasing from left to right, when the components are ordered by decreasing frequencies. However, it should also be clear that any improvement in size may at best be incremental. To see this, one needs only to remark that current rough estimates for the total number of small organic molecules are in the 10⁶⁰ range¹⁴ which corresponds to an absolute minimum of 200 bits per molecule (2²⁰⁰ ≈ 10⁶⁰). Beyond the current level, any improvements in size are also likely to be more costly in terms of speed of decoding and computing similarity measures. In this respect, the proposed algorithm requires only a relatively small computational price. For circular fingerprints, in our implementation this overhead is within a factor of two in the worst case scenario. As we approach the limits of lossless compression and wish to search increasingly larger portions of chemical space, the emphasis may shift to speed considerations.

Besides space and time, a third important consideration is accuracy. Because the compression scheme proposed is lossless, it ought to lead to better retrieval performance than lossy compression schemes. In controlled leave-one-out cross validation experiments, using several pharmacologically-relevant datasets against a large random background of molecules, we have shown that the lossless representations yield better retrieval than the lossy representations by any classification measure. In particular, we observed significant improvements of 11%−18% for the average area under the ROC curves, depending on the length of the lossy-compressed fingerprints.. These results highlight the utility of these fingerprints for chemists to effectively find new molecules of interest from large chemical repositories. While in time, one can hope that improved chemoinformatics methods will make their way into proprietary systems like CAS, a direct comparison to their retrieval capabilities is currently impossible due to the closed nature of these systems.

Finally, it is important to note that the MOV/MOL compression algorithms we have derived are completely general and not specific to chemical fingerprints. They can be applied in any situation where monotone or quasi-monotone, increasing or decreasing, sequences of integers need to be compressed. In particular, they can be applied in other domains where binary vector representations of power-law distributed features are commonly found, such as in the compression of web pages or written texts when treated as “bags of words”.^27,28

Table 2.

Golomb-Rice encoding of integers j = 0 − 33 with k = 2 (m = 4) and k = 3 (m = 8). Integer j is encoded by concatenating [j/2^k] 1-bits, one 0-bit, and the k least significant bits of j.

Number	Encoding (k = 2)	Number	Encoding (k = 3)
0−3	0xx	0−7	0xxx
4−7	10xx	8−15	10xxx
8−11	110xx	16−31	110xxx
33	11111111001	33	11110001