An Age-Stratified Poisson Model for Comparing Trends in Cancer Rates Across Overlapping Regions

Summary

The annual percent change (APC) has been used as a measure to describe the trend in the age-adjusted cancer incidence or mortality rate over relatively short time intervals. The yearly data on these age-adjusted rates are available from the Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute. The traditional methods to estimate the APC is to fit a linear regression of logarithm of age-adjusted rates on time using the least squares method or the weighted least squares method, and use the estimate of the slope parameter to define the APC as the percent change in the rates between two consecutive years. For comparing the APC for two regions, one uses a t-test which assumes that the two datasets on the logarithm of the age-adjusted rates are independent and normally distributed with a common variance. Two modifications of this test, when there is an overlap between the two regions or between the time intervals for the two datasets have been recently developed. The first modification relaxes the assumption of the independence of the two datasets but still assumes the common variance. The second modification relaxes the assumption of the common variance also, but assumes that the variances of the age-adjusted rates are obtained using Poisson distributions for the mortality or incidence counts. In this paper, a unified approach to the problem of estimating the APC is undertaken by modeling the counts to follow an age-stratified Poisson regression model, and by deriving a corrected Z-test for testing the equality of two APCs. A simulation study is carried out to assess the performance of the test and an application of the test to compare the trends, for a selected number of cancer sites, for two overlapping regions and with varied degree of overlapping time intervals is presented.

1 Introduction

The American Cancer Society (ACS) in its annual publication Cancer ACS 2007 (http://www.cancer.org/) reports that in 2007 about 1.5 million new cancer cases are expected to be diagnosed, and approximately 560,000 Americans are expected to die of cancer. Cancer is the most common cause of death in US, exceeded only by heart disease, and accounts for 1 of every 4 deaths. The same report also reveals that, for a number of cancer sites (such as breast, stomach, colon and rectum, lung and bronchus and leukemia), the age-adjusted cancer mortality rates have been steadly decreasing in recent years. In addition, the National Surveillance, Epidemiology, and End Results (SEER) Program of the National Cancer Institute (NCI) periodically publishes similar reports on trends of cancer incidence at http://seer.cancer.gov/csr; see Ries et al. (2003) So much has been at stake in terms of human life and cost - for example, the government agencies such as the National Health of Institutes (NIH), and many private sectors spend billions of dollars every year on cancer research, health insurance and medical and other costs - that there is an urgent need for new methods that produce more accurate and reliable estimates of measures of cancer trends.

The annual percent change (APC) has been used as a measure of cancer trends over short time periods, and to compare the recent cancer trends by gender or by geographic regions, one compares their APC values using the two-sample pooled t-test ( Kleinbaum et al., 1988) that assumes that the datasets on age-adjusted rates under the study are independent. However, a fundamental statistical difficulty arises when such comparisons, largely for policy making purposes, have to be made for regions or time intervals that overlap, e.g. comparing the most recent changes in trends of cancer rates in a local area (e.g. the mortality rate of breast cancer in California) with a more global level (i.e. the national mortality rate) over two overlapping time periods. For example, as detailed in the data analysis section, it is of substantial interest to compare the changes in California cancer mortality rates with the national cancer mortality rates in the last 15 years.

Recently, Li and Tiwari (2007) and Li et al. (2007) developed Z-tests which adjust for the dependence between the two APCs, and are more efficient than the naive test which assumes independence. However, these tests are based on the logarithmic transformation of the age-adjusted rates, and fits a simple linear regression model of the transformed data on time using either the ordinary least squares (OLS) or the other weighted least squares (WLS) procedures. The proposed test procedure is based on the natural assumption that the age-specific mortality or incidence counts are results of underlying Poisson processes (Brillinger, 1986), and hence are realizations of independent Poisson random variables. The age-specific instantaneous hazards are modeled by a log-link function, thus leading to an age-stratified Poisson model. The estimation of the parameters is then carried out using a likelihood-based approach.

The rest of the paper is organized as follows. In Section 2, we briefly review the existing tests, and derive the new test in Section 3. To compare the performance of the proposed test with respect to the above mentioned tests, a simulation study is carried out in Section 4. In this section, we also give application to breast cancer mortality data from California (CA) and the US extracted from the SEER*STAT software of the SEER Program. Section 5 ends this paper with a short discussion.

2 A Brief Review of Existing Tests

Consider two regions, and let d_kji denote the number of counts (deaths or new cancer cases) from the population at risk n_kji observed in Region k (k = 1, 2) in age-group j (j = 1, …, J) and at times T₁, …, T_m for Region 1 and T_s+1, …, T_s+n for Region 2, where T₁ ≤ T_s+1 < T_m ≤ T_s+n, with 0 ≤ s < m leading to overlapping time intervals. Note that this formulation is general and allows one region to have fewer time points than the other. In the SEER program, it is common to choose n_kji (at year T_i) to be the mid-year population representing the total person-years in one year, with the assumption of “drop-outs” being uniform over the unit-intervals. The age-adjusted rates are defined as

$$r_{ki}=\sum _{j=1}^J{w}_j\frac{d_{\mathit{kji}}}{n_{\mathit{kji}}}$$

where w_j > 0, j = 1, …, J, are the known standards for the age group j so that ${\sum }_{j=1}^J{w}_j=1$. For the SEER analysis, there are J = 19 standard age-groups consisting of 0–1, 1–4, 5–9, …, 85+, and w_j are chosen to be the year 2000 population standards (Fay et al. 2006).

Let y_ki = log(r_ki), be the logarithmic transformations of the age-adjusted rates. Consider the linear regression models

$$y_{ki}={\beta }_{0k}+{\beta }_{1k}{t}_{ki}+e_{ki},i=1,\dots ,I_k,$$ (1)

for k = 1, 2, flagging Regions 1 and 2, respectively. Here e_ki are random errors with mean 0, and t_ki corresponds to the calendar times of data collection in region k with I₁ = m and I₂ = n. More specifically, (t₁₁, …, t_1I1) = (T₁, …, T_m), while (t₂₁, …, t_2I2) = (T_s+1, …, T_s+n). For the two regions, the annual percent change (APC) are defined as APC_k = 100(e^β1k − 1)= 100β_1k, for a small β_1k, e.g. in the order of 10⁻² (Kim et al., 2000; Fay et al., 2006; Tiwari et al., 2006).

Then under the assumptions that e_ki are independent and have common variance σ², the two-sample pooled t-test (Kleinbaum et al., 1988) for testing the null hypothesis H₀: APC₁ = APC₂ versus the alternative H_a: APC₁ ≠ APC₂ is given by

$$T_t=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}}{\sqrt{{\widehat{\sigma }}^2\left({({\sum }_{i=1}^{I_1}(t_{1i}-{\overline{t}}_1)}^2{)}^{-1}+{({\sum }_{i=1}^{I_2}(t_{2i}-{\overline{t}}_2)}^2{)}^{-1}\right)}}\sim t_{(I_1+I_2-4)},$$ (2)

where ${\overline{t}}_k={\sum }_{i=1}^{I_k}{t}_{ki}/I_k$ for k = 1, 2, and σ̂² is the “pooled” unbiased estimate of σ² given by

$${\widehat{\sigma }}^2=\frac{{\sum }_{i=1}^{I_1}(y_{1i}-{\widehat{y}}_{1i}{)}^2+{\sum }_{i=1}^{I_2}{(y_{2i}-{\widehat{y}}_{2i})}^2}{I_1+I_2-4},$$

where ŷ_ki = β̂_0k + β̂_1kt_ki are the predictions for k = 1, 2. Here, β̂_0k and β̂_1k are obtained from the least squares estimation. That is,

$${\widehat{\beta }}_{1k}=\frac{{\sum }_{i=1}^{I_k}(t_{ki}-{\overline{t}}_k)(y_{ki}-{\overline{y}}_k)}{{\sum }_{i=1}^{I_k}{(t_{ki}-{\overline{t}}_k)}^2},{\widehat{\beta }}_{0k}={\overline{y}}_k-{\beta }_{1k}{\overline{t}}_k$$

where ${\overline{y}}_k={\sum }_{i=1}^{I_k}{y}_{ki}/I_k.$

The above test is not appropriate, however, when there is an overlap between the two regions or the two time periods. For this case, Li and Tiwari (2007) proposed the following corrected Z-test

$$Z_{CT}=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}}{{\left\{{\widehat{\sigma }}^2\left({\sigma }_1^{-2}+{\sigma }_2^{-2}-2{\sigma }_{12}{\sigma }_1^{-2}{\sigma }_2^{-2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right)\right\}}^{1/2}},$$ (3)

where ${\sigma }_k^2={\sum }_{i=1}{(t_{ki}-{\overline{t}}_k)}^2$, ${\sigma }_{12}={\sum }_{s+1}^m(T_i-{\overline{t}}_1)(T_i-{\overline{t}}_2)$, $n_k={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{\mathit{kji}}$ for k = 1, 2, $n^{(O)}={\sum }_{i=s+1}^m{\sum }_{j=1}^J{n}_{ji}^{(O)}$ and and $n_{ji}^{(O)}$ are the numbers of at-risk population in the overlapping region. Note that there is no suffix k in $n_{ji}^{(O)}$. The sign of σ₁₂ determines, whether the covariance between β̂₁₁ and β̂₁₂ is positive or negative, and when there is no overlap in time intervals, σ₁₂ = 0. Under the log-normal model, the corrected Z_CT test was shown to follow a standard normal distribution under the null hypothesis, and to be more efficient than the pooled t-test; see Li and Tiwari (2007).

However, one assumption in Li and Tiwari (2007) is the equal variance in both regression models, which may not be realistic, especially for rare cancers. A further refinement has been made to derive the variance of y_ki by using the Poisson assumptions on the first two moments of the counts d_kji, i.e. E(d_kji) = var(d_kji). Under these assumptions, the consistent estimate of the error variance of e_ki is given by $v_{ki}^2=\frac{1}{r_{ki}^2}{\sum }_{j=1}^J{w}_j^2\frac{d_{\mathit{kji}}}{n_{\mathit{kji}}^2}$, leading to the following weighted least squares test proposed by Li et al. (2007), referred to as Z_WLS:

$$Z_{WLS}=\frac{{\stackrel{\sim }{\beta }}_{11}-{\stackrel{\sim }{\beta }}_{12}}{{\left\{{\stackrel{\sim }{\sigma }}_1^{-2}+{\stackrel{\sim }{\sigma }}_2^{-2}-2{\stackrel{\sim }{\sigma }}_{12}{\stackrel{\sim }{\sigma }}_1^{-2}{\stackrel{\sim }{\sigma }}_2^{-2}\frac{{(n^{(O)})}^2}{n_1{n}_2}\right\}}^{1/2}}.$$ (4)

with ${\stackrel{\sim }{\sigma }}_1^2={\sum }_{i=1}^m{(T_i-{\stackrel{\sim }{t}}_1)}^2/v_{1i}^2$ and ${\stackrel{\sim }{\sigma }}_2^2={\sum }_{i=s+1}^{s+n}(T_i-{\stackrel{\sim }{t}}_2{)}^2/v_{2i}^2$,

$${\stackrel{\sim }{\sigma }}_{12}=\sum _{i=s+1}^m(T_i-{\stackrel{\sim }{t}}_1)(T_i-{\stackrel{\sim }{t}}_2)\frac{v_{12i}^{(o)}}{v_{1i}^2{v}_{2i}^2},$$

where

$$v_{12i}^{(o)}=\frac{1}{r_{1i}{r}_{2i}}\sum _{j=1}^J{w}_j^2\frac{d_{ji}^{(o)}}{{(n_{ji}^{(o)})}^2},$$

and $d_{ji}^{(o)}$ are the counts in the overlapping region and during the overlapping period. Here,

$${\stackrel{\sim }{t}}_1=\frac{{\sum }_{i=1}^m{T}_i/v_{1i}^2}{{\sum }_{i=1}^{m}1/v_{1i}^2},{\stackrel{\sim }{t}}_2=\frac{{\sum }_{i=s+1}^{s+n}{T}_i/v_{2i}^2}{{\sum }_{i=s+1}^{s+n}1/v_{2i}^2},$$

and β̃₁₁, β̃₁₂ are weighted least square estimates of β₁₁, β₁₂.

Under the null hypothesis, because of the normal approximation, Z_WLS approximately follows a standard normal distribution. The Z_WLS has been shown to be more conservative than Z_CT in retaining the size of the test, but is more powerful for the common cancer sites; see Li et al. (2007). However, there are several disadvantages of the existing methods. First, one key step of Li et al. (2007) is the normal approximation of the age-adjusted rates. Secondly, both Li et al. (2007) and Li and Tiwari (2007) need adjustments for zero counts.

3 Age-stratified Poisson Regression Model

As the existing approaches to dealing with age-adjusted cancer rates were all based on the normal approximation, we take a more natural route in the sequel by considering the Poisson nature of the underlying count data and propose an age-stratified Poisson regression to describe the change trend of incident (or death) counts on time. Based on this model, a proper test that accounts for overlapping is proposed.

Specifically, since d_kji, the number counts (deaths or new cancer cases) observed in Region k (k = 1, 2) in age-group j, is a count, we assume that

$$d_{\mathit{kji}}{}^{\underset{\sim }{\mathit{ind}}}\mathit{Pois}(n_{\mathit{kji}}{\lambda }_{\mathit{kji}}),$$

with

$$log{\lambda }_{\mathit{kji}}={\beta }_{0kj}+{\beta }_{1k}{t}_{ki},$$ (5)

which is referred to as the Age-stratified Poisson Regression Model as the age-specific intercept β_0kj is assumed for age-group j. The common slope β_1k is of particular importance as it transcribes the trends of mortality or incidence and, in particular, determines the APC value.

Again let APC₁ and APC₂ be the corresponding APC values for these two Poisson regressions. A natural test for the null hypothesis H₀: APC₁ = APC₂ versus the alternative hypothesis H₁: APC₁ ≠ APC₂ would be

$$Z_{\mathit{POIS}}=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}}{\sqrt{\mathit{Var}\{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}\}}},$$

where β̂₁₁ and β̂₁₂ are the maximum likelihood estimates of β₁₁ and β₁₂ derived in the Appendix.

Because of the possible overlapping of Regions 1 and 2, β̂₁₁ and β̂₁₂ may be correlated. Thus the key to the derivation of the test lies in a correct evaluation of Cov(β̂₁₁, β̂₁₂).

3.1 Derivation of the Test

To proceed, we let β_k = (β _1k, β _0k1, …, β _0kJ)′, k = 1, 2, whose estimates β̂_k can be btained by solving the score equations [based on (5)]

$$U_k({\beta }_k)=0,$$

for k = 1, 2, where U_k = (U_1k,1, U_0k,1, …, U_0k,J)′ and

$$\begin{array}{l}{U}_{1k,1}=\sum _{i=1}^{I_k}\sum _{j=1}^J{n}_{\mathit{kji}}{t}_{ki}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki})-\sum _{i=1}^{I_k}\sum _{j=1}^J{d}_{\mathit{kji}}{t}_{ki},\\ U_{0k,j}=\sum _{i=1}^{I_k}{n}_{\mathit{kji}}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki})-\sum _{i=1}^{I_k}{d}_{\mathit{kji}},\end{array}$$

for j = 1, …, J.

As U_k(β̂_k) = 0, expanding it around the true value β_k, and ignoring the higher order terms yields

$$0\equiv \frac{1}{\sqrt{I_k}}{U}_k({\widehat{\beta }}_k)=\frac{1}{\sqrt{I_k}}{U}_k({\beta }_k)+\frac{1}{I_k}{U}_k^{(1)}({\beta }_k)\left\{\sqrt{I_k}\left({\widehat{\beta }}_k-{\beta }_k\right)\right\}+o_p(1),$$

where $U_k^{(1)}=\partial U_k({\beta }_k)/\partial {\beta }_k$ are (J+1) × (J+1) matrices with its 1^st row as $(U_{1k,11}^{(1)},U_{1k,01}^{(1)},\dots ,U_{1k,0J}^{(1)})$ and the (j + 1)^th row (j = 1, …, J) as $(U_{0k,j1}^{(1)},U_{0k,0j1}^{(1)},\dots ,U_{0k,0jJ}^{(1)})$, for k = 1, 2. Here

$$\begin{array}{l}{U}_{1k,11}^{(1)}=\frac{\partial U_{1k,1}}{\partial {\beta }_{1k}}=\sum _{i=1}^{I_k}\sum _{j=1}^J{n}_{\mathit{kji}}{t}_{ki}^{2}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki}),\\ U_{1k,0j}^{(1)}=\frac{\partial U_{1k,1}}{\partial {\beta }_{0kj}}=\sum _{i=1}^{I_k}{n}_{\mathit{kji}}{t}_{ki}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki}),\\ U_{0k,j1}^{(1)}=\frac{\partial U_{0k,j}}{\partial {\beta }_{1k}}=\sum _{i=1}^{I_k}{n}_{\mathit{kji}}{t}_{ki}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki}),\\ U_{0k,0j{j}^{\prime }}^{(1)}=\frac{\partial U_{0k,j}}{\partial {\beta }_{0k{j}^{\prime }}}={\delta }_{j{j}^{\prime }}\sum _{i=1}^{I_k}{n}_{\mathit{kji}}exp({\beta }_{0kj}+{\beta }_{1k}{t}_{ki}),\end{array}$$

and δ_jj′= 1 if j = j′ and 0 otherwise.

Denote by $A_k=\mathit{pli}{m}_{I_k\to \infty }-U_k^{(1)}({\beta }_k)/I_k$ for k=1, 2, where plim denotes the limit in probability. Then for large I₁(≡m) and I₂(≡n), standard probabilistic arguments yield

$$\left\{\sqrt{I_1}({\widehat{\beta }}_1-{\beta }_1),\sqrt{I_2}({\widehat{\beta }}_2-{\beta }_2)\right\}\underset{\sim }{d}\left\{A_1^{-1}\frac{1}{\sqrt{I_1}}{U}_1({\beta }_1),A_2^{-1}\frac{1}{\sqrt{I_2}}{U}_2({\beta }_2)\right\}.$$

Here, $\underset{\sim }{d}$denotes approximate equivalence in joint distribution functions. Hence,

$$\begin{array}{l}\mathit{Var}(\sqrt{m}({\widehat{\beta }}_1-{\beta }_1),\sqrt{m}({\widehat{\beta }}_1-{\beta }_1))\doteq A_1^{-1}\frac{1}{m}\mathit{Cov}(U_1({\beta }_1),U_1({\beta }_1))A_1^{-T},\\ \mathit{Var}(\sqrt{n}({\widehat{\beta }}_2-{\beta }_2),\sqrt{n}({\widehat{\beta }}_2-{\beta }_2{)}^{\prime })\doteq A_2^{-1}\frac{1}{n}\mathit{Cov}(U_2({\beta }_2),U_2({\beta }_2))A_2^{-T},\\ \mathit{Cov}(\sqrt{m}({\widehat{\beta }}_1-{\beta }_1),\sqrt{n}({\widehat{\beta }}_2-{\beta }_2{)}^{\prime })\doteq A_1^{-1}\frac{1}{\sqrt{mn}}\mathit{Cov}(U_1({\beta }_1),U_2({\beta }_2))A_2^{-T},\end{array}$$

Let $V=\frac{1}{m}\mathit{Cov}(U_1({\beta }_1),U_1({\beta }_1))$, $W=\frac{1}{n}\mathit{Cov}(U_2({\beta }_2),U_2({\beta }_2))$, $\sum =\frac{1}{\sqrt{mn}}\mathit{Cov}(U_1({\beta }_1),U_2({\beta }_2))$, and V̂, Ŵ, Σ̂ be the corresponding estimates, whose derivations are given in the Appendix.

Then,

$$\begin{array}{l}\widehat{C}ov({\widehat{\beta }}_1,{\widehat{\beta }}_1)=m{\{U_1^{(1)}({\widehat{\beta }}_1)\}}^{-1}\widehat{V}{\{U_1^{(1)}({\widehat{\beta }}_1)\}}^{-T};\\ \widehat{C}ov({\widehat{\beta }}_2,{\widehat{\beta }}_2)=n{\{U_2^{(1)}({\widehat{\beta }}_2)\}}^{-1}\widehat{W}{\{U_2^{(1)}({\widehat{\beta }}_2)\}}^{-T};\\ \widehat{C}ov({\widehat{\beta }}_1,{\widehat{\beta }}_2)=\sqrt{mn}{\{U_1^{(1)}({\widehat{\beta }}_1)\}}^{-1}\widehat{\sum }{\{U_2^{(1)}({\widehat{\beta }}_2)\}}^{-T};\end{array}$$

These are three (J +1) × (J +1) matrices, the (1, 1) entries of which are ${\widehat{\sigma }}_1^2=\widehat{V}ar({\widehat{\beta }}_{11})$, ${\widehat{\sigma }}_2^2=\widehat{V}ar({\widehat{\beta }}_{12})$and σ̂₁₂ = Ĉov(β̂₁₁, β̂₁₂), respectively. From this we compute V̂ar (β̂₁₁ − β̂₁₂) = V̂ar (β̂₁₁)+V̂ar (β̂₁₂) − 2Ĉov(β̂₁₁, β̂₁₂). Hence, the Z-test for comparing APC values is given by

$$Z_{\mathit{POIS}}=\frac{{\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}}{{({\widehat{\sigma }}_1^2+{\widehat{\sigma }}_2^2-2{\widehat{\sigma }}_{12})}^{1/2}},$$ (6)

which follows the standard normal distribution under H₀: β₁₁ = β₁₂. The computation of β̂₁₁, β̂₁₂ is given in the Appendix.

3.2 ARE Comparison with the WLS test

It is of substantial interest to evaluate the gains in efficiency of the proposed test compared with the WLS test. First note (5) implies that $E(r_{ki})\equiv E({\sum }_j{w}_j\frac{d_{\mathit{kji}}}{n_{\mathit{kji}}})=({\sum }_j{w}_j{e}^{{\beta }_{0kj}})e^{{\beta }_{1k}{T}_i}$. This in turn implies that

$$E(log{r}_{ki})\doteq logE(r_{ki})=log\left(\sum _j{w}_j{e}^{{\beta }_{\text{0}kj}}\right)+{\beta }_{1k}{t}_{ki},$$ (7)

when Var(r_ki) is small, which is often the case for the cancer incidence and mortality data (Kim et al., 2000).

A comparison between (1) and (7) reveals that models (1) and (5) approximately specify the same first moment of the age-adjusted cancer rates, making it possible to compare the efficiency of the tests based on these two models via the measure of the Pitman Asymptotic Relative Efficiency. Specifically, standard asymptotic analysis will yield

$${\widehat{\beta }}_{11}-{\widehat{\beta }}_{12}\sim N({\beta }_{11}-{\beta }_{12},{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_2^2-2{\widehat{\sigma }}_{12}),$$

while, for the WLS estimates,

$${\stackrel{\sim }{\beta }}_{11}-{\stackrel{\sim }{\beta }}_{12}\sim N({\beta }_{11}-{\beta }_{12},{\stackrel{\sim }{\sigma }}_1^{-2}+{\stackrel{\sim }{\sigma }}_2^{-2}-2{\stackrel{\sim }{\sigma }}_{12}{\stackrel{\sim }{\sigma }}_1^{-2}{\stackrel{\sim }{\sigma }}_2^{-2}\frac{{(n^{(O)})}^2}{n_1{n}_2}).$$

Hence, the Pitman Asymptotic Relative Efficiency (ARE) comparing tests (6) and (4), which is the ratio of the noncentralities of the above two normal distributions, is given by

$$\text{ARE}=\frac{{\stackrel{\sim }{\sigma }}_1^{-2}+{\stackrel{\sim }{\sigma }}_2^{-2}-2{\stackrel{\sim }{\sigma }}_{12}{\stackrel{\sim }{\sigma }}_1^{-2}{\stackrel{\sim }{\sigma }}_2^{-2}\frac{{(n^{(O)})}^2}{n_1{n}_2}}{{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_2^2-2{\widehat{\sigma }}_{12}}$$ (8)

The evaluation of (8) typically involves numerical computations.

4 SEER mortality data analysis and Simulations

Li et al. (2007) demonstrated that Z_WLS performs better than Z_CT, via the calculation of ARE, as Z_CT relies on the common variance assumption, which may not be realistic. Hence, we focus this paper on comparing Z_POIS with Z_WLS. To comprehensively evaluate these tests, we consider several scenarios of overlap in two regions and in two different time intervals. Specifically, we assume that Region 1 consists of Georgia (GA), South Carolina (SC), and North Carolina (NC), and that Region 2 consists of NC, Virginia (VA) and Maryland (MD); with NC as the overlapping state between the two regions. The three different time intervals, with varying degree of overlap in the intervals, are taken to be: (a) [1980,1989] for Region 1, and [1990,1999] for Region 2 so that there is no overlap between the two time intervals and, hence, σ₁₂ = 0; (b) [1980,1989] for Region 1, and [1983,1992] for Region 2 so that there a considerable overlap of six years between the two intervals and σ₁₂ = 12.25; (c) [1980,1989] for Region 1, and [1987, 1996] for Region 2 so that there is a little overlap of three years’ between the two intervals and σ₁₂ = −34.75.

The counts, d_kji were generated based on model (5) with t_ki taking values in the intervals corresponding to the two regions stated above. More specifically, the t_1i take values of {0, 1, …, 9}, while the t_2i take values of {10, …, 19}, {3, …, 12}, and {7, …, 16}, respectively for cases (a)–(c).

In order to fully specify λ_kji in (5), we assume that β_0kj = log(d_kj1/n_kj1) − β_1kt_k1, where d_kj1 and n_kj1 are respectively the observed number of deaths and the number of at-risk population at the beginning of the intervals considered, and take β_1k = log(APC_k/100 + 1), based on the specified values of APC_k. The age-specific counts for the overlapping state, NC, are generated from Poisson distributions with means, $n_{ji}^{(o)}\times \frac{1}{2}({\lambda }_{1ji}+{\lambda }_{2ji})$, where $n_{ji}^{(o)}$ denotes the at-risk population in the overlapping region. When λ_1ji =λ_2ji, this reduces to the situation specified by the null hypothesis. The number of at risk population and the observed number of deaths were obtained from the SEER database for all malignant male cancers and prostate cancer. The values of APC were assumed to range from −0.3% to 3.0%. For each parameter configuration, a total of 1000 simulated data were obtained. The results for the three time-overlapping cases are summarized in Tables 1–3.

Table 1.

Comparison of the power functions under various hypotheses between the Poisson-based test Z_POIS and the weighted-least-squares based test Z_WLS for two overlapping regions over disjoint time intervals, Region 1 (1980–1989) vs Region 2 (1990–1999). APC1 and APC2 are the annual percent changes in Regions 1 and 2, respectively.

Cancer Sites	APC1	APC2	ARE	ZWLS	ZPOIS
All Malignant	0.100	0.100	1.1490	0.059	0.050
	−0.300	−0.300	1.1491	0.049	0.045
	0.500	0.500	1.1492	0.060	0.049
	1.000	1.000	1.1493	0.048	0.053
	3.000	3.000	1.1504	0.047	0.057
	0.100	0.500	1.1507	0.877	0.907
	−0.300	0.300	1.1509	0.998	1.000
	1.000	2.000	1.1515	1.000	1.000
	1.000	3.000	1.1518	1.000	1.000
Prostate	0.100	0.100	1.1610	0.043	0.045
	−0.300	−0.300	1.1611	0.041	0.047
	0.500	0.500	1.1612	0.051	0.041
	1.000	1.000	1.1613	0.046	0.051
	3.000	3.000	1.1614	0.045	0.051
	0.100	0.500	1.1617	0.182	0.212
	−0.300	0.300	1.1619	0.357	0.40
	1.000	2.000	1.1622	0.773	0.830
	1.000	3.000	1.1634	1.000	1.000

Table 3.

Comparison of the power functions between the Poisson based Z_POIS and the weighted-least-squares based Z_WLS for two overlapping regions over slightly overlapping time intervals, Region 1 (1980–1989) vs Region 2 (1987–1996). APC1 and APC2 are the annual percent changes in Regions 1 and 2, respectively.

Cancer Sites	APC1	APC2	ARE	ZWLS	ZPOIS
All Malignant	0.100	0.100	1.1350	0.044	0.044
	−0.300	−0.300	1.1350	0.044	0.046
	0.500	0.500	1.1351	0.046	0.051
	1.000	1.000	1.1351	0.045	0.051
	3.000	3.000	1.1352	0.043	0.047
	0.100	0.500	1.1354	0.834	0.891
	−0.300	0.300	1.1355	0.994	0.994
	1.000	2.000	1.1362	1.000	1.000
	1.000	3.000	1.1367	1.000	1.000
Prostate	0.100	0.100	1.1410	0.045	0.051
	−0.300	−0.300	1.1410	0.043	0.049
	0.500	0.500	1.1412	0.060	0.051
	1.000	1.000	1.1423	0.061	0.055
	3.000	3.000	1.1426	0.052	0.052
	0.100	0.500	1.1428	0.170	0.184
	−0.300	0.300	1.1431	0.319	0.361
	1.000	2.000	1.1436	0.706	0.759
	1.000	3.000	1.1439	0.998	1.000

We remark that that, even though both Z_WLS and Z_POIS are derived under different model assumptions, they are both valid tests for testing the equality of two APCs and hence the ARE defined in (8) is valid. The tables show that the ARE of Z_POIS with respect to Z_WLS is greater than 1 for all the three cases, meaning that Z_POIS would be more powerful than Z_WLS when the alternative hypothesis is true. The tables also show that in most situations Z_POIS outperforms the Z_WLS in retaining the Type I error probabilities and, hence, yields a more valid test. Also the powers of both WLS and Poisson-based tests are sensitive to the delta values (the differences of APC values). The larger the delta values are, the more powerful the tests are. The larger delta values also lead to slightly larger AREs, though the differences are not so obvious.

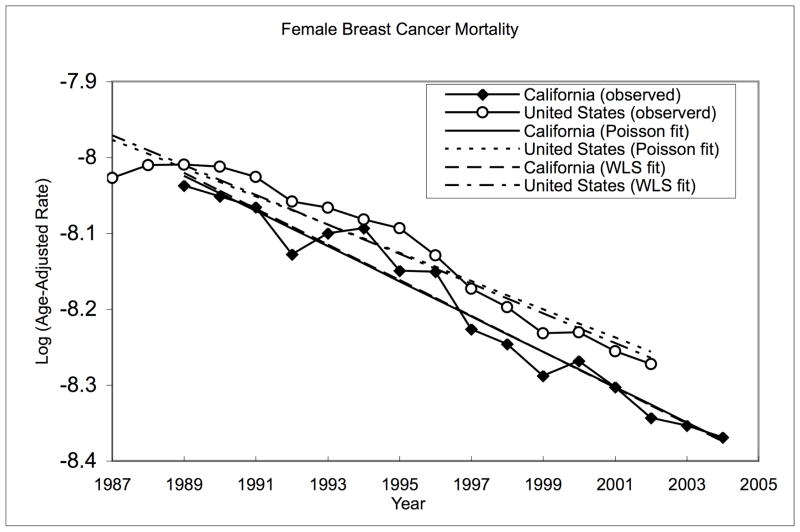
It is of substantial interest to compare the changes in cancer mortality rates in California with the national levels starting late 1980’s as a California law (Health and Safety Code, Section 103885) was passed then, which mandated the reporting of malignancies diagnosed throughout the state. For this purpose, we applied the proposed methodology to compare the annual percent change (APC) in the age-adjusted mortality rates for the United States (US) for the period from 1988–2002 to that of California (CA) for the period from 1990 to 2004. We fitted the weighted linear models as well as the age-stratified Poisson model, and applied both tests to compare the age-adjusted mortality rates of female breast cancer in CA for the 16-year period from 1989–2004 to that of US for the 16-year period from 1987–2002, for which the national mortality data were available. The observed values of the log-transformed annual age-adjusted rates and fitted regression lines from the Z_POIS test procedure are plotted in Figure 1. The parameter estimates and the values of the test statistics are summarized in Table 4. The results indicated the mortality rates of Breast cancer for California and the US have decreased. Both tests reject the null hypothesis of equality of the two APCs, indicating that the annual percent change (APC) of California, is significantly different from the national level. However, the p-value for Z_POIS is much smaller than that of Z_WLS, rendering more evidence again the null hypothesis.

Fig. 1.

Observed and fitted log-transformed age-adjusted breast cancer mortality rates in CA [1989–2004] and US [1987–2002]

Table 4.

Comparing APC of Breast Cancer Mortality Between CA and the US

	CA	US
APCWLS	−2.33	−1.94
SEWLS	0.084	0.027
ZWLS	−4.95	(p=0.000000757)
APCPOIS	−2.29	−1.84
SEPOIS	0.083	0.026
ZPOIS	−5.62	(p= 0.000000019593)

5 Discussion

In this paper, we have considered an important problem where comparisons have to be made for regions or time intervals that overlap. As opposed to the existing work, e.g Li and Tiwari (2007) and Li et al. (2007), this project advances this area in two distinct ways. First, the developed test does not rely on the normal approximation of the cancer rate, but directly model the counts to follow a Poisson regression model. The parameters are then estimated using their maximum likelihood estimates, and the Z-test is derived for testing the equality of two APCs. Secondly, the developed Poisson regression model can easily accommodate 0 count data (for the rare cancers), as opposed to the log normal model (Li and Tiwari, 2007; Li et al., 2007) which needs to involve extra zero-corrected adjustment. We have applied the developed methodology to the analysis of the major cancer sites from the SEER Program and have found that the corrected Z-test renders more power than the existing tests. A Bayesian Poisson regression would be a useful approach. However, choice of priors is always difficult and computation may not be so straightforward compared to this current work, wherein analytical solutions have been derived. Hence, we envision that the proposed method would be preferable because of simple interpretation of the model parameters, natural choice of the model and computational readiness.

In our technical development, we have modelled the logarithm transformation of the age-adjusted rates as a linear regression on time in (5) and have indeed explicitly assumed parallelism across age groups. That is, the growth curves of the cancer rates for various age groups share the same slope, which carries the information for the APC. Indeed, linearity parallelism for the cancer rates could be a debatable issue in cancer surveillance, which is likely to be violated for some cancers. One alternative, along the line of generalized mixed models, is to assume a random slope (as opposed to a constant slope) across age groups. This ongoing work will be reported in a subsequent communication.

Table 2.

Comparison of the power functions between the Poisson based Z_POIS and the weighted-least-squares based Z_WLS for two overlapping regions over roughly the same time intervals, Region 1 (1980–1989) vs Region 2 (1983–1992). APC1 and APC2 are the annual percent changes in Regions 1 and 2, respectively.

Cancer Sites	APC1	APC2	ARE	ZWLS	ZPOIS
All Malignant	0.100	0.100	1.1710	0.055	0.057
	−0.300	−0.300	1.1710	0.056	0.057
	0.500	0.500	1.1711	0.048	0.050
	1.000	1.000	1.1712	0.047	0.049
	3.000	3.000	1.1723	0.051	0.056
	0.100	0.500	1.1726	0.872	0.908
	−0.300	0.300	1.1729	0.994	0.997
	1.000	2.000	1.1733	1.000	1.000
	1.000	3.000	1.1737	1.000	1.000
Prostate	0.100	0.100	1.1820	0.043	0.047
	−0.300	−0.300	1.1821	0.043	0.043
	0.500	0.500	1.1822	0.046	0.041
	1.000	1.000	1.1823	0.035	0.053
	3.000	3.000	1.1823	0.034	0.055
	0.100	0.500	1.1825	0.170	0.197
	−0.300	0.300	1.1827	0.341	0.393
	1.000	2.000	1.1832	0.742	0.802
	1.000	3.000	1.1835	1.000	1.000

Appendix A: Derivation of V̂, Ŵ, Σ̂

Write

$$V={\left(\begin{array}{cc}{V}_{11}& V_{12}\\ V_{12}^{\prime }& V_{22}\end{array}\right)}_{(J+1)\times (J+1)};W={\left(\begin{array}{cc}{W}_{11}& W_{12}\\ W_{12}^{\prime }& W_{22}\end{array}\right)}_{(J+1)\times (J+1)};\sum ={\left(\begin{array}{cc}{\mathrm{\sum }}_{11}& {\mathrm{\sum }}_{12}\\ {\mathrm{\sum }}_{12}^{\prime }& {\mathrm{\sum }}_{22}\end{array}\right)}_{(J+1)\times (J+1)}$$

where

$$V_{11}=\frac{1}{m}\mathit{Var}(U_{11,1})=\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^J{T}_i^2\mathit{Var}(d_{1ji})=\frac{1}{m}\sum _{i=1}^m\sum _{j=1}^J{T}_i^{2}E(d_{1ji}).$$

Hence a consistent estimate is ${\widehat{V}}_{11}=\frac{1}{m}{\sum }_{i=1}^m{\sum }_{j=1}^J{T}_i^2{d}_{1ji}.$

Similarly,

$${\widehat{V}}_{12}=({\widehat{V}}_{12,1,\dots ,}{\widehat{V}}_{12,J})$$

where

$${\widehat{V}}_{12,j}=\widehat{C}ov(U_{11,1,}{U}_{01,j})=\frac{1}{m}\sum _{i=1}^m{T}_i{d}_{1ji}.$$

Also, V₂₂ = ((V_22,jj′)) with V̂_22,jj′= Ĉov (U_01,j; U_01,j′) = 0; j ≠ j′; $\frac{1}{m}{\sum }_{i=1}^m{d}_{1ji,}j=j^{\prime }.$

Next compute the estimate of W:

$$W_{11}=\frac{1}{n}\mathit{Var}(U_{12,1})=\frac{1}{n}\sum _{i=s+1}^{s+n}\sum _{j=1}^J{T}_i^2\mathit{Var}(d_{2ji})=\frac{1}{n}\sum _{i=s+1}^{s+n}\sum _{j=1}^J{T}_i^{2}E(d_{2ji})$$

so that ${\widehat{W}}_{11}=\frac{1}{n}{\sum }_{i=s+1}^{s+n}{\sum }_{j=1}^J{T}_i^2{d}_{2ji}$ Similarly, Ŵ₁₂ = (Ŵ_12,1, …, Ŵ_12,J) where ${\widehat{W}}_{12,j}=\widehat{C}ov(U_{12,1},U_{02,j})=\frac{1}{n}{\sum }_{i=s+1}^n{T}_i{d}_{2ji}$. Also, Ŵ₂₂ = ((Ŵ_22,jj′)) with ${\widehat{W}}_{22,j{j}^{\prime }}=0,j\ne j^{\prime };=\frac{1}{n}{\sum }_{i=s+1}^{s+n}{d}_{2ji,}j=j^{\prime }$. Finally, the estimate of Σ is computed as follows:

$$\begin{array}{l}{\mathrm{\sum }}_{11}=\frac{1}{\sqrt{mn}}\mathit{Cov}(U_{11,1},U_{12,1})\\ =\frac{1}{\sqrt{mn}}\mathit{Cov}\left(\sum _{i=1}^m\sum _{j=1}^J{T}_i{d}_{1ji},\sum _{i=s+1}^{s+n}\sum _{j=1}^J{T}_i{d}_{2ij}\right)\\ =\frac{1}{\sqrt{mn}}\mathit{Cov}\left(\sum _{i=1}^m\sum _{j=1}^J{T}_i\left(d_{1ji}^{(NO)}+d_{ji}^{(O)}\right),\sum _{i=s+1}^{s+n}\sum _{j=1}^J{T}_i\left(d_{2ji}^{(NO)}+d_{ji}^{(O)}\right)\right)\end{array}$$

where $d_{\mathit{kji}}=d_{\mathit{jki}}^{(NO)}+d_{ji}^{(O)}$ and the superscripts “NO” and “O” denote the non-overlapping and overlapping regions, respectively. Thus, ${\widehat{\mathrm{\sum }}}_{11}=\frac{1}{\sqrt{mn}}{\sum }_{i=s+1}^m{\sum }_{j=1}^J{T}_i^2{d}_{ji}^{(O)}$. Let Σ̂₁₂ = (Σ_12,1, …, Σ̂_12,J ) where ${\widehat{\mathrm{\sum }}}_{12,j}=\frac{1}{\sqrt{mn}}{\sum }_{i=s+1}^m{T}_i{d}_{ji}^{(O)}$. Also, Σ̂₂₂ = ((Σ̂_22,jj′)) with ${\widehat{\mathrm{\sum }}}_{22,j,j^{\prime }}=0,j\ne j^{\prime };\frac{1}{\sqrt{mn}}{\sum }_{i=s+1}^m{d}_{ji}^{(O)},j=j^{\prime }$.

Appendix B: Computation of the MLEs

Note that the MLEs of β_0jk and β_1k satisfy:

$$\begin{array}{l}{e}^{{\beta }_{0jk}}=\frac{{\sum }_i{d}_{\mathit{kji}}}{{\sum }_i{e}^{{\beta }_{1k}{T}_i}{n}_{\mathit{kji}}};\\ \stackrel{\sim }{U}({\beta }_{1k})=\sum _{j,i}{n}_{\mathit{kji}}{T}_i\left(\frac{{\sum }_i{d}_{\mathit{jki}}}{{\sum }_i{e}^{{\beta }_{1k}{T}_i}{n}_{\mathit{kji}}}\right)e^{{\beta }_{1k}{T}_i}-\sum _{j,i}{d}_{\mathit{kji}}{T}_i\\ =\sum _j{d}_{kj.}\left(\frac{{\sum }_i{n}_{\mathit{kji}}{T}_i{e}^{{\beta }_{1k}{T}_i}}{{\sum }_i{e}^{{\beta }_{1k}{T}_i}{n}_{\mathit{kji}}}\right)-\sum _i{d}_{k.i}{T}_i\\ =\sum _j{d}_{kj.}[A_{kj}(1)A_{kj}^{-1}(0)]-\sum _i{d}_{k.i}{T}_i=0;k=1,2,\end{array}$$

where d_kj· =Σ_i d_kji, d_k·i =Σ_j d_kji, and $A_{kj}(a)={\sum }_i{n}_{\mathit{kji}}{T}_i^a{e}^{{\beta }_{1k}{T}_i}$ for a = 0, 1, 2.

Since Ũ(β_1k) is a monotonic function of β_1k, there is a unique solution to this equation. Let β̂_1k be the solution. This is the MLE of β_1k. We can use a Newton-Raphson method to obtain β̂_1k as follows. Let β̂_1k(l) be the estimate at the l^th iteration, then the estimate at the (l + 1)^th iteration is given by β̂_1k(l + 1) = β̂_1k(l) − [Ũ⁽¹⁾(β̂_1k(l))]^{− 1}Ũ(β̂_1k(l)), where Ũ⁽¹⁾(β) is the first (partial) derivative of Ũ(b) with respect to b evaluated at b = β. We stop iterating wh en |β̂_1k(l + 1) − β̂_1k(l)| < ε for some pre-specified value of ε. Note that

$$\begin{array}{l}{\stackrel{\sim }{U}}^{(1)}({\beta }_{1k})=\sum _{j,i}{n}_{\mathit{jki}}{T}_i^2{e}^{{\beta }_{1k}{T}_i}\left(\frac{{\sum }_i{d}_{\mathit{kji}}}{{\sum }_i{e}^{{\beta }_{1k}{T}_i}{n}_{\mathit{kji}}}\right)-\sum _{j,i}{n}_{\mathit{jki}}{t}_i{e}^{{\beta }_{1k}{t}_i}\frac{{\sum }_i{n}_{\mathit{kji}}{t}_i{e}^{{\beta }_{1k}{t}_i}}{{\left({\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}\right)}^2}\\ =\sum _j\left(\frac{\left({\sum }_i{n}_{\mathit{kji}}{t}_i^2{e}^{{\beta }_{1k}{t}_i}\right)\left({\sum }_i{d}_{\mathit{kji}}\right)}{{\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}}\right)-\sum _j\frac{{\left({\sum }_i{n}_{\mathit{kji}}{t}_i{e}^{{\beta }_{1k}{t}_i}\right)}^2}{{\left({\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}\right)}^2}\\ =\sum _j{d}_{kj.}\left(\frac{{\sum }_i{n}_{\mathit{kji}}{t}_i^2{e}^{{\beta }_{1k}{t}_i}}{{\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}}\right)-\sum _j\frac{{\left({\sum }_i{n}_{\mathit{kji}}{t}_i{e}^{{\beta }_{1k}{t}_i}\right)}^2}{{\left({\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}\right)}^2}\\ =\sum _j\mathit{dkj}.[A_{kj}(2){(A_{kj}(0))}^{-1}]-\sum _j[{(A_{kj}(1))}^2{(A_{kj}(0))}^{-1}],k=1,2.\end{array}$$

Substituting the MLE β̂_1k in place for β_1k in $e^{{\beta }_{0kj}}=\frac{{\sum }_i{d}_{\mathit{kji}}}{{\sum }_i{e}^{{\beta }_{1k}{t}_i}{n}_{\mathit{kji}}}$ gives the MLE ${\widehat{\beta }}_{0kj}=log\left({\sum }_i{d}_{\mathit{kji}}\right)-log\left({\sum }_i{e}^{{\widehat{\beta }}_{1k}{t}_i}{n}_{\mathit{kji}}\right).$