Effects of Small-Group Tutoring with and without Validated Classroom Instruction on At-Risk Students' Math Problem Solving: Are Two Tiers of Prevention Better Than One?

Abstract

The purpose of this study was to assess the effects of small-group tutoring with and without validated classroom instruction on at-risk (AR) students' math problem solving. Stratifying within schools, 119 3^rd-grade classes were randomly assigned to conventional or validated problem-solving instruction (Hot Math [schema-broadening instruction]). Students identified as AR (n = 243) were randomly assigned, within classroom conditions, to receive Hot Math tutoring or not. Students were tested on problem-solving and math applications measures before and after 16 weeks of intervention. Analyses of variance, which accounted for the nested structure of the data, revealed the tutored students who received validated classroom instruction achieved better than tutored students who received conventional classroom instruction (ES = 1.34). However, the advantage for tutoring over no tutoring was similar whether or not students received validated or conventional classroom instruction (ESs = 1.18 and 1.13). Tutoring, not validated classroom instruction reduced the prevalence of math difficulty. Implications for responsiveness-to-intervention prevention models and for enhancing math problem-solving instruction are discussed.

Mathematics word problems require the transfer of knowledge to novel situations, and this form of transfer can be difficult to effect (cf. Bransford & Schwartz, 1999; Mayer, Quilici, & Moreno, 1999) especially for primary-grade children (Durnin, Perrone, & MacKay, 1997; Foxman, Ruddock, McCallum, & Schagen, 1991, cited in Boaler, 1993; Larkin, 1989). Whereas a calculations problem is already set up for solution, a word problem requires students to use text to determine what information is unknown and to construct and solve a number sentence for finding that unknown information. So, although calculation skill is foundational to word problems (e.g., Fuchs et al., 2006), it seems likely that for some students, word-problem skill will not develop automatically from instruction on math calculations, but rather that instruction needs to be designed specifically to prevent difficulty with word problems.

The context for preventing academic difficulty in the schools has changed over the past 5 years with the introduction of multi-tiered prevention systems.¹ Adapted from the health care system, school-based multi-tier prevention systems typically involve three tiers. The first tier is research-principled or validated classroom instruction. Students who are deemed at risk for difficulty with the classroom program, usually on the basis of screening near the beginning of the school year, also receive a second tier of prevention, using a standard, validated small-group tutoring protocol (that can be expected to benefit most students). Only students who prove unresponsive to classroom instruction and to tutoring are referred for a comprehensive evaluation to consider the possibility of a disability that requires a third, more individualized tier of prevention, usually special education. Because such a multi-tier prevention system involves assessing a student's responsiveness-to-intervention (RTI), it is conventionally referred to as an RTI prevention system (e.g., see Vaughn & Fuchs, 2003).

Most RTI studies have addressed reading (e.g., Fuchs, Compton, Fuchs, & Davis, in press; Vaughn, Linan-Thompson, & Hickman, 2003; Vellutino et al., 1996). In mathematics, where fewer studies have been conducted, the bulk of the literature has been conducted by VanDerHeyden, Witt, and colleagues. For example, VanDerHeyden, Witt, and Gilbertson (2007) screened elementary-grade students on grade-level computational fluency. Classrooms scoring below a criterion received classroom instruction to build computational fluency. Individual students who scored below the 16^th percentile of their own class, with classroom intervention when needed, were assessed to determine whether students could score above the 16^th percentile if offered a reward. Only students who could not achieve the criterion even when rewarded entered tutoring, which involved 10 minutes per day of computation instruction using modeling, guided practice with immediate error correction, independent timed practice with slightly delayed error correction, and the opportunity to earn a reward. VanDerHeyden et al. evaluated this multi-tiered RTI math prevention model using a multiple-baseline across schools design with five schools. Referrals to and evaluations for special education decreased with implementation, but effects on students' math performance were not reported. In related work, VanDerHeyden and Witt (2005) used a similar model to screen first and second graders in one school using basic fact assessments. With the subset of children who scored poorly, nine practice sessions with feedback and reinforcement were conducted to increase basic fact fluency. On this basis, the researchers identified nonresponders and examined decision utility with respect to final outcomes, but they did not explore effects on student learning.

These studies and others in the VanDerHeyden line of work are ambitious and important, but are restricted to calculations, rely on a narrow approach to math instruction, and do not assess effects on students' math performance. Fuchs et al. (2005) extended this line of work by conducting a randomized field trial to assess the effects of second-tier small-group tutoring on a broader math curriculum at first grade, including number sense and concepts, addition and subtraction concepts and procedures, number combinations, missing addends, place value, and word problems. A more comprehensive instructional design and a more sustained intervention were used, and the study supported the efficacy of the small-group tutoring on students' learning outcomes. However, the focus on word problems was limited to one week of the 16-week tutoring program, and the researchers did not consider whether tutoring efficacy was enhanced when classroom instruction relied on a validated approach.

In fact, we identified only one prior RTI or prevention study that assessed the efficacy of tutoring with and without validated classroom instruction. It was conducted at first grade in reading. Gilbert, Compton, Fuchs, and Fuchs (2007) showed that tutoring was similarly effective for at-risk children with or without validated classroom reading instruction as the backdrop for tutoring. However, in contrast to most RTI models where risk status is identified on the basis of initial screening, at-risk students entered the Gilbert et al. study only after a full semester of progress monitoring showed inadequate response to the classroom instructional program; so, it is not surprising that the nature of classroom instruction during tutoring did not enhance tutoring's efficacy.

The issue of how tutoring interacts with classroom instruction among students at risk for poor learning outcomes is important for designing efficient and effective RTI prevention systems. If tutoring is differentially efficacious when combined with validated classroom instruction, then both tiers are critical, and classroom instruction needs to be designed deliberately with AR students in mind, even when they receive tutoring. By contrast, if tutoring promotes comparable outcomes regardless of the classroom instructional context, then findings would set the stage for research on whether tutoring might occur as a replacement for, rather than as a supplement to, classroom instruction. Tutoring as replacement for classroom instruction would make RTI prevention systems more feasible and efficient and would permit resources to be infused at the tutoring tier. Of course, in considering tutoring efficacy as a function of the classroom's instructional context, it is important not only to compare the response of at-risk students who do and do not receive tutoring, but also to contrast the learning of those at-risk students against not-at-risk peers. This has not been addressed in prior work.

The purpose of the present study, therefore, was to examine students' mathematics problem-solving learning and to explore the prevalence of mathematics difficulty as a function of validated classroom prevention, as a function of small-group tutoring, and as a function of whether tutoring occurs with or without validated classroom instruction. (We refer to small-group tutoring as tutoring in this paper.) In this introduction, we describe the theoretical basis for our approach to word-problem instruction and summarize previous related work. Then we consider previous studies assessing the effects of one or two tiers of prevention on the prevalence of mathematics difficulty. Finally, we review the study's purpose and design.

Transfer, Schema Theory, and Related Work on Word-Problem Instruction

The mathematics education literature shows that children experience difficulty transferring the math competence they develop in school. For example, Larkin (1989) demonstrated that children fail to apply simple computational skills when problems change in minor ways. Other work (Foxman, Ruddock, McCallum, & Schagen, 1991, cited in Boaler, 1993) illustrates how students fail to realize connections between math problems presented in and out of context. Such findings are supported by theoretical frameworks for understanding the development of transfer that challenge the assumption of vertical transfer, whereby mastery of simple skills facilitates acquisition of more complex skills (Gagne, 1968; Resnick & Resnick, 1992). The notion of vertical transfer has been replaced with the concept of lateral transfer, by which children recognize problems across numerous experiences to abstract generalized problem-solving strategies.

Some refer to the abstraction of generalized problem-solving strategies as the development of schemas (Brown et al., 1992; Gick & Holyoake, 1983). A schema is a category that encompasses similar problems; it is a problem type (Chi, Feltovich, & Glaser, 1981; Gick & Holyoake, 1983; Mayer, 1992; Quilici & Mayer, 1996). The broader the category for the problem type, the greater the probability individuals will recognize connections between familiar and novel problems, so they will know when to apply the solution methods they have learned. Essentially, students are expanding the domain of problems for which they recognize that they have the mathematical means to find answers, thereby facilitating transfer to novel problems. To facilitate schema development, teachers must first teach problem-solution rules, as they conventionally do. Then, however, teachers must help students develop schemas and awareness of those schemas (Cooper & Sweller, 1987) and provide students with a wealth of problem-solving activities that emphasize knowledge application (Brown, Collins, & Duguid, 1989; Prawat, 1992). The hope is that schemas can influence behavior in a broad set of situations and thereby affect breadth of learning or transfer (Brown et al., 1992; Glaser, 1983). Research has substantiated the importance of mastering rules for problem solution (e.g., Mawer & Sweller, 1982; Sweller & Cooper, 1985), but less is known about how to help students develop schemas and awareness of those schemas (e.g., Bransford & Schwartz, 1999; Cooper & Sweller, 1987; Mayer et al., 1999).

Some studies have relied on explicit instruction based on schema theory to enhance word-problem skill. Working primarily at the second or third tier of the RTI prevention system in small groups, Jitendra and colleagues have demonstrated acquisition, maintenance, and transfer effects for students with serious math deficits or with risk for math difficulty at eighth grade (Jitendra, DiPipi, & Perron-Jones, 2002), sixth grade (Xin, Jitendra, & Deatline-Buchman, 2005), and third and fourth grades (Jitendra, Griffin, Haria, Leh, Adams, & Kaduventtor, 2007; Jitendra, Griffin, McGoey, Gardill, Bhat, & Riley, 1998; Jitendra & Hoff, 1996). In our work on, we have also relied on schema theory. In contrast to Jitendra, our work has been conducted exclusively at third grade, with more difficult problem types, with a focus on far transfer that extends beyond the transfer requirements in Jitendra's studies, and with a key difference in the way schema theory is applied. Similar to Jitendra's schema-based strategy instruction, we teach students to understand the underlying mathematical structure of the problem type, to recognize the basic problem-type category, and to solve the problem type. In contrast to Jitendra's teaching methods, we incorporate a fourth instructional feature by explicitly teaching students to transfer their problem-solving skills. In keeping with Cooper and Sweller (1987), our goal is to help students recognize connections between problems like those worked during instruction and problems with unexpected features, such as problems that include irrelevant information, or that present a novel question requiring an extra step, or that include relevant information presented in charts or graphs, or that combine problem types, and so on. The hope is that the addition of explicit, transfer instruction will lead to more flexible and successful problem solving. We refer to the combination of all four instructional components as schema-broadening instruction, or SBI. Teachers and students refer to this approach as “Hot Math.”

In our first randomized field trial, Fuchs, Fuchs, Prentice, Burch, Hamlett, Owen et al. (2003a) separated the effects of the first three instructional components (teaching students to understand the underlying mathematical structure of the problem type, to recognize the basic schema for a problem type, and to solve the problem type) from the last instructional phase (explicitly teaching students to transfer). The study was conducted at the first tier of the RTI prevention system, in general education classrooms, using whole-class instruction and involving all students on whom we had consent. The basic word-problem types targeted for instruction were more complex than had been studied to date with third graders, including finding half, step-up functions, 2-step problems involving pictographs, and 2- and 3-step shopping list problems. Also, far transfer was assessed on taught and untaught problem types within a highly novel and complex context that resembled real-life problem-solving situations. Third-grade classes were randomly assigned to teacher-designed word-problem instruction, to experimenter-designed instruction on the first three instructional components, or to experimenter-designed SBI that incorporated the first three components but also explicitly taught students to transfer. With the addition of this last instructional component, teachers explained how problem features such as format or vocabulary can make problems seem unfamiliar without modifying the problem type or the required solution rules; they discussed examples emphasizing the same problem type, as superficial features such as format or vocabulary changed; they provided practice in sorting novel problems in terms of superficial problem feature changes and in solving those problems; and they prompted students to search novel problems for familiar problem types. Results indicated that on near- and far-transfer word-problem tasks, Hot Math SBI (i.e., all four components) strengthened problem-solving performance over and beyond experimenter-designed instruction that only addressed the first three components (understanding the underlying mathematical structure, recognizing the basic schema, and solving problems) and beyond teacher-designed instruction.

In subsequent work (Fuchs et al., 2004b), SBI that addressed transfer instruction on three superficial features was more effective than SBI that addressed transfer instruction on six superficial features. However, the present study is the first to assess the efficacy of SBI tutoring on relatively complex problem types. Moreover, in our own prior work, as in other math and reading RTI research, the combined and separate effects of classroom instruction and tutoring has not been assessed, and the prevalence of math difficulty with one and/or two tiers of prevention has not been examined.

Prevalence of Math Difficulty

Studies (e.g., Gross-Tsur et al., 1996; Lewis et al., 1994; Shalev, 2007) indicate that 5−9% of the school-age population experience some form of math disability. Four problems, however, limit the utility of available figures. First, much of the literature is limited to math facts and simple computation. Second, many studies do not rely on individual tests, as used in the schools to identify disability. Third, to recruit adequately large samples, high cut-scores have often been applied. For example, Jordan and Hanich (2000) and Jordan and Montani (1997) demarcated math difficulty as falling below the 30^th percentile on a group-administered test; Hanich, Jordan, Kaplan, and Dick (2001) used the 35^th percentile. Russell and Ginsburg (1984) included students performing one level below expected grade, and Geary (1990) identified children participating in Chapter 1 (in which mean study scores corresponded to percentile ranks of 25 in grade 1 and 40 in grade 2). The fourth problem is that in the absence of sound prevention activities, math disability estimates may be artificially high because they fail to eliminate inadequate instruction as a possible explanation for low math achievement.

In the present study, we sought to address these problems. We focused on applied math problems. We investigated the prevalence of math difficulty on an individually-administered math test, as done in the schools to identify disability, and we applied a cut-score more similar to those used in the schools (i.e., 15^th percentile). Finally, to understand how sound prevention activities may affect the prevalence of math disability, we examined prevalence with and without SBI classroom instruction and with and without SBI tutoring.

Study Purposes and Overview

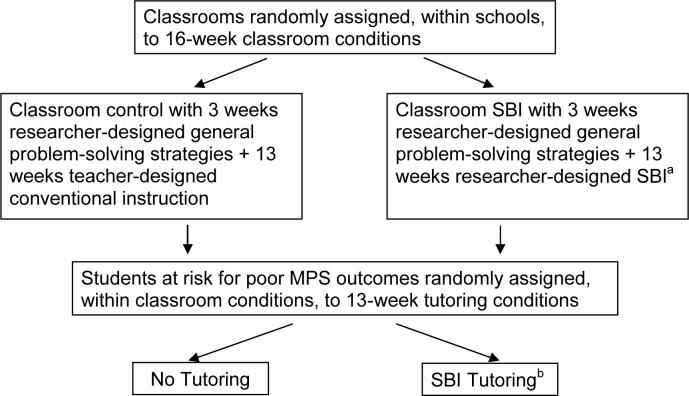
The primary purpose of the present study was to assess the effects of SBI tutoring when it occurs with and without SBI classroom instruction on at-risk (AR) students' math problem solving and their learning relative to not-AR (NAR) peers. We also examined the prevalence of mathematics difficulty with and without one or two tiers of SBI math problem-solving prevention, and assessed the efficacy of the classroom and tutoring SBI instructional protocols. Within schools, we randomly assigned third-grade classrooms to receive classroom SBI or to receive the math problem-solving instruction designed by their teachers. In these classrooms, we designated NAR and AR students based on their incoming math scores and, within classroom conditions, randomly assigned AR students to continue in their classroom conditions with or without SBI tutoring. Students were pre- and posttested in a 3-week window before and after prevention occurred. See Figure 1 for the study design.

Figure 1. Study Design.

^aIn Years 1−3, SBI classrooms were randomly assigned to receive standard SBI or a variant of SBI

^bIn Years 1−2, SBI tutoring students were randomly assigned to receive standard SBI tutoring or a variant of SBI tutoring

Method

Participants

Classrooms and their teachers

In a southeastern metropolitan school district, 120 third-grade classrooms participated. Stratifying so that each condition was represented approximately equally in each school, we randomly assigned 40 classrooms to control (i.e., 3 weeks of researcher-designed general math problem-solving instruction plus 13 weeks of teacher-designed math problem-solving instruction) and 80 classrooms to Hot Math SBI (i.e., 3 weeks of researcher-designed general math problem solving plus 13 weeks of researcher-designed SBI). The study occurred over four school years during a time when the school district was relatively stable²; one-quarter of the sample entered the study each year. During the first three years, SBI classrooms were randomly assigned to Hot Math SBI or to a variant designed to strengthen Hot Math SBI (see Table 1 for a summary of the classroom SBI variants). In the first three cohorts, the effects of the two SBI conditions were not statistically significant different, but both were reliably better than control. So we did not test a variant in Cohort 4 (all Cohort 4 teachers were randomly assigned to control or to the standard version of SBI). We consider all students in the SBI classrooms to have participated in one SBI condition; however, to assess SBI variants, we include cohort effects in the analytic model. One Cohort 3 classroom in the SBI condition left the study during the first month of participation due to the classroom teacher's personal reasons. The remaining 119 classroom teachers were predominantly female (97.4% in control; 97.5% in SBI), and European-American (79.5% in control; 66.7% in SBI; the other teachers were African American). In control and SBI, respectively, average years teaching was 14.18 (SD = 10.49) and 16.09 (SD = 10.27), and class size was 18.69 (SD = 2.40) and 18.45 (SD = 2.62). There were no significant differences on these variables by classroom condition.

Table 1.

Instructional Variants by Tier and by Cohort¹

Tier	Cohort	Variant	Incorporated as Standard SBI in Subsequent Years
Classroom	1	Once per week, RA-teacher led discussion of how transfer features apply to a video portraying a real-life math situation that included second-grade problem types	No
	2	Each session, in paired practice, students extended one partially developed problem into a specific problem type. This was guided by “Problem Production Steps” (What kind of problem? What do you know? What should you add?)	No
	3	Every problem, students asked themselves meta-questions to guide the problem-solving process (Who is the most important person in the story? What is the most important thing the Who is doing? What question do we need to answer using math? What's the problem type? What transfer features are included?)	No
Tutoring2	1	Self-regulated learning strategies incorporated within tutoring sessions	Yes and strengthened in Cohorts 2, 3, and 4 to enhance motivation
	2	Drill-and-practice warm-ups to build fluency with a foundational skill necessary for the specific problem type	No

¹When variants required additional time, students in the standard SBI condition had more practice to keep instructional time comparable.

²See text for more information.

Research assistants, not classroom teachers, delivered researcher-designed general problem-solving strategies instruction to all 119 classrooms during the first 3 weeks of instruction. For the final 13 weeks of instruction, research assistants delivered classroom SBI whereas classroom teachers delivered conventional instruction. We refer to research assistants who taught general problem-solving strategies or classroom SBI as “RA-teachers,” and we refer to the real classroom teachers as “classroom teachers.” Whenever an RA-teacher was delivering instruction, the classroom teacher was present to help distribute materials, maintain order, and provide corrective feedback. (When there was more than one variant of classroom SBI, each RA-teacher taught in both conditions.) We also note that the math program in all classrooms went beyond the instructional procedures described in the study; that is, experimental procedures were incorporated within the classroom teachers' broader mathematics instructional program. We describe research assistants later.

Students

To obtain a representative sample, we screened 2,023 students on whom we had consent. That is, in the 119 third-grade classrooms, we randomly sampled 1,200 students for participation, blocking within classroom and within three strata: (a) 25% of students with scores 1 SD below the mean of the entire distribution on the Test of Computational Fluency (Fuchs, Hamlett, & Fuchs, 1990); (b) 50% of students with scores within 1 SD of the mean of the entire distribution on the Test of Computational Fluency; and (c) 25% of students with scores 1 SD above the mean of the entire distribution on the Test of Computational Fluency. Of these 1,200 students, 59 moved prior to posttesting (including 45 AR students; see below). The 59 children who moved prior to posttesting were demographically comparable to the pupils who remained in the study. Among these 1,141 students, IQ, as measured on the 2-subset Wechsler Abbreviated Intelligence Scale (WASI; Wechsler, 1999), averaged 97.29 (SD = 13.93). Standard scores on the Woodcock-Johnson III Tests of Achievement (WJ III; Woodcock, McGrew, & Mather, 2001) Applied Problems averaged 102.56 (SD = 13.60), and standard scores on the Woodcock Reading Mastery Test-R (Woodcock, 1998) Word Identification averaged 100.83 (SD = 10.09). Of these students, 559 (49.0%) were male, and 626 (54.9%) received subsidized lunch. Ethnicity was distributed as follows: 480 (42.1%) African American; 464 (40.7%) European American; 120 (10.5%) Hispanic; 17 (1.5%) Kurdish; and 60 (5.3%) other. Thirty-seven students (3.2%) were English language learners.

Among these students, we identified 288 students as AR of poor problem-solving outcomes. To derive a parsimonious equation for predicting problem-solving outcomes, we conducted regression analyses on a previous database (Fuchs, Fuchs, Prentice, Hamlett, Finelli, & Courey, 2004) of third-grade students who had received Hot Math SBI. The final prediction equation included pretest performance on the immediate transfer problem-solving measure (see Measures) and pretest performance on the Test of Computational Fluency (Fuchs et al., 1990). For each cohort, we rank ordered students on the predicted score and selected the lowest 72 students in that year's sample. Within cohort, these students were assigned to tutoring conditions, while stratifying by classroom condition. In this way, some AR students received neither classroom nor tutoring Hot Math SBI; some received classroom but not tutoring Hot Math SBI; some received tutoring but not classroom Hot Math SBI; and some received classroom and tutoring Hot Math SBI. Of the 288 AR students, 45 moved prior to posttesting. On demographic and pretest performance variables, the 45 children who moved prior to posttesting were comparable to the 243 pupils who remained in the study, and there were no significant interactions between AR students' tutoring condition and attrition status.

During the first two years of the study, AR students were randomly assigned to control (no tutoring) or to one of two versions of tutoring SBI. For Cohort 1, the two versions of SBI tutoring were SBI with and without self-regulated learning strategies; the addition of self-regulated learning strategies appeared promising (the cohort sample was too small to apply inferential statistics). For Cohort 2, we strengthened the motivation system within self-regulated learning strategies. Students were randomly assigned to receive SBI with strengthened self-regulated learning strategies, with and without drill/practice activities designed to build fluency with low-level skills. Strengthened self-regulated learning strategies appeared promising but the drill/practice activities did not (again, cohort sample was too small to apply inferential statistics). For Cohorts 3 and 4, we built power by randomly assigning AR students to only two tutoring conditions: control versus Hot Math SBI that incorporated strengthened self-regulated learning strategies. In our model, Hot Math SBI tutoring is treated as one condition; however, to gain insight into the effects of the variants, we consider cohort effects. (See Table 1 for a summary of the SBI variants.) Research assistants delivered SBI tutoring, and we refer to these research assistants as “RA-tutors.” (When there was more than one variant of SBI tutoring, each RA-tutor taught in both conditions.) Information on research assistants is provided later.

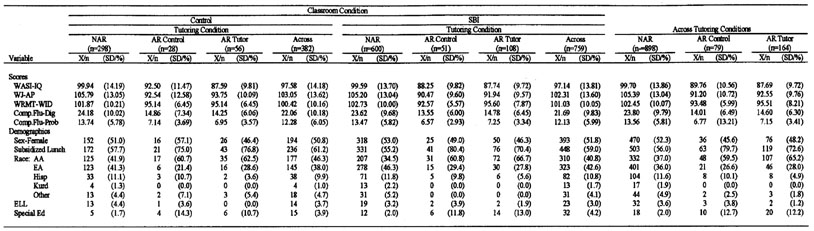
For the classroom factor, we had two conditions: classroom control and classroom SBI. For the tutoring factor, we had three conditions: NAR (i.e., not eligible for tutoring), AR control, and AR tutored. See Table 2 for demographics by classroom and tutoring conditions (for a table that provides this information by cohort as well, contact the first author). See Table 2 for standard scores on WASI IQ, WJ III Applied Problems, and Woodcock Reading Mastery Test-R Word Identification and raw scores on the Test of Computational Fluency (digits correct and problem correct) and for demographic data by classroom and by tutoring conditions (for tables with this information by cohort as well, contact the first author). We ran 3-way analyses of variance on these performance data using classroom condition, tutoring condition, and cohort as factors. The only significant effect was for tutoring condition. As expected, on each measure, NAR students scored significantly higher than both AR groups, which scored comparably to each other. We ran chi-square analyses to examine the relation between demographics and classroom condition; none was significant. For tutoring condition, we used one degree of freedom to examine the relation between demographics and risk status. Compared to AR students, NAR students were significantly less likely to receive subsidized lunch, to be African-American, and to receive special education (but were comparably likely to be ELL). We used the other degree of freedom to examine the relation between demographics and AR control versus AR tutored; none was significant.

Table 2.

Students' Math and Reading Scores^a and Demographics^b by Classroom Condition and Tutoring Condition

WASI-IQ is standard scores on the Wechsler Abbreviated Scale of Intelligence. WJ-AP is standard score on Woodcock-Johnson III Tests of Achievement-Applied Problems; WRMT-WID is standard score on the Woodcock Reading Mastery Tests-Word Identification; Comp. Flu is raw score on the Test of Computational Fluency (Dig is digits correct; Prob is problems correct); AA is African American; EA is European American; Hisp is Hispanic; Kurd is Kurdish; ELL is English Language Learners; Special Ed is Special Education.

^aScores are means (X) and standard deviations (SDs).

^bDemographics are numbers (n) and percentages (%).

Classroom Conditions

For a manual with the researcher-designed general problem-solving strategies, classroom SBI, or SBI tutoring teaching scripts and materials, contact the first author. Scripts and materials provided a road map for research assistants to implement the instructional methods. The scripts were studied, not read.

Problem types

We centered the study on four word-problem types, chosen from the district curriculum to ensure that classroom control students had instruction relevant to the study. The four problem types were “shopping list” problems (e.g., Joe needs supplies for the science project. He needs 2 batteries, 3 wires, and 1 board. Batteries cost $4 each, wires cost $2 each, and boards cost $6 each. How much money does he need to buy supplies?), “half” problems (e.g., Marcy will buy 14 baseball cards. She'll give her brother half the cards. How many cards will Marcy have?), step-up function or “buying bags” problems (e.g., Jose needs 32 party hats for his party. Party Hats come in bags of 4. How many bags of party hats does Jose need?), and 2-step “pictograph” problems (e.g., Mary keeps track of the number of chores she does on this chart [pictograph is shown with label: each picture stands for 3 chores]. She also took her grandmother to the market 3 times last week. How many chores has Mary done?).

Classroom control condition

To guide instruction relevant to the four problem types, classroom control teachers relied primarily on the core math instructional program. For Cohorts 1 and 2, this was Math Advantage (Burton & Maletsky, 1999). For Cohorts 3 and 4, this was Houghton Mifflin Math (Greenes et al., 2005). In both programs, instruction addressed one problem type at a time (as did SBI) and focused on the concepts underlying the problem type. In addition, a prescribed set of problem-solution rules was taught, with explicit steps for arriving at solutions to the problems presented in the narrative. There was no attempt to broaden students' schemas for these problem types to address transfer. However, in comparison to classroom SBI, classroom control group instruction provided more practice in applying problem-solution rules and provided greater emphasis on computational requirements. Classroom control group instruction was explicit and relied on worked examples, guided group practice, independent work with checking, and homework. Compared to Math Advantage, Houghton Mifflin Math had a greater emphasis on problem-solving strategies, including guiding questions to help students understand, plan, solve, and reflect on the content of problems (we note, however, that our analyses did not reveal cohort effects involving the control group).

In addition, classroom control (as well as classroom SBI) incorporated a 3-week researcher-designed and delivered general problem-solving strategies unit (see below) to control for foundational problem-solving strategies that were necessary for but conceptually unrelated to SBI. Previous research (Fuchs, Fuchs, Prentice, Burch, Hamlett, Owen et al., 2003b) shows that this 3-week unit alone is insufficient to enhance outcomes on the math problem-solving measures used in the present study. We conceptualized the classroom control group as representing conventional classroom problem-solving instruction in order to estimate the contribution of classroom SBI over conventional instruction.

General problem-solving strategies instruction (classroom control and classroom SBI)

Classroom control and classroom SBI students received a researcher-designed 3-week (2 lessons per week) instructional unit on general math problem-solving strategies, which was conceptually unrelated to SBI and was delivered by research assistants. It addressed making sure answers make sense; lining up numbers from text to perform math operations; checking computation; and labeling work with words, monetary signs, and mathematical symbols. These six lessons, each lasting 30−40 min, relied on worked examples with explicit instruction, dyadic practice, independent work with checking, and homework, for a total of 210 min.

Classroom SBI

After classroom SBI students received the 3-week general math problem-solving unit, they received four researcher-designed 3-week SBI units. Each SBI unit comprised six sessions. Also, two cumulative review sessions were delivered the week after winter break. In each unit, Sessions 1 and 5 lasted about 40 min; the others lasted about 30 min. This totaled 200 min per unit and 856 min across the units (including the two cumulative review sessions). Each 3-week unit addressed one of the four problem types: shopping list, buying bag, half, and pictograph.

Within each unit, the sequence of lessons was as follows. In Sessions 1−4, problem-solution instruction was delivered, using problems that varied only cover stories. A poster listing the steps of the solution method was displayed in the classroom. In Session 1, RA-teachers addressed the underlying concepts and structural features for the problem type, presented a worked example and, as they referred to the poster, explained how each step of the solution method had been applied in the example. Students responded frequently to questions. After reviewing the concepts and presenting several worked examples in this way, RA-teachers shared partially worked examples while students applied the solution steps. Students then completed 1−4 problems in dyads, where stronger students helped weaker students solve problems and check work with answer keys. Sessions 2−4 were structured similarly, with a greater proportion of time spent on partially worked examples and dyadic practice. Also, at the end of Sessions 2−4, students completed one problem independently; the teacher checked work against an answer key; and students graphed scores.

Sessions 5−6 were designed to broaden schemas, with each problem varying the cover story and one of the four superficial features addressed in SBI. RA-teachers first taught the meaning of the word transfer, and then taught the four superficial features (referred to as transfer features), which change a problem without altering its type or solution: A familiar problem type, for which a solution is known, can use unfamiliar vocabulary, can pose an additional question, can incorporate irrelevant information, can combine problem types. A poster, “Transfer: Ways Problems Change,” was displayed. In Session 5, teachers explained the poster, illustrating each superficial feature with a worked example. They gradually moved to partially worked examples. Then, students worked in pairs to apply the solution method to problems that varied superficial features. In Session 6, RA-teachers reviewed the four superficial features using similar procedures, except students spent more time working in dyads and then completed a problem independently, scored work against a key, and graphed scores.

Delivery

When more than one SBI variant was used for Cohorts 1−3, classroom research assistants had responsibility for classes in both SBI conditions. To ensure comparable mathematics instructional time across conditions, experimental sessions occurred within the confines of the class teachers' mathematics instructional block. At the end of the study, classroom teachers reported the number of minutes per week they spent on math, including time on this research project. Math instructional minutes (including research-designed general math problem-solving strategy instruction and SBI) were 274.23 (SD = 72.96) and 282.50 (SD = 80.59) for classroom control and for classroom SBI, respectively.

Treatment fidelity

Prior to the first delivery of each session, classroom research assistants agreed on the essential information in the script and made a checklist of points. Each session was audiotaped. At the study's end, two research assistants independently listened to tapes while completing the checklist to identify the percentage of points addressed. We sampled tapes so that, within conditions, RA-teachers and lesson types were sampled equitably. In class-level control, 1−2 tapes were sampled per class (for Unit 1); in class-level SBI, 6−7 tapes were sampled per class (distributed equally across Units 1−5). Intercoder agreement, calculated on 20% of the sampled tapes, was 95.3%. The mean percentage of points addressed was 97.20 (SD = 3.06) for classroom control and 96.71 (SD = 2.37) for classroom SBI, F(1,117) = 0.88, p = .351.

Tutoring Conditions

NAR and AR control students continued in their classroom conditions without modification, with one-third of AR students randomly assigned to the tutoring control condition and two-thirds of AR students randomly assigned to tutoring. AR tutored students received SBI tutoring. Tutoring SBI centered on the same four word-problem types.

Tutoring began after the general math problem-solving unit had been implemented, with AR students identified, randomly assigned, and scheduled for tutoring during the general math problem-solving unit. Tutoring addressed the four 3-week SBI units, with three tutoring sessions conducted each week and with two cumulative review sessions delivered the week after winter break. Tutoring groups were 2−4 students, and each session lasted 20−30 min (i.e., 225 min per unit and 940 min across the units, including the two review sessions). Each 3-week unit addressed one of the four problem types: shopping list, buying bag, half, and pictograph.

The content of Hot Math SBI tutoring mirrored the content covered in classroom SBI. However, in tutoring, the most difficult concepts from classroom SBI were targeted; manipulatives were incorporated more frequently; additional scaffolding to support student learning was employed; and self-regulated learning strategies with tangible reinforcement (depending on cohort) were incorporated.

During the first 5 sessions of each unit, problem-solution instruction was delivered, using problems that varied only cover stories. A poster listing the steps of the solution method was displayed during the tutoring session. In Session 1, RA-tutors addressed the underlying concepts and structural features for the problem type, using concrete objects. Together with the students, RA-tutors worked several examples and, as they referred to the poster and the concrete objects, explained why and how each step of the solution method had been applied in the examples. Next, students responded frequently to questions as they worked 2−4 problems together with their tutor. Beginning in Session 2, students then completed one problem independently, which the tutor reviewed and scored.

Sessions 6−9 were designed to broaden schemas, with each problem varying the cover story and one of two transfer features: different question or irrelevant information. RA-tutors first taught the meaning of the word transfer, and then taught the two transfer features, utilizing a poster, “Transfer: To Move.” Though 5 bulleted types of transfer features were included on the poster for continuity with the whole class sessions, the two covered in tutoring sessions were bolded and in larger font for emphasis. In Session 6, RA-tutors explained the poster, illustrating both superficial features by working examples. In Sessions 6−9, students still completed a problem independently, though never a transfer problem.

For Cohort 1, AR tutored students were randomly assigned to SBI without self-regulated learning strategies (see preceding description) or SBI with self-regulated learning strategies. Self-regulated learning strategies were designed to help students become more metacognitively, motivationally, and behaviorally active in their own learning (cf. De Corte, Vershaffel, & Eynde, 2000; Zimmerman, 1995). The strategies incorporated the following components. First, RA-tutors reminded students to stay “on-task” by working hard, listening carefully, and following directions. RA-tutors set timers for three irregular intervals throughout the session (the timing for each session was standardized across tutors); when the timer sounded, each student earned a point if all students in the group were on task. If any student was off task, no student received a point. Second, students received up to three points per session for accurate work, with the task for which accuracy was rewarded varied across sessions (but standardized across RA-tutors). Third, students completed one problem, called the Hot Math Problem of the Day. This problem was scored on a 20-point scale by the RA-tutors according to a specific rubric; students were encouraged to participate in the scoring and to meet or beat their previous day's score. Fourth, following Hot Math Problem of the Day, students shaded their Hot Math thermometers with the number of points they had earned over the session. Fifth, students used their Hot Math thermometers to set a goal for next day. Sixth, students were awarded stickers for each point. At the end of each session, students totaled their points and noted their totals on a game board.

In Year 2, self-regulated learning strategies were incorporated into both experimental tutoring-level conditions as part of the regular treatment, with students earning “dollars” instead of stickers and having the opportunity to spend dollars at the Hot Math Store each week or to save their dollars. Both tutoring conditions utilized this strengthened self-regulated learning strategies, but with or without drill-and-practice warm-ups at the beginning of each lesson. These warm-ups were designed to build fluency with a foundational skill necessary for the specific unit (e.g., repeated addition for the stepping-up problem type). So AR tutored students were randomly assigned to SBI with strengthened self-regulated learning strategies or SBI with strengthened self-regulated learning strategies plus warm-ups. All students in Cohorts 3 and 4 who were randomly assigned to tutoring received SBI with strengthened self-regulated learning strategies.

Delivery

RA-tutors had responsibility for tutoring (for Cohorts 1 and 2, each RA-tutored groups in both SBI tutoring conditions). Consistent with an RTI prevention system, tutoring occurred in addition to, not as a substitute for, classroom math instruction and was conducted by someone other than the classroom teacher, in this case the RA-tutor. Also, as with an RTI prevention system, students within a given tutoring group were not necessarily from the same classroom.

Treatment fidelity

Prior to the first delivery of each session in each condition, RA-tutors agreed on the essential information in the script and made a checklist of points. Each tutoring session was audiotaped. At the study's end, four research assistants independently listened to tapes while completing the checklist to identify the percentage of points addressed. We sampled tapes so that, within conditions, RA-tutors, groups, and session numbers were sampled equitably. For each of 64 tutoring small groups, 20% of sessions were sampled (7−8 tapes distributed equally across the four units). Intercoder agreement, calculated on 20% of the sampled tapes, was 96.4%. The mean percentage of points addressed across all units was 98.12 (SD = 1.28).

Research Assistants

Across the four years of the study, the typical research assistant was one to two years beyond undergraduate education, studying for a graduate degree in education, special education, counseling, or education policy. The majority of research assistants worked for the project one year, with six RA-teachers remaining for more than one year and three RA-tutors working for more than one year. During each year of the study, two full-time project coordinators, typically with bachelor's or master's level degrees typically outside of education, also served as RA-teachers and RA-tutors. Each year, five or six RA-teachers and another five or six RA-tutors were needed. The same research assistants did not conduct classroom SBI and tutoring sessions.

For classroom SBI, a typical RA-teacher was responsible for the same four classrooms across 16 weeks of intervention, teaching each classroom two times each week, usually two classes per day, and alternating days within a given classroom. For example, an RA-teacher might teach classrooms 1 and 2 on Monday, 2 and 3 on Tuesday, 1 and 2 again on Wednesday, and 2 and 3 again on Thursday.

Each RA-tutor was responsible for one or two control classrooms for general problem-solving strategies during the first 3 weeks and then for three or four tutoring groups during the next 13 weeks. A typical RA-tutor taught the same 3 or 4 tutoring groups across the 13 weeks, three times per week. The RA-tutor's schedule was usually the same each of the three tutoring days, with students typically receiving tutoring Tuesday, Wednesday, and Thursday. Tutoring groups were determined based on preferred schedules provided by classroom teachers.

To train research assistants, we conducted the following activities. In an introductory meeting, all research assistants were trained on research ethics and procedures, including professional behaviors in schools. Then research assistants were trained for their specific role within the project (RA-teacher or RA-tutor) in one full-day session. Research assistants were introduced to the project and its goals, assigned roles (RA-teacher or RA-tutor), and provided instruction, demonstrations, and scripted materials to study. They were paired to practice the treatment. Then, they conducted one lesson for a project coordinator and were judged on a point-by-point system for fidelity to treatment. A research assistant who achieved 95% fidelity was considered reliable. A research assistant who scored lower than 95% fidelity was coached on points he/she missed, asked to practice more, and then re-rated at a later time on another lesson. At weekly meetings, project staff met for problem-solving sessions separately with RA-teachers and with RA-tutors. At the beginning of each unit, a 3-hour training sessions was conducted to orient research assistants and to distribute supporting materials. In addition, all sessions were audio tape recorded, which were used in part to monitor research assistants for fidelity throughout treatment. Research assistants were provided written corrective feedback and provided one-to-one retraining as needed.

Measures

Math problem solving

We employed three measures of problem solving. These measures all sampled novel problems (i.e., never seen before or used for instruction). They incorporated the four targeted problem types, but the measures differed from each other in terms of transfer distance in relation to problems used for problem-solution instruction. We refer to the three measures as immediate transfer, near transfer, and far transfer (increasing numbers signify greater transfer distance).

Immediate transfer incorporated novel problems in the same format as the problems used for problem-solution instruction. Near transfer incorporated novel problems that varied from the problems used for problem-solution instruction in terms of one or more of the transfer features addressed in SBI: unfamiliar vocabulary, different question, irrelevant information, or combination of problem types. Far transfer, which was designed to mirror real-life problems, varied from the problems used for instruction in multiple ways. It was formatted to look like a commercial, standardized test; it presented a multi-paragraph with four questions; some of the information needed to answer the question was removed from the multi-paragraph narrative and placed in figures or question stems; it contained multiple pieces of numeric and narrative irrelevant information; it provided opportunities for students to formulate decisions; it combined all four problem types; and it varied all four SBI transfer features.

None of the cover stories had been used for instruction. Each measure had two alternate forms; problems on both forms required the same operations and presented text with the same number/length of words. Immediate-transfer alternate forms incorporated the same numbers; near-transfer alternate forms incorporated the same numbers; and far-transfer alternate forms used similar numbers. In half the classes in each condition, we used Form A at pretest and Form B at posttest; in the other half, forms were reversed.

Immediate transfer

comprised 10 word problems, equally representing the problem-solving units. Across the 10 problems, the maximum score was 44. On this sample, Cronbach's alpha was .84 and .95 at pre- and posttest, respectively; concurrent validity with WJ-III Applied Problems (Woodcock et al., 2001) was .56 at pretest and .42 at posttest. Interscorer agreement, computed on 20% of protocols by two independent, “blind” scorers, was .983 at pretest and .960 at posttest.

Near transfer

comprised nine problems: a shopping list problem with a novel format (information shown in bulleted format, with a selection rather than an open-ended response format); a shopping list problem with a novel question (asking for money left at the end); a buying bags problem with a different key word (packages instead of bags); a buying bags problem with a novel question (comparing prices of two packaging options); a half problem with unfamiliar vocabulary (share equally instead of half); a pictograph problem with a novel question (asking for money left at the end); a pictograph problem with a novel question (comparing quantities at the end); a problem with irrelevant information that combined a buying bags problem with a pictograph problem and combined novel vocabulary with a novel question; and a problem with irrelevant information that combined a shopping list problem with a buying bags problem and combined a novel format with a novel question. On this sample, across items, the maximum score was 79. Cronbach's alpha was .87 and .96 at pre- and posttest, respectively; concurrent validity with WJ-III Applied Problems (Woodcock et al., 2001) was .52 at pretest and .40 at posttest. Interscorer agreement, computed on 20% of protocols by two independent, “blind” scorers, was .985 at pretest and .973 at posttest.

Far transfer

simultaneously assessed transfer of all four problem types and the four transfer features addressed in SBI. Also, to decrease association between the task and classroom or tutoring SBI, far transfer was formatted to look like a commercial test (printed with a formal cover, on green paper, with photographs and graphics interspersed throughout the test booklet). Two assessments were constructed as alternate forms: Although the context of the problem situations differed, the structure of the problem situation and the questions were identical, and the problem solutions and reading demands were equivalent.

Performance was scored according to a rubric with four dimensions: conceptual underpinnings, computational applications, problem-solving strategies, and communicative value. The original rubric (Kansas Board of Education, 1991) scored responses on a 6-point scale. To enhance reliability, we awarded points on a finer basis (e.g., the problem-solving strategies score included points for finding relevant information, accumulating to a total, showing all computation, working the answer in distinct multiple parts, labeling at least half of the multiple parts, and labeling work with monetary and operation signs). Across the four questions and four scoring dimensions, the maximum score is 72. On this sample, Cronbach's alpha was .91 at pretest; .94 at posttest; concurrent validity with WJ-III Applied Problems (Woodcock et al., 2001) was .47 at pretest; .61 at posttest. Interscorer agreement, computed on 20% of protocols by two independent “blind” scorers, was .987 at pretest; .949 at posttest. Given the deleterious effects of student unfamiliarity with performance assessments (Fuchs, Fuchs, Karns, Hamlett, Dutka, & Katzaroff, 2000), research assistants delivered a 45-min “test-wiseness” lesson before pre- and posttesting in all conditions. (The mean score across immediate, near, and far transfer correlated .62 with WJ-III Applied Problems (Woodcock et al., 2001) at pretest; .57 at posttest.)

Math applications

WJ-III Applied Problems (Woodcock et al., 2001) measures skill in analyzing and solving practical math problems with 60 items. The tester orally presents items involving counting, telling time or temperature, and problem solving. Testing is discontinued after six consecutive errors. The score is the number of correct items. As reported by McGrew and Woodcock (2001), 1-year test-retest reliability is .85; the ratio of true score variance to observed variance is .88−.91. Coefficient alpha on this sample was .85.

Data Collection

Trained research assistants administered the three problem-solving measures in whole-class arrangement. For immediate transfer and near transfer, research assistants read aloud each item and provided students time to complete work before progressing to the next item. For far transfer, research assistants read the entire assessment and re-read portions to individuals, upon request, as they worked. Trained research assistants administered WJ-III Applied Problems individually, outside the classroom in a quiet location in the school. All pretesting occurred during the 3 weeks before treatment; posttesting during the 3 weeks following treatment. To avoid familiar research assistants prompting awareness that SBI might apply, students were unfamiliar with their testers. The RA-teachers and RA-tutors administered the three whole-class problem-solving measures using scripted sets of direction. In many cases, the RA-teachers and RA-tutors could identify study conditions, but given the whole-class, scripted administration, it seems unlikely that testers could influence performance. An entirely different pool of research assistants administered individual WJ-III Applied Problems, so these testers had no way of knowing the study conditions in which students had participated.

Data Analysis

We converted scores on the three problem-solving measures to percentage correct so performance on the three measures could be compared. To examine how much of the total variance in improvement on the three problem-solving measures was explained by the clustering of children in classrooms and in tutoring groups, we estimated variance components with SAS PROC MIXED (Littell, 2006). The resulting intraclass correlations showed that the effect for classroom clustering explained 16.10% of the variance (p <.001) and the effect for tutoring-group clustering explained 4.10% of the variance (p = .006). We therefore incorporated each as a random effect into our model, which also included four fixed effects: one within-subjects factor (problem-solving measure) and three between-subjects factors (classroom condition, tutoring condition, and cohort). To assess pretreatment comparability, we fit a full model that included all main effects, 2-way, 3-way, and 4-way interactions as well as estimated the impact of classroom as a random effects factor.

To index learning as a function of study condition, we used improvement on the three problem-solving measures. (Fitting a model using improvement scores produces identical effects as would considering the interaction between test occasion [pre vs. posttest] and study conditions. We opted for improvement scores because their interpretation is more straightforward.) In this full model, the variance component for tutoring group decreased to zero (indicating that all of the variance associated with tutoring group clusters was explained in the model). So we fixed the random effects of tutoring group to zero and also eliminated from the final model all higher-order interactions that were not statistically significant. To follow-up significant effects, we Bonferroni-corrected p-values by the number of follow-up tests we ran for that significant effect. To compute effect sizes (ESs), we subtracted the difference between improvement means and then divided by the pooled standard deviation of the improvement/square root of 2(1-r_xy) (Glass, McGaw, & Smith, 1981).

To examine the effects of the classroom and tutoring tiers of SBI prevention on the prevalence of math difficulty, we designated difficulty as performing below the 16^th percentile on WJ Applied Problems at the end of intervention and applied chi-square analyses.

Results

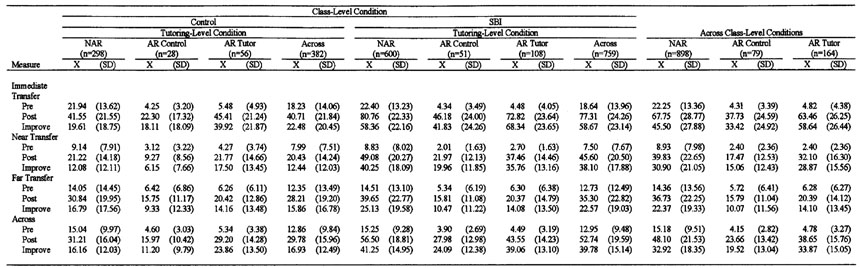
See Table 3 for means and standard deviations by classroom condition and by tutoring condition (for a of means and standard deviations by classroom condition, tutoring condition, and cohort, contact the first authors). See Table 3 for rates of difficulty status by classroom and tutoring conditions. See Table 3 for ESs.

Table 3.

Performance on Problem-Solving Measures by Classroom Condition and Tutoring Condition (Across Cohorts)

Pretreatment Comparability on Math Problem-Solving

See Table 3 for means and standard deviations. There were no significant effects for classroom condition, F(1,274) = 0.06, p = .811, or for cohort, F(3,3274) = 0.14, p = .938. As expected, there was a significant effect for tutoring condition, F(2,3274) = 236.75, p < .001, with NAR students performing higher than each of the two AR tutoring groups (both p < .001), which performed comparably to each other (p = .587). Also, there was a significant effect for measure, F(2,3274) = 27.43, p < .001. Across classroom conditions, across tutoring conditions, and across cohorts, students performed higher on immediate transfer than on near transfer; higher on immediate transfer than on far transfer (p < .001); but higher on far transfer than on near transfer (p < .001). The reason students scored higher far than on near transfer at pretreatment was that far transfer incorporated a greater variety of problem types, some of which were simpler than the problem types on near transfer. Neither of these main effects threatens the internal validity of the study. (Moreover, as shown below, improvement on far transfer was harder to effect, supporting its far-transfer designation.) The 2-way interactions were as follows: for classroom condition by tutoring condition, F(2,3274) = 0.22, p < .799; for classroom condition by measure, F(2,3274) = 0.21, p < .814; for tutoring condition by measure, F(4,3274) = 28.75, p < .001; for classroom condition by cohort, F(3,3274) = 0.52, p < .666; for tutoring condition by cohort, F(6,3274) = 0.68, p < .663; and for measure by cohort, F(6,3274) = 2.76, p = .011. For Cohorts 1, 2, and 4, students performed higher on immediate transfer than on near transfer (all p < .001); higher on immediate transfer than on far transfer (all p < .001); but higher on far transfer than on near transfer (all p < .001 except for Cohort 1, p = .005). By contrast, the third cohort scored comparably on near and far transfer (p = .022) (with immediate transfer scores higher than both other measures, as was the case for the other three cohorts, both p < .001). Because neither classroom nor tutoring conditions was involved in this interaction, it does not threaten the validity of the study. None of the 3- or 4-way interactions was significant.

Math Problem-Solving Learning as a Function of Prevention Conditions

See Table 3 for means and standard deviations; see Table 5 for ESs. We first consider the primary question addressed in the present study: Is tutoring more effective with validated classroom instruction? Then, we consider other effects involving treatment. Finally, we list results for the remaining effects, which are of less interest.

Table 5.

Effect Sizes^a on Improvement Scores by Classroom Condition and Tutoring Condition (Across Cohorts)

	Measure
Contrast	Immediate Transfer	Near Transfer	Far Transfer	Across
Within Classroom Control
NAR vs. AR Tutored	-1.16	-0.42	0.15	-0.50
NAR vs. AR Control	0.09	0.51	0.43	0.37
AR Tutored vs. AR Control	1.47	1.03	0.49	1.18
Within Classroom SBI
NAR vs. AR Tutored	-0.46	0.36	0.86	0.14
NAR vs. AR Control	0.80	1.73	1.23	1.17
AR Tutored vs. AR Control	1.52	0.99	0.23	1.13
Across Classroom Conditions
NAR vs. AR Tutored	-0.54	0.11	0.44	-0.05
NAR vs. AR Control	0.53	0.86	0.64	0.73
AR Tutored vs. AR Control	1.34	1.09	0.37	1.17
Across Tutoring Conditions
SBI vs. Control	1.90	1.73	0.36	1.51

^aPositive value indicates that the first condition named was higher. Negative value indicates that the second condition named was higher. NAR is not-at-risk; AR is at-risk; SBI is schema-broadening instruction.

Is tutoring more effective with validated classroom instruction?

The interaction between classroom condition and tutoring condition was significant, F(2,3320) = 24.33, p < .001. We pursued this interaction in three ways. First, exclusively with AR students, we tested the difference between tutoring with and without validated classroom instruction directly; this was significant (p < .001; ES = 1.34). Second, again focusing exclusively on AR learners, we contrasted the difference between tutored and control students who received conventional classroom instruction (ES = 1.18) versus the difference between tutored and control students who received validated SBI classroom instruction (ES = 1.13). This was not significant (p = .308), suggesting that the effects of two tiers of prevention are additive, not synergistic. Finally, we considered the pattern of improvement between NAR versus AR students as a function of tutoring condition within each classroom treatment. With classroom control, improvement of NAR students and AR control students was comparable (p = .011); NAR students improved less than AR tutored students (p < .001); and AR tutored students improved more than AR controls (p < .001). By contrast, when students received classroom SBI, NAR students outgrew AR control students (p < .001); AR tutored students continued to outgrow AR controls (p < .001); and the improvement of NAR and AR tutored students was comparable (p = .108).

Interactions with problem-solving measure

The main effect for classroom condition was significant, F(1,3320) = 160.32, p < .001. Classroom condition did, however, interact significantly with measure, F(2,3320) = 176.37, p < .001. The effect of classroom condition was significant on immediate transfer (p < .001) and on near transfer (p < .001), but not on far transfer (p = .495).

The main effect of tutoring condition was also significant, F(2,3320) = 51.67, p < .001. There was, however, a significant interaction between tutoring condition and measure, F(4,3320) = 27.61, p < .001. On immediate transfer, NAR students outgrew AR control students (p < .001). Importantly, however, AR tutored students outgrew AR control students (p < .001) and most impressively, AR tutored students also outgrew NAR (p < .001). On near transfer, although NAR and the AR tutored students again outgrew AR control students (both p < .001), the improvement of the NAR and the AR tutored students was comparable on this measure (p = .813). A different pattern emerged on the far-transfer measure. Although the contrast between AR tutored students and AR control students only approached significance (p < .043), the NAR students outgrew both AR groups of learners (both p < .001).

Interaction between tutoring and cohort

Tutoring also interacted significantly with cohort, F(6,3320) = 3.45, p = .002. The follow up to this interaction focused exclusively on AR students, by looking at the effect of receiving versus not receiving tutoring for Cohorts 2, 3, and 4, each compared to the effect for Cohort 1. This is interesting because with tutoring SBI, none of Cohort 1 had the strengthened version of self-regulated learning strategies, and although all of Cohort 2 had the strengthened version of self-regulated learning strategies, half of this cohort had the warm-up drill/practice activities. By contrast, all the Cohort 3 and 4 SBI tutored students received the strengthened version of self-regulated learning strategies strengthened motivation without warm-up activities In line with this instructional design feature, the contrast between tutored Cohorts 1 and 2 was not significant (p = .194; ESs comparing AR tutored against AR control of 0.60 for Cohort 1 vs. 0.97 for Cohort 2) but was significant for the contrast between Cohorts 1 and 3 (p < .001; ESs comparing AR tutored against AR control of 0.60 for Cohort 1 vs. 1.86 for Cohort 3) and between Cohorts 1 and 4 (p = .002; ESs comparing AR tutored against AR control of 0.60 for Cohort 1 vs. 1.57 for Cohort 4).

Remaining effects

The measure effect was significant, F(2,3320) = 219.97, p < .001. As expected, across classroom conditions, tutoring conditions, and cohorts, improvement on immediate transfer exceeded improvement on near transfer (p < .001); improvement on immediate transfer exceeded improvement on far transfer (p < .001); and improvement on near transfer exceeded improvement on far transfer (p < .001). The cohort effect was not significant, F(1,3320) = 0.43, p < .733 (indicating the across classroom conditions, tutoring conditions, and measures, improvement of the four cohorts was comparable).

Math Difficulty as a Function of Prevention Conditions

See Table 4 for math difficulty by classroom and tutoring conditions. Chi-square analyses indicated no relation between math difficulty status and classroom condition, X² (1, N=1141) = 0.18, p = .672. To examine the relation between math difficulty status and tutoring condition (where we had three levels: NAR, AR control, and AR tutored), we allocated one degree of freedom to the contrast between NAR versus AR (control and tutored), which revealed a significant relation: X² (1, N=1141) = 104.27, p < .001. We allocated the other degree of freedom to the contrast between the two AR groups, which also revealed a significant relation: X² (1, N=243) = 7.08, p = .008.

Table 4.

Difficulty Status by Classroom Condition and Tutoring Condition (Across Cohorts)

	Classroom Condition
	Control		SBI		Across
Tutoring Condition	n	(%)	n	(%)	n	(%)
With MDa
NAR	2	(0.6)	11	(1.8)	13	(1.4)
AR Control	8	(28.5)	13	(25.5)	21	(26.6)
AR Tutor	7	(12.5)	14	(12.9)	21	(12.8)
Across	17	(4.5)	38	(5.0)	55	(4.8)

^aFinal Woodcock-Johnson Applied Problems score below 16^th percentile.

We then estimated overall prevalence of math difficulty as a function of whether AR students received tutoring. To estimate overall prevalence without tutoring, we did the following calculation: [(number of NAR students identified as having math difficulty + number of AR control students identified as having math difficulty + [proportion of AR control students identified as having math difficulty times X AR tutored students]) divided by the number of students in the 89 classrooms who completed the study (n = 1141)]. We added the [proportion of AR control students identified as having math difficulty times X AR tutored students] because we wanted to include the base rate of expected math difficulty in the tutored group if they had not been tutored. In a similar way, to estimate overall prevalence with tutoring, we did the following calculation: [(number of NAR students identified as having math difficulty + number of AR tutored students identified as having math difficulty + [proportion of AR tutored students identified as having math difficulty times X AR control students]) divided by the number of students in the 89 classrooms who completed the study (n = 1141)]. Here, we added the [proportion of AR tutored students identified as having math difficulty times X AR control students] because we wanted to include the rate of MD expected in the control group if they had been tutored. Without tutoring, we estimate a math difficulty prevalence rate of 6.8%; with tutoring, 3.9%.

Discussion

The primary purpose of this large-scale randomized field trial was to assess the effects of third-grade small-group tutoring with and without validated classroom instruction on AR students' math problem solving and their learning relative to NAR peers. The issue of how tutoring interacts with classroom instruction among students at-risk for poor learning outcomes is important for designing efficient and effective RTI prevention systems. If tutoring is differentially efficacious when combined with validated classroom instruction, then both tiers are critical and classroom instruction needs to be designed deliberately with AR students in mind, even when they receive tutoring. By contrast, if tutoring promotes comparable outcomes regardless of the classroom instructional context, then findings would set the stage for research on whether tutoring might occur as a replacement for, rather than as a supplement to, classroom instruction. This would make RTI prevention systems logistically easier and more efficient, facilitating scheduling and permitting resources to be infused at the tutoring tier. In addition, when considering tutoring efficacy as a function of the classroom context, it is important not only to compare the response of AR students who do and do not receive tutoring, but also to contrast the learning of AR students against their NAR peers. This has not been addressed in prior work.

So, in the present study, we randomly assigned classrooms to validated or conventional instruction; designated incoming risk status (NAR vs. AR); and within classroom conditions, randomly assigned AR students to receive tutoring or not. This allowed us to compare the learning of AR students (with one, two, or no tiers of SBI) and NAR students (with/without validated classroom prevention). We considered this an efficacy study, where the key question is whether interventions have their intended effects when they are actually implemented Toward that end, we relied on research assistants to implement SBI classroom instruction and SBI tutoring. We note, however, that within most RTI models, someone other than the classroom teacher implements Tier 2 tutoring; so the use of research assistants to conduct tutoring does not compromise external validity.

Results revealed an interaction between the two tiers of prevention and, importantly, tutoring was significantly and substantially more effective when it occurred in combination with validated classroom instruction than when tutoring occurred with conventional classroom instruction (ES = 1.34). This suggests that two tiers are better than one tier of prevention and indicates the importance of providing AR students validated instruction in the classroom and then supplementing that instruction with high quality tutoring. In the present study, the two tiers of instruction were closely aligned, both addressing the same types of word problems at the same time and both relying on the same theoretical (SBI) and operational approach (Hot Math) to instruction. It is possible that when the two tiers of instruction are less well aligned, as is often the case, results would differ. Moreover, it is possible that aligning Tier 1 and Tier 2 instructional content may differ as a function of academic domain. Consequently, we emphasize that future studies should assess the value-added of validated classroom instruction that is more and less aligned with tutoring for different academic content. At the same time, even with closely aligned instruction at the two tiers of the prevention system, our results showed that the advantage for AR tutored students over AR control students was comparable with (ESs = 1.18) and without (ES = 1.13) validated classroom instruction. So, the effects of two tiers of prevention appear to be additive rather than synergistic.

It is also interesting to consider the effects of one versus two tiers of validated prevention by comparing the performance of AR students against NAR peers (at least in the area within which intervention occurred, i.e., in math problem solving). When contrasting AR tutored students' learning with that of NAR peers, two tiers of prevention again appear to make a difference, but in an unanticipated way. With only one tier of prevention (i.e., tutoring for AR students combined with conventional classroom instruction for AR and NAR students), AR tutored students improved more than NAR students, by an impressive half a standard deviation. So when AR and NAR students receive conventional classroom math problem-solving instruction, with AR students receiving tutoring, the achievement gap between AR and NAR students narrows substantially (at pre-intervention, ES = 1.09, with the mean difference between AR and NAR students representing 2.80 standard errors of measurement; at post-intervention, ES = 0.13, with the mean difference between AR and NAR students less than 1 standard error of measurement). This unexpected finding shows the power of SBI tutoring to effect strong learning among AR students, who initially performed substantially below NAR classmates. It also suggests that classroom teachers require guidance about how to promote math problem-solving learning. On the other hand, with two tiers of prevention (i.e., validated classroom and tutoring for AR students combined with validated classroom instruction for NAR students), AR tutored and NAR students achieved comparably (ES=0.14). So when AR and NAR students receive validated classroom math problem-solving instruction, with AR students also receiving a second tier of tutoring, the achievement gap between AR and NAR students remains sizeable and comparable (at pre-intervention, ES = 1.29, with the mean difference between AR and NAR students representing 3.11 standard errors of measurement; at post-intervention, ES = 0.72, with the mean difference between AR and NAR students representing 2.71 standard errors of measurement).

In terms of the contrast between AR control and NAR students, NAR consistently improved more than AR controls, with an ES of 0.37 without classroom SBI and an ES of 1.17 with classroom SBI. This was expected. So when AR and NAR students receive the same, single tier of validated classroom math problem-solving instruction, without AR students receiving a second tier of preventive tutoring, the achievement gap between AR and NAR students grows (at pre-intervention, ES = 1.30, with the mean difference between AR and NAR students representing 3.28 standard errors of measurement; at post-intervention, ES = 1.55, with the mean difference between AR and NAR students representing 5.95 standard errors of measurement; hence, the gap between AR and NAR students at pre- versus post-intervention increased by 2.69 standard errors of measurement). The differential effect of validated classroom practices, favoring NAR over AR students, has been documented in prior work (e.g., Fuchs et al., 1997).

Together, findings indicate that intensive instruction, in the form of preventative tutoring, is essential for AR students. Without it, the gap between AR and NAR students continues to widen, even when NAR students suffer the disappointing effects of conventional problem-solving classroom instruction. Accordingly, results highlight the importance of validated problem-solving instruction in the Tier 1 classroom and suggest that tutoring occur as a supplement to, not a replacement for, classroom instruction. This is the case for AR students: When they receive tutoring combined with validated classroom instruction, their learning exceeds that of students who receive tutoring without validated classroom instruction – by a practically important ES of 1.34 standard deviations. At the same time, the importance of validated classroom instruction is also clear for NAR students, whose problem-solving learning is superior with validated classroom SBI. Readers should take note, however, that when AR students receive two tiers of validated instruction while their NAR classmates receive validated classroom instruction, the AR students' performance gap is unlikely to narrow. We also caution that these results cannot be generalized beyond third grade, beyond math problem solving, and beyond instruction that is closely aligned across tiers. Additional research exploring these issues at other grades and in other academic areas and testing the effects with and without instructional alignment is warranted.

This need for additional studies at other grades and in other areas is illustrated by comparing our results to those of Gilbert et al. (2007). Working in reading at first grade, Gilbert et al. showed that validated classroom instruction did not contribute to tutoring efficacy. At least two differences between Gilbert et al. and the present study help explain the inconsistency of findings. First, because Gilbert et al. tutored students at instructional levels that were substantially below classmates' levels, classroom teachers and tutors did not work on identical skills at the same time (as was the case in the present study). Second, Gilbert et al.'s AR sample had already proven unresponsive to the fall semester's validated classroom instruction; so it is not surprising that second-semester Tier 2 tutoring was not differentially effective when combined with Tier 1 validated instruction. By contrast, we used a more typical RTI method for identifying students for risk and for tutoring: initial performance on predictors of outcome.

In addition to studying the contribution of validated classroom instruction to the efficacy of tutoring in terms of math problem-solving outcomes, we also examined the prevalence of mathematics difficulty with and without validated classroom instruction and with and without tutoring. We operationalized math difficulty with a widely-used tool for identifying math disability in the schools. Also, WJ-III Applied Problems (Woodcock et al., 2001) is broader than our math problem-solving outcome measures, assessing skill in analyzing and solving practical math problems that involve counting, telling time or temperature, as well as problem solving. In addition, we selected a relatively stringent cut-point (the 15^th percentile) for designating difficulty, and we note that students were not identified for participation and or designated as AR using this measure. Even so, the prevalence of math difficulty was clearly associated with tutoring. Although AR students were, as expected, disproportionately represented in the math difficulty category compared to NAR students, AR tutored students were significantly and dramatically less likely than AR controls to be designated as having math difficulty at the end of the study. That is, tutoring cut the proportion of students with math difficulty in half: from 26.6% of AR control students (or 6.8% of the general population) to 12.8% of AR tutored students (or 3.9% of the general population). At the same time, math difficulty status was not associated with classroom condition, even when looking exclusively at AR students who received validated classroom SBI versus convention classroom instruction. So, it appears that tutoring, not validated classroom instruction, is the active agent that reduces math difficulty status for AR students, suggesting that tutoring is the tier that moves student ranking around the cut-points used to designate disability and corroborating the strong need for tutoring among the population of learners at-risk for poor math problem-solving learning.

Four additional findings, although not the primary purpose of the present study, also merit discussion. First, results strengthen previous work (Fuchs et al., 2003a, 2004a) showing that Hot Math SBI enhances mathematical problem solving. Across the three problem-solving measures and across tutoring conditions, the ES favoring classroom SBI over conventional teachers' mathematics problem-solving instruction was 1.51 standard deviations. So SBI was superior to teachers' conventional instruction, even when the problem types addressed within SBI were selected to correspond with the schools' (i.e., control group's) curriculum. Given that the researchers designed SBI with considerable effort over years, it may seem unsurprising that SBI was more effective than conventional classroom instruction. So it is important to note that Fuchs et al. (2003a) demonstrated that SBI makes a sizeable contribution beyond researcher-designed problem-solution instruction, which does not teach students to broaden schemas for transfer to novel problems. We therefore conclude that effects are due to schema-broadening instruction, not just simply researcher-designed problem-solution instruction.

Second, findings demonstrate the efficacy of SBI for tutoring AR students on problem types that extend beyond total, difference, and change relationships addressed in prior work (Fuchs et al., in press; Jitendra & Hoff, 1996; Jitendra et al., 1998, 2002; Xin et al., 2005. By contrast, the problem types addressed in the present study involve multiple quantities of more than one kind of item, halving quantities, step-up functions, and pictograph problems, with emphasis on multi-step problem solving, combining problem types, and ignoring irrelevant information. Across the three problem-solving measures and across classroom SBI and control conditions, the ES favoring SBI tutoring over control among AR learners exceeded one standard deviation (ES = 1.17), even though two-thirds of untutored (control) AR students received SBI at the classroom level. Few validated tutoring protocols exist at the second tier of RTI multi-tier prevention systems. Results provide an option for schools to use within their RTI systems for math problem solving on problem types appropriate for third grade.

Third, the interaction between tutoring condition and cohort suggests that for AR learners, systematic motivation may be important for promoting learning within small-group tutoring. For Cohort 1, although tutoring incorporated self-regulated learning strategies, the motivation system within those self-regulated learning strategies was weak. By contrast, for Cohorts 3 and 4, tutoring incorporated a strengthened motivation system within self-regulated learning strategies, which relied on tangible reinforcers for listening carefully, following directions, paying attention, working hard, and producing accurate work. Accordingly, the differences in outcome for Cohort 1 versus Cohort 3 and for Cohort 1 versus Cohort 4 were statistically significant, with ESs of 1.86 and 1.57. (This strengthened motivation system was first incorporated with the Cohort 2 tutored sample; however, half of the Cohort 2 tutored sample also received warm-up drill and practice, which proved problematic. The difference in learning outcome for Cohort 1 vs. Cohort 2 was not statistically significant, even though the ES was a sizeable 0.60). These findings suggest the need for systematic motivation systems to address task persistence deficits among AR learners (Deci & Chandler, 1986; Deci & Ryan, 1985; Dweck & Leggett, 1988; Garber & Seligman, 1980). This may be particularly relevant when solving mathematical word problems, which requires metacognition and persistence in the face of challenge (De Corte et al., 2000). Causal-comparative studies (e.g., Lester & Garofalo, 1982; Schoenfeld, 1992; Silver, Branca, & Adams, 1980) illustrate how self-regulation differs between weak and skilled problem solvers: Experts spend more time analyzing problems before initiation solutions, reflect more frequently on their problem solving, and alter their approach more flexibly. Motivation to think through challenging tasks and to persist with the task even when initial efforts are not successful may be critical, and future research should address this question more directly.

Fourth, results illustrate the difficulty of enhancing students' real-life problem solving, as revealed with a significant interaction between classroom condition and problem-solving measure. Learning was significantly stronger for classroom SBI compared to classroom control on immediate- and near-transfer measures, both of which included entirely novel math problems, with near-transfer problems extending well beyond what had been directly taught within SBI. The ESs for immediate- and near-transfer, respectively, were 1.90 and 1.73. On far transfer, however, the effect was not statistically significant. The far-transfer measure, designed to mirror real-life problems, varied from the problems used for instruction in multiple ways. It presented a multi-paragraph with four questions; some of the information needed to answer the question was removed from the multi-paragraph narrative and placed in figures or question stems; it contained multiple pieces of numeric and narrative irrelevant information; it provided opportunities for students to formulate decisions; it combined all four problem types; and it varied all four SBI transfer features. Given the transfer distance involved in the far-transfer measure, the ES of 0.36 is notable, especially because effects were demonstrated with relatively young students for whom schema-induction (e.g., Chen, 1999) and problem-solving competence (Chen; Durnin et al., 1997; Foxman et al., 1991, cited in Boaler, 1993; Larkin, 1989) have proven hard to effect. Present findings do, however, suggest the need for additional research to examine how to strengthen real-life problem solving.

In a similar way, an interaction between problem-solving measure and tutoring condition was also documented. On immediate transfer, AR tutored students improved more than NAR students (ES = 0.54), while both groups grew more than AR control (ES = 1.34 for AR tutored and 0.53 for NAR). On near transfer, the improvement of NAR and AR tutored students was comparable (ES = 0.11), but again both groups grew better than AR controls (ES = 0.86 for NAR and 1.09 for AR tutored). Only on far transfer did the improvement of NAR students exceed that of AR tutored students (ES = 0.44), and the improvement of AR tutored versus AR control students only approached statistical significance (p = .043; ES = 0.37). Again, given the transfer distance involved in the far-transfer measure and the sizeable deficits the AR students brought to the tutoring table, the ES of 0.37 favoring AR tutored over AR control students appears promising, but additional work exploring methods for promoting real-life problem solving is required.

In sum, relying on a randomized field trial while accounting for the nested structure of the data, the present study provides evidence for the efficacy of SBI for classroom and for tutoring use in promoting superior math problem solving with AR and NAR students. Moreover, in terms of RTI prevention systems, results indicate that two tiers of validated instruction are better than one tier, but that the effects of two tiers are additive, not synergistic. Findings also illustrate the disappointing efficacy of conventional math problem-solving instruction and the need for improved methods to teach math problem solving in general education classrooms. SBI appears to represent one potentially strong method for achieving that goal. At the same time, as shown previously (e.g., Bransford & Schwartz, 1999; Brown et al., 1992; Durnin et al., 1997; Foxman et al., 1991, cited in Boaler, 1993; Larkin, 1989; Mayer et al., 1999), findings once again corroborate the difficulty of promoting far transfer, in this study operationalized as real-life problem solving. Additional studies exploring methods for enhancing far transfer are warranted. Given the promising ESs on this study's far-transfer measure, researchers might consider marrying SBI with other approaches toward that end.

Before closing, we note that research assistants, not teachers, delivered classroom and tutoring SBI, with close monitoring of the fidelity of implementation. So, this investigation qualifies as an efficacy, not an effectiveness study. That is, findings demonstrate that SBI promotes superior outcomes, at the classroom and tutoring prevention tiers, under conditions that ensure strong SBI implementation. The present study does not address issues of effectiveness, i.e., whether SBI effects can be realized when implemented by teachers (for classroom SBI) and school-based support staff (for tutoring SBI), and does not address issues about how to scale-up Hot Math SBI. Given the demonstration of Hot Math SBI efficacy in the present study, research focused on issues of effectiveness and scaling up appear warranted.

Supplementary Material

1

Instructional Components of Hot Math Classroom SBI Whole Class and Hot Math Tutoring SBI for One Unit: Half (H)