Summary
This article introduces methods for use in vaccine clinical trials to help determine whether the immune response to a vaccine is actually causing a reduction in the infection rate. This is not easy because immune response to the (say HIV) vaccine is only observed in the HIV vaccine arm. If we knew what the HIV-specific immune response in placebo recipients would have been, had they been vaccinated, this immune response could be treated essentially like a baseline covariate and an interaction with treatment could be evaluated. Relatedly, the rate of infection by this baseline covariate could be compared between the two groups and a causative role of immune response would be supported if infection risk decreased with increasing HIV immune response only in the vaccine group. We introduce two methods for inferring this HIV-specific immune response. The first involves vaccinating everyone before baseline with an irrelevant vaccine, for example, rabies. Randomization ensures that the relationship between the immune responses to the rabies and HIV vaccines observed in the vaccine group is the same as what would have been seen in the placebo group. We infer a placebo volunteer’s response to the HIV vaccine using their rabies response and a prediction model from the vaccine group. The second method entails vaccinating all uninfected placebo patients at the closeout of the trial with the HIV vaccine and recording immune response. We pretend this immune response at closeout is what they would have had at baseline. We can then infer what the distribution of immune response among placebo infecteds would have been. Such designs may help elucidate the role of immune response in preventing infections. More pointedly, they could be helpful in the decision to improve or abandon an HIV vaccine with mediocre performance in a phase III trial.
Keywords: AIDS, Causal inference, Correlate of protection, Counterfactual, HIV, Missing data, Principal stratification, Surrogate endpoint
1. Introduction
A vaccine contains innocuous material that provokes a response by the adaptive immune system. Following vaccination, the immune system mounts a multifaceted, and exquisitely specific, counterattack based on two types of white blood cells, B-lymphocytes and T-lymphocytes. These cells respond to specific proteins of the vaccine material, proliferate, and wait to subsequently attack either floating microbes or infected cells that display such peptides. B-lymphocytes produce antibodies that recognize proteins in the outer surface of the virus and neutralize their ability to infect cells. T-lymphocytes produce cells that either kill or aid in killing infected cells. The magnitude of each component of the adaptive immune response to the vaccine can be measured. Vaccine development focuses on inducing a strong, measurable immune response while ensuring that the vaccine is safe (see, e.g., Halloran, 1998; Nabel, 2001; or Chan, Wang, and Heyse, 2003).
Establishing the role of vaccine-induced immune response on actual protection of infection and disease is an important open problem in vaccine studies (Halloran, 1998). A “correlate of protection” is the threshold for immune response, say xp, beyond which infections and disease do not occur (Lachenbruch et al., 2000). Methods for estimating such a threshold are discussed in Carey, Barker, and Platt (2001), Chan et al. (2002), and Plikaytis and Carlone (2005). However, when immune response only occurs in the vaccinated group, validation of a correlate of protection, or more generally validation of immune response as a true surrogate with a causative role, is problematic (Chan et al., 2003). The use of Prentice’s criteria to establish surrogacy, conditional independence of treatment, and outcome given the surrogate (Prentice, 1989) breaks down here because immune response to the vaccine basically only occurs in the vaccine group and thus the value of the surrogate basically identifies the treatment group. Strictly speaking, one cannot know whether the measured immune responses, or other unmeasured vaccine-induced changes, are actually responsible for an efficacious vaccine. For example, it could be that those individuals who achieve xp in response to a weak vaccine are more intrinsically fit than others so that even if a more powerful vaccine achieved xp in everyone, not all would be protected.
That this might be an actual problem was demonstrated in VAX004, the first phase III trial of an HIV vaccine (Gilbert et al., 2005; The rgp120 HIV Vaccine Study Group, 2005). Overall, the vaccine was not effective, with infection rates of 0.067 and 0.070, respectively, in the vaccine and placebo groups based on 5403 volunteers. However, the antibody response to the HIV vaccine was strongly associated with infection risk in the vaccine group. Tables 1 and 2 provide the relative hazard of infection as a function of antibody response quartiles, first within the vaccine group and then when the placebo group is used as a control (see Gilbert et al., 2005). Because antibody response to the HIV vaccine is only measured in the vaccine group, Table 2 has question marks in the placebo cells—we do not know what HIV immune response they would have had, had they been vaccinated.
Table 1.
The relative hazard of infection, based on a Cox model, as a function of antibody response to the HIV vaccine, which is only measured in the vaccine group. It seems the vaccine-induced antibodies are doing their job.
| Quartile of antibody response following HIV vaccination
|
||||
|---|---|---|---|---|
| Group | Weak | Modest | Good | Best |
| Vaccine | 1.00 | 0.35* | 0.28* | 0.22* |
p < 0.05.
Table 2.
When we calculate the relative hazard for the four quartiles compared to the placebo group, a different picture emerges (Gilbert et al., 2005). The numbers provide the hazard relative to the overall placebo group, while the ?’s emphasize that immune response following HIV vaccination is not measurable in the placebo group and thus the relative hazards are unknown.
| Quartile of antibody response following HIV vaccination
|
|||||
|---|---|---|---|---|---|
| Group | Weak | Modest | Good | Best | Overall |
| Placebo | ? | ? | ? | ? | 1.00 |
| Vaccine | 1.86* | 0.99 | 0.99 | 0.81 | |
p < 0.05.
Two hypotheses were postulated to explain these results (Gilbert et al., 2005; Graham and Mascola, 2005). The first was that antibody response is identifying volunteers with different constitutional ability to avoid infection but the vaccine-induced immune response had no causative role. We call this the association hypothesis. The second was that the vaccine caused infections in those with the weakest immune response and prevented infections in those with the strongest immune response. We call this the causation hypothesis. As it stands, neither of these hypotheses can be evaluated on the basis of data.
In this article we introduce two new designs to help understand the role of immune response in vaccines. These designs can discriminate between the two hypotheses outlined above. The first design is to inoculate everyone in both arms prior to randomization with an irrelevant vaccine, say rabies. We call this baseline irrelevant vaccination (BIV), and let W0 be the immune response to the rabies vaccine at baseline. Also, we define X0 as the immune response to the HIV vaccine, which is measured just after randomization in the vaccine group. Randomization ensures that the relationship between W 0, X0 observed in the vaccine group is the same in the placebo group. Based on this relationship, the observed W0 of a placebo participant can be used to infer his X0. Figure 1 illustrates how W0 can be used to impute X0 in the placebo group when they are very highly correlated (ρ= 0.98). It is important to note that a rabies vaccine is not required—any baseline measurement that correlated well with X0 would work, but an irrelevant vaccination is a good choice. This type of thinking to predict a post-randomization characteristic only observed in the treatment group has been used before in heart disease (see, e.g., Follmann, 2000, or Hallstrom et al., 2001).
Figure 1.
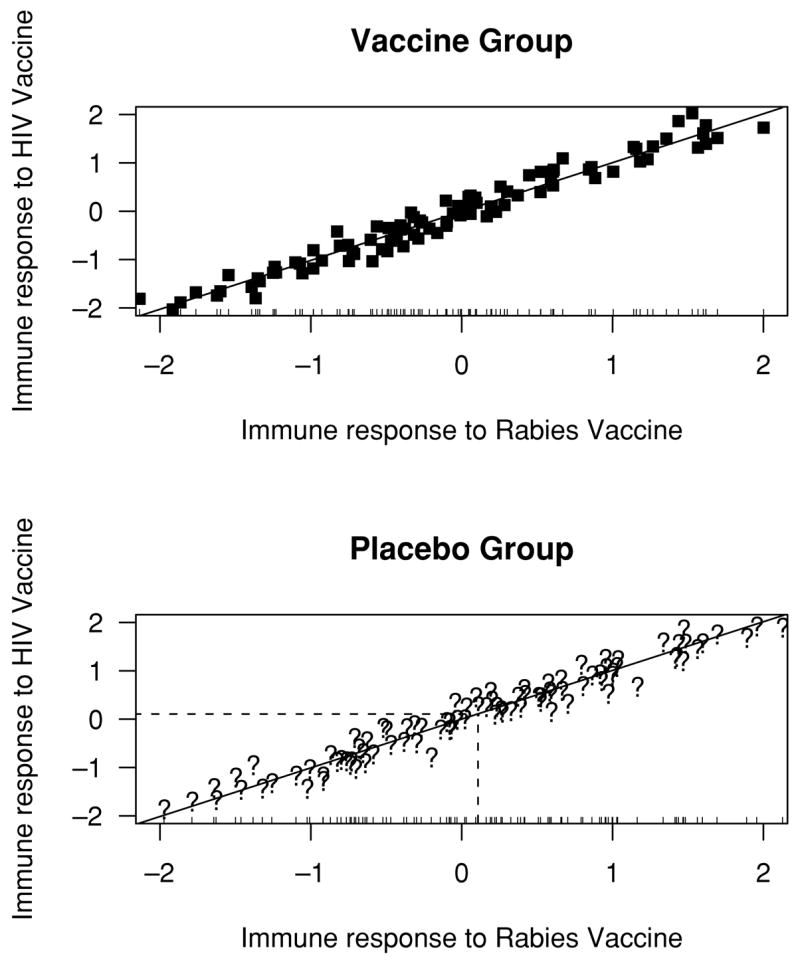
Made-up scatterplot illustrating imputation of the immune response to an HIV vaccine (X0) in the placebo group based on the observed immune response to a rabies vaccine (W0) for a single patient. The bivariate distribution between X0, W0 is observed in the vaccine group. Randomization assures that this distribution and regression line also apply to the placebo group. While X0 cannot be observed in the placebo group, W0 can and provides the basis for imputation. A very high correlation between X0, W0 is used to illustrate the concept.
The second way to get at X0 in the placebo group would be to vaccinate all the uninfected placebo recipients at the closeout of the trial with the HIV vaccine and then measure their immune response, say XC. If we make the assumption that XC is the same as X0, we effectively obtain X0 in many. We call this closeout placebo vaccination (CPV). Table 3 provides hypothetical data illustrating how CPV can be used to suggest that X0 is associated with constitutional ability to remain uninfected, but has no causative role.
Table 3.
Hypothetical data set of a trial where 800 patients are randomized. The vaccine group has an immune response to the HIV vaccine that is measured just after randomization/vaccination. The placebo volunteers who remain uninfected are vaccinated at the end of the study and immune response is measured then. Bold numbers are directly observed, italicized numbers are inferred. Randomization assures that roughly 100 placebo patients would be in each quartile, as occurred in the vaccine group. In this example, consistent with the association hypothesis, the vaccine has no overall effect but identifies patients with an intrinsic ability to avoid infection.
| Quartile of antibody response following HIV vaccination
|
|||||
|---|---|---|---|---|---|
| Group | 1st | 2nd | 3rd | 4th | Total |
| Vaccine | |||||
| Total | 100 | 100 | 100 | 100 | 400 |
| Infected | 30 | 15 | 10 | 5 | 60 |
| Uninfected | 70 | 85 | 90 | 95 | 340 |
| Placebo | |||||
| Total | ±100 | ±100 | ±100 | ±100 | 400 |
| Infected | ±29 | ±16 | ±9 | ±4 | 58 |
| Uninfected | 71 | 84 | 91 | 96 | 342 |
Figure 1 and Table 3 are meant to informally illustrate how to infer X0 in the placebo group. In the sequel, we develop formal methods that rely on the thinking of counterfactuals, causal inference, and principal stratification. We also describe some simple methods, investigate performance of different methods by simulation, and discuss some more elaborate approaches.
2. Model-Based Approach
Suppose that n patients per group are randomized to placebo or vaccine. Prior to randomization, all patients receive a rabies vaccine and the immune response to rabies vaccine (W0) is measured before randomization. Patients are then randomized to either a placebo or HIV vaccine injection and shortly thereafter, immune response to the HIV vaccine (X0) is measured in the vaccine group. At the closeout or end of the trial, all uninfected placebo recipients receive the HIV vaccine and shortly thereafter, immune response to this vaccine is measured (XC). Let Y be the infection indicator and Z be the vaccine indicator. A schematic representation of a vaccine trial augmented with BIV and CPV is given in Figure 2.
Figure 2.
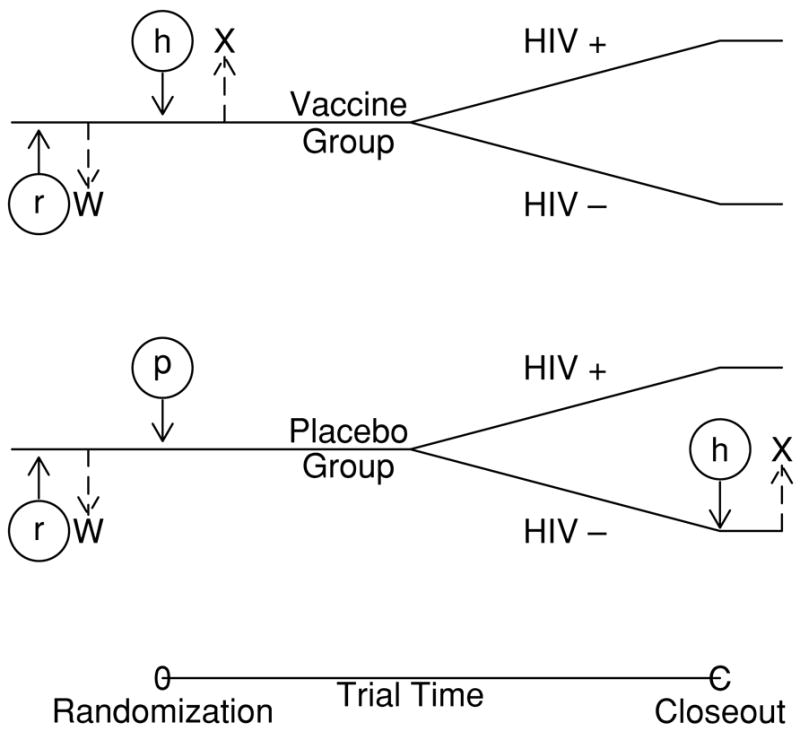
Schematic representation of augmented designs. Circles and lowercase letters denote inoculations, immuneresponse is denoted by capital letters. Under a traditional design, patients are vaccinated either with HIV vaccine (h) or placebo (p) and immune response to the HIV vaccine (X = X0) is measured shortly thereafter in the vaccine group. Under BIV, both groups are vaccinated against rabies (r) and the immune response to rabies vaccine (W = W0) is measured prior to randomization. Under CPV, placebo patients who are uninfected at the end of the trial receive HIV vaccine at close-out and their immune response is measured then (X = XC).
Our approach to using these data is perhaps best described using counterfactual reasoning (Rubin, 1974, 1977, 1978; Halloran and Struchiner, 1995) and principal stratification (Frangakis and Rubin, 2002). First, let W0i be the baseline rabies-specific adaptive immune response for patient i. This is seen in everyone. The response to HIV vaccination is different. One can write X0i(z) as the (post) baseline HIV-specific immune response to HIV vaccination. We call X0i(0), X0i(1) potential covariates; X0i(1) is measured in vaccine recipients while X0i(0) would be 0 in nearly everyone. We say that X0i(1) is realized in the vaccine group and unrealized in the placebo group. Using the terminology of Frangakis and Rubin (2002), Xi (1) = x, Xi (0) = 0 defines a principal stratum indexed by x. Principal strata are a classification of subjects defined by the potential values of a post-treatment variable under each of the treatments being considered. They also call X0(1) a principal surrogate and distinguish it from a “statistical” surrogate, which for our setup would be Xobs = X0(1)Z + X0(0) (1 − Z). We next define Yi(z) as the outcome for person i following treatment z. We call the pair Yi(0), Yi(1) potential outcomes. We also define XCi(z, y) as the closeout HIV-specific adaptive immune response for person i when given treatment z and following outcome y. Only XCi(0, 0) is measured and meaningful:
We make the following simplifying assumptions:
All patients receive the assigned injections so there is no noncompliance.
There are no missing data; W0, Y0 are measured on everyone, X0 is measured on all vaccinees, and XC is measured on all placebo uninfecteds.
No infections occur between the time of randomization and when X0 is measured, say the interval [0, m].
The first two are for simplicity and can be relaxed. For example, if there is some noncompliance but it is governed by an independent random mechanism, our methods could be applied to just the compliers. With data missing completely at random the methods can be applied directly to the observed data. If the data are missing at random, methods that incorporate covariates associated with missingness can be used. The last assumption is more likely to be met if m is small. If a few infections occur in [0, m], an analysis that throws them out may be acceptable. We discuss how to modify our approach to incorporate infections during [0, m] in Section 6.
We next specify probit models for the effect of the “baseline covariate” X0(1) on the probability of infection in both groups:
| (1) |
where Φ( ) is the standard normal c.d.f. (cumulative distribution function). This equation specifies a model for a standard covariate by treatment interaction for a clinical trial. The probit is handy because it is easy to integrate over x, which we will need to do later. Note that (1) assumes that W0 has no effect on Y(z) once X0(1) and Z are in the model. This can also be relaxed, as we discuss in Section 5.
Different causal estimands can be used to quantify the effect of the vaccine as a function of X0(1). For example, following Hudgens and Halloran (2004) we define vaccine efficacy as
With our probit model, a natural estimand is
Note that when β3 = 0, ΔP(x) is free of x, this is not true for VE(x).
If X0i(1) were observed in everyone, estimation would be straightforward. As X0i(1) is not observed in the placebo group, we require at least one of the following two assumptions to proceed:
X0i(1) can be viewed as a baseline covariate or
For placebo uninfecteds, X0i(1) = xi + U1 and XCi(0, 0) = xi + U2 where U1 and U2 are i.i.d. (independent and identically distributed) mean 0. We call this time constancy of immune response.
The first assumption is true by design in randomized trials and allows us to impute X0i (1) based on W0i in the placebo group. While technically measured post-randomization, this “post-baseline” covariate can be used as a baseline covariate. The second assumption allows us to replace X0i(1) with XCi(0, 0) as a covariate in the probit model for placebo uninfecteds. Under the model X = x + U, one can think of x as the true time constant immune response, which is observed subject to measurement error and our interest focuses on the regression of Y on X. This assumption cannot be accepted uncritically as immune response can diminish with age, such as for herpes zoster, if the trial is long enough. Additionally, volunteers might get subinfectious exposures to a virus that modifies immune response. This is thought possible for HIV where commercial sex workers showed immune responses to HIV but remained uninfected. However even here, the assumption might hold if the immune response is effectively primed by subinfectious exposure pre-baseline and this response is maintained during the course of the trial. Additionally, this assumption can be examined, as we will discuss in Section 5.
Our final assumption allows us to easily integrate over the distribution of X0(1)|W0:
The distribution of X0(1), W0 is bivariate normal with moments μx, μw, , , ρ.
This assumption can also be relaxed but the integration would be more complicated.
To estimate β = (β0, β1, β2, β3), we use maximum likelihood. We begin by constructing a likelihood incorporating both BIV and CPV. The likelihood contribution for vaccinees is simple,
where V is the set of vaccinees. For uninfected placebo volunteers we use XCi in lieu of X0i and their contribution is
where ℘ (U) is the set of uninfected placebo recipients. In the placebo infecteds, X0(1) is missing and we need to integrate p0(X0(1)) over the distribution of X0(1)|W0 to obtain their likelihood contribution. Under our last assumption, it follows that X0(1)|W0 = w is normal with mean μ*(w0) = μx + ρσx/σw(w0 − μw)and variance . The (integrated) probability of infection for a person with W0 = w0 is thus
The right-hand side obtains the result that for U normal(μ, σ2). The overall likelihood is thus
Note that depends on the moments of X0(1), W0, which are unknown. We advocate estimating these moments using vaccine group data and regard them as fixed in LBC. Because of this, the standard error estimates obtained by the Fisher information matrix are incorrect and we suggest using the nonparametric bootstrap method to obtain standard errors.
We can also construct likelihoods based on augmenting the usual design with BIV alone or CPV alone. These are, respectively,
where ℘ is the set of placebo recipients, and
where #℘(I) is the number of placebo infecteds. The last Φ( ) in LC(β) is just the probability that a generic placebo patient is infected and equals E{β0 + β1X0(1)}, where X0(1) is normal (μx, ). Based on the estimated β’s it is a simple matter to plug them into a causal estimand. Standard errors and confidence intervals for causal estimands can be computed from the bootstrap.
3. Closeout Placebo Vaccination Alone
The previous section outlined how BIV and CPV can be used to estimate the effect of immune response using a model and likelihood. In this section, we show how closeout placebo vaccination by itself can be used without a model to assess immune response. The approach is inspired by Tables 1 and 2 and Gilbert, Bosch, and Hudgens (2003).
Denote by f0(x) and f1(x) the densities of X0(1) for the placebo and vaccine groups, respectively. In each group we can decompose the distribution of immune response into a mixture of those who would/did become infected and those who would not/did not. Thus we can write the immune response densities in mixture form,
| (2) |
| (3) |
where θℓ is the true proportion of infected volunteers in group ℓ. In the vaccine group the mixed density and the two constituent densities are directly estimable as is θ1. In the placebo group θ0 and f0(x|Y = 0) are directly estimable, provided . To get f0(x|Y = 1) we replace f0(x) with f1(x) and solve by subtraction.
With these arguments and Bayes’ theorem, one can deduce that
| (4) |
| (5) |
The terms on the right-hand side can be estimated nonparametrically and thus so can the left-hand side.
Interestingly, the different conditional distributions of X0(1) can be compared to test the role of X0(1). To motivate these tests, consider Table 3. Suppose the counts in the placebo uninfected row were very similar over the four quartiles. This would suggest that unrealized potential immune response was unassociated with infection risk. Using the fact that f1(x) = f0(x), the continuous analog to see whether the counts in the placebo uninfected row are similar can be written as
Note that if the probit model (1) is correct, then is equivalent to β2 = 0. Also note that corresponds to the causation hypothesis that was suggested to explain Tables 1 and 2.
At the other extreme, suppose that the counts in the vaccine uninfected row were quite similar to the counts in the placebo uninfected row. This would suggest that immune response has no causative effect on infection. The continuous analog is
Unlike does not correspond to β3 = 0 even if (1) is correct, unless β1 = 0. Note that corresponds to the association hypothesis suggested to explain Tables 1 and 2.
Different methods could be used to test equality of the densities specified by and such as t-tests, rank tests, or Kolmogorov-type tests. For a t-test of , one compares all X0i(1)’s in the vaccine group to the XCi ’s of the placebo uninfecteds. For a t-test of , one compares the X0i(1)’s of the vaccine uninfecteds to the XCi’s of the placebo uninfecteds.
4. Simulation
To assess these designs, we conducted a simulation under the model assumptions given in the previous section. We generated data where P{Y(z) = 1 |Z = z, X0(1) = x} is given by (1), and W0, X0(1) are bivariate Gaussian with correlation ρ. We set E[p0{X0(1)}] = θ0 = 0.10 and θ1 = 0.08. We selected β2, β3 in terms of relative risk,
where Q(7/8), Q(1/8) are the seventh and first octiles of the distribution of X0(1). Three scenarios were considered, chosen with the hazards of Tables 1 and 2 in mind:
Association: Here R1 = R0 = 0.2, β3 = 0, and ΔP(x) is free of x.
Causation: Here R0 = 1, R1 = 0.2, β2 = 0, and ΔP(x) depends on x.
Both: Here R0 = 0.33, R1 = 0.11, βk < 0, k = 0, 1, and ΔP(x) depends on x.
For each simulated data set maximum likelihood using LBC, LB, and LC was used to estimate β. We also constructed a probit likelihood based on observing X0(1) exactly in everyone. Estimates based on this likelihood correspond to an unattainable benchmark.
The first set of simulations used 10,000 replications and varied by 0.25, 0.5, 0.75, 1. We do not evaluate ρ= 0 as the model using BIV alone is unidentifiable. Replications were not tallied when convergence was not attained, which was very rare except for BIV alone with ρ= 0.25 when the estimates did not converge 2–3% of the time.
Figure 3 provides the sample variance for the four estimates of β, divided by the sample variance when X0(1) is used, as a function of ρ under the Association and Causation scenarios. Relative behavior of the different estimates is similar under the Both scenario and hence not reported. For the estimates using CPV (C) alone or the benchmark (X), the sampling variability is free of ρ. The sample variance with CPV alone is from nearly 10 times to almost 25 times larger than with the benchmark. The performance of BIV (B) alone depends profoundly on ρ with ρ= 0.25 exhibiting extremely large sample variances for the Association scenario, and variances similar to CPV alone for the Causation scenario. For ρ > 0.5, BIV and CPV + BIV have similar variance ratios. We see that for large ρ CPV is unnecessary and for small ρ BIV performs poorly. As ρ = 0.25, both CPV and BIV are helpful.
Figure 3.
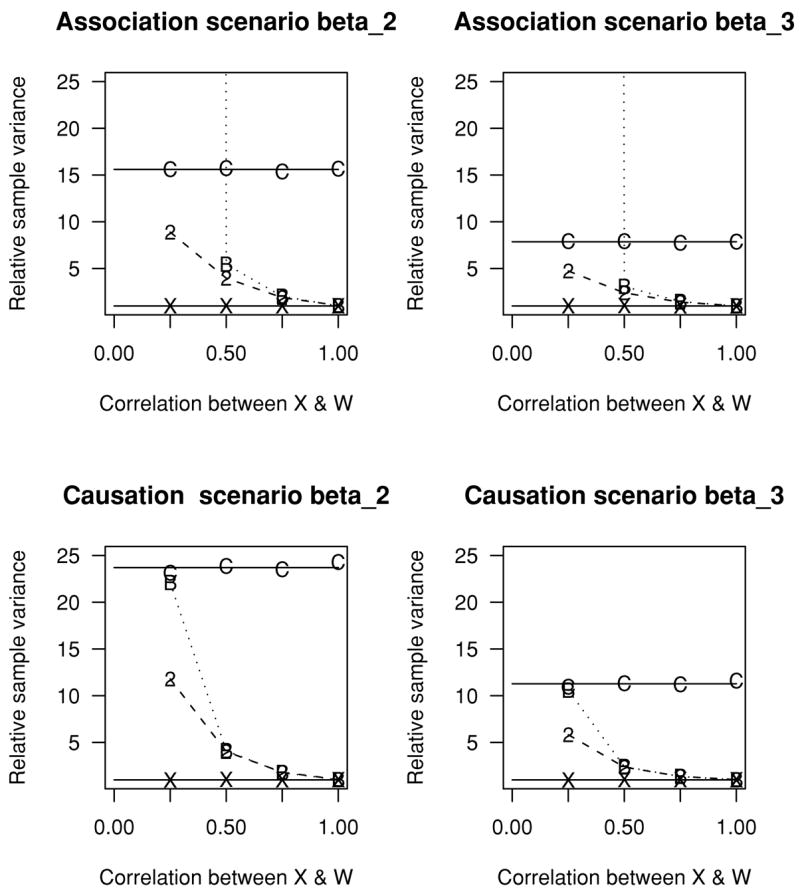
Sample variance of estimates of β divided by the sample variance when the X0(1) is used. Estimates denoted by B, C, 2, and X correspond to designs using BIV alone, CPV alone, BIV + CPV, and the impossible benchmark where X0(1) is known in everyone, respectively. For BIV alone when ρ = 0.25 the relative sample variance is enormous and off the chart for the Association scenario. One can extrapolate the behavior of the designs using CPV alone and the benchmark ρ= 0 as their behavior is free of ρ. Each symbol is based on 10,000 simulated trials.
Our second set of simulations evaluates power and is given in Table 4 with n = 1000 or 2500, ρ = 0.25 or 0.50, for the three scenarios Association, Causation, and Both. For the Wald tests, a nonparametric bootstrap standard error was calculated using the sample variance of 100 bootstrap resamples for each simulated trial. Resamples where convergence was not attained were thrown out, which was rare except for BIV alone with ρ = 0.25. As before, BIV alone with ρ = 0.25 had problems with convergence and these were exacerbated in the bootstrap resamples.
Table 4.
Simulated power for Wald and t-test of and under various augmented designs. The Wald tests for the X0 design is when the actual X0 is used in (1) and thus serves as an unattainable benchmark. The t-test compares the XCi ’s from the placebo uninfecteds to the X0i of the vaccine (vaccine uninfecteds) to test . Standard errors for Wald tests are based on a bootstrap standard error with 100 bootstrap resamples. Power exceeding 80% is bolded. Each line is based on 1000 simulated vaccine trials.
| Test of
or β2 = 0
|
Test of
or β3 = 0
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Wald tests
|
Wald tests
|
|||||||||||
| n | ρ | Scenario | t-test CPV | CPV | BIV | CPV + BIV | X0 | t-test CPV | CPV | BIV | CPV + BIV | X0 |
| 1000 | 0.25 | A | 0.34 | 0.40 | 0.01 | 0.58 | 1.0 | 0.06 | 0.04 | 0.03 | 0.04 | 0.05 |
| 0.50 | A | 0.35 | 0.40 | 0.86 | 0.91 | 1.0 | 0.06 | 0.05 | 0.03 | 0.04 | 0.05 | |
| 0.25 | C | 0.07 | 0.08 | 0.00 | 0.06 | 0.04 | 0.23 | 0.30 | 0.13 | 0.43 | 0.98 | |
| 0.50 | C | 0.06 | 0.06 | 0.04 | 0.04 | 0.05 | 0.24 | 0.30 | 0.78 | 0.78 | 0.99 | |
| 0.25 | B | 0.19 | 0.22 | 0.00 | 0.32 | 0.99 | 0.09 | 0.17 | 0.11 | 0.22 | 0.66 | |
| 0.50 | B | 0.20 | 0.23 | 0.57 | 0.64 | 0.99 | 0.08 | 0.16 | 0.35 | 0.40 | 0.71 | |
| 2500 | 0.25 | A | 0.70 | 0.74 | 0.38 | 0.91 | 1.0 | 0.07 | 0.05 | 0.03 | 0.05 | 0.05 |
| 0.50 | A | 0.68 | 0.74 | 1.0 | 0.99 | 1.0 | 0.07 | 0.05 | 0.05 | 0.06 | 0.05 | |
| 0.25 | C | 0.06 | 0.07 | 0.02 | 0.05 | 0.040 | 0.47 | 0.52 | 0.63 | 0.78 | 1.0 | |
| 0.50 | C | 0.05 | 0.07 | 0.05 | 0.06 | 0.050 | 0.48 | 0.52 | 0.99 | 0.99 | 1.0 | |
| 0.25 | B | 0.39 | 0.44 | 0.22 | 0.64 | 1.0 | 0.12 | 0.31 | 0.30 | 0.46 | 0.97 | |
| 0.50 | B | 0.43 | 0.48 | 0.95 | 0.97 | 1.0 | 0.11 | 0.28 | 0.65 | 0.71 | 0.97 | |
We begin by evaluating the Wald test. First, the benchmark has extremely high power, except for β3 under scenario B with n = 1000. For CPV + BIV, power is generally good to excellent for all scenarios with n = 2500. For n = 1000, power is degraded, especially with ρ = 0.25. For BIV alone, power is similar to CPV + BIV for ρ = 0.50 and much worse for ρ = 0.25. Generally, power for CPV alone is much worse than for BIV alone with ρ = 0.50 and moderately better with ρ = 0.25. The power of the t-tests is usually similar to CPV alone and close to at least 0.50 for scenarios A and C with n = 2500.
We also did a few limited simulations to address specific issues. In practice, one might want to perform CPV on a fraction of the placebo uninfecteds. For scenario A, we compared the estimates using CPV alone, where XC was obtained in everyone to where it was obtained in 1/2, 1/4, or 1/10 of the placebo uninfecteds. The sampling variance for either β̂2 or β̂3 was about 60%, 300%, and 1000% larger than when XC was obtained in everyone, respectively. Second, we evaluated the procedures when the moments were set to their true values and not estimated. The sampling variance for CPV alone and for BIV alone was nearly halved when true values were used instead of estimated values. For CPV + BIV, the sampling variability was only modestly reduced. For larger trials, for example, n = 8000 with low event rates, the performance of CPV and BIV relative to BIV + CPV might be better than shown in Figure 3 and Table 4 as the estimated moments of X0(1), W0 would be more reliable. It also suggests that one might want to consider use of a full likelihood. For example, for CPV alone uses
where φ(x; μ, σ2) is the normal density and f0(xiC|Yi = 0; μx, ) is the density for uninfecteds, derived under (1) and a Gaussian model for X0(1).
In summary, the new designs can be efficient and powerful even with n = 1000 if ρ > 0.5. If ρ is modest, a larger sample size is required to achieve strong power as CPV is necessary. If ρ is large enough, CPV may be unnecessary, while if ρ is too small, BIV alone may be useless. With n = 2500 we have excellent power for scenarios A and C with ρ = 0.5 using BIV alone and good to excellent power with the BIV + CPV combination with ρ = 0.25. Even with CPV alone, power is greater than 50% for these two scenarios. This configuration is not unlike VAX004 suggesting augmented designs could have helped inform the debate about these two hypotheses. It is clear that the performance of the designs depends dramatically on specific scenarios. In practice, careful analysis of performance would be required to settle on a specific augmented design.
We note that a correlation of close to 0.5 may be a realistic aspiration. In the VAX004 trial, the vaccine consisted of two strains of viral gp-120, which is a sequence of 120 amino acids that comprise the outer envelope of the virus. The two strains were denoted MN and GNE8. Two nonoverlapping regions of the envelope, prone to mutations, are called the V2 and V3 loops. The amino acid sequences for the V2 loop and the V3 loop of the gp120 are completely different and thus the immune response induced by these two different loops should behave like responses to irrelevant vaccinations. Correlations between these loops were 0.42 and 0.44, respectively, for the MN and GNE8 strains. Correlations across strains were 0.34 and 0.48 (Figure 3 of Gilbert et al., 2005).
5. Elaborations
The methods of this article can help decide whether an improved vaccine is worth evaluating in a phase III trial. Suppose that after tinkering with the old vaccine, a new version was created, which shifted the distribution of the immune response to the right by Δ. So in an obvious notation, we have X0(1)old with moments μx and , while X0(1)new has moments μx + Δ and . We assume that a person with response x under the old vaccine is infected with probability
under the new vaccine. Note that Δ is missing from β2 as only β3 reflects the causative effect of immune response. Overall, we calculate the expected event rate with the new vaccine
Based on the data from the trial of the old vaccine, one can estimate θ 0 and and then estimate the sample size required for a phase III trial of the new vaccine with improved immune response Δ. Or one might conclude that is too modest to proceed.
Closeout placebo vaccination requires time constancy of immune response. One way to examine this assumption would be to close out some fraction of the placebo uninfecteds midway through the trial, vaccinate them, and obtain their immune response, say XC/2. Equality of the distributions of XC/2 and XC supports time constancy of immune response provided the effect of X0(1) on Y does not vary with time. To formalize this, let YC/2, YC be the infection indicators over half the trial and the entire trial, respectively. If
| (6) |
then
is consistent with time constancy of immune response on an individual level. Note that if (6) does not hold, there is no point in examining .
Testing need not be very costly. Simple power calculations show that for a 8800 person trial with 90% power to detect a 10% versus 8% difference in infection rates, removing 10% of placebo uninfecteds halfway through would retain at least 88% power. Additionally, comparing XC/2 in 440 “halfway” placebo uninfecteds to XC in say the 3520 final placebo uninfecteds would give 97% power to detect a standardized difference (mean difference over standard deviation) of 0.20.
Another way to examine time constancy of immune response is to see whether the relationships between W0, X0(1) and W0, XC are the same in the two arms. But this also requires assumptions. For example, if the following probit model holds
| (7) |
then
is consistent with time constancy of immune response. Note that can be tested using data readily available from a CPV trial and does not require a partial closeout halfway through the trial.
Model (1) assumes that there is no effect of W0 on infection risk once X0(1) is in the model. One can specify generalizations to (1) that include W0 as an additional main effect, or even allow for interaction with treatment,
| (8) |
and likelihood construction for this model would parallel construction based on (1). It is perhaps surprising that even for our setting, where X0(1) is missing in the placebo group, this model with two interactions can be estimated provided CPV is performed. If CPV is not done, (8) is identifiable provided, for example, β5 = 0. With CPV one could test whether β5 and/or β3 were 0. However, such tests would likely have poor power, as trials are powered for a treatment main effect and estimating two interactions may be difficult.
In principle, W0 could be any baseline variable correlated with X0(1) and a baseline irrelevant vaccination need not be performed. Presumably, however, W0 based on BIV should have a much stronger relationship with X0(1) than a variable such as race, gender, or age. An additional issue with nonimmunologically based W0 is the perhaps greater concern that β3 and or β5 in (8) might not be zero. It is important to realize that if (8) holds with (β3, β5) ≠ (0, 0) then inference derived from fitting (the incorrect) model (1) would be misleading.
We made a simplifying assumption that there were no infections in either group until X0(1) was measured. If infections do occur over the interval [0, m] we can still obtain consistent estimates of the parameters provided we derive a likelihood under more assumptions. We illustrate one way. Consider a BIV design. Because the likelihoods in Section 2 factor L(β) = Lv(β0 + β1, β2 + β3)Lp(β0, β2) we can estimate β0, β2 using Lp ( ), given consistent estimates of θ = (μx, μz, , , ρ) (recall that Lp depends implicitly on θ). For the vaccine group, let V(m) be the set of vaccinees who become infected over the interval [0, m] and V(R) be the rest of the vaccinees. Then under assumption (6) applied over [0, m], the likelihood for the vaccine group is proportional to
where φ is the bivariate normal density function.
6. Final Comments
While this article has focused on immune response to an HIV vaccine, it is clear that the methods would apply to any vaccine trial. Chan et al. (2003) describe the role of immune response in vaccine development and point out the difficulty of establishing immune response as a surrogate for protection or disease burden as immune response is only measured in the vaccine group. The designs of this article allow one to use the principal surrogacy approach of Frangakis and Rubin (2002).
This article has focused on evaluating the effect of immune response on preventing infections. Current thinking on HIV vaccines is that they may have their major effect on post-infection outcomes, such as the viral load setpoint, the steady-state amount of virus in the bloodstream shortly after infection. The approach of this article could also be applied to post-infection endpoints, though this is necessarily more assumption dependent as the infected groups are not balanced by virtue of randomization (see Gilbert et al., 2003; Hudgens, Hoering, and Self, 2003).
The simulations show the profound dependence of these methods on ρ. Fortunately, ρ can be estimated well before closeout. However, even if ρ is large, there is some benefit in obtaining some CPV data as they provide a check of the imputation-based W0 alone. Additionally, if it turns out to be an unanticipated immune response to the HIV vaccine, say X0(1)u is strongly associated with infections and W0 is independent of X0(1)u, a BIV-alone design would have been a mistake. CPV offers protection against this possibility. Finally, a simple t-test based on CPV data alone is appealing for its simplicity and transparency. Of course, CPV requires the strong assumption of time constancy of immune response.
In practice, several vaccinations over several months may be necessary during which time infections might accrue and the immune responses might wax and wane in conjunction with the vaccinations so thought is required to choose a precise time to measure X0(1). Another approach would be to develop methods that explicitly model the time-varying nature of X0(1) and use time to infection as the outcome rather than a binary indicator of infection.
Implementation of these designs could be done in an incremental fashion. Initially, small studies could be conducted to establish the extent of correlation between W0 and X0(1), which irrelevant vaccine was most useful, and whether time constancy of immune response were plausible. If promising, an adaptive augmented phase III design could then be initiated.
Acknowledgments
I am grateful to Peter Gilbert, Jorge Flores, Michael Hudgens, Michael Fay, and an associate editor for providing helpful comments on drafts of this article.
References
- Carey VJ, Baker CJ, Platt R. Bayesian inference on protective antibody levels using case-control data. Biometrics. 2001;57:135–142. doi: 10.1111/j.0006-341x.2001.00135.x. [DOI] [PubMed] [Google Scholar]
- Chan I, Li S, Matthews H, Chan C, Vessey R, Sadoff J, Heyse J. Use of statistical models for evaluating antibody response as a correlate of protection against varicella. Statistics in Medicine. 2002;21:3411–3430. doi: 10.1002/sim.1268. [DOI] [PubMed] [Google Scholar]
- Chan I, Wang W, Heyse J. Vaccine clinical trials. In: Chow S-C, editor. Encyclopedia of Biopharmaceutical Statistics. 2. New York: Marcel Dekker; 2003. pp. 1005–1022. [Google Scholar]
- Follmann D. On the effect of treatment among treatment compliers: An analysis of the Multiple Risk Factor Intervention Trial. Journal of the American Statistical Association. 2000;95:1101–1109. [Google Scholar]
- Frangakis CE, Rubin DB. Principal stratification in causal inference. Biometrics. 2002;58:21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P, Bosch R, Hudgens M. Sensitivity analysis for the assessment of causal vaccine effects on viral load in HIV vaccine trials. Biometrics. 2003;59:531–541. doi: 10.1111/1541-0420.00063. [DOI] [PubMed] [Google Scholar]
- Gilbert P, Peterson M, Follmann D, et al. Correlation between immunologic responses to rgp120 vaccine and incidence of HIV-1 infection in a phase 3 HIV-1 preventive vaccine trial. Journal of Infectious Diseases. 2005;191:666–677. doi: 10.1086/428405. [DOI] [PubMed] [Google Scholar]
- Graham B, Mascola J. Lessons from failure—Preparing for future HIV-1 vaccine efficacy trials. Journal of Infectious Diseases. 2005;191:647–649. doi: 10.1086/428406. [DOI] [PubMed] [Google Scholar]
- Halloran ME. Vaccine studies. In: Armitage P, Colton T, editors. Encyclopedia of Biostatistics. Vol. 6. New York: Wiley; 1998. pp. 4687–4694. [Google Scholar]
- Halloran ME, Struchiner C. Causal inference in infectious diseases. Epidemiology. 1995;6:142–151. doi: 10.1097/00001648-199503000-00010. [DOI] [PubMed] [Google Scholar]
- Hallstrom AP, McAnulty JH, Wilkoff BL, Follmann D, Raitt MH, Carlson MD, Gillis AM, Shih HT, Powell JL, Duff H, Halperin BD. Patients at lower risk of arrhythmia recurrence: A subgroup in whom implantable defibrillators may not offer benefit. Journal of the American College of Cardiology. 2001;37:1093–1099. doi: 10.1016/s0735-1097(00)01208-0. [DOI] [PubMed] [Google Scholar]
- Hudgens M, Halloran ME. Technical Report 04-03. Department of Biostatistics, Emory University; Atlanta, Georgia: 2004. Causal vaccine effects on binary post-infection outcomes. [Google Scholar]
- Hudgens M, Hoering A, Self S. On the analysis of viral load endpoints in HIV vaccine trials. Statistics in Medicine. 2003;22:2281–2298. doi: 10.1002/sim.1394. [DOI] [PubMed] [Google Scholar]
- Lachenbruch PA, Horne DA, Lynch CJ, Tiwari J, Ellenberg S. Biologics. In: Chow S-C, editor. Encyclopedia of Biopharmaceutical Statistics. New York: Marcel Dekker; 2000. pp. 47–54. [Google Scholar]
- Nabel G. Challenges and opportunities for development of an HIV vaccine. Nature. 2001;410:1002–1007. doi: 10.1038/35073500. [DOI] [PubMed] [Google Scholar]
- Plikaytis B, Carlone G. Statistical considerations for vaccine immunogenicity trials. Part 2: Noninferiority and other statistical approaches to vaccine evaluation. Vaccine. 2005;23:1606–1614. doi: 10.1016/j.vaccine.2004.06.047. [DOI] [PubMed] [Google Scholar]
- Prentice RL. Surrogate endpoints in clinical trials: Definition and operational criteria. Statistics in Medicine. 1989;8:431–440. doi: 10.1002/sim.4780080407. [DOI] [PubMed] [Google Scholar]
- The rgp120 HIV Vaccine Study Group. Placebo-controlled trial of a recombinant glycoprotein 120 vaccine to prevent HIV infection. Journal of Infectious Diseases. 2005;191:654–665. doi: 10.1086/428404. [DOI] [PubMed] [Google Scholar]
- Rubin D. Estimating causal effects of treatments in randomized and nonrandomized studies. Journal of Educational Psychology. 1974;66:688–701. [Google Scholar]
- Rubin D. Assignment to a treatment group on the basis of a covariate. Journal of Educational Statistics. 1977;2:1–26. [Google Scholar]
- Rubin D. Bayesian inference for causal effects. Annals of Statistics. 1978;6:34–58. [Google Scholar]


