Changes Across Time in the Temporal Responses of Auditory Nerve Fibers Stimulated by Electric Pulse Trains

Abstract

Most auditory prostheses use modulated electric pulse trains to excite the auditory nerve. There are, however, scant data regarding the effects of pulse trains on auditory nerve fiber (ANF) responses across the duration of such stimuli. We examined how temporal ANF properties changed with level and pulse rate across 300-ms pulse trains. Four measures were examined: (1) first-spike latency, (2) interspike interval (ISI), (3) vector strength (VS), and (4) Fano factor (FF, an index of the temporal variability of responsiveness). Data were obtained using 250-, 1,000-, and 5,000-pulse/s stimuli. First-spike latency decreased with increasing spike rate, with relatively small decrements observed for 5,000-pulse/s trains, presumably reflecting integration. ISIs to low-rate (250 pulse/s) trains were strongly locked to the stimuli, whereas ISIs evoked with 5,000-pulse/s trains were dominated by refractory and adaptation effects. Across time, VS decreased for low-rate trains but not for 5,000-pulse/s stimuli. At relatively high spike rates (>200 spike/s), VS values for 5,000-pulse/s trains were lower than those obtained with 250-pulse/s stimuli (even after accounting for the smaller periods of the 5,000-pulse/s stimuli), indicating a desynchronizing effect of high-rate stimuli. FF measures also indicated a desynchronizing effect of high-rate trains. Across a wide range of response rates, FF underwent relatively fast increases (i.e., within 100 ms) for 5,000-pulse/s stimuli. With a few exceptions, ISI, VS, and FF measures approached asymptotic values within the 300-ms duration of the low- and high-rate trains. These findings may have implications for designs of cochlear implant stimulus protocols, understanding electrically evoked compound action potentials, and interpretation of neural measures obtained at central nuclei, which depend on understanding the output of the auditory nerve.

INTRODUCTION

There are three primary stimulus dimensions that govern how cochlear implants transfer information to auditory nerve fibers (ANFs):

Stimulus level

By modulating level, the population of excited fibers is altered and the firing and stochastic characteristics of that population are also changed.

Place of stimulation

Through the use of multiple-electrode arrays, implants can excite different fiber subpopulations and exploit, to some extent, the cochleotopic arrangement of ANFs.

Temporal pattern of stimulation

As most cochlear implants encode stimuli as trains of modulated electric pulses, both the pulse (carrier) rate and modulation rate are important determinants of the spike codes. It has long been known that the degree of within- and across-fiber synchrony elicited by electric stimuli is much greater than that caused by acoustic stimulation (Kiang et al. 1965). This loss of “randomness” in the responses of deaf and electrically stimulated ANFs has led to the investigation of the use of high-rate (e.g., 5,000 pulse/s) trains to improve temporal uncertainty (e.g., Rubinstein et al. 1999). In a systematic study of feline ANFs, Litvak et al. (2001) demonstrated that such electric pulse trains produced responses that were desynchronized relative to those evoked by lower-rate trains.

This study builds on the work of Litvak et al. (2001), focusing on the temporal response patterns of ANFs stimulated by relatively low- (250 pulse/s) to high-rate (5,000 pulse/s) electric pulse trains. It goes beyond that work by examining how temporal response properties change over the course of 300-ms-long pulse trains. In this way, we address the important topic of how response changes may affect the temporal representation of electric stimuli of durations similar to those of speech tokens. This area of inquiry may be relevant to the design of future speech processors. For example, there are two competing versions of speech processors that employ relatively high-rate (i.e., >1,000 pulse/s) pulse trains. One modulates the carrier with the envelope of incoming sound, while the other constantly presents a steady carrier, to which a modulated pulse train (of the same rate and phase) is added (see Wilson 2004 for a discussion of stimulation strategies). It could be argued that the latter is more appropriate in that the “quiescent” high-rate train maintains excitable fibers in adapted states, whereas the former transiently presents high-rate pulses and, thus, may repeatedly drive fibers “in” and “out” of adapted states. However, the output of either type of processor will tend to transiently excite fiber subpopulations due to the fact that activation of any stimulus electrode results in a spread of excitation to populations of fibers that have a distribution of thresholds. Thus, the response of ANFs to gated pulse trains is relevant to understanding the nerve’s response to modulated pulse trains used by auditory prostheses.

We measured four ANF temporal response properties. First spike latency characterized the mean time between stimulus onset and the occurrence of the first action potential. Vector strength (VS, Goldberg and Brown 1969) was used to assess temporal uncertainty relative to the stimulus pulses and, thus, the degree of “stochasticity” of ANF responses. The statistics of interspike intervals (ISIs) were examined to assess the degree of temporal regularity in the responses. Fano factor (FF, Teich and Khanna 1985), a measure of the variability in the number of nerve-fiber responses across repeated stimulus presentations, was used to determine the degree to which fibers responded like a random (Poisson) process. We would expect that measures dependent on spike rate (i.e., ISIs and VS) would undergo changes over the course of ongoing pulse-train stimuli. The nature of such changes is the subject of this paper.

METHODS

Subject preparation

Eight adult cats free of middle ear infections were used as acute (nonsurvival) subjects. These animals were also used in a study of spike-rate adaptation (Zhang et al. 2007). The auditory nerve was accessed through a posterior fossa approach (Kiang et al. 1965), and seven of eight cats were chemically deafened immediately prior to data collection to eliminate spontaneous or electrophonically induced activity. Click-evoked compound action potentials were used to assess the hearing status of the cats prior to and after deafening with cochlear perfusion of neomycin sulfate. Chemical deafening was not performed in one cat (which provided data from three fibers) due to a measured 70-dB loss in auditory brainstem response sensitivity during the experiment prior to ANF recordings. That loss was accompanied by an absence of acoustic-evoked and electrophonic responses, as well as spontaneous activity, from the three fibers. Throughout each experiment, the animal was kept at surgical levels of anesthesia, while vital signs (noninvasive oxygen saturation, heart rate, expired CO₂, and core temperature) were monitored to assist with anesthetic maintenance. All animal procedures were approved by the University of Iowa Animal Care and Use Committee and complied with NIH standards. Additional methodological details are provided in Zhang et al. (2007).

Stimuli

An eight-band Nucleus electrode array (Cochlear, Lane Cove, Australia) was inserted in an apical direction through a cochleostomy into the scala tympani to depths between 5 and 6 mm. The most apical band was used to present monopolar stimuli, with the return current path provided by a needle electrode positioned in muscle. Stimuli were controlled by Labview programs written in-house, which drove an Instrutech ITC-18 data acquisition board with 16-bit resolution and 100,000 sample/s output rate. This, in turn, drove an optically isolated, capacitively coupled, current source. Search stimuli consisted of single, 40-μs/phase biphasic pulses (cathodic leading phase) presented at 30 pulse/s. This stimulus was also used for recording electrically evoked compound action potentials (ECAPs) to assess nerve sensitivity and determine the search level (defined as the level that evoked ECAP amplitudes approximately 90% of maximum). Experimental stimuli consisted of pulse trains of 300 ms in duration. Stimulus pulse rates of 250, 1,000, and 5,000 pulse/s were used to span those used by cochlear prostheses. To obtain ANF firing statistics, trains were presented repeatedly with 900-ms intertrain intervals for a total of 30 to 100 presentations, depending upon the evoked firing efficiency. Whenever possible, ANFs were presented with trains of all rates and at several levels. As fiber-contact time permitted, levels were chosen to span a range that resulted in a low (20–40%) firing probability to the first pulse to one that produced a maximal (saturated) response rate over the final 100-ms epoch of the stimulus train.

Recording conditions

ECAPs were recorded prior to ANF data collection and at later intervals to assess nerve sensitivity using electrodes placed on the nerve trunk. Micropipettes pulled from 0.58 mm ID/1.0 mm OD glass (A-M Systems) and filled with 3 M KCl were used to record spike activity. Potentials were amplified (10×) and filtered (first-order 10 kHz low pass) by an Axon Instruments Axoprobe amplifier. Additional filtering was provided by a 100-Hz, two-pole Butterworth high-pass filter and by a 30-kHz six-pole Butterworth low-pass filter. Power-line induced artifacts were reduced using a HumBug noise-template subtraction circuit (Quest Scientific Instruments, North Vancouver, Canada). All ECAP and spike waveforms were sampled at a rate of 100,000 sample/s with 16-bit resolution by the aforementioned Instrutech board and saved to mass storage for later spike picking and analyses.

Data analysis

Spike analyses were conducted using custom Matlab programs (Natick, MA, USA; version 6.5). Stimulus artifact reduction was performed by a subthreshold “template subtraction” method (Miller et al. 1999) for the responses collected using a pulse rate of 1,000 pulse/s or lower. For highest pulse rates, a “box-car” finite impulse response filter was used (Litvak 2002). Details of these two procedures, including examples of the before-and-after results, are shown in Zhang et al. (2007). Our spike-picking software required human review of automatically picked peaks to reduce reporting false spikes due to atypically large noise spikes or stimulus artifacts. While time-consuming, this provided us with a higher level of confidence in our data. In a small minority of cases, response waveforms evoked by 5,000-pulse/s trains required two stages of artifact reduction. Specifically, in cases where a large ECAP was recorded at the train onset, the template method was applied after the box-car filter was used.

To quantify temporal properties across the pulse-train duration, ANF responses were analyzed in several temporal windows defined by the stimulus onset. These windows were 0–12, 12–24, 24–48, 48–100, 100–200, and 200–300 ms after train onset. Empirically, the 12-ms window width for the first two analysis windows was found to be the shortest that would typically yield stable rate estimates for all pulse rates studied. The first window (0–12 ms) was used to characterize what we termed “onset” spike rate, computed by counting all spikes that occurred within that window (across all repeated train presentations) and dividing by the total time of those repeated windows. ISIs were computed for each of the aforementioned analysis windows. To avoid biasing ISI statistics toward low values, ISIs for each analysis window were computed for spike pairs that fell within each window, as well as the last spike within each window and the subsequent spike. Either the 100–200- or the 200–300-ms window was used to assess what we termed the “steady state” response. In data plots, these epochs are specified by their linear midpoints. In certain situations, additional analysis epochs were used, as noted in the text. For graphically displaying interval histograms (IHs), bin widths of 50 μs were used. In computing spike timing statistics (latency, VS, etc.), the resolution of our digital sampling (i.e., 10 μs) was used. In this paper, most analyses of stimulus-rate effects were conducted by comparing responses evoked by 250- and 5,000-pulse/s stimuli. In characterizing group (across-fiber) trends, median values were typically used so that group measures were not unduly influenced by outliers.

RESULTS

ISIs and example waveforms

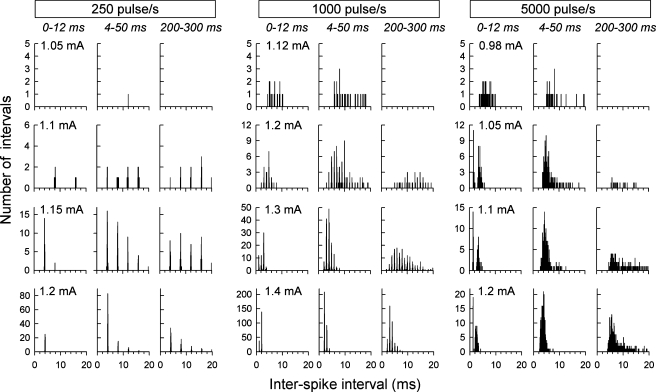
Analyses were performed on data from 88 fibers of eight cats. None of the ANFs exhibited spontaneous activity or electrophonic responses. Figure 1 shows example IHs obtained from one fiber in response to 250-, 1,000-, and 5,000-pulse/s trains (left, middle, and right columns, respectively). Within each row, IHs are shown for three different analysis time windows, as labeled above the top row. Within each column, IHs are shown for different stimulus levels. For all three pulse rates, the centroids of the IHs tended toward shorter intervals with increasing level, consistent with level-dependent increases in ANF excitation that allows refractoriness to be overcome. In the case of 5,000-pulse/s stimulation, a pattern is seen in the onset (0–12 ms) epoch in which spike intervals are distributed around two sharp peaks, with the first peak having very low temporal variance. This pattern is unique in that it is not predicted from the stimulus characteristics per se but is likely determined by refractory properties. In the examples shown here, the shorter-interval peak has modes ranging from about 1 to 2 ms and arose from spike pairs that occurred within the 0–4-ms epoch. Two-peaked IHs were observed in 24 of 88 fibers of three cats for 5,000-pulse/s stimuli but were not observed in response to lower-rate stimuli. This response pattern is thus different from the relatively rare double peaking reported in Miller et al. (1999) in response to single-pulse stimuli, which was hypothesized to be due to excitation of two neural membrane sites.

FIG. 1.

Examples IHs obtained from one ANF stimulated at three pulse rates (columns) and four levels (rows). In each of the three columns and for each level, three IHs are shown, corresponding to three temporal analysis windows (as labeled near the top of each column in italic print). Stimulus levels are indicated at the top left of each of the 12 panels. Comparisons across IHs for the three analysis windows reveal effects of adaptation that occur across the duration of each pulse train. Unique, two-peaked IHs can be seen for the three higher-level IHs produced by the 5,000-pulse/s stimuli over the “onset” (0–12 ms) response epoch. In all cases, bin width was 50 μs.

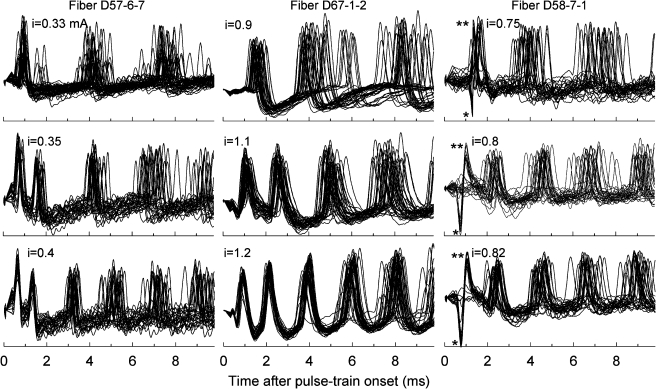
Figure 2 presents examples of spikes evoked by 5,000-pulse/s trains for three fibers of three cats. All waveforms were processed by “box-car” filtering to remove the high-rate stimulus artifacts. In each case, responses are shown for three stimulus levels and 30 repeated pulse-train presentations. As was seen in Figure 1, the intervals between successive volleys of spikes became smaller as level was increased. Responses shown in the left column have two distinctly different sets of ISIs among the first three spikes of each response, characteristic of the aforementioned two-peaked IHs. For the responses of the middle column, intervals vary in a somewhat different manner, with a more gradual increase in ISI over time. The spikes of the lowest panel of that series clearly demonstrate increasing temporal dispersion within each volley of spikes. This increased temporal variation should not be considered due simply to increased jitter, as it likely also represents greater uncertainty as to the specific pulse that resulted in spike initiation. This point is reinforced by the fact that spikes to high-rate trains can exhibit significant phase locking, as will be shown below. The right column of Figure 2 includes examples of “worst-case” spike waveforms of marginal, yet useful, quality. These waveforms suffered contamination by poorly cancelled stimulus-onset artifacts that affected the morphology of the earliest spikes. The probabilistic nature of those early spike events enabled us to confirm that these were, most likely, neural in origin.

FIG. 2.

Examples of spikes evoked by 5,000-pulse/s trains from three fibers of three cats. Superimposed responses to the first 10 ms of repeated pulse trains are shown. In the spikes shown in the left column, two distinctly different ISIs are evident in response to the two highest stimulus levels, consistent with a two-peaked IH. Spikes from a second fiber (middle column) demonstrate somewhat different timing, with smaller differences between the first and second ISIs. That fiber also demonstrates a cumulative effect of increasing temporal variation within successive volleys of spikes. That pattern should not be interpreted simply as increased “jitter” but also as greater uncertainty in the stimulus pulse number that causes spike initiation. In the case of fiber D58-7-1 (right column), two-stage artifact reduction (box-car filtering followed by template subtraction) was required to reduce the impact of a relatively large ECAP potential that occurred across the first 1.5 ms of each trace. The ECAP subtraction resulted in distorted first spikes; specifically, those spikes had a large preceding negative peak (single asterisk) and a narrowed action potential (double asterisks). In this case of poor artifact subtraction, the occurrence of spike failures (i.e., relatively flat lines over the 0–1.5-ms epoch) reinforce the fact that the distorted spikes are, indeed, action potentials.

First-spike latency

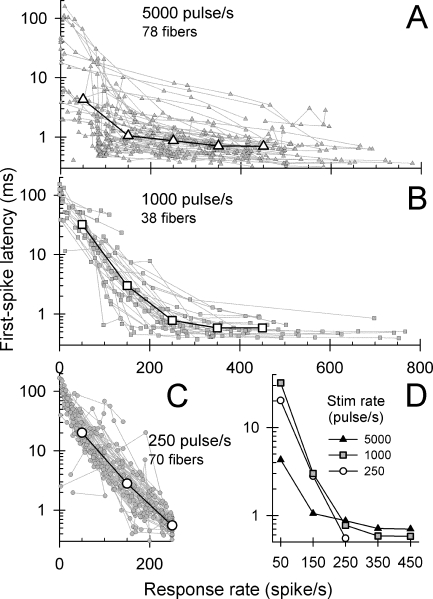
The latency of the first spike in response to a pulse train was examined as a function of overall spike rate for all ANFs and pulse rates. “Mean first-spike latency” was computed for each fiber and stimulus condition by averaging the latencies of the first spike to repeated pulse-train presentations. With respect to the familiar dot-raster plot, this measure is obtained by averaging the latencies of the first dot in each row of the plot in which a response occurred. For inclusion in this group analysis, each fiber contributed data at a minimum of three stimulus levels. To facilitate across-fiber comparisons, the latencies are plotted as a function of overall spike rate (i.e., the rate computed across the 300-ms response epoch) for 5,000-, 1,000-, and 250-pulse/s stimuli in Figure 3A, B, and C, respectively. Data from individual ANFs are plotted in these three graphs (plots with smaller gray symbols), along with across-ANF median values computed within spike-rate windows that are typically 100-spike/s wide (plots with larger white symbols). Note that there is greater across-fiber variation in latencies for the 5,000-pulse/s responses than is evident in the 250-pulse/s responses (Fig. 3A versus Fig. 3C). While the latency functions of a small proportion of fibers have sharply sloped functions for high-rate stimulation, overall, the high-rate functions are flatter than those obtained at the two lower pulse rates.

FIG. 3.

The effect of pulse rate and response rate on first-spike latency. Mean first-spike latencies from individual ANFs are plotted using gray symbols and dotted lines, whereas across-fiber median values are plotted using larger, open symbols and solid lines. Response rates were computed by averaging spike activity across the entire 300-ms duration of the pulse-train stimuli (A 5,000-pulse/s, B 1,000-pulse/s, and C 250-pulse/s stimuli). The median values were computed using analysis windows centered at 50, 150, 250, 350, and 450 spike/s. The median data of A, B, and C, are replotted together in D to facilitate comparison of pulse-rate effects.

To visualize general stimulus-rate effects, the across-ANF medians are replotted for the three pulse rates in Figure 3D. Over the range of response rates from 20 to 250 spike/s, across-fiber latency trends for the 250 and 1,000-pulse/s stimuli are similar. The group latency plot for the 5,000-pulse/s trains differs from the lower-rate plots in two ways. First, for response rates of 150 spike/s and less, the first-spike latencies are shorter than those evoked for the lower pulse rates. This suggests that, for low response rates, ANF excitability is improved with the use of high pulse rates, consistent with a current-integration mechanism (Dynes 1996; Cartee et al. 2000). At higher spike rates, however, the first-spike latencies in response to 5,000-pulse/s stimuli are greater than those for the two lower pulse rates. This result may seem somewhat counterintuitive. If latency is assumed to be an indicator of excitability, it is perhaps surprising that the addition of energy (i.e., use of higher pulse rates) results in an increase in the first-spike latency.

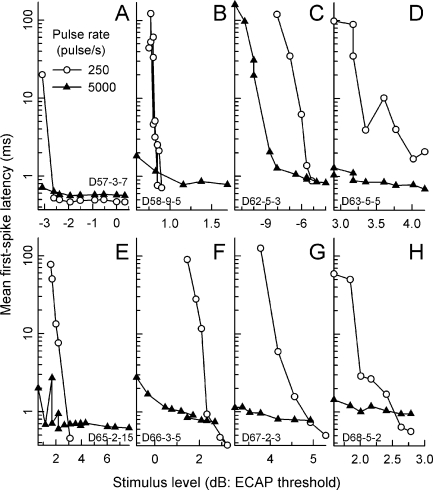
The longer asymptotic latencies for high-rate stimuli may reflect a level effect not captured in the plots of Figure 3. It is possible that low levels can elicit spikes with 5,000-pulse/s stimuli but are subthreshold for low-rate pulses. The influence of level is addressed in Figure 4 by plotting mean first-spike latencies vs. level for 250- and 5,000-pulse/s stimuli for individual ANFs. The eight fibers of this figure were chosen to provide data from as many cats and on the basis that each ANF yielded data from a relatively large number of stimulus levels. While the 250- and 5,000-pulse/s functions typically share overlapping regions of stimulus level, responses to the high-rate train were obtained at lower levels in five of the eight cases (panels B, C, E, F, and G). Also, at relatively low levels, the mean first-spike latency for 5,000-pulse/s stimuli was less than that measured for low-rate pulses for all eight fibers. These trends are consistent with an integrative mechanism that is more effective at high pulse rates. However, at higher stimulus levels, in six of eight cases (panels A, B, E, F, G, and H), the two functions cross, consistent with group trends (i.e., Fig. 3D). Thus, the data suggest that, as level is increased, the “efficiency” of high-rate stimuli can decrease relative to that of low-rate (or single) pulses. It is important to note that this study did not attempt to drive ANFs to their highest spike rates. Thus, the relationship between the latency plots for the two pulse rates may be different at higher stimulus levels.

FIG. 4.

Further examination of mean first-spike latencies. In contrast to the data of Figure 3, mean first-spike latencies from eight representative ANFs (from eight cats) are plotted vs. stimulus level (A–H). Data obtained with low-rate (250 pulse/s) stimuli are plotted using open circles, whereas data obtained using 5,000-pulse/s trains are plotted using filled triangles. Stimulus level is expressed in decibels relative to each subject’s ECAP threshold level. The scaling of each ordinate axis is identical.

Changes over time: group trends

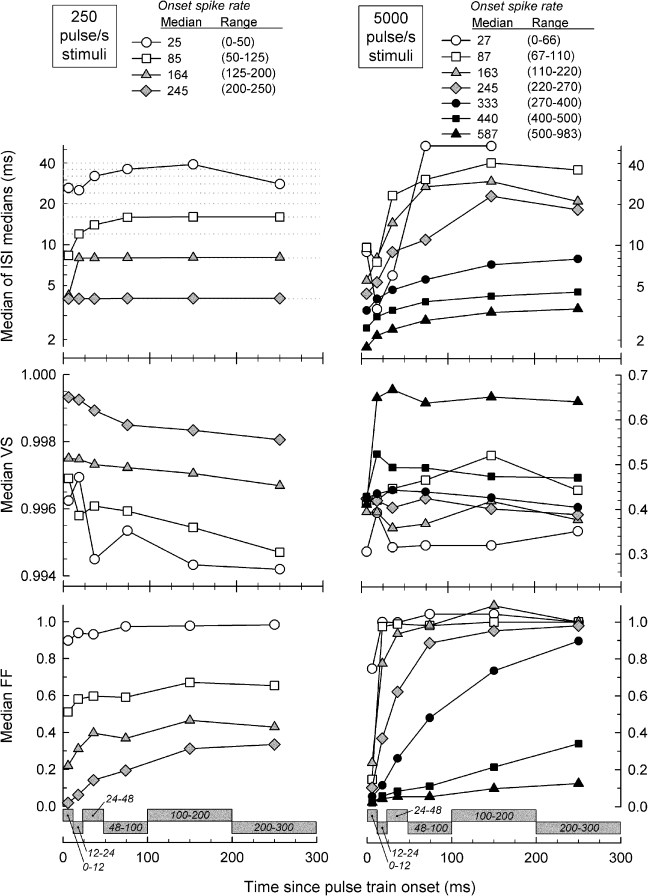
To characterize ANF response trends across time, ANF data were pooled and grouped into several ranges of onset spike rates to also account for level effects. Group median ISI, VS, and FF values are plotted vs. time after pulse-train onset in Figure 5, with onset spike rate as the parameter. Temporal functions obtained with 250-pulse/s stimuli are plotted in the left column and data obtained with 5,000-pulse/s stimuli are plotted in the right column. Note that data were parsed into groups so that the individual plots cover median onset spike rates that are similar for both stimulus rates. Thus, comparisons can be made across stimulus rate by matching the symbol types across each of the three rows of Figure 5.

FIG. 5.

Summary plots demonstrating how ISI, VS, and FF vary over the duration of the 300-ms stimuli for low, 250-pulses/s stimuli (left panels) and high, 5,000-pulse/s stimuli (right panels). The several plots within each panel demonstrate response-rate effects. Data from all fibers were grouped according to “onset spike rate” (computed over the first 12-ms epoch) to facilitate across-ANF comparison of spike-rate effects. The spike-rate ranges were chosen so that the median values of each plot were similar for the low- and high-rate responses (e.g., plots with the same symbol type can be compared across the pulse rates). All plots report median values computed across fibers. The temporal analysis windows are shown, using gray rectangles, along the bottom abscissae. Note that different ordinate scales are used to plot the VS data for the two pulse rates. The dotted lines in the upper left panel indicate integer multiples of the stimulus period.

For both pulse rates, median ISIs were affected by stimulus level and time after train onset. Level (i.e., spike rate) effects were observed at both stimulus rates, and their magnitudes were greater than the temporal effects. Increases in stimulus level resulted in decreased spike intervals, presumably due to the increased membrane excitation provided by higher current levels. For 250-pulse/s stimuli, median ISIs (upper left panel) follow integer multiples of the stimulus period for all but the lowest response rate category. These functions generally increase across time, with the exception that median ISIs at the highest response-rate category were constant at the reciprocal of the pulse rate. In some instances, the median ISI “jumped” to a higher integer number of pulse periods over time. The strong locking of spike intervals to integer numbers of low-rate pulse periods is consistent with the very high VS reported for these fibers.

ISI trends for the high-rate pulses differ from the low-rate trends. While the magnitude of the level effect is similar to that observed for low-rate stimuli, the temporal pattern contrasts with the low-rate pattern in that ISIs increased over time along relatively smooth contours that trend toward asymptotic values. With high-rate stimulation, the interpulse period (0.2 ms) is shorter than the absolute refractory period of feline ANFs (Miller et al. 2001). Thus, the refractory property is expected to have a more dominant effect than in the case of low-rate stimulation. We assume that, for a fixed stimulus level, the shape of an ISI-vs.-time plot is largely governed by the combined effects of refractoriness, which strongly affects the maximum spike rate, and adaptation, which acts cumulatively to reduce spike rate across the stimulus duration.

Median VS plots are shown in the middle panels of Figure 5. For 250-pulse/s stimuli, median VS values are high, with all values greater than 0.994 (middle left panel). Small VS decreases are observed across time, whereas decreases in onset spike rate result in relatively larger VS decreases. Changes in VS over time for the low-rate trains typically do not reach asymptotic values over the 300-ms epoch. In comparison to the low pulse-rate data, VS for 5,000-pulse/s stimuli (middle right panel) is much more variable across response rates and time. Across the seven plots covering different onset spike rates, no simple dependence of VS on spike rate is evident. For the plots covering low- to mid-onset spike rates, the changes in VS across time are relatively small and are not consistent. In contrast, the two plots covering the highest onset spike rates (i.e., >400 spike/s) undergo sharp increases within the first 24 ms of the response and then remain relatively constant, with VS values greater than almost all values obtained at lower onset rates. Systematic increases in VS with onset response rate are evident only across the plots covering the three highest rates. We speculate that the initially low VS values at these high spike rates are due to refractory-driven spike intervals. For the plots covering the five lowest onset rates, VS plots are roughly flat across time and asymptotic values cluster between 0.35 and 0.45.

While the responses to both pulse rates indicate that median FF increased over time and with decreases in the onset spike rate (bottom panels, Fig. 5), there were significant differences in the functions across the two stimulus rates. For 250-pulse/s stimuli, median FF values undergo relatively small increases across time for all four onset-rate ranges plotted, with most of the increases complete by 150 ms after pulse-train onset (bottom left panel). The asymptotic FF value for the lowest onset rate plot approached 1.0, whereas, for the highest onset rate, the asymptotic value was about 0.35. Larger FF changes were observed over time and across response rates for spikes evoked by 5,000-pulse/s stimuli (bottom right panel). In four of the six plots for 5,000-pulse/s stimuli, FF increased over time from initial values below 0.2 to final values of 0.9 or greater. However, at the two highest onset rates plotted, temporal changes in FF are relatively slow and incomplete by the end of the 300-ms stimulus.

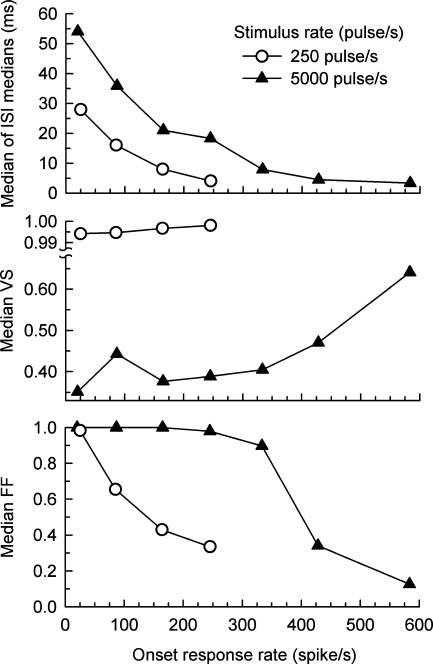
The effect of spike rate on the “steady state” measures of Figure 5 (i.e., data obtained for the 200–300-ms time window) are shown in Figure 6, which plots the group median values of ISI, VS, and FF as functions of onset spike rate for both pulse rates. The larger ISIs produced by the high-rate pulse train for a given onset rate (top panel) are consistent with a greater level of rate adaptation observed with high-rate stimulation (Zhang et al. 2007). The increasing trend of VS at higher spike rates is obvious in the 5,000-pulse/s plot of the middle panel. Comparisons of VS values across the two pulse rates are problematic due to the change in pulse period; this issue is addressed in a later analysis. Finally, unlike the responses obtained with 250-pulse/s stimuli, the high-rate FFs are high (between 0.9 and 1) for onset rates up to about 300 spike/s, consistent with a random, Poisson-like, process over a wide range of onset spike rates.

FIG. 6.

“Steady state” values ISI, VS, and FF plotted as a function of onset spike rate. Data for low-rate (250 pulse/s) and high-rate (5,000 pulse/s) pulse trains are plotted using open circles and filled triangles, respectively. Group (across-fiber) values of each measure were computed for spike activity occurring within the final (200–300 ms) response epoch. “Onset spike rate” was computed over the initial (0–12 ms) response epoch. These data were derived from the plots of Figure 5 to more clearly demonstrate the effects of response rate on the measures assessed in the final response epoch.

Effect of spike rate on ISI modes produced by high-rate pulses

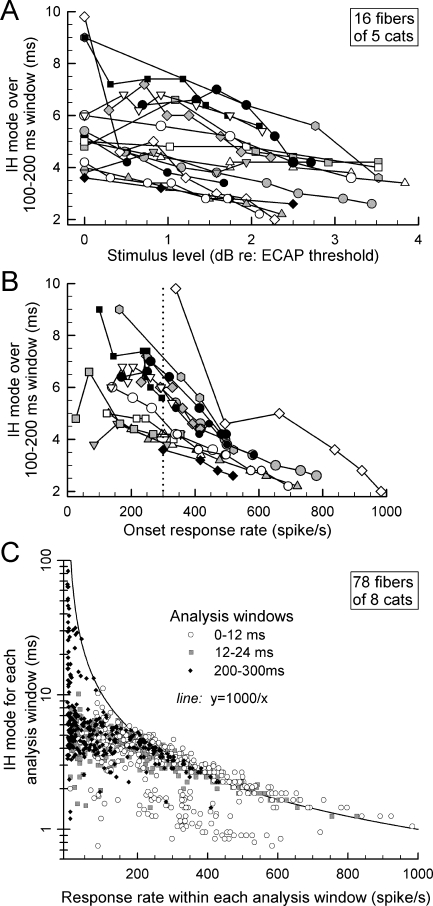
One question of interest is whether or not all ANFs produce comparable ISIs under similar stimulus (or response) conditions. To address this, 16 ANFs from five cats were chosen using the criterion that each yielded responses to 5,000-pulse/s stimuli over relatively wide ranges of level (i.e., typically 2 dB or greater). As our null hypothesis is that no ISI changes would be observed across ANFs, the mode of the IH was chosen as the metric to test the hypothesis as, relative to mean or median ISI, the mode is less sensitive to changes in the ISI distribution. IH modes were computed over the 100–200-ms response window, the epoch that provided sufficient spikes for stable ISI statistics across fibers while sampling a window beyond the largest changes due to rate adaptation. Figure 7A plots IH modes of the 16 fibers vs. stimulus level, normalized to each cat’s ECAP threshold. Figure 7B plots the same data vs. onset spike rate. These plots indicate consistent variations in IH mode across ANFs, suggesting that there are across-fiber differences in refractory and/or adaptation properties in the ANF population. We did not find a statistically significant correlation between each fiber’s IH mode (measured at a 300-spike/s onset rate, dotted line in panel B) and its degree of adaptation, as defined in our study of rate adaptation (Zhang et al. 2007).

FIG. 7.

The effects of stimulus level and response rate on ISIs for ANF excited by 5,000-pulse/s trains. The effect of stimulus level on IH mode for 16 ANFs is plotted in A, whereas the effect of onset spike rate on IH mode for the same fibers is plotted in B. Systematic differences in IH mode can be seen across this group of fibers. In C are plotted IH modes for 78 ANFs as a function of response rate. Three sets of data are included in this graph, covering three response epochs. IH mode vs. spike rate are plotted for (1) the onset (0–12 ms) window, (2) the subsequent 12–24-ms window, and (3) the final (200–300 ms) response window. The hyperbola indicates the IH mode expected for ANFs firing at a constant rate. For response rates >200 spike/s, most data cluster near the hyperbola, with the exception of a subset of responses assessed over the onset (0–12 ms) epoch.

A second analysis, performed across all ANFs, shows how the IH mode in each of three selected response epochs (0–12, 12–24, and 200–300 ms) varied with the mean spike rate measured in each epoch (Fig. 7C). The hyperbolic curve indicates how IH mode would vary if spikes fired at a constant rate across each analysis epoch. Three trends are worth noting. First, for relatively low spike rates (i.e., <150 spike/s), the modes are almost always smaller than the hyperbolic prediction. This trend holds across the three response epochs. Second, for higher (>200 spike/s) response rates, the intervals generally follow the hyperbolic relationship for the two later analysis windows. Third, for the onset (0–12 ms) epoch and higher (>200 spike/s) response rates, the modes are clustered into two groups, one following the hyperbola and another ranging over intervals from about 1 to 2 ms. This latter group reflects the relatively short ISIs observed in some fibers that likely correspond to “double spiking” associated with responses dominated by the refractory property.

Stochastic response measures

Vector strength

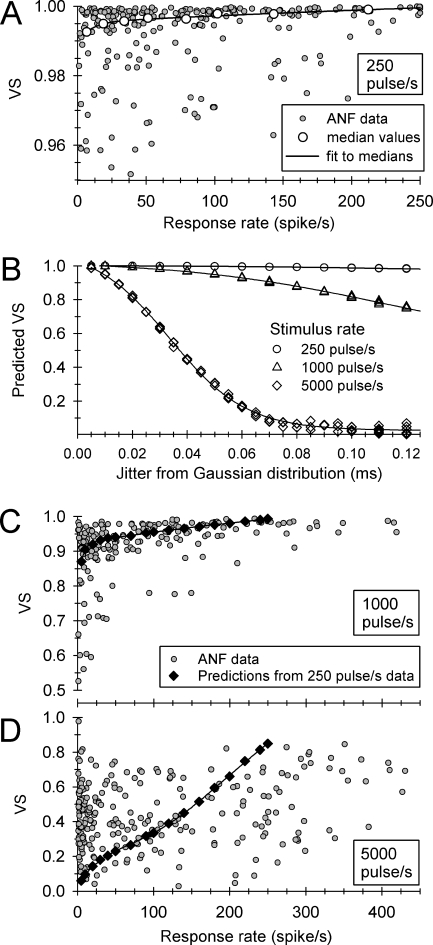
Also of interest is the degree to which high-rate stimuli increase temporal-response uncertainty (Rubinstein et al. 1999; Litvak et al. 2001). Comparisons of jitter across stimulus rates are problematic, as the magnitude of jitter can be greater than the interpulse period for stimulus rates greater than 1,000 pulse/s (Miller et al. 1999), rendering the assignment of a spike to a particular pulse difficult. Furthermore, for a fixed value of jitter, VS will decrease as the analysis window (stimulus period) is reduced, as will occur when pulse rate is increased. Thus, we sought a means of comparing VS across pulse rates to test the hypothesis that, relative to low-rate stimuli, high-rate trains desynchronize spike timing. This effort is summarized in the plots of Figure 8.

FIG. 8.

Summary of a method used to compare VS values obtained at three pulse rates. The small, filled symbols of A, C, and D show VS values obtained from 37 ANFs at stimulus rates of 250, 1,000, and 5,000 pulse/s, respectively. Across-pulse-rate VS comparisons require accounting for the effect of different pulse periods on VS. This effect is shown in B, where simulated distributions of spike times were used to relate VS and jitter for the three pulse rates. Multiple symbols for fixed jitter and pulse rate reflect multiple simulations; smooth curves connect these points. These curves provided a means of predicting VS (for 1,000- and 5,000-pulse/s rates) under the assumption that an ANF’s jitter is not affected by stimulus rate. The predicted (constant jitter) VS values are plotted in C and D using filled diamond symbols. In the case of 5,000-pulse/s stimuli, all experimental data lie below the prediction curve for response rates greater than 200 spike/s, indicating spike desynchronization.

Figure 8A, C, and D plot VS values for ANFs stimulated at 250, 1,000, and 5,000 pulse/s, respectively (small, grayed circles). The plots are based on data from 37 ANFs that provided VS measures at all three pulse rates. To characterize “steady-state” responses, all data were based on spikes within the 200–300-ms epoch. The VS data obtained at the 250-pulse/s rate provided baseline measures for the across-rate comparisons. In Figure 8A, the larger, unfilled circles indicate median values assessed across eight contiguous windows of spike rate, along with a smooth curve fit to those medians. That curve, based on a double-exponential model, provided the means of specifying VS at any spike rate. To compare VS across pulse rates, we predicted VS values for all three pulse periods (e.g, 4, 1, and 0.2 ms) by generating 1,000 spike times from Gaussian distributions, with the standard deviation of those distributions equal to the ANF jitter measured with 250-pulse/s stimuli. Figure 8B plots the predicted VS values for the three pulse rates across a range of jitter values typical for low-rate stimuli (Miller et al. 1999). Equivalent VS values for a given jitter value (across the three pulse rates) can be read by intersecting a vertical line with the plots, providing a means of testing the hypothesis.

The predicted VS values for 1,000 and 5,000-pulse/s stimuli (based on the 250-pulse/s VS data) are plotted in Figure 8C, D using diamond symbols and smooth curves. For 5,000-pulse/s stimuli, note that all ANF data fall below the predicted VS curve for response rates of 200 spike/s or greater, indicating that this high-rate stimulus results in spike desynchronization. With respect to the 1,000-pulse/s data, the observed VS values (for response rates >200 spike/s) were closer to the prediction line. Finally, we note that the large scatter evident in the VS data for 5,000-pulse/s stimulation may be due, in part, to the lower phase resolution at that high pulse rate.

Fano factor

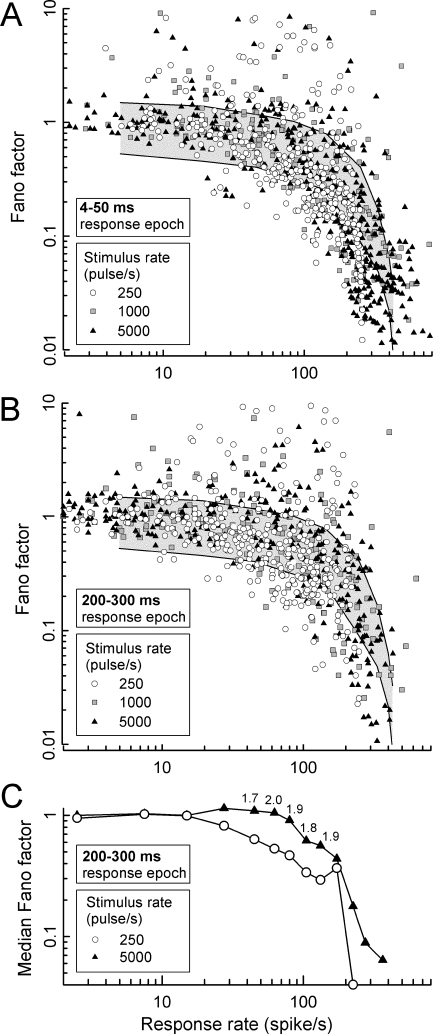
Fano factor (FF), the normalized variance (i.e., σ²/μ) in the number of spikes produced across repeated train presentations, has been used to assess the degree of randomness in ANF responses (Teich and Khanna 1985; Litvak et al. 2001). We examined FF across pulse rates (250, 1,000, and 5,000 pulse/s) for responses within the “steady state” (200–300 ms) epoch. We also measured FFs over an early (4–50 ms) epoch to provide a comparison condition for the assessment of time effects. FF values for the early epoch and three pulse rates are plotted vs. spike rate in Figure 9A, whereas “steady state” FF values for the three rates are shown in Figure 9B. The gray regions indicate 99% of the expected range of FFs produced by a model based on a Poisson process with a 2-ms dead time. As in Litvak et al. (2001), the 2-ms dead time value was chosen to provide a rough approximation of the range of spike delays due to refractoriness (Miller et al. 2001). As might be expected with rate adaptation (Zhang et al. 2007), the high-rate data for the early (4–50 ms) analysis window appear to be skewed to somewhat high spike rates relative to the late-epoch data of panel B. Consistent with the report of Litvak et al. (2001), experimental FFs largely fell within the modeled Poisson process for low-to-moderate response rates. However, deviation of the FF trend across spike rates from the Poisson model is evident at response rates greater than about 30–40 spikes/s.

FIG. 9.

Summary of the effects of (1) response rate, (2) stimulus rate, and (3) time after stimulus onset on FF. In A and B, FFs for all ANFs are plotted vs. response rate. The gray background regions in these graphs indicate the expected region (within 99% of cases) of FFs for a Poisson process with a 2-ms dead time (i.e., a refractory-driven process). In A, FFs computed over an early response epoch (4–50 ms) are plotted for each fiber and the three stimulus rates. In B, FFs are plotted for spikes occurring in the “steady state” (200–300 ms) response epoch. In C, median FFs – computed across fibers and several ranges of response rates – are plotted for 250- and 5,000-pulse/s stimuli, again computed over the “steady state” (200–300 ms) response epoch. Consistent symbol types are used across the three panels. The small numbers appearing above selected data in C indicate the ratios of FF obtained at 5,000 and 250 pulse/s, demonstrating increased stochasticity for the high-rate responses.

Careful examination of the data of Figure 9B might lead one to suspect that FF values for 250-pulse/s stimuli are generally lower than those obtained with 5,000-pulse/s stimuli. To compare “steady state” FF values obtained with low- and high-rate stimuli, data of Figure 9B were reduced to a series of median values covering contiguous analysis windows. In Figure 9C, median values for 250- and 5,000-pulse/s stimulus rates are plotted vs. spike rate for the “steady state” response epoch. Each median was based on a minimum of 14 samples, with 22 samples as the median number of samples. Note that higher FFs were obtained for the high-rate stimuli over a significant range of response rates. Using a paired-comparison t test over the data of the two curves of Figure 9C, this effect of pulse rate was found to be statistically significant (t = 4.06, d.f. = 24, p_error < 0.01). Over a region of response rates from about 40 to 140 spike/s, median FF values for the high-rate stimuli are roughly twice as large as those obtained at 250 pulse/s. We failed to observe a statistically significant difference between the “steady state” FF values obtained at 250 and 1,000 pulse/s.

DISCUSSION

A novel aspect of this study is the characterization of the time course of ANF temporal response properties across the duration of pulse train stimuli presented at rates spanning ranges likely encountered in prosthetic devices. In recent work (Zhang et al. 2007), we demonstrated spike-rate adaptation to electric pulse trains that was characterized by a “rapid” and a “short-term” time constant. For 250-pulse/s trains, median values of these time constants were 11 and 91 ms, respectively, whereas for 5,000-pulse/s trains, median values were 7.7 and 70 ms, respectively. Thus, for the higher-rate pulses, short-term adaptation was largely (95%) complete by about 200 ms, justifying our use of a 200–300-ms analysis window for evaluating “steady state” temporal response characteristics. We believe that short-term adaptation is relevant to issues associated with cochlear prostheses, as the durations of speech sounds are on the order of hundreds of milliseconds. We acknowledge that slower adaptation effects (occurring over seconds or longer) may also occur and be relevant to stimulus coding. Such longer-term effects were not examined in this study.

Onset effects – response timing occurring within the first 12 ms after stimulus onset – varied significantly with stimulus level and pulse rate. Increased levels resulted in shorter ISI, as may be expected by an increase in membrane excitation. Double-peaked IHs, evident in 27% of ANFs stimulated at 5,000 pulse/s, occurred at mid-to-high levels of a fiber’s dynamic range. These short intervals were only observed within the “onset” epoch, indicating a rapid succession of three spikes shortly after stimulus onset. This was not reported by Litvak et al. (2001), perhaps because they did not analyze the first 5 ms of their ANF responses. As evident in the spike trains of Figure 2, there is also significant across-fiber variation in the pattern of intervals observed shortly after stimulus onset. The spiking of the ANF shown in the left column of Figure 2 produced IHs with two distinct and sharp peaks at short intervals. At the highest stimulus level shown (bottom left panel), the first intervals were all less than 1 ms, whereas intervals of the second set ranged from about 1.5 to 2 ms. The temporal pattern of the spikes shown in the middle column of Figure 2, however, demonstrated a more gradual increase in ISIs over time.

Our current hypothesis is that the progression of ISIs observed immediately after stimulus onset results from the combined effects of refractoriness and rapid adaptation. The latter effect was recently described by Zhang et al. (2007) in response to electric pulse trains. After onset of a high-rate pulse train, refractory and recovery cycles result in repeated spiking, and the superposition of a rapid adaptation component over this epoch would cause additional threshold elevation and prolonged ISIs. Across-fiber variations in the extent of refractoriness and adaptation may account for across-fiber differences in timing, such as those seen in Figures 1, 2, and 7. It is possible, however, that two-peaked histograms may be produced by refractoriness, without the need for an adaptation mechanism. Using a computational model of an ANF based upon a Hodgkin–Huxley approach and stochastic sodium channels (cf. Rubinstein et al. 1999), Mino (2007) demonstrated double-peaked IHs in response to stimulation of a model axon by 5,000-pulse/s electric pulses. It should be noted that the second peak of those IHs was considerably wider than those reported here and was attributed to the modeled fiber achieving “pseudospontaneous” firing that is associated with states of relative refractoriness.

The across-fiber differences in spiking patterns (evident in the examples of Fig. 2) raises the possibility that characteristics of refractoriness and adaptation may vary significantly across the population of ANFs. In a population of feline fibers, Miller et al. (2001) reported a range of refractory characteristics, i.e., across-fiber variations in the absolute refractory period and the recovery time constant. These variations may be linked to a variable fiber characteristic, such as axon diameter or the nature of the membrane at the site of excitation (e.g., degree of myelination). It is also possible that differing fiber-to-electrode orientations and distances may result in changes in excitation, as Mino et al. (2004) have suggested with the results of model simulations. At any rate, a range of temporal responses can be seen across a small set of fibers, as was demonstrated in the data from 16 fibers (Fig. 7). Functional across-fiber diversity deserves consideration when approaching issues of subsequent processing by the central auditory nervous system.

Response latencies to electric pulse trains have not been previously reported. Across fibers, the mean first-spike latency for low-rate (250 pulse/s) trains followed a remarkably consistent downward trend with increases in onset spike rate (Figs. 3 and 4). The functional relationship observed in response to 1,000-pulse/s trains was similar to the 250-pulse/s data. For both rates, first-spike latency could be as great as 100 ms, consistent with a Poisson process operating at very low probability. In the case of the 5,000-pulse/s stimuli, greater across-fiber variability was evident. A small proportion of fibers stimulated at that high rate followed the same trend across response rates that was observed with lower-rate stimulation. However, overall, the latency-rate functions for the responses to 5,000-pulse/s stimuli were considerably flatter.

The group summary data and individual ANF data sets of median first-spike latency vs. spike rate (or stimulus level) demonstrated a tendency toward longer first-spike latencies with increases in stimulus pulse rate (Figs. 3D and 4). For high-rate (5,000 pulse/s) stimuli, relatively long first-spike latencies may be expected at low stimulus levels due to across-pulse current integration. However, finding that latencies for high-rate stimuli were greater than those obtained with low-rate pulses for relatively high stimulus levels was unexpected. Note that the comparisons afforded by the latency-vs.-level plots of Figure 4 indicate that longer mean first-spike latencies observed (for a range of stimulus levels) are not due to the fact that lower levels were used to evoke the 5,000-pulse/s responses. Indeed, the 250- and 5,000-pulse/s functions often overlap to a significant degree. We speculate that, for a range of current levels examined, the presence of a pulse preceding a second pulse by only 0.2 ms may have reduced ANF excitability to the combined presentation of two pulses. Prolonged latencies at high pulse rates have been reproduced by a single-node Hodgkin–Huxley model of an ANF that has been developed in our laboratory (Woo et al. 2007). However, with this model, as level is increased further, the latencies to the high-rate stimuli shorten to equal those of the single-pulse responses. It may be the case that the levels explored in our experiments were inadequate to achieve that condition. Clearly, this phenomenon requires further investigation. We propose developing a more realistic computational model (one using a multinodal axon) and examining responses to pulses presented at various rates and with different pulse shapes (i.e., biphasic vs. monophasic).

ANF temporal responses to high-rate stimuli demonstrated significant across-fiber variability, as demonstrated by plots of IH modes vs. onset spike rate (Fig. 7B), which indicated a spread of ISI distributions across the small fiber population examined. We did not find a correlation between measures of spike rate adaptation (Zhang et al. 2007) and the ISI mode variability seen across the 16 fibers illustrated in the graph. Litvak et al. (2001) also found across-fiber variability (in reported FFs) that could not be attributed to adaptation. Other possible contributors to the observed variability are across-fiber differences in refractory properties that could arise from across-fiber differences in membrane properties (such as fiber diameter) or a spread of distances between the stimulus electrode and target sites of excitation. Using computer simulations, the latter has been shown to affect spike timing by influencing the number of nodes active in action potential initiation (Mino et al. 2004; Mino and Rubinstein 2006).

The summary plot of IH mode vs. response rate (Fig. 7C) illustrates how temporal responses are influenced by response rate and by time relative to stimulus onset. For the earliest epoch (0–12 ms), ANF responses had IH modes that appeared to fall into one of two distributions. One distribution (centered at intervals from about 1 to 2 ms) is consistent with the short ISIs observed shortly after stimulus onset that we attribute to firing driven (or limited) by the refractory property. As ANFs were driven to rates greater than about 200 spike/s, the dominant ISI often closely approximated the hyperbola of Figure 7C, indicating firing at a constant rate. At lower spike rates (<200 spike/s), IH modes departed from the hyperbolic relationship. We suspect that this ANF response timing is still influenced and determined by refractory properties at these lower spike rates (hence the smaller-than-predicted ISIs), although with a larger contribution of a random process.

There has been considerable interest in the salutary effect of high-rate stimulation on temporal response patterns. Our study suggests that high-rate stimuli indeed provide greater “stochasticity,” albeit with some limitations. Our results indicate that reductions in the predicted VS were observed with 5,000-pulse/s stimulation, but only at steady-state response rates greater than 200 spikes/s (Fig. 8D). The measure of a stochastic process provided by the FF presented a somewhat different picture. The data indicate that enhanced steady-state “stochasticity” due to high-rate stimulation occurred for response rates between about 20 and 100 spike/s (Fig. 9B). With respect to changes over time, VS and FF measures demonstrated different trends. For all but very high spike rates, VS was generally constant across time, whereas FF underwent large increases for low-to-moderate (<220 spike/s) onset response rates (Fig. 5). These large increases were generally complete within the first 100 ms of the ANF responses. Increases in FF over time became proportionally smaller as the response rate was increased beyond 220 spike/s. It is important to note, however, that VS and FF indicate different aspects of ANF firing and could therefore describe very different membrane phenomena that are dominant at different firing rates.

It is beyond the scope of this study to determine which of these two measures of randomness in ANF response (VS and FF) is more relevant to speech perception with electric stimulation. The changes in VS would be expected to occur for each ANF. Changes in FF would, by definition, occur across pulse-train presentations. However, given that electric stimuli likely excite an ensemble of fibers, changes in FF would be evident in the ANF ensemble response. The 100-ms temporal window over which VS and FF (generally) underwent the greatest changes is comparable to formant transition times and the duration of shorter speech segments. These temporal changes, along with the spike-rate and amplitude changes previously reported by our group, require consideration. Given that several aspects of ANF responses undergo temporal changes, one approach to this general problem would be to use computational models that can consider the response of an ensemble of ANFs, with variables such as fiber diameter and electrode-to-axon distance incorporated into the model.

We noted that our model of spike timing, a Poisson process with a 2-ms dead time, demonstrated predictive error at the highest response rates (Fig. 9A, B). The systematic bias of the experimental data toward lower FFs evident in the figure suggests that the model was more deterministic than the ANFs, consistent with an overly large dead time. A smaller dead time is likely appropriate for fibers driven to high rates, consistent with reports of the absolute refractory periods of feline ANFs (Cartee et al. 2000; Miller et al. 2001). Also, at high rates, a large proportion of the experimental data lie outside the 99% confidence intervals of the model, indicating that the model fails to account for the variance observed in our ANF population. We suggest that a Poisson process with a single dead time is inadequate in describing a population of excited fibers. In a survey of fibers driven to refractory states, Miller et al. (2001) found that both the recovery time constant and the absolute refractory period demonstrated significant across-fiber variability. We speculate that this variability may be due to intrinsic ANF differences (such as fiber diameter) or across-fiber differences in the manner in which the fibers are excited by the external electric field (owing to fiber-to-electrode distance and orientation variables).

The data presented here, in conjunction with our characterization of spike rate adaptation (Zhang et al. 2007) help in the interpretation of ECAPs that are recorded from humans with implanted auditory prostheses (e.g., Abbas and Brown 2000). Wilson et al. (1994) noted that ECAPs recorded from implant users can undergo fast reductions in amplitude (within a few milliseconds) and that these reductions increase in magnitude as stimulus pulse rate is increased. The Zhang et al. (2007) study demonstrated that spike large amplitude changes indeed occur at the single-fiber level shortly after the onset of high-rate stimuli. The across-pulse-rate comparison of VS (Fig. 8) of this present study also indicates that, for spike rates greater than about 200 spike/s, VS for 5,000-pulse stimuli is lower than what is expected from the responses to low-rate stimuli, indicating not only that refractory properties may result in smaller ANF contributions to ECAP amplitude (Zhang et al. 2007), but spike desynchronization may play a role for high-rate stimulation. Thus, two ANF mechanisms may need to be considered for accurate modeling of the ECAP for stimulation at different pulse rates.

Computational modeling approaches may prove particularly useful in addressing longstanding issues of across-species differences in cochlear or nerve-fiber anatomy (Hatsushika et al. 1990; Nadol et al. 1990; Felix 2002) that could render some of our results inapplicable to the physiology of electrically stimulated human ANFs. For example, while feline and human cochleae are similar, they vary in gross dimensions and shape of the first turn. Also, the extent (or existence) of myelin around ANF cell bodies may prove to be an important species variable. Finite-element computational models of the cochlea, surrounding tissues, and nerve fibers can be developed for multiple species within a single laboratory to address the influence of across-species differences, as Frijns et al. (2001) have done a comparison of electrical excitation patterns for guinea pig and human cochleae.

A related concern is that most ANF studies conducted using research animals are based upon acute experimental preparations that do not suffer from retrograde ANF degeneration that is typical of chronically deaf ears (Spoendlin 1975; Nadol 1997). With loss of myelination, for example, membrane excitation may be expected to become less efficient, and action potential propagation would be expected to occur more slowly and with greater vulnerability to conduction failure. For that reason, we are planning follow-up studies in chemically deafened cats that are allowed to survive for periods known to result in nerve degeneration secondary to deafness.

Finally, we note that, whereas our stimulus-artifact procedure was effective, our experience indicates that the use of artifact subtraction schemes requires care, as none of them work perfectly. Examples of suboptimal spike waveforms were included in Figure 2 (right column) to demonstrate possible distortion of spike waveforms. Such distortion could contribute to altered latency and, in some cases, increases in apparent spike synchrony. We found no simple way of predicting when distortion would occur, although it was correlated with stimulus level. We visually inspected all waveforms for such distortion to avoid reporting false spike events. Such human intervention, of course, can introduce observer bias and data errors. It may be possible to automate this procedure through a cross-correlation algorithm that measures the degree of deviance from an ideal spike shape (template). As spike morphology can vary across fibers (due, perhaps, to different fiber/electrode orientations and micropipette variability, such a spike template scheme would likely need to be updated on a per-fiber basis.