Measurement of the Distribution of Medial Olivocochlear Acoustic Reflex Strengths Across Normal-Hearing Individuals via Otoacoustic Emissions

Abstract

A clinical test for the strength of the medial olivocochlear reflex (MOCR) might be valuable as a predictor of individuals at risk for acoustic trauma or for explaining why some people have trouble understanding speech in noise. A first step in developing a clinical test for MOCR strength is to determine the range and variation of MOCR strength in a research setting. A measure of MOCR strength near 1 kHz was made across a normal-hearing population (N = 25) by monitoring stimulus-frequency otoacoustic emissions (SFOAEs) while activating the MOCR with 60 dB SPL wideband contralateral noise. Statistically significant MOCR effects were measured in all 25 subjects; but not all SFOAE frequencies tested produced significant effects within the time allotted. To get a metric of MOCR strength, MOCR-induced changes in SFOAEs were normalized by the SFOAE amplitude obtained by two-tone suppression. We found this “normalized MOCR effect” varied across frequency and time within the same subject, sometimes with significant differences between measurements made as little as 40 Hz apart or as little as a few minutes apart. Averaging several single-frequency measures spanning 200 Hz in each subject reduced the frequency- and time-dependent variations enough to produce correlated measures indicative of the true MOCR strength near 1 kHz for each subject. The distribution of MOCR strengths, in terms of SFOAE suppression near 1 kHz, across our normal-hearing subject pool was reasonably approximated by a normal distribution with mean suppression of approximately 35% and standard deviation of approximately 12%. The range of MOCR strengths spanned a factor of 4, suggesting that whatever function the MOCR plays in hearing (e.g., enhancing signal detection in noise, reducing acoustic trauma), different people will have corresponding differences in their abilities to perform that function.

INTRODUCTION

Although there are considerable data showing that there is a medial olivocochlear reflex (MOCR) in humans, most studies show averages and only a few show MOCR effects across individual subjects (Micheyl et al. 1995; Micheyl and Collet 1996; De Ceulaer et al. 2001; Wagner et al. 2005). De Ceulaer et al. (2001) presented the first measured distribution of MOCR strengths across individuals using otoacoustic emissions (OAEs). However, it is uncertain how much their results are affected by MOC activity evoked by their test clicks (Veuillet et al. 1991; Guinan et al. 2003) and by their use of the “nonlinear click method”, which misses the linear part of the MOCR effect. Furthermore, a major drawback of the De Ceulaer study is that no mention is made of how repeatable the measurements were on each individual. Thus, it is not possible to determine how much of the variation in their measured distribution is caused by actual variation in MOCR strengths across individuals and how much is caused by measurement errors. A major goal of the present work was to determine the distribution of MOCR strengths across individuals, i.e., to obtain a strength distribution in which the measurements are sufficiently accurate that the measurement-related variations account for only a small fraction of the observed variation in MOCR strengths across subjects.

Establishing the range and variation of MOCR strengths in normal-hearing subjects and making clear the issues involved in measuring such reflex strengths via OAEs promises to have both scientific and clinical impact. For example, the correlation of MOCR strengths from different individuals with results from psychoacoustic tests, such as speech detection in noise, may help to better understand the roles the MOCR plays (Bar-Haim et al. 2004; Kumar and Vanaja 2004). Clinically, a reflex strength test may prove useful for screening individuals for susceptibility to acoustic trauma because data from guinea pigs suggest that a stronger reflex affords greater protection (Maison and Liberman 2000).

We used stimulus-frequency otoacoustic emissions (SFOAEs) to measure MOCR strengths for the cochlear region near 1 kHz. SFOAEs were chosen because they offer several advantages over other OAE types, namely: (1) SFOAEs provide a frequency-specific measure, (2) the single 40 dB SPL tone used to produce the SFOAEs elicits little or no MOCR activity itself, (Guinan et al. 2003) and (3) at 40 dB SPL, SFOAEs are produced by a single, easily interpreted mechanism—coherent reflection (Shera and Guinan 1999).

At the start of the experiment, our working hypothesis was that the percentage change in the SFOAE at a single frequency would provide a good metric of MOCR strength. In other words, when the MOCR’s effect on an SFOAE at a single frequency was normalized by that SFOAE’s amplitude, it would be strongly related to an individual’s MOCR strength throughout the frequency region near the test frequency. We presumed that any randomness in the innervation patterns of individual MOC fibers (Liberman and Brown 1986) would be averaged out because our wideband sound activates many MOC fibers and their effects would be averaged over the relatively wide region of cochlear-amplifier gain that influences an SFOAE. However, to our surprise, we found that such normalized MOCR effects often varied significantly across nearby frequencies within the same individual.

Our data indicate that when combined across frequency, normalized MOCR effects on SFOAEs can be indicative of MOCR strength. It is therefore important to make a distinction between (1) the MOCR effect on an SFOAE, the value obtained from a measurement at a single frequency, (2) an OAE metric for MOC strength (e.g., MOCR normalized effects on SFOAEs averaged across frequencies), and (3) an individual’s MOCR strength as would be measured neurally. By combining multiple measures of MOCR effects across frequency and time, we were able to produce a single overall subject-specific metric of MOCR strength and obtain a distribution of those strengths across our subjects.

METHODS

Overview

A constant probe-tone (PT) was played into an ear canal to generate an SFOAE from within the cochlea. This SFOAE combined with the probe-tone to produce a compound-tone, C(t) = PT + SFOAE(t), which is the ear canal sound pressure at the probe-tone frequency (bold notation is used for complex measured variables—variables with both magnitude and phase). If the probe-tone stimulus and middle ear transmission are invariant, e.g., if there is no middle ear muscle contraction, changes in the compound tone can be wholly attributed to changes in the SFOAE, i.e., ΔSFOAE(t) = ΔC(t).

To measure MOCR effects, the compound-tone, C(t), was monitored via a heterodyne technique over a time period during which a contralateral wideband noise burst was presented to activate the MOCR. The changes in the compound-tone, ΔC(t), caused by MOCR activation were used to quantify the MOCR raw effect (i.e., the unnormalized effect). This raw effect was then normalized by the native SFOAE amplitude (the SFOAE before presentation of the contralateral sound, estimated from two-tone suppression) to produce an MOCR normalized effect, expressed as the percent of the native SFOAE altered by MOCR activation.

Subjects

Twenty-five normal-hearing adult subjects (18 female, 7 male), aged 19 to 54 years (mean = 26, SD = 8 years) participated in the study. The only requirement for participation was ‘normal hearing’ in both ears. A two-interval forced choice audiogram using 1/3 octave band noise bursts (noise bands were used instead of tones to avoid possible effects of threshold microstructure) centered at 250 Hz, 500 Hz, 1 kHz, 2 kHz, and 4 kHz were used to determine whether subjects had normal hearing in both ears (within 20 dB re: ANSI S3.2 1996 pure tone thresholds). All subjects who had normal hearing were included. Two subjects who did not have normal hearing were excluded.

Subjects were seated in a sound-absorbing chamber and fitted with two Etymotic Research ER10c acoustic assemblies (each had two sound sources and a microphone) for approximately 30 min measuring sessions interleaved with approximately 15 min breaks. One ear from each subject, the ‘test ear’, was chosen at random (by a coin flip). The total time allotted to measuring a subject depended on subject availability. The maximum total session time (not including the audiogram) was 266 min for subject M157L; and the minimum was 128 min for subject M68R (mean = 177, standard deviation [SD] = 39 min). In subjects who produced significant effects with only a few minutes of averaging time, we often continued gathering data while the subject was still available. Our measurement procedures have not been optimized for speed or for clinical use. To use the present test methods in a clinical setting, criteria would need to be determined for when to stop gathering data, either because a statistically significant response has been demonstrated or because the data show that any response must be below some criteria level. However, developing such criteria was beyond the scope of the present work. It may also be possible to speed the process by screening for the SFOAE frequencies with the highest signal-to-noise ratios (SNRs) using TEOAEs and/or probing multiple SFOAEs simultaneously.

Measurements of spontaneous emissions in quiet showed that no measurement ear had spontaneous emissions >−10 dB SPL within 50 Hz of any probe-tone. A middle ear muscle reflex group delay test (Guinan et al. 2003) was used to insure that MOCR effects dominated the measured changes in the ear canal sound pressure.

Stimuli

To generate SFOAEs, a continuous 40 dB SPL probe-tone was played bilaterally through one sound source in each ER10c earphone. Tones near 1 kHz were used because they provide high SNRs for SFOAEs. Bilateral presentation was not necessary but was used to facilitate comparison with our prior work. To elicit MOCR activation, a 4-s 60 dB SPL contralateral (re: the ‘test ear’) wideband (100 Hz–10 kHz, flat ear canal spectrum) noise burst (5 ms rise/fall) was presented through the second source of the contralateral earphone. This wideband activator was chosen because it provides good MOCR activation and does not generally elicit middle ear muscle responses (Guinan et al. 2003). Narrow-band activators are less potent (Maison et al. 2000). To estimate the native SFOAE amplitude by two-tone suppression, two 400 ms, 60 dB SPL tone bursts at 110 Hz below the probe-tone frequency were played through the second sound source in the ipsilateral earphone, one during MOCR activation and one alone (Fig. 1b). A suppressor placed 110 Hz below the SFOAE suppresses the SFOAE by approximately 80% (Backus and Guinan 2006); 110 Hz was used because it falls outside the heterodyne analysis filter width. MOCR-activator noise bursts and suppressor-tone bursts were alternated in polarity every stimulus repetition such that when an even number of responses were averaged together, their acoustic contributions to the response signal in the ear canal canceled. Response pairs were rejected as being contaminated with artifacts (usually from subject movement) when the difference between one pair of responses and the next pair exceeded a criterion (pairs were used because the signs of the activator and suppressor sounds ware reversed on alternate trials).

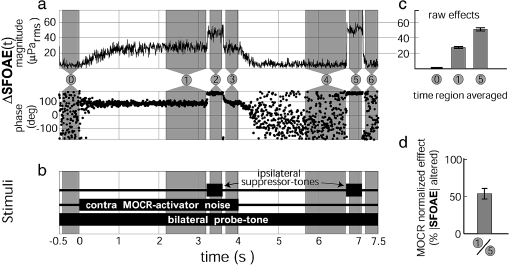
FIG. 1.

Averaged response (a), stimulus timing (b), and analysis (c and d) from a single measurement of MOCR normalized effects. a Shows the average change (relative to region #0) in ear canal sound pressure at the probe-tone frequency, ΔSFOAE(t), caused by the contralateral noise. c Shows the magnitude of this response in three numbered time regions: 0 noise floor region, 1 MOCR response region A, 5 two-tone suppression response region (for SFOAE estimate). Bars 1 and 5 are from vector averages in these regions, and bar 0 is from the SD (see text). Error bars are 95% confidence intervals about the means. d Shows the MOCR normalized effect calculated from c, i.e., the ratio of the MOCR effect to the two-tone suppression effect with error bar = 1 SE. As shown in b, the probe-tone was a continuous, bilateral, 40 dB SPL, 1 kHz tone. The MOCR-activator was a contralateral, 60 dB SPL, wideband (100 Hz–10 kHz), 4 s, noise burst. Suppressor-tones were 60 dB SPL, 400 ms, ipsilateral tone bursts at 110 Hz below the probe-tone frequency. MOCR-activators and tone-suppressors were alternated in polarity on successive presentations. Subject F150R

Analysis

The magnitude and phase of the ear canal sound pressure at the probe-tone frequency was extracted by heterodyning the averaged waveform (Kim et al. 2001; Guinan et al. 2003). The changes in the ear canal sound pressure over time as a result of changes in the SFOAE, ΔSFOAE(t), were calculated by vector subtracting the preelicitor baseline average (−420 ms < t < −20 ms, region “0” in Fig. 1a) from each time point resulting in Figure 1a. Then vector (complex) time-averages of ΔSFOAE(t) were made for seven time regions to quantify:

• The MOCR raw effect; Figure 1, region 1.

• The native SFOAE amplitude from the two-tone suppression; Figure 1, region 5 or 2.

• The noise floor, from the standard error of Figure 1, region 0. This was done from the variation of the amplitude points, not the vector average, as described below. Note that region 0 was also used to obtain the preelicitor baseline average, as described above.

• Various measurement controls; Figure 1, regions 3, 4, and 6.

To estimate the standard errors (SEs) of these window time-averages, a bootstrap technique was used. This was done because the SE of the magnitude of such a ‘mean vector’ depends upon its constituent magnitudes and phases and cannot be calculated in the same way as the SE of real-valued numbers (Backus 2007). The bootstrap estimate of SE also had the advantage of not requiring assumptions about the underlying magnitude and phase distributions and how they were coupled. For the bootstrap, the N vectors that were averaged in computing a mean vector (i.e., the waveform points) were pooled. Statistically similar data sets of N vectors were then generated by taking N samples at random with replacement from the pool. One thousand such sets were generated and were used to compute 1,000 new mean estimates. The SD of these window time-averages was used as the estimate of the SE.

To compare ΔSFOAEs across ears and/or frequencies that have SFOAEs of different amplitudes, we normalized the MOCR raw effects by the SFOAE native amplitudes. The native amplitude of the SFOAE is inaccessible from a simple ‘probe-tone with contralateral acoustic stimulation’ measurement because the SFOAE and the probe-tone both occur at the same time and frequency. To estimate the SFOAE native amplitude, we incorporated a two-tone suppression measure (Shera and Guinan 1999) into our stimulus paradigm (e.g., Fig. 1, region 5). The combined effects of MOCR inhibition plus two-tone suppression (Fig. 1, region 2) were generally statistically indistinguishable from the two-tone suppression effect alone (Fig. 1, region 5), except subject F168L whose combined effect was significantly larger than her two-tone-suppression alone. In all cases, we used the larger value from the two regions because our goal was to estimate the total |SFOAE|. Thus, the measured suppression was, on average, greater than the 80% achieved by the suppressor alone.

Ideally, if the SFOAE is completely suppressed in regions 2 and 5, the native SFOAE amplitude equals the change in ear canal sound pressure (e.g., the difference from region 0 to region 5 in Fig. 1). After normalization, the MOCR normalized effect (at each frequency) is expressed in %|SFOAE|. This normalization is explicit for SFOAEs, but it is conceptually the same measure that is tacitly used by researchers who report their MOCR effects as a dB change in transient-evoked OAEs (TEOAEs) or distortion-product OAEs (DPOAEs).

Measurement protocols

Each test ear was initially measured from 900 to 1,100 Hz in 20 Hz steps with ‘low-N’ averages of four responses. Two of these frequencies, 1 kHz and a frequency that produced a comparatively large SFOAE, were used for ‘high-N’ measurements (except subject M166 who was measured at 1 kHz, but in both ears). The largest SFOAE was usually selected as the non-1 kHz frequency to measure, but if the largest SFOAE was within 21 Hz of 1 kHz, 900 Hz or 1,100 Hz was chosen at random to be the second high-N frequency.

‘High-N’ measurements averaged 8–284 responses (mean = 102, SD = 50), in subgroups of four responses with the number depending on subject signal-to-noise-ratio (SNR >6 dB), subject availability, and whether statistical significance was achieved. Because heterodyne measurements yield values that are vectors, traditional statistical methods that assume normally distributed scalar measurements do not apply (Backus 2007). To determine that a set of high-N measurements was statistically significant relative to the background noise, we used the following procedure: (1) Use only subgroup averages that had low (<−10 dB SPL) noise (calculated from the SD of the Fig. 1 “window 0” points, as described earlier). (2) Calculate 95% confidence interval circles in the complex plane, for the mean values of both the signal and the noise. (3) A signal was considered as statistically significant if its 95% confidence interval circle did not overlap the noise 95% confidence interval circle. This is a conservative criterion for statistical significance and corresponds approximately to p < 0.006. Statistical significance was checked for at the end of each 30-min session. If an obvious and statistically significant MOCR raw effect was observed before the end of the allotted time, averaging was sometimes stopped. A high-N measurement averaged all responses to the high-N stimulus, across sessions, except those rejected as having artifacts or excessive noise.

RESULTS

MOCR effects could be measured in 25/25 subjects

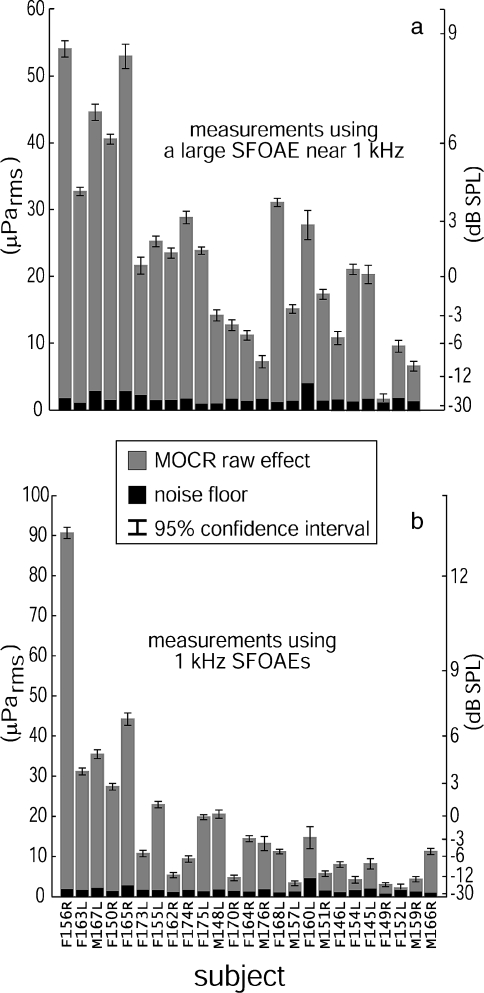
Within the allotted experiment time, we were able to measure statistically significant (p < 0.006, i.e., the 95% confidence interval circles for the mean signal and noise do not overlap—see the “Methods” section) MOCR raw effects for all ears, although not at all frequencies. Figure 2 shows the MOCR raw effects and the noise floors for the high-N measurements. Subjects F152L and F149R had very weak SFOAEs between 900 and 1,100 Hz but both were ultimately measurable at 900 Hz (100 presentations averaged) and 1 kHz (284 presentations averaged), respectively. These subjects did not generate statistically significant MOCR raw effects at their other test frequency (neither F152L at 1 kHz with 96 presentations nor F149R at 940 Hz with 148 presentations). The weakest responder, F149R, required 284 trials or 38 min of averaging time to demonstrate a significant effect.

FIG. 2.

Plots of the magnitudes of MOCR raw effects on SFOAEs (gray bars) relative to measurement noise (black bars) from two SFOAE frequencies measured in each of the 25 subjects. Although not all ears could be measured at all frequencies, all ears registered statistically significant (p < 0.006, i.e., the 95% confidence interval circles for the mean signal and noise do not overlap—see the “Methods” section) MOCR raw effects on at least one SFOAE near 1 kHz. a Shows the measurements of MOCR raw effects made using a large SFOAE (estimated from two-tone suppression) between 900 and 1,100 Hz for each subject (excluding 1 kHz). b Shows the MOCR raw effects measured in the same subjects using 1 kHz SFOAEs. The F or M prefix indicates male or female, L or R suffix indicates left or right ear; subject M166R was only measured at 1 kHz. The subjects are arranged left to right in decreasing order of the sum of the high-N native |SFOAEs| (the sums are not shown)

MOCR raw effects

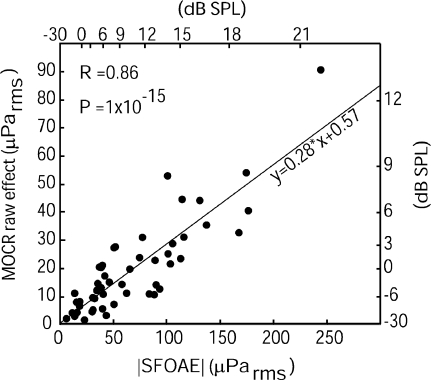
MOCR raw effects on SFOAEs were roughly proportional to the corresponding SFOAE amplitudes measured via two-tone suppression. Activating the MOCR with 60 dB SPL wideband noise generally resulted in approximately 30% change in SFOAE amplitude (30% is the slope in Fig. 3). A high Pearson’s product-moment correlation coefficient and low p value (R = 0.86; p = 1e-15) indicates there is a generally linear relationship between MOCR raw effects and SFOAE native magnitudes (note that the deviations from a purely linear relationship are attributable to the differences in MOCR strengths across subjects). This linear relationship is consistent with the notion that bigger SFOAEs lead to bigger MOCR raw effects.

FIG. 3.

The plot of SFOAE amplitudes vs MOCR raw effects on those SFOAEs shows that most SFOAEs are changed by approximately 30% during contralateral MOCR activation with 60 dB SPL wideband noise. Data from the two high-N frequencies are both included. All error bars are smaller than, and obscured by, the points used to represent the data, indicating that the departures of the points from the linear relationship are not caused by measurement noise. Correlation (R = 0.86) was highly significant (p = 1e-15). The line represents a linear regression fit to the data

Single-frequency MOCR normalized effects

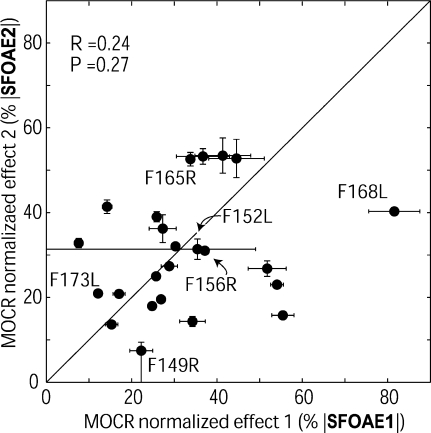
Single-frequency MOCR normalized effects measured in the same ear at nearby frequencies showed unexpected frequency-dependent variation. To account for the fact that larger SFOAEs produce larger MOCR raw effects (Fig. 3), MOCR raw effects were normalized by the native SFOAE amplitudes estimated from two-tone suppression to yield MOCR normalized effects. For the 24 subjects with two high-N measurements in the same ear (from 1 kHz and a nearby frequency), the MOCR normalized effects are plotted against each other in Figure 4. These two measures were not significantly correlated (Fig. 4). This lack of correlation was surprising because the two measures were taken from frequencies within 100 Hz of each other and the stimulus presentations that generated them were interspersed over the same time period (e.g., Fig. 5).

FIG. 4.

Two SFOAE-based measures of MOCR normalized effects for 24 subjects plotted against each other. The two measures were not significantly correlated (Pearson’s product-moment R = 0.24, p = 0.27) although they were made over the same time, in the same ear, and at nearby SFOAE frequencies. ‘SFOAE1’ used the 1 kHz SFOAE and ‘SFOAE2’ used a large SFOAE within 10% of 1 kHz. Error bars are ±1 SE; but most error bars are obscured by the data points. Subjects who are referred to in the text are labeled here and in subsequent graphs. Subjects F152L and F149R have asymmetric error bars that reach to zero because a statistically significant MOCR raw effect was not measured at one SFOAE frequency for these subjects (see Fig. 2). Subject M166R from Figure 2 is not included in this plot because that subject only had high-N data at 1 kHz

FIG. 5.

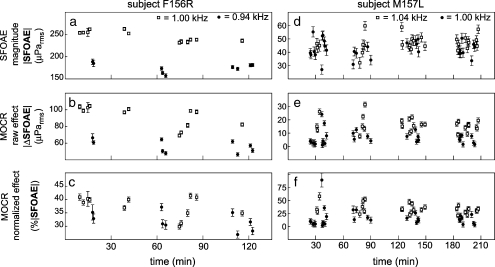
Repeated SFOAE measurements in the same subject show that small changes in frequency (10 s of Hz) can cause significant differences in normalized single-frequency MOCR effects. As expected, SFOAE magnitudes (a, d) and raw MOCR effects (b, e) can differ significantly over small differences in frequency (1.0 and 0.94 kHz in F156R; 1.0 and 1.04 kHz in M15L). Normalization reduced, but surprisingly did not remove, these differences (c, f). Each point is the average from four responses to 60 dB SPL contralateral noise. Error bars are 1 SE. The 1-kHz SFOAE amplitude of subject F156R varied significantly with time (i.e., across sessions) but this was not a general trend. Only four subjects had 1 kHz SFOAE magnitude-versus-time slopes that were statistically significant at the 0.05 level, and the slopes went in both directions

The single-frequency MOCR normalized effects measured at nearby frequencies showed no bias between the effect at 1 kHz and the effect at the nearby frequency with a high SFOAE amplitude. The means of the two measures were statistically indistinguishable, i.e., in Figure 4, data points were scattered equally above and below the line y = x (measure 1: mean = 32%, SD = 17%, SE = 3.4% and measure 2: mean = 31%, SD = 13%, SE = 2.6%). However, the SD of the MOCR normalized effects measured using the largest SFOAE near 1 kHz (measure 2) was slightly less than measure 1’s. These findings indicate that (1) no systematic bias was introduced by electing to measure at frequencies with large SFOAEs near 1 kHz as opposed to always selecting 1 kHz and (2) that larger SFOAEs may produce more consistent measurements.

Figure 5 shows the variation across time for submeasurements (four presentations averaged) from two subjects with high SNRs. For subject F156R, the native SFOAE (Fig. 5a) and the raw MOCR effect (Fig. 5b) were significantly different at the two test frequencies. Normalization removed much of this frequency-specific difference but the variations in normalized MOCR measurement still spanned approximately 15% range (Fig. 5c) and it is difficult to tell whether the variation is caused by frequency-dependent differences or time-dependent variation. By contrast, subject M157L (Fig. 5, right) had relatively little difference between the native SFOAE amplitudes at the two frequencies (Fig. 5d) but clearly demonstrates the existence of fine-scale (in this case, 40 Hz) frequency-dependent variations in normalized MOCR effects (Fig. 5f—note that most of the filled symbols are below the open symbols). The approximately 18% difference between the means of the two measures was statistically significant (1 kHz: mean = 16.4%, SD = 16.8%; 1.04 kHz: mean = 34.3%, SD = 9.2%; Student’s t test: t = −4.9, p = 9e-6) and could not be explained by time-dependent variation. Furthermore, when the 1 kHz outlier at approximately 90% was omitted from SD calculations, SDs from the two frequencies were quantitatively similar (1 kHz: SD = 9.26%; 1.04 kHz: SD = 9.22%), suggesting that the cause of the variations might be the same for both measurements.

The data of Figures 4 and 5 show that single-frequency normalized |ΔSFOAE| values can vary significantly for small changes in frequency. Of the 24 subjects, 15 demonstrated significant fine-scale (within 100 Hz) frequency-dependent variations by passing a Student’s t test, which indicated there was a significant difference between the means of the measures taken from nearby frequencies, and a Kolgormorov–Smirnov test, which showed that datasets from different but nearby frequencies were indeed from different distributions, both with p values <0.05. Larger differences between MOCR normalized effects were usually observed when the frequency separation was larger.

Four possible sources of variation in our measurements can be identified: (1) equipment measurement noise, (2) “drift” as a result of changes in the position of the acoustic assembly in the ear canal, (3) variation of MOCR strength across time, e.g., as a result of variations in subject alertness, and (4) variation in the SFOAE reflex metric across frequency. Of these, only (4) is expected to remain after extensive averaging of interspersed measurements. Thus, the high-N data do demonstrate real variation across frequency in ΔSFOAE values, even for closely spaced (≤40 Hz difference) frequencies.

Estimates of MOCR strength by combining low-N and high-N SFOAE data

Because our high-N single-frequency measures did not produce significantly correlated values, we reasoned that assessing MOCR strength using SFOAEs might be done by averaging SFOAEs across frequency. Our high-N dataset was not designed for this. We did, however, have low-N (4 responses averaged) data that provided an alternate, albeit noisier, dataset with 11 different frequencies.

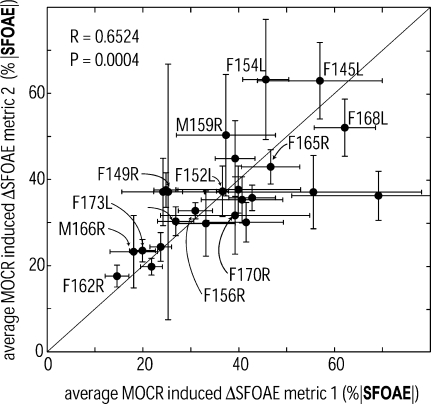
To test whether averaging across frequency might yield significantly correlated measures, we partitioned the measures into two groups: (1) the frequencies 920, 960, 1,000, 1,040, and 1,080 Hz and (2) the frequencies 900, 940, 980, 1,020, 1,060, and 1,100 Hz. Only measurements that were above the noise floor magnitude by two SDs—after vector averaging all submeasurements at the same frequency, high-N, and low-N—were included, so not all subjects had all frequencies included in the frequency averages. The mean number of frequencies included was 4.46, SD = 1.28 (differences in the number of frequencies averaged are captured in the 1 SE error bars in Fig. 6).

FIG. 6.

Two estimates of MOCR strength near 1 kHz for each of the 25 subjects plotted against each other. The two estimates are significantly correlated (R = 0.65, p = 0.0004) and spanned a range from 15% to 69%, indicating that there is statistically significant intersubject variation in MOCR strength near 1 kHz. Measure 1 was an average involving three to five (measurements had to be >2 SD above the noise floor magnitude to be included) SFOAEs at probe frequencies of 920, 960, 1,000, 1,040, and/or 1,080 Hz; measure 2 was an average involving three to six SFOAEs of 900, 940, 980, 1,020, 1,060, and/or 1,100 Hz. Error bars are ±1 SE

Overall, Figure 6 shows that when two independent sets of several single-frequency MOCR normalized effects were averaged, frequency- and time-dependent variations were reduced enough to produce correlated MOCR measures in a given subject. The simplest hypothesis by which averaging these measurements would produce an increased correlation between the two measures is if each measurement is caused by (1) a component from an underlying MOCR effect common to a wide frequency region and (2) a component that varies randomly across frequency (and perhaps time). In this case, averaging data from two sets of interleaved frequencies reduces the variations caused by the random frequency-specific component and reveals the underlying MOCR effect. In contrast, for the single frequency measures (Fig. 4), many averages were obtained, which reduced the effects of time variations, but all the measurements in a set were at the same frequency so they fully show the randomness across nearby frequencies. Because Figure 6 plots two independent variables against each other, R rather than R² represents the variance explained by an underlying cause. Thus, the R value is consistent with 65% of the variance of these two measures originating from the same underlying cause, presumably the intersubject variation in MOCR reflex strength. The two measures were also statistically indistinguishable (measure 1: mean = 37%, SD = 14%; measure 2: mean = 36%, SD = 12%). That is, each of these frequency-averaged normalized ΔSFOAEs produced very similar metrics for MOCR strength.

The distribution of MOCR strengths across subjects

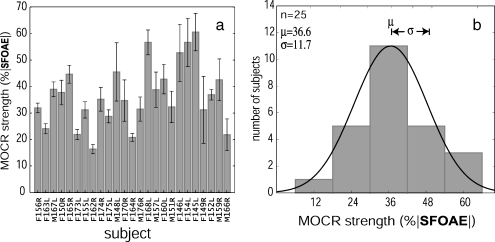
To get the most reliable estimate of MOCR strength for each subject, we combined both of the metrics of Figure 6. That is, all of the 11 frequencies for which the measurement was more than 2 SDs above the noise floor (range = 4–11 frequencies; mean = 8.92; SD = 2.28) were averaged. Figure 7 shows the resulting estimates of MOCR strength for the 25 normal-hearing subjects (Fig. 7a) and a histogram of the distribution of MOCR strengths across subjects (Fig. 7b). In Figure 7, subjects with high SNRs (smaller error bars) had MOCR strengths that were slightly lower than subjects with low SNRs, but the difference was not significant at the p = 0.05 level. This indicates that choosing only frequencies that had measurements >2 SD above the noise floor resulted in there being little SNR-related bias in these data (Backus 2007).

FIG. 7.

a Estimates of MOCR strength near 1 kHz for 25 normal-hearing subjects show the subject variations in efferent strength; error bars are ±1 SE. b Distribution of MOCR strengths near 1 kHz across subjects (mean = 36.6%, SD = 11.7%). The distribution is well approximated by a Gaussian (solid curve). MOCR activation with contralateral 60 dB SPL wideband noise generally suppressed SFOAEs near 1 kHz in a given subject by approximately 35% (range = 15–60%)

Figure 7b shows the distribution of MOCR strengths in a normal-hearing population. The distribution was essentially symmetric with a slight positive skew of 0.36 but was well modeled by a Gaussian. A Shapiro–Wilks test confirmed that the distribution could easily be Gaussian (W statistic = 0.96, p = 0.51; a p < 0.05 would indicate a non-Gaussian). In general, MOCR activation with a 60-dB SPL contralateral wideband noise altered a subject’s SFOAEs by approximately 35% (mean = 36.6%, SD = 11.7%) in the frequency region near 1 kHz. MOCR strengths spanned a range from 16.3% to 60.5%.

Estimating the amount of true subject-dependent variability in our MOCR strength measures

How much of the variability in Figure 7 is subject-dependent and how much is noise? The answer is crucial to understanding how the distribution of Figure 7 relates to the real distribution of MOCR strengths in the population. First, note that the two metrics that were averaged to get the points in Figure 7 came from independent measurements (i.e., they were from separate measurements at separate frequencies). Of course, the results of these measurements are not independent because of the underlying cochlear processes involved. If each metric is considered to have an underlying component caused by subject-dependent MOCR strength plus a normally distributed error (which includes both measurement noise and fine-frequency variations), then the 65% correlation of the metrics indicates that 65% of the variance is caused by the subject-dependent MOCR strength, leaving 35% to be error. Averaging the two metrics will reduce the variance of the error by a factor of 2 (or reduce the SD of the error by the square root of 2). Therefore, in the new distribution, Figure 7, the fraction of the variance that is attributable to the variation in the population MOCR strength, 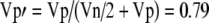. Thus, if the assumption of additive, normally distributed error is correct, 79% of the variation in the distribution of Figure 7 is caused by the distribution of MOCR strengths in the population.

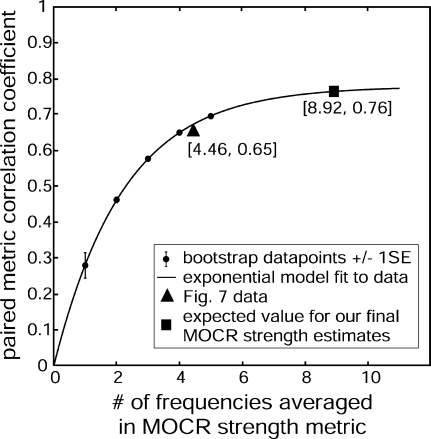
A bootstrap method provides an alternative approach that can also show the effects of including more frequencies in the frequency average. To illustrate the procedure, consider the effect of averaging data from two different frequencies. We obtained a pair of averages, A and B for each subject, each with N = 2 frequencies averaged and with the frequencies selected such that none of the frequencies in B were included in A. We then calculated the Pearson’s product-moment correlation across subjects between these A and B averages. Next, we incremented N = 3, made the same correlation calculation, and continued this to as high an N as the data allowed. Because there were 11 frequencies, the highest N possible was 5 (2 pairs of 5 using 10 frequencies). In all cases, we only used frequencies for which the data met the SNR criterion, i.e., (average value − noise value) >2 SD of the noise. For the statistics at each N, all possible combinations of the frequencies were used (selecting frequencies without replacement so that each pair represents simulated independent measurements). With this method, the effect of increasing the number of frequencies on the correlation between pairs of averages could be observed (Fig. 8). The large triangle at N = 4.46, R = 0.65 is the result from the combination of frequencies used in Figure 6. An exponential constrained to go through the origin fit the data (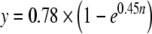; R² = 0.99995). By extrapolating this curve to 8.92 frequencies included for each subject (the mean number included in Fig. 7), the expected correlation is 0.76. That indicates that 76% of the variance in our final representation of MOCR strengths (Fig. 7b) is caused by subject-specific variation in MOCR strength. This is in agreement with the 79% estimated via the first method.

FIG. 8.

The plot shows how increasing the number of frequencies included in an SFOAE-based MOCR strength measure produces more subject-dependent (correlated) measures. Dots represent the mean bootstrapped values from the collected data for 25 subjects; error bars are ±1 SE, but all error bars are obscured except at N = 1. The curve is an exponential fit to these points described by the equation shown. The triangle shows the value from the grouping used in Figure 6. The square represents the extrapolated expected value when all the frequencies for each subject (that meet the SNR criteria) are combined as in Figure 7

DISCUSSION

How well does our MOCR strength distribution match the real strength distribution?

Our statistical tests indicate that 76–79% of the variance seen in the MOCR strength distribution of Figure 7b is caused by the differences in the MOCR reflexes across subjects. The remainder is attributable to measurement variation. However, how well the distribution of Figure 7 captures the actual distribution of MOCR strengths depends on how closely MOCR-induced changes in SFOAEs follow MOCR-induced inhibition within the cochlea. One metric for intracochlear inhibition is the MOCR-induced attenuation of cochlear neural responses. In anesthetized cats, MOC-induced changes in SFOAEs have been reported to be roughly proportional to the MOC-induced inhibition of the compound action potential (CAP) from tone pips at the same frequency (Guinan 1991). If this result holds for humans, the results of Figure 4 indicate that the ΔCAP/ΔSFOAE proportionality constant changes with small changes in frequency. We overcame this fine-scale frequency variation by averaging across frequency and obtained consistent measures from each subject (Fig. 6). It should be noted that the proportionality constant of ΔSFOAE to ΔCAP might vary across subjects, although there is no reason to expect that it does.

The relationship between MOCR effects on OAEs and MOCR effects on cochlear gain is not known for any OAE and is, therefore, an issue when using any OAE to determine MOCR strength. There is only one published comparison of MOCR-induced OAE changes to neural changes. MOCR-induced changes in DPOAEs measured at a single frequency with a single parameter combination are not well correlated to the MOCR effective attenuation determined neurally (Puria et al. 1996). In contrast, Maison and Liberman (2000) found that MOCR effects on DPOAEs measured in a matrix of F1 and F2 levels near a response dip yielded a metric that was correlated in group averages with a MOCR physiological effect protection from acoustic trauma. Maison and Liberman’s result shows that this MOCR metric does provide information about MOCR strength (Wagner et al. 2007). In short, whereas it seems clear that MOCR inhibition of OAEs provides some information about the neural effects produced, we do not know, for any OAE metric, how well correlated OAE changes are with neural attenuation or whether that relationship is a linear one.

We speculate that the relationship between MOCR-induced changes in neural responses and OAEs is more straightforward for SFOAEs than for DPOAEs because SFOAEs from low-level tones are produced by a single mechanism, coherent reflection (for 40 dB SPL probe-tones), whereas DPOAEs are produced by two processes, distortion and coherent reflection (Shera and Guinan 1999), and these two sources interact in a complex way to produce the DPOAE. TEOAEs, which appear to be the inverse FFT of component SFOAEs (Kalluri and Shera 2007), might also have a high correlation with MOCR attenuation. However, a confound when using TEOAEs is that the TEOAE-evoking stimulus is itself a strong elicitor of MOC activity (Guinan et al. 2003). Whereas OAEs are good for testing MOCR strengths across individuals because the tests are easy to do, the accuracy of OAE tests is unknown. In particular, the relationship between MOCR effects on OAEs and on neural responses must be determined experimentally to put these tests on a firm basis.

In addition to the uncertain correspondence between MOCR-induced changes in OAEs versus in neural attenuation, several other things must be kept in mind in interpreting the MOCR strength distribution of Figure 7b: (1) The distribution is for the frequency region near 1 kHz with MOC activity produced by 60 dB broadband contralateral noise. The relative strengths across subjects could be different in other frequency regions, at other sound levels, or between the ipsilateral and the contralateral reflexes, although there is no reason to expect systematic variation in relative strengths across subjects because of any of these. (2) Our elicitor level and our SFOAE probe level were set in dB SPL, and it is possible that a different distribution would have been obtained if they had been set relative to each subject’s individual threshold. It seems likely that for levels near threshold, tighter distributions would be obtained by setting the levels relative to the individual’s threshold of hearing, but it is not clear if this would be true for high elicitor levels. For instance, faster recruitment in subjects with poor hearing tends to make the middle ear muscle reflex thresholds to contralateral tones be more tightly distributed when expressed in dB SPL than when expressed in sensation level (Gelfand and Piper 1984). Thus, for this reflex, the strength distribution is a function of sound level. (3) The 60-dB SPL elicitor is within the range in which the reflex is still growing as sound level is increased (Backus and Guinan 2006). It is possible that the reflex effect saturates, and that saturation levels differ across individuals in a way that is not highly correlated with the reflex strength at 60 dB SPL. If this is the case, then what we have measured is the strength at one elicitor level, as opposed to the total capacity of the reflex at very high levels. The importance of this distinction depends on what the MOCR distribution is used for. For correlations with possible MOCR antimasking effects, reflex strength might be most important, whereas for correlations with the prevention of damage as a result of intense sounds, the reflex total capacity might be most important.

Comparison with prior work

De Ceulaer et al. (2001) was the first study to explicitly recognize that individual MOCR strengths vary and to attempt to plot a normative distribution of MOCR strengths. There are also several other papers that show individual MOCR effects across subjects from which MOCR strength distributions might be calculated (Micheyl et al. 1995; Micheyl and Collet 1996; Kumar and Vanaja 2004; Muller et al. 2005; Wagner et al. 2005, 2007). A major drawback of the De Ceulaer et al. distribution is that no information was provided on the amount of measurement error in the data. Indeed, the skewed distribution presented by De Ceulaer et al. is precisely what would be expected for a distribution infused with noise (Backus 2007). Distributions calculated from the other published data would also have poorly described measurement variance. Knowing how much of the distribution variance arises from the underlying variations in subject MOCR strength versus in measurement variation is a basic requirement of any putative strength distribution. Ideally, the data presentation would include both a measure of the error in the strength determinations for each subject (as in Fig. 7a) and the amount of variance caused by error in the final distribution (as done for Fig. 7b).

The De Ceulaer et al. (2001) study also calls attention to several other issues in using TEOAEs to obtain an MOCR strength distribution: (1) The stimulus De Cuelaer et al. used to evoke TEOAEs is likely to have also activated the ipsilateral MOCR in both the control and contralateral sound-on conditions, and how that may change the MOCR effect produced by the contralateral sound is unknown. (2) The click levels used by De Ceulaer et al. (2001) may have been high enough to produce middle ear muscle reflex effects that went unseen using a clinical reflex test. (3) The TEOAEs were obtained using the “nonlinear clicks” method of Kemp et al. (1986) which cancels out the linear part of the response. How well the remaining nonlinear part of the response mimics the whole response is unknown. (4) The TEOAE results of De Cuelaer et al. were analyzed by subtracting overall time-domain averages, which mixes MOCR-induced level and phase changes. On the other hand, one possible advantage of the TEOAE method over our SFOAE method is that TEOAE responses usually contain many frequency components thereby providing inherent averaging across frequency. If low-level, linear TEOAEs were used, the disadvantages listed above might be avoided so that TEOAEs might be the preferred method for measuring MOCR strength. However, in TEOAE studies to date, high levels were used and the disadvantages were present.

The origin of fine-scale frequency-dependent variations in MOCR effects on SFOAEs

Initially, our working hypothesis was that MOCR activation would cause an approximately constant-fraction reduction in cochlear amplifier gain with the fraction changing only slowly with frequency. Instead, we found that for small changes in frequency (e.g., 40 Hz) there could be significant changes in the fraction, i.e., in the normalized MOCR-induced change in the SFOAE, ΔSFOAE (Figs. 4 and 5). In mathematical terms, our working hypothesis was:

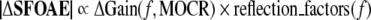1

This says that the change in the magnitude of an SFOAE would be proportional to the change in the cochlear amplifier gain evoked by MOCR activation multiplied by reflection factors. Equation 1 is a simplification. According to coherent-reflection theory, the SFOAE magnitude is the integration across the length of the cochlea of a local scattering factor times the square of the local cochlear amplifier gain (Zweig and Shera 1995), thus Eq. 1 is an approximation valid only for small |ΔSFOAE|.

Because both the cochlear amplifier for a given frequency and the MOC innervation affecting this frequency are spread along the cochlea, we assumed that those factors in Eq. 1 would change slowly with frequency. Evidently, this is not true. If our thinking about how the MOCR changes cochlear gain and how SFOAEs are generated is correct, then this finding indicates that there is an unappreciated interaction between these factors in Eq. 1—one that is different from the simple multiplication shown there. It is well established that SFOAE amplitudes can vary rapidly over frequency, an effect that presumably originates in the irregularity of the reflection factors as a function of frequency (Zweig and Shera 1995; Talmadge et al. 2000). Lowering cochlear amplifier gain makes less energy available for reflection, but it also makes the traveling wave amplitude less peaked and this change in the traveling wave envelope will change the pattern of reflected wavelet cancellations versus coherence and might lead to rapid changes in ΔSFOAE across frequency. It is also possible that SFOAE reflection factors (e.g., the gains of individual OHCs) are affected by MOCR activation. We do not know whether the rapid changes in ΔSFOAEs over frequency should be ascribed mainly to changes in traveling wave shape or to changes in reflection factors. Because SFOAEs are the integral over the length of the cochlea of both gain and reflection factors, both can be involved.

The effect of the reflex strength distribution on MOCR roles in hearing

There are currently many postulated roles for the MOCR in hearing: developmental (Walsh et al. 1998), protective (Rajan and Johnstone 1983; Reiter and Liberman 1995), dynamic range adjustment (Geisler 1974; Winslow and Sachs 1988), enhancing signal detection in noise (Winslow and Sachs 1988; Kawase et al. 1993). All of these, except perhaps the developmental, would be affected by variations of reflex strength across individuals. The approximate factor of 4 variation we have found in MOCR reflex strengths can be expected to produce a similar variation in the extent to which the MOCR does each of these things. Thus, tests done to discern the extent of such MOCR effects on hearing would benefit from measuring reflex strength in the same individuals. The present work demonstrates the feasibility of doing such tests, along with caveats regarding the methods used. More work is required to adapt OAE-based measurements of MOCR strength so they can be routinely and efficiently done in a clinical setting.

Conclusions

1. We found unexpected fine-scale frequency dependence in the effect of contralateral acoustic stimulation on SFOAEs to an extent that renders MOCR effects on an SFOAE at a single frequency a poor measure of MOCR strength.

2. By averaging MOCR effects on SFOAEs across several frequencies, we were able to obtain a metric for MOCR strength that yielded a distribution in which 76–79% of the variance was caused by subject-specific variations in MOCR strength.

3. Using 60 dB SPL wideband contralateral noise, this metric showed a distribution of MOCR strengths in a normal-hearing population that is relatively symmetrical, produced an average change in the SFOAE of 35% of the normal SFOAE amplitude, and had a SD approximately 1/3 of the mean. The neural attenuation corresponding to this SFOAE change remains to be determined.