Absence of Voltage-Dependent Compliance in High-Frequency Cochlear Outer Hair Cells

Abstract

Cochlear outer hair cells are the key element in a mechanical amplification process that enhances auditory sensitivity and tuning in the mammalian inner ear. The electromotility of outer hair cells, that is, their ability to extend or contract at acoustic frequencies, is proposed to be the source of the mechanical amplification. For amplification to take place, some stiffness is required for outer hair cells to communicate force to the organ of Corti, the sensory epithelium of the inner ear. Modulation of this stiffness would be expected to have a significant effect on inner ear function. Outer hair cell compressive stiffness has recently been shown to be dependent on membrane potential, but this has only been demonstrated for cells originating in the apical, low-frequency segment of the cochlea, whereas cochlear amplification is arguably more important in the more basal high-frequency segment. The voltage-dependent compliance (the reciprocal of stiffness) of high-frequency outer hair cells was investigated by two methods in cells isolated from the basal turns of the guinea pig cochlea. In contrast to previous findings, no evidence was found for voltage-dependent changes in compliance. The results call into question the importance of outer hair cell voltage-dependent compliance as a component of cochlear amplification.

INTRODUCTION

The outer hair cells (OHCs) of the mammalian cochlea are sensory hair cells that are also electromotile, that is, they contract or lengthen in direct response to membrane potential change (Ashmore and Gale 2000; Kachar et al. 1986). This electromotility, driven by the sound-induced OHC receptor potential, is believed to supply a mechanical amplification step to the vibration pattern of the cochlea’s sensory substrate, the basilar membrane (Santos-Sacchi 2003; Nobili et al. 1998). The amplification is believed to be necessary to overcome viscous forces due to the rapid movement of the basilar membrane at acoustic frequencies and to confer high sensitivity and frequency selectivity at low sound pressure levels, although how this might work is not clear.

For OHC motility to have a significant effect on basilar membrane motion, the OHC must have sufficient axial stiffness (Hallworth 1995). The properties of this stiffness are clearly important, and agents such as osmotic challenge and the efferent neurotransmitter acetylcholine that are known to affect cochlear function have also been shown to modulate OHC axial stiffness (Hallworth 1997a, b; Dallos et al. 1997). More recently, OHC stiffness has been demonstrated to be modulated directly by OHC membrane potential (He and Dallos 1999, 2000; He et al. 2003). OHC stiffness decreased when depolarized and slightly increased when hyperpolarized. The membrane potential range of modulation corresponded directly with electromotility itself, which indicated that the two processes were intimately linked.

This phenomenon is potentially very important to our understanding of cochlear function, and not only for the effective communication of OHC force to its load. Assuming that OHC axial stiffness represents a substantial portion of total basilar membrane stiffness, dynamic changes in OHC stiffness could modify basilar membrane vibration on a cycle-by-cycle basis. A stiffness decrease (the elastic component of impedance) could even represent the basis of cycle-by-cycle mechanical amplification (Diependaal et al. 1986).

Such amplification should be most significant in the high-frequency basal turn of the cochlea where viscous forces would be greatest. However, the previous studies were performed on OHCs derived from the low frequency cochlear apical turns. In this study, the voltage-dependent compliance (the reciprocal of stiffness) of OHCs from the high-frequency cochlear basal turns has been examined for the first time. Both compressive pulse stimuli and sinusoidal mechanical stimuli (resembling those in He and Dallos 2000) were used. No evidence for voltage dependence was found with either method. The results suggest that voltage-dependent compliance does not exist in high-frequency OHCs, and therefore, any voltage-dependent stiffness observed in low-frequency OHCs may not be relevant to normal hearing.

MATERIALS AND METHODS

Preparation of isolated OHCs

Isolated OHCs were prepared from guinea pig cochleas according to previous methods (Hallworth 1995, 1997a, b) with small modifications. Barbiturate anesthesia was induced via intraperitoneal injection. Strips of organ of Corti were incubated at room temperature for 30 min in a solution of 1% papain (Calbiochem, San Diego, CA) in Hank’s solution with no calcium or magnesium ions. The experimental solutions were Leibovitz’s L-15 supplemented with 10 mM HEPES and 0.1% bovine serum albumin (pH 7.25, adjusted to 300 mOsm). Leibovitz’s L-15 consists of (inorganic salts only) 139.6 mM NaCl, 5.3 mM KCl, 1.3 mM CaCl₂, 1.0 mM MgCl₂, 0.8 mM MgSO₄, 1.3 mM Na₂HPO4, and 0.4 mM KH₂PO4. Unlike previous studies, no ion channel blocking solutions were used. Enzyme-treated organ of Corti pieces were triturated into an experimental chamber on an inverted microscope. Shorter OHCs, presumed to be from the high-frequency cochlea (turns 1 and 2), were used preferentially in this study (Pujol et al. 1992; Tsuji and Liberman 1997). Cells selected for experimentation were less than 50 μm in length, straight with diameter constant between 8 and 9 μm, had cytoplasm free of moving particles, and had nuclei properly located at the basal pole.

Experimental approach

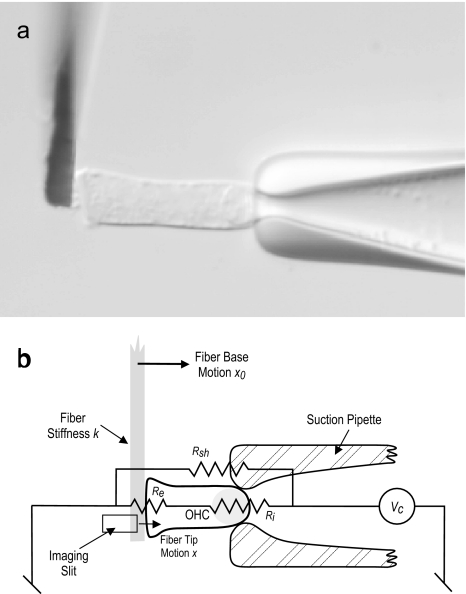
The configuration of a typical experiment is shown in Figure 1. Isolated cells were held by their basal poles by a suction pipette fabricated from 2-mm outside diameter borosilicate glass. The pipette orifice diameter was smaller than the diameter of an OHC. OHC axial compliance (the reciprocal of stiffness, used here for comparison with previous data) was measured using square-wave compression or sinusoidal fiber motions delivered using a calibrated glass fiber of known stiffness (Hallworth 1995, 1997a, b). Details of the fiber motion waveforms are given below. As shown in Figure 1, the fiber with cell attached was placed such that it overlapped the edge of a slit placed in front of a photodiode-based motion measurement system. Lateral motion of the fiber therefore modulated the intensity of the light falling on the photodiode, thereby providing a measure of fiber motion (Hallworth 1995). Motion of the fiber was driven using a piezoelectric pusher and driver (Burleigh PZO-015 and PX-150, Fishers, NY). Sinusoidal voltage commands and bias pulses were delivered via the suction pipette using a patch clamp amplifier (Model 8900, Dagan Corp., Minneapolis, MN). Motion of the fiber was measured using a photodiode-based measurement system and calibrated by image deflection using an optical lever (Clark et al. 1990). Fiber motion waveforms were averaged from up to eight consecutive presentations.

FIG. 1.

Experimental method. a Photomicrograph of an isolated OHC (length 38 μm) held by a suction pipette with a calibrated glass fiber placed at the apex. b Diagram of the experimental situation indicating membrane resistances of the OHC (R_i and R_e) and the shunt resistance R_sh.

Stimulus waveforms were generated and motion waveforms acquired using an A/D-D/A board (KCPI 3801, Keithley Instruments, Taunton, MA) in an IBM PC-type computer. The fiber motion waveform was digitized at 800 Hz after low-pass filtering at 400 Hz. Stimulus presentation and data acquisition and analysis functions were written in TestPoint (CEC Corporation, Burlington, MA).

Although most aspects of the methods used in the study are common to previous studies (Hallworth 1995, 1997a, b), several technical differences need to be emphasized. The OHC plasma membrane segment in the pipette (called the included segment) is in series with the remainder of the membrane outside of the pipette (the excluded segment). The resistances of the two membrane segments (R_i and R_e) are in series (shunted by the seal resistance R_sh) and form a voltage divider biased towards the much smaller, and therefore much higher resistance, included segment (Fig. 1b). Thus, the effective voltage command delivered to the excluded segment, V_e, is related to the voltage command applied to the pipette interior, V_c, by the following relationship:

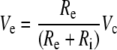Shorter OHCs were used exclusively, which, because of the relatively smaller excluded segment area, enabled larger bias voltage polarizations in the excluded segment without breaking down the included segment membrane in the suction pipette. In addition to a more favorable voltage divider than longer cells, basal cells also have larger resting membrane conductances in the basal pole (Housley and Ashmore 1992; Santos-Sacchi et al. 1997) which further favorably reduces the bias of the voltage divider in favor of the excluded segment. It was to take advantage of these larger resting currents that no blocking ions such as tetraethyl ammonium or cobalt were used. A third advantage of shorter cells is that they are intrinsically straighter than longer cells and therefore easier to align. A fourth advantage is that shorter cells undergo smaller length changes than longer cells and, therefore, are less likely to lose contact with the fiber or to move the fiber out of range of the photodiode motion measurement system.

Measurement of voltage-dependent compliance

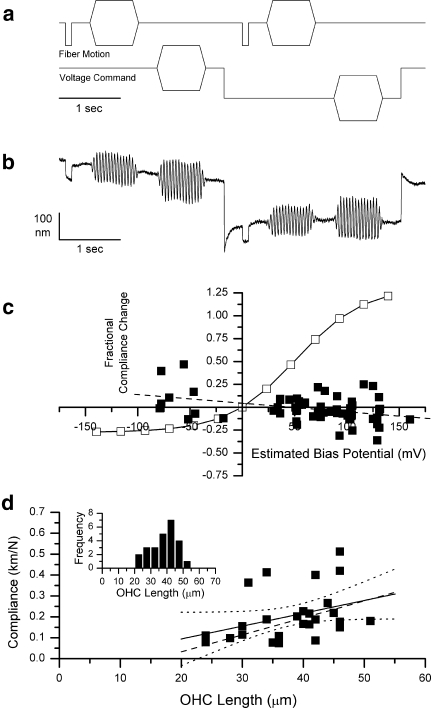
For comparison with previous data, all mechanical measures on OHC are expressed as compliance, the reciprocal of stiffness. For measurement of compliance and compliance change by the pulse method, the fiber motion consisted of: (1) a compressive pulse of amplitude −300 nm and duration 100 ms, followed by (2) a sinusoidal burst of frequency 20.3 Hz [chosen as an exact fast Fourier transform (FFT) component of the stimulus waveform], amplitude 300 nm, duration 800 ms, with onset and offset ramp duration of 100 ms. OHC compliance was calculated from the amplitude of the fiber tip motion in response to the compressive pulse. The simultaneous pipette voltage commands consisted of: (1) a sinusoidal burst waveform of frequency 20.3 Hz, amplitude 120 mV, duration 800 ms, onset and offset ramp duration of 100 ms, (2) a bias voltage command pulse of variable amplitude and of duration 2,900 ms initiated at 3,200 ms from the start of acquisition, and (3) a repetition of the sinusoidal voltage burst during the bias pulse. The fiber rectangular pulse and sinusoidal motion were also repeated during the bias pulse. The waveforms are depicted in Figure 3a.

FIG. 3.

Determination of voltage dependence of compliance by the compressive pulse method. a Voltage command and fiber motion command waveforms as a function of time. b Typical fiber motion waveform in response to the above fiber and voltage commands. This cell was 39 μm long, and the biasing step voltage command was 300 mV. The calculated compliance was 0.183 km/N before and 0.178 km/N during the bias voltage command. c Fractional compliance change as a function of estimated membrane potential change for 63 measurements from 26 cells (all cells studied from six animals). The solid line represents the expected fractional compliance change if the cell behaved like the reference cell. The dashed line fitted to the data has a slope of 0.00094/mV and an intercept of 0.044. d Resting compliance as a function of cell length for the 26 cells used in this part of the study. The fitted line (R = 0.37) has a slope of 0.00614 km M⁻¹ μm⁻¹. The dashed line represents the compliance versus length function for the 89 cells in Hallworth (1997b). Inset Histogram of lengths of cells used in this part of the study.

For measurement of compliance and compliance change by the continuous sinusoid method, fiber motion consisted of a continuous sinusoid of amplitude 300 nm, frequency 20.3 Hz, and duration 5,800 ms, latency 100 ms. The waveforms are depicted in Figure 5a. For some experiments, the frequency of the sinusoidal fiber motion was increased to 100.0 Hz. The simultaneous pipette voltage command consisted of a bias voltage command pulse of variable amplitude and of duration 2,900 ms initiated at 3,200 ms from the start of acquisition.

FIG. 5.

Determination of voltage-dependent compliance change by the sinusoidal method. a Voltage command waveform and fiber motion command waveform as a function of time. The fiber sinusoid amplitude was 300 nm. The voltage command sinusoid amplitude was usually 120 mV. The step voltage command was varied. b Typical fiber motion waveform (cell extension upward) in response to the above fiber and voltage commands. This cell was 35 μm long, and the biasing step voltage command was 240 mV. The calculated compliance was 0.20 km/N before and 0.23 km/N during the bias voltage command. c Fractional compliance change as a function of estimated membrane potential change for 32 measurements from 26 cells (all cells studied from six animals). The solid line represents the expected fractional compliance change if the cell behaved like the reference cell. The line fitted to the data has a slope of 0.00094 and an intercept of 0.044. d Correlation between compliance measures for the same cells (12 cells). The fitted line has a slope of 1.20 and an intercept of 0.013 (R = 0.962).

When the driven frequency of the fiber motion was 20.3 Hz, the peak-to-peak amplitude in response to sinusoidal fiber motion was measured as twice the 20.3-Hz component of the FFT of the motion waveform. Similarly, the AC component of the force waveform was measured as twice the 20.3-Hz component of the FFT of the force waveform. The DC component of the force waveform was determined from the zeroth frequency component of the same FFT. When the driven frequency of the fiber was 100.0 Hz, twice the 100.0-Hz Fourier component was used as the amplitude measure.

Calculation of compliance and compliance change

Fiber deflection in response to a square-wave pulse was computed as the difference between the averages of five sample points immediately after and immediately before the initial rapid phase of the deflection. Compliance C was calculated as:

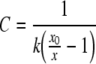where k is the fiber stiffness, x is the fiber deflection and x₀ is the amplitude of motion of the fiber base. Nearly all of the data presented here were obtained using one fiber, of stiffness 1.02 mN/m. The fractional compliance change due to electrical bias δC was calculated as:

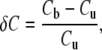where C_b and C_u are the compliances in the electrically biased and unbiased states, respectively.

Measurement of voltage to length change function

The voltage to length change function for each cell was determined by application of a series of 17 consecutive voltage command segments, each 100 ms long, consisting of a 10-ms positive pulse followed by a 10-ms negative pulse. The stimulus waveform is depicted in Figure 2a. Pulse magnitudes increased in steps of 20 mV from 0 to 300 mV.

FIG. 2.

Estimation of membrane potential change due to voltage commands. aAbove Voltage command waveform as a function of time. The maximum pulse amplitude is ±300 mV. Below Typical fiber motion waveform (cell extension upward) in response to the above voltage command. Inset Diagram of a single pulse pair showing their relative timing and typical fiber motion response waveform (±300 mV). This cell was 30 μm long. b Amplitudes of fiber motion as a function of voltage command for the same cell as a and b. The fitted curve is given by V_e = −67.31 mV, dx = 74.32 mV, A₁ = 61.60 nm, A₂ = −159.74 nm (R² = 0.99).

Estimation of membrane potential change due to bias voltage command

To estimate membrane potential change of the excluded segment due to a voltage command, a reference cell of known membrane potential to length change function was needed. Because few complete membrane potential to length change functions have been published, a membrane non-linear charge function from Figure 10 of Santos-Sacchi (1991) was assumed to be representative of normalized total length change from the hyperpolarized state. Using the published first-order Boltzmann function fit to that data, the quantities V_m20 and V_m80, the values of membrane potential at which the charging curve was 20 and 80% of its maximum value, were obtained. For each cell in this study, a first-order Boltzmann function of the form:

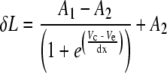was fit to the measured length changes as a function of voltage command V_c using the sigmoid fitting function in Origin (Microcal, Northampton, MA) where V_e is the voltage command in millivolt at 50% of the maximum length change, dx is a scaling factor, also in millivolt, A₁ is the maximum extension in nanometer, and A₂ is the range of length change observed, also in nanometer. This fitting function also returned the values of V_c20 and V_c80, the voltage commands that evoked 20 and 80% of the maximum length changes for the cell. Thus, the membrane potential change δV_m due to the voltage command V_c for each cell was calculated as:

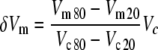Control for fiber contact artifacts

During a depolarizing bias voltage command, an OHC contracts and moves away from the measurement fiber. It was found to be essential to monitor the symmetry of the sinusoidal fiber motion even when the pulse was being used for compliance measurement. If the initial contact between fiber and cell is insufficient, after depolarization, the fiber will not be in contact with the cell during part of its motion, which would appear as an increase in compliance, that is, a decrease in stiffness. Asymmetry in the sinusoidal fiber motion was taken as an indication of improper contact between OHC and fiber, and the data obtained were not considered.

RESULTS

Estimation of membrane potential change induced by voltage commands

As described in “MATERIALS AND METHODS”, the range of fiber motion (reflecting OHC length change) that was evoked by voltage commands was measured using a series of biphasic voltage pulses extending from ±20 to ±300 mV in 20-mV steps. The voltage command waveform and a typical evoked fiber motion response to that waveform are shown in Figure 2a. The fiber motion is plotted as a function of voltage command amplitude in Figure 2b. As expected, the amplitudes were a non-linear function of the voltage command amplitude. Elongation saturation was evident to hyperpolarizing commands, while the beginnings of contraction saturation were evident to depolarizing commands. For each cell, the results were fitted to a first-order Boltzmann function and then scaled to the voltage range of the total charge transfer function of a cell under voltage clamp, as described in “MATERIALS AND METHODS”. This information was then used to estimate the membrane potential change due to biasing voltage commands.

Compliance change as a function of estimated membrane potential bias

Compliance and compliance change were measured using the fiber motion and voltage command waveforms shown in Figure 3a. After the compressive pulse and sinusoidal 10-Hz fiber motions were applied to measure compliance and a 10-Hz sinusoidal voltage command burst was applied to measure electromotive force, a voltage bias command of magnitude ranging from −120 to +300 mV was presented and the three measures repeated. The compliance and the compliance change were calculated as described in “MATERIALS AND METHODS”. Generally, several different voltage bias commands were tested for each cell.

An example of such an experiment is shown in Figure 3b. The biasing voltage command (in this case, 200 mV) evoked an initial contraction that then sometimes, but not always, relaxed, either further in the compression direction or back towards the baseline. The origin of this relaxation may be mechanical or it may be a function of the relationship between the membrane electrical time constants of the two segments, which are in series with each other. This question will be examined later. Note that as was almost always observed, the mechanical compression induced by the square-wave fiber motion was essentially identical before and during the bias voltage command. The compliance was therefore unchanged by the biasing voltage command. Note also that the amplitude of the fiber response to the sinusoidal fiber motion bursts was also unchanged.

The membrane potential change evoked in this cell by the bias voltage command was estimated to be 90.68 mV. In support of this estimate, it was observed that the sinusoidal voltage command evoked a fiber motion that was originally asymmetrical in the compression direction in the unbiased state, but was asymmetrical in the extension direction during the depolarizing bias command. This strongly suggests that the bias voltage command had sufficiently depolarized the OHC to move the operating point of the voltage to length change function close to the contraction saturation point (Santos-Sacchiw 1991; Evans et al. 1991).

Figure 3c shows the fractional compliance change observed as a function of estimated bias membrane potential. The results are from 63 trials on 26 cells obtained from five animals. For comparison, the open symbols and thin line indicate the predicted compliance change based on the reference cell depicted in Figure 5 of (He and Dallos 2000). The original data, which were expressed as stiffness as a function of voltage command, were converted to compliance, then to compliance change from resting compliance, and were scaled to estimated membrane potential by the same procedure as described in “MATERIALS AND METHODS”.

In contrast to the prediction from the reference cell, essentially no change in compliance was seen in the current experiments over an estimate membrane potential bias range of −80 to +130 mV. The slope of the line of best fit was −0.00094 per mV. While the fit was poor (R = −0.388), it was apparent from the data that the observed change in compliance was essentially zero and was, in any case, much smaller than that predicted from the previously published results.

In Figure 3d, the resting compliance of the same cells is plotted as a function of cell length. The line of best fit (R = 0.367) is shown in black. For comparison, the line of best fit from a previously published data set from this laboratory is shown as a dashed line (Hallworth 1997b). The slope of this line of best fit falls within the 95% confidence limits of the slope of the present data. Thus, the population of cells examined in this study is comparable with those examined in the previous study. The range of cell lengths studied is depicted in the inset of Figure 3d. The population of cells studied appeared to be otherwise normal. Based on morphological data, the OHC lengths correspond to cochlear locations of best frequencies from 0.7 to 22.5 kHz, depending on OHC row (Pujol et al. 1992).

Compliance change as a function of mechanical bias

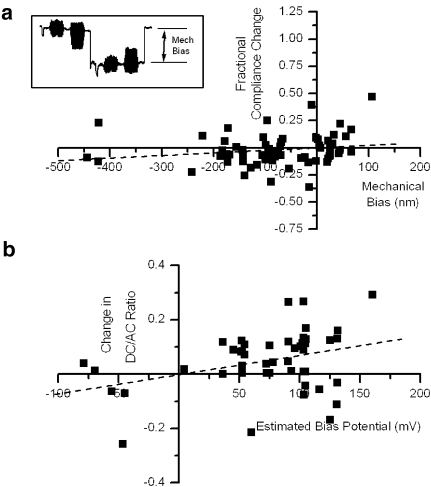
As previously described, the relaxation of length change after application of the bias pulse may reflect a slow mechanical process or it may reflect filtering by the electrical network composed of the basal membrane of the OHC in series with the apical membrane. If electrical filtering were occurring, the length relaxation may be a consequence of relaxation of the imposed membrane potential bias. In turn, the estimated membrane potential bias may not be accurate at the time that the test compressive pulse was applied. To test this possibility, the fractional compliance change was plotted as a function of the mechanical bias evoked at the time of the compressive pulse. The results of this analysis are plotted in Figure 4a for the same 63 measures in 26 cells as Figure 3c. The results could be fit weakly (R = 0.18) by a line with almost zero slope (0.00023/nm) as a function of mechanical bias. Thus, there was no indication that the actual deflection, as distinct from the estimate of the imposed electrical bias, significantly altered compliance.

FIG. 4.

a Fractional compliance change as a function of mechanical bias (change in cell length from resting to just before the compliance measurement, for the same cells and measurements as in Figure 3c. The fitted line (R = 0.18) has a slope of 0.00023 and an intercept of −0.00066. b Change in DC/AC ratio of the force waveform as a function of estimated membrane bias potential change. The fitted line (R = 0.347) has a slope of 0.00071 and an intercept of −0.002.

Change in DC/AC ratio of the force waveform by bias voltage command

Changes in the evoked motion of the fiber in response to a sinusoidal voltage command were examined as a partial confirmation that the biasing membrane potential command had the desired effect on membrane potential. From previous studies (Evans et al. 1991; Dallos et al. 1991), a contraction asymmetry of the waveform is normally seen at the resting membrane potential, and this asymmetry becomes less pronounced as the cell is depolarized. If the depolarization is sufficiently large, the asymmetry may become positive (the extension direction; see Figure 3b). As an unbiased estimator of the DC component, the zeroth frequency component of the Fourier transform of the force waveform was calculated and was then compared to the stimulus frequency AC component as the DC/AC ratio. The observed changes in the DC/AC ratio are plotted in Figure 4b as a function of estimated bias potential. Consistent with the hypothesis that the membrane potential was being substantially changed by the bias potential, the DC/AC ratio was overwhelmingly biased in the extension direction by depolarizing bias pulses. Further, the change in DC/AC ratio was weakly but positively correlated with the magnitude of the estimated bias potential (slope 0.00071/mV, R = 0.347).

Sinusoidal measurements of compliance change as a function of estimated membrane potential bias

Previous studies (He and Dallos 1999, 2000) used long-duration continuous sinusoidal fiber motion to measure OHC compliance and compliance change. To determine if the measurement of voltage-dependent compliance is influenced by the measurement method, OHC compliance change was studied using a 20.3 Hz sinusoidal fiber motion (amplitude 300 nm) in a separate sample of OHCs. The fiber motion and voltage command waveforms are illustrated in Figure 5a, and a representative fiber motion waveform in response to these stimuli are shown in Figure 5b. The fractional compliance change results for 31 measurements from eight cells are shown in Figure 5c as a function of estimated bias potential. Again, for comparison, the predicted compliance change based on the reference cell is shown as open symbols and a thin line. While there is a weak positive correlation between fractional compliance change and bias potential (R = 0.41), the magnitude of the change was evidently nowhere near that predicted (slope 0.00027/mV). Thus, there appeared to be little compliance change in OHCs as a function of membrane potential by either of the two methods.

Relationship between pulse and sinusoidal measures of OHC compliance

Although pulse and sinusoidal measures of compliance and voltage-dependent compliance change were made mainly on different OHCs, to ensure that the two methods measured essentially the same quantity, in a limited number of cases, compliance and compliance change for both methods were compared in the same OHCs. The measured compliance by the sinusoid method is plotted in Figure 5d as a function of the measured compliance by the pulse method from 12 measures in six cells from three animals. The straight line fit is shown as a dashed line. The correlation between the two methods is strong (slope 1.20, R = 0.962), which indicates that the two methods are essentially equivalent, with the sinusoidal method systematically estimating compliance at about 20% higher than the pulse method.

Frequency independence of sinusoidal compliance measurements

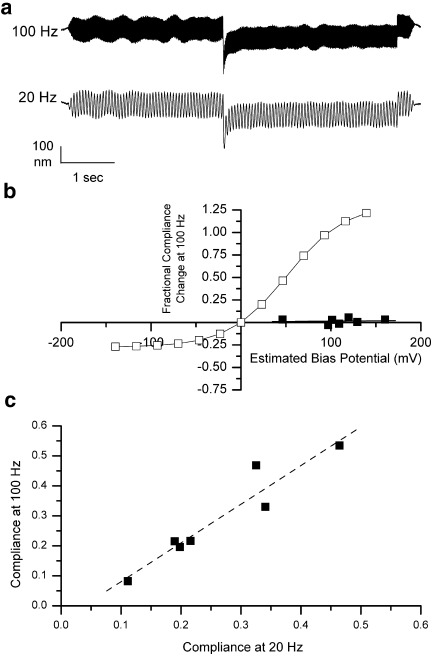
The previous measurements were taken using a 20.3-Hz sinusoidal fiber motion. To eliminate the possibility that the absence of voltage-dependent compliance was frequency-specific, a small sample of cells (seven) were studied at 20.3 and 100.0 Hz using a 240-mV bias voltage command. An example is shown in Figure 6a. As shown in Figure 6b, no significant compliance change was observed in response to voltage commands. Further, the compliance at 100.0 Hz strongly correlated to the compliance measured at 20.3 Hz (Fig. 6c). As no voltage-dependent compliance change was observed at 20.3 Hz, this is further evidence that the absence of compliance change is not a frequency-specific phenomenon.

FIG. 6.

a Comparison of sinusoidal compliance measures obtained at two different frequencies in the same cell. b Fractional compliance change measured using a 100 Hz sinusoidal fiber motion as a function of estimated membrane potential change for seven measurements from seven cells (from two animals). The solid line represents the expected fractional compliance change if the cell behaved like the reference cell. The line fitted to the data has a slope of 0.000067/mV and an intercept of 0.0083. c Correlation between compliance measures at 20.3 and 100 Hz for the same seven cells. The regression line has a slope of 1.29 and an intercept of 0.013 (R = 0.95).

DISCUSSION

This study has observed in high-frequency OHCs a strikingly different result from that previously observed in low-frequency OHCs (He and Dallos 1999, 2000; He et al. 2003). High-frequency OHCs exhibited essentially no voltage-dependent compliance change by three different methods. The cells used in this study are entirely comparable to cells of similar lengths used in previous studies from this laboratory (see Fig. 3d and “RESULTS”). In comparison, the range of stiffnesses of the OHCs used in He and Dallos (2000) was not given. The reference cell had a stiffness of approximately 5.8 mN/m (compliance 0.17 km/N), which is comparable to the OHCs reported here.

There are, however, some remaining differences in the methods between the studies. Firstly, the OHCs used in this study are shorter (only up to 50 μm long) than those in the previous studies. Shorter OHCs have several advantages over long OHCs for axial compliance measurements. They are easier to align than longer OHCs, and the fiber motions observed in response to voltage commands are smaller. The latter is especially important during depolarizing voltage commands for which the resulting contraction may disconnect the OHC from the fiber. Secondly, this study used a suction pipette to provide a firm base for the OHC, whereas the previous study used the microchamber method in which the cell may slide in and out (Evans et al. 1991; Dallos et al. 1991; Hallworth et al. 1993). The microchamber method permits a larger membrane potential change to be delivered to the OHC excluded segment. However, the use of shorter OHCs makes this difference less significant. Further, the voltage to length change functions obtained in this study indicated that the bias commands covered most of the dynamic range of OHC motility. A third difference is that the primary method used in this study for determining compliance is a compressive pulse, compared with the sinusoidal method used in the previous study. However, this study has also demonstrated that the compressive pulse method gives equivalent results to the sinusoidal method at two different frequencies. Finally, the fiber motion commands used in this study were smaller than in the previous studies. However, such compressions may be more realistic in that they are closer to the motion amplitudes anticipated during normal operation.

Of the prior studies referred to earlier, the study most closely resembling this one in method (He and Dallos 2000) used the microchamber to secure the OHC, 100-Hz sinusoidal fiber motion to measure stiffness, and 1- to 10-Hz sinusoidal voltage commands to apply bias. Although a complete breakdown is not given, the preponderance of the OHCs specifically described in that study had lengths greater than 60 μm. Only one cell (out of nine described) was less than 50 μm long. It is interesting that only 38 of 46 cells were reported to show voltage-dependent stiffness, which suggests a measure of vulnerability, although it is unclear to what extent stiffness was modulated in the reported examples. The reference cell varied in stiffness from 7.6 to 2.5 mN/m, a factor of 3, while in another cell (their Fig. 6), the apparent stiffness range is a factor of 8. Whether these are representative, atypical, or even extreme values is unclear, but in the present study, nothing like this amount of modulation was observed (Fig. 3).

As a partial comparison with the previous studies, a small number of longer OHCs were studied using the methods of this paper (four cells from two animals). The results of those cells are shown in Table 1. Changes in compliance due to depolarizing bias were small and of apparently random sign. Thus, there appears to be little evidence of voltage-dependent compliance change in longer cells by these methods. It is difficult to extend the methods of this study to longer cells for purely technical reasons. The voltage divider is so unfavorable in longer cells that it becomes impossible to drive the excluded segment to motility saturation without risking breakdown of the included segment membrane. Further, motion of the fiber in response to depolarizing biasing commands is sufficiently large (several hundred nanometers) that there is a risk of the fiber moving out of the slit or of becoming disconnected from the fiber.

TABLE 1.

Fractional compliance change and effective bias command for four cells with lengths greater than 50 μm

Length (μm)	Bias command (mV)	Effective bias command (mV)	Compliance (km/N)	Fractional compliance change
54	240	116.9	0.503	−0.074
64	240	186.2	0.365	0.069
72	300	58.9	1.477	−0.075
62	300	162.4	0.509	−0.023
			Average	−0.02575
			SD	0.067673

Theoretical treatments of OHC mechanics showed that a piezoelectric OHC does exhibit a voltage-dependent compliance, but the effect was, at most, 20% (Iwasa 2000). As was noted in that paper, this change is less than the experimental result of He and Dallos (2000). However, it is more in line with the present experimental findings.

In summary, it appears that voltage-dependent stiffness as reported in apical low-frequency OHCs does not exist in high-frequency OHCs. Therefore, assuming that the same mechanisms for mechanical amplification apply throughout the cochlea, voltage-dependent compliance is unlikely to be a component.