The Effect of Gaussian Noise on the Threshold, Dynamic Range, and Loudness of Analogue Cochlear Implant Stimuli

Abstract

The deliberate addition of Gaussian noise to cochlear implant signals has previously been proposed to enhance the time coding of signals by the cochlear nerve. Potentially, the addition of an inaudible level of noise could also have secondary benefits: it could lower the threshold to the information-bearing signal, and by desynchronization of nerve discharges, it could increase the level at which the information-bearing signal becomes uncomfortable. Both these effects would lead to an increased dynamic range, which might be expected to enhance speech comprehension and make the choice of cochlear implant compression parameters less critical (as with a wider dynamic range, small changes in the parameters would have less effect on loudness). The hypothesized secondary effects were investigated with eight users of the Clarion cochlear implant; the stimulation was analogue and monopolar. For presentations in noise, noise at 95% of the threshold level was applied simultaneously and independently to all the electrodes. The noise was found in two-alternative forced-choice (2AFC) experiments to decrease the threshold to sinusoidal stimuli (100 Hz, 1 kHz, 5 kHz) by about 2.0 dB and increase the dynamic range by 0.7 dB. Furthermore, in 2AFC loudness balance experiments, noise was found to decrease the loudness of moderate to intense stimuli. This suggests that loudness is partially coded by the degree of phase-locking of cochlear nerve fibers. The overall gain in dynamic range was modest, and more complex noise strategies, for example, using inhibition between the noise sources, may be required to get a clinically useful benefit.

INTRODUCTION

Typical cochlear implants mimic the normal place coding of frequency by filtering the input signal by a bank of bandpass filters, each of which stimulates a different region of the cochlea. We have previously proposed that the deliberate addition of Gaussian noise to the outputs of the bandpass filters could lead to improved speech comprehension (Morse and Evans 1996). As discussed below, there are two primary arguments for adding noise: a physiological one and a theoretical one based on the enhanced time-coding of information. There is also a secondary theoretical argument for adding noise based on the expected effect of noise on the psychophysical threshold and dynamic range of cochlear implant signals (from threshold to uncomfortable loudness level). The aim of the present work was to investigate these hypothesized secondary effects.

Primary benefits of adding noise

The primary physiological argument for adding noise to cochlear implant signals is that noise, random fluctuations in an information-carrying commodity, is a conspicuous feature of the normal auditory system. The inner hair cells are the primary sources of the noise, and their loss, which is associated with profound deafness, results in much reduced variability in the response to electrical stimulation, and the normal spontaneous activity of fibers is completely abolished or greatly reduced (Kiang 1965; Hartmann et al. 1984; Shepherd and Javel 1997). Therefore, with standard cochlear implant stimulation (without noise), the response of the cochlear nerve to electrical stimulation is vastly different from its response to normal acoustic stimulation. The addition of Gaussian noise to cochlear implant signals, however, makes responses to electrical and acoustic stimulation much more similar (Morse and Evans 1996, 1999).

Although the electrical response without noise is physiologically abnormal, it might be thought that noise in the normal hearing system is an obstacle to faithful stimulus coding (e.g., Harris 1968). The addition of noise, however, could result in the “linearization” of the nonlinear system from which the instantaneous amplitude of an input signal can be deduced from the probability of getting an action potential at each point in time, and with optimal noise, the amount of information transmitted could be increased; we anticipate that this would lead to increased speech comprehension. The study of noise-enhanced coding in similar systems has recently been studied under the generic umbrella of stochastic resonance (Gammaitoni et al. 1998; Wiesenfeld and Moss 1995). Of particular relevance to cochlear implant coding, Stocks (2000; 2001) have investigated a new form of SR termed suprathreshold stochastic resonance (SSR) and have shown that signals need not be subthresholds for noise to be advantageous; on the contrary, noise can be more advantageous for suprathreshold signals.

Our more theoretical studies for the primary use of noise (Morse and Evans, 1999; Stocks et al. 2002) are supported by psychophysical experiments with cochlear implant users. Zeng et al. (2000) have found that noise can increase frequency discrimination at 300 Hz; no results are given at other frequencies. Furthermore, noise can also enhance the sensitivity to amplitude modulation (Chatterjee and Robert 2001; Chatterjee and Oba 2005). Benham and Zeng (2003) have also shown that noise can reduce the minimum detectable level of a harmonic in a complex tone, although it is not clear whether this effect is based on temporal or loudness cues.

Hypothetical secondary benefits of adding noise

The addition of noise to cochlear implants could also have some potentially useful effects secondary to improving time coding. Because of the threshold nature of a nerve fiber, the addition of any waveform (in this case noise) to an information-bearing signal would be expected to lower the threshold to the information-bearing signal; as the threshold decrease would be expected with the addition of a non-stochastic signal, this is not necessarily a stochastic resonance effect. Zeng et al. (2000) confirmed the expectation of decreased threshold, but only for stimulus frequencies below 300 Hz. Hong et al. (2003) have also reported that the addition of a 5-kHz pulse train, i.e., a deterministic waveform, can lead to a decrease in threshold. The use of such “high-rate conditioners” is discussed later.

Furthermore, there is some evidence that the loudness of low-frequency acoustic stimuli (<5 kHz) is partially encoded by the degree of phase-locking of cochlear nerve spikes to the stimulus (Carlyon and Moore 1984); louder stimuli are thought to correspond to tighter phase-locking. An effect of phase-locking on loudness might also account for the observation by Gockel et al. (2003) that for a given overall level, complex stimuli in cosine phase are louder than stimuli in random phase; these effects cannot be accounted for by models of loudness perception that ignore the phase spectrum (Moore et al. 1997) and are only partially accounted for by loudness models that include peripheral compression. It has also been observed that a high-frequency tone presented continuously in background noise may become inaudible after a few tens of seconds, whereas a low-frequency tone does not (Wright 1959). This lack of fading at low frequencies may reflect the use of phase locking to maintain the percept (Moore and Peters 1997).

The addition of noise to an electrically coded stimulus might therefore be expected to decrease the loudness of a stimulus if it was originally some way above threshold. Near threshold, a crossover would be expected between the noise lowering the threshold, and therefore, making a stimulus louder and the noise decreasing the phase-locking, in turn, making the stimulus quieter. If the effect persisted when the stimulus without noise was at the uncomfortable loudness level for a cochlear implantee, then noise would increase the uncomfortable loudness level. The expected effects of noise, to decrease threshold and increase the uncomfortable loudness level, would both lead to an increase in the dynamic range for electrical stimulation. An increased dynamic range would be expected to result in greater speech comprehension, particularly in adverse listening conditions (Zeng and Galvin 1999; Loizou et al. 2000). Furthermore, the acoustic signals received by a cochlear implant must be compressed because the dynamic range of speech, typically about 50 dB for multiple talkers (Cox et al. 1988; Boothroyd et al. 1994; Zeng et al. 2002), is much greater than the dynamic range for electrical stimulation, which is typically 4 to 30 dB (Hochmair-Desoyer et al. 1981; Michelson 1971; Shannon 1983); we would expect an increase in the dynamic range by the addition of noise to make the choice of compression parameters, e.g., the ‘T’ and ‘M’ levels (Loizou 1999), for a particular implantee less critical because the rate-of-change in loudness with stimulus level would be less severe.

In this study, we have investigated the potential secondary benefits of noise with users of the Clarion® cochlear implant (Kessler 1999); as described above, we hypothesized that noise would decrease the threshold to a signal, increase the dynamic range, and reduce the loudness of greatly suprathreshold signals.

METHODS

The psychophysical experiments were performed on eight subjects in a total of 20 sessions. The subjects were post-lingually deafened adults who had been implanted with the S-Series Clarion® Implant (Advanced Bionics Corporation) for at least 6 months before the experiments. All the experiments were performed at St Thomas’ Hospital, London, except for subject CA who was tested at Keele University. Experiments were performed with the informed consent of the subjects and with prior approval of the local ethics committee at Keele University. Advanced Bionics (UK) Ltd. reimbursed the travelling expenses of the subjects, but no other financial inducement was given. The number of subjects in this experiment was limited by accessibility and the required familiarity with computers for the automated testing.

Access to the intracochlear electrodes was via a Clarion Research Interface (CRI) connected to a personal computer. This interface was designed by the House Ear Institute (Wygonski et al. 1999) and enables researchers to have almost unimpeded access to the electrodes via a custom telemetry link. To perform this study, the demonstration programs that were supplied with the interface were substantially modified. The modified programs enabled the presentation of arbitrary stimuli and the transmission of control commands to the speech processor to change the type of stimulation (e.g., monopolar/bipolar) or the stimulating electrode. For the automated forced-choice tests, the subjects responded using a mouse to click the appropriate buttons displayed on a computer screen. The modified CRI was used to investigate the effect of noise on the threshold and dynamic range of sinusoidal stimuli at frequencies of 100, 1,000, or 5,000 Hz. The effect of noise on the loudness of the sine waves presented at different amplitudes was also investigated.

Presentation of the sinusoidal stimuli and the noise waveforms was made using monopolar electrode coupling and the sinusoidal stimulus was always presented on electrode 4 (a mid-electrode for the S-series implant, which can use up to eight current sources). The clinically measured thresholds and most comfortable loudness levels for electrode 4 were normal for all subjects, and the electrode was always used by their standard (take-home) speech processor. Stimulus amplitudes of the waveforms were controlled in clinical units (CUs); in the Clarion S-Series implant, the actual mapping between input words to the digital-to-analogue convertor (DAC) and the output in clinical units was a power function, but this was compensated by the program such that the DAC input was logarithmically compressed to get, for example, a sinusoidal output. Assuming perfect current sources, one clinical unit would correspond to 1 μA; in practice, slight nonlinearities in the current sources result in increments of 1 CU corresponding to less than 1 μA, particularly at high stimulus levels. Because we used monopolar stimulation, however, the peak stimulation level used (486 CU) was much less than the maximum possible output current (2,500 CU), and this nonlinearity would not therefore be expected to have substantially affected the results.

The maximum sampling frequency for the S-Series cochlear implant is about 13 kHz (Loizou 1998), and the 5-kHz stimulus was therefore only just below the Nyquist frequency, although it is well within the passband of the highest frequency filter for the Simultaneous Analog Strategy (SAS) with the S-Series implant (Loizou 1998). Even though the 5-kHz stimulus is below the Nyquist frequency, the response of a cochlear nerve to the sampled signal would be expected to have harmonics at 1 kHz and above because of its nonlinear “all-or-nothing” response. To some extent, this will be mitigated by the lowpass filtering action of a cochlear nerve fiber, the linearizing effect of neural noise (Stocks et al. 1996), and the linearizing effect of having a distribution of nerve thresholds (McDonnell et al. 2006). Nonetheless, in a computational study using a leaky-integrate-and-fire nerve model we found that the nerve fibers did phase-lock to the 1-kHz harmonic (results not shown). Therefore, such synchronization with the 5-kHz stimulation might also have occurred in the psychophysical experiments.

In the experiments by Zeng et al. (2000) and by Chatterjee and Robert (2001), noise was applied to only one electrode. The noise at each cochlear nerve fiber was therefore likely to have been highly correlated with the noise at neighboring fibers. When the information-bearing stimulus is suprathreshold, a high degree of independence between the noise waveforms exciting different fibers is essential for stochastic resonance (Stocks 2000; Stocks et al. 2002). For this study, each of the eight intracochlear electrodes was therefore stimulated by a Gaussian noise waveform that was independent of the noise waveforms at the other electrodes. Because of the distribution of nerve fibers within the conductive media of the cochlea, each fiber would be expected to receive a different weighted sum of all the noise currents. Therefore, with noise stimulation by multiple electrodes, the noise excitation at neighboring fibers would be expected to be less correlated than with noise stimulation by a single electrode (Morse and Meyer 2000).

The amplitude of individual samples of the noise waveforms was calculated using the Box–Muller equation (Box and Muller 1958) at 76.9-μs intervals, the update rate dictated by the implant. The background root-mean-square (rms) noise level for the experiments was measured with respect to a noise threshold, which was defined to be the minimum audible level of the noise waveforms presented simultaneously to the electrodes; the rms noise level on each electrode was identical, and no attempt was made to determine the threshold noise level for individual electrodes. The noise threshold could therefore have been dominated by the response of a few highly sensitive neurons, which would have led to greater variability between subjects. Nonetheless, we adopted this initial method because without baseline results, we could not justify the substantial extra time that would have been required by the subjects to find the noise thresholds individually.

Before measurement of the noise threshold, the maximum noise level for comfortable listening was determined. Noise bursts lasting one second were presented at 2-s intervals, and after each noise burst, the amplitude was increased. The subject was asked to stop the test when the level of noise burst would be too loud for comfort if presented continuously. Bornstein and Musiek (1993) have found that when listeners are asked to judge whether a stimulus level is uncomfortable based on the criterion that they would choose “not to listen for any period of time” then the discomfort level can be up to 9 dB higher than if the criterion is whether they would choose “not to listen for 15 minutes or longer.” Our final noise level, where the criterion was for continuous listening, was therefore taken to be a conservative estimate of the level of discomfort for the short stimulus presentations used in this study. The noise threshold was then determined using a two-alternative forced choice (2AFC) paradigm in which the maximum noise level was constrained to be below the conservative level of discomfort. In each trial, two intervals were cued by colored bars on the computer screen, and during one randomly selected interval, a noise burst was presented; the intervals lasted 1 s and were separated by a 1-s gap. The subject was asked to judge during which interval the noise burst was presented. Based on the correctness of the subject’s response, the noise level was automatically adjusted according to the Parameter Estimation by Sequential Testing (PEST) algorithm (Taylor and Creelman 1967) such that correct answers generally led to a decrease in the noise level and vice versa. The experiment continued until the subject could no longer reliably determine the interval in which the noise was presented (target probability 75%, Wald level 0.5). The threshold and conservative uncomfortable loudness level (CULL) of the noise were remeasured at the start of each test session.

For the sine wave threshold experiments, the threshold level to a sinusoidal stimulus of either 100 Hz, 1 kHz, or 5 kHz (duration 1 s, rise/fall time of 100 ms) on electrode 4 was measured for two conditions: sinusoidal stimulation alone or sinusoidal stimulation in the presence of background noise. In the second condition, independent Gaussian noise currents at 95% of the threshold level were applied to each electrode in addition to the sinusoidal stimulation on electrode 4; the Gaussian noise alone was therefore predominantly inaudible to the subject given that a stimulus at the 100% level was audible in only 75% of presentations. Because the expected threshold decrease was not thought to involve stochastic resonance (see Introduction section), we used only one noise level. The 95% level was chosen simply because a larger noise level would be expected to lead to a larger decrease in threshold for the sinusoidal signal, but a noise level much greater than 95% of the threshold level would be liable to be intermittently above the audible threshold through chance alone. At the 95% level, the subjects never commented on hearing a sound in both stimulus intervals, but when the sine wave level was low, they did comment that they heard nothing in either interval. Although we did not rigorously map the psychometric function for noise detection, this suggests that the noise was predominantly subthreshold as intended. Furthermore, some pilot studies were done with noise at 50% of the threshold level, and the conclusions from these studies were substantially the same as for 95% noise. The threshold for the sinusoidal stimulus was measured using a method similar to that used to measure the noise threshold. First, a conservative estimate of the level of discomfort was made and then a 2AFC task was used to find the threshold. For the condition with noise, noise was presented in both intervals, but the interval that also contained the sinusoidal stimulus was randomized. The experiment was repeated five times for each condition, and the order of the trials with and without background noise was randomized. Some subjects were not available to be tested with all the frequencies, and the experiments were therefore, unbalanced.

In an initial analysis of variance (ANOVA) for the effect of noise on threshold, the residual errors departed considerably from normality. All thresholds were therefore converted using a logarithmic transformation to force the residuals to be approximately normal. Given that the decibel is ubiquitous in acoustics, the exact transformation was to convert clinical units into decibels re 1 CU. An ANOVA was performed on the transformed thresholds with the main effects being noise treatment (present or absent), subject, and stimulus frequency; all interactions between the main effects were considered.

Although the conservative estimate of the uncomfortable loudness level with sinusoidal stimulation was made primarily for safety reasons and without repetition, the effect of noise on the CULL was analyzed. In common with the sine wave threshold experiments, the initial ANOVA of the difference in the uncomfortable level when noise was added (with subject and frequency as the main effects) resulted in residuals that were not normally distributed. The CULLs were therefore transformed to decibels re 1 CU before further analysis. The overall effect of noise on the dynamic range was also investigated using an ANOVA with subject and frequency as the main effects and including their interaction.

To investigate the effect of background noise on the loudness of sinusoidal stimuli (100 Hz, 1 kHz, or 5 kHz), loudness balance experiments were performed using a 2AFC paradigm. In one interval, the sinusoidal stimulus was presented without noise (duration, 1 s; rise/fall time of 100 ms) at one of five randomized levels between threshold and 80% of the conservative uncomfortable loudness level (i.e., 0, 20, 40, 60, or 80% of {CULL − θ}, where θ is the threshold level in clinical units). In the other interval, the sinusoidal stimulus was presented in background noise (duration, 1 s; rise/fall time of 100 ms, noise at 95% of threshold level); the time between stimulus intervals was 1 s. The subject was asked to judge which interval was the loudest. Based on the subject’s response, the level of the sinusoidal component of the stimulus with background noise was adjusted according to the PEST algorithm until the subject could no longer reliably discriminate between the loudness of the two intervals (target probability, 0.75; Wald level, 0.5). To control for the effects of masking or facilitation by the two stimulus intervals, the experiment was repeated twice. In one experiment, the sinusoidal stimulus was always presented in background noise in the first interval and presented alone in the second interval. In the other experiment, the order was reversed.

The levels for the balanced sine waves were converted from clinical units to decibels, and the effect of noise on loudness was analyzed using an ANOVA to predict the difference between the dB levels of the balanced sine waves. The main effects were subject, the level of the reference stimulus (as a level from 1 to 5), sine wave frequency, and presentation order (noise in the first or second interval of the 2AFC). The analysis included the following interactions: subject and level, subject and presentation order, level and frequency, frequency, and presentation order.

RESULTS

With the noise presented in the absence of a sinusoidal stimulus, the subjects reported that the loudness of the noise increased gradually between threshold and the CULL. The mean noise threshold for the eight subjects was 3.2 ± 0.6 CU, the mean CULL was 35.4 ± 4.4 CU, and the mean dynamic range was 21.3 ± 2.1 dB. Suprathreshold noise stimulation was reported to sound like a “fluttering wing beat” or “bubbly”.

Effect of noise on sine wave threshold

Without noise, the mean dynamic range of the sinusoidal stimuli was 27.1 dB at 100 Hz (σ = 2.1 dB, N = 7), 23.0 dB at 1 kHz (σ = 1.7 dB, N = 6), and 25.3 dB at 5 kHz (σ = 2.0 dB, N = 5).

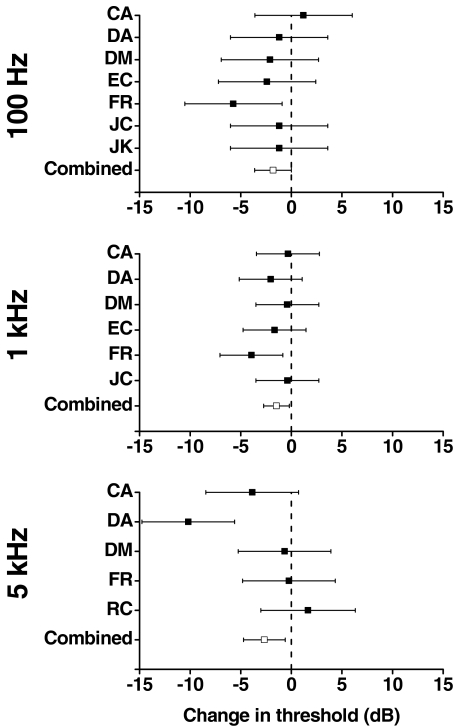
The effect of noise on the threshold of sinusoidal stimuli is shown in Figure 1. The figure shows that the addition of noise typically resulted in a reduction of the mean sine wave threshold for each subject. The analysis showed that averaged over all subjects and frequencies, the decrease in sine wave threshold with added noise is significant (p = 0.0011). The other main effects of subject and frequency are also significant (both p = 0.0001). Neither of these effects are surprising given the large literature on intersubject variability (e.g., Summerfield 1985) and the effect of frequency on stimulus threshold (e.g., Pfingst 1988). None of the interactions involving the effect of noise are significant, which implies that the effect of noise was similar for all subjects and across all frequencies.

FIG. 1.

The change in threshold of a sinusoidal stimulus by the addition of Gaussian noise. The figure shows estimates from a least square means analysis of the mean threshold change and 95% confidence intervals for each subject (denoted by their initials) at three frequencies: 100 Hz, 1 kHz, and 5 kHz. The analysis enabled the combined effect across subjects (combined) to be estimated at each frequency.

Because the design of the experiment was unbalanced, it was not possible to estimate the change in sine wave threshold due to noise from the full model. Separate analyses were therefore performed for each of the stimulus frequencies of 100 Hz, 1 kHz, and 5 Hz with noise and subject as the main effect. The effect of noise on sine wave threshold approaches significance at 100 Hz (p = 0.0514) and is significant at 1 and 5 kHz (p = 0.0246 and p = 0.0124, respectively).

The overall size of the effect of adding noise was estimated across subjects and frequency by an ANOVA with noise, subject, and frequency as the main effects and with noise and subject as the only interaction. The analysis showed that the overall mean effect of adding noise to a sine wave was to decrease the threshold by 2.0 ± 0.56 dB.

Effect of noise on the conservative estimate of the uncomfortable loudness level

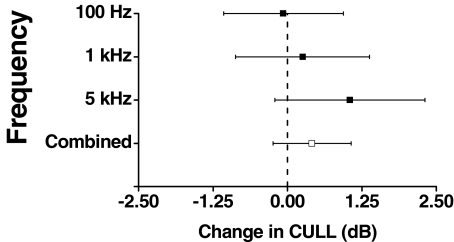
The analysis for the effect of noise on the CULL showed that noise had no significant effect on the CULL for sinusoidal stimulation (p > 0.05); furthermore, there were no significant differences between frequencies or subjects. The power, however, of the experiment was low because of the small number of observations (13 observations across three frequencies). To enable comparison of the effect of noise across stimulus frequency with an unbalanced design, the mean and 95% confidence intervals for the CULLs were estimated from the ANOVA using the method of least square means (Fig. 2). In Figure 2, it appears that the change in the CULL with added noise is greater at higher frequencies. This trend, however, is not significant (p = 0.1644).

FIG. 2.

The change in conservative estimate of the uncomfortable loudness level (CULL) of a sine wave by the addition of Gaussian noise. The figure shows the estimated mean and 95% confidence interval for 100 Hz, 1 kHz, and 5 kHz stimulation across all subjects based on a least square means analysis. The combined effect across frequencies and subject is also shown.

Effect of noise on sine wave dynamic range

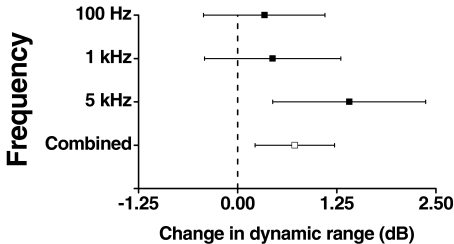
Noise increased the mean dynamic range of a sinusoidal stimulus at all frequencies tested. The change in the dynamic range with added noise is significant overall (p = 0.0103) and is significant at 5 kHz (p = 0.0099). The size of the effect with the unbalanced design was estimated using the method of least square means (Fig. 3) and the mean change in dynamic range over all frequencies was 0.7 dB; this analysis simultaneously accounted for the variability in the thresholds and the CULL and provides a better estimate of the change in dynamic range than would have been obtained by simply adding the mean effect of noise on threshold to the mean effect of noise on the CULL (Winer 1971). The effect of noise was greatest at 5 kHz (1.4 ± 0.4 dB), but the apparent trend with increasing frequency is not significant. There were no significant differences between subjects, but in common with the CULL measurements, the power of the experiment was low because of the small number of observations (18 observations over 3 frequencies).

FIG. 3.

The change in the dynamic range of a sine wave (from threshold to the conservative estimate of the uncomfortable loudness level) by the addition of Gaussian noise. The figure shows the estimated mean and 95% confidence interval for 100 Hz, 1 kHz, and 5 kHz stimulation across all subjects based on a least square means analysis. The combined effect across frequencies and subject is also shown.

Effect of noise on sine wave loudness

The effect of noise on the loudness of a sinusoidal stimulus was measured in a loudness balance experiment for frequencies of 100 Hz, 1 kHz, and 5 kHz at five equal steps in the level of the reference sine wave from threshold to 80% of the CULL; apart from loudness, subjects did not report any qualitative difference between the sinusoids presented alone or in noise. The analysis showed that all main effects except order are statistically significant (subject, p = 0.0049; frequency, p = 0.0068; level, p = 0.0001). Three of the second order effects are also significant (subject and presentation order, p = 0.0141; subject and level, p = 0.0177, frequency and level, p = 0.0004). Of particular concern was the interaction between subject and presentation order, which shows that the presentation order affected the balance levels differently for different subjects. For some subjects, the stimulus in the first interval tended to make the second stimulus louder; for other subjects, the first stimulus tended to make the second stimulus quieter. To evaluate the effect of noise, the differences in level between the balanced sine waves (noise and no noise) were therefore averaged over the two presentation orders.

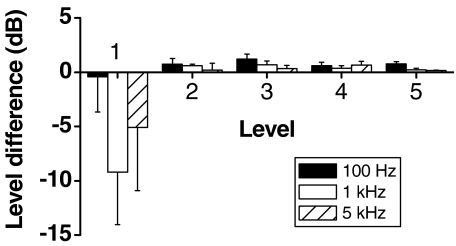
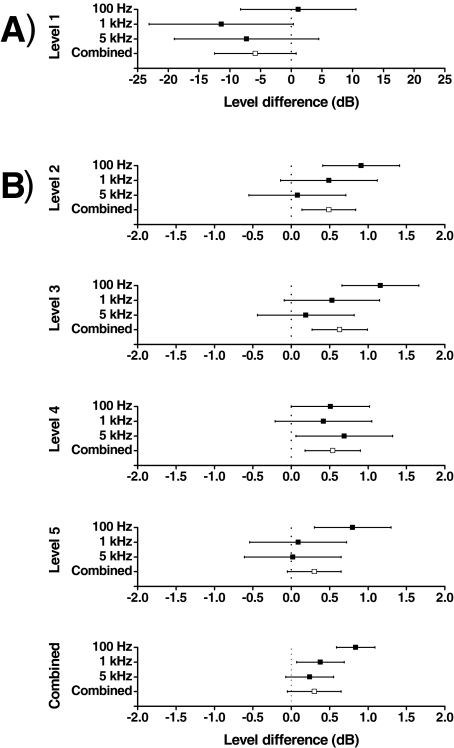
As indicated above, the difference in level required to balance the paired sine waves was significantly dependent on the level of the reference sine wave. When the reference sine wave (without noise) was at the threshold level (Fig. 4: level 1), the level of sine wave with noise generally had to be smaller than that of the reference to be equally loud. This is consistent with the finding above that noise lowers the detection threshold for an information-bearing signal. At higher levels of the reference sine wave (Fig. 4: levels 2 to 5), the level of the sine wave with noise, generally, had to be larger than that of the reference to be equally loud. In other words, for moderately to highly suprathreshold stimuli, the effect of noise was to make the information-bearing signal quieter.

FIG. 4.

The level difference required to make a sine wave with noise as loud as a reference sine wave at the same frequency but without noise. The level of the reference sine wave for each subject was at five levels from threshold to 80% of the conservative estimate of the uncomfortable loudness level (denoted as levels 1 to 5). The error bars show the standard error about the mean at each frequency and level (100 Hz: five subjects, 1 kHz: four subjects, and 5 kHz: four subjects).

These findings are supported by two further ANOVAs: one for stimulus level 1 alone (just suprathreshold), and the other, for levels 2 to 5. The ANOVA for level 1, which had subject and frequency as the main effects showed that there were no significant differences between subjects or between frequencies. The mean differences in stimulus level between the balanced sine waves at each frequency and for the combined frequency were estimated from the ANOVA using the method of least square means (Fig. 5A). The figure suggests that loudness was higher when noise was added to a just suprathreshold sine wave, but this result is not significant at any frequency although it approaches significance at 1 kHz (p = 0.0547). A lack of significance is not surprising given that there were only 13 observations at level 1. It has, however, already been shown above that noise had a significant effect of threshold for 1 kHz and 5 kHz sine waves. The significant effect of noise on threshold, which was found in an experiment with more observations, supports the hypothesis that noise increases the loudness of a sine wave at threshold.

FIG. 5.

The level difference required to make a sine wave with noise as loud as a reference sine wave at the same frequency but without noise. The level of the reference sine wave for each subject was at five levels from threshold to 80% of the conservative estimate of the uncomfortable loudness level (denoted as levels 1 to 5). The figure shows the mean and 95% confidence intervals across subjects for each level and frequency estimated from the unbalanced data using the method of least square means. (A) Level 1 (just suprathreshold). (B) Levels 2 to 5. The bottom plot shows the overall effect of noise on loudness for levels 2 to 5.

The ANOVA for levels 2 to 5 had subject, frequency, and level as the main effects and included the following interactions: subject and level, and frequency and level. This analysis revealed a significant difference between subjects (p = 0.0003) and between frequencies (p = 0.0025); there was no significant difference between levels, or for the interaction terms of the model. In common with the level 1 data, the mean differences in stimulus level between the balanced sine waves at each frequency and for the combined frequency were estimated using the method of least square means (Fig. 5B). The analysis suggests that the level of a sine wave with noise had to be about 0.5 dB greater than that of the reference to be equally loud. This result is significant for the combined levels at 100 Hz (p = 0.0001) and 1 kHz (p = 0.0197); it is also significant for the combined frequencies and levels (p = 0.0001).

Figure 5B also shows that the level difference for balanced loudness decreased with increasing frequency. This observation was confirmed by the analysis of variance for trend with frequency, which showed statistical significance (p = 0.0076).

CONCLUSIONS AND DISCUSSION

The dynamic range for noise stimulation (21.3 ± 2.1 dB) was similar to the dynamic range for sinusoidal stimulation (about 23 dB at 100 Hz and about 19 dB at 5 kHz). From subject feedback, however, the criteria for judging a stimulus to be uncomfortable may have differed; with noise stimulation, subjects often considered that a particular level would be uncomfortable if continued indefinitely based on irritability rather than on loudness. Benham and Zeng (2003) have also found the noise dynamic range to be relatively large (20 to 25 dB) when Gaussian noise is applied to a single electrode.

The gradual increase in loudness of the noise stimulus with stimulus level implies that the exact level of the noise is probably not critical for an effect on threshold; indeed, preliminary experiments with different noise levels (either 50 or 75% of threshold) led to similar results (Morse et al. 2000). This is important for the practical implementation of a noise strategy. An increase in the dynamic range of an information-bearing signal by the addition of noise may make the choice of the compression parameters less critical, but this would not be useful if a precise noise level was required: the fitting problem would simply be moved from selection of the compression parameters to selection of the noise level.

The lack of significance for the effect of noise on the threshold to a 100 Hz stimulus may have resulted from the minimum step-size of 1 CU, which was large relative to the sine wave threshold without noise. Our threshold results are not entirely consistent with those from Zeng et al. (2000), who demonstrated that the addition of noise to a single channel of the Ineraid implant (Eddington et al. 1978) can lower the threshold to sinusoidal stimuli only if the frequency is less than 300 Hz. Given the threshold nature of nerve fibers, this result is unexpected because the root-mean-square amplitude of the combined noise and sine wave stimuli would be expected to be larger than the root-mean-square amplitude of the sine wave alone; the threshold to the summed stimulus should therefore be lower. The different findings from the two experiments may have resulted from the different methods for presenting the noise. In the experiments by Zeng et al., the noise was presented on a single electrode and was continuous throughout an experiment; whereas in the present study, the noise was presented on multiple electrodes simultaneously with the sine wave. Zeng et al. have hypothesized that the unexpected frequency dependence they observed may have resulted from a hypothetical low-pass filtering process in the auditory brainstem. This hypothesis, however, is inconsistent with results from the present study.

The direct effect of noise on the conservative estimate of the uncomfortable loudness level was not found to be significant. The results showed, however, that noise could significantly decrease the loudness of a sine wave at levels from 20 to 80% of the range from threshold to the CULL (levels 2 to 5). Because the loudness balance experiments used a 2AFC paradigm and had a reference stimulus, they would be expected to be more sensitive to the effects of noise than the staircase procedure used to measure the CULL. This gives credence to the hypothesis that noise might also decrease the loudness of a sine wave originally at the conservative level for discomfort (equivalent to increasing the CULL) and that the lack of significance for the CULL experiments simply resulted from the low power of the experiments and the imprecise nature of the subjects’ criteria for uncomfortableness. There is, however, a potential for bias in the loudness balance experiments because the level of the sine wave in background noise was the adjusted stimulus, and for acoustical stimulation, the adjusted stimulus is typically larger than the reference for equal loudness (Stevens 1956; Zwicker et al. 1957). It is notable, however, that the decrease in the effect of noise on loudness was frequency dependent and that the effect was almost negligible (and nonsignificant) at 5 kHz; this would not be expected if the loudness decrease resulted solely from subjective bias.

Notwithstanding the finding that the effect of noise on the CULL was not significant, the combined effect of noise on the threshold and CULL of sinusoidal stimulation was to increase the dynamic range by about 0.7 dB. For many subjects, however, this was a small fraction of the dynamic range without noise. Therefore, although the overall effect across subjects and frequency was statistically significant, the effect was not substantial.

The effect might have been small because the noise level on each electrode was identical. The noise threshold for each electrode almost certainly differed, so the noise level at fibers most intensely stimulated by the sine wave on electrode 4 could have been some way below threshold. A more substantial effect might have been observed if the noise level on each electrode had been balanced according to the different thresholds for the individual electrodes; this would, however, have required a longer setup time. The effect might also have been more substantial if there was inhibition between the independent noise sources, e.g., each electrode current was the sum of the current from one noise source minus half the sum of the currents from the two neighboring noise sources. A computational investigation of this opponent noise strategy (Morse and Meyer 2000) showed that it resulted in less correlation between the noise exciting neighboring fibers than the simpler strategy used in this study. Therefore, compared with the simpler strategy, the opponent noise strategy might lead to a greater decrease in loudness of moderate to high intensity sinusoidal stimuli.

Taken at face value, the increase in dynamic range using additive noise is small compared with the 6.7 dB increase reported for “high-rate conditioners,” such as a 5-kHz pulse train (Hong and Rubinstein 2003; Hong et al. 2003). It is not clear, however, that a direct comparison is possible. First, results from Hong et al. relate to the largest change in dynamic range observed change over all conditioner levels, electrode positions, and stimulus frequencies, which is likely to exaggerate the degree of benefit compared with our results where we have calculated the mean. Figure 1 shows that repeated measures of the threshold with and without noise showed large variability and the upper 95% confidence interval was typically about 5 dB greater than the mean; naturally, the largest difference would be expected to be even further from the mean, and in the limit of a large number of repeated measures, would be considered an outlier. The difference in the results may therefore merely reflect our use of standard statistical methods rather than a difference in the underlying data. Second, the measurements of threshold and MCL by Hong et al. were performed sequentially from no conditioner up to the maximum conditioner level. This makes it very difficult to distinguish between the longer-term effects of adaptation and other putative mechanisms, notably stochastic resonance, which they claim may lead to an increased dynamic range. Cochlear nerve fibers are known to adapt markedly in response to a high-rate conditioner over the first 100 s of stimulation; indeed, in physiological experiments by Litvak et al. (2003), 46% of fibers produced less than 5 spikes/s after the first 100 s of a 5-kHz stimulus, whereas the spike rate in response to the onset was up to 700 spikes/s. Furthermore, 75% of the fibers that were still responding after 100 s did not have exponential interspike intervals following the refractory period, and the temporal response of the majority of cochlear nerve fibers was therefore unlike spontaneous activity in the normal ear. Moreover, 13% of fibers had discharge rates greater than the maximum spontaneous rate found in normal hearing. Therefore, although use of a high-rate conditioner may have benefits for cochlear implantation, the mechanisms involved are unclear and the responses are markedly different to those in the normal ear.

As noted in the introduction, our prime motivation for using additive noise is to enhance the transmission of temporal information through suprathreshold stochastic resonance, which ideally leads to independent nerve activity in the absence of a stimulus. However, computer simulations using a deterministic nerve model have shown that the direct addition of an independent noise waveform to every electrode in a 16-channel implant is unlikely to lead to completely independent nerve activity (Morse and Meyer 2000); the practical use of additive noise may therefore require more advanced electrode design or the use of stochastic beam forming to achieve greater independence. Given the added complexity that might be needed for successful implementation with the additive noise strategy, the use of a high-rate conditioner might seem preferable because based on a computational model, it has been suggested that a 5-kHz high-rate conditioner does lead to independent nerve activity (Rubinstein et al. 1999). We find it hard, however, to conceive of a neural mechanism that would lead to independent responses to a deterministic pulse train on a single channel and yet lead to coherent responses to a multichannel, stochastic, and broadband waveform such as our basic additive noise strategy. Moreover, physiological experiments have shown synchronization in response to sinusoidal stimulation up to at least 10 kHz (Hartmann and Klinke 1990; Dynes and Delgutte 1992), and the response to a 5-kHz conditioner would therefore also be expected to be synchronized. An explanation for this discrepancy between the computational and physiological results may be that the forward-recurrence time analysis used by Rubinstein et al. in the computational study was not powerful enough to find the synchronization between the stimulus and the modelled response. Johnson and Kiang (1976) have previously used the forward-recurrence time method to investigate the independence of discharges recorded simultaneously from two cochlear nerve fibers for over 100 s; in this analysis, they used a bin width of 0.1 ms. The null hypothesis of the test is that the discharges are independent. Johnson and Kiang were careful to note that their failure to reject the null hypothesis was not proof of independence but merely consistent with the alternative hypothesis. In the analysis by Rubinstein et al., only 8 s of data was used, and the bin width was increased to 0.5 ms to get “useful recurrence-time histograms.” With these changes, the resulting forward recurrence-time histogram was just within the set bounds so that the hypothesis of independence could not be rejected and the results have been taken to show a pseudospontaneous response (Hong and Rubinstein 2003; Hong et al. 2003). These changes, however, would have substantially reduced the power of the statistical test, which may well have shown a lack of independence if a smaller bin size had been used—particularly, given that the associated calculation of the vector strength was 0.26 (Rubinstein et al. 1999), which is suggestive of synchronization. It is therefore not clear that the use of a high-rate conditioner leads to a completely desynchronized response.

The decrease in the loudness of moderate to intense sine waves by the addition of noise cannot be explained in terms of the spread of excitation because the rms level of the combined signal and noise would have been higher than for the noise alone. Therefore, the finding directly suggests that the loudness of electrical stimuli is partially coded by the degree of phase-locking of cochlear nerve fibers. As discussed above, however, the decrease in loudness with noise was almost negligible at 5 kHz. This may have resulted from the more complex response to the sampled 5-kHz stimulus (see Methods section). Moreover, although the phase-locking limit for electrical stimulation can be up to 10 kHz, rather than just 5 kHz for acoustic stimuli, the change in phase-locking for electrical stimuli above 5 kHz is unnatural. Nonetheless, given the results for 100 Hz and 1 kHz stimulation, these experiments support the finding that the loudness of low-frequency acoustic stimuli may be partially cued by phase-locking (Carlyon and Moore 1984).

The findings from this study support the original conjecture that the addition of noise to cochlear implant signals could decrease the threshold to an information-bearing signal and make a moderate-to-intense information-bearing signal quieter. Further studies are required to determine whether the increased dynamic range by the addition of noise is consequential for patient fitting and improved speech comprehension and whether alternative methods for stochastic stimulation with additive noise produce a greater effect. Further studies are also required to determine whether the increased dynamic range with additive noise is associated with an increase in the number of discriminable loudness levels, particularly because recent studies by Runge-Samuelson et al. (2004) have shown that the use of a high-rate conditioner actually decreases sensitivity to intensity change.