Abstract
Entropic and enthalpic contributions to the hydrophobic interaction between nanoscopic hydrophobic solutes, modeled as graphene plates in water have been calculated using molecular dynamics simulations in isothermal-isobaric (NPT) ensemble and with free energy perturbation methodology. We find the stabilizing contribution to the free energy of association (contact pair formation) to be the favorable entropic part, the enthalpic contribution being highly unfavorable. The desolvation barrier is dominated by the unfavorable enthalpic contribution in spite of a fairly large favorable entropic compensation. The enthalpic contributions, incorporating the Lennard-Jones solute-solvent terms, largely determine the stability of the solvent separated configuration. We decompose the enthalpy into a direct solute-solute term, the solute-solvent interactions and the remainder that contains pressure-volume work as well as contributions due to solvent reorganization. The enthalpic contribution due to changes in water-water interactions arising from solvent reorganization around the solute molecules is shown to have major contribution in the solvent induced enthalpy change.
I. INTRODUCTION
The hydrophobic interaction (HI) causes1–4 a nonpolar solute dissolved in water to display various forms of aggregation, organization and self assembly.5 It is generally believed that manifestations of hydrophobicity are length scale dependent. Therefore, a complete understanding of hydrophobicity remains elusive.
Water is a network forming liquid due to extensive hydrogen bonding between the molecules. Due to lack of hydrogen bonding between water and hydrophobic units, dissolution of a hydrophobic solute in water results an energetic cost due to the disruption of the hydrogen bond network in water for larger solutes.6 When the hydrophobic unit is small, it can often be accommodated into the spontaneous cavities present in water8 with some reorganization of the hydrogen bond network. A molecular level understanding that supports this picture for a small solute has emerged from a number of studies.7–16 Results from these studies for small length scale solutes provided useful information regarding solvation and stability of dilute aqueous solutions of many hydrophobic molecules such as methane, rare gases etc. However, direct use of these results to understand the nature of hydrophobicity at a larger length scale relevant to aggregation and association phenomena in biological systems has been difficult. Therefore, in order to understand various aggregation and association phenomena as diverse as protein folding, and self assembly of hydrophobic nano materials, a thorough understanding of hydrophobicity at a larger length scale, although far from macroscopic, is essential.
A variety of physically appealing arguments have been used to explain such aggregation phenomena involving hydrophobic macro molecules. Persistence of the complete hydrogen bond network of contact water near a large or extended hydrophobic solute surface is geometrically impossible by mere rearrangement of the water molecules. Thus some have proposed that resulting energetic imbalance can induce drying near such surfaces leading to the formation of a thin vapor layer6,17 around the solute. In such a picture, when two such water depleted large hydrophobic units come close to each other, number fluctuations near the interfaces lead to expulsion of the remaining water molecules from the inter solute region and induce collapse of the solute units. Various theoretical6,18–20 and simulation21–25 studies using an idealized model of the solute have supported the water expulsion mechanism for the hydrophobic association. However, a number of recent studies26–33 using more realistic models for the solute have contradicted the idea of dewetting induced collapse of large hydrophobic groups. Studies of stability of water26 inside a carbon nanotube, in between two nanoscopic hydrophobic surfaces,30,31 and wetting of large methane clusters by water29 showed solvent participation in the HI without dewetting. The evidence from simulations of a stable one dimensional chain of water molecules inside a carbon nanotube26 and that of a two dimensional monolayer of water30 between two nanoscopic planar hydrophobic solutes contradict the idea that energetic cost of some local disruption in the hydrogen bond network induces drying in or near a hydrophobic environment. Even a cluster of a few water molecules has been shown27 to be stable in a spherical hydrophobic cavity.
One of the compensating effects to the energetic cost due to minor disruption of hydrogen bond of water appears to come from the solute-solvent attractive dispersion interactions. In a series of recent studies30,32,34,35, the importance of attractive solute-solvent interaction on the wetting/dewetting behaviour of nanoscopically large solutes has been clearly demonstrated. It has been explicitly shown30–32 that the cumulative effect of a large number of small solute-solvent attractive interactions can change large solute hydration behaviour. In particular, the mechanism of the contact pair formation for a purely repulsive model nanoscopic solutes in water has been shown30 to be completely different from that for a system with reasonable dispersion interactions. The importance of an attractive interaction between solute and the solvent on the hydration and domain collapse of proteins has also been demonstrated28 recently.
Solutes in water at ambient conditions can change the vapor-liquid phase boundary. In particular, location of the vapor-liquid phase boundary in the vicinity of a large nanoscopic hydrophobic solute is highly dependent35 on the extent of solute-water attractive interactions. Molecular level understanding of hydrophobicity at this length scale is thus far from being complete.36
A large increase in heat capacity when a hydrophobic solute is solvated in water is a defining thermodynamic signature of hydrophobic interaction. Understanding the thermodynamics of nonpolar solvation37 is thus central to the understanding of the hydrophobic interaction. Relative contributions of entropy and enthalpy to the free energy of association determines the thermodynamic driving force of hydrophobicity induced aggregation. For small hydrophobic solutes in water, it is well established that nonpolar solvation in water near room temperature is dominated by favorable entropic contribution. A large number of simulation studies of methane association in water have shown12,14–16 the contact pair state to be entropically stabilized. As has been already mentioned, extrapolation and generalization of these small length scale results to understand aggregation phenomenon of large bio-macromolecules may not be straight forward, because of the multifaceted nature of hydrophobic hydration. It has been proposed48 and recently demonstrated,49 based on the hydration behavior of a purely repulsive model hydrophobic solute, that hydration thermodynamics changes from entropic for small solutes to enthalpic for large solutes. As has been shown earlier inclusion of small van der Waals attractions between solute atoms and water changes the mechanism of association for nanoscopic solutes from that of its purely repulsive analogue.30 It is, therefore, important to investigate whether thermodynamics of association of more realistic solutes with slowly varying weakly attractive dispersion interactions (in addition to the usual repulsive interaction) follow the same thermodynamic crossover as observed in case of hard sphere solutes.
In our previous work, we have calculated the free energy as function of separation, commonly known as the potential of mean force (PMF), between two nanoscopic hydrophobic solutes in explicit water. The PMF was obtained from molecular dynamics sampling in the isothermal-isobaric (NPT) ensemble in combination with free energy perturbation (FEP) methodology30,38,39. In the present work, we decompose the PMF into entropic and en-thalpic contributions and investigate the mechanistic implications.
II. METHOD
We have used computer simulation to study the thermodynamic behavior of the hydrophobic interaction between two nanoscopic, hydrophobic, planar solutes in water. The entropy of association has been calculated from the temperature derivative of the PMF via finite differences.50
We label solutes ,u, and solvent, v. The solvent water molecules were modeled by the 3 site SPC/E40 model. Each of the hydrophobic solutes considered here was modeled as a graphite-like sheet or plate made up of sp2 carbon atoms placed in a flat, hexagonal lattice with carbon-carbon bond lengths of 1.4 Å with force field parameters from the AMBER force field41. Each of the solute plates for our study has 60 carbon atoms with dimensions of ~11 Å × 12 Å between nuclear centers or around 15 Å total van der Waals diameter.
Entropy is calculated from the finite difference temperature derivative of the PMF or ΔG(r) at each inter solute separation r, viz.,
| (1) |
In the present calculation values of T and ΔT are chosen to be 298 K and 20 K respectively. The enthalpy contribution to the free energy, ΔH(r), can be obtained from entropy S(r) and the PMF ΔG(r) at temperature T.
| (2) |
In order to elucidate the contribution from solvent molecules to the PMF we evaluate the solvent contribution ΔWv(r) to the PMF ΔG(r) by subtracting the direct potential between two solutes, Uuu(r) from the PMF i.e.
| (3) |
Here ΔWv(r) is the solvent induced contribution to the adiabatic work surface. As a free energy we may split this into enthalpic and entropic contribution. Since the potential is independent of temperature, we decompose the solvent contribution to the enthalpy of association as
| (4) |
In order to clarify the role of the reorganization of water molecules around large hydrophobic solutes, further analysis of ΔHv(r) is necessary. The solvent contribution to the enthalpy of association can be split16 further into two terms namely, a solute-solvent direct interaction, ΔUuv, which represents the potential energy of interaction of a pair of solute plates separated by a distance r with the surrounding water molecules relative to its value at r = ∞ and the remaining contributions ΔHrem(r) that include mechanical pressure-volume work and changes in the solvent-solvent interaction in presence of a pair of solute plates at distance r, i.e.
| (5) |
The solute-solvent contribution, ΔUuv(r) can be averaged directly from the simulation runs; one can then easily get the remaining contribution, ΔHrem(r) from the above equation.
Simulations in the isothermal isobaric (NPT) ensemble were carried out using the molecular dynamics (MD) extended system approach of Nose and Anderson42–44. Periodic boundary conditions were applied and electrostatic interactions were calculated using the Ewald method45. The bonds and angles between oxygen and hydrogen atoms of the water molecules were constrained by use of the RATTLE algorithm45,46 and the solutes were kept rigid. All the systems were simulated at a target pressure of 1 atm and at target temperatures of 298 K and 318 K. The equations of motion were integrated using velocity Verlet algorithm45,47 with a 2 fs time step. The PMFs were calculated using a Free Energy Perturbation (FEP) technique. Details of the procedure are described elsewhere30.
III. RESULTS AND DISCUSSIONS
A. Decomposition of potential of mean force into enthalpic and entropic contributions
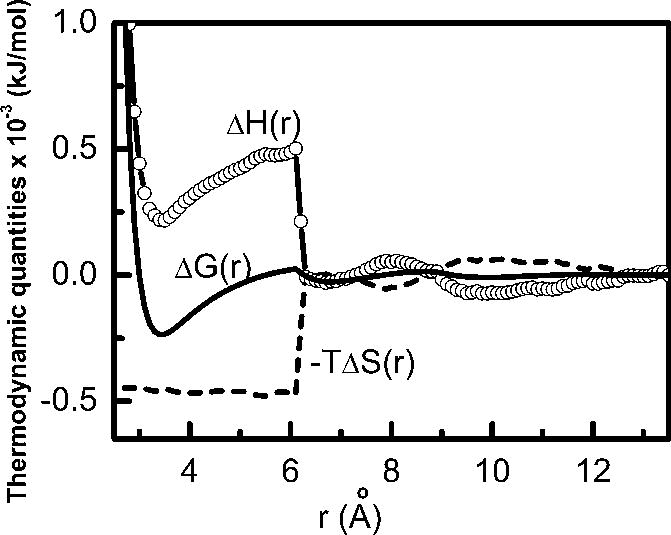
The potential of mean forces, ΔG(r), as a function of the separation r between the two large (60 atoms) parallel plates at normal pressure and two different temperatures have been calculated by the FEP technique using MD simulation for sampling. The entropic contribution, −T ΔS(r) to the PMF, ΔG(r), at 298 K is obtained through Eq. (1). The entropic (−T ΔS(r)) and enthalpic (ΔH(r)) contributions to the PMF at 298 K are shown in Fig. 1 along with the PMF. The stabilizing effects of entropic and enthalpic contributions of the PMF act in opposite direction to each other and the relative proportion of the two contributions depends on the inter solute distances. This is a form of the familiar macroscopic entropy-enthalpy compensation which has been seen for local quantities like these reflected in a PMF for some time.50
Fig. 1.

Enthalpic contribution, ΔH(r), (open circles with line) and entropic contribution, −TΔS(r), (dashed line) to the potential of mean force, ΔG(r), (solid line) for a pair of planar nanoscopic nonpolar solutes in water at 298 K and 1 atm pressure.
The contact pair state is entirely stabilized by the favorable entropic contribution, en-thalpic contribution being highly unfavorable. The favorable entropic contribution is so huge that it stabilizes the solute association even after compensating the unfavorable en-thalpic effect. The entropic contribution at the contact state in the present case is around −460 kJ/mol. The entropy of association for a methane pair is around −4 kJ/mol,13,16 which amounts to around −240 kJ/mol for 60 atom pairs, say those directly opposite to each other. The additional entropic stabilization thus arises from cross correlations in the solute-solute and solute-solvent contributions.
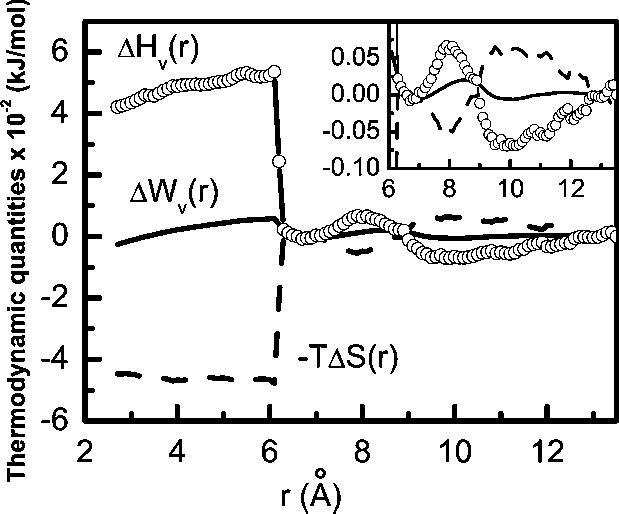
At lower inter particle separations the enthalpic contribution is dominated by the steep repulsive part of the direct solute-solute potential Uuu(r) and therefore, change in the solvent contribution to enthalpy is masked. Eliminating the direct solute-solute potential part, Uuu(r) from the PMF, we obtain the solvent contribution to the PMF, ΔWv(r). Since the direct solute-solute interaction is independent of temperature, the solvent contribution to enthalpy, ΔHv(r) can easily be obtained by subtracting the Uuu(r) from the enthalpy term. The solvent contribution to the PMF is shown in Fig. 2 along with its entropic (−T ΔS(r)) and solvent induced enthalpic (ΔHv(r)) contributions.
Fig. 2.
Solvent contribution, Wv(r) to the PMF, G(r) and its entropic (−TΔS(r)) and enthalpic (ΔHv(r)) contributions for the same system as in Fig. 1. The keys are same as in Fig. 1. In the inset the same plots are shown for inter solute separations of 6 Å and larger.
Stability of the first solvent separated state at an inter solute separation of around 7 Å, is determined mostly by the stabilizing effect of the enthalpy, the entropic contribution at this separation being relatively small. However, the barrier between the contact pair state and first solvent separated state at around 6 Å is dominated by unfavorable enthalpy in spite of a considerable favorable contribution from the entropy. When the inter solute distance is shorter than 6 Å, a substantial increase in ΔHv(r) and decrease in −TΔS(r) are observed. We have shown earlier30 that water forms a highly structured layer between the two solutes at an inter solute distance of 7.0 Å and it remains so down to around an inter solute distance of 6.0 Å. The large increase in entropy (decrease in −TΔS(r) as shown in Fig. 2) below 6 Å results from the release of the highly structured water from the inter solute region to the bulk. On the other hand, as a result of expulsion of water molecules from the inter solute region, an amount of favorable energy arising from attractive interactions between the solute and water in the confined region is lost. This results in sharp increase in solvent reflected enthalpy below an inter solute distance of 6 Å.A slight downward trend in ΔHv term from this point downward can be either due to increase in favorable interactions between the water and the solute or due to changes in water-water interactions. A decomposition of ΔHv into solute-solvent and water-water interactions has, therefore, been performed and presented in the next subsection.
Beyond the first solvent separated minimum in free energy we find another minimum at around an inter solute separation of 10 Å that corresponds30 to the second solvent separated state with a solute-solvent configuration having two intervening water layers which is stabilized by enthalpy. The barrier between the first and the second solvent separated minima is determined from a slight imbalance between the stabilizing enthalpic contribution and the destabilizing entropic contribution.
B. Contributions from water-water interactions due to solvent reorganization around the solute
With a change in inter solute distance, it is expected that water around the solute molecules will reorganize themselves and therefore a change in water-water interaction should result. As mentioned earlier, quantification of this contribution due to change in water-water interaction to the solvent induced enthalpy is possible16 if the direct solute water interaction can be calculated from the simulation trajectory. In the present study, we have calculated, from the configurations obtained from the MD trajectory, the interaction between the water and the pair of solute plates at various inter particle distances. The variation of this term with respect to its value at a large inter solute separation is designated here as ΔUuv(r) and is shown in Fig. 3. At large inter solute separation, ΔUuv(r) is nearly zero and it deviates only slightly when the inter solute distance is reduced to 9 Å. On further reduction of the inter solute distance, the change in this contribution is noticeable. When the inter solute separation is further reduced below 6 Å, ΔUuv(r) becomes highly unfavorable, essentially constant and contributes significantly to the unfavorable ΔHv term. The drop in interaction energy between the solute and confined water when the inter solute separation is reduced from say 6.2Å, where a monolayer of water exists in the confined region, to 5.8 Å, where no water molecules are sterically allowed in the inter solute region, is around 150 kJ/mol (see Table I of Ref.30). This is almost the same as the increase in ΔUuv(r) at this point as shown in Fig. 3. Thus, the increase in ΔUuv(r) at this point originates solely from the reduction in favorable interactions of the confined water with the solute plates due to expulsion of water from between the two solute plates.
Fig. 3.
The solvent induced contribution to enthalpy of association, ΔHv(r) (solid line) is split into the change in energy of interaction of the solute pair with water molecules, ΔUuv(r), (dotted line) and the remaining contributions from the change in water-water interactions and other mechanical work, ΔHrem(r), (dashed line). In this plot all quantities are referenced to the solute pair at 13 Å.
When the contribution due to direct solute-solvent interactions, ΔUuv(r) is subtracted from the solvent contribution to the enthalpy (ΔHv(r)), one obtains the remaining contributions (ΔHrem(r)) arising from the change in water-water interactions around the solute plates and from the pressure-volume work, PΔV. At 1 atm pressure, the PΔV term is small and the behavior of ΔHrem is mainly dictated by the contributions from the changes in interactions. It is important to observe that the contribution from ΔHrem(r) term is substantial in the ΔHv(r) through out the entire range of inter particle separations considered here. As already shown, near the contact pair state a significant unfavorable contribution in ΔHv(r) comes from the direct solute-water interaction part, ΔUuv(r), which accounts for more than 30 % of the increase in the solvent induced enthalpy change. However, an unfavorable contribution also arises from the change in the interactions represented by ΔHrem. When all the water molecules are expelled from the inter solute region into the bulk a reorganization is required to accommodate these expelled water molecules and so some less favorable interactions of the water molecules may result. The nature and amount of decrease in ΔHv(r) in the region of inter solute separations of 6 Å to 3 Å is entirely due to the similar change in the ΔHrem term.
IV. CONCLUSIONS
We have investigated the detailed thermodynamics of nanoscopically large hydrophobic solute plates modeled as graphene sheets in explicit water. The entropic and enthalpic contributions to the PMF were calculated from the temperature dependence of the PMF obtained from the MD simulation in conjunction with FEP techniques. Here we mainly confirm an old theoretical picture of the hydrophobic interaction. In particular we find contact (solvent excluding) configurations are entropically stabilized. Solvent separated configurations are enthalpically stabilized or show entropy-enthalpy compensation or cancellation.
The stabilization of the contact pair state is mainly due to an increase in entropy arising from the expulsion of the highly structured water layer from the inter solute region. It is however important to note that the expulsion of water between the plates occurs only due to steric constraints. The highly unfavorable solvent induced contribution to the enthalpy change at the contact pair state arises from the changes in water-water interactions. The PMF at the first solvation barrier is dominated by unfavorable enthalpic contributions as compared to the stabilizing entropic term.
The results presented here clearly demonstrate the relative roles of entropy and enthalpy in stabilizing various solute-solvent configurations of nanoscopic hydrophobic solutes in water at ambient conditions. We have shown that thermodynamic behavior of association of solutes with realistic interactions in water does not show any crossover from entropic to enthalpic behavior in this solute size range which is similar to that expected for many biomolecular assemblies. In order to better understand the association of large hydrophobic solutes in water and its relation to the aggregation phenomena observed in biological systems, future studies will include the effects of pressure, salt concentrations and denaturant on the PMF as well as on the relative contributions of entropy and enthalpy to the PMF.
Acknowledgments
We gratefully acknowledge NIH, the R.A. Welch foundation, and TiiMES, funded by NASA Cooperative Agreement No. NCC-1-02038 for partial financial support of this work. The computations were performed in part using the NSF meta center facilities and the Molecular Science Computing Facility in the W.R. Wiley Environmental Molecular Sciences Laboratory, a national scientific user facility sponsored by DOE’s Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, operated for DOE by Battelle.
References
- 1.Kauzmann W. Adv Protein Chem. 1959;14:1. doi: 10.1016/s0065-3233(08)60608-7. [DOI] [PubMed] [Google Scholar]
- 2.Pratt LR, Pohorille A. Chem Rev. 2002;102:2671. doi: 10.1021/cr000692+. [DOI] [PubMed] [Google Scholar]
- 3.Tanford C. The Hydrophobic Effect: Formation of Micelles and Biological Membranes. John Weiley; New York: 1973. [Google Scholar]
- 4.Dill KA. Biochemistry. 1990;29:7133. doi: 10.1021/bi00483a001. [DOI] [PubMed] [Google Scholar]
- 5.Ludemann S, Schreiber H, Abseher R, Steinhauser O. J Chem Phys. 1996;104:286. [Google Scholar]
- 6.Lum K, Chandler D, Weeks JD. J Phys Chem B. 1999;103:4570. [Google Scholar]
- 7.Pangali C, Rao M, Berne BJ. J Chem Phys. 1979;71:2975. [Google Scholar]
- 8.Hummer G, Garde S, Garcia AE, Pohorille A, Pratt LR. Proc Natl Acad Sci USA. 1996;93:8951. doi: 10.1073/pnas.93.17.8951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Perkyns JS, Pettitt BM. J Phys Chem. 1996;100:1323–1329. [Google Scholar]
- 10.Hummer G, Garde S. Phys Rev Lett. 1998;80:4193. [Google Scholar]
- 11.Smith DE, Haymet ADJ. J Chem Phys. 1993;98:6445. [Google Scholar]
- 12.Smith DE, Zhang L, Haymet ADJ. J Am Chem Soc. 1992;114:5875. [Google Scholar]
- 13.Shimizu S, Chan HS. J Am Chem Soc. 2001;123:2083. doi: 10.1021/ja0034390. [DOI] [PubMed] [Google Scholar]
- 14.Rick SW, Berne BJ. J Phys Chem. 1997;101:10488. [Google Scholar]
- 15.Rick SW. J Phys Chem B. 2000;104:6884. [Google Scholar]
- 16.Ghosh T, Garcia AE, Garde S. J Chem Phys. 2002;116:2480. [Google Scholar]
- 17.Stillinger J Solution Chem. 1973;2:141. [Google Scholar]
- 18.Huang DM, Chandler D. Proc Natl Acad Sci USA. 2000;97:8324. doi: 10.1073/pnas.120176397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huang DM, Geissler PL, Chandler D. J Phys Chem B. 2001;105:6704. [Google Scholar]
- 20.Huang DM, Chandler D. J Phys Chem B. 2002;106:2047. [Google Scholar]
- 21.Berard DR, Attard P, Patey GN. J Chem Phys. 1993;98:7236. [Google Scholar]
- 22.Wallqvist A, Berne BJ. J Phys Chem. 1995;99:2885. [Google Scholar]
- 23.Wallqvist A, Berne BJ. J Phys Chem. 1995;99:2893. [Google Scholar]
- 24.Huang X, Margulis CJ, Berne BJ. Proc Natl Acad Sci USA. 2003;100:11953. doi: 10.1073/pnas.1934837100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Walqvist A, Gallicchio E, Levy RM. J Phys Chem. 2001;105:6745–6753. [Google Scholar]
- 26.Hummer G, Rasaiah JC, Noworyta JP. Nature. 2001;414:188. doi: 10.1038/35102535. [DOI] [PubMed] [Google Scholar]; Sansom MSP, Biggin PC. Nature. 2001;414:156. doi: 10.1038/35102651. [DOI] [PubMed] [Google Scholar]; Sansom MSP, Biggin PC. Nature. 2001;414:156. doi: 10.1038/35102651. [DOI] [PubMed] [Google Scholar]
- 27.Waghe A, Rasaiah JC, Noworyta JP, Hummer G. J Chem Phys. 2002;117:10789. [Google Scholar]
- 28.Zhou R, Huang X, Margulis CJ, Berne BJ. Science. 2004;305:1605. doi: 10.1126/science.1101176. [DOI] [PubMed] [Google Scholar]
- 29.Ashbaugh HS, Paulaitis ME. J Am Chem Soc. 2001;123:10721–10728. doi: 10.1021/ja016324k. [DOI] [PubMed] [Google Scholar]
- 30.Choudhury N, Pettitt BM. J Am Chem Soc. 2005;127:3556. doi: 10.1021/ja0441817. [DOI] [PubMed] [Google Scholar]
- 31.Choudhury N, Pettitt BM. J Phys Chem B. 2005;109:6422. doi: 10.1021/jp045439i. [DOI] [PubMed] [Google Scholar]
- 32.Choudhury N, Pettitt BM. Mol Sim. 2005;31:457. [Google Scholar]
- 33.Subramanian V, Yin H, Rasaiah JC, Hummer G. Proc Natl Acad Sci USA. 2004;101:17002. doi: 10.1073/pnas.0407968101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Choudhury N, Pettitt BM. Special Volume of the Royal Society of Chemistry entitled. In: Naidoo KJ, Hann M, Gao J, Field M, Brady J, editors. Modeling Molecular Structure and Reactivity in Biological Systems. (communicated) [Google Scholar]
- 35.Choudhury N, Pettitt BM. Phys Rev Lett. (Communicated) [Google Scholar]
- 36.Ball P. Nature. 2003;423:25. doi: 10.1038/423025a. [DOI] [PubMed] [Google Scholar]
- 37.Ben-Neim A. Hydrophobic Interactions. Plenum Press; New York: 1980. [Google Scholar]
- 38.Zwanzig RW. J Chem Phys. 1954;22:1420. [Google Scholar]
- 39.Linse P. J Am Chem Soc. 1993;115:8793. [Google Scholar]
- 40.Berendsen HJC, Grigera JR, Straatsma TP. J Phys Chem B. 1987;91:6269. [Google Scholar]
- 41.Cornell DW, Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, Spellmeyer DC, Fox T, Caldwell JW, Kollman PA. J Am Chem Soc. 1995;117:5179. [Google Scholar]
- 42.Nose S. Mol Phys. 2002;100:191. [Google Scholar]
- 43.Andersen HC. J Chem Phys. 1980;72:2 384. [Google Scholar]
- 44.Nose S, Klein ML. Mol Phys. 1983;50:1055. [Google Scholar]
- 45.Allen MP, Tildesley DJ. Computer Simulation of Liquids. Oxford University; New York: 1987. [Google Scholar]
- 46.Andersen HC. J Comput Phys. 1983;52:24. [Google Scholar]
- 47.Swope WC, Andersen HC, Berens PH, Wilson KR. J Chem Phys. 1982;76:637. [Google Scholar]
- 48.Chandler D. Nature. 2002;417:491. doi: 10.1038/417491a. [DOI] [PubMed] [Google Scholar]
- 49.Rajamani S, Truskett TM, Garde S. Proc Natl Acad Sci USA. 2005;102:9475. doi: 10.1073/pnas.0504089102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Pettitt BM, Rossky PJ. J Chem Phys. 1986;84:5836. [Google Scholar]


