An Optical Signal Correlated with the Allosteric Transition in Scapharca inaequivalvis HbI

Abstract

The transient absorbance change in the first 2 μs after photolysis of COHbI (from Scapharca inaequivalvis) reported by Chiancone et al. (1) has been studied in several mutants. Evidence is presented that this change (rts) is associated with the allosteric transition between R- and T-states. Two different rts spectra relate to Hb₂ and Hb₂CO. No rts has been observed for mutants at position 97 (normally Phe). Correlation of ligand binding and rts shows that protein function changes at or near the rates of rts – typically 2 × 10⁶ s⁻¹ (Hb₂) and 5 × 10⁵ s⁻¹ (Hb₂CO). Unique values of allosteric parameters for several mutants have been obtained by combining kinetic and equilibrium data. The effect of mutation on function thus may be assigned to allostery or to change in intrinsic heme reactivity.

Cooperativity in ligand binding by mammalian hemoglobins, expressed in their sigmoid equilibrium curves, was established about a century ago. These studies initiated attempts, still ongoing, to describe the curves in physicochemical terms. Difficulties in studying these hemoglobins have arisen from: (a) two kinds of subunits, (b) four subunits per molecule, (c) a strong dependence on pH and salts and (d) tetramer to dimer dissociation. Clearly, a dimeric hemoglobin would be much easier to study. There are, however, few dimeric types of hemoglobin, and fewer still that bind ligands cooperatively. The hemoglobin from Scapharca inaequivalvis that has two identical subunits, no effect of pH and salts, marked cooperativity, and a very small dimer to monomer dissociation constant even when liganded, perhaps comes closest to the ideal.

This homodimeric hemoglobin was first studied in relation to an Adriatic clam fishery. References to the early work may be found in Antonini et al. (2). In that paper the kinetics of the reactions of the native protein with oxygen and carbon monoxide were described in terms of the two-state model (MWC) of Monod, Wyman and Changeux (3). They noted, however, that unique values of the allosteric parameters could not be assigned from ligand binding studies alone because of the close correlation between L (the ratio of the R and T forms of deoxyhemoglobin) and c (the change in L on binding each ligand molecule). The structures of both liganded and deoxy forms of the wild type and of many mutants have been determined to high resolution (4,5). Unlike mammalian hemoglobins, there are no major quaternary structural changes on ligand binding, allowing fully cooperative oxygen binding to crystals (6). However, residue F97 does move away from the heme group and water molecules in the interface between the subunits change in number and position. The importance of residue 97 has been underscored by site-directed mutagenesis (7,8), and the role of interfacial water probed by the isosteric substitution T72V (9,10). It does not alter the structure apart from these water molecules but the mutation raises oxygen affinity some 50-fold. Royer et al. (9) have shown that the kinetic and equilibrium effects may be explained by changing the MWC parameter L, without alteration of c. We now describe a spectrophotometric signal (rts), present evidence of its relation to allostery, and illustrate how the properties of F97 mutants (8) may be used to assign unique values of the allosteric parameters L and c in the MWC model. Edelstein (11) proposed that the rough relation between affinity and cooperativity (expressed as Hill’s n, a measure of inflection of a sigmoid curve) of several naturally occurring mutants of human hemoglobin may be explained in terms of the MWC model on the assumption that the mutants share common tense and relaxed (T and R) states. An analogous relation has been found among mutants of Scapharca and both the principle and deviations from it contribute to understanding the detailed mechanism.

Materials and Methods

Flash photolysis data were collected by feeding the output of a fast photomultiplier into the 50-ohm input of a Tektronix oscilloscope model TDS620. During data collection a 75W xenon arc light source was pulsed using a lumped component network to flatten the peak of the output pulse. No corrections were required for total collection times up to 10 μs. An interval of 6 sec between laser flashes was obtained by counting the pump flashes of the laser both to minimize heating of the sample and to standardize charging time for the pulser network. The data were displayed as collected, and collection continued until a satisfactory signal was obtained, using up to 50 flashes. Data were collected between 450 and 400 nm at intervals of 5 nm. In most cases neutral density filters were used to give 5 or 6 levels of photolysis. The 8-bit resolution of the oscilloscope is not sufficient to display the relatively small R-T signal, so a second expanded trace was also collected on a more sensitive scale. The expanded traces by themselves do not give meaningful absorbance information because the trace is off screen until the laser fires. The change in absorbance from zero time to the end of the normal trace served to scale the expanded trace. The scaled traces were represented as the sum of two, or more rarely, three exponentials. The data at all wavelengths and a single light level were fitted as a group, using the same rates for the components. The correlations from the covariance matrix were used as an index of the interdependence of the rate constants. This procedure separated the contributions of geminate recombination and the rts signal. In addition to the difference in spectrum, geminate recombination was usually an order of magnitude faster than the rts signal. In analysis, the expanded traces were usually treated as starting from zero time. When treated as differences from the last recorded data, slower processes would be ignored, but in practice comparisons between the two methods seldom showed discrepancies, suggesting the absence of slower processes apart from bimolecular recombination. This rate was not taken into account, as it was always more than two orders of magnitude slower than the first order processes. Comparisons of the effect of change in level of photolysis on the amplitude of the rts signal used the absorbance at the end of the normal traces, when geminate and R-T processes were complete, as a measure of effective photolysis, and the rts signal was taken as the sum of the weighting coefficients for the appropriate rate component between 420 and 435 nm.

Results and Discussion

Nature and Assignment of Signal

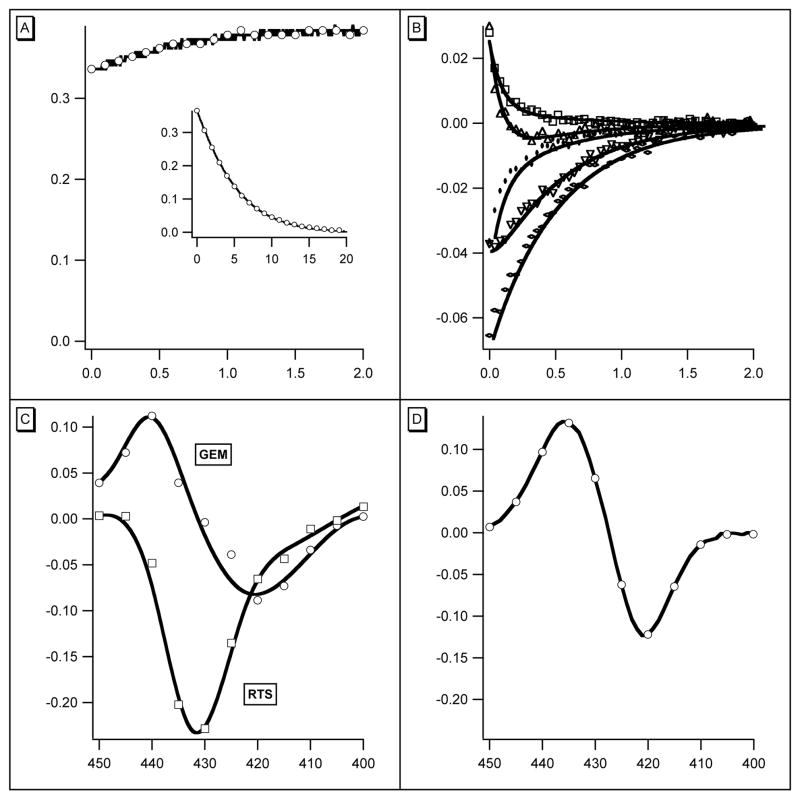
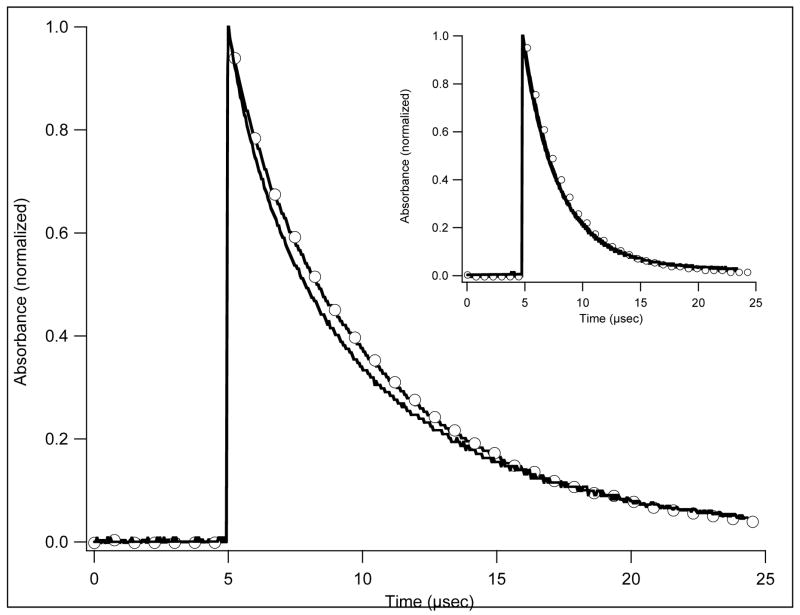
An extract from the rts data collected during the first 1.6 μs after photolysis of w/t COHbI is shown in Figure 1. A single shot at one wavelength shows ligand binding and the rts signal and gives an idea of their relative amplitudes and time scales (Figure 1A). Eleven wavelengths were used with 6 light levels at each wavelength and 400 points in each trace; an extract is shown in Figure 1B. In analysis, the data were first described by fitting the full photolysis data set with two exponentials. There were two rates at each light level, an invariant one of 2.2 × 10⁷ s⁻¹, and another dropping from 2.0 × 10⁶ s⁻¹ to about 5.0 × 10⁵ s⁻¹ as the photolysis level decreased. The precision at low light is much less because of increased noise. The rates are only weakly correlated, with a value from the covariance matrix of 0.13. At each wavelength and level of photolysis the coefficients of the exponentials define the contributions of the underlying processes at that point, and are plotted to give the spectrum of each component (Figure 1C). The spectrum and rate of the faster component (upper curve) suggest its source is geminate recombination. The spectrum is that of ligand binding, and the rate of 2.2 × 10⁷ s⁻¹ is the same as that for oxygen. Both components scale with hemoglobin photolysis. The geminate rebinding component corresponds to 4.2% of the total ligand binding difference spectrum (Figure 1D).

Figure 1.

(A) Absorbance change at 435 nm during the first 2μs (abscissa) after photolysis. At the beginning of the curve, absorbance (ordinate) increases after the flash. The rts is the relatively slow change that follows. Conditions: 1 mM CO, 18μM heme, 0.05M KPi, 20°, path 2mm. Inset: Complete rebinding of CO, abscissa 20 ms. (B) Data for 5 representative wavelengths from the same experiment, expanded scale. (WER comment – I think we need to identify the five wavelengths used here.) Abscissa 2.0 μs. Ordinate, change in absorbance. Points are experimental; the lines are fits to two exponentials using the same rates for all traces. Full photolysis was used in the experiment shown. (C) Coefficients for the rates used in panel B plotted against wavelength. Rates were 1.9 x 10⁷ s⁻¹ for curve GEM (geminate) and 2.9 × 10⁶ s⁻¹ for RTS (rts). (D) Static difference spectrum Hb2 – Hb2(CO)2 for comparison with curve GEM of panel C.

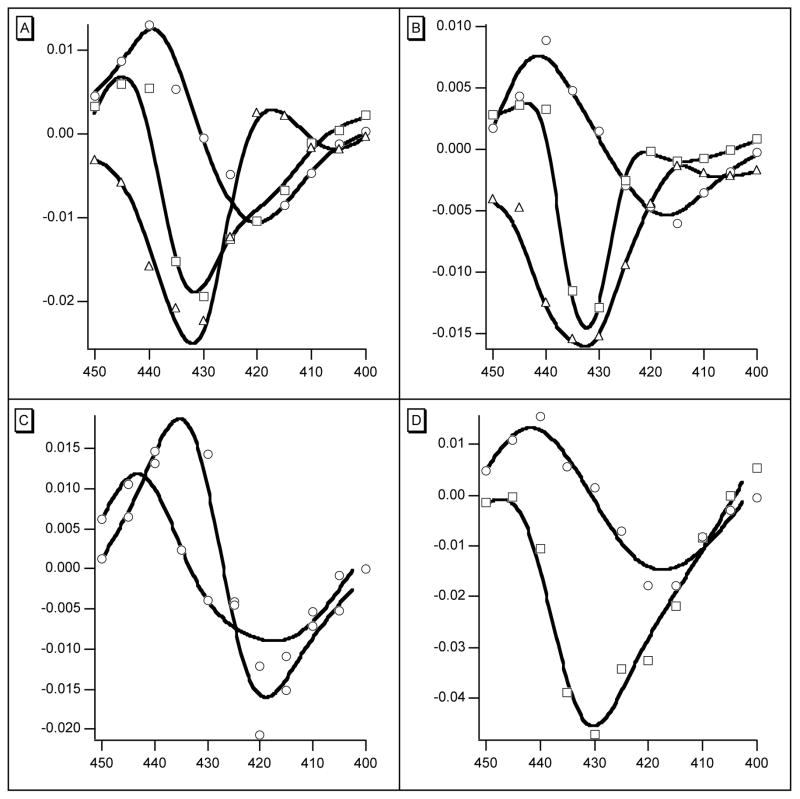
As the products of photolysis are Hb₂ and Hb₂CO it is plausible to associate their formation with the second rate. Immediately after photolysis, the distribution between R- and T-states of both products is that of Hb₂(CO)₂. Royer et al. (9) have suggested that about 80% of w/t Hb₂(CO)2 is in the R-state and that both Hb₂CO and Hb₂ are more than 97% T-state at equilibrium. It follows that both photoproducts (Hb₂ and Hb₂CO) may be expected to relax to the T-state. As the level of photolysis falls the proportion of Hb₂CO relative to Hb₂ increases and its R to T rate has an increasing influence on the overall observed rts rate. The data were therefore refit using 3 exponentials giving the rates of three processes as 1.37 × 10⁷ s⁻¹, 2.1 × 10⁶ s⁻¹, and 0.9 × 10⁵ s⁻¹ for the full data set and all 6 light levels. The rms residual remained at 0.001: the largest correlation of 0.38 was between the two rts rates. Neither rts rate was strongly correlated with the geminate rate (0.23 and 0.25). The use of 3 exponentials therefore appears to be justified although the difference between the two rts rates was too small to be apparent when data for single light levels were examined separately. The three spectra are presented in Figure 2A. Comparison shows that the rts signal in Figure 1C is indeed the sum of the two rts spectra in Figure 2A. Analogous results obtained with L73M, F97Y and T72V are also presented in Figure 2: they will be discussed later.

Figure 2.

The panels show the weights of the components used to represent the absorbance changes (ordinates) during the first 2μs after photolysis of the mutants indicated. In each panel the curve with the highest point is assigned to geminate rebinding of ligand. In panels (A) w/t and (B) L73M, the middle spectrum is assigned to the rts signal of Hb2, the lowest spectrum is assigned to Hb2(CO). (C) Two geminate recombination spectra associated with F97Y. (D) The single, and only rts spectrum associated with T72V. In all panels abscissa is wavelength in nm.

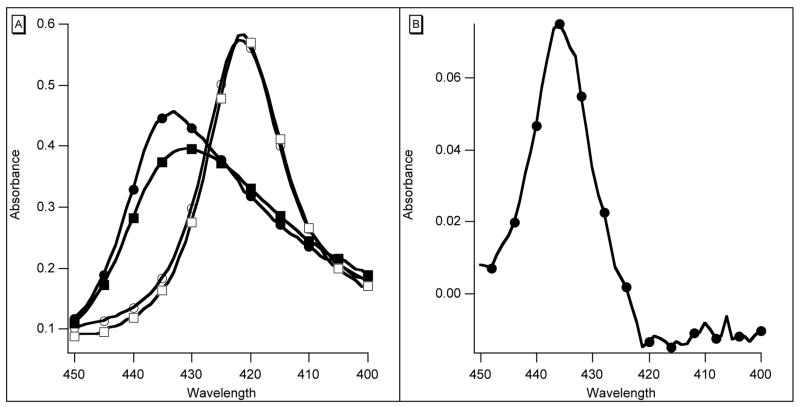
Further evidence of a relation between the rts signal and conformation change comes from the high affinity species F97L, F97Y, and F97V, none of which has an rts signal. F97Y, in particular, has been studied in detail recently (8). The characteristic movement of residue F97, packing close to the heme in the deoxy form and moving out on ligand binding, does not occur. Several features of the behavior of this mutant following photolysis are presented in Figure 2C and Figure 3. There are two rapid geminate reactions with different difference spectra and rates, and as already reported (8), bimolecular binding of CO is also biphasic. Although the static spectra of oxy- and carboxy F97Y hemoglobins are closely similar to those of w/t, the spectrum of deoxy F97Y has lower absorbance at the Soret maximum (Figure 3). There is apparently more than one stable conformation. The longer wavelength species has a geminate rate of 7.4 × 10⁷ s⁻¹ and accounts for some 40% of the total geminate reaction. The rate for the slower component is 1.0 × 10⁷ s⁻¹. The mutant F97V behaves similarly (not illustrated). The high affinity mutants F97L, F97Y and F97V also share a large observed rate of oxygen binding of 40–50 μM⁻¹s⁻¹ (cf. w/t 17 μM⁻¹s⁻¹) and have the same rate of oxygen dissociation (2.8 s⁻¹) measured either with dithionite or by replacement of oxygen with CO. This commonality leads us to suggest that these rates may define a standard R-state.

Figure 3.

(A) Absorption spectra of w/t (deoxy–● and CO–○) and F97Y (deoxy–■ and CO–□). (B) Difference spectrum F97Y Hb2 – w/t Hb2· Heme 4 micromolar, path 1 cm.

Experiments with other mutants are consistent with this suggestion. The structure of the isosteric mutant T72V has been studied in detail (9,10). Its structure is identical to that of w/t except for water molecules in the T-state interface between the subunits. Its rates of combination with O₂ and CO are much faster and there is a 40-fold increase in affinity for oxygen, coupled to an increase in Hill’s n from 1.45 to 1.55. These findings may be accommodated in the MWC model by a decrease in the allosteric parameter L without change in the intrinsic T and R properties (9). At equilibrium the distribution of R and T is quite different from that of w/t: Hb₂(CO)₂ and Hb₂CO are effectively all in the R-state and even Hb₂ is about 10% R. During the first few microseconds after photolysis, in addition to a geminate reaction, there is an rts signal with the same spectrum as the slower broader w/t rts signal. Unlike w/t, however, its appearance is accurately described by the single rate constant of 1.0 × 10⁵ s⁻¹ at all levels of photolysis. With a value of 10 for L and the standard value of 600 for c, Hb₂CO is 98% R-state and Hb₂(CO)₂ is almost all R-state, thus the change from Hb₂(CO)₂ to Hb₂CO would not be expected to contribute a significant rts change. The rts observed must therefore be attributed to the change from Hb₂CO to Hb₂ and it has the form of the broader spectrum of Figure 2, already attributed to this change in w/t. When flash intensity is changed, the amplitude of the rts signal scales with the square root of photolysis, consistent with a relation between the rts signal and change of Hb₂CO from R to T.

The absence of an rts signal in all mutants at position 97 suggests that it may be linked to the effect of Phe 97 packing against the heme in the T-state. Raman studies (12) on wild-type HbI have identified resonances that follow an approximately similar time-course following CO photodissociation to that observed here for the rts. Among these changes, the heme macrocycle resonance at 756cm⁻¹ and the iron-proximal histidine stretching mode at 203cm⁻¹ may be correlated with the R to T transition of Phe 97 and thus may be related to the rts signal observed here. The rts time course is slightly faster than suggested by time-resolved crystallography (13), which probably reflects real differences between crystalline and solution experiments.

Rate of the R-T transition

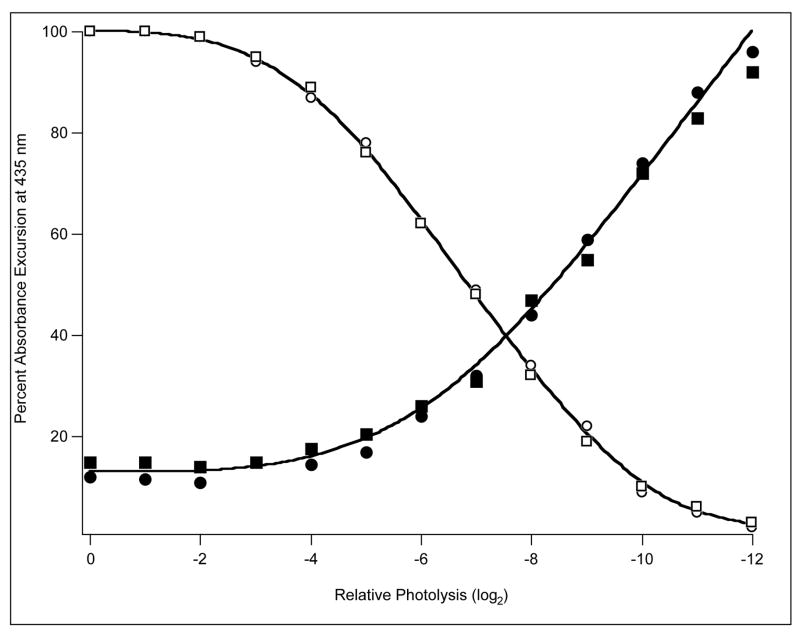
Measurement of the rate of appearance of the rts signal immediately raises the question of its relation to the rate of change of the functional properties of the protein. One approach was to use the laser flash to generate empty sites suddenly and follow the bimolecular reaction thereafter. The first mutant examined was T72V reacting with 1 atm. CO. The time of observation was extended to include bimolecular recombination over a 4000-fold range of intensities. Two rates of 1.8 μM⁻¹s⁻¹ and 5.2 μM⁻¹s⁻¹ were attributed to binding to T- and R-states respectively. In this experiment the doubly liganded species should be over 99.9% R-state so the immediate photoproduct is expected to be in the R-state. The finding of a low rate of binding shows that T-state function appears quickly, but quantization is complicated by a small amount of protein with R-state properties that does not appear to enter into allosteric reactions. The proportion of the main reaction accounted for by the slower (1.8 μM⁻¹s⁻¹) component (Figure 4) increases at high light levels as the proportion of Hb₂ relative to Hb₂CO increases: it fails to reach 100% at high light intensity tending towards an asymptote at 88% of the total absorbance change. Repetition of the experiment with 10% CO in place of 1 atm. CO yielded similar results, eliminating ligand binding kinetics as a source of the anomaly. A further point of interest arises when CO binding is followed at several wavelengths. With the parameters given previously and with full photolysis, most of the hemoglobin is in the T-state very soon after dissociation of CO. As binding proceeds, R-state accumulates and the rts signal reverses. The result is that the measured course of ligand binding should not be quite the same at different wavelengths. The effect, though small, is quite demonstrable. The time course of CO binding to T72V is slightly different when followed at 435 nm and at 425 nm (Figure 5). The data from a control experiment with myoglobin (inset) share the same time course at these wavelengths.

Figure 4.

CO binding to T72V. Abscissa log2, relative photolysis intensity. Absorbance excursion at 435 nm, percent of value with full light (□ – 1 mM CO, ○ – 0.1 mM CO) and corresponding fraction of faster reaction (■ – 1 mM CO, ●– 0.1 mM CO). Path 1 mm, flash 6 ns.

Figure 5.

CO (0.1 mM) binding to T72V followed at 435 nm (○) and at 420 nm (□). Inset: Sperm whale myoglobin treated similarly.

The rapid appearance of the rts signal in w/t (2.0 × 10⁶ s⁻¹) suggested it mightn well precede the functional change of R to T. With a large value of L (4.8 × 10⁴), however, even if this rate were also the rate of appearance of T-state ligand binding, the rate of the T₀–R₀ reaction (2.0 × 10⁶ L) would only be about 20 s⁻¹. A qualitative test of this rate was made by comparing the time courses of CO binding with 10% CO and with 1 atm. CO. An accelerating time course had been reported earlier in a flash photolysis experiment using 10% CO (2). If the T₀–R₀ rate is only 20 s⁻¹, the rate of binding with 1 atm. CO, some 150 s⁻¹, would be too great to allow significant acceleration to develop, with binding to T-state only. Experiments (Figure 6) confirmed the earlier result with 10% CO whereas acceleration with 1 atm. CO was negligible. It appears that the T₀–R₀ time course cannot be much greater than about 20 s⁻¹ so that the appearance of the rts signal and the change from R to T must share the same rate. Additional steps may precede and follow the rts signal, but must be rapid as compared with the rate of the ligand reactions. The corollary is that the R₀ to T₀ rate of appearance of T-state function should be the same as that of the appearance of the rts signal (2.0 × 10⁶ s⁻¹).

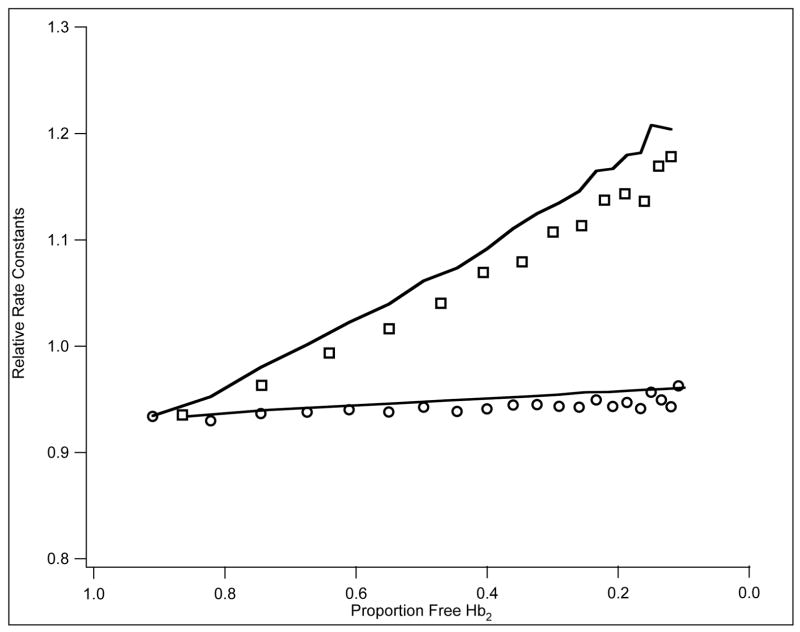
Figure 6.

Combination of CO, 1mM (○) and 0.1mM (□) with w/t followed at 435 nm. Abscissa: proportion free Hb2· Ordinate: corresponding relative rate constants obtained by smoothing the 400 total data points using a moving average of 5 points. Rates were calculated from point to point. The lowest point (ordinate) corresponds to 0.18 μM⁻¹s⁻¹, the highest to 0.27 μM⁻¹sμ⁻¹.

The reaction of w/t with oxygen is faster, and more difficult to deal with: the effective quantum yield is low, pointing to picosecond or faster geminate reactions. Nanosecond geminate rebinding also returns 45% of photodissociated oxygen to the heme contributing to a mix of R- and T-states, presumably in a binomial distribution. The resulting initial rate of oxygen rebinding is therefore intermediate between R- and T-state rates and, in the practically accessible range, is very slightly dependent on amplitude of photolysis. The initial rate observed with 1 atm. O₂ following photolysis of Hb₂O₂ was 17 μM⁻¹s⁻¹. To increase the proportion of Hb₂ after the laser flash, the sample was equilibrated with CO and O₂ gases in the ratio 80:20. The value of M, (the ratio of the affinities for O2 and CO of the second molecule of ligand to bind), is 200 (1) so effectively all the protein is present as Hb₂CO and is largely in the R-state. The full flash removes more than 99% of bound CO in some 5 ns, delivering R-state Hb₂. Relaxation after the flash was followed at 6 wavelengths in the Soret region. The results were modeled using the standard R-state rates and T-state values for oxygen (7) together with the revised value of L and a separate measurement of the T-state combination rate for CO on the same sample. The T-state rate of combination was the only variable used. The rms residual was 0.0016 and the oxygen on rate 17 μM⁻¹s⁻¹. There is no evidence of the R-state rate of 40 μM⁻¹s⁻¹, corresponding to a pseudo first order rate of 60,000 s⁻¹ with 1 atm. O₂. Although the experiment does not lead to numerical value, the rate of the functional R to T change must be at least 1.0 x 10⁵ s⁻¹, and no steps slower than that can be prerequisites of the functional R to T transition in w/t. Note that the rate constant for oxygen binding to the T-state was significantly larger than previously suggested (1,7).

Application of the model to other mutants

As was suggested by Edelstein (1971) the rough relation between the cooperativity of naturally occurring hemoglobin mutants and their affinity might be explained if T- and R-states were shared by several hemoglobins which would then have widely different values of L. His proposal could not be tested fully because of difficulty in determining the value of L, though a clear relation between affinity and Hill’s n was found. By analogy, for Scapharca, if the affinity of the mutant F97Y sets a standard for a general R-state, there should be no mutants with higher affinity, and indeed none has yet been found. Similarly, if the T-state of w/t defines a standard T-state, there should be no mutant with a dissociation constant for oxygen greater than 47 μM. The mutant L73M has a dissociation constant of 33 μM, (cf. w/t at 16 μM) and has been examined with the Edelstein proposal in mind.

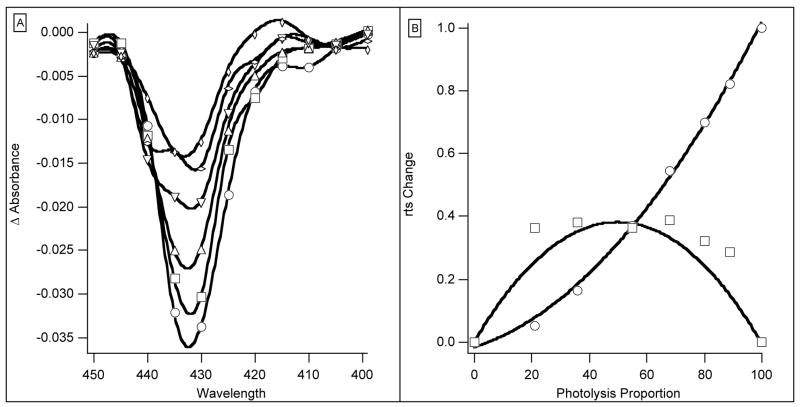
The value of L for L73M has been estimated in two different ways. In kinetic experiments, assuming the standard parameters, with L as the sole variable, its value was 6.1 × 10⁵. Computer runs with slightly different values for the kinetic parameters showed that the sensitivity of the solutions to the value of L was low because L is already so large. The equilibrium curve calculated from the same set of parameters and p50 gave L of 5.5 × 10⁵ but lower n of 1.18 (observed 1.24). With these numbers, 55% of fully liganded Hb₂O₂ remains in the T-state so the amplitude of the rts is reduced (Figure 2). When the appearance of the rts was represented by two exponentials the apparent rate of the rts component fell off as photolysis was reduced and its spectrum (Figure 7A) changed in shape. The data permitted analysis with 3 exponentials. The fastest rate had the form of a ligand binding difference spectrum. The spectrum associated with the lowest rate has the same form as the rts spectrum of T72V, already identified with the change of Hb₂ from R to T. The contributions of the two rts components are strongly dependent on level of photolysis (Figure 7B). The lines in the figure show the change in the amounts of Hb₂ and Hb₂CO appearing on photolysis calculated from the model. Although the scatter of the points is large reflecting the small absorbance changes, there is little doubt that the data form two groups. The identification of the R-T changes of Hb₂ and Hb₂CO with the faster and slower rts signals is also clear. The upper curve in Figure 7B refers to the fast component, and the lower curve to the slower component.

Figure 7.

(A) Spectra of rts components for L73M. Ordinate: Absorbance change for six photolysis intensities. The photolysis intensity was halved between each record. Abscissa: wavelength in nm. (B) L73M rts coefficients and photolysis. Ordinate: (○) Faster rts signal associated with Hb2 R to T change. (□) Slower rts signal associated with Hb2(CO). Lines represent simulations of each signal; symbols are experimental data. Abscissa: proportion of photolysis.

With so large a value of L, singly liganded hemoglobin should be over 99% T-state, which would predict no observable difference in rates for different levels of photolysis. This was examined in experiments with CO. There was no clear difference between the rates of rebinding following full and partial photolysis with both giving a rate of 0.1 μM⁻¹s⁻¹. The rate of oxygen binding to T-state L73M was measured by equilibrating a sample with 80% CO, 20% O₂. The rate for T-state binding was 11.5 μM⁻¹s⁻¹, regarded as being the same as the rate for w/t (Table 1). This is the result expected on the Edelstein principle.

Table 1.

Parameters describing oxygen binding to some mutants

Mutant	L	Ton	Toff	rms	COTon	[O2]50 calc	[O2]50 obs	n calc	n obs
w/t	48,000	10	500	0.0027	0.2	16.6	16.2	1.54	1.47
T72V	5	0	550	0.0051	0.2	0.2	0.3	1.43	1.55
L73M	650,000	11.6	550	0.0014	0.15	31.9	34.3	1.24	1.24
F97L	330	33	47	0.0025	0.5	1.0	1.6	1.16	1.15
I114F	210,000	4.8	200	0.0015	0.2	26.5	34	1.22	1.08

L is the ratio Hb_T/Hb_R for deoxyhemoglobin. T_on is the rate of combination of oxygen with T–state hemoglobin, units are μM(dimer) ⁻¹seconds⁻¹. T_off units are seconds⁻¹. r.m.s is the square root of the sum of the squares of differences between observed and calculated values of absorbance for all points in an experiment (usually 14000). CO_Ton units as for oxygen. [O₂]₅₀ is the concentration of oxygen (μM) required to give half-saturation using the kinetic parameters listed in the allosteric model. n is Hill’s n, a measure of sigmoidicity. For a dimer its limits are 1, no cooperativity, and 2, full cooperativity. Note that due to experimental error, the results of individual experiments given in the text may not agree with the averaged values of the Table.

Results with the mutant F97L are of particular interest both because it was the first mutant prepared (7) and because of its behavior. The substitution did not lead to a total loss of cooperativity with Hill’s n decreasing from 1.45 to 1.16 coupled with a 8-fold increase in affinity. The spectra in the usual time frame, however, show no sign of an rts signal, but there are two difference spectra: the faster (2.7 × 10⁷ s⁻¹) has an isosbestic at 433 nm in a ligand binding difference spectrum; the slower rate (3.9 × 10⁶ s⁻¹) also has a ligand binding spectrum with an isosbestic at 425 nm. In this respect F97L resembles F97Y. The standard 35-trace dataset was treated as described for w/t and L73M varying L only. The results were unacceptable. The rms residual was 0.0057 with L of 1280. Hill’s n was 1.8, very far from the experimental 1.16, though pO₂ at 1.6 mm Hg was not far from the experimental value. This mutant, though demonstrating the importance of residue F97, is not represented satisfactorily by the 2-state model with the constraints of “standard” R- and T-states. The failure of this analysis is reasonable, however, given that crystal structures indicate that the R- and T-states of F97L are likely to be quite different from those of wild-type (7)

Another mutant, I114F, has low affinity and reduced cooperativity (p50 = 21 mm. Hg, n = 1.08), although it has an rts signal similar to that of w/t. The results of the 35-trace experiment, constrained by standard R- and T-states, gave quite different values, and as with F97L, new values had to be sought. It was found that the on rates for both R- and T-states had to be reduced substantially to the values given in Table 1. Modification of the standard values may make suggestions about mechanism – in this case as both R and T on rates must be substantially reduced, the Phe at 114 may be blocking a pathway for ligands.

Conclusions

The origin of the rts is not known: it has not been observed in any mutant at position 97 and to that extent is linked to that residue. Although not quite so fast, rts occurs in the same time range as geminate recombination, and examination of the transient spectra is required to establish the nature of the absorbance changes during the first 2 microseconds after photolysis. The experiments and calculations described in the main section of this paper may be summarized by saying that the two-state model affords an internally consistent description of ligand binding kinetics by all of the mutants so far examined except for F97L and I114F. This does not, of course, prove that is how the protein reacts. The model may be used to classify mutants into those whose behavior may be described by change in allostery and those where access to the heme group or change in its intrinsic reactivity is more significant. It may, indeed, be necessary to use the model to describe kinetic data generally because the phenomenological rates are all, to a greater or lesser extent, composites of several allosteric and kinetic parameters. The rate of combination of oxygen, for example, may be influenced by the extent of geminate combination, the length of a photolysis flash, the rate of the R₀–T₀ transition, and the partition of Hb₂O₂ between R- and T-states, as well as by the on and off rates for ligands. The precision of the allosteric parameters is not readily accessible: experience suggests between 5 and 10% may prove reasonable except for L which, as its influence is indirect, may have an uncertainty of 30% or more.

The rate of dissociation of oxygen from w/t is given by the proportion of T multiplied by the rate of dissociation plus the proportion of R multiplied by the rate of dissociation. This is (0.15 × 500) + (0.85 × 3) = 78 s⁻¹, a rate in reasonable agreement with experiment (100 s⁻¹). Analogous calculations for L73M lead to rates of several hundreds per second. The observed rate with dithionite is high, but poorly determined because the time required by dithionite to react with oxygen in physical solution is of the same order as that of oxygen dissociation. The dissociation reaction is certainly rapid, however. The work described here with Scapharca appears to have fulfilled the expectation and hopes raised for a dimeric hemoglobin in the Introduction. The two-state model has often been used in describing ligand binding experiments and with carbon monoxide, sometimes with very great precision (14). We believe that this may be the first time a complete description of oxygen binding to a cooperative hemoglobin has been given in terms of the allosteric model in which values of the allosteric parameters were supported by both kinetic and equilibrium experimental data.

Abbreviations

Hb

hemoglobin

HbI

Scapharca dimeric hemoglobin I

rts

spectrophotometric signal correlated with allosteric change from T- to R-state

CO

carbon monoxide

p50

partial pressure of oxygen at which 50% of ligand binding sites are occupied

rms

root-mean square

atm

atmosphere

MWC

Monod, Wyman and Changeux two state model

L

ratio of R & T forms of deoxy-Hb

c

change in L on binding each ligand molecule