Decreases in dengue transmission may act to increase the incidence of dengue hemorrhagic fever

Abstract

Dengue hemorrhagic fever (DHF) is a potentially fatal manifestation of an infection with the mosquito-borne dengue virus. Because of the social and economic costs of DHF, many countries in Asia and South America have initiated public health measures aimed at vector control. Despite these measures, DHF incidence rates do not appear to be declining. The effectiveness of vector control in reducing dengue transmissibility has thereby been questioned. Here, we revisit this conclusion using epidemiological data from Thailand. We first show, with age incidence data, that dengue transmission rates have fallen since 1981; surprisingly, however, these declines are not associated with decreases in DHF incidence. Instead, district-level analyses indicate a nonmonotonic relationship between the basic reproductive number R₀ and DHF incidence. To understand this relationship, we formulated three mathematical models, which differ in their assumptions of transient between-serotype cross-protection. Unlike the first two models, the previously unconsidered third model with clinical cross-protection can reproduce this nonmonotonic relationship. Simulation of this model with nonstationary R₀ reproduces several previously unexplained patterns of dengue dynamics, including a transition from a ≈2-year cycle to a ≈4-year cycle and a transient trough in DHF incidence in provinces with rapid R₀ declines. These results imply that DHF incidence can be effectively controlled with a sufficiently large reduction in R₀ but that moderate reductions may be counterproductive. More broadly, these results show that assuming parameter stationarity in systems with approximate stationarity in disease incidence is unjustified and may result in missed opportunities to understand the drivers of disease variability.

Dengue virus is endemic to Asia but has recently been classified as an “emergent” or “reemergent” vector-borne disease in many other parts of the world, including Africa and South America (1). In human hosts, dengue infections cause a spectrum of symptoms, from a mild febrile illness to severe, life-threatening dengue hemorrhagic fever (DHF). The virus exists as four distinct serotypes, with the proportion of dengue cases caused by each serotype changing dramatically between years. Epidemiological studies indicate that homologous immunity provides nearly permanent protection against reinfection with a previously experienced serotype; in contrast, heterologous immunity does not provide protection against reinfection in the long term (2, 3). Instead, after a brief period of heterologous cross-protection (2), previous infections are considered risk factors for DHF (4, 5). [Similarly, maternal antibodies have also been shown to be a risk factor for DHF in infants (6, 7).] Because preexisting antibodies have long been held as the causative agent for this enhancement in secondary (or later) infections, this effect is commonly called antibody-dependent enhancement (ADE), although whether antibodies are the sole explanation for this enhancing effect is still unclear (8).

Because of the severity of DHF infections, public health initiatives have been developed worldwide in an effort to control dengue's burden. Here, we focus exclusively on Thailand, where many of the annual 200,000–500,000 DHF cases occur (9). This region is also where the World Health Organization first developed their diagnostic criteria for DHF (10); Thailand is, therefore, one of the regions with the longest available time series of dengue and DHF. Starting as early as the 1960s, Thailand initiated programs of vector control through insecticide use, including the application of both adulticide and larvicide (11, 12). Larvicide has been shown to be especially effective in reducing larval abundance when properly applied (13). These programs continued over the following decades. Thailand formed a national committee to synthesize and reinforce its Aedes aegypti control programs (14), and throughout the 1990s, health authorities continued to reinforce the practice of applying larvicide to individual households (15). In parallel with these insecticide-based vector control programs, Thailand initiated programs based on health education (16) and trained health workers regularly visited individual houses to encourage reduction of water containers (17).

Despite these public health initiatives, a long-term decline in DHF incidence has not been evident in Thailand. After the first epidemics of DHF in Thailand in 1958 (18), DHF was reported annually from all parts of Thailand by the end of the 1970s (19). The next two decades witnessed the three largest epidemics of DHF in Thailand, occurring in 1987, 1998, and 2001. Currently, dengue illness is a source of considerable economic loss to health authorities (20), as well as to patients (21). Long-term increases in DHF incidence rates are evident not only at the national level, but also at local scales, indicating that DHF has not simply extended spatially. When averaged over a 5-year sliding window, DHF incidence rates across Thai changwats (provinces) between 1981 and 2004 have either remained relatively constant (e.g., Fig. 1e) or have shown evidence of increase (e.g., Fig. 1 a and i). The absence of a long-term decline in DHF incidence (and its overall increase at the national level) is hypothesized to arise from a combination of transmissibility-increasing factors: human population growth, urbanization, expanding traffic (22), and ineffective public health measures (23).

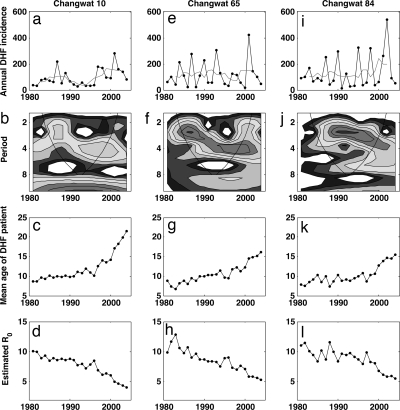
Fig. 1.

Temporal patterns of DHF in three representative Thai changwats (provinces) over the period 1981–2004. (a–d) Time series data for centrally located changwat 10 (Bangkok, lat 13°72′). (e–h) Data for northern changwat 65 (Phitsanulok, lat 17°03′). (i–l) Data for southern changwat 84 (Surat Thani, lat 9°02′). (a, e, and i) Annual DHF incidence per 100,000 (black). Gray lines show average annual DHF incidence per 100,000 over a 5-year sliding window. (b, f, and j) Wavelet plots of DHF incidence patterns, showing transitions from a short (≈2-year) cycle to a longer-period (≈4-year) cycle in all three changwats. (c, g, and k) Average age of DHF cases. (d, h, and l) Estimated R₀ trajectories over the period 1981–2004, computed from the average age of DHF cases (SI Appendix). DHF incidence and age data were obtained from the Ministry of Public Health of Thailand, as reported elsewhere (58). Wavelet analyses were performed on log-transformed incidence data, by using the Morlet wavelet. Wavelet software was provided by C. Torrence and G. Compo and is available at http://paos.colorado.edu/research/wavelets.

However, the interpretation of these temporal DHF patterns in terms of rising transmissibility becomes problematic in light of additional epidemiological data. Specifically, the mean age of DHF patients has steadily risen since the 1980s (Fig. 1 c, g, and k), doubling from 8.7 to 17 years between 1981 and 2004 in Thailand as a whole. This dramatic increase in mean age of DHF cases has occurred despite the age structure of the population remaining relatively stable: according to the National Statistics Office of Thailand, the average age in the entire population has only risen from 26 to 33 years of age during this time period. This pattern is also supported by data from a children's hospital in Bangkok (24), where the mean and mode age of children hospitalized with dengue infection have both significantly increased during the period 1973–1999. Moreover, the observed increase in mean age of DHF cases cannot simply be due to a recent serotype expansion in Thailand: Phylogenetic analyses provide evidence that at least three of the four dengue serotypes have been cocirculating in this region since 100–1,500 years ago (25), although DHF epidemics are a much more recent phenomenon. An increase in the mean age of infection has generally been interpreted as a decrease in the force of infection; a classic result for a pathogen that induces permanent immunity is that the basic reproductive number, R₀, which is proportional to pathogen transmissibility, can be computed by dividing the average host life span by the average age of infection (R₀ = L/A) (26). By modifying this expression to allow for four serotypes and the heightened risk of developing DHF with secondary or later infections, we calculated approximate values for R₀ over the time period 1981–2004 [supporting information (SI) Appendix]. These rough estimates show that there has been a steady decline in transmission rates from an R₀ value of ≈10–12 in 1981 to ≈4–6 in 2004 (Fig. 1 d, h, and l), and, therefore, that public health measures have indeed been effective at reducing dengue transmissibility.

Given this finding and its consistency with previous research suggesting long-term reductions in transmissibility (24), the question of why DHF incidence rates have been increasing in Thailand in the long term needs to be addressed. One possibility is that DHF incidence rates have in fact been decreasing and that increases in incidence rates are simply artifacts of increases in reporting rates. However, this possibility is precluded by a spatial analysis across districts in northern Thailand showing that areas of relatively low transmissibility have high DHF incidence rates, whereas areas of higher transmissibility have lower DHF rates. Using data from districts in northern Thailand between the years 1994 and 1996, we calculated the mean Breteau Index (a measure of mosquito prevalence), the mean DHF incidence rate, and the mean age of DHF cases for each district, where available. As expected, the mean age of DHF infection is higher in districts with lower mosquito abundance (i.e., with lower Breteau Index values) (Fig. 2a), providing support for the inverse of age being a good indicator of transmissibility. Plotting annual DHF incidence levels against the districts' Breteau Index values reveals that DHF levels generally decrease with higher transmissibility, except at very low levels of transmissibility (Fig. 2b). Again approximating R₀ from the mean age of DHF infections (SI Appendix), we find that at high R₀, DHF incidence is negatively correlated with increasing transmissibility, whereas at very low levels of R₀, DHF incidence is positively related to transmissibility (Fig. 2 c and d). These results are consistent with the temporal patterns shown in Fig. 1 in the region of high R₀: DHF incidence rates slightly increase with transmissibility decreases.

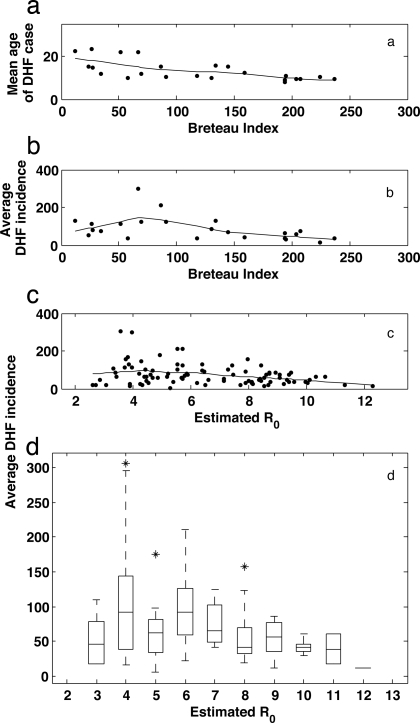
Fig. 2.

Spatial patterns of DHF across Thai amphoes (districts, which are subdivisions of provinces) over the years 1994–1996. In northern Thailand, entomological surveillance was conducted in 91 amphoes in 1994, 1995, and 1996 (43, 59); 23 of these amphoes had available Breteau Index values for the month of June for each of the 3 years. (a) Mean age of DHF cases plotted against the mean June Breteau Index of each of the 23 amphoes. The Breteau Index, defined as the number of positive water containers for mosquito larvae/pupae in 100 randomly sampled households (60), is known to be a relatively sensitive indicator of transmission (61). Mean age of DHF was obtained as described elsewhere (58). (b) DHF incidence rates per 100,000, averaged over 1994–1996, plotted against the mean June Breteau Index for the 23 amphoes. DHF incidence rates were averaged over 3 years to minimize the effects of high DHF interannual variability. Patterns in a and b were robust to changes in the month for which the Breteau Index was computed. (c) Average DHF incidence rates per 100,000 plotted against each amphoe's estimated R₀ for each of the 91 amphoes. Each amphoe's R₀ was estimated from the mean age of DHF cases over the years 1994–1996 (SI Appendix). Lines in a, b, and c are Lowess curves with a 50% span, fit to the scatterplot data. (d) Box plot of c, showing more clearly the nonmonotonic relationship between R₀ and average DHF incidence rates.

Here, we present a mathematical model that can explain this unexpected pattern of higher DHF incidence rates at lower transmission rates. Using a deterministic model of dengue's four serotypes, we first show that neither ADE alone nor ADE together with short-term cross-protection, as it has been classically modeled, can reproduce these empirical observations. Using a third model, we then show that ADE together with short-term clinical cross-protection, which prevents clinical illness but allows sero-conversion, can capture the empirical patterns shown in Fig. 2d. Finally, we show that deterministic simulations of the clinical cross-protection model reproduce the nonstationary patterns of DHF interannual variability (Fig. 1 a, b, e, f, i, and j) as well as observed patterns of interannual serotype fluctuations.

Results

Clinical Cross-Immunity Can Account for the Nonmonotonic Relationship Between Transmissibility and DHF Incidence.

To determine the critical processes that can account for the nonmonotonic relationship between transmissibility and DHF incidence (Fig. 2d), we formulated three distinct models. Each of them models the four serotypes of dengue virus through modifications of a multistrain model first introduced by Andreasen et al. (27) (see Methods). Each model assumes that immunity to reinfection with a previously experienced serotype is permanent, consistent with empirical data (3), and in agreement with previous mathematical models of dengue (28–32). On the basis of findings from epidemiological studies, we also assume that the risk of developing DHF is higher in secondary (or later) infections than in primary infections; we consider this increased risk to be the sole effect of ADE, in contrast to previous models wherein ADE is assumed to enhance either susceptibility to reinfection with a heterologous serotype (28, 33, 34), an infected individual's transmissibility (30, 31, 34), or a host's mortality (34, 35).

The three models differ only in the type of heterologous cross-protection. The first model can be considered a null model, with no period of heterologous cross-protection, and it represents the class of models, such as the one by Ferguson and colleagues (30), in which ADE sets in immediately after recovery from infection. The second model includes a transient period of heterologous cross-protection against reinfection, consistent with research by Sabin (2) showing that viral challenges to patients who have recently experienced dengue are unsuccessful for a short period. A transient period of heterologous cross-protection is further supported by a concordance between episodic within-serotype clade replacements and serotype abundance (29). Cross-protection against reinfection is modeled “classically” here: During the period of transient cross-protection, a challenge with a previously unexperienced serotype results in neither infection nor a gain in immunity (i.e., sero-conversion) toward the challenging strain. This model captures the immunological assumptions present in a dengue model by Wearing and Rohani (28). When parameterized for permanent (but imperfect) heterologous cross-protection, this second model is also capable of representing the genre of multistrain models introduced by Kamo and Sasaki (36), which has been used by Adams and coauthors (29, 32, 34), most notably to reproduce the asynchronous serotype fluctuations of DENV-1 and DENV-4 (29). Similar to the second model, the third model also includes a transient period of heterologous cross-protection. However, instead of modeling cross-protection classically, the third model assumes clinical cross-protection: A challenge with a previously unexperienced serotype during the cross-protected period does not result in clinical manifestation of DHF nor in transmissible infection; however, the challenge does result in a gain of immunity toward the challenging serotype. The occurrence of clinical cross-protection in dengue is supported by three studies. First, Kochel et al. (37) showed that cross-protected monkeys sero-convert upon inoculation with a heterologous serotype. Second, Kraiselburd et al. (38) reported that detectable viremia was not necessary for sero-conversion. Third, Sabin (2) noted the occurrence of mild systemic inflammation after the inoculation of cross-protected subjects, which suggests sero-conversion.

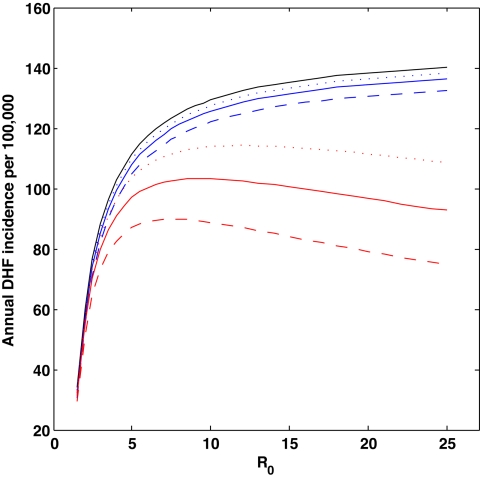
Fig. 3 shows the results of simulating these three models deterministically over a wide range of R₀. The first model generates a monotonic relationship between R₀ and DHF incidence, with higher DHF incidence at higher R₀. This result is easily interpretable: At higher R₀, the fraction of infected individuals in the population is higher, and there are more secondary (or later) infections, leading to higher DHF incidence. The second model, with classical cross-protection, also generates a monotonically increasing relationship between DHF incidence and R₀. In comparison to the first model, this model predicts a lower DHF incidence rate for any value of R₀, as would be expected.

Fig. 3.

DHF incidence rates as a function of the basic reproductive number, R₀. Results from the model without temporary cross-protection are shown in black, results from the model with classical cross-protection are shown in blue, and results from the model with clinical cross-protection are shown in red (SI Appendix). Model parameters were: host life span 1/μ = 70 years (62), degree of susceptibility-reduction σ _Jⁱ = 1 for all i and J, and duration of infection 1/ν = 9 days. The 9-day duration of infection is consistent with the observed viremic period of 4–12 days (63). Transmission rate β was computed from R₀: β = R₀ (υ + μ). For the two models with transient cross-protection, three durations of cross-protection were considered: 1/δ = ½ year (dotted), 1/δ = 1 year (solid), and 1/δ = 2 years (dashed). We parameterized the proportion of dengue infections that resulted in DHF symptoms from data published by Sangkawibha et al. (4): p₁ = 0.0020 for primary infections and p_x = 0.0338 for secondary or later infections. The nonmonotonic patterns generated by the clinical cross-protection model are robust to the following explored parameter choices of p₁ through p₄: {p₁, p₂, p₃, p₄} = {0, 0.0338, 0.0338, 0.0338}, {p₁, p₂, p₃, p₄} = {0.0020, 0.0338, 0, 0}, and {p₁, p₂, p₃, p₄} = {0, 0.0338, 0, 0} (SI Appendix). All simulations were run deterministically for 600 years. Annual DHF incidence rates were computed by averaging the total number of DHF cases accumulated during the last 500 years of simulation (the first 100 years were removed as transients). Simulations run with a degree of seasonal forcing of ε = 0.05 and a low immigration rate of m = 1 × 10⁻⁶ per serotype per host per year (i.e., with parameter values identical to those used for Figs. 4 and 5) generated results that were consistent and quantitatively very similar (results not shown). Additional predictions and patterns arising from the clinical cross-protection model are included in the SI Appendix.

In contrast to the first two models, the third model, with clinical cross-protection, reproduces the nonmonotonic relationship estimated in Fig. 2d. At low R₀, we find a positive relationship between DHF incidence and transmissibility. At high R₀, we observe a long, slightly decreasing plateau of DHF incidence. This pattern is evident for any duration of cross-protection, although the negative relationship between R₀ and DHF incidence is more pronounced for longer durations of protection (Fig. 3). The negative relationship between R₀ and DHF at high R₀ is due to the increasing number of individuals that gain immunity to heterologous serotypes while being transiently cross-protected from becoming infectious and from manifesting DHF clinically.

Interannual DHF Variability and Serotype Fluctuations.

Previous models of dengue, including those represented by the first two models described above, have been able to reproduce some of the observed patterns of interannual DHF variability and serotype dynamics. In a two-serotype model of dengue, Ferguson et al. (30) showed that enhancement (acting to increase the probability of transmissibility) facilitates serotype coexistence and can generate complex, and even chaotic, disease dynamics. A recent two-serotype model by Adams et al. (29), which allowed for either cross-protection or cross-enhancement but not a sequential combination of them, reproduced the out-of-phase serotype–cycling of DENV-1 and DENV-4. In another analysis that modeled four distinct serotypes and a number of different possible immunological factors (including a transient period of classical cross-protection, ADE, and asymmetry in virulence), Wearing and Rohani (28) were able to reproduce the ≈3-year cycle in DHF incidence and cyclical patterns of serotype dominance. All of these models, however, assume a stationary system, with transmissibility constant in time (with the exception of seasonal forcing).

Given that the mean age of DHF cases in Bangkok and other Thai provinces has been increasing since the 1980s (Fig. 1 c, g, and k), and that transmissibility of dengue has, therefore, likely decreased (Fig. 1 d, h, and l) in response to vector control measures and health education, we sought to determine whether, in a nonstationary transmission environment, the clinical cross-protection model generates dynamic patterns in DHF incidence and serotype dominance that are consistent with empirical disease patterns. These patterns include a transition from a short, ≈2-year cycle to a longer, ≈4-year cycle in DHF incidence, robustly observed across changwats (Fig. 1 b, f, and j) and also present in a higher-resolution monthly time series from Bangkok (Fig. 4h). A second pattern is one of alternating serotypes, with serotype-specific outbreaks occurring approximately every 8–10 years (Fig. 5b) (24, 28).

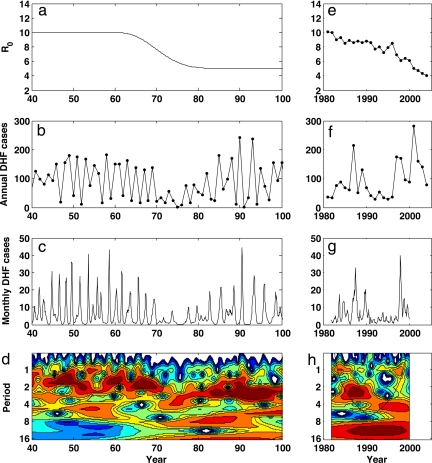
Fig. 4.

Simulated vs. observed DHF dynamics. (a–d) Simulation results of the clinical cross-protection model, run deterministically with a temporal decrease in R₀. (e–h) Empirical data (and analyses of these data) for Bangkok. (a) Input trajectory of R₀ over time, with a reduction from R₀ = 10 to R₀ = 5 over 20 years. (b) Simulated annual DHF incidence per 100,000. (c) Simulated monthly DHF incidence per 100,000. (d) Wavelet plot of simulated monthly DHF incidence rates. Wavelet analyses of simulated data were performed on log-transformed monthly incidence rates, by using the Morlet wavelet. Parameters used in the simulation were population size N = 5 million hosts (the size of Bangkok), 1/δ = 1 year, degree of seasonality ε = 0.05, immigration rate m = 1 × 10⁻⁶ per serotype per host per year. Other parameters were as in Fig. 3. (e) Estimated trajectory in R₀, computed from the observed mean ages of DHF cases over time, reproduced from Fig. 1d. (f) Observed annual DHF incidence per 100,000, reproduced from Fig. 1a. (g) Observed monthly DHF incidence per 100,000 (obtained from Ministry of Public Health of Thailand). (h) Wavelet plot of observed monthly DHF incidence. Data were analyzed as for d. Sensitivity analyses of model parameters ε and m were conducted. Changes in seasonality parameter ε between 0.0 and 0.15 did not affect results appreciably, although ε = 0.0 simulations did not reproduce the faint annual period observed in Fig. 4h. Changes in immigration rate m between 1 × 10⁻¹⁰ per serotype per host per year and 1 × 10⁻² per serotype per host per year showed that the value of m affected the degree of interannual variability. At high values of m (m > 1 × 10⁻⁴), DHF dynamics lost their interannual variability (results not shown); at low values of m (m < 1 × 10⁻⁸), DHF dynamics became more explosive than empirically observed (results not shown). The transition from a ≈2-year cycle to a ≈4-year cycle with a decrease in R₀ from 10 to 5 was robust to the additional parameter choices of p₁ through p₄ explored in Fig. 3 (SI Appendix).

Fig. 5.

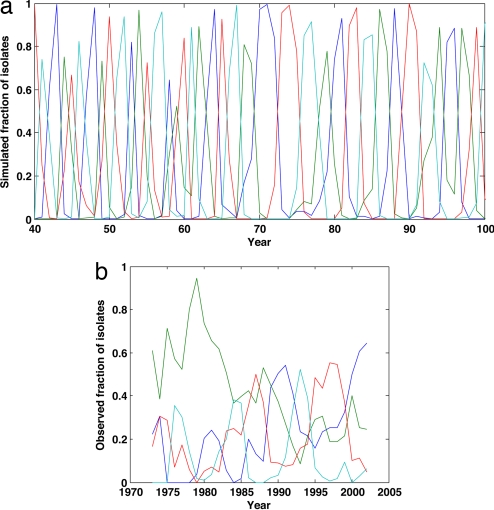
Fluctuations in serotype dominance in simulated vs. observed time series. (a) Proportion of dengue cases belonging to serotypes DENV-1 to DENV-4 over time, computed from model simulations shown in Fig. 4. (b) Proportion of dengue fever and DHF cases belonging to serotypes DENV-1 to DENV-4 over the period 1973–2002, computed from serotype-specific time series (24, 64). Although DENV-2 appears to be displaced in the mid-1980s, its dominance between 1973 and the early 1980s appears to be due to the low numbers of DENV-1, DENV-3, and DENV-4 dengue fever and DHF cases, instead of a decrease in its absolute incidence rate (see figure 3 of ref. 24).

We simulated the clinical cross-protection model deterministically, in a population the size of Bangkok, with R₀ decreasing from 10 to 5 over 20 years (Fig. 4a and SI Appendix). The simulations produce annual and monthly DHF incidence rates on the order of those observed (Fig. 4 b and c), with no apparent long-term decreasing trend in DHF incidence. More importantly, the simulated dynamics (Fig. 4d) exhibit patterns of interannual variability consistent with those observed (Figs. 1 b, f, and j, and 4h): The model-generated periodicity of dengue epidemics transitions from 1- to 3-year cycles at high values of R₀ to 3- to 4-year cycles at lower values of R₀. Changes in periodicity followed reductions in R₀ by 10–20 years, in agreement with our expectations if our estimated R₀ values were temporally lagged (SI Appendix, Section II). The observed transition in periodicity can thus be explained by changes in long-term changes in transmissibility and may, therefore, be independent from changes in the periodicity of potential climatic drivers.

Unexpectedly, the simulations also show a transient decrease in DHF incidence after the onset of the transmissibility decrease. This pattern is consistent with the trough in Bangkok's DHF time series (Fig. 4f). The magnitude of the transient trough in DHF incidence depends on the speed and magnitude of changes in transmissibility (results not shown), with the transient trough becoming deeper with a faster or a larger decrease in R₀.

In addition to reproducing the patterns of overall DHF variability, the clinical cross-protection model is also consistent with previously observed temporal changes in serotype dominance (Fig. 5 a and b). Specifically, the model predicts serotypes to sequentially cycle in dominance, with ≈8–10 years between returns to dominance. Previous dengue models, assuming classical cross-protection, have also been able to reproduce characteristics of these serotype cycles (28, 29, 32); the strength of the clinical cross-protection model over these previous models is, therefore, specifically in its ability to reproduce the nonmonotonic relationship shown in Fig. 2 and its ability to reproduce the temporary trough in DHF incidence that accompanies the decrease in R₀ (Fig. 4f).

Discussion

Other Processes Driving DHF Dynamics.

Although the clinical cross-protection model presented here can reproduce the observed increases in DHF incidence that previous dengue models are incapable of explaining in a system with decreasing transmission rates, it does not preclude that other immunological and ecological processes may play additional roles in driving the dynamics of this infectious disease. Given that the abundance and longevity of the mosquito vectors, as well as the virus' amplification rate, are critically affected by temperature, rainfall, and resulting humidity (e.g., refs. 39–43), one of the most important processes further regulating dengue dynamics is likely to be climate variability. Previous analyses that consider these environmental covariates or weather “packages” (44) such as the El Niño Southern Oscillation (ENSO) have shown statistically significant correlations between dengue epidemics and climatic drivers (e.g., ref. 45), and wavelet approaches have shown that dengue's biennial cycle is phase-locked (i.e., synchronized with a temporal lag) with rainfall in the region (46).

Another important process that is likely to regulate dengue dynamics is within-serotype evolution. Phylogenetic analyses (47–51) indicate that lineage turnover occurs in each of the four viral serotypes. In many of these documented cases, lineage turnover has occurred through punctuated clade replacements. Although these replacements may result from genetic bottlenecks in times of low dengue incidence (47), another hypothesis is that adaptive evolution (52), perhaps through the emergence of immune escape mutants (53), shapes these patterns of within-serotype evolution. In the context of influenza, immune escape mutants that sweep through the host population have previously been shown to affect the interannual dynamics of the virus (54); immune escape in dengue may have similar effects.

Finally, it has recently been argued that an increase in dengue cases at lower transmission rates might result from “endemic stability” (55). Endemic stability, a term that is used to describe the pattern of lower levels of disease at higher transmissibility, requires two factors: (i) that immunity is long lasting and (ii) that the risk of developing symptoms increases with age of infection. Like clinical cross-protection, endemic stability acts to decrease disease incidence at high levels of transmission. Indeed, the increase of dengue fever in Singapore after decades of effective vector reduction is likely to be due to endemic stability (56), in agreement with theoretical predictions that take into account the age-dependency of dengue fever (57). However, the dependency of clinical manifestation of DHF on age is still unclear. Instead, it has been established that the development of DHF relies mainly on history of previous infections and/or the presence of immunological memory. A more detailed analysis will need to take into consideration not only the type of heterologous cross-protection but also how age itself affects the probability of developing DHF.

The model presented here hypothesizes that decreases in transmission rates from high levels to moderate ones have had the counterproductive effect of increasing DHF incidence. However, on a more uplifting note, it should be remembered that the relationship between transmissibility and DHF incidence that clinical cross-immunity produces is nonmonotonic. Therefore, we expect DHF incidence rates to rapidly fall with a significant reduction in R₀ from today's moderate levels. Public health measures such as mosquito control and dengue vaccination programs are, therefore, critical in ultimately reducing DHF. To be productive, however, these initiatives require high efficacy in transmissibility reduction; a gradual, half-hearted attempt at lowering transmissibility could instead make the situation worse.

Methods

To model the disease dynamics of dengue's four serotypes, we modified a history-based multistrain model previously published by Andreasen et al. (27) in an application to influenza. All three of the models described in Results, and in more detail in the SI Appendix, assume permanent immunity to reinfection with serotypes to which one has previously been exposed, consistent with the immunity patterns of dengue. The critical difference between the models is the way in which heterologous serotypes interact immunologically (SI Appendix). Fig. 3 shows the results for the deterministic simulations of all three models. Figs. 4 and 5 show the deterministic simulations of the clinical cross-protection model, run with a temporal decrease in R₀.