Skip to main content
PMC home page
Molecular Systems Biology logoLink to Molecular Systems Biology
. 2008 Aug 5;4:210. doi: 10.1038/msb.2008.48

Constraints imposed by non-functional protein–protein interactions on gene expression and proteome size

Jingshan Zhang 1, Sergei Maslov 2, Eugene I Shakhnovich 1,a
PMCID: PMC2538908  PMID: 18682700

Abstract

Crowded intracellular environments present a challenge for proteins to form functional specific complexes while reducing non-functional interactions with promiscuous non-functional partners. Here we show how the need to minimize the waste of resources to non-functional interactions limits the proteome diversity and the average concentration of co-expressed and co-localized proteins. Using the results of high-throughput Yeast 2-Hybrid experiments, we estimate the characteristic strength of non-functional protein–protein interactions. By combining these data with the strengths of specific interactions, we assess the fraction of time proteins spend tied up in non-functional interactions as a function of their overall concentration. This allows us to sketch the phase diagram for baker's yeast cells using the experimentally measured concentrations and subcellular localization of their proteins. The positions of yeast compartments on the phase diagram are consistent with our hypothesis that the yeast proteome has evolved to operate closely to the upper limit of its size, whereas keeping individual protein concentrations sufficiently low to reduce non-functional interactions. These findings have implication for conceptual understanding of intracellular compartmentalization, multicellularity and differentiation.

Keywords: non-functional interaction, protein–protein interaction, proteome size, yeast cytoplasm

Introduction

The properties of individual proteins ranging from their structure and folding to function and evolution have been extensively studied. Recently, protein–protein interactions (PPIs) became popular subjects of both experimental (Uetz et al, 2000; Ito et al, 2001; Giot et al, 2003; Li et al, 2004; Stelzl et al, 2005; Rual et al, 2005; Gavin et al, 2006) and theoretical scrutiny (Bogan and Thorn, 1998; Lo Conte et al, 1999; Kortemme and Baker, 2002; Aloy et al, 2004; Aloy and Russell, 2006; Kim et al, 2006). In addition to the traditional studies, which mainly focus on the detailed understanding of protein interactions within small sets of functionally related proteins, the new systems biology perspectives have emerged (Sear, 2004; Deeds et al, 2007; Maslov and Ispolatov, 2007), which address the behaviour of large sets of proteins of diverse types operating together inside living cells. However, our understanding of the coexistence of different proteins in crowded cellular environments remains quite limited. The key issue we discuss here is whether the possibility to form numerous non-functional interactions (Box 1) in such environments impedes proteins' ability to engage in highly specific biologically functional interactions. Here, the non-functional interaction refers to a transient complex between two functionally unrelated proteins. Such complexes are formed following random encounters between proteins as they diffuse in the cell searching for their functional (specific) partners. Apparently, one way for nature to reduce non-functional interactions is to keep the concentrations of individual proteins in a cell to a minimum. However, there is a limit to how low this concentration can go, as it must allow for the efficient biological functioning of the cell as well as formation of the specific complexes (both transient and permanent). Obviously, under these conditions, the only remaining way to reduce the overall concentration of proteins and hence the formation of non-functional complexes is to limit the diversity of the proteome, that is, the number of different protein types that are co-expressed in a given subcellular compartment. If such limit on the proteome diversity does indeed exist, how far below it are the environments inside real cells? For instance, among the ∼4500 yeast protein types simultaneously expressed under the normal conditions (Ghaemmaghami et al, 2003; Huh et al, 2003), about 1800 types are known to be co-localized in the cytoplasm (Huh et al, 2003). How far is this number from the theoretical upper bound?

Box 1 A non-functional interaction refers to formation of a transient complex between two functionally unrelated proteins. Such complexes are formed following random encounters between proteins as they diffuse in the cell searching for their functional (specific) partners. If there are many types of coexisting proteins in a cell compartment, the chance to encounter an arbitrary partner in such random walk is much greater than to encounter a protein's specific partner. For functional interactions to dominate, this entropic factor has to be compensated by making functional interactions, on average, much stronger than random non-functional ones. This is achieved by evolutionary selection of interacting surfaces for functionally interacting proteins. Proteins expressed at lower concentrations are subject to stronger evolutionary pressure, as they need a smaller dissociation constant to form specific complexes. To enhance their strength and specificity, functional interactions may involve the formation of additional hydrogen bonds and, in some cases, salt bridges. On the other hand, non-functional interactions, which have not been evolutionarily optimized, result from random encounters between surfaces of two proteins. The physical nature of these interactions is hydrophobic: it is mainly due to burial of hydrophobic groups on the transient interface from water.

A related question is to what extent non-functional interactions affect the biochemical efficiency of formation of functional protein complexes? That is to say, by how much proteins' search for their specific partners is slowed down by transient non-functional complexes? The answer depends upon both the proteome diversity and individual protein concentrations. Were individual protein concentrations evolutionarily tuned to assure the sufficient efficiency to form specific protein complexes?

We hypothesize that in general the biological evolution pushes an organism towards higher protein diversity. The diversity increases until it reaches the limit beyond which non-functional interactions start to significantly interfere with proteins' functions. At the same time, the average concentration of individual proteins is pushed down in evolution to reduce the impairment of non-functional interactions to biochemical efficiencies, until it reaches the lower limit defined by stability of specific complexes as well as the overall functioning of the cell.

In this study, we quantitatively address these questions and check this hypothesis by comparing the equilibrium concentrations of specific and non-functional complexes and that of unbound proteins in the monomeric form. The typical binding energy of specific PPIs is obtained from a database (Kumar and Gromiha, 2006) generated by manual curation of the literature. As the information about non-functional PPIs is not usually reported in the literature, we infer the distribution of their binding energies from the data generated in high-throughput Yeast 2-Hybrid (Y2H) experiments (Uetz et al, 2000; Ito et al, 2001; Giot et al, 2003; Li et al, 2004; Rual et al, 2005; Stelzl et al, 2005). As presented in Box 2, the PPIs detected in these experiments are known to include many false-positives (Ito et al, 2001; Aloy and Russell, 2002; Deane et al, 2002; Vidalain et al, 2004; Huang et al, 2007), which are likely caused by non-functional interactions (Deeds et al, 2006). Therefore, the results of proteome-wide Y2H assays provide a unique opportunity to estimate both the average strength and the distribution of non-functional interactions.

Box 2 Interactions between many proteins are systematically tested in large-scale Y2H screens. In Y2H approach, proteins are overexpressed to high concentration of 1 μM or higher (Estojak et al, 1995). To this end, the Y2H approach detects PPI with binding affinities stronger than Kd*≈1 μM. Some reported interactions (up to 19%; Nakayama et al, 2002) may not be real, but owing to experimental artefacts such as bait self-activation (Vidalain et al, 2004). However, the remaining of the reported interactions, although being real in Y2H assay, may not all be observed in living cells. Many proteins are expressed in vivo at lower concentrations than baits and preys in Y2H experiments, and therefore they will not form complexes in cells, although in Y2H assay they can form complexes due to overexpression. Pairs of proteins with binding affinities close to Kd* form transient complexes in Y2H, which may be detected in some experiments and missed in others, hence lack of reproducibility for weaker complexes. Although these limitations may affect the ability of Y2H to reliably detect functional PPIs, the Y2H data is very useful to estimate strength of non-functional PPI because it massively reports on relatively weak interactions between proteins. Here we use the Y2H data for that purpose, assuming that fraction α of PPIs are real yet non-functional, which are detected under high concentration conditions of the Y2H experiment. The uncertainty in the estimate of parameter α gives rise to the uncertainty in the estimate of mdead—the maximal number of protein types that can be coexpressed in a cell. In the future, to obtain the complete set of non-functional PPIs within a given interactome, it will be necessary to systematically disrupt each interaction and test the impact of such a disruption on biological functioning of the cell. Eventually, when large-scale experimental information about the binding affinities of individual PPIs will become available, one would be able to exactly calculate the effect of non-functional interactions on biochemical efficiency of individual proteins.

Using these estimates, we find that the size of the yeast proteome is close to the theoretical upper limit imposed by competition between specific and non-functional interactions. Namely, the number of protein types co-expressed and co-localized in the cytoplasm, which is the largest compartment of the yeast cell, is close to its theoretical upper limit. It could be further increased only by the virtue of intracellular compartmentalization or (in multicellular organisms) by cell-type differentiation. At the same time, we find that the average concentration of individual proteins expressed in the yeast cytoplasm is close to its theoretical lower limit at which functional interactions with a typical specific binding energy are possible. On average, the time proteins waste in various non-functional complexes is typically comparable with the time they spend in the monomeric (unbound) form. However, for some of the stickiest proteins, this lost time ratio can be significantly higher. We conjecture that the impact of non-functional PPIs on biochemical efficiencies of specific protein complexes is close to the tolerable limit. Other relatively large compartments of the yeast cell, the nucleus and mitochondria, have fewer protein types than the cytoplasm and higher average individual protein concentrations, although these differences do not exceed an order of magnitude.

Results

The upper limit on protein diversity: a simple estimate

Non-functional interactions are ubiquitous in crowded cellular environments. As a large variety of different proteins are forced to coexist in the same intracellular compartment, a protein encounters non-functional interaction partners much more frequently than the few protein types with which it has evolved to specifically interact. As was pointed out by Janin (1996) and Deeds et al. (2007), the specific interactions must be significantly stronger than non-functional ones to guarantee that specific complexes are more common than random, non-functional complexes. We begin the discussion of the role of non-functional interactions from a simplified conceptual example where we assume that: (1) all binding energies Es in a small set (one interaction partner per protein) of specific PPIs are the same; (2) the binding energies En of non-functional interactions between all possible pairs of proteins are also identical to each other and (3) the concentrations Ci of every protein in the cell are the same. Furthermore, we consider the case in which the biologically functional state of each protein is when it is bound with its specific interaction partner. Although, as will be shown below, these assumptions are certainly an oversimplification, they represent a conceptually useful first step towards addressing the problem of the competition between specific and non-functional complexes.

Consider a protein of a certain type i that interacts with other proteins of a unique type i′ through specific binding, and with all other proteins R through non-functional binding. We assume that proteins participating in pairwise specific and non-functional complexes do not bind to other proteins. Then the total concentration Ci=C̃ of the protein i is formed by

graphic file with name msb200848-i1.jpg

where [i], [ii′] and [iR] are the concentrations of the three states of the protein i: the monomeric (unbound), bound in a specific complex and bound in any of the promiscuous non-functional complexes. These three concentrations are related to each other by the law of mass action

graphic file with name msb200848-i2.jpg
graphic file with name msb200848-i3.jpg

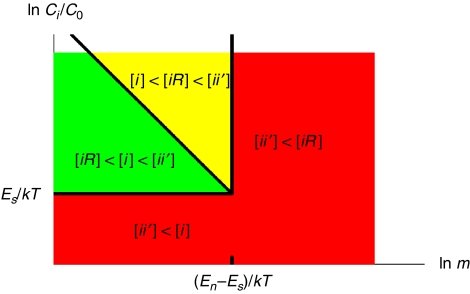
Here the normalization concentration C0=1M is the convention and 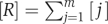Inline graphic sums over nearly all of the m protein types co-localized in the same compartment. The binding energies are related to the dissociation constants by K=C0 exp (E/kT) and are usually negative. Among the three terms in Equation (1), the concentration [ii′] should be the dominant one to ensure the abundance of specific complexes needed for proper functioning of the cell. We refer to a situation in which [ii′] is not the largest of the three terms as a biologically prohibitive ‘dead zone' shown in red colour in Figure 1. One way, the system can fall into the dead zone if [ii′]<[i]. For a simple estimate of the boundary of this zone, let us ignore for a moment the contribution of non-functional interactions. In this case, precisely at the border of the dead zone, one has [ii′]=[i]=[i′]=C̃/2. Thus, according to Equation (2b), the system is in the dead zone if the individual protein concentration C̃ is below the critical value

Figure 1.

Figure 1

Open in a new tab

The conceptual illustration of possible states of a protein in a compartment of a living cell. The green, yellow and red regions represent the ‘safe zone', the ‘dangerous zone' and the ‘dead zone', respectively. The boundaries between them are given by Equations (3, 4 and 5).

graphic file with name msb200848-i5.jpg

We emphasize that the choice of [ii′]=[i] to define the boundary of the dead zone is purely on the basis of convenience. In reality, the ratio [ii′]/[i] changes continuously with C̃. Therefore, the dead zone is separated from the other zones by a smooth crossover rather than a sharp phase transition. The dead zone also includes the situation when [ii′]<[iR]. By comparing Equations (2a) and (2b), we find that this happens when the number m of co-expressed and co-localized protein types exceeds the critical value

graphic file with name msb200848-i6.jpg

Similar to Equation (3), mdead is a characteristic value of the crossover. The inequality mdead≫1 follows from the observation (Janin, 1996; Deeds et al, 2007) that specific, functional, interactions are significantly stronger, statistically, than non-functional ones. We further divide the biologically allowed region into two parts: the ‘safe zone' with [iR]<[i]<[ii′] (shown in green in Figure 1), and the ‘dangerous zone' with [i]<[iR]<[ii′] (shown in yellow in Figure 1). The boundary between them in this simplified example is determined by Equation (2a) to be:

graphic file with name msb200848-i7.jpg

where Kn is the dissociation constant for non-functional interactions. If one fixes the concentration C̃ of each individual protein type and increases the number of protein types m, starting from the safe zone, one first enters the dangerous zone at m=mwarning, and finally reaches the dead zone at m=mdead. As C̃ decreases, mwarning increases, and the separation between mwarning and mdead shrinks. Eventually, when C̃ reaches the lowest value Ccrit given by Equation (3), the separation between mwarning and mdead disappears altogether. In other words, the three lines corresponding to Equations (3), (4) and (5) intersect approximately at the same ‘triple point' (see Figure 1), where all three terms in Equation (1) are equal to each other.

A protein in the dangerous zone has disadvantages compared with those in the safe zone. First, to ensure the dominance of the specific complex, [ii′]>[iR], its specific interaction must be strong enough to resist the interference from non-functional interactions (see Supporting Information for details). Although this could be achieved in evolution, it is an extra requirement the cell needs to satisfy. Moreover, even if the specific interaction is strong enough, a protein in the dangerous zone would waste a considerable amount of time on non-functional interactions with non-functional partners. This increases the time it takes for it to find its specific partner by the factor 1+[iR]/[i]>2 and thus affects the temporal efficiency of all biochemical processes involving this protein. Therefore, it indeed represents a ‘dangerous', or suboptimal, situation and imposes a soft upper limit on the protein diversity. Outside of the dead zone, compartments of living cells need to minimize the average losses of biochemical efficiency experienced by proteins inside the dangerous zone.

Physical model of non-functional interactions

What happens inside intracellular compartments of real cells is more complicated than the simplified example presented above. Most importantly, the binding energies of both specific and non-functional interactions as well as the concentrations of individual proteins vary in a broad range. Therefore, different proteins in a cell are characterized by different ‘danger levels' [iR]/[i]. In spite of these complications, can we still quantitatively analyse the general situation inside compartments of real cells, for example, in the cytoplasm of yeast cells under normal conditions? How many protein types fall inside the dangerous zone? What is the largest value of [iR]/[i] among all protein types present in the yeast cytoplasm? What is the phase diagram in terms of the proteome diversity m and the distribution of individual protein concentrations? To address these questions, we start with a basic physical model of non-functional interactions.

To enhance their strength, functional interactions may involve the formation of additional hydrogen bonds and, in some cases, salt bridges. On the other hand, non-functional interactions, which have not been evolutionarily selected, are formed primarily due to the hydrophobic effect. Indeed, non-functional interactions result from random encounters between surfaces of two proteins, and the free energy gain associated with such an encounter was shown to be proportional to the total amount of buried hydrophobic residues on these two surfaces (Janin, 1995; Bahadur et al, 2004). It has become standard to relate the binding (free) energy to surface hydrophobicity (Eisenberg and McLachlan, 1986; Noskov and Lim, 2001; Bahadur et al, 2004; Deeds et al, 2006). Here, we adopt a simple model from Deeds et al (2006) to describe the distribution of non-functional interactions. The major premise of the model is that the free energy of a non-functional PPI is determined by the total hydrophobic surface that is screened from the water upon the formation of a complex. This assumption is strongly supported by the structural and energetic analysis of many functional and non-functional protein complexes (Bahadur et al, 2004). The interaction energy between any two proteins i and j is therefore additive:

graphic file with name msb200848-i8.jpg

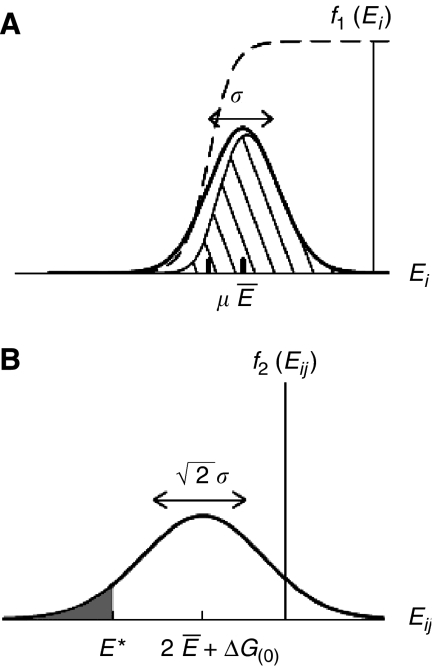
Here, Ei and Ej describe the ‘stickiness' of proteins i and j, indicating how hydrophobic their surfaces are. In support of this model, Figure 3 of Janin (1995) showed that experimental result of binding energies can be described by the sum of stickiness terms and a constant term. The constant term ΔG(0), determined as ∼6 kcal/mol≈10kT from experiments (Janin, 1995; Tamura and Privalov, 1997), comes from the translational and rotational entropy the two proteins lose while binding to each other. In other words, the effective ‘interaction volume' is much smaller than the convention of 1/C0=1M−1 in Equation (2). The fraction P of hydrophobic residues on proteins' surfaces has an approximately Gaussian distribution, with the average P̄≅0.22 and the standard deviation σP≅0.058 (Deeds et al, 2006). As Ei is proportional to the surface hydrophobicity, Ei/Ej=Pi/Pj, the distribution of Ei is also expected to be Gaussian (Figure 2a)

Figure 2.

Figure 2

Open in a new tab

Gaussian distributions: (A) f1(Ei) of ‘stickiness' parameters Ei of individual proteins (B) f2(Eij) of binding energies Eij=Ei+Ej+ΔG(0) of pairwise non-functional interactions. The dashed line in the panel (A) shows the fraction of proteins in the monomer defined by Equation (10) with the chemical potential μ. The shadowed area is the product of f1(Ei) and Equation (10), and represents the distribution of Ei in protein monomers. The shadowed region in panel (B) corresponds to non-functional PPIs that are stronger than the detection threshold E* and thus appear in high-throughput Y2H screens. The fraction of such interactions among ∼N2/2 pairs is given by Equation (16).

Figure 3.

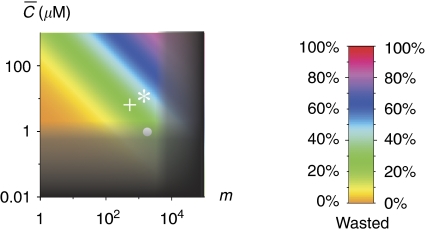
Figure 3

Open in a new tab

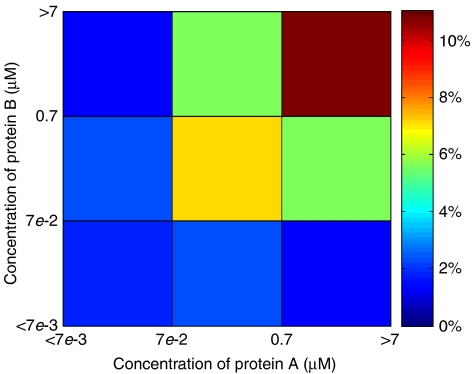
The phase diagram for baker's yeast. The area in shade is the ‘dead zone'. Its boundaries, defined by Equations (13) and (15), are blurred to indicate they are crossover rather than sharp transitions. The colours indicate the average fraction of proteins tied up inside non-functional complexes in the yeast cytoplasm as defined in Equation (12). The white circle shows the C̄ and m for a group of proteins coexpressed and colocalized in the yeast cytoplasm, whereas the white star and cross represents these parameters for the cell nucleus and mitochondria.

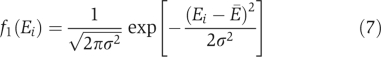graphic file with name msb200848-i9.jpg

where

graphic file with name msb200848-i10.jpg

(Deeds et al, 2006). The distribution of binding energy Eij=Ei+Ej+ΔG(0) of two-body non-functional interactions is then given by

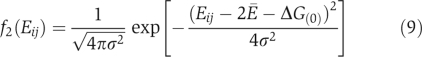graphic file with name msb200848-i11.jpg

with the average value 2Ē+ΔG(0) and the standard deviation 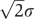Inline graphic (Figure 2b). This model has been used to successfully explain most global topological properties of PPI network (Deeds et al, 2006).

In fact, the details of the (hydrophobic) physical nature of non-functional interactions are not crucial for our model. What is indeed important is the assumption that the free energy of such interactions is proportional to the total hydrophobic surface covered upon formation of a non-functional complex involving these two proteins. There exists a significant evidence (Janin, 1995; Tamura and Privalov, 1997) that this may indeed be the case. The key aspect underlying this assumption is that non-functional interactions, having not been evolutionarily selected, represent random encounters between protein surfaces and as such adequately reflect the average surface composition of proteins. We use the Y2H data (see Materials and methods) to evaluate the significant parameters of this free energy model. In contrast, protein surfaces participating in functional PPIs have been presumably selected by evolution for stability and specificity, and various types of interactions were employed to achieve that (Lukatsky et al, 2007). As a result, these evolutionarily selected interactions are not adequately described by the sum of hydrophobicities of covered surfaces.

Fraction of proteins wasted in non-functional complexes: the phase diagram

If a protein with the surface energy Ei is not bound in a specific complex, it can either exist in a monomeric form or be bound to any of the non-functional partners. The ratio [iR]/[i]=e−(Ei−μ)/kT between the last two concentrations depends on the chemical potential μ of the pool of all non-functional interaction partners (see Supporting Information for details). Then the probability for a protein to be in a monomeric form obeys the Fermi–Dirac distribution

graphic file with name msb200848-i13.jpg

shown by the dashed line in Figure 2a. The value of μ can be found by solving

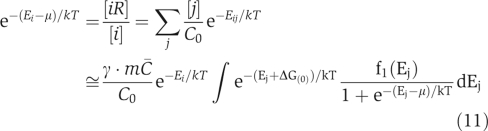graphic file with name msb200848-i14.jpg

self-consistently. Here, we implicitly assume that the possible correlation between individual protein concentrations Ci and their stickiness parameters Ei can be neglected (see Supporting Information for the justification). The parameter γ is defined as the effective fraction of the total protein concentration mC̄ that is not tied up inside the specific complexes and thus could participate in non-functional interactions. Although we assumed above that specific complexes do not participate in non-functional PPIs, in fact some of them do (however, with a reduced affinity). Indeed, their constituent proteins typically have more than one ‘surface side' (Kim et al, 2006) and could use their other (usually less hydrophobic) surface sides for non-functional interactions. This would push the effective fraction γ closer to 1. For simplicity, throughout the manuscript we use γ=1. This is justified, as the value of μ determined by the solution of Equation (11) only depends weakly on the value of γ within its plausible range (see Supporting Information for details).

The chemical potential μ goes up when the total protein concentration mC̄ in the cytoplasm increases. As shown in Figure 2a, proteins with too sticky surfaces Ei<μ actively participate in non-functional bindings, and the interference of non-functional bindings for such proteins is strong: [iR]>[i]. On the other hand, less sticky proteins with Ei>μ have [iR]<[i] and thus belong to the safe zone in which the effects of non-functional interactions are weak. As will be described in the Materials and methods section, the high-throughput Y2H experiments allow us to estimate the parameters Ē≅−7.0kT and σ≅1.8kT of the distribution f1(Ei). For any given number of protein types m and average concentration C̄, one could use Equation (11) to calculate the chemical potential μ and the individual danger levels [iR]/[i] for proteins with any energy Ei. The total fraction of proteins wasted in the non-functional complexes

graphic file with name msb200848-i15.jpg

is shown in colour in Figure 3. For the cytoplasm of a yeast cell with m≅1800 and C̄≅1 μM (Ghaemmaghami et al, 2003), Equation (11) gives μ≅−8.9kT. Thus, according to Equation (12), at any time point about 22% of proteins that are not in specific complexes are bound in non-functional complexes. Figure 3 also shows the nucleus and the mitochondria of a yeast cell by the white star and the white cross.

The next question is whether these compartments, especially the cytoplasm, fall in the dead zone. The range of the dead zone depends on specific and non-functional binding energies as well as concentrations, and these quantities vary greatly for proteins within a compartment. Therefore, Equations (3) and (4) can only find the boundaries of the dead zone for the simplified example system. However, for a realistic compartment such as the cytoplasm, we can still find the representative boundaries of the dead zone using the median values. Namely, we focus on a protein with median values of concentration, specific interaction Es≈−16.5kT and stickiness Ei=Ē≅−7.0kT, which correspond to the median non-functional interaction En=2Ē+ΔG(0)=−4.0kT (see the next section and Materials and methods for these values). Owing to the variability of stickiness and concentrations of proteins, Equations (3) and (4) should be modified. First, as the distribution of individual protein concentrations is nearly lognormal, the median concentration of individual proteins is higher than the average value. We find Cmed≅C̄/6 from data of the yeast cytoplasm. So Equation (3) becomes

graphic file with name msb200848-i16.jpg

This gives C̄=0.82 μM as the boundary of the dead zone for the protein with median-specific interactions. Second, variation of surface ‘stickiness' changes Equation (2a) to

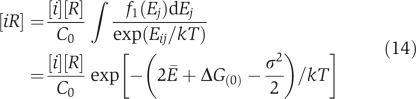graphic file with name msb200848-i17.jpg

Comparing Equations (2b) and (14), we obtain a modification of Equation (4)

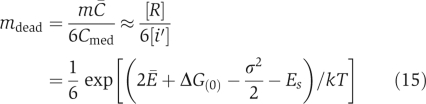graphic file with name msb200848-i18.jpg

This results in mdead≅8200 for the cytoplasm. This value is not necessarily very precise, as shown in Table I. mdead is smaller if we use other Y2H data sets, or we obtain mdead≅4900 if the full Ito data set is used. Figure 3 shows the dead zone in shade. The boundaries of the dead zone, characterized by Equations (13) and (15), are blurred to indicate that they are crossover rather than sharp transitions. We can see from Figure 3 that the cytoplasm of a yeast cell avoids the dead zone but locates near the corner corresponding to the upper limit of m and the lower limit of C̄. The nucleus and the mitochondria are also away but not far from the dead zone.

Table 1.

The summary of data from high-throughput Y2H experiments in different organisms and calculation results using the databases

Species ν N
 Fraction 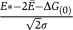Inline graphic mdead 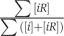Inline graphic
    Nbait Nprey        
Yeast 1600 6000 6.2 e−5 3.8 8200 22%
Worm 4000 1900 1000 1.5 e−4 3.6 5300 26%
Fly 2000 1100 1000 2.4 e−4 3.5 4100 28%
Human1 3200 4500 5600 1.8 e−4 3.6 4900 26%
Human2 2800 7200 7.4 e−5 3.8 7500 23%
Open in a new tab

The data set of yeast merges interaction data in Uetz et al (2000) and the core data of Ito et al (2001), which contain interactions identified by at least three interaction sequence tags. The source of other data sets are as follows: worm (Li et al, 2004), fly (Giot et al, 2003), human1 (Stelzl et al, 2005) and human2 (Rual et al, 2005). The fraction is calculated as αν/(N2/2) if Nbait≅Nprey, and αν/(NbaitNprey) otherwise. The parameter α=0.7 is used in calculations.

The phase diagram shown in Figure 3 represents all proteins in a given subcellular compartment by a single point. This is just an approximation, as different proteins would have different distances from the boundaries of the dead zone due to the variation in their energies of specific and non-functional interactions as well as in their concentrations. For instance, proteins with relatively strong specific binding could afford to have smaller concentrations Ci or, conversely, proteins with low concentrations have more difficulty maintaining the stability of specific complexes and thus need to have a stronger binding energy of specific interactions. Also, sticky proteins have stronger than average non-functional interactions and thus tend to be more sequestered in non-functional complexes than the average fraction colour-coded in Figure 3. The complete description of the system should include the ratio [i]:[ii′]:[iR] for every protein. However, the presently available experimental data (most notably the scarcity of data on binding energies of individual-specific interactions) does not allow for such a complete description.

All this imposes additional evolutionary constraints on the system. As was proposed by one of us (Maslov and Ispolatov, 2007), the result of such evolutionary pressure is that interactions between proteins with lower Ci would be stronger, that is, have lower (more negative) binding energy Es translating into smaller dissociation constant Ks. However, from the evolutionary standpoint, the strength of these interactions must not be much stronger than the minimum required to ensure a sufficient concentration of a specific complex [ii′] (Maslov and Ispolatov, 2007).

Variability of individual protein concentrations and specific binding energies

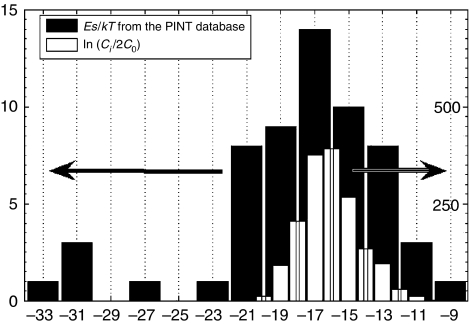
Let us compare the histogram of specific binding energies with that of individual protein concentrations (Figure 4). The concentrations of individual proteins in yeast cells vary greatly (Ghaemmaghami et al, 2003; Belle et al, 2006) (open bars in Figure 4), with the median (typical) value Cmed≅0.2 μM or ln(Cmed/2C0)≈−16.1.

Figure 4.

Figure 4

Open in a new tab

The histograms of individual protein concentrations ln (Ci/2C0) (white bars) and binding energies Es of specific interactions (filled bars) (Kumar and Gromiha, 2006). Note that the peaks of these two distributions almost precisely agree with each other, whereas the distribution of binding energies is broader, especially on the negative side.

The dissociation constants (or corresponding binding energies) of specific interactions between yeast proteins have not been measured systematically. The binding energy data available from the PINT (Protein–protein Interaction Thermodynamic) database (Kumar and Gromiha, 2006) is quite limited. To gather sufficient statistics, we had to combine the binding energy data from different species including yeast, rat, human and so on (see Table S1, in Supporting Information). The resulting histogram is shown with filled bars in Figure 4. The data we choose are interactions between two types of wild-type proteins from the same species. Although most data are not from yeast cells, it could still provide some helpful information, because protein systems in different species have certain similarities.

Comparing the two histograms shown in Figure 4, we find that the median of ln (Ci/2C0)∼−16.1 is just slightly above that of Es/kT∼−16.5. Therefore, most individual protein concentrations Ci are only slightly larger than the typical limiting value given by Equation (3). This would be enough for proteins within the safe zone where [iR]≪[i]. On the other hand, the distribution of Es/kT below the median is noticeably broader than that of ln (Ci/2C0). This corresponds to the contribution of proteins that are inside the dangerous zone ([iR]>[i]) where specific interactions are required to be even stronger than required as per Equation (3).

This validates our observation that concentrations of most proteins are kept at or near the lower limit to ensure the formation of specific complexes. Maintaining low individual protein concentrations allows the cell to reduce the interference of non-functional interactions and, therefore, enhance the evolutionarily important protein diversity (the number of protein types that are simultaneously expressed and co-localized in the same compartment).

Discussion

In this work, we compared the concentrations of the three states of protein inside compartments of living cells: bound in specific complexes [ii′], bound in non-functional complexes [iR] and free (monomeric) [i]. As shown in Figure 1, the lower limit of the individual protein concentration is controlled by the requirement that [ii′]>[i], and the upper limit on the number of types of proteins that are co-expressed in the same intracellular compartment is set by the requirement that [ii′]>[iR]. The average concentration of a single protein and the protein diversity inside the yeast cytoplasm are in fact rather close to these two limits (see Figure 3). The size of the proteome is likely to be pushed up to the upper limit by evolution, because higher protein diversity allows for more complex biological functions. The average concentration of individual proteins is then pushed down towards the lower limit to reduce the waste of proteins in non-functional complexes and to improve the spatial and temporal efficiency of biochemical processes in a cell. Therefore, we suggest that the systems of coexisting proteins inside compartments of living cells, especially the cytoplasm, are located near the corner of the allowed region in the phase diagram. This requires the value of mcytoplasm/mdead to fall in the interval 0.1–0.8 and 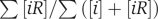Inline graphic in the interval 0.1–0.35, and for Ito core data this further requires α to be in the interval 0.05–15.0. Our estimated ranges α∼0.3–0.9, mcytoplasm/mdead∼0.11–0.4 and 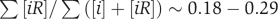Inline graphic are consistent with the hypothesis. Another argument in favour of keeping the specifically bound concentration [ii′] comparable with the free concentration [i] relies on the observation that along this horizontal line of the phase diagram in Figure 3, the functionally important concentration [ii′] is most sensitive to changes in total concentration Ci. This can be used for regulatory purposes allowing the cell to effectively turn on and off this particular biological function by changing the expression level of the protein i.

The phase diagram presented in Figure 3 highlights the major trade-off faced by compartments of living cells. To ensure the robust function, concentrations of individual proteins should be high enough to provide for sufficient formation of specific complexes. On the other hand, higher concentrations lead to an increase and possible dominance of non-functional interactions sequestering proteins and wasting precious resources. To overcome this limitation, the evolution could either strengthen the specific interactions, or weaken the non-functional ones, or (better yet) do both things at once. Nature has certainly exercised the first possibility by evolving stronger specific PPIs between proteins in functional complexes (e.g., by the virtue of cooperative binding). However, this route has its limitations, as designing strong specific interactions requires a prolonged evolutionary search in sequence space, which might be quite challenging to achieve. An alternative possibility is to evolve proteins with less hydrophobic surfaces. An interesting manifestation of this possibility could be seen in comparison of mesophilic with (hyper-)thermophilic proteins. It is clear from Equation (3) that the gap between specific and non-functional interaction energies should increase for organisms living at higher temperatures to keep the same proteome size. In this regard, it is important to note that surfaces of proteins from hyperthermophilic organisms are enriched with charged residues (Glyakina et al, 2007) and that majority of those residues do not form salt bridges (Goldstein, 2007). It is therefore tempting to speculate that the main reason for this enrichment with charged residues is to reduce non-functional PPIs in hyperthermophiles to keep their proteome size at a physiologically acceptable level.

Multicellular organisms, however, can go around the upper limit of protein diversity. By separating different kinds of proteins in different cell types, they can avoid coexistence of too many protein types and reduce the amount of non-functional interactions. Therefore, they are allowed to develop more complicated functions through cellular differentiation. This could be one of the crucial reasons for multicellular organisms to emerge in the course of the evolution. It will be also interesting to study whether there is a systematic difference in stickiness of proteins from prokaryotes with less compartmentalized cells and higher organisms whose cells are highly compartmentalized. It could be an interesting undertaking to systematically compare surface hydrophobicities with specific interaction energies between groups of proteins from simplest—not compartmentalized—cells to single-cell eukaryotes to multicellular organisms.

The specific estimates of tolerable concentrations and proteome sizes made in this study are on the basis of assessment of the specific and non-functional interactions, which are not necessarily very accurate. An important source of uncertainty lies in the estimate of the parameter α, the fraction of non-functional interactions among all interactions detected in Y2H data sets. To see the impact of α on the results, if α is in the interval 0.4–0.9, the value of mdead is in the interval 7300–10 500 and 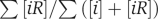Inline graphic is in the interval 21–23%. We also face a dilemma in choosing either the full or the core data from Ito et al (2001). As the filtered Ito core data requires three interaction sequence tags, many non-functional interactions that are only slightly stronger than the threshold Kd*≈1 μM (Estojak et al, 1995) may not be included in the data set. The number of non-functional PPIs is better reflected by the full Ito data set, which contains ∼4500 interactions and results in mdead=4900 and average fraction [iR]/([iR]+[i])=26% for yeast cytoplasm. However, the full Ito data set might contain many false interactions due to experimental artefacts such as bait self-activation. To be cautious, we choose the united data of Uetz et al (2000) and Ito core rather than the full Ito data set for yeast PPIs to avoid experimental artefacts, and keep in mind that the result mdead=8200 might be overestimated and the average fraction [iR]/([iR]+[i])=22% might be slightly underestimated. In consistence with this expectation, the result of mdead is also smaller if we try the calculation with Y2H data sets of other organisms (see Table I).

There are other sources of uncertainties in the calculation besides the estimate of non-functional interactions in Y2H data sets. For binding energies of specific interactions, we used the PINT database (Kumar and Gromiha, 2006), which contains the experimentally measured strength of specific interactions between some of the proteins from various organisms, which we subsequently extrapolated to yeast. The data on such interactions are still scarce and its accuracy is not entirely clear. For non-functional interactions, our estimates are on the basis of a straightforward analysis of Y2H experiments that assumes a ‘hard cutoff' E* on binding energy Eij of detected PPIs. A more sophisticated method that uses a ‘soft' cutoff assumption (Shi et al, 2006) for the detection of PPI in Y2H experiments may give somewhat different estimates for strength and variation of non-functional interactions. For example, using the soft-cutoff model modifies our estimates for the non-functional interaction energy, but still predicts that around 15% of proteins are sequestered in non-functional complexes (Maslov, unpublished data). However, the fundamental finding of this work concerns the deep interrelation between specific and non-functional interactions and sizes of proteomes in living cells and is independent on the specific numeric values used in our estimates.

Above, we assumed that the biologically active state of all proteins is in the complex with their specific binding partner. Although this is certainly the case for a significant fraction of all proteins in the cell, there also exist proteins that are biologically active in their monomeric form. Our definition of death zone for such proteins should be adjusted to require [i]>[iR]. Instead of Equation (3), the lower bound on concentrations of monomeric proteins is imposed by purely physiological factors. For example, the abundance of metabolic enzymes is likely to be dictated by typical concentrations of their substrates. There are also cases of proteins with more than one specific partner. Under these circumstances, the condition [ii′]>[iR] should hold independently for each of the functionally important partners.

The interference of non-functional PPIs with biochemical efficiency of all intracellular functional processes is quantified by the ratio [iR]/[i], indicating whether proteins that do not participate in specific complexes are free in cytoplasm or non-functionalally bound to non-functional partners. Although the average ratio [iR]/([iR]+[i])=22% does not seem particularly large, due to the variation in stickiness, certain proteins would have much greater ratio [iR]/[i] than average (see Materials and methods for details). Thus, the requirement of biochemical efficiency is pushing individual protein concentrations down in the cytoplasm. As a result, the cytoplasm of a cell can only stay at the corner near the triple point in the phase diagram. This conclusion might be generalized to apply to many other cells.

Materials and methods

Obtaining individual protein concentrations from experimental results

The expression level of proteins in yeast cell cytoplasm, nucleus and mitochondria are taken from experiments (Ghaemmaghami et al, 2003; Huh et al, 2003; Belle et al, 2006). The average volume of a haploid yeast cytoplasm is ∼25 fL (Jorgensen et al, 2007), which is similar to the cell volume. The volume of nucleus (Jorgensen et al, 2007) and mitochondria (Visser et al, 1995) are both about 7% of cell volume, although early results of mitochondria (Grimes et al, 1974; Stevens, 1977) vary from 3 to 14%.

Most proteins within a given subcellular compartment diffuse over its whole volume. Although some proteins enhance their local concentrations through co-localization (Kuriyan and Eisenberg, 2007) near the membrane, such membrane-bound proteins are only a small fraction among all protein types, for example, no more than 15% for the cytoplasm (Kumar et al, 2002). Thus, this effect constitutes just a small correction to our estimates for individual subcellular compartments and will not be considered in this study.

These individual protein concentrations were obtained mainly for the cells in the G1 stage in the cell cycle. Are they really representative of what happens at other stages of the cell cycle? To address this concern, we point out that the median half-life of yeast proteins is ∼40 min (Belle et al, 2006) whereas the cell cycle takes ∼90 min. Therefore, the concentrations of most yeast proteins do not change dramatically in the course of a cell cycle, and the above estimate using the average concentration in the G1 stage remains valid.

Our calculations are quite robust with respect to random errors in measurements of concentrations of individual proteins, as we use only the total concentration of all proteins and the number of protein types. Even large systematic errors in protein concentrations will not significantly impact our qualitative results. For example, a factor of 2 or 1/2 error in the total protein concentration will change the fraction 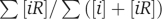Inline graphic from 22% to only 28 or 17% correspondingly.

Estimating the strength of non-functional interactions from Y2H experiments

In this section, we estimate the mean and the standard deviation of the binding energy of all non-functional PPI from the Y2H experiments. This estimate was used in the previous section to derive the phase diagram (Figure 3) for the fraction of non-functional complexes in the cytoplasm of yeast cells.

The distribution of binding energy of non-functional interactions is determined by its average 2Ē+ΔG(0) and variation 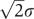Inline graphic as defined by Equation (7). High-throughput Y2H experiments systematically inspect PPIs between nearly all pairs of proteins encoded in the genome of a given organism. Thus, they contain a useful information, allowing one to estimate the values of Ē and σ.

A positive signal is detected in a Y2H experiment if a PPI is sufficiently strong, and the detection threshold for the dissociation constant is experimentally estimated as Kd*≈1 μM or E*≈kT ln(Kd*/C0)=−14kT (Estojak et al, 1995).

The interactions detected in Y2H experiments are not necessarily biologically functional. For one thing, the in vivo concentrations of individual proteins (Ghaemmaghami et al, 2003; Huh et al, 2003; Belle et al, 2006) are often considerably lower than those of bait-and-prey proteins used in Y2H experiments. As a result, there is no guarantee that even a reproducible interaction detected in a Y2H screen will occur with any significant probability for in vivo concentrations of interacting proteins. This view is supported by our observation (Figure 5) that the overlap between Y2H interactions from the full set of Ito et al (2001) and the curated set of biologically functional interactions is biased towards proteins with high in vivo concentrations. Below, we use the large-scale Y2H data sets to determine the parameters of non-functional interactions necessary for our model. As pointed out above, the Y2H technique detects interactions between baits and preys at elevated concentrations, and therefore it samples a much broader set of PPIs than those that are occurring with high probability at in vivo concentration of proteins. Another advantage of large-scale Y2H screens is that they check for possible interactions among all possible pairs of proteins without any bias towards functionally related pairs. As a result, large-scale Y2H data sets contain ample information about the distribution of affinities for non-functional interactions, especially for proteins with low in vivo concentrations (see Figure 5).

Figure 5.

Figure 5

Open in a new tab

The fraction of Y2H interactions from the full set of Ito et al (2001) confirmed in a curated set of biologically functional interactions that were independently reported in two or more publications not using the Y2H technique. The x and y axis are the in vivo protein concentrations (Ghaemmaghami et al, 2003) in yeast cytoplasm. One can see that Y2H interactions between proteins with relatively high in vivo concentrations (>0.1 μM) have considerably higher chances of being biologically functional.

We define α as the fraction of non-functional interactions among all interactions detected in large-scale Y2H screens. The list of all interactions detected in the largest Y2H screen of yeast proteins (Ito et al, 2001) contains many false-positives (Deane et al, 2002; Vidalain et al, 2004; Huang et al, 2007) due to reproducible yet non-functional interactions as well as methodological artefacts such as bait self-activations (Nakayama et al, 2002). The Ito core data set, formed by the interactions repeatedly detected in the course of the experiment (three times or more) is more reliable and reproducible, but is still thought to contain over 40% false-positives (Deane et al, 2002). Most importantly, the internal reproducibility condition used to generate this data set likely eliminates most of the artefacts due to bait self-activation. Indeed, the interaction partners of a self-activating bait are essentially randomly selected from a large pool of prey proteins. Hence, it is exceedingly improbable to repeatedly detect the same prey protein three or more times. We assume that the remaining false-positives in the Ito core data set are real and reproducible, but not formed under the in vivo conditions inside a living cell and thus do not contribute to its biological functioning. The lower bound on the fraction of non-functional interactions in the Ito core data set is set by the following observation: among the 522 interacting pairs with known subcellular localizations of both proteins (Huh et al, 2003), 15% correspond to pairs of proteins that are never co-localized in the same intracellular compartment, and thus in principle cannot bind each other in vivo. We expect the fraction of all non-functional interactions (including those caused by concentration effects of co-localized proteins) to be significantly higher than 15%.

On the other hand, many strong and functional interactions must be missed in large-scale Y2H screens as false-negatives, because another filtered Y2H data set (Uetz et al, 2000) of yeast proteins has few overlaps with the Ito core data set. Thus, we expect that many strong enough non-functional interactions can be missed in Y2H data sets. To take this effect into account, we merge the Ito core data set and the filtered Uetz data set to obtain a more complete data set of yeast proteins. Combining the estimate of false-positives in Y2H data sets reported by Deane et al (2002) with this false-negative effect, we propose α=0.7 as the ballpark fraction of non-functional PPIs among all interactions detected in Y2H screens. The impact of uncertainty in our estimation of this parameter α is assessed in Discussion.

For N types of proteins tested in a high-throughput experiment, there are N(N+1)/2≈N2/2 possible interactions. If ν distinct interacting pairs pass the dissociation constant cutoff and αν interactions are non-functional, their fraction among all pairs is given by

graphic file with name msb200848-i24.jpg

where Erf is the error function. This equation defines a relationship between the parameters Ē and σ of the distribution of binding energies of non-functional interactions and the parameters ν and N of a high-throughput Y2H experiment. The genome-wide Y2H studies in baker's yeast Saccharomyces cerevisiae (Uetz et al, 2000; Ito et al, 2001) contain ν≈1600 interacting pairs between about N≅6000 tested proteins. We use α=0.7 to find the number of non-functional interactions and solve Equation (16) to get

graphic file with name msb200848-i25.jpg

We solve Equations (8) and (17) to find Ē≅−7.0kT and σ≅1.8kT. Hence, the estimated median value of non-functional interactions is 2Ē+ΔG(0)=−4.0kT or Kn∼18 mM. This value is in agreement with the suggestion (Kuriyan and Eisenberg, 2007) that Kn is a little larger than 10 mM for non-functional PPIs.

In Table I, we also show the value of 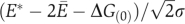Inline graphic for several large-scale Y2H experiments, which are strikingly similar for different species. Although in this study we focus on the baker's yeast for which protein concentrations were systematically measured, our estimates of the parameters of non-functional interactions could be applicable to other organisms listed in Table I.

Protein-to-protein variability of non-functional sequestration ratio

As estimated above for yeast cytoplasm, the average fraction [iR]/([iR]+[i]) of proteins sequestered inside non-functional complexes is about 22%. As the chemical potential μ≅−8.9kT is lower than the median energy Ē≅−7.0kT, the ratio [iR]/[i]=exp[−(Ei−μ)/kT] is below one for most of the proteins. Around 20 of the most sticky types of proteins have [iR]/[i]>10, and for the protein with highest hydrophobicity, the ratio reaches [iR]/[i]≈60. If we add the correction that proteins in specific complexes have reduced affinity for non-functional interactions, the highest ratio is reduced to [iR]/[i]≈35 (see Supporting Information).

Supplementary Material

Supplementary Information

msb200848-s1.doc (262KB, doc)

Supplementary Table

msb200848-s2.xls (31KB, xls)

Acknowledgments

We are grateful to Paul Choi, Eric Deeds, Lucas Nivon and Boris Shakhnovich for discussions, and Orr Ashenberg for sharing hydrophobicity data. This work was supported by the National Institutes of Health. Work at Brookhaven National Laboratory was carried out under Division of Material Science, US Department of Energy Contract DE-AC02-98CH10886.

References

  1. Aloy P, Bottcher B, Ceulemans H, Leutwein C, Mellwig C, Fischer S, Gavin AC, Bork P, Superti-Furga G, Serrano L, Russell RB (2004) Structure-based assembly of protein complexes in yeast. Science 303: 2026–2029 [DOI] [PubMed] [Google Scholar]
  2. Aloy P, Russell RB (2002) Potential artefacts in protein-interaction networks. FEBS Lett 530: 253–254 [DOI] [PubMed] [Google Scholar]
  3. Aloy P, Russell RB (2006) Structural systems biology: modelling protein interactions. Nat Rev Mol Cell Biol 7: 188–197 [DOI] [PubMed] [Google Scholar]
  4. Bahadur RP, Chakrabarti P, Rodier F, Janin J (2004) A dissection of specific and non-specific protein–protein interfaces. J Mol Biol 336: 943–955 [DOI] [PubMed] [Google Scholar]
  5. Belle A, Tanay A, Bitincka L, Shamir R, O'Shea EK (2006) Quantification of protein half-lives in the budding yeast proteome. Proc Natl Acad Sci USA 103: 13004–13009 [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bogan AA, Thorn KS (1998) Anatomy of hot spots in protein interfaces. J Mol Biol 280: 1–9 [DOI] [PubMed] [Google Scholar]
  7. Deane CM, Salwinski L, Xenarios I, Eisenberg D (2002) Protein interactions: two methods for assessment of the reliability of high throughput observations. Mol Cell Proteomics 1: 349–356 [DOI] [PubMed] [Google Scholar]
  8. Deeds EJ, Ashenberg O, Gerardin J, Shakhnovich EI (2007) Robust protein protein interactions in crowded cellular environments. Proc Natl Acad Sci USA 104: 14952–14957 [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Deeds EJ, Ashenberg O, Shakhnovich EI (2006) A simple physical model for scaling in protein–protein interaction networks. Proc Natl Acad Sci USA 103: 311–316 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Eisenberg D, McLachlan AD (1986) Solvation energy in protein folding and binding. Nature 319: 199–203 [DOI] [PubMed] [Google Scholar]
  11. Estojak J, Brent R, Golemis EA (1995) Correlation of two-hybrid affinity data with in vitro measurements. Mol Cell Biol 15: 5820–5829 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gavin AC, Aloy P, Grandi P, Krause R, Boesche M, Marzioch M, Rau C, Jensen LJ, Bastuck S, Dumpelfeld B, Edelmann A, Heurtier MA, Hoffman V, Hoefert C, Klein K, Hudak M, Michon AM, Schelder M, Schirle M, Remor M et al. (2006) Proteome survey reveals modularity of the yeast cell machinery. Nature 440: 631–636 [DOI] [PubMed] [Google Scholar]
  13. Ghaemmaghami S, Huh WK, Bower K, Howson RW, Belle A, Dephoure N, O'Shea EK, Weissman JS (2003) Global analysis of protein expression in yeast. Nature 425: 737–741 [DOI] [PubMed] [Google Scholar]
  14. Giot L, Bader JS, Brouwer C, Chaudhuri A, Kuang B, Li Y, Hao YL, Ooi CE, Godwin B, Vitols E, Vijayadamodar G, Pochart P, Machineni H, Welsh M, Kong Y, Zerhusen B, Malcolm R, Varrone Z, Collis A, Minto M et al. (2003) A protein interaction map of Drosophila melanogaster. Science 302: 1727–1736 [DOI] [PubMed] [Google Scholar]
  15. Glyakina AV, Garbuzynskiy SO, Lobanov MY, Galzitskaya OV (2007) Different packing of external residues can explain differences in the thermostability of proteins from thermophilic and mesophilic organisms. Bioinformatics 23: 2231–2238 [DOI] [PubMed] [Google Scholar]
  16. Goldstein RA (2007) Amino-acid interactions in psychrophiles, mesophiles, thermophiles, and hyperthermophiles: insights from the quasi-chemical approximation. Protein Sci 16: 1887–1895 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Grimes GW, Mahler HR, Perlman RS (1974) Nuclear gene dosage effects on mitochondrial mass and DNA. J Cell Biol 61: 565–574 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Huang H, Jedynak BM, Bader JS (2007) Where have all the interactions gone? Estimating the coverage of two-hybrid protein interaction maps. PLoS Comput Biol 3: e214. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Huh WK, Falvo JV, Gerke LC, Carroll AS, Howson RW, Weissman JS, O'Shea EK (2003) Global analysis of protein localization in budding yeast. Nature 425: 686–691 [DOI] [PubMed] [Google Scholar]
  20. Ito T, Chiba T, Ozawa R, Yoshida M, Hattori M, Sakaki Y (2001) A comprehensive two-hybrid analysis to explore the yeast protein interactome. Proc Natl Acad Sci USA 98: 4569–4574 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Janin J (1995) Protein–protein recognition. Prog Biophys Mol Biol 64: 145–166 [DOI] [PubMed] [Google Scholar]
  22. Janin J (1996) Quantifying biological specificity: the statistical mechanics of molecular recognition. Proteins 25: 438–445 [DOI] [PubMed] [Google Scholar]
  23. Jorgensen P, Edgington NP, Schneider BL, Rupes I, Tyers M, Futcher B (2007) The size of the nucleus increases as yeast cells grow. Mol Biol Cell 18: 3523–3532 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kim PM, Lu LJ, Xia Y, Gerstein MB (2006) Relating three-dimensional structures to protein networks provides evolutionary insights. Science 314: 1938–1941 [DOI] [PubMed] [Google Scholar]
  25. Kortemme T, Baker D (2002) A simple physical model for binding energy hot spots in protein-protein complexes. Proc Natl Acad Sci USA 99: 14116–14121 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kumar A, Agarwal S, Heyman JA, Matson S, Heidtman M, Piccirillo S, Umansky L, Drawid A, Jansen R, Liu Y, Cheung KH, Miller P, Gerstein M, Roeder GS, Snyder M (2002) Subcellular localization of the yeast proteome. Genes Dev 16: 707–719 [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kumar MD, Gromiha MM (2006) PINT: protein–protein interactions thermodynamic database. Nucleic Acids Res 34: D195–D198 [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Kuriyan J, Eisenberg D (2007) The origin of protein interactions and allostery in colocalization. Nature 450: 983–990 [DOI] [PubMed] [Google Scholar]
  29. Lo Contc L, Chothia C, Janin J (1999) The atomic structure of protein-protein recognition sites. J Mol Biol 285: 2177–2198 [DOI] [PubMed] [Google Scholar]
  30. Li S, Armstrong CM, Bertin N, Ge H, Milstein S, Boxem M, Vidalain PO, Han JD, Chesneau A, Hao T, Goldberg DS, Li N, Martinez M, Rual JF, Lamesch P, Xu L, Tewari M, Wong SL, Zhang LV, Berriz GF et al. (2004) A map of the interactome network of the metazoan C. elegans. Science 303: 540–543 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Lukatsky DB, Shakhnovich BE, Mintseris J, Shakhnovich EI (2007) Structural similarity enhances interaction propensity of proteins. J Mol Biol 365: 1596–1606 [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Maslov S, Ispolatov I (2007) Propagation of large concentration changes in reversible protein-binding networks. Proc Natl Acad Sci USA 104: 13655–13660 [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Nakayama M, Kikuno R, Ohara O (2002) Protein–protein interactions between large proteins: two-hybrid screening using a functionally classified library composed of long cDNAs. Genome Res 12: 1773–1784 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Noskov SY, Lim C (2001) Free energy decomposition of protein-protein interactions. Biophys J 81: 737–750 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Rual JF, Venkatesan K, Hao T, Hirozane-Kishikawa T, Dricot A, Li N, Berriz GF, Gibbons FD, Dreze M, Ayivi-Guedehoussou N, Klitgord N, Simon C, Boxem M, Milstein S, Rosenberg J, Goldberg DS, Zhang LV, Wong SL, Franklin G, Li S et al. (2005) Towards a proteome-scale map of the human protein–protein interaction network. Nature 437: 1173–1178 [DOI] [PubMed] [Google Scholar]
  36. Scar RP (2004) Specific protein-protein binding in many-component mixtures of proteins. Phys Biol 1: 53–60 [DOI] [PubMed] [Google Scholar]
  37. Shi YY, Miller GA, Qian H, Bomsztyk K (2006) Free-energy distribution of binary protein–protein binding suggests cross-species interactome differences. Proc Natl Acad Sci USA 103: 11527–11532 [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Stelzl U, Worm U, Lalowski M, Haenig C, Brembeck FH, Goehler H, Stroedicke M, Zenkner M, Schoenherr A, Koeppen S, Timm J, Mintzlaff S, Abraham C, Bock N, Kietzmann S, Goedde A, Toksoz E, Droege A, Krobitsch S, Korn B et al. (2005) A human protein–protein interaction network: a resource for annotating the proteome. Cell 122: 957–968 [DOI] [PubMed] [Google Scholar]
  39. Stevens BJ (1977) Variation in number and volume of the mitochondria in yeast according to growth conditions. Biologie Cellulaire 28: 37–56 [Google Scholar]
  40. Tamura A, Privalov PL (1997) The entropy cost of protein association. J Mol Biol 273: 1048–1060 [DOI] [PubMed] [Google Scholar]
  41. Uetz P, Giot L, Cagney G, Mansfield TA, Judson RS, Knight JR, Lockshon D, Narayan V, Srinivasan M, Pochart P, Qureshi-Emili A, Li Y, Godwin B, Conover D, Kalbfleisch T, Vijayadamodar G, Yang M, Johnston M, Fields S, Rothberg JM (2000) A comprehensive analysis of protein–protein interactions in Saccharomyces cerevisiae. Nature 403: 623–627 [DOI] [PubMed] [Google Scholar]
  42. Vidalain PO, Boxem M, Ge H, Li S, Vidal M (2004) Increasing specificity in high-throughput yeast two-hybrid experiments. Methods 32: 363–370 [DOI] [PubMed] [Google Scholar]
  43. Visser W, van Spronsen EA, Nanninga N, Pronk JT, Gijs Kuenen J, van Dijken JP (1995) Effects of growth conditions on mitochondrial morphology in Saccharomyces cerevisiae. Antonie Van Leeuwenhoek 67: 243–253 [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

msb200848-s1.doc (262KB, doc)

Supplementary Table

msb200848-s2.xls (31KB, xls)

Articles from Molecular Systems Biology are provided here courtesy of Nature Publishing Group

RESOURCES