High-order combination effects and biological robustness

Abstract

Biological systems are robust, in that they can maintain stable phenotypes under varying conditions or attacks. Biological systems are also complex, being organized into many functional modules that communicate through interlocking pathways and feedback mechanisms. In these systems, robustness and complexity are linked because both qualities arise from the same underlying mechanisms. When perturbed by multiple attacks, such complex systems become fragile in both theoretical and experimental studies, and this fragility depends on the number of agents applied. We explore how this relationship can be used to study the functional robustness of a biological system using systematic high-order combination experiments. This presents a promising approach toward many biomedical and bioengineering challenges. For example, high-order experiments could determine the point of fragility for pathogenic bacteria and might help identify optimal treatments against multi-drug resistance. Such studies would also reinforce the growing appreciation that biological systems are best manipulated not by targeting a single protein, but by modulating the set of many nodes that can selectively control a system's functional state.

Introduction

Even the simplest organisms are robust, in that they are able to maintain functional stasis to a remarkable degree in the face of environmental changes or functional component losses (Kitano, 2004, 2007; Stelling et al, 2004). For example, mutation studies in yeast (Winzeler et al, 1999), nematodes (Fraser et al, 2000), flies (Boutros et al, 2004), and mice (Walke et al, 2001) find that surprisingly few genes (typically 10–20%) affect viability when deleted from the genome. In humans, this robustness is reflected in the fact that many drug candidates discovered using the prevailing one-drug-one-target paradigm fail because of a lack of efficacy (Hopkins and Groom, 2002). Clearly, there is sufficient flexibility in biological systems to overcome even severe attacks to isolated components (Hartman et al, 2001).

Another quality of biological systems is their complexity (Carlson and Doyle, 2002; Stelling et al, 2004), which is apparent in the topology of network models that are constructed from interactions between the many thousands of genes (Lee et al, 2002), proteins (Uetz et al, 2000), and metabolites (Duarte et al, 2004) that make up cells in an organism. These networks are organized into modules (Hartwell et al, 1999; Gavin et al, 2002) of interconnected nodes (functional elements) with relatively few highly connected nodes (functional elements) that then link to other subnetworks. These networks have relatively few highly connected modules at their center with many more peripheral nodes, giving rise to approximately power-law node degree distributions (Barabási and Albert, 1999). But the topological structure also involves interlocking serial pathways of metabolic reactions and genetic regulatory networks involving transcription factors that affect many target genes (Ideker and Lauffenburger, 2003). Functional robustness arises from the many redundancies and feedbacks inherent to this structure that allow the system to dynamically adapt or compensate for losses or environmental changes (Stelling et al, 2004).

Simulated network systems become less robust when they are attacked by node removals or other perturbations, especially if the perturbations are combined. Power-law networks that have been constructed using random node attachment are topologically robust against removal of randomly selected nodes (Albert et al, 2000), because most nodes are peripheral, but they become increasingly fragile as more nodes are removed (Agoston et al, 2005). More realistic network simulations of metabolism with combined node removals find many ‘synthetic lethal' interactions (∼4 per enzyme), where a combination disrupts the system's function strongly even when both single deletions have no effect (Segrè et al, 2005). Dynamic simulations of more realistic pathways also produce synergistic responses (Araujo et al, 2004; Lehár et al, 2007) that increase with combination order (Araujo et al, 2007).

Combinations are also very effective in biological experiments (Sharom et al, 2004; Keith et al, 2005). Synthetic lethality rates of ∼8 per gene are observed in yeast double-mutant screens (Tong et al, 2004) and siRNA gene silencing on nematodes (Ceron et al, 2007). Comparable rates are also found when targeted pairs are only partially inhibited, for either mutant chemical sensitivity screens (Giaever et al, 2004; Lum et al, 2004; Parsons et al, 2004) or chemical combination experiments (Borisy et al, 2003; Yeh et al, 2006; Lehár et al, 2007). Finally, clinical experience shows that drug combinations can be more effective than single agents (Zimmermann et al, 2007), especially for resistant bacteria (Walsh, 2000), viruses (Bonhoeffer et al, 1997), and many cancers, where combinations have become the main treatment strategy (Dancey and Chen, 2006). At higher order, in vitro studies of resistant bacteria show that third-order combinations are more effective than drug pairs (Bhusal et al, 2005), and clinical regimens for resistant tuberculosis (Anonymous, 2003) or AIDS infections (Bonhoeffer et al, 1997) routinely require more than two drugs together.

For both the simulated and experimental studies, there is a trend toward more functional fragility as the system is subjected to perturbations of increasing combination orders. This can be explained by the high-order combinations overwhelming any functional redundancy in the system (Figure 1). From this it follows that by determining the ‘combination order of fragility' (COF), high-order perturbation experiments can be used to probe the robustness of a biological system. This can be demonstrated by adapting random attachment network algorithms (Barabási and Albert, 1999) to produce networks with intrinsic functional redundancy, and examining their robustness to successively higher order node removals (Box 1). A similar process could be followed experimentally to evaluate the complexity of a biological system. Here, we explore how high-order perturbation experiments can use this approach not only to identify key sets of agents that can selectively control the state of a robust system but also to functionally dissect a network in terms of its functional complexity.

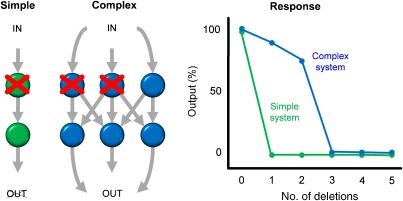
Figure 1.

How complex systems are less fragile to high-order perturbations. Biological processes are often modeled as networks of interacting components that generate output responses based on input conditions. For a trivially simple system with a single pathway and no feedback, removing a single node will eliminate all output, so applying additional deletions will yield no synergistic responses. Networks that have more redundancy provide opportunities for synergy because cutting off alternative pathways or feedbacks can lead to lower output levels. If we monitor the output response as well-chosen nodes are successively removed from the network, the output should be only weakly affected until it reaches a ‘combination order of fragility' (COF), where all available alternative pathways have been blocked.

Measuring synergy in high-order experiments

Realizing the potential of high-order combinations for probing biological robustness requires the selection of relevant probe sets and measured end points, the definition of appropriate synergy metrics, and efficient strategies for exploring the vast combinatorial space of high-order perturbations.

Systematic biological perturbation studies require quantitative phenotypes that monitor the system's function, in most cases a global phenotype such as cellular proliferation (Tong et al, 2004; Yeh et al, 2006). Such integrative phenotypes permit the system to be monitored simultaneously across many functions with relatively few measurements, and can probe the system's responses to perturbations even when the direct targets are not known. Thus for large-scale investigations of high-order combinations, it is likely that global phenotypes will be most practical in the foreseeable future.

The perturbations must target particular functional components, and be flexible enough to permit high-order combinations to be assembled. Large-scale genetic studies are limited to organisms with mutant libraries, and current efforts to extend systematic double-mutant studies (Tong et al, 2004; St Onge et al, 2007) to high-order mutations will be very challenging. Combined siRNA gene silencing experiments (Sahin et al, 2007) are promising, but this work has only been explored to third order. By contrast, biologically active chemical probes can be readily combined in mixtures up to very high order. Chemicals also offer the advantage of variable dosing, as the system's behavior can be monitored in response to different concentrations alone and in combination (Zimmermann et al, 2007). This added detail can be used to identify both synthetic effects at high concentration and potentiation interactions (where the presence of one agent makes the other achieve its maximum effect at lower doses) that could be missed entirely using knockout experiments. The dose–response surfaces from chemical combinations can contain useful mechanistic information (Lehár et al, 2007), and chemicals also provide an excellent starting point for therapeutically exploiting any promising synergies. For these reasons, chemical probes have great potential for high-order testing.

To detect synergy, appropriate experimental designs and combination effect measures are required. For genetic mutations, the necessary data are the responses to the full combination and to all constituent subcombinations. Chemical combinations also require appropriate concentration sampling to make the most of dose responses (Greco et al, 1995). A factorial design, where all permutations of serially diluted single-agent doses are tested, makes very few assumptions about the response surface shape, but is prohibitively expensive for high-order combinations. A more efficient format is to test fixed dose ratio responses, by mixing the component drugs at a high concentration (e.g. twice their 50% effective concentrations, or the highest achievable concentration for singly inactive compounds) and serially diluting that mixture. If response curves are collected for all submixtures of any high-order combination as part of a systematic experiment, there will be sufficient information to fully describe most high-order synergies and antagonisms. Most synergy measures compare a combination's response to those of the constituent single agents (Greco et al, 1995). For genetic interactions, synergy is measured by comparing the combined effect to a model that represents the expectation for non-interaction (Anastassiou, 2007; Mani et al, 2008). For chemical combinations, synergy can be measured either as a high concentration effect boost using one of the genetic interaction models, or as a potency shift at a chosen effect level (Chou and Talalay, 1984; Lehár et al, 2007). These definitions generalize readily to high-order combinations and can be used to quantify the ‘absolute synergy' of a combination compared to its single agents (see Figure 2). Although there is considerable debate concerning which null-interaction model is most generally applicable to biological contexts (Chou and Talalay, 1984; Greco et al, 1995; Lehár et al, 2007; Mani et al, 2008), all of them permit the calculation of an absolute synergy score as described here. At high order, it is also useful to consider the ‘differential synergy' (Figure 2) that measures the extra benefit gained by increasing the combination order. Differential synergy can be calculated from the differences between an mth order combination's synergy score and those of its (m−1)th order submixtures, and should peak at the combination order where the system becomes fragile and the absolute synergy increases most rapidly.

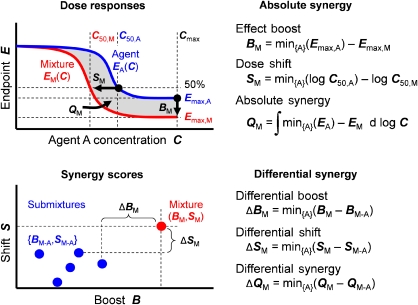
Figure 2.

Synergy scores for high-order combinations. Absolute synergy measures the activity gained in combination over the responses of the single agents, and differential synergy measures the incremental benefit from adding one more agent. For a mixture M comprising a set of chemical agents {A}, the combination can improve the end point response E(C) either by boosting the high-concentration effect level E_max or by shifting the effective dose at a chosen level C₅₀ to lower doses. Synergy scores quantify boosts and shifts relative to the single agents using one of many possible null models (Chou and Talalay, 1984; Anastassiou, 2007; Lehár et al, 2007; Mani et al, 2008), and here we refer simply to the most effective single agent. Overall absolute synergy can be measured by integrating the area between curves. Differential synergies compare the absolute score of an mth order mixture to those of its (m−1)th order ingredients. Here, we show how the submixtures might score for a sixth-order synergy, and define differential synergy using the smallest gain due to adding an mth compound. Differential synergy will peak at the COF, providing a convenient empirical measure of system robustness relevant to a measured end point.

Finally, efficient sampling methods are needed to explore the vast space of possible high-order combinations. Comprehensively testing all pairs of 10 perturbers and their single agents would require only 55 tests, but that number grows to 845 up to sixth order, and for 20 perturbations there are over 60 000 permutations up to sixth order. High-throughput experimental testing should enable screens on that scale (Zimmermann et al, 2007), but it will be some time before comprehensive coverage at higher order or for more than 20 agents is feasible. It is still possible, however, to sample such high-order spaces using informed searching methods. For example, one strategy is to employ an iterative maximal damage search (Agoston et al, 2005) where each perturber is first tested alone and the most effective agent is combined and tested with all the other agents. Higher orders are tested by combining the most active mixture from the previous order with the full set of single agents. This will identify progressively more effective combinations as the order is increased, but is guaranteed to miss the most dramatic high-order synergies between inactive agents. If information on the mechanistic targets of the perturbers is available, such a greedy search can be improved by selecting more than one agent for testing at the next order, based on both activity and mechanistic diversity.

Synergy as a window into network complexity

Combination order of fragility (COF) determinations from systematic experiments should provide useful probes of biological complexity, providing global constraints on corresponding network models. A set of perturbations encompass a subnetwork between the target nodes and the measured end point, and as each such set probes different subnetworks, its differential synergy trend provides a new perspective on the overall structure. Sets of probes that cover a large and redundant portion of the network are likely to have high COFs, whereas those encompassing a low-complexity subnetwork should peak at relatively low orders (Figure 3). Thus, by examining differential synergy for many high-order combinations across different end points, it should be possible to probe the complexity of the network at many levels. For example, high-order perturbation studies could be conducted using bacterial growth assays under different media conditions to determine which media lead to more fragile states and to identify particular sets of probes involved with fragility. It would also be instructive to compare differential synergy results from experiments performed on bacteria, yeasts, and mammalian cells, where one might expect trends toward higher COFs for more complex organisms.

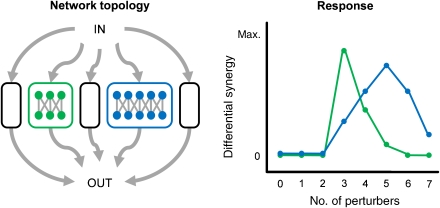
Figure 3.

Expected differential synergy in modular systems. Biological networks are organized into modules, some with differing levels of functional redundancy (Hartwell et al, 1999; Gavin et al, 2002; Ideker and Lauffenburger, 2003). Experiments that focus on different modules, based on which perturbing agents and end points are chosen, should yield differential synergy peaks at combination orders that reflect the complexity of the sampled modules. In this example with multiple essential modules, probe sets targeting nodes in the green module will have COFs at three agents, whereas those targeting the blue module will peak at five perturbers. In this way, systematically testing increasing combination orders for a variety of probe end point sets can yield information on many aspects of the total system's complexity and robustness.

Individual high-order synergies can also expose critical vulnerabilities of the system under study. If a high-order combination experiment reveals a set of perturbers whose differential synergy peaks lower than most of the other sets, the targeted nodes will encompass a subnetwork that can most effectively control the mechanisms involved with the measured end point. Such combinations correspond to minimal cut sets (Schilling et al, 1999), which delineate the eigenstates that underlie the dynamic behavior of a system (Schuster et al, 1999), and that can also suggest optimal combination therapies. This approach could be especially useful when applied to the mounting threat of multi-drug-resistant bacteria (Lowy, 2003; Normark and Normark, 2002). Antibiotic combinations are more effective than single agents at slowing both the proliferation of resistant strains (Saginur et al, 2006) and the emergence of resistance under sustained exposure (Kosowska-Shick et al, 2006). Thus, by impairing the pathogens and raising barriers to evolutionary adaptation, high-order antibacterial synergies show great promise. Systematic high-order experiments may even reveal particular combinations that cripple bacteria to such an extent as to preclude the development of any resistance. COF combinations that show strong antibacterial synergy could also include drugs that on their own are not especially selective for bacteria over human toxicity, increasing the number of targets that can be usefully explored for antibacterial effect. Because antibacterial combinations at the COF can counter many functional redundancies relevant to bacterial proliferation, they have potential for preventing the emergence of any resistance, and could even prove effective even against strains of bacteria that are resistant to all of their constituent drugs when applied individually. As there is always a trade-off between efficacy and toxicity, especially for high-order combinations, the COF should provide a useful guide for optimizing the choice of such antiresistance combinations. Once demonstrated in bacteria, this approach could be used against other pathologies where resistance is an obstacle, including AIDS and cancer.

Finally, investigations of high-order synergy will help reinforce the growing realization that a useful paradigm for a therapeutic or bioengineering target is the set of nodes (e.g. metabolites, genes, proteins, or pathways) in a network that can selectively control the state of a biological system (Kitano, 2007; Kubinyi, 2003). In principle, the behavior of biological systems should be controllable by individually adjusting the state of many components, and the precision with which the system can be manipulated should depend on the number of such state settings. Because of this increased precision, high-order perturbations are more likely than single agents to produce a therapeutic outcome without triggering toxic side effects. In practice, therapeutic selectivity can result both from having more points of control and from the ability to reduce the doses of individual perturbers if they cooperate toward a beneficial end point. High-order experiments can identify such selective synergies and determine the optimal number of ingredients. Although there will always be some conditions that are best treated by a single drug, high-order multi-target combinations represent a strategy that addresses the very complexity of biological systems.

How fragility to combined perturbations depends on system complexity.

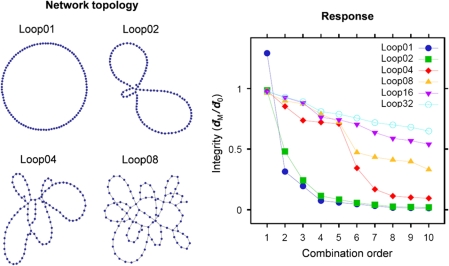
To illustrate how the combination order of fragility (COF) depends on system complexity, we used a simple simulation of graphs with looped topology. A family of networks with the same number of nodes but increasing numbers of loops can be created using a modified attachment algorithm (Barabási and Albert, 1999), starting with a single closed loop and randomly connecting both ends of fixed-length linear ‘pathways' to the existing network. Such networks can be tested for vulnerability to dismemberment by deleting a set of nodes M and measuring the average distance 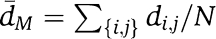between nodes in network fragments, where N is the number of distinct node pairs {i,j}, and d_i,j is the number of steps along the shortest path between nodes i and j, excluding node pairs across fragments. The integrity of perturbed network can be assessed by calculating the ratio between d̄_M and the corresponding d̄₀ for the unperturbed network. Using this procedure to generate 100-node networks with 1 through 32 loops (left), and applying a maximal damage algorithm that selects the most disruptive node at each order for the next set of combined deletions (Agoston et al, 2005), the robustness to high-order perturbations shows a clear trend with system complexity. Simple networks are rapidly disrupted by second- or third-order combinations, whereas networks with many loops are steadily eroded at slower rates. Networks with intermediate levels of complexity are able to maintain integrity under low-order attacks, but are rapidly dismembered once the combination order exceeds a critical level related to the network's level of redundancy. Note that these networks are robust not only to the removal of random peripheral nodes but also to the removal of the highly connected central nodes until the COF has been exceeded. More realistic simulations would require a biologically relevant modeling approach (e.g. flux balance analysis; Segrè et al, 2005), but are likely to find similar trends.

Conflict of interest The authors declare competing financial interests.