Polarizable empirical force field for the primary and secondary alcohol series based on the classical Drude model

Abstract

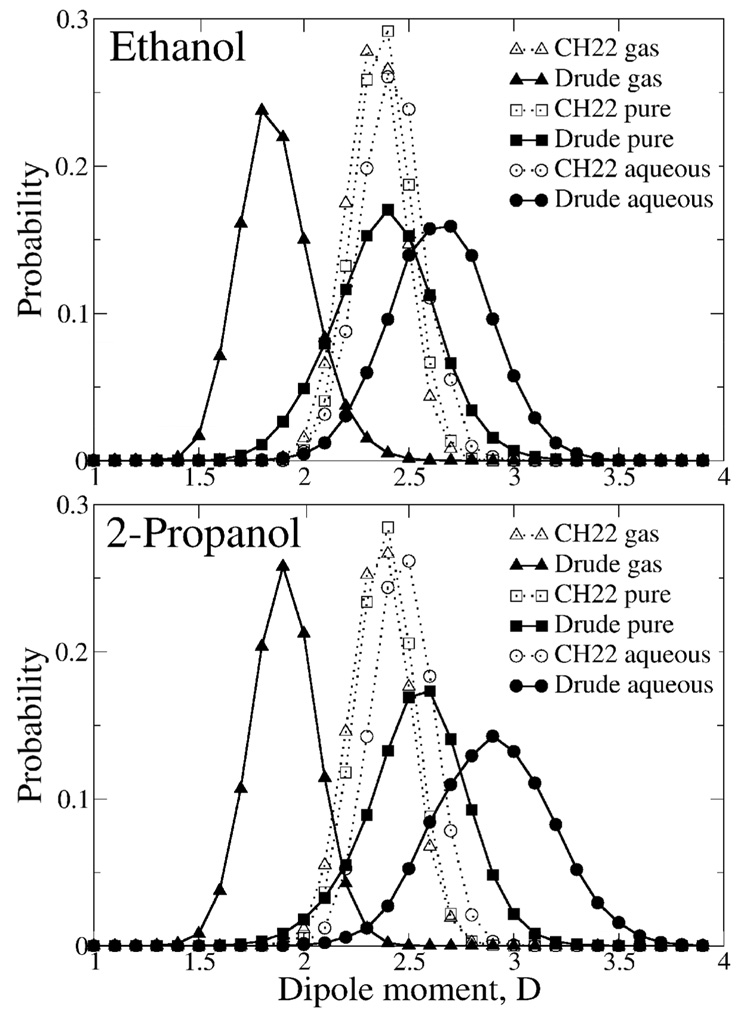
A polarizable empirical force field based on the classical Drude oscillator has been developed for the aliphatic alcohol series. The model is optimized with emphasis on condensed-phase properties and is validated against a variety of experimental data. Transferability of the developed parameters is emphasized by the use of a single electrostatic model for the hydroxyl group throughout the alcohol series. Aliphatic moiety parameters were transferred from the polarizable alkane parameter set, with only the Lennard-Jones parameters on the carbon in methanol optimized. The developed model yields good agreement with pure solvent properties with the exception of the heats of vaporization of 1-propanol and 1-butanol, which are underestimated by approximately 6%; special LJ parameters for the oxygen in these two molecules that correct for this limitation are presented. Accurate treatment of the free energies of aqueous solvation required the use of atom-type specific O_alcohol-O_water LJ interaction terms, with specific terms used for the primary and secondary alcohols. With respect to gas phase properties the polarizable model overestimates experimental dipole moments and quantum mechanical interaction energies with water by approximately 10 and 8 %, respectively, a significant improvement over 44 and 46 % overestimations of the corresponding properties in the CHARMM22 fixed-charge additive model. Comparison of structural properties of the polarizable and additive models for the pure solvents and in aqueous solution shows significant differences indicating atomic details of intermolecular interactions to be sensitive to the applied force field. The polarizable model predicts pure solvent and aqueous phase dipole moment distributions for ethanol centered at 2.4 and 2.7 D, respectively, a significant increase over the gas phase value of 1.8 D, whereas in a solvent of lower polarity, benzene, a value of 1.9 is obtained. The ability of the polarizable model to yield changes in dipole moment as well as the reproduction of a range of condensed phase properties indicates its utility in the study of the properties of alcohols in a variety of condensed phase environments as well as representing an important step in the development of a comprehensive force field for biological molecules.

Introduction

Alcohol moieties are one of the most ubiquitous classes of functional groups, representing building blocks of proteins, nucleic acids, lipids and carbohydrates as well as being found in a wide range of industrial chemicals, including pharmaceuticals. For example, hydroxyls are present in the amino acids serine, threonine and tyrosine, the presence of the hydroxyl group at the 2’ position of the ribose ring in RNA leads to its unique properties as compared to DNA and hydroxyls dominate the structure and function of carbohydrates. Notable is the presence of both polar and non-polar moieties in their structures, allowing alcohols to participate both in hydrophobic and hydrophilic interactions. To better understand the properties of alcohols a number of theoretical chemistry studies have been undertaken,^1–9 including empirical force field based studies investigating their condensed phase properties. To date a majority of these have been based on non-polarizable (fixed-charge additive) models, such as those available in the popular all-atom bio-molecular force fields CHARMM^{10, 11}, Amber¹², and OPLS-AA^{4, 13}, among others.^{3, 14, 15} The additive models use fixed partial atomic charges and in all cases it is necessary to overestimate the gas phase dipole moment of alcohols by approximately 40 % in order to accurately treat the condensed phase (including alcohols in aqueous solution). Despite their usefulness, the assumption of additivity in the treatment of electrostatic interactions prevents an accurate treatment of the full range response in polar and nonpolar environments where the alcohol function groups exist in biomolecules. To overcome the limitation of additive empirical force fields, models that include explicit treatment of electronic polarizability are being developed and a number of classical polarizable models for alcohols have been presented.^16–23 These models have been based on induced dipoles^{16–18, 24}, fluctuating charges^20–22 and the Drude model^{19, 23} to treat the electronic polarizability. In some of the models the internal parameters were transferred directly from the corresponding additive models with few remaining parameters being optimized to reproduce condensed-phase properties^{18, 19, 24}. In other models parameters for hydroxyl groups are set to be unique for the particular alcohol being studied and can not be regarded as transferable across the alcohol series.^21–23 In the present work we extend these efforts via the development of a polarizable model for the alcohol series (Figure 1) with emphasis on maximizing the transferability of the developed parameters to biological macromolecules. In addition, a systematic, iterative approach is applied to rigorously optimize all aspects of the force field parameters to maximize the overall accuracy of the model.

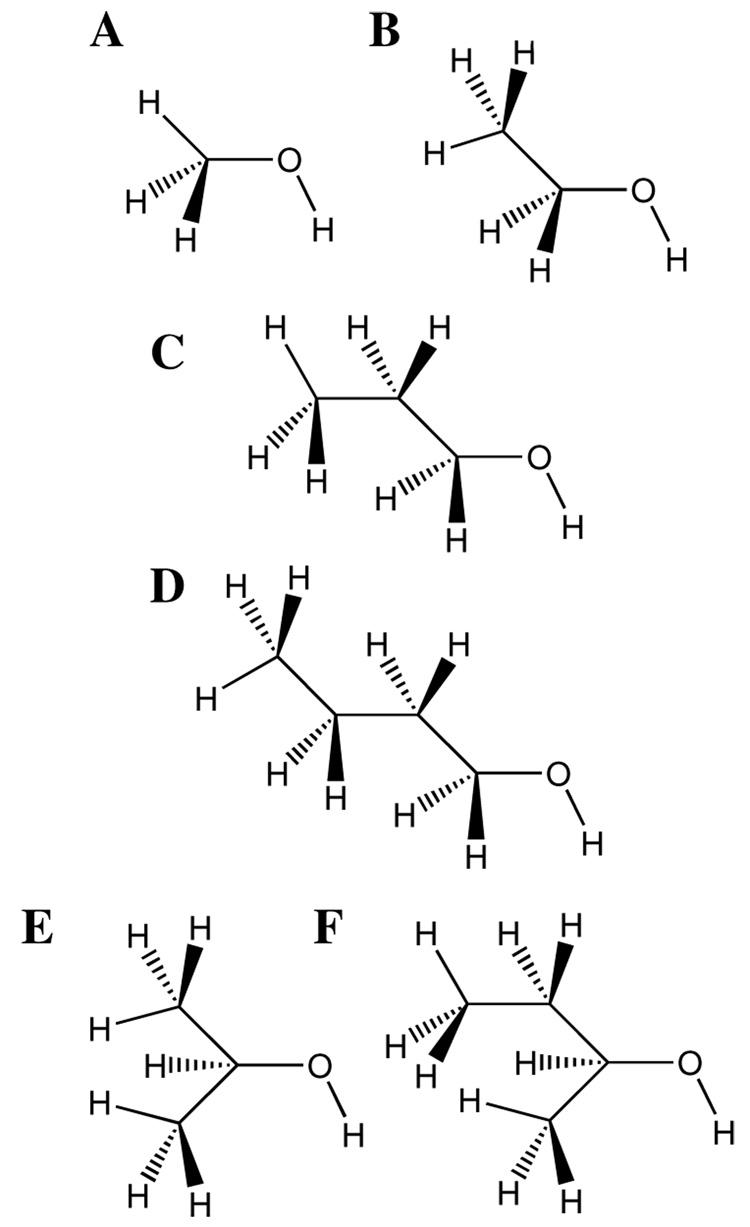
Figure 1.

Model compounds used in the parameter optimization. Primary alcohols A) methanol, B) ethanol, C) 1-propanol and D) 1-butanol and secondary alcohols E) 2-propanol (isopropanol) and F) 2-butanol.

The present work follows the hierarchical approach towards the optimization of force field parameters that was originally developed for the CHARMM all-atom biomolecular force field.¹¹ This work builds on the classical Drude polarizable models developed for water^{25, 26}, the alkane series,²⁷ aromatics²⁸ and ethers.²⁹ As before the optimization of all necessary parameters including atomic charges, atomic polarizabilities, internal equilibrium parameters, force constants, torsion potentials and Lennard-Jones terms is undertaken. In the polarizable alcohol series the alkyl group parameters are transferred directly from the alkanes with only the methyl group in methanol being partially optimized as described below.

Methods

The induced polarization framework employed in this work is based on the classical Drude oscillator model as described previously.³⁰ According to this model each non-hydrogen atom is described by two point charges q_core and δ connected by a harmonic spring with a force constant of k_D. The sum of the two point charges yields the partial atomic charge q_A associated with atom A (i.e., q_A = q_core + δ). The host atom in the Drude model is also the center of the Lennard-Jones (LJ) radius whereas the Drude particle typically does not carry LJ parameters (although LJ parameter can be assigned in principle). Placement of atom in an external field E causes a displacement of the charged Drude particle, which gives rise to an induced dipole µ=αE; the displacement (x) of Drude particles from their corresponding atomic centers in response to the external field is opposed by the restoring force of the harmonic spring F_harm=−k_Dx, which defines the polarizability α=δ²/k_D of an atom. When there are many polarizable atoms responding to a field E, the calculation of the total electrostatic interactions can be achieved by relaxing the charged Drude particles iteratively until self-consistency. Alternatively, in the case of MD simulations an extended Lagrangian may be applied allowing the treatment of the electronic degrees of freedom as dynamic variables.^{30, 31}

Electrostatic interactions of Drude particles with other charged centers involving 1,4 pairs and beyond are treated according to Coulomb’s Law as commonly used in classical force fields.³² 1,2 and 1,3 intramolecular electrostatic interactions between covalently connected atoms, which are typically turned off in additive models, are reintroduced in the polarizable model at the level of dipole-dipole interactions. Here, the Drude particles inherit the position index of their corresponding host atoms. The presence of 1,2 and 1,3 dipole interactions increases the internal polarizability of molecules as well as the anisotropy of that polarizability.³³ Effective inclusion of the 1,2 and 1,3 interactions requires their scaling to avoid polarization catastrophe. Scaling is performed using the approach of Thole^{34, 35} where the interaction energy of the induced dipoles on the atomic centers i and j is calculated according to the modified Thole scheme:

$$\frac{{\delta }_i{\delta }_j}{r_{\mathit{\text{ij}}}}\left[1-\left(1-\frac{{\overline{r}}_{\mathit{\text{ij}}}}{2}\right)·\text{exp}\left(-{\overline{r}}_{\mathit{\text{ij}}}\right)\right]$$ (1)

where the normalized distance is defined as

$${\overline{r}}_{\mathit{\text{ij}}}=a\frac{r_{\mathit{\text{ij}}}}{\sqrt[6]{{\alpha }_i{\alpha }_j}}$$ (2)

and r_ij is the distance between the interacting centers, α_i is the atomic polarizability of center i, and a is a Thole parameter with a default value of 2.6, originally selected to produce the correct polarizability anisotropy ratio of benzene.^{34, 35}

Optimization of the electrostatic parameters is performed using the FITCHARGE module in the program CHARMM^{10, 11} and is an extension of our previously published protocol.³⁶ Modifications include the placement of an additional “near” grid and the inclusion of virtual charged particles at the position of oxygen lone-pairs (LP).³³ The effective charge of the oxygen atom is moved entirely to the corresponding LP sites (two LPs per oxygen atom), while the polarizability is retained on the atomic center. Initial optimization of charges and polarizabilities was done by fitting to quantum mechanical (QM) electrostatic potential (ESP) maps. One “unperturbed” EPS map is calculated for the isolated molecule of interest and a number of additional “perturbed” maps are calculated in the presence of small point charges (0.5e) placed at different locations to probe the polarization response. Grids defining the ESP were placed on concentric surfaces at multiples of the van der Waals (vdW) radii of atoms. The perturbating point charges as required for the production of perturbed ESPs are placed along bonds, and at additional locations to approximate an isotropic distribution around the molecule, using the parameters listed in Table 1. In Table 1 the vdW scale factor indicates the distance of the Connolly surfaces from the atomic centers in multiples of the corresponding atomic vdW radius. The total number of points on each surface is a multiple of the “density factor”. The “distance to atoms” parameter does not allow placement of a perturbation ion or a grid point at a distance less than the specified value to any atom in the molecule. The “distance to perturbation ions” parameter prevents newly added perturbation ions being closer to other ions than the specified distance. Finally, “type” descriptor specifies the way the points are generated. The type “ions (bonds)” means that the perturbation ions are placed along vectors extended from covalent bonds while “ions (gaps)” places ions in vacant regions on a surface between the ions originally placed based on the bonds criteria. The type “grids” indicates placement of grid points. The present work extends our previous methodology by adding a layer (#1) of perturbation ions and a corresponding layer of grid points (#4) at a vdW scale factor of 1.3, thereby taking into account the electrostatic response at distances corresponding to direct hydrogen bonds, as described below. Further, an additional layer (#5) of grid points at distances corresponding to the separation of heavy atoms involved in hydrogen bonds was added.

Table 1.

Specification of Connolly surfaces for perturbation ion and grid point placement

Surface #	vdW scale factor	density factor	Dist. to atoms	Dist to pert. ions	Type
1a	1.3	5.0	0.0	0.0	Ions(bonds)
	1.3	5.0	1.4	2.0	Ions(gaps)
2	2.2	1.1	1.5	2.0	Ions(bonds)
	2.2	1.1	2.0	2.0	Ions(gaps)
3	4.0	0.1	2.0	2.0	Ions(bonds)
4a	1.3	6.0	0.0	2.0	Grids
5	2.2	1.1	1.0	2.0	Grids
6	3.0	1.3	1.0	2.0	Grids
7	5.0	0.6	1.0	2.0	Grids
8	6.0	0.2	1.0	2.0	Grids

^aOnly in vicinity of polar atoms

Initial guesses of the charges for ESP fitting were based on the CHARMM22 force field.¹¹ Initial values for the polarizabilities were obtained from the additive atomic polarizabilities of Miller³⁷ modified for the present non-hydrogen polarizability model, as described previously.³⁶ Fitting was performed on monomer geometries optimized at the MP2(fc)/6-31G(d) level of theory³⁸ using the Gaussian 03 package³⁹ with ESPs calculated using the B3LYP functional^40–44 with aug-cc-pVDZ basis set.⁴⁵ Gauche- and trans-conformations of ethanol and iso-propanol were included in the fitting. The positions of the LPs were determined by varying the LP geometry to minimize the RMS error between the QM and empirical ESPs and to reproduce the relative interaction energies of alcohols with water for different orientations.

QM calculations of alcohol-water complexes were done by constraining the geometry of the alcohols to the corresponding MP2(fc)/6-31G(d) optimized geometry and water geometry to that of SWM4-NDP model²⁵. The position of the water relative to the alcohol molecule was optimized at the MP2(fc)/6-31G(d) level of theory for the interaction distance, C-O…H_water angle, and H(O)…C-O…H_water torsion. Single point LMP2/cc-pVQZ^{46, 47} calculations were performed on the minimum energy geometry to obtain the interaction energy using the program Jaguar (Schrodinger Inc.) as previously described.⁴⁸ Water-alcohol orientations used in the present study are shown in Figure 2. Empirical alcohol-water interactions were performed on preliminarily relaxed geometry of alcohols with the water orientation obtained from corresponding QM calculations. Only the interaction distance was optimized in the empirical calculations with other geometrical parameters held fixed at their initial values.

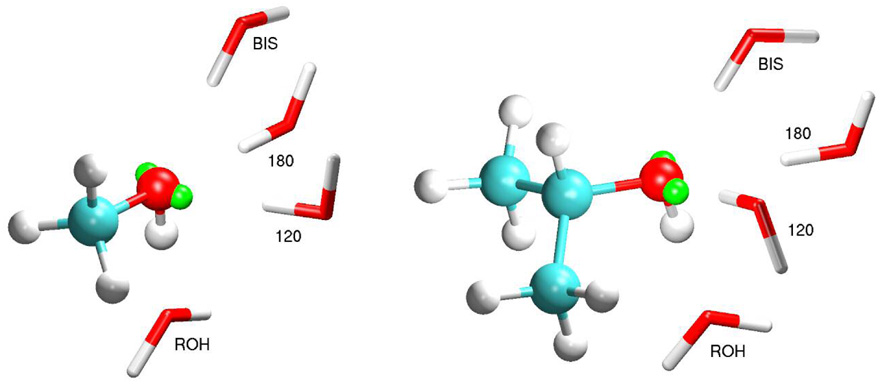
Figure 2.

Interaction orientations between water and the alcohols using methanol (left) and 2-propanol (right) as examples. Lone-pair sites are shown in green. BIS-orientation C-O-Hw angle is 115.8, 117.4, and 117.2° for methanol, ethanol, and isopropanol, respectively; 120-orientation C-O-Hw angle is 104.4, 108.3, and 105.1°, respectively; 120-orientation H(O)-C-O-Hw torsion is 108.0, 131.3, and 118.0°, respectively.

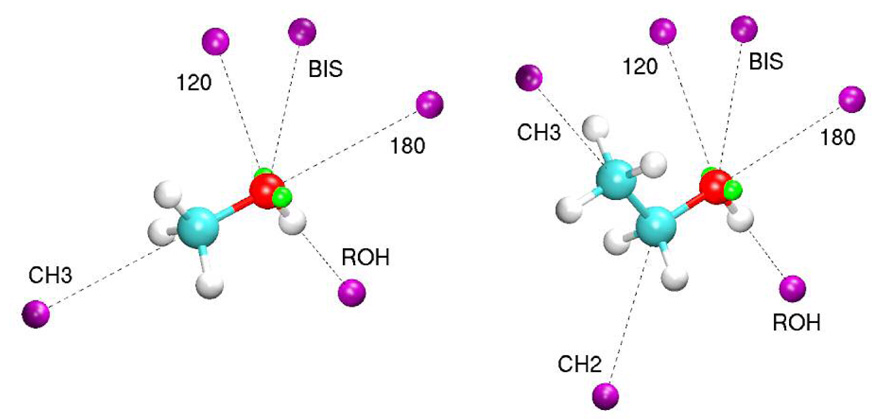
QM calculations of the alcohol complexes with rare gas atoms were performed using MP2(fc)/6-31G(d) optimized geometry of the corresponding alcohols. Relative position of rare-gas atom was adopted from alcohol-water interactions with additional positions added to probe the alkyl carbon atoms. Minimum interaction energies and distances for rare gas – alcohol complexes were determined using interaction distance scans with 0.01Å increments. Energy of the complex was evaluated at the MP3(fc)/6-311++G(3d,3p) level of theory for each point on the scan path.⁴⁹ The rare gas atom placement is illustrated in Figure 3.

Figure 3.

Interaction orientation of the rare gases with the alcohols methanol (left) and ethanol (right). Rare-gas atoms are shown in purple and lone-pair sites are shown in green.

Empirical force field calculations were performed with program CHARMM. Energy minimizations of model compounds in the gas phase were performed with the adopted basis Newton-Raphson minimizer (ABNR)^{10, 50} to a final RMS gradient of 10⁻⁵ kcal/(mol * Å). All gas phase calculations were performed using infinite cutoffs.

Equilibrium parameters and force constants associated with the bonds, valence and torsion angles were optimized targeting the mean values of geometric parameters from the survey of crystal structures⁵¹, QM geometries and QM vibrational spectra of the model compounds. The QM calculations were performed at the MP2/6-31G(d) level and a scale factor of 0.9434 was applied to vibrational modes to account for limitations in the level of theory.⁵² Second derivatives of energy with respect to atomic coordinates of real atoms were obtained numerically with position of Drude particle self-consistently adjusted to every change in coordinates of the real atoms. Potential energy decomposition analysis was performed using the MOLVIB utility⁵³ in CHARMM. Internal coordinate assignment was done according to Pulay et al.⁵⁴

Target data for optimization of the dihedral parameters were torsion energy profiles obtained from QM calculations. Dihedral angle scans were performed in 10° increments for the torsion angle with subsequent geometry relaxation performed at the MP2(fc)/6-31G(d) level, which was followed by single-point energy evaluation at the MP2/cc-pVTZ⁵⁵ level. A similar procedure was repeated in the force field calculations where the torsion angle of interest was scanned while other geometrical parameters were fully relaxed. Dihedrals were restrained to their target values using harmonic force constants of 10⁵ kcal/(mol * Ų) and energy minimizations were performed with ABNR method to RMS gradients of 10⁻⁵ kcal/(mol * Å). Empirical torsion parameters were optimized to minimize the difference between the potential energy profile and the MP2/cc-pVTZ data.

Molecular dynamics (MD) simulations of condensed phases were performed at a constant pressure of 1 atm with cubic periodic boundary conditions using the velocity Verlet integrator that includes treatment of Drude particles via an extended Langrangian.³⁰ The integration time step was 1 fs for both polarizable and additive simulations with temperatures maintained at 298.15 K using the Nose-Hoover thermostat⁵⁶ with a relaxation time of 0.1 ps applied to all real atoms. A modified Andersen-Hoover barostat^{30, 57} with a relaxation time of 0.1 ps was used to maintain the system at constant pressure. The SHAKE algorithm was used to constrain covalent bonds involving hydrogens.⁵⁸ Lennard-Jones (LJ) interactions were treated explicitly out to 12 Å with force switch smoothing⁵⁹ applied over the range of 10 to 12 Å. Nonbond pair lists were maintained out to 14 Å and the long range correction for LJ interactions⁶⁰ was applied in the condensed-phase simulations. Electrostatic interactions were treated using particle mesh Ewald (PME) summation⁶¹ with a coupling parameter 0.34 and 6^th order spline for mesh interpolation. The extended Lagrangian double-thermostat formalism³⁰ was used in all polarizable MD simulations where a mass of 0.4 amu was transferred from real atoms to the corresponding Drude particles. The amplitude of Drude oscillations was controlled with a separate low-temperature thermostat at 1 K to simulate near-SCF conditions.³⁰

Pure solvent MD simulations included 128 alcohol molecules. To obtain convergent results 5 independent MD simulations were run for 250 ps with different initial velocities being assigned to the particles. The first 50 ps of the simulations were treated as equilibration and the final 200 ps were used for the analysis. Averages were obtained from the 5 independent simulation averages which were also used to calculate the standard errors for the calculated properties. Heats of vaporization, ΔH_vap and molecular volume V_m were determined following the standard procedure.²⁷ Gas-phase simulations were performed using Langevin dynamics in the SCF regimen with infinite cutoffs for nonbonded interactions. The friction coefficient of 5 ps⁻¹ was applied to all atoms except for Drude particles. The gas-phase simulations were performed on all 128 individual monomers extracted from the respective equilibrated alcohol box from the condensed-phase MD simulations. The simulations were run for 250 ps for each molecule with the resultant energies obtained from last 200 ps. The gas-phase energy was the average of the averages from the 128 monomer simulations.

Radial distribution functions, isothermal compressibilities, and self-diffusivities were calculated for the alcohols from condensed-phase MD trajectories. Isothermal compressibilities were calculated from

$${\beta }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial P}\right)}_T=\frac{\langle \partial V^2\rangle }{{\mathit{\text{Vk}}}_{B}T}$$ (3)

according to Klauda et al.,⁶² where V is the volume, 〈δV²〉 is the volume fluctuation, and k_B is Boltzmann’s constant. The slope of the mean squared displacement versus time was used to determine the self-diffusivity for the periodic boundary condition, D_PBC. The self-diffusivity was corrected for system-size effects using the hydrodynamic model of Yeh and Hummer⁶³ of a particle surrounded by a solvent with viscosity, η,

$$D_S=D_{\mathit{\text{PBC}}}+\frac{k_{B}T\xi }{6\pi \eta L}$$ (4)

where L is the cubic box length and ξ=2.837297. The shear viscosities were taken at their experimental values.

Free energies of aqueous solvation (relative to gas phase), ΔG_sol, were obtained as a sum of nonpolar, ΔG_np, and electrostatic, ΔG_elec, contributions via a free energy perturbation (FEP) approach^{64, 65} according to the step-by-step staged protocol developed by Deng and Roux.⁶⁶

$$\mathrm{\Delta }{G}_{\text{sol}}=\mathrm{\Delta }{G}_{\text{np}}+\mathrm{\Delta }{G}_{\text{elec}}$$ (5)

The nonpolar contribution was obtained from the perturbation formula^{64, 65}, where the free energy change ΔG, corresponding to the change in the potential energy from U_i to U_j, can be calculated as an average over the ensemble of configurations generated with the potential energy U_i:

$$\mathrm{\Delta }G=-kT\text{ln}{\langle \text{exp}\left(-\frac{U_j-U_i}{kT}\right)\rangle }_{\left(U_i\right)}$$ (6)

The nonpolar contribution was calculated with all atomic and Drude charges of the solute set to 0. In the protocol the nonpolar term was decomposed into dispersive, U^dis, and repulsive contributions, U^rep, using the Weeks, Chandler, and Andersen scheme.⁶⁷

$$U_{\text{uv}}^{\text{np}}\left(X,Y,\xi \right)=U_{\text{uv}}^{\text{rep}}+\xi U_{\text{uv}}^{\text{dis}}\left(X,Y\right)$$ (7)

The dispersive contribution was calculated using a linear coupling scheme with the coupling parameter ξ such that the interaction energy U_uv(X,Y) between solute u with coordinates X and solvent v with coordinates Y was calculated as ξ was changed from 0 to 1 in increments of 0.1. The repulsive term, due to its sharp r¹² dependence, cannot be treated accurately via a linear perturbation and instead was transformed into a soft-core potential. It was calculated in multiple stages with a staging parameter s. The staging parameter s was set to 0.0, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0. The free energy contributions from simulations using different staging parameters were summed. The weighted histogram analysis method (WHAM)⁶⁸ was used to obtain the dispersive and repulsive contributions to free energies from the simulations. The electrostatic component of the free energy of hydration was computed by decoupling a molecule of the solute from the solvent by thermodynamic integration (TI)^69–71:

$$\mathrm{\Delta }{G}_{\mathit{\text{elec}}}={\displaystyle \underset{0}{\overset{1}{\int }}d\lambda \langle \frac{\mathit{\text{dU}}\left(\lambda \right)}{d\lambda }\rangle }$$ (8)

where the coupled state (λ=1) corresponds to a simulation where the solute is fully interacting with the solvent and the uncoupled state (λ=0) corresponds to a simulation where the solute dose not interact with the solvent. In the perturbations λ was changed from 0 to 1 in 0.05 increments with a 0.1 window size and half of the window overlapping with the previous window. Each contributing term to the free energy was obtained as a difference in the free energy of the solute in water and in vacuum.

For the free energy calculations gas-phase simulations were performed using Langevin dynamics with SCF Drudes as described above. Aqueous phase calculations were performed with the alcohol molecule solvated in a box of 250 SWM4-NDP polarizable water²⁶ molecules and restrained to the center of mass of the box by a harmonic potential with a force constant of 0.5 kcal/(mol * Ų) acting on all solute atoms except Drudes. The system was then subjected to a 110 ps NPT simulation at 298.15 K and 1 atm pressure at each value of the coupling/staging parameter. The FEP analysis was performed on the final 100 ps of these dynamics runs. The reported free energy value was averaged over five independent runs each performed with individual seed numbers. Corresponding non-polarizable simulations were performed using the TIP3 water model.⁷² During free energy calculation the molecular dynamics simulations did not include long-range correction (LRC) for dispersion forces. However, the latter were estimated from 50 ps MD simulations of a single alcohol molecule placed in a box of 250 water molecules. The MD calculations were performed using the protocol described for simulations of the condensed phase. The energy due to LRC was calculated for the fixed configuration of the solute-solvent system as difference of the van der Waals energy contribution calculated using 10 and 30Å non-bonded cutoffs and averaged for 30 snapshots each written at 1 ps time intervals.

The static dielectric constants ε of the neat alcohols were calculated from the total

$$\epsilon ={\epsilon }_{\mathrm{\infty }}+\frac{4\pi }{3\langle V\rangle k_{B}T}\left(\langle {\mathrm{M}}^2\rangle -{\langle \mathrm{M}\rangle }^2\right)$$ (10)

dipole moment M fluctuations of the box;^{25, 30, 73} <V> is the average volume of the box, and ε_∞ is the high-frequency dielectric constant. Time series of M were obtained from 5 independent simulations of 5 ns using data from the last 4 ns of each simulation following the previously discussed protocol.²⁷ The high-frequency contribution ε_∞, representing the dielectric constant at the limit of infinitely high frequency of light, is estimated from the Clausius-Mossotti equation:

$$\frac{{\epsilon }_{\mathrm{\infty }}-1}{{\epsilon }_{\mathrm{\infty }}+1}=\frac{4\pi \alpha }{3V_m}$$ (11)

where α is gas-phase molecular polarizability; V_m is molecular volume.

Results and Discussion

Optimization of the alcohol parameters targeted the compounds methanol, ethanol, and 2-propanol (isopropanol), with greater emphasis placed on ethanol for the primary alcohols. The derived parameters were then validated on 1-propanol, 1-butanol, and 2-butanol to test their transferability. This was followed by additional optimization on the oxygen LJ parameters for 1-propanol and 1-butanol to obtain better agreement with experimental molecular volume and enthalpy of vaporization (see below). The molecules, which include both primary and secondary alcohols, are shown in Figure 1. Hydroxyl groups located on tertiary carbon atoms are not common in biological macromolecules and, therefore, were not considered in this study. For the alcohol series the aliphatic carbon and hydrogen parameters previously determined in our laboratory²⁷ were applied directly with the exception of the electrostatic parameters on CH_(1–3) fragments directly adjacent to the oxygen and of the LJ parameters for the methyl group in methanol. The remaining parameters were optimized as part of the present work.

The parameter optimization was performed using the following protocol. The electrostatic part of the polarizable model was initially derived from fitting to QM unperturbed and perturbed ESP maps with the geometry of the model compounds being fixed at their corresponding QM values. The internal parameters were initially taken from the additive CHARMM22 force field. Next, optimization of the LJ parameters was undertaken based on condensed-phase simulations and rare gas - model compound interactions. After the LJ parameters were initially determined (within 5% of target heat of vaporization and molecular volume) the internal parameters were updated to reproduce target geometries and vibrational spectra. Next the torsion parameters were optimized to reproduce the QM dihedral potential energy surfaces. After the first round of optimization was completed the atomic charges and polarizabilities were manually adjusted to reproduce QM data on interactions with water as well as dipole moments and condensed phase properties. The LJ parameters were then reoptimized and the internal parameters, including the dihedral parameters, were correspondingly updated. These steps were repeated until convergence.

Intramolecular parameters

Target data for the equilibrium bonded parameters were intramolecular geometries obtained from surveys of the Cambridge Crystallographic Database.⁵¹ Structural data involving hydrogen atoms were obtained from MP2(fc)/6-31G(d) gas-phase optimized geometries. Equilibrium geometries of the model compounds for the final parameters are summarized in Table 2 along with the corresponding target data. The empirical model shows good overall agreement with the target data. The maximum deviation is 0.04 Å for C-C bond (C-COH) and 0.7 degrees for C-C-C angle. The C-C bond was not optimized due to adopting the hierarchical approach for parameter development requiring the parameters for the previously defined alkane atom types be preserved. Such constraint is an important precondition for maintaining transferability of the developed parameters and it also helps reduce the number of parameters to be optimized.

Table 2.

Equilibrium geometries of alcohols in the trans conformations^a

	Methanol		Ethanol		iso-Propanol		RMSD
	Drude	Target	Drude	Target	Drude	Target
C-Ob	1.43	1.40 (0.05)	1.43	1.42 (0.04)	1.43	1.43 (0.03)	0.02
C-Cc,e	-	-	1.53	1.48 (0.05)	1.53	1.50 (0.03)	0.04
O-Hd	0.97	0.97	0.97	0.97	0.97	0.97	0.00
C-Hd	1.11	1.09	1.11	1.10	1.12	1.09	0.02
C-C-Ob	-	-	111.4	111.5 (3.2)	110.4	109.7 (2.8)	0.5
C-C-Cb,e	-	-	-	-	113.2	112.5 (2.6)	0.7
C-O-Hc	107.6	107.4	107.5	107.6	106.7	106.6	0.1
H-C-Oc	109.9	110.3	110.7	110.9	103.6	103.8	0.3
H-C-Hc,d	109.1	108.6	107.3	107.6	-	-	0.4

^aBond lengths, Å; Valence angles, degrees; data are shown for carbon atom adjacent to oxygen.

^bCambridge crystallographic survey based on 2037 hits for methanol, 913 hits for ethanol, and 130 hits for iso-propanol; CSD version 5.27 (Nov 2005); standard deviations are shown in parentheses.

^cMP2(fc)/6-31G(d) gas-phase optimized geometry.

^dNot optimized; corresponding parameters were directly transferred from the polarizable alkanes.

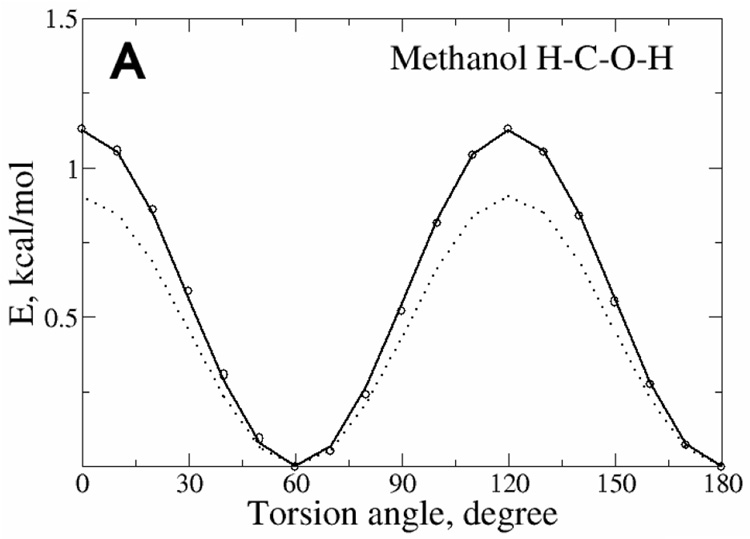
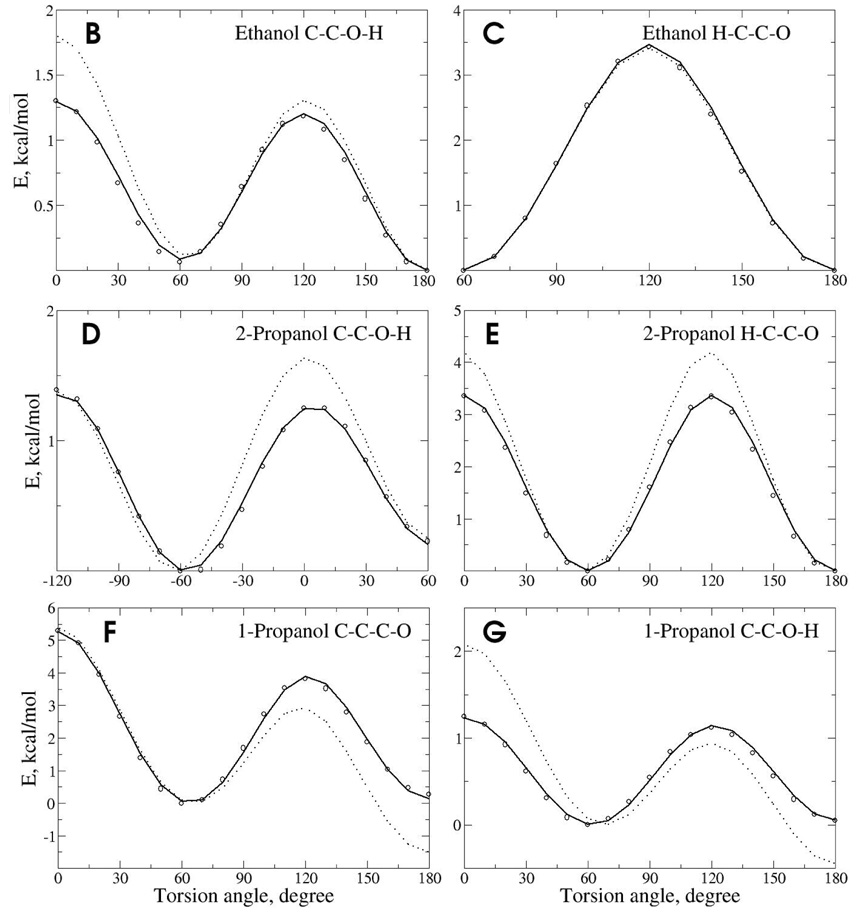
Reproduction of vibrational spectra along with potential energy surfaces for rotation about selected dihedrals was used to optimize the force constants. Presented in Table S1, S2 and S3 of the supporting information are the Drude and target QM vibrational spectra for methanol, ethanol and 2-propanol. Inspection of those results shows the agreement of both the magnitudes of the frequencies and the assignments to be excellent. The largest difference, the CO torsion in the IR-spectrum of methanol, was due to final adjustment of the associated parameter based on the energy surface, as follows. Final optimization of the dihedral parameters was based on the reproduction of QM energy surfaces. Shown in Figure 4 are the surfaces for the three molecules. It is evident that the Drude model satisfactorily reproduces the QM surfaces and is significantly better than CHARMM22, which was originally optimized targeting lower level QM data. The level of agreement of the Drude model for both the vibrational and dihedral surfaces indicates that the alcohols will sample the correct intramolecular conformations during MD simulations.

Figure 4.

Potential energy surfaces for rotation of selected dihedrals in methanol (A), ethanol (B and C), 1-propanol (D and E) and 2-propanol (F and G). Data is included from the QM (circles), Drude (solid line) and CHARMM22 (dotted line) models.

Electrostatic model

Atoms in classical molecular mechanics are traditionally treated as point charges. This leads to a certain degree of arbitrariness in the derivation of partial atomic charges from electrostatic fitting that cannot be eliminated due to the inherent ambiguities in partitioning the electron distribution with respect to a set of atomic centers. Therefore the point charge fitting to a QM electrostatic potential is often conducted under restraints enforcing that the derived charges follow chemical intuition.⁷⁴ The CHARMM additive force field¹¹ was developed according to a slightly different methodology. Because of the aforementioned limitations in the fitting of atomic charges to electron distributions, plus additional uncertainty as to how well gas-phase fitted charges would work in the condensed-phase, the additive CHARMM force field treated the atomic charges as adjustable parameters. These terms were then optimized to reproduce energetics and geometries of test molecules interacting with water along with condensed phase properties. This approach was successfully validated in the development of CHARMM22 and CHARMM27 additive force fields.^{11, 75} In the classical Drude polarizable model the number of electrostatic parameters has increased due to the inclusion of atomic polarizabilities. To address this additional complexity the Drude electrostatic parameter determination protocol in CHARMM has been extended to include ESP fitting.³⁶ However, as the final goal of the resultant force field is the reproduction of condensed phase properties as well as atomic details of gas phase interactions with water, manual corrections of the ESP fitted values are considered acceptable.

An additional factor that has to be taken into account during the optimization of electrostatic parameters is the placement of virtual charged particles representative of oxygen lone pairs (LP). Inclusion of LPs was motivated by the inability of force field models without them to accurately reproduce the angular dependence of ESP maps in the case of hydrogen bond acceptors.^{33, 76} The charge on LP sites and their geometry were initially determined from the ESP fitting procedure to reduce the RMS error during fitting. The resulting fitted charges, polarizabilities and LP geometry were then tested on interactions with water and LP positions were further adjusted to better reproduce the local anisotropy of interactions with water. Because calculation of the interactions with water requires LJ parameters on the hydroxyl the CHARMM22 values were used as an initial guess. In later stages of the optimization the LP position and atomic charges were reevaluated based on interactions with water each time a new set of oxygen LJ parameters became available from the condensed-phase optimization (see below). This elaborate optimization procedure was performed for ethanol only with the derived LP positions applied without change to the other alcohols. The final oxygen lone pair position were as follows: distance between oxygen atom center and lone pair center = 0.35 Å; C-O-LP angle = 110°; virtual torsion angle H(O)-C-O-LP = ±91°.

Placement of water molecules around the hydroxyl group in the primary and secondary alcohols is illustrated on Figure 2 and the interaction energies and distances are presented in Table 3 and Table 4, respectively, for both the additive and polarizable models. Additive CHARMM22 force field results are presented as a representative example of those for an additive alcohol force field. Examination of the CHARMM22 energy differences, ΔE, show them to be significantly more favorable than the QM target data and the balance amongst the interaction orientations to be poor with the differences ranging from −0.6 to −2.2 kcal/mol for ethanol (Table 3). The more favorable interaction energies are expected given the need to overpolarize the effective fixed charges in the additive model to account for the lack of explicit polarizability. However, the limitation in the balance of the interactions for different placements of water molecule around the test molecule is due to limitations in the anisotropy of the electrostatic representation. This problem was also seen in the Drude model without LPs.³³ Therefore the Drude model of alcohols was extended to include LPs on the oxygen atom, yielding a more anisotropic electrostatic model. This anisotropy was further extended by assigning anisotropic polarizability on the oxygen atom. This anisotropic polarizability was introduced by treating the Drude force constant (k_D) of the oxygen as a tensor, as previously described.³³ The X-axis of the tensor is defined along C-O bond; the Y-axis goes through the oxygen atom perpendicular to the plane created by C-O-H atoms; the Z-axis is orthogonal to the X and Y axes. Increased stiffness of the Drude constant along the C-O bond (X-axis) reduces the overestimation of alcohol-water interaction in the 180-orientation (e.g. 180 in Table 3 for the C22 models). In addition, reducing the force constant along the Y-axis effectively increases oxygen polarizability along the lone-pair directions (e.g. 120 in Table 3 and Figure 2). More details of the impact of the inclusion of LPs and anisotropy on methanol and other molecules with hydrogen bond acceptors is presented in Harder et al.³³ Thus, by increasing the force constant along the X direction and decreasing it along the Y-axis leads to improvements in the balance of interactions of the hydroxyl with water. The final values of the tensor are k_Dxx=600, k_Dyy=400, k_Dzz=500 kcal/(mol * Ų) with the same anisotropic Drude constants used for all the alcohols. In addition, the use of anisotropic polarizability leads to a more accurate representation of the polarization response around the hydroxyl group.³³

Table 3.

Alcohol-water minimum interaction energy differences relative to QM data.

	EQMa	ΔEC22b	ΔEDrude2	ΔEC22, %	ΔEDrude, %	RRMSC22c	RRMSDrudec
MeOH						0.44	0.19
BIS	−4.40	−1.83	−0.34	42	8
180	−2.09	−2.29	−0.71	110	34
120	−4.90	−1.12	−0.22	23	4
ROH	−4.12	−2.09	−0.33	51	8
EtOH						0.63	0.11
BIS	−4.82	−1.72	−0.70	36	15
180	−2.33	−2.23	−0.50	96	21
120	−4.80	−0.61	−0.52	13	11
ROH	−4.24	−2.07	−0.39	49	9
1-PrOH						0.69	0.12
BIS	−5.01	−1.38	−0.29	28	6
180	−2.64	−1.86	−0.13	70	5
120	−5.09	−0.21	−0.01	4	0
ROH	−4.40	−1.95	−0.31	44	7
2-PrOH						0.93	0.21
BIS	−4.68	−1.59	0.25	34	−5
180	−2.46	−2.31	−0.24	94	10
120	−4.76	0.16	0.13	−3	−3
ROH	−3.99	−1.83	0.28	46	−7

Energies in kcal/mol. See Figure 2 for interaction orientations. Results for the polarizable model include off-diagonal (i.e. NBFIX) O_alcohol…O_water LJ parameters.

^aQM calculations are performed at LMP2/cc-pvQZ//MP2/6-31G* level of theory.

^bΔEⁱ _model = Eⁱ _int (model) − Eⁱ _int(QM), where Eⁱ _int(model) is interaction energy corresponding to CHARMM22 or Drude models for i^th orientation.

^cRelative RMS error calculated for the difference ΔEⁱ _alcohol − ΔE^ave _alcohol, where ΔE^ave _alcohol is the average difference between model and QM calculations for a given alcohol molecule.

Table 4.

Alcohol-water minimum interaction distance differences relative to QM data.

	RQMa	ΔRC22b	ΔRDrudeb	ΔRC22,%	ΔRDrude,%	RRMSC22c	RRMSDrudec
MeOH						0.05	0.05
BIS	1.98	−0.14	−0.08	−7	−4
180	2.12	−0.23	−0.14	−11	−7
120	1.95	−0.11	−0.09	−6	−5
ROH	1.95	−0.13	−0.01	−7	−1
EtOH						0.06	0.04
BIS	1.98	−0.12	−0.09	−6	−5
180	2.12	−0.24	−0.13	−11	−6
120	1.97	−0.08	−0.10	−4	−5
ROH	1.95	−0.13	−0.02	−7	−1
1-PrOH						0.06	0.04
BIS	1.98	−0.12	−0.09	−6	−5
180	2.12	−0.24	−0.13	−11	−6
120	1.97	−0.08	−0.09	−4	−5
ROH	1.95	−0.13	−0.02	−7	−1
2-PrOH						0.07	0.04
BIS	1.97	−0.13	0.00	−7	0
180	2.10	−0.23	−0.04	−11	−2
120	1.96	−0.05	−0.01	−3	−1
ROH	1.97	−0.09	0.06	−5	3

Distance in Å, See Figure 2 for interaction orientations. Results for the polarizable model include off-diagonal (i.e. NBFIX) O_alcohol…O_water LJ parameters.

^aQM calculations are performed at LMP2/cc-pvQZ//MP2/6-31G* level of theory.

^bΔRⁱ _model = Rⁱ _min(model) − Rⁱ _min(QM), where Rⁱ _min(model) is minimum energy distance corresponding to CHARMM22 or Drude models for i^th orientation.

^cRelative RMS error calculated for the difference ΔRⁱ _alcohol − ΔR^ave _alcohol, where ΔR^ave _alcohol is the average difference between model and QM calculations for a given alcohol molecule.

As discussed above the additive model systematically overestimates the water-alcohol interactions energies (i.e. too favorable) and there is an imbalance in the treatment of the energies as a function of orientation. These effects are indicated by the large negative ΔE_C22 values in Table 3 for the former and the greater values of the RRMS_C22 values for the latter in comparison with the polarizable model. In the Drude model both of these problems are largely alleviated. There is still a tendency for the interaction energies to be slightly too favorable, though the magnitude is generally much less than with the additive model. While such a problem may have contributions from the level of theory used in the ab initio calculations, the need to overestimate the interaction energies was necessary to obtain the correct pure solvent properties (see below). It should be noted that the data in Table 3 and Table 4 represent the use off diagonal LJ terms for the O_hydroxyl—O_water interactions, as discussed in the following section. Ideally, the need to overestimate the gas phase interactions with water is not required for a polarizable model; future investigations will address this result. With respect to the balance of the interactions, the Drude model behavior is satisfactory, with the tendency to overestimate the 180-orientation significantly decreased with respect to the additive model. Thus, the polarizable alcohol model that incorporates oxygen atom charge anisotropy (due to LPs) and oxygen polarization anisotropy more accurately reproduces the change in interaction energy with water as a function of orientation as compared to the additive model.

Due to parameter correlation, the optimization of the electrostatic terms has to be repeated whenever the LJ parameters are changed, because new LJ parameters alter the interactions with water. Therefore, the LJ optimization from condensed phase simulations and electrostatic model optimization steps are repeated until convergence as judged by the agreement with the target condensed phase data typically being 2% or less. This iterative optimization procedure leads to maximizing agreement with the condensed phase properties while gas phase interactions are sacrificed to some extent. However, inclusion of the water interaction data assures that the model satisfactorily describes atomic details of hydrogen bonding as discussed above, an attribute that is anticipated to have paramount influence on the utility of the model in biomolecular simulations.

As mentioned above, small corrections to the ESP fitted charges were necessary during the parameter optimization. The manual adjustment of charges addresses two issues. First, it circumvents the present limitation that the ESP fitting procedure be applied to only one test molecule at a time (although simultaneous fitting of multiple conformations is performed in this work). Ideally, for a series of compounds for which transferable parameters are desired, they all should be fit simultaneously, including the application of equality restraints on those groups of atoms that should be transferable (e.g. the hydroxyl O and H atoms for the primary alcohols). The second issue is related to the requirement that the derived transferable charges and polarizabilities should ultimately reproduce as correctly as possible the interaction energies of the model compounds with water. Conceivably, one could implement an extended global optimization procedure simultaneously including the ESP for a set of molecules in multiple conformations as well as their interactions with water molecules in specific hydrogen binding configurations to achieve such goal. However, it is not trivial to perform such global optimization with all the different target data weighted appropriately. For the sake of simplicity, in the present work manual adjustment of the electrostatic parameters was performed, addressing the two issues in two steps. To evaluate the robustness of this approach as well as the transferability of the parameters additional calculations were performed on alcohols not included in the training set.

Another modification to the ESP fitting procedure³⁶ is the addition of several new Connolly surface layers for placement of perturbation ions and grid points. This was motivated by the inability of the published procedure to yield an electrostatic model that reproduced condensed-phase properties of alcohols. Application of the original approach produced electrostatic models that significantly (about 2 kcal/mol) underestimated the enthalpy of vaporization of ethanol (experimental value 10.11 kcal/mol), such that LJ parameter optimization could not correct the deficiency of the derived charge model. Comparison of the hydroxyl charges for the additive CHARMM22 (q_O=−0.66; q_H=0.43) with those derived using the original³⁶ grid (q_O=−0.436; q_H=0.312) indicates substantial underestimation of polarity of the hydroxyl group, leading to underestimation of the electrostatic contribution to the enthalpy of vaporization. To correct for this deficiency the fitting protocol was extended to include an additional “near” grid and perturbation ions in the vicinity of polar atoms thereby increasing the contribution of polar atoms in ESP fitting. The location of this grid is shown in Figure 5. The ethanol charges derived from the extended grid fitting procedure (q_O=−0.462; q_H=0.355) show an increased local dipole of the hydroxyl group and indeed allowed identification of LJ parameters that yielded satisfactory condensed-phase properties. Despite the improvement brought by the near grid the fitting procedure gave different charges for methanol, ethanol, and 2-propanol (Table 5), whereas to enforce the parameter transferability a single set of charges was required. Therefore, the fitted charges and polarizabilities were subjected to manual adjustment, leading to the final optimized charges for alcohols of q_O=−0.46 (q_LP=−0.23); q_H=0.36, which are quite close to the ESP fitted values. Basically, the ESP fitting provided a good initial guess for the electrostatic model although empirical adjustment was required to derive the final fully balanced electrostatic model.

Figure 5.

Image of the additional Connolly surfaces around methanol at vdW scale factors of 1.3 and 2.2. See Table 1 for details of all grid surfaces and perturbation ion positions used in the electrostatic parameter fitting.

Table 5.

ESP Fitted atomic charges (q) and polarizabilities (α) of the model compounds

Atom	Methanol		Ethanola		2-Propanola
	q	α	q	α	q	α
O	0.000	0.90	0.000	0.44	0.000	0.99
Lone-pair	−0.242	0.00	−0.231	0.00	−0.223	0.0
H (O)	0.352	0.00	0.355	0.00	0.365	0.0
C (O)	−0.006	1.92	−0.021	1.45	−0.003	1.08
H (CO)	0.046	0.00	0.064	0.00	0.084	0.00
Calk (CH2)	n/a	n/a	n/a	n/a	n/a	n/a
Halk (CH2)	n/a	n/a	n/a	n/a	n/a	n/a
Calk (CH3)	n/a	n/a	−0.18	2.05	−0.18	2.05
Halk (CH3)	n/a	n/a	0.06	0.00	0.06	0.00

n/a indicates not applicable

^aGauche- and trans-conformations were fitted simultaneously.

The final electrostatic parameters are presented in Table 6. Two additional adjustments were made to the electrostatic model prior to finalization. As discussed previously,^{25, 26} it appears to be necessary to empirically scale gas phase polarizabilities by a factor smaller than 1.0 to yield accurate properties of polar molecules for the condensed phase. This was necessary for the SWM4-NDP water model and is applied to account for increased Pauli exclusion that occurs in the condensed phase due to surrounding molecules in the environment over that in the gas phase. Further support for the reduced polarizabilities are studies on macromolecules in the condensed phase, where unscaled values can lead to polarization catastrophe.^{25, 77–79} Accordingly, the polarizabilities of aliphatic moieties in the alcohols were scaled by 0.7 consistent with the scaling applied to the SWM4-NDP water model. This yielded a polarizability of 1.4 for the CH₃ group (alkane value 2.05) and 1.2 for CH₂ group (alkane value 1.66). A sp3 carbon atom is considered an alkane type if it is not covalently bound to a heteroatom. The electronic properties of carbon atoms directly connected to heteroatoms are influenced by the electronegative character of such atoms and, therefore, are included in ESP fitting. Therefore, the polarizability of the carbon atom connected to oxygen was taken as the average from the ESP fitted values for methanol, ethanol, and 2-propanol and scaled by 0.7 giving the final polarizability value of 1.0. The oxygen atom was treated differently. Here the polarizability was set to the Miller value of 1.0³⁶ and not scaled as the unscaled value was required to reproduce the dipole moments, the interactions with water, and the condensed phase properties all in the context of enforcing transferability across the alcohols studied. Importantly, tests indicated that the oxygen polarizability was not causing electrostatic collapses in either the pure solvent or aqueous environment MD simulations.

Table 6.

Final atomic charges (q) and polarizabilities (α) of the model compounds

Atom	Methanol		Ethanol		2-Propanol		1-Propanol		2-Butanol
	q	α	q	α	q	α	q	α	q	α
O	0.00	1.0	0.00	1.0	0.00	1.0	0.00	1.0	0.00	1.0
Lone-pair	−0.23	0.0	−0.23	0.0	−0.23	0.0	−0.23	0.0	−0.23	0.0
H (O)	0.36	0.0	0.36	0.0	0.36	0.0	0.36	0.0	0.36	0.0
C (O)	−0.14	1.0	−0.06	1.0	0.00	1.0	−0.06	1.0	0.00	1.0
H (CO)	0.08	0.0	0.08	0.0	0.10	0.0	0.08	0.0	0.10	0.0
Calk (CH2)	n/a	n/a	n/a	n/a	n/a	n/a	−0.12	1.2	−0.12	1.2
Halk (CH2)	n/a	n/a	n/a	n/a	n/a	n/a	0.06	0.0	0.06	0.0
Calk (CH3)	n/a	n/a	−0.18	1.4	−0.18	1.4	−0.18	1.4	−0.18	1.4
Halk (CH3)	n/a	n/a	0.06	0.0	0.06	0.0	0.06	0.0	0.06	0.0

n/a indicates not applicable.

Dipole moments for the final electrostatic models are shown in Table 7 along with CHARMM22 and target experimental and QM values. The fixed-charge additive CHARMM22 values are approximately 44% larger than the target values, which is necessary for the additive model to reproduce condensed phase properties. The agreement with experimental gas-phase dipole moments is improved in the polarizable model; however, the values are still overestimated by 10%. This is consistent with the polarizable model yielding more favorable interactions energies with water (Table 3) as required to reproduce the condensed phase properties throughout the alcohol series. A similar approach was utilized by Gao¹⁸ in development of the PIPF polarizable model for alcohols by treating the dipole moment as an adjustable parameter to improve agreement with condensed-phase properties and is necessary to obtain the targeted condensed phase properties as discussed below.

Table 7.

Dipole moments for alcohols in the trans-conformation

Alcohol	µ (C22)	µ (Drude)	µ (exp)	µ (QM)	Δµ (C22), %	Δµ (Drude), %
MeOH	2.38	1.83	1.70	1.72	40	8
EtOH	2.36	1.81	1.71	1.63	38	6
2-PrOH	2.43	1.87	1.58	1.73	54	18
2-BuOH	2.42	1.79	…	1.76	38	2
1-PrOH	2.35	1.82	1.55	1.54	52	17
1-BuOH	2.36	1.80	1.66	1.60	42	8
Average	n/a	n/a	n/a	n/a	44	10

Units in Debye. QM dipole moments at the MP2(fc)/aug-cc-pVQZ// MP2(fc)/6-31G(d) level. Percent differences with respect to the experimental data. Experimental data from ⁸⁷.

Final atomic charges and polarizabilities, presented in Table 6, represent a balance required to reproduce target data of all alcohols throughout the series with primary importance in reproducing condensed-phase properties. Grid scans (Tables S8, S9 and S10, Supporting Information) of point charges and atomic polarizability parameters performed in the vicinity of the optimized parameter values confirm their optimal choice. Attempts to improve the agreement with the target data through variations of the charges do show improvement for individual properties but the overall agreement with the multiple target properties considered becomes poorer. For example, decreasing the value of point charges followed by a corresponding increase in atomic polarizabilities would improve agreement with gas-phase dipole moment, but it would also negatively impact the already too favorable dielectric susceptibility of 1-butanol. Therefore, the current electrostatic parameters represent a balance for the entire alcohol series within the limitations of a transferable parameter set for the hydroxyl group. Such a constraint is a necessary prerequisite for subsequent transfer of the developed parameters to corresponding fragments of biological macromolecules.

Lennard-Jones parameters

Optimization of LJ parameters represents the most difficult aspect of empirical force field development as this term impacts the strength of ionic and hydrogen bond interactions as well as dispersion types of interactions. Adjustment of the LJ parameters was performed to reproduce experimental molecular volumes and enthalpies of vaporization of the neat alcohols, with the relative values of the LJ parameters checked via interactions with rare gases, as previously performed.⁴⁹ All alkyl groups were constrained to the previously determined alkane LJ values²⁷ and the polar hydrogen LJ parameters were constrained to a well depth of 0.01 kcal/mol and radius, R_min/2, of 0.4 Å. Such LJ parameters on the polar H introduce a repulsive potential on the hydrogen atom to diminish the possibility of overpolarization during hydrogen or ionic bonding interactions. Based on these assumptions only the oxygen LJ parameters were optimized subject to the constraint that the same oxygen LJ parameters were to be utilized throughout the alcohol series, with the only exception being the LJ parameters of the methyl group in methanol. This strategy was selected to facilitate parameter transferability to a biomacromolecular force field and to limit the overall number of atom types in the force field. However, such a limitation will diminish the quality of the fit for the individual alcohols, though the compromise to be made is moderate (see below). Final optimized values of the oxygen well depth and R_min/2 were 0.15 kcal/mol and 1.765 Å, respectively. The derived oxygen LJ parameters are relatively close to the polarizable SWM4-NDP water model LJ parameters where the well depth is 0.21 kcal/mol and R_min/2 is 1.79 Å. Additionally well depth parameters on the methyl carbon and hydrogen in methanol were optimized to obtain better agreement with the experimental molecular volume, which was otherwise too large. The LJ radii on the methyl atoms were constrained to the alkane values,²⁷ as condensed-phase properties of methanol were considerably less sensitive to changes in the LJ radii than in the well depths, ε. Final values of well depth for methanol were ε(C)=0.11 and ε(H)=0.035 kcal/mol. The Lennard-Jones parameters on other aliphatic C,H atoms were preserved at their alkane values.²⁷

One of the common assumptions in empirical force fields is the use of combining or mixing rules to convert LJ parameters for individual atom types to those for atom pairs.^80–82 This assumption is largely for convenience avoiding the need to individually determine LJ terms for each atom type pair. However, in the present work it was observed that the LJ parameters of the hydroxyl oxygen that yielded good pure solvent condensed phase properties lead to both the interaction energies with individual water molecules as well as the free energies of aqueous solvation being too favorable. This motivated the use of a specific, or off-diagonal (ie. NBFIX), LJ term for the O_alcohol…O_water atom pairs, with individual terms for the primary and secondary hydroxyl oxygens. As shown above in Table 3 and Table 4 and presented below, this leads to good agreement for the aforementioned properties and will be part of the present alcohol force field.

Computed and experimental properties for the neat liquids are summarized in Table 8. Data were obtained for the training set molecules, methanol, ethanol and 2-propanol as well as for the test molecule 2-butanol, 1-propanol and 1-butanol. Overall, the level of agreement of the polarizable model is quite good, especially with methanol, ethanol, 2-propanol and 2-butanol. For all the compounds the molecular volumes are generally improved over CHARMM22, the exception being 2-propanol. Concerning the heats of vaporization both the polarizable and additive models are good for methanol, ethanol and 2-propanol, with CHARMM22 significantly underestimating the value for 2-butanol while the polarizable model significantly underestimates the heats for 1-propanol and 1-butanol. Thus, it appears that neither of the models is capable of accurately reproducing pure solvent properties for the full series of primary and secondary alcohols. While this may be associated with constraints on the number of parameters optimized to assure transferability, similar problems have been observed in polarizable alcohol force fields based on both induced dipole and fluctuating charge models.^{18, 21, 22} In the induced dipole model, the heats of vaporization were typically in good agreement with experiment while molecular volumes were overestimated for the smaller alcohols and underestimated for the larger compounds.¹⁸ With the fluctuating charge force field distinct parameters were used for methanol²¹ and ethanol²² to obtain agreement with experiment. Thus, despite the inclusion of polarizability, it appears that the current form of the energy function, combined with limitations associated with the need to develop transferable parameters, is not capable of accurately treating the full series of primary and secondary alcohols.

Table 8.

Pure solvent properties of neat alcohols

Property	MeOHa	EtOH	2-PrOH	2-BuOH	1-PrOH	1-BuOH
Vm(C22)	69.18 (0.34)	99.09 (0.31)	128.41 (0.39)	157.25 (0.56)	128.98 (0.40)	157.37 (0.42)
	2.90%	2.20%	0.50%	3.00%	3.40%	3.50%
Vm(Drude) finalb	67.21 (0.15)	97.11 (0.19)	125.79 (0.30)	153.36 (0.32)	125.78 (0.20)	153.09 (0.49)
	0.00%	0.20%	−1.60%	0.50%	0.80%	0.70%
Vm(Drude) alternativec	66.02 (0.17)	95.42 (0.28)	124.11 (0.46)	152.13 (0.41)	124.06 (0.66)	151.87 (0.59)
	−1.8%	−1.5%	−2.9%	−0.3%	−0.6%	−0.1%
Vm(exp)	67.23	96.92	127.79	152.65	124.78	152.05
ΔHvap(C22)	9.11 (0.04)	10.20 (0.05)	10.81 (0.06)	10.63 (0.33)	11.22 (0.29)	12.42 (0.27)
	1.80%	0.90%	−0.30%	−10.50%	−1.10%	−0.70%
ΔHvap(Drude) finalb	8.94 (0.04)	10.07 (0.06)	10.99 (0.07)	11.76 (0.18)	10.55 (0.13)	11.68 (0.19)
	−0.10%	−0.40%	1.20%	−1.00%	−7.00%	−6.60%
ΔHvap(Drude) alternativec	9.58 (0.04)	10.86 (0.05)	11.83 (0.08)	12.51 (0.19)	11.36 (0.13)	12.49 (0.19)
	+7.0%	+7.4%	+9.0%	+5.3%	+0.2%	−0.1%
ΔHvap(exp)	8.95	10.11	10.85	11.88	11.34	12.51

Heats of vaporization in kcal/mol and molecular volumes in ų; values in parenthesis are the standard deviations; percent differences are with respect to experiment. Experimental data from ⁸⁷.

^aMethanol LJ well-depth: Carbon ε=0.11, Hydrogen ε=0.035.

^bFinal polarizable model Oxygen LJ ε=0.15, R=1.765.

^cAlternative polarizable model Oxygen LJ ε=0.15, R=1.74.

A natural extension of the present parameterization will be to model longer aliphatic-chain alcohols. To this end, the development of LJ parameters for the oxygen targeting the 1-propanol and 1-butanol pure solvent properties was undertaken. This model only differed in those LJ parameters; the remainder of the force field was maintained. Results in Table 8 (the alternative LJ model) show the second LJ model to yield good agreement for 1-propanol and 1-butanol. This second model, with a well depth = 0.15 kcal/mol and R_min/2 = 1.74 Å on the alcohol oxygen, is recommended for use on long chain primary alcohols. Also included in Table 8 are results using that alternative LJ model for ethanol, 2-propanol and 2-butanol, for comparison with the original model. Basically, the utility of the alternative LJ set for hydroxyl oxygen is limited to long-chain primary alcohols only.

To minimize the impact of parameter correlation during the optimization of LJ parameters, interactions with rare gases were monitored to facilitate optimization of the relative values of the LJ parameters. The target data from the rare gas interactions were the RMS fluctuations about the average difference (or ratios) for the minimum interaction energies and distances. Use of this target data allows for the LJ parameters to produce interactions that are systematically offset from the QM data to indicate that the relative LJ parameters for different atom types are properly balanced while accounting for limitations in QM methods to treat dispersion interactions⁴⁹. Shown in Table 9 are the RMS fluctuations for CHARMM22 and the final polarizable model for methanol and ethanol, with additional details supplied in Table S4 of the supporting information. The RMS values for the two models are similar, indicating that the polarizable model did not improve the balance of the LJ parameters using interactions with rare gases as a metric. Analysis of the individual minimum interaction distance differences shows those associated with direct interactions with the lone pairs (120 interaction) and hydroxyl hydrogen (ROH interaction, Figure 3) to be significantly shorter for the empirical models as compared to the target QM data. Such difference suggests that the empirical models may benefit from assignment of LJ parameters on lone-pair sites and the hydroxyl hydrogens. However, in the present model LJ parameters are not applied to the lone pairs for simplicity and a standard LJ parameter is applied to the polar hydrogen to facilitate transferability of the model.

Table 9.

Differences between empirical and QM values and RMS fluctuations about the average differences and ratios for the rare gas interactions with methanol and ethanol.

Orientation	MeOH+He		MeOH+Ne		EtOH+He		EtOH+Ne
CHARMM22	ΔRmin	ΔEint	ΔRmin	ΔEint	ΔRmin	ΔEint	ΔRmin	ΔEint
BIS	−0.12	−0.01	0.03	0.15	−0.18	−0.03	0.02	0.26
180	0.03	0.02	0.14	0.23	0.00	0.02	0.12	0.25
120	−0.32	−0.03	−0.08	0.16	−0.36	−0.06	−0.10	0.17
ROH	−0.33	0.01	−0.16	0.37	−0.36	0.01	−0.15	0.38
CH3	0.19	0.06	0.20	0.34	0.00	0.02	0.10	0.37
CH2	n/a	n/a	n/a	n/a	−0.15	−0.01	0.03	0.28
RMS	0.20	0.03	0.15	0.10	0.15	0.03	0.10	0.07
Drude	ΔRmin	ΔEint	ΔRmin	ΔEint	ΔRmin	ΔEint	ΔRmin	ΔEint
BIS	−0.14	−0.02	−0.03	0.11	−0.20	−0.02	−0.04	0.23
180	0.02	0.02	0.10	0.22	0.00	0.02	0.10	0.24
120	−0.33	−0.04	−0.13	0.12	−0.39	−0.05	−0.16	0.15
ROH	−0.35	0.01	−0.28	0.28	−0.37	0.01	−0.28	0.31
CH3	0.16	0.03	0.17	0.29	−0.02	0.01	0.08	0.37
CH2	n/a	n/a	n/a	n/a	−0.26	−0.03	−0.08	0.23
RMS	0.20	0.03	0.16	0.08	0.15	0.03	0.13	0.07

Interaction energy differences (kcal/mol) and distance differences (Å) are calculated as X^model-X^QM.

Additional condensed phase properties of the alcohols

Additional properties of the pure solvents investigated include the dielectric constants, diffusion constants, isothermal compressibilities and structural features based on radial distribution functions. In addition, free energies of solvation of the final models were evaluated.

An important feature of a model is proper treatment of the dielectric constant as this term is important in dictating the energetics of dissolution of solutes in the alcohols. Dielectric constants for both the Drude and additive models as well as the experimental data are presented in Table 10. The additive model systematically underestimates the dielectric constant on an average percent difference of −35.9 %, an inherent limitation of the model due to the lack of explicit polarizability, as previously described for alkanes.²⁷ With the Drude model, larger dielectric constants are obtained, leading to systematically better agreement with experiment with an average percent difference of −2.3%. As the internal parameters in the additive and polarizable models are similar the improvement in description of dielectric constant is clearly due to the explicit description of electronic polarization. Small underestimations are observed for ethanol and 2-propanol, the results for methanol, 1-propanol and 2-butanol are quite good, whereas 1-butanol overestimates the experimental data. Computations of dielectric constant show that this is a very slow converging property. In the current study five independent condensed-phase runs of 5 ns were performed for each alcohol molecule yield a total of 25 ns of simulation time. Longer simulations may be beneficial to obtain more reliable estimates; however, the present results already illustrate the advantage of the polarizable model over the additive one.

Table 10.

Dielectric constant

Alcohol	C222	Drude, ε∞a	Drude, εb	Exp., εb
MeOH	17.2 (0.1)	1.5	30.1 (0.1)	32.61
EtOH	18.8 (0.3)	1.6	21.4 (0.2)	24.85
2-PrOH	13.7 (0.1)	1.7	17.6 (0.5)	19.26
2-BuOH	7.8 (0.1)	1.7	15.8 (0.4)	15.94
1-PrOH	15.2 (0.2)	1.6	19.5 (1.1)	20.52
1-BuOH	10.8 (0.1)	1.7	21.2 (0.7)	17.33
Ave. % diff.	−35.9	n/a	−2.3	n/a

^aε_∞ estimation from the Clausius-Mossotti equation using experimental polarizabilities of alcohols.

^bT=298.15K; Experimental data from ⁸⁷. Ave. % diff. is the average of the percent difference with respect to experiment over the six alcohols studied.

Self-diffusion coefficients and isothermal compressibilities for four of the alcohols are presented in Table 11 and Table 12. Diffusion constant data include the values obtained directly from the periodic boundary simulations, a correction for PBC effects on the diffusion⁶³, and the total values along with the experimental values. The results demonstrate that the polarizable model to be an improvement over the additive one, although there is a tendency to slightly overestimate the experimental values. Concerning the isothermal compressibilities the calculated results show better agreement with the additive model for methanol and 2-propanol while the polarizable model is equivalent or better for ethanol and 1-propanol. Overall, there is a tendency for the polarizable model to underestimate the compressibilities, with the exception of ethanol at 343 K.

Table 11.

Self-diffusion coefficients of alcohols, (D_tot), 10⁻⁵ cm²/s

Alcohola	DPBC		Dcorr	Dtot		Exp.
	C22	Drude		C22	Drude
MeOH	2.16 (0.16)	2.03 (0.44)	0.56	2.72	2.59	2.4
EtOH	1.08 (0.15)	0.93 (0.13)	0.25	1.33	1.18	1.0
2-PrOH	0.60 (0.13)	0.52 (0.07)	0.12	0.72	0.64	0.6
1-PrOH	0.66 (0.13)	0.66 (0.16)	0.13	0.79	0.79	0.6

^aData calculated as in reference: methanol²¹, ⁸⁸–⁹⁰, ethanol, ²², ⁸⁸–⁹¹ iso-propanol,⁸⁹,⁹⁰ n-propanol. ⁸⁹–⁹¹ D_pbc is the direct result obtained from MD simulation involving periodic boundary condition; D_corr is the correction for system-size effect according to eq. 4.

Table 12.

Isothermal compressibility of alcohols, MPa⁻⁴

Alcohol	Temp., K	C22	Drude	Exp.a
MeOH	313.15	11.98 (0.96)	8.68 (0.97)	13.83
EtOH	293.15	10.12 (1.08)	10.03 (0.69)	11.19
EtOH	343.15	15.24 (1.44)	16.58 (1.53)	15.93
2-PrOH	313.15	13.62 (2.13)	11.71 (1.42)	13.32
1-PrOH	273.15	8.73 (0.99)	8.17 (1.01)	8.43

^aExperimental data from reference ⁸⁷.

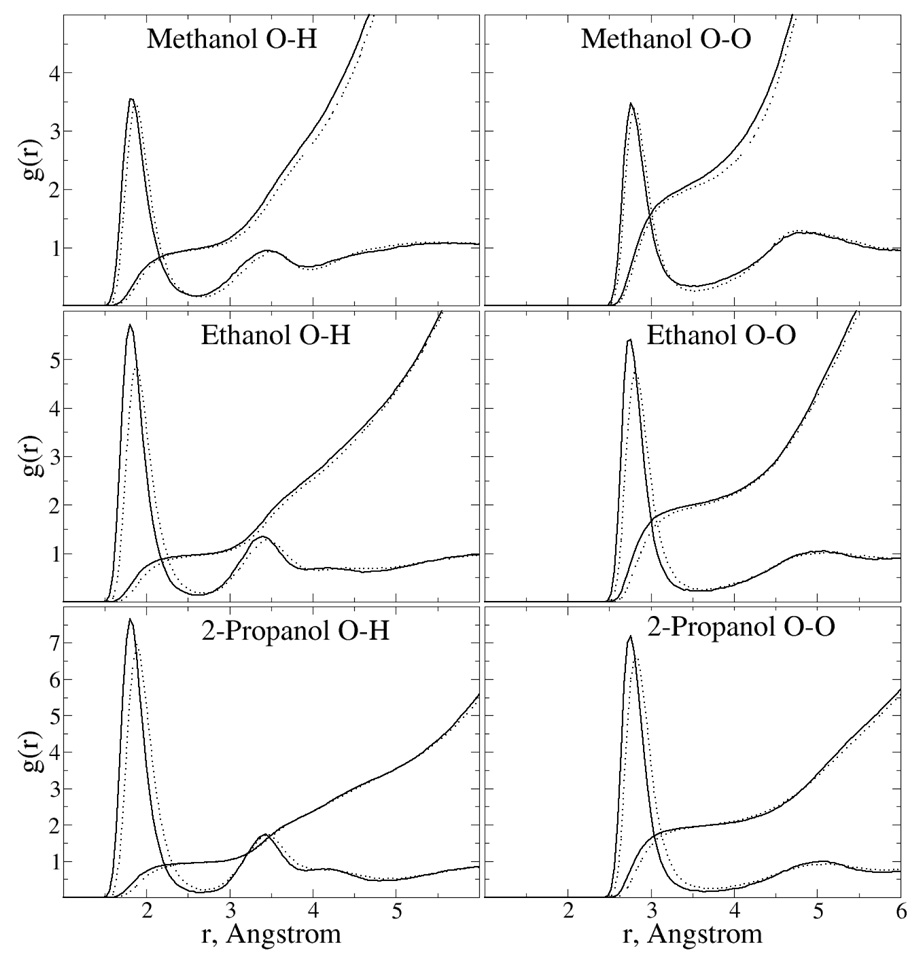
Radial distribution functions (RDF) for the methanol, ethanol, and 2-propanol were obtained to analyze structural features of those pure solvents. O-H and O-O radial distribution functions for these solvents along with coordination numbers as a function of distance are shown in Figure 6. Comparison of the polarizable and additive g(r)s show minor but systematic differences. In all cases the first peak is higher in the polarizable model, indicating a higher degree of structural organization. The peak is also shifted to shorter distances in the polarizable model. For example, the first peak in the O-H RDF shifts in from 1.87 to 1.81 Å upon going from the additive to the polarizable model for all studied alcohols. A similar shift from 2.81 to 2.75 Å occurs in the O-O RDFs. The computed RDFs of the O-O and O-H distances in ethanol are in satisfactory agreement with experimental data. Neutron scattering⁸³ and X-ray diffraction⁸⁴ show the first peak in the O-O RDF to occur in the range 2.7–2.8 Å. The calculated coordination numbers are 2.00 and 1.99 to the first minimum occurring at 3.54 and 3.61 Å in the O-O RDFs for the polarizable and additive model, respectively, which compare well with the experimental value of 2.0 reported at 3.0 Å, the location of the minimum in the experimental work. Empirical O-H coordination numbers out to the first minima integrate to 0.97 at 2.68 Å and 0.98 at 2.64 Å for additive and polarizable models, respectively. These are in good agreement with neutron scattering data for liquid ethanol where oxygen is surrounded by 0.95 hydroxyl atoms up to the first minima at 2.1 Å. Beyond the first peak the g(r)s are similar for the two solvents. Thus, upon going from the additive to the polarizable model there is a significant change in the O-O and O-H pair correlation function for ethanol and 2-propanol, although the second peaks and the coordination numbers are similar for the two models.

Figure 6.

Radial distributions functions of the pure solvents of ethanol and 2-propanol for both the CHARMM22 additive and Drude polarizable force fields. Results for the O-H (left panels) and O-O (right panels) intermolecular interactions are shown. Solid line: polarizable model; dotted line: CHARMM22 model.

While the optimization process was dominated by the pure solvent properties, free energies of aqueous solvation values were also considered during the optimization, though their weight in the selection of the final parameter set was less than that assigned to the pure solvents. Table 13 shows the additive, Drude and experimental free energies of solvation for the alcohols studied; the free energies include a long-range correction (LRC) for the truncation of the LJ atom-atom interactions. The CHARMM22 results are in good agreement with experiment, though they tend to be too favorable than the experimental data by 4 to 19 percent. In the polarizable model this tendency was enhanced when LJ parameters based on the pure solvent simulations were used (see Table 13, ΔG_uncorr), with the largest percent difference being 34 % for 2-butanol (Table S5 of the supplemental information). To overcome this trend atom type O_alcohol-O_water LJ terms were developed. These terms lead to improved agreement for the interactions of the alcohols with water (Table 3 and Table 4) and for the free energies of solvation (Table 13). During this process it was observed that the O_alcohol-O_water LJ term developed based on ethanol led to the ΔG_solv values still too favorable for the secondary alcohols by −0.5 to −0.6 kcal/mol (not shown). Therefore, a secondary alcohol specific O_alcohol…O_water LJ term was optimized, yielding the results shown in Table 3, Table 4 and Table 13. The resulting pair specific O_alcohol…O_water LJ terms were (ε_ij=0.18 kcal/mol; R_{min_ij}=3.58 Å for the primary alcohols and ε_ij=0.21 kcal/mol; R_{min_ij}=3.60 Å for the secondary alcohols) replacing the corresponding terms (ε_ij=0.17788 kcal/mol; R_{min_ij}=3.5519 Å for both primary and secondary alcohols) generated by the combining rule. While the use of a specific O_alcohol-O_water LJ terms for the primary and secondary alcohols deviates from the goal of a fully transferable alcohol model, the significant improvement in the aqueous solvation warrants this decision.

Table 13.

Free energies of solvation, kcal/mol

Alcohol	CHARMM22			Drude				Exp
	LRCa	ΔGsolv	%diff	LRCa	ΔGuncorr	ΔGsolv	%diff	ΔGsolv
MeOH	−0.20	−4.98 (0.08)	−3	−0.26	−5.20 (0.19)	−4.64 (0.18)	−9	−5.11b
EtOH	−0.31	−5.34 (0.12)	7	−0.35	−5.66 (0.31)	−4.97 (0.13)	−1	−5.01b
2-PrOH	−0.39	−5.07 (0.09)	7	−0.45	−6.06 (0.23)	−4.82 (0.16)	1	−4.76b
2-BuOH	−0.45	−4.93 (0.27)	8	−0.57	−6.11 (0.18)	−4.75 (0.43)	4	−4.57c
1-PrOH	−0.42	−5.33 (0.24)	10	−0.46	−5.38 (0.16)	−4.85 (0.15)	0	−4.83b
1-BuOH	−0.53	−5.60 (0.21)	19	−0.57	−5.72 (0.16)	−4.67 (0.23)	−1	−4.72b
Aver			9				−1

^aThe long range correction (LRC) is estimated for dispersion forces. In the polarizable model, ΔG_uncorr represents free energy obtained using standard combining rule for intermolecular LJ interactions and ΔG_solv is free energy that included an off-diagonal (i.e. NBFIX) for the O_alcohol…O_water LJ parameters (R_min=3.60, ε=0.18 for primary alcohols, and R_min=3.60, ε=0.21 for secondary alcohols).

^bExperimental results as reported in reference ⁹²

^creference.⁹³

With respect to previous studies ΔG_solv values of −4.88 and −4.08 kcal/mol for methanol and ethanol, respectively, were obtained by Deng and Roux for the CHARMM22 force field using a spherical solvent boundary potential (SSBP).⁶⁶ Pande and coworkers⁸⁵ used periodic boundary conditions (PBC) simulations with thermodynamic integration along with extensive sampling (with 5 ns per window versus 100 ps in the present work) to obtain free energies of solvation of −4.59 and −4.22 kcal/mol for the CHARMM22 methanol and ethanol models, respectively. Comparison with the CHARMM22 additive results shows the present results to be more favorable than the published values by 0.4 to 1.1 kcal/mol. Further analyses indicate that the variations are associated with methodological differences. The present computations were done using PBC with 250 water molecules, atom-based truncation, LJ switch truncation from 10 to 12 Å, treatment of long range electrostatic interactions via PME. The computations of Deng and Roux were done using 100 water molecules, LJ switch truncation from 10 to 12 Å, treatment of long range electrostatics with extended electrostatics and the SSBP continuum model. The computations of Pande and coworkers used PBC with 900 water molecules, group-based truncation, treatment of both LJ and electrostatic interactions with switch truncation over 10 to 12 Å (i.e. no long range electrostatic correction). These results emphasize the sensitivity of free energy perturbation calculations to differences in computational methodology.

Beyond methodological difference, the impact of the conformation of the alcohol on the obtained ΔG_solv was considered. This was performed by calculating the free energy of solvation of ethanol with the hydroxyl in either the gauche (60°) or trans (180°) conformation via inclusion of a harmonic restraint on the C-C-O-H dihedral of 1000 kcal/mol/rad². The resulting ΔG_solv values for the gauche and trans states, assuming the same LRC corrections reported in Table 13, were −5.01 and −5.61 kcal/mol, respectively, for CHARMM22 and −4.48 and −5.52 kcal/mol, respectively, for the Drude model. Thus, the relative g versus t conformations may lead to significant differences in the obtained free energy of solvation. While ethanol stayed in the trans conformation in the present study, with the same behavior presumably occurring in the studies discussed in the preceding paragraph, the potential impact of the conformation of the hydroxyl should be noted.

It is interesting to note that the observed trends in hydration free energies of ethanol as a function of conformation is opposite to the gas-phase dipole moments of polarizable ethanol (µ_gauche=1.96 D, µ_trans=1.81 D). Such a difference indicates that the relative free energy of solvation of ethanol is dictated by the higher degree of availability of the hydroxyl group in the trans-conformation to intermolecular hydrogen bonds rather than the intrinsic dipole moment. This speaks to the importance of the proper treatment of intermolecular interactions in the gas versus condensed phases, including proper polarization contribution, and their impact on condensed phase properties.

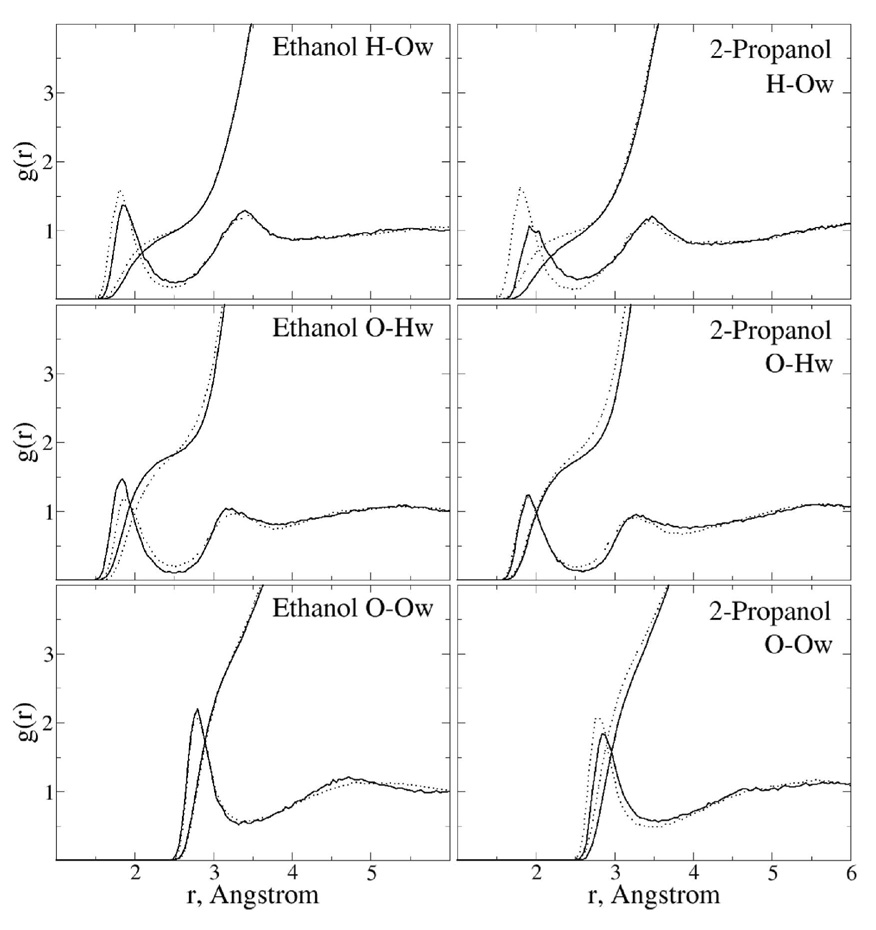
RDFs of water with ethanol and 2-propanol were analyzed to check the impact of the polarizable model on structural properties in solution with respect to CHARMM22. Analysis of Figure 7 shows there to be significant difference between the polarizable and additive force fields. In the O_alcohol-H_water RDFs the polarizable model has the first peak shifted to longer values versus the additive model while the opposite is true for the H_alcohol-O_water RDF. In addition, with the O_alcohol-H_water RDF there are differences in the first minimum as well as the second peak. With the secondary alcohol, 2-propanol, even larger differences between the additive and polarizable models are observed, with the largest change in the H_alcohol-O_water RDF followed by the O_alcohol-O_water RDF. Thus, significant differences in the atomic details of the additive versus polarizable models are observed for in aqueous solution.

Figure 7.

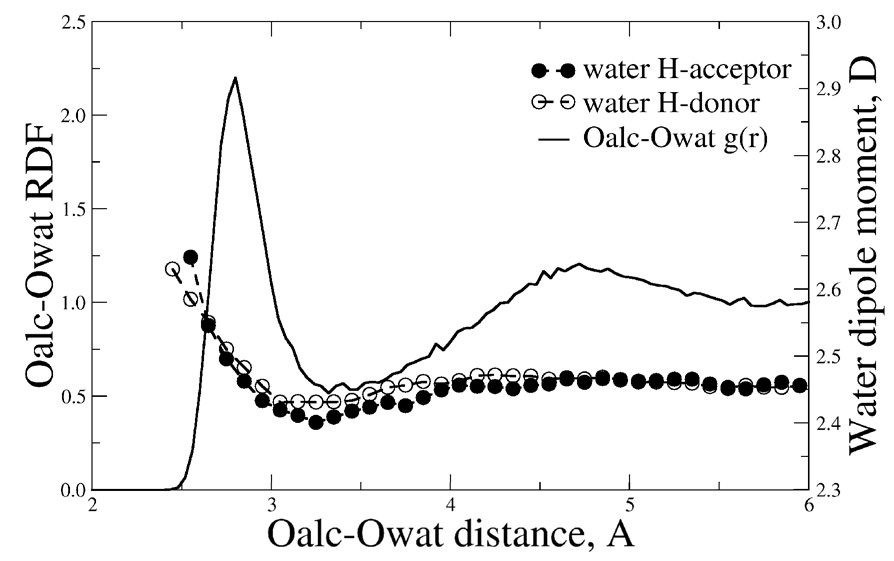
Radial distributions functions of ethanol and 2-propanol in aqueous solution for both the CHARMM22 additive and Drude polarizable force fields. Solid line: polarizable model; dotted line: CHARMM22 model.

Explicit inclusion of electronic polarizability is anticipated to allow for more accurate modeling as a function of the polarity of the environment. To see if such effects occur in the Drude polarizable force field dipole distributions were obtained from MD simulations in the gas phase, the pure solvent and in aqueous solution for both the additive and polarizable models (Figure 8). Analysis of the figures shows extreme differences. The additive model has the three distributions clustered together with the maximum close to 2.4 D for both ethanol and 2-propanol. Such similar distributions are expected due to the lack of explicit polarizability, with the value of 2.4 being significantly larger than the gas phase experimental value for both molecules, as required to implicitly overpolarize the molecule to obtain reasonable condensed phase properties. With the polarizable model, significant differences are seen as a function of environment. From the MD simulations in the gas phase, which may be considered a hydrophobic environment, the distribution is centered around the gas phase experimental values (Table 7). Upon going to the pure solvent an upshift in the distribution which is centered around 2.4 and 2.5 D for ethanol and 2-propanol, respectively. Upon moving to the more polar aqueous environments additional upshifting occurs, where the distributions are now centered around 2.7 and 2.9 D for ethanol and 2-propanol, respectively. The value for ethanol is in good agreement with a Car-Parrinello MD prediction of the dipole moment of ethanol of 3.1 D for ethanol solvated in water.⁸⁶ Interestingly, the implicitly overpolarized additive model has a distribution similar to that of the polarizable model in the pure solvent, consistent with the satisfactory agreement for ΔH_vap for both models.

Figure 8.

Dipole moment distributions of ethanol and 2-propanol in the gas phase, in pure solvents and in aqueous solution for both the CHARMM22 additive and Drude polarizable force fields. Solid line: polarizable model; dotted line: CHARMM22 model.

Further comparison of the dipole moment distributions were obtained from 500 ps MD simulation of ethanol in a box of 128 benzene molecules. The simulation using the polarizable model yields an average ethanol dipole moment of 1.86 D, close to the gas-phase value, while the additive model yields a value of 2.34 D. This result suggests that a model where polarizability changes as a function of environment has a distinct advantage over the fixed charge additive model.

Also of interest is the impact of the presence of the alcohol on the electrostatic properties of the surrounding water molecules. This was analyzed by calculating the average dipole moment of water molecules as a function of O_alcohol-O_water distance for ethanol in water (Figure 9). While the overall change in the dipole moment is 0.2 D, there is a clear trend for the water dipole moment to decrease from the bulk value in the vicinity of the first minimum in the O_alcohol-O_water RDF followed by an increase upon moving in to shorter distance. The overall trends in the average dipole moment of water molecules interacting with ethanol as H-bond donors or acceptors are similar, though minor differences are present. It is observed that the variations in the total dipole of water molecules relax back to the average bulk value only after the second hydration shell (4–5 Å away from the solute). Incorporating such subtle effects clearly requires going beyond the mean field picture provided by effective additive force fields, in which all the water molecules are modeled with the same electrostatic charge distribution. These results further indicate the power of a polarizable model for the investigation of condensed phase properties.

Figure 9.

Average water dipole moment around ethanol as a function of O_alcohol-O_water distance overlaid on the O_alcohol-O_water radial distribution function (solid line) of ethanol in water. Open circles indicate water molecules acting as H-bond donors and filled circles indicate water molecules acting as H-bond acceptors.

Conclusions

An empirical polarizable force field for the alcohol series has been developed. Explicit incorporation of electronic polarizability via the classical Drude oscillator facilitates more realistic response of the model compounds to the degree of polarity of the environment, with the molecular dipole changing significantly upon transition from hydrophobic to hydrophilic environments. This represents a considerable improvement over the additive model of alcohols, indicating the polarizable model to yield a better balance of the types of interactions dictating structural and thermodynamic properties of condensed phases. Significant improvement is obtained in prediction of dielectric susceptibility of liquid alcohols due to the explicit incorporation of electronic polarizability. Notable improvement over the additive model in the prediction of self-diffusivity of alcohols is also obtained. The potential energy profiles for rotation about selected bonds show the Drude model to accurately reproduce the high-level QM correlated energy maps. The Drude model is in good agreement with experiment for both pure solvent and aqueous solvation properties, though the agreement with the free energies of solvation required the use of atom type specific terms for the O_alcohol-O_water LJ interactions, including individual terms for the primary and secondary alcohols. This represents a departure of the goal of transferability where the LJ parameters for the hydroxyls are identical in all the molecules and the LJ parameters for the aliphatic moieties were transferred directly from the alkanes.²⁷ In contrast, transferable LJ parameters were used in the additive model yielding a level of agreement with experiment typically better than that for the Drude model before the use of the atom type specific LJ terms. This poorer agreement is suggested to be due to additional sensitivity of the polarizable model to changes in the polarity of its environment leading to the constraint of transferability having a more adverse impact on that model versus than on the additive model, where the fixed-charge model diminishes the sensitivity of the model to the environment (including changes in the neighboring atoms forming the intramolecular “environment” of a given atom type). Supporting this are results from previously published polarizable models of alcohols were it was observed that the same LJ parameters could not be used for methanol and ethanol to yield agreement with experiment^{18, 21, 22} and in a second study on a polarizable alcohol series where constraining the LJ parameters on the hydroxyl to be identical lead to a systematic variation of the pure solvent molecular volumes with respect to experiment.¹⁸ Addressing this issue will be beneficial in gaining an understanding about effective ways to improve the predictive potential of empirical force fields.

Supplementary Material

1File002. Supporting Information Available.

The comparison of empirical and target QM IR-spectra, the data on interaction with rare gases, optimized parameter values, parameter scans in vicinity of the optimized values, and free energy computation details. This material is available free of charge via the Internet at http://pubs.acs.org.