Dynamic Population Coding of Category Information in Inferior Temporal and Prefrontal Cortex

Abstract

Most electrophysiology studies analyze the activity of each neuron separately. While such studies have given much insight into properties of the visual system, they have also potentially overlooked important aspects of information coded in changing patterns of activity that are distributed over larger populations of neurons. In this work, we apply a population decoding method to better estimate what information is available in neuronal ensembles and how this information is coded in dynamic patterns of neural activity in data recorded from inferior temporal cortex (ITC) and prefrontal cortex (PFC) as macaque monkeys engaged in a delayed match-to-category task. Analyses of activity patterns in ITC and PFC revealed that both areas contain “abstract” category information (i.e., category information that is not directly correlated with properties of the stimuli); however, in general, PFC has more task-relevant information, and ITC has more detailed visual information. Analyses examining how information coded in these areas show that almost all category information is available in a small fraction of the neurons in the population. Most remarkably, our results also show that category information is coded by a nonstationary pattern of activity that changes over the course of a trial with individual neurons containing information on much shorter time scales than the population as a whole.

INTRODUCTION

The concept of population coding, in which information is represented in the brain by distributed patterns of firing rates across a large number of neurons, arguably dates back over 200 years (McIlwain 2001). Yet, despite this long conceptual history, and an extensive amount of theoretical work on the topic (Rumelhart et al. 1986; Seung and Sompolinsky 1993; Zemel et al. 1998), most electrophysiological studies still examine the coding properties of each neuron individually.

While much insight has been gained from studies analyzing the activity of individual neurons, these studies can potentially overlook or misinterpret important aspects of the information contained in the joint influence of neurons at the population level. For example, many analyses make inferences about what information is in a given brain region based on the number of responsive neurons or on the strength of index values that are averaged over many individual neurons. However, much theoretical and experimental work (Olshausen and Field 1997; Rolls and Tovee 1995) has indicated that information can be coded in sparse patterns of activity. Under a sparse representation, a brain region that contains fewer responsive neurons during a particular task might actually be more involved in the use of that information, and averaging over many neurons might dilute the strength of the effect, which could give rise to a misinterpretation of the data.

Another shortcoming of most single-neuron analyses is that they do not give much insight into how information is coded in a given brain region. Several theoretical studies have examined how information is stored in ensembles of units including attractor networks, synfire chains (Abeles 1991) and probabilistic population codes (Zemel et al. 1998) among others. However, because of the paucity of population analyses of real neural data, there is currently little empirical evidence on which to judge the relative validity of these models.

To better understand the content and nature of information coding in ensemble activity, we used population decoding tools (Duda et al. 2001; Hung et al. 2005; Quiroga et al. 2006; Stanley et al. 1999) to analyze the responses of multiple individual neurons in inferior temporal cortex (ITC) and prefrontal cortex (PFC) recorded while monkeys engaged in a delayed match-to-category task (DMC) (Freedman et al. 2003). Previous individual neuron analyses of these data had suggested that ITC is more involved in the processing of currently viewed image properties, whereas PFC is more involved in signaling the category and behavioral relevance of the stimuli and in storing such information in working memory (Freedman et al. 2003). Here, by pooling the activity from many neurons, we are able to achieve a finer temporal description of the information flow, and we can better quantify how much of the category information in these areas is due to visual properties of the stimuli versus being more abstract in nature. Additionally, by looking at the activity in a population over time, we find that the selectivity of those neurons that contain abstract category information changes rapidly. Information is being continually passed from one small subset of neurons to another subset over the course of a trial. This work not only clarifies the roles of ITC and PFC in visual categorization, but it also helps to constrain theoretical models on the nature of neural coding in these structures (Riesenhuber and Poggio 2000; Serre et al. 2005).

METHODS

Behavioral task and recordings

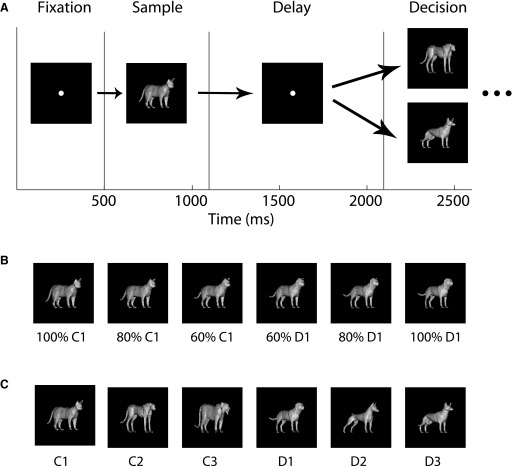
We used the data recorded in the study of Freedman et al. (2003). Briefly, responses of 443 ITC and 525 PFC neurons were recorded from two Rhesus Macaque monkeys as the monkeys engaged in a delayed match-to-category task. Each DMC trial consisted of a sequence of four periods: a fixation period (500-ms duration), a sample period in which a stimulus was shown (600-ms duration), a delay period (1,000 ms), and a decision period in which a second stimulus was shown and the monkey needed to make a behavioral decision (Fig. 1A). The stimuli used in the task were morphed images generated from three prototype images of cats and three prototype images of dogs (Fig. 1, B and C). A morph stimulus was labeled a “cat” or “dog” depending on the category of the prototype that contributed >50% to its morph. During the sample period of the task, a set of 42 images (Fig. S11 ) were used that consisted of the six prototype images and morphs that were taken at four even intervals between each dog and cat prototype. The stimuli shown in the decision period consisted of random morphs that were ≥20% away from the cat/dog category boundary, so that the category that these stimuli belonged to was unambiguous. The monkeys needed to release a lever if the sample-stimulus matched the category of the decision-stimulus to receive a juice reward (or to continue to hold the lever and release it for a second decision-stimulus in the nonmatch trials). Performance on the task was ∼90% correct. Figure 1 illustrates the time course of an experimental trial, one morph line used in the experiment, and the six prototype dog and cat images. The experimental design and recordings were previously reported by Freedman et al. (2001, 2003); and more details about the stimuli, the task, and the recordings can be found in those publications.

FIG. 1.

Organization of the stimuli and behavioral task. A: time course of the delayed match to category experiment. B: an example of 1 of the 9 morph lines of the stimuli from the cat 1 prototype to the dog 1 prototype (the actual stimuli used in the experiment were colored orange) (see Freedman et al. 2002). C: the 6 prototype images used in the experiment. All the stimuli used in the experiment were either the prototype images, or morphs between the cat (C) and dog (D) prototypes.

DATA ANALYSIS.

To estimate the information conveyed by a neuronal ensemble about a particular stimulus or behavioral variable, we used a decoding-based approach (Hung et al. 2005; Quiroga et al. 2006). We trained a pattern classifier on the firing rates from a population of m neurons recorded across k trials (i.e., we have k training points in R^m, where R^m is an m-dimensional vector space). For each trial, one of c different conditions is present, and the classifier “learns” which pattern of activity across the m neurons is indicative that condition c_i was present. We assessed how much information is present in the population of neurons by using a “test data set” (firing rates from the same m neurons, but from a different set of h trials) and quantifying how accurately the classifier could predict which condition c_i was present in these new trials. Classifier performance was evaluated and reported throughout the text as the percentage of test trials correctly labeled. In the text we use the terms “decoding accuracy” and “information” interchangeably because there is an injective monotonic mapping between these two measures (Gochin et al. 1994; Samengo 2002). Variables (i.e., different groups of conditions) we decoded include 1) which of the 42 stimuli was shown during the sample period (c = 42), 2) the category of the stimulus shown during the sample period (c = 2), 3) the category of the stimulus shown during the decision period (c = 2), and 4) whether a trial was a match or nonmatch (c = 2). Occasionally, in the text we are informal and we say we trained a classifier on a given set of images X, by which we mean we trained the classifier on neural data that was recorded when images in set X were shown.

Because most of the neurons used in these analyses were recorded in separate sessions, it was necessary to create pseudo-populations that could substitute for simultaneous recordings. Although creating these pseudo-populations ignores correlated activity between neurons that could potentially change estimates of the absolute level of information in the population (Averbeck et al. 2006), having simultaneous recordings would most likely not change the conclusions drawn from this work because we are mainly interested in relative comparisons over time and between brain regions.

To create this pseudo-population for the decoding of identity information (i.e., which of the 42 stimuli were shown during the sample period) the following procedure was used. First we eliminated all neurons that had nonstationary trends (those with an average firing rate variance in 20 consecutive trials was less than half the variance over the whole session). Because the stimuli were presented in random order, the average variance in 20 trials should be roughly equivalent to the variance over the whole session (only 42 ITC and 34 PFC neurons met the trend criterion, and the decoding results were not significantly different when these neurons were included). Next we found all neurons that had recordings from at least five trials for each of the 42 stimuli shown in the sample period. This left 283 ITC and 332 PFC neurons for further analysis. From the pools of either ITC neurons or PFC neurons we applied the following procedure separately at each time period.

First, 256 neurons were randomly selected from the pool of all available neurons. This allowed a fair comparison of ITC to PFC even though there were more neurons available in the PFC pool.

Second, for each neuron, we randomly selected the firing rates from five trials for each of the 42 stimuli.

Third, the firing rates of the 256 neurons from each of the five trials were concatenated together to create 210 data points (5 repetitions × 42 stimuli) in R²⁵⁶ space.

Fourth, a cross-validation procedure was repeated five times. In each repetition, four data points from each of the 42 classes were used as training data and one data point from each class was used for testing the classifier (i.e., each data point was only used once for testing and 4 times for training). Prior to training and testing the classifier, a normalization step was applied by subtracting the mean and dividing by the SD for each neuron (the means and SD were calculated using only the data in the training set). This z-score normalization helped ensure that the decoding algorithm could be influenced by all neurons rather than only by those with high firing rates. Similar results were obtained when this normalization was omitted.

Fifth, the whole procedure from steps 1–4 was repeated 50 times to give a smoothed bootstrap-like estimate of the classification accuracy. The main statistic shown in Figs. 2–7 is the classification accuracy averaged over all the bootstrap and cross-validation trials.

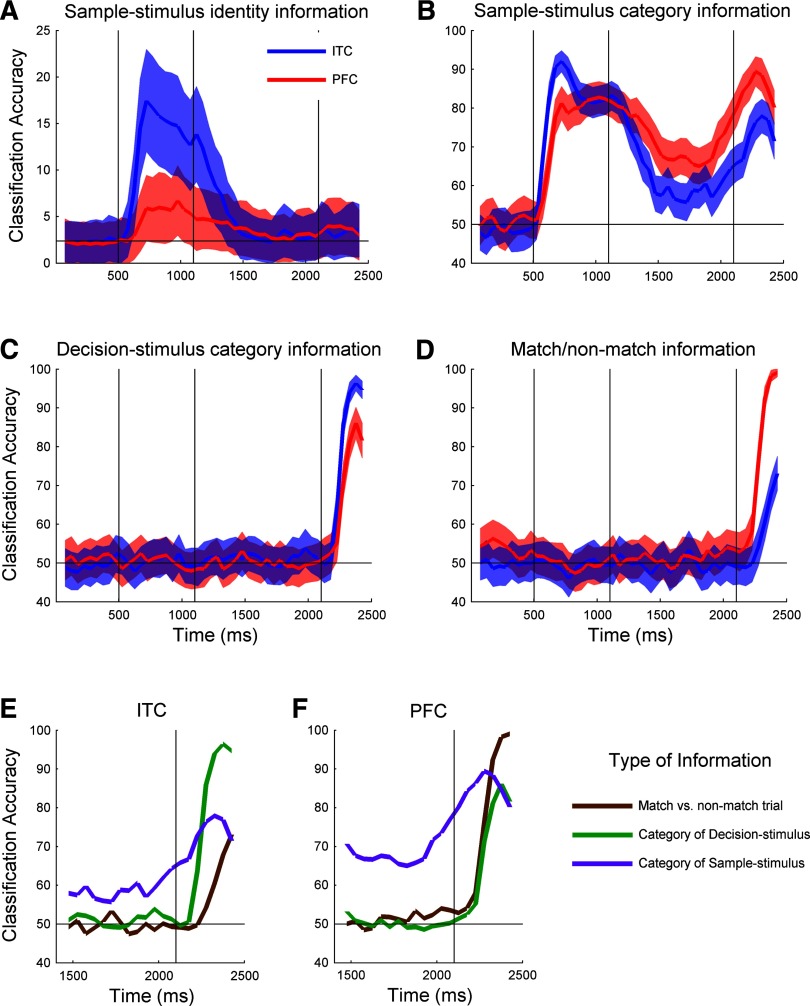
FIG. 2.

Basic decoding results for 4 different types of information. A–D: blue lines indicates results from inferior temporal cortex (ITC) and red lines indicate results from prefrontal cortex (PFC; red, and blue shaded regions indicate one SD over the bootstrap-like trials). The 3 vertical black lines indicate SAMPLE-STIMULUS onset, SAMPLE-STIMULUS offset, and DECISION-STIMULUS onset from left to right respectively. E and F: comparison of SAMPLE-STIMULUS category decoding accuracy (purple), DECISION-STIMULUS category decoding accuracy (green), and whether a trial is a match or nonmatch trial (brown) for ITC (E) and PFC (F).

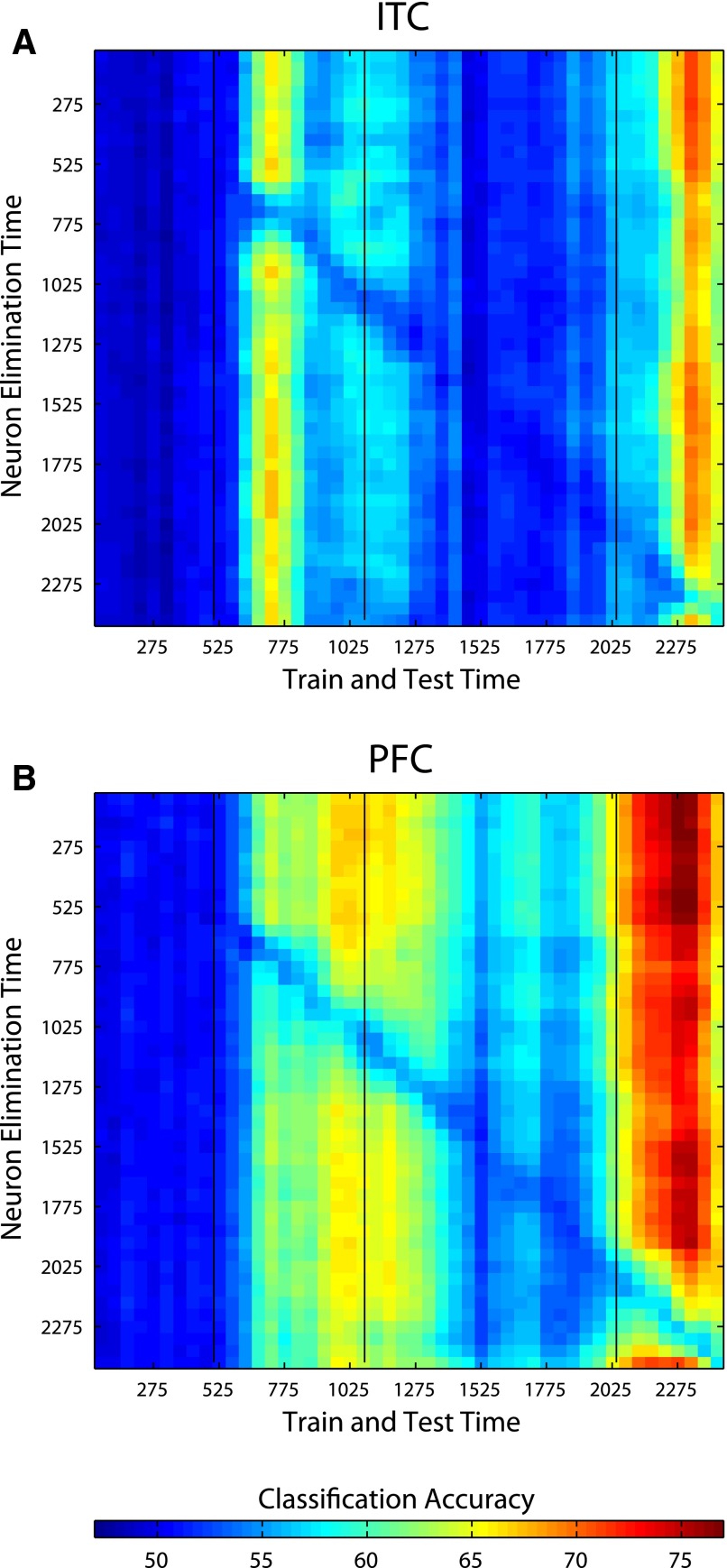
FIG. 7.

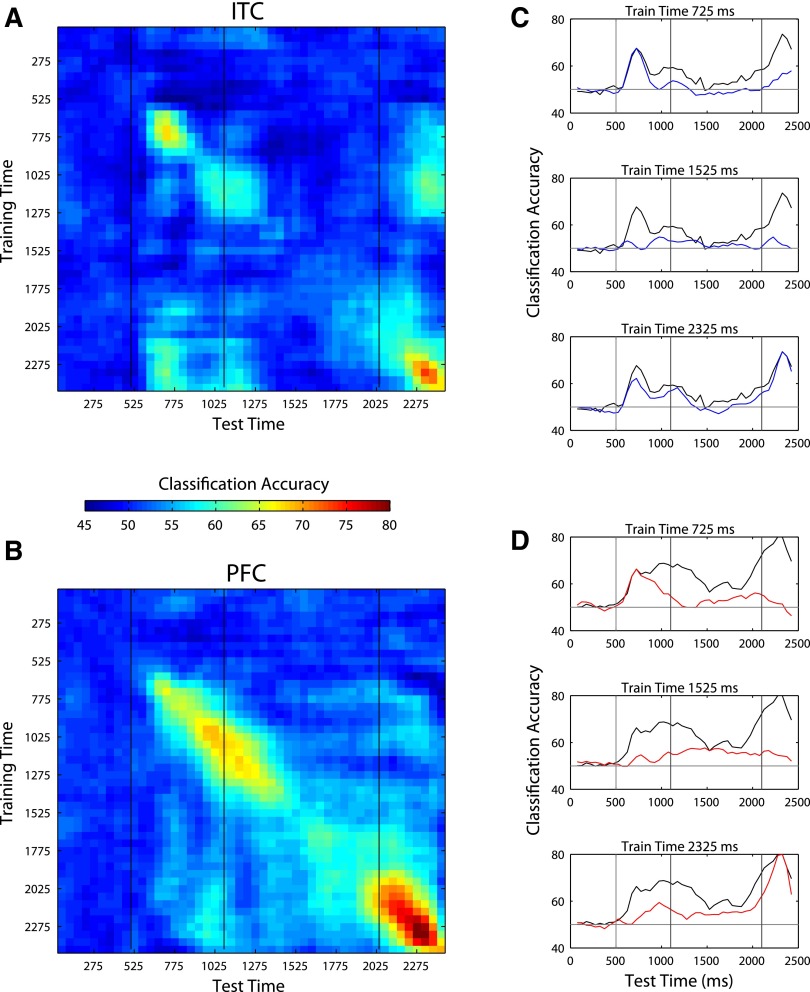
Elimination of the best 64 neurons from the time period t₁ (specified on the y axis) and then training and testing with all the remaining 192 neurons at time period t₂ (as specified by the x axis) for ITC (A) and PFC (B). Eliminating the best neurons from the training set at one time period only has a large affect on decoding accuracy at that same time period and leaves other time period unaffected as can be seen by the fact that there is only lower performance long the diagonal of the figure. This indicates that the neurons in the population that carry the majority of the information change with time. Additionally, one can see a decrease only along the diagonal even during periods where the stimulus is constant (areas between the black vertical bars). This indicates that the neural code is changing at a faster rate than changes in the stimulus.

A similar procedure was used to create pseudo-population vectors for decoding of sample-stimulus category, decision-stimulus category, and match-nonmatch information as shown in Fig. 2, except that 50 data points for each class were used in each of the five cross-validation splits (i.e., there were 400 training points and 100 test points), and the trial condition labels were changed to reflect the information that we were trying to decode. For the decoding of “abstract category” information in Figs. 3–7, the procedure was used exactly as described in the preceding text except that the 42 identity labels were remapped to their respective dog and cat categories, and different prototypes were used for training and testing (see section on decoding abstract category information).

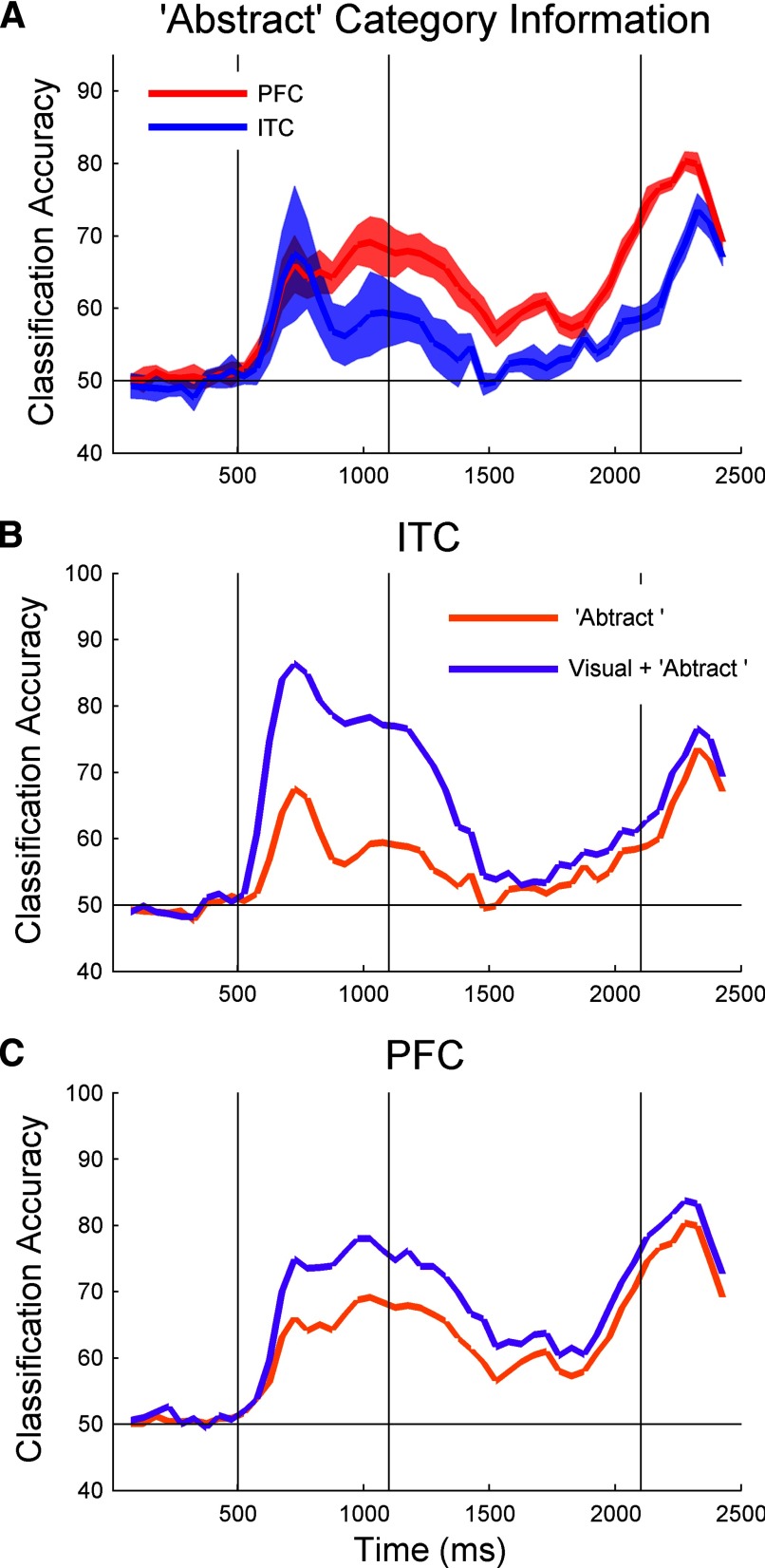
FIG. 3.

Decoding task-relevant “abstract” category information. A: decoding accuracies for ITC (blue) and PFC (red) when training on data from 2 dog and 2 cat prototype images and testing on the remaining dog and cat prototype images. The results are the average over all 9 permutations of training/test splits and the shaded results show the SDs over the 9 permutations (the individual traces are shown in Supplementary Fig. S4A). B and C: comparison of visual plus category stimulus decoding accuracies (purple line) to abstract category information (orange line) for ITC (B) and PFC (C). Note that there is a larger difference between these two types of information in ITC compared with the difference between these information types seen in PFC. This is a strong indication that the high SAMPLE-STIMULUS category decoding accuracies seen in ITC in Fig. 2B are largely due to visual information and not abstract category information during the sample period. During the decision period, for both ITC and PFC, most of information about the category of the SAMPLE-STIMULUS is in a more abstract representation, as there is little difference between abstract category information and “basic” category information during this period.

Unless otherwise noted, all figures that show smooth estimates of classification accuracy as a function of time are based on using firing rates in 150-ms bins sampled at 50-ms intervals with data from each time bin being classified independently. Because the sampling interval we used is shorter than the bin size (50-ms sampling interval, 150-ms time bin), the mean firing rates of adjacent points were calculated using some of the same spikes, leading to a slight temporal smoothing of the results.

In the body of the text, we also report classification accuracy statistics. Unless otherwise stated, classification accuracy results from the sample periods are reported for bins centered at 225 ms after sample stimulus onset, results from the delay period are reported for 525 ms after sample stimulus offset, and results from the decision period are reported for 225 ms after decision stimulus offset (this corresponds to 725, 1,625, and 2,325 ms after the start of a trial, with each bin width being 150 ms). The results reported for “basic” decoding accuracies are the means ± 1 SD of the decoding accuracies over all the bootstrap trials and cross-validation splits. The results reported for decoding abstract category information are the average ±1 SD of basic decoding results taken over the nine combinations of training and test splits (see the section on decoding abstract category information for more details). Also, because there are two stimuli presented in each trial, to avoid confusion when reporting basic decoding results, we denote the first stimulus shown as the SAMPLE-STIMULUS and the second stimulus shown as the DECISION-STIMULUS with capitalized letters used to avoid confusion with the sample, delay, and decision periods (which are time periods where properties of these stimuli can be decoded). It should be noted that in this paper, we refer to the time period after the second stimulus is shown as the decision period rather than the test period as used by Freedman et al. (2003) to avoid confusion with the test set that is used to evaluate the trained classifier.

All results reported in this paper use a correlation coefficient-based classifier. Training of this classifier consists of creating c “classification vectors” (where c is the number of classes/conditions used in the analysis), and each classification vector is simply the mean of all the training data from that class (thus each classification vector is a point in R^m, where m is the number of neurons). To assess to which class a test point belongs, the Pearson's correlation coefficient is calculated between the test point and each classification vector; a test data point is classified as belonging to the class c_i, if the correlation coefficient between the test point and the classification vector of class c_i is greater than the correlation coefficient between the test point and the classification vector of any other class. The classification accuracy reported is the percentage of correctly classified test trials.

There are several reasons why we use a correlation coefficient-based classifier. First, because this is a linear classifier, applying the classifier is analogous to the integration of presynaptic activity through synaptic weights; thus decoding accuracy can be thought of as indicative of the information available to the postsynaptic targets of the neurons being analyzed. Second, computation with this classifier is fast, and it has empirically given classification accuracies that are comparable to more sophisticated classifiers such as regularized least squares, support vector machines and Poisson naïve Bayes classifiers, which we have tested on this and other data sets (see Supplemental Fig. S2). Third, this classifier is invariant to scalar addition and multiplication of the data, which might be useful for comparing data across different time periods in which the mean firing rate of the population might have changed. And finally, this classifier has no free adjustable parameters (that are not determined by the data) which simplifies the training procedure.

For several analyses, we trained a classifier on one condition and tested the classifier on a different related condition. These analyses test how invariant the responses from a population of neurons are to certain transformations, and they help to determine whether a population of neurons contains information beyond what is directly present in the stimulus itself. We also performed analyses in which a classifier is trained with data from one time period and tested with data from a different time period; this allowed us to assess whether a pattern of activity that codes for a variable at one time period is the same pattern of activity that codes for the variable at a later time period. It is important to emphasize that for all analyses, training and test data come from different trials. Finally, for several analyses, we calculated the classification accuracy using only small subsets of neurons, ranked based on how category-selective these neurons were. The rank order was based on a t-test applied to all cat trials versus all dog trials on the training dataset, and the k neurons with the smallest P values were used for training and testing. This “greedy” method of feature selection is not guaranteed to return the smallest subset that will achieve the best performance, so the readout accuracies obtained with this feature selection method might be an underestimate of what could be obtained with an equivalent number of neurons from the same population if an ideal feature selection algorithm was applied.

Finally, for one set of analyses (Fig. 8), we estimated the amount of mutual information (MI) between the category of the stimuli s and individual neurons' firing rates r, using the average firing rates in 100-ms bins sampled at 10-ms intervals. To compute the mutual information, we assumed the prior probability of each stimulus category was equal, and we used the standard formula, I = ∑_s,rP[r, s] log₂ (P[r, s]/P[r] P[s]) (Dayan and Abbott 2001). The joint probability distribution between stimulus and response, P[r, s], was estimated from the empirical distribution using all trials. Although there exists potentially more accurate methods for estimating mutual information (Paninski 2003; Shlens et al. 2007), because our results do not depend critically on the exact MI values, we preferred the simplicity of this method.

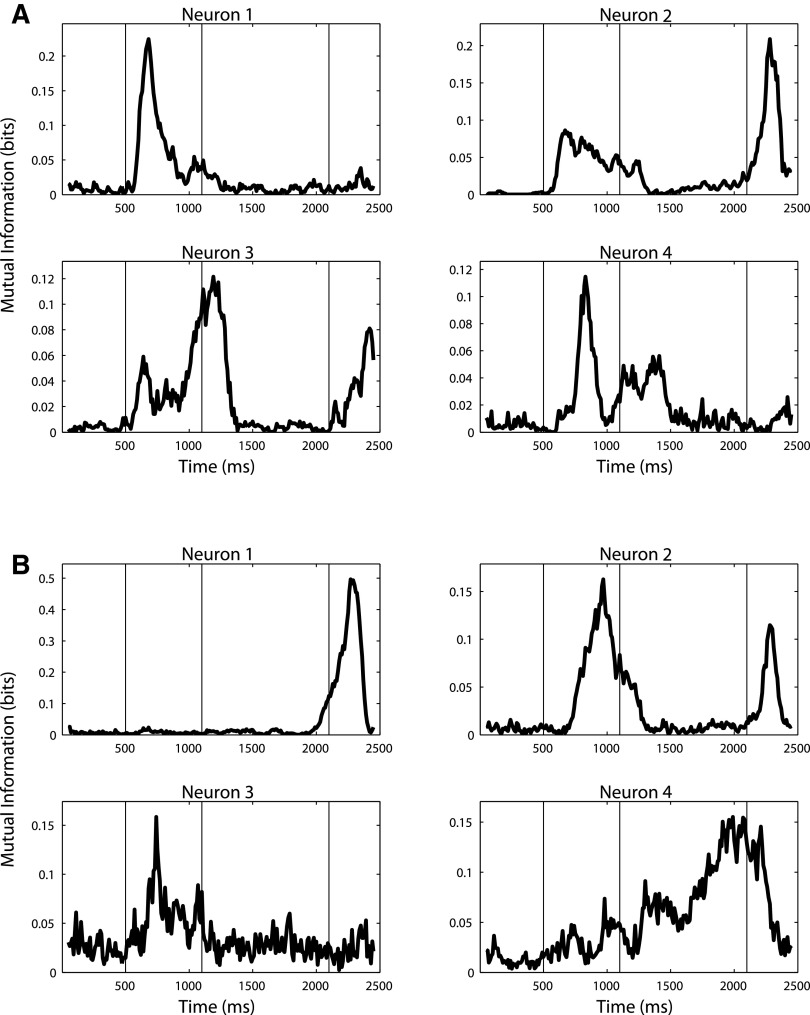
FIG. 8.

Illustration showing that many individual neurons have short periods of selectivity for ITC (A) and PFC (B). The figure plots the 4 neurons for ITC and PFC that had the highest the mutual information between the category of the SAMPLE-STIMULUS and neuron's firing rate (firing rates where calculated using 100-ms bin periods sampled every 10 ms). As can be seen, most neurons show high mutual information (MI) values for only short time periods, which is what is expected for a population code that changes with time. It is also interesting to compare neurons 1 and 4 in ITC (A) because it shows that individual neurons have different peak selectivity times even when the stimulus being shown is constant. Thus the changing of the neural code is not just due to changes in the stimulus.

Additional material can be found at http://cbcl.mit.edu/people/emeyers/jneurophys2008/.

RESULTS

Decoding information content in ITC and PFC

BASIC RESULTS.

We used a statistical classifier to decode information from neuronal populations that were recorded as monkeys engaged in a delayed match-to-category task (Fig. 1A) (Freedman et al. 2003). Figure 2 shows the accuracy levels obtained when decoding four different types of information. The decoding of identity information (i.e., which of the 42 stimuli was shown during the sample period) is shown in Fig. 2A and provides an indication of how much detailed visual information is retained despite the variability in spike counts that occur from trial to trial. Given the high physical similarity among the images along a given morph line (Fig. 1B), this is a very challenging task. There was a significant amount of information only during the sample period when the stimulus was visible, and there was much more information in ITC than in PFC (17.5 ± 5.5 vs. 5.9 ± 3.5% respectively, chance = 1/42 = 2.4%). Because information about the details of the visual stimuli was not relevant for the task in which the monkey was engaged, these results are consistent with the notion that ITC is involved in the detailed analysis of the visual information that is currently visible, whereas PFC activity only contains the information necessary for completing the task (Freedman et al. 2001; Riesenhuber and Poggio 2000).

Next we examined decoding the category of the SAMPLE-STIMULUS (i.e., whether the stimulus shown at the beginning of the sample period was a cat or a dog, Fig. 2B). When the SAMPLE-STIMULUS was first presented, ITC had a slightly higher accuracy level than PFC (92.0 ± 2.8 vs. 81.3 ± 4.3%, at t= 225 ms, chance = 50%). However, by the middle of the sample period (t = 425 ms after stimulus onset), the information in these two areas was approximately equal (82.1 ± 4.0 vs. 82.0 ± 4.2%). During the delay and decision periods, PFC had more category information about the SAMPLE-STIMULUS than ITC [delay: 66.7 ± 4.1% (PFC) vs. 56.6 ± 4.8% (ITC); decision: 88.4 ± 4.3% (PFC) vs. 77.9 ± 4.4% (ITC), chance = 50%]. Because category information is behaviorally relevant to the monkey in this task, these results support the role of the PFC in storing task-relevant information in memory during the delay period (Miller and Cohen 2001). That ITC initially had more information about the category of the SAMPLE-STIMULUS is largely due to ITC having more information related to visual properties of the stimuli, and this visual information is being used by the classifier to decode the category of the stimuli (see section on decoding abstract category information in the following text).

Figure 2C shows accuracy levels from decoding the category of the DECISION-STIMULUS (i.e., the stimulus that is presented in the beginning of the decision period). ITC had slightly more information about the category of the DECISION-STIMULUS than PFC during the decision period (93.9 ± 2.7 vs. 81.1 ± 4.3%). This is probably due to the combination of visual and abstract category information by the classifier and because there is more visual information in ITC the performance level is higher there. In contrast, PFC showed higher accuracy levels when decoding whether a trial was a match or nonmatch trial during the decision period (92.3 ± 2.7 vs. 60.5 ± 4.8% Fig. 2D), which is again consistent with PFC containing more task-relevant information than ITC.

In addition to comparing ITC to PFC, it is also instructive to directly compare different types of information within each of these areas. Figure 2, E and F, compares the decoding accuracies for three different variables: whether a trial is a match/nonmatch trial (brown), the category of the DECISION-STIMULUS (green), and the category of the SAMPLE-STIMULUS (purple) (we start the comparison in the middle of the delay period because there is no information about trial status and DECISION-STIMULUS category until the decision period). Results from ITC (Fig. 2E) reveal that during the decision period, there is much more information about the category of the DECISION-STIMULUS (green line) than about the category of the SAMPLE-STIMULUS (purple line) or about whether a trial is a match or nonmatch trial (brown). Also the match/nonmatch trial information showed the longest latency. This pattern shows that the variable that ITC has the most information about (of the 3 variables listed in the preceding text) is the most recently viewed visual stimulus and that there is less information about task-related variables. The pattern in PFC is quite different (Fig. 2F), with the most information being about task-related variables; i.e., whether a trial is a match or nonmatch trial. Also the latency of the match/nonmatch status of a trial in PFC is the same as the latency of information about the category of the DECISION-STIMULUS (and shorter than the ITC latency in the same task). It is also interesting to note that for both PFC and for ITC, the information about the category of SAMPLE-STIMULUS seems to increase just prior to the onset of the DECISION-STIMULUS presentation. This anticipatory increase of information might subserve the quick reaction times seen in the experiment.

ABSTRACT CATEGORY INFORMATION.

From a cognitive science perspective, a category often refers to a grouping of objects based on their behavioral significance, and objects within such a group do not necessarily share any common physical characteristics (Tanaka 2004). In Fig. 2B, however, the decoding accuracy level for the category of the SAMPLE-STIMULUS is influenced not only by the “abstract” behaviorally relevant category of the stimulus but also by physical visual properties of the image that are also predictive of the category that the stimulus belongs to (see Supplemental Fig. S3 for more details). To better assess how much abstract category information is in ITC and PFC that is related to the behavioral grouping of the stimuli (and that not due to physical properties of the stimuli), we trained a classifier on images derived from two dog prototypes and two cat prototypes and then tested the classifier's decoding accuracy on images derived from the remaining dog and cat prototypes (by “derived from a prototype,” we mean the images that contain ⩾60% of their morph from a given prototype). The logic behind this analysis is that if the within-category prototype images were just as visually similar to each other as they are to the between-category prototype images, then using different prototypes for training and testing should eliminate the ability of visual feature information to be predictive of which class a stimulus belongs to (because there would be as many visual features shared between the training and test sets within the same category, as there are between the two different categories; see Supplemental Fig. S3). Thus obtaining above chance classification performance in this analysis would imply that a brain region had more abstract category information. While determining the visual similarity between two images is currently an ill-defined problem, we note that the prototype images used in this experiment did vary greatly in their visual appearance (Figs. 1C and S1). Therefore this decoding method should greatly reduce the influence of visual features (see discussion for more details on image similarity). In fact, because many of the images used to test the classifier were morphs that were blended with prototype images from the opposite category, images from opposite categories were more similar in terms of the morph coefficients than images from the same category (similar results were obtained when we did not use images that were morphs between the training and test set prototypes; see Supplemental Fig. S4B).

Figure 3A, shows the decoding results of this more abstract category information for ITC (blue) and PFC (red) averaged over all nine training/test permutations [e.g., train on (c1, c2 vs. d1, d2) test on (c3, d3); training on (c1, c2 vs. d1, d3) tested on (c3, d2) etc.]. Supplemental Fig. S4A shows the results for the nine individual runs for both PFC and ITC; all individual results are the average of 50 bootstrap-like trials. During the sample period when the stimuli are first shown, PFC has as much abstract category information as ITC. During the delay and decision periods, PFC has more category information than ITC. This strongly suggests that the larger amount of category information in ITC during the sample period seen in Fig. 2B is due to the classifier combining category information in a visually based format with information in a more abstract format.

Figure 3, B and C compare the visual plus abstract category information (purple trace) that was shown in Fig. 2B with the abstract category information (orange trace) that was shown in Fig. 3A, for ITC (B) and PFC (C). For ITC, most of the category information during the sample period is visual; however, during the delay and decision periods, almost all the category information is abstract. PFC shows a similar pattern; however, there is more abstract category information (and less visual category information) during the sample period than for ITC. Thus both ITC and PFC have category information in a visual format while the stimulus is visible, and both represent information in an abstract, task-relevant format during the delay and decision period. However, the overall ratio of abstract category information relative to total category information is greater in PFC than in ITC during the sample period.

Coding of information in ITC and PFC

COMPACT AND REDUNDANT INFORMATION.

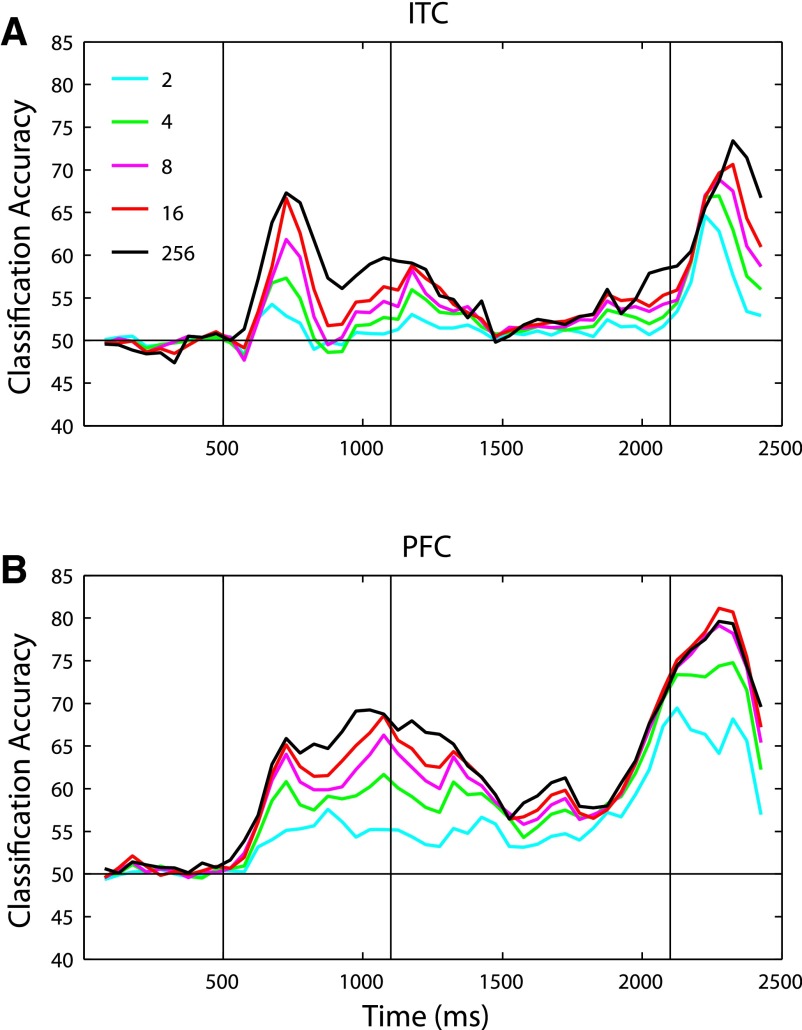
In addition to assessing what information is contained in ITC and PFC, the decoding analysis also allows us to examine how information is coded across a population of neurons. One important question of neural coding concerns whether information is contained in a widely distributed manner such that all neurons are necessary to represent a stimulus or if at a particular point in time, there is a smaller “compact” subset of neurons that contains all the information that the larger population has (Field 1994). To assess if there is a smaller compact subset of neurons in ITC and PFC conveying as much information as the larger population using population decoding, we first selected the “best” k neurons using the training data (where k < 256) and then trained and tested our classifier using only these neurons (Fig. 4) . The best k neurons were defined as those neurons with the smallest P values based on a t-test applied to all cat-trials versus all dog-trials on the training data set (see methods). The selection process was done separately for each time bin. Using the 16 best neurons, we were able to extract almost all the information that was available using 256 neurons at almost all time points for both PFC and ITC. The level of compactness of information was particularly strong in PFC during the decision period where, strikingly, eight neurons contained nearly all the information (decoding accuracy = 78.2 ± 1.2%) that was available in the whole population (79.4 ± 1.7%). It should also be noted that because our algorithm for selecting the best neurons works in a greedy fashion, the top k neurons selected might not be the best k neurons available in combination. Therefore all the information present in the entire population could potentially be contained in even fewer neurons. We also examined if there is a smaller subset of neurons that contains all the identity information (Supplemental Fig. S5) and found that for ITC, identity information seems to be less compact with the decoding accuracy not saturating until around 64 neurons. We speculate that this might be related to the fact that it takes more bits of information to code 42 stimuli than to code the binary category variable and also perhaps because identity information is not relevant for the task the monkey is engaged in.

FIG. 4.

Readout using the “best” 2, 4, 8, or 16 neurons, compared with readout using all 256 neurons, for ITC (A) and PFC (B). As can be seen for almost all time periods, the abstract category information available in whole population is available in only ≤16 neurons. The best neurons were determined based on t-test between cats and dogs using the training data. Because the algorithm used to select the best neurons works in a greedy manner and is not necessarily optimal, the information reported in the subsets of neurons is an underestimate of how much information would be present if the optimal k neurons were selected.

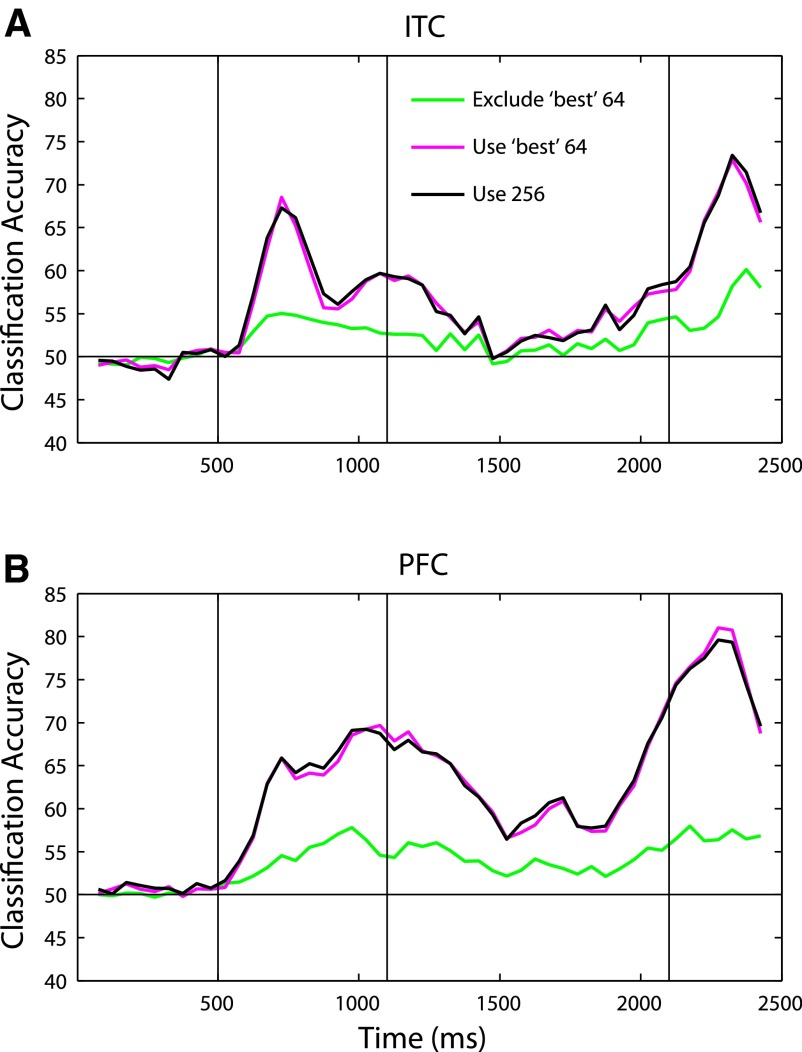
Redundancy allows a system to be robust to degradation of individual neurons or synapses. This robustness constitutes a key feature of biological systems. To asses if there is redundant information present in the population of neurons, we again selected the k best neurons from the training set, but this time we excluded these neurons from training and testing and used the remaining 256 − k neurons for our analyses. We note that this analysis aims to assess whether there is redundant information (as opposed to estimating how much redundant information there is in the Shannon sense of redundancy). Figure 5 compares the classifier's performance using the best 64 neurons to its performance excluding the best 64 neurons. The best 64 neurons contain as much information as the whole population (magenta line). However, even when these best 64 neurons are excluded, and the remaining 192 neurons are used instead, classification performance is above chance at almost all time points (green line). Because the best 64 neurons contain as much information as the whole population, the fact the excluding these neurons does not lead to chance classification performance implies that these remaining 192 neurons contain a nonnegligible amount of redundant information with the best 64 neurons. In fact, even when half the neurons are removed, decoding accuracy is still above chance at almost all time points (Supplemental Fig. S6).

FIG. 5.

Illustration of redundant information in ITC (A) and PFC (B). The magenta line indicates the readout performance when the top 64 neurons were used, and the green line indicates when the top 64 neurons were excluded and the remaining 192 neurons were used. As can be seen, the top 64 neurons achieve a performance level that is as good as using the whole population of 256 neurons. However, even when these neurons are excluded, readout is above chance, indicating that there is redundant information in these populations.

TIME-DEPENDENT CODING OF INFORMATION.

Another interesting question in neural coding is whether a given variable is coded by a single pattern of neural activity in a population, as in a point attractor network (Hopfield 1982), or whether there are several patterns that each code for the same piece of information (Laurent 2002; Perez-Orive et al. 2002). To address this question, we trained a classifier with data from one time bin relative to stimulus onset and tested the classifier on data from different time bins (in all the results reported in the preceding text, training and testing were done using the same time period relative to stimulus onset). If, at all time periods, the same pattern of activity is predictive of a particular variable, then the decoding accuracy should always be highest (or at least should not decrease) when training a classifier with data from time periods that have the maximum decoding accuracy levels because the data from these time periods presumably have the least noise and would therefore lead to the creation of the best possible classifier. Alternatively if the pattern of activity that is indicative of a relevant variable changes with time (and is time-locked to the onset of a stimulus/trial), then high decoding accuracies would only be achieved when using training and testing data from the same time period.

Figure 6, A and B, shows accuracy levels for decoding abstract category information when training a classifier with data from one time period (indicated by the y axis) and testing with data from a different time period (indicated on the x axis). As can be seen for both ITC and PFC, the highest decoding accuracies for each time bin occur along the diagonal of the figure, indicating that the best performance is achieved when training and testing is done using data from the same time bin relative to stimulus/trial onset. Additionally, for ITC, the decoding performance is also high when training using data from the sample period and testing using data from the decision period and vice versa, whereas for PFC, there seems to be little transfer between any different time periods. The pattern of transfer between the sample and the decision periods in ITC might indicate that there is indeed one pattern of activity in ITC that codes for the abstract category of the stimulus regardless of time; alternatively, this result might be due to visual information that is similar in the sample and decision stimuli, as the decision stimuli were created from random morphs between the prototype images. Figure 6, C and D, compares the decoding accuracies from training on three of these “fixed” time points (colored lines) to training and testing a classifier using data from the same time period (black lines) in a format that is similar to Figs. 2 and 3 (i.e., these are plots of 3 rows of Fig. 6, A and B, at time points during the sample, delay, and decision periods and compares them to the results in Fig. 3A). These plots again show that the highest decoding accuracy occurs when training and testing using data from the same time period, which implies that indeed the pattern of activity that codes for a particular piece of information changes with time.

FIG. 6.

Evaluating whether the same code is used at different times for abstract category information. A: in ITC there is some similarity in the neural code for abstract category information in the sample and the decision periods, as can be seen by the green patches near the top right and bottom left of the figure. Also there appears to be two different codes used during the sample period as can be seen by the two blob regions occurring 775–1,275 ms after the start of the trial. B: for PFC, the code for abstract category information seems to be constantly changing with time as indicated by the fact that the only high decoding accuracies are obtained along the diagonal of the plot. C and D: examples of decoding accuracies using 3 fixed training times from the sample, delay and decision periods (colored lines) compared decoding accuracies obtained when training and testing using the same time period (black line) for ITC (C) and PFC (D); (each of these plots corresponds to 1 row from the from A or B and the black line corresponds to the diagonal of this figure and is the same line as shown in Fig. 3A). These figures again illustrate that the highest performance is always obtained when training and testing is done using the same time bin relative to stimulus/trial onset, which suggests that the neural coding of abstract category information is time-locked to stimulus/trial onset.

Next we tested whether this changing pattern of activity was only due to neural adaptation in a fixed set of neurons or whether indeed different neurons were carrying the relevant information at different points in time. To address this question, we conducted analyses in which we eliminated the best 64 neurons (of 256 random neurons selected on each bootstrap trial) at one 150-ms time period (indicated on the y axis in Fig. 7) and training and test data were taken from a different 150-ms time period (indicated on the x axis). If the same small subset of neurons codes for abstract category information at all time periods, then eliminating these neurons from one time period should result in poor decoding accuracy at all time periods. Alternatively if different small subsets of neurons contain the abstract category information at different time periods, then there should only be a decrease in performance in the time period where the best neurons were removed. Results for both ITC and PFC show a clear pattern of lower decoding accuracies along the diagonal but largely unchanged decoding accuracies almost everywhere else, which indicates that different neurons contain the category information at different time points in a trial. Figure 7 also clearly shows that the neural code is changing faster than changes in the stimuli as illustrated by the fact that there is also a decrease only along the diagonal during the sample, delay, and decision periods even though the stimulus is not changing during these times. Additionally, Supplemental Fig. S7 shows that the neurons that code for identity information also change through the course of a trial, although the changes in code seem to be much less dramatic than is seen for the changes in code for abstract category information.

To further examine the duration of selectivity for individual neurons, we calculated an estimate of the mutual information (MI) between the category of the stimulus, and the average firing rate of neurons in 100-ms bins (see methods). Figure 8 shows the MI as a function of time for the four neurons that had highest MI at four different time bins. As can be seen for both PFC and ITC, individual neurons have short time windows of selectivity as expected from the results showing changing patterns of coding at the population level. It is also interesting to compare neurons 1 and 4 in Fig. 8A, where we can see two ITC neurons that are selective at slightly different times during the sample period even though the stimulus is constant during this time. This further supports the point that individual neuron's selectivity are occurring on a faster time scale than the changes in the stimuli.

DISCUSSION

We applied population decoding methods to neuronal spiking data recorded in PFC and ITC to gain more insight into what types of information are contained in these regions as well as how information is represented in these regions. By pooling information from hundreds of neurons, we were able to observe the time course of the flow of information in these areas with a fine time scale. Results from basic decoding analyses (Fig. 2) showed that ITC contained more information related to the currently viewed stimulus than PFC, while PFC contained more task-relevant information than ITC, which is largely consistent with the results originally reported by Freedman et al. (2003). The finer temporal precision in our analyses also revealed an anticipatory response in both ITC and PFC, in which information about the category of the SAMPLE-STIMULUS reemerged just prior to the onset of the DECISION-STIMULUS, which seems similar to the increase in firing rate seen just prior to the onset of the decision period reported by Rainer et al. (Rainer and Miller 2002; Rainer et al. 1999) in macaque delayed match-to-sample experiments. We speculate that this anticipatory reemergence of category information might be involved in preparing the network for processing the imminent decision stimulus as soon as it is shown, which could account for the monkeys' fast reaction times.

The ability to train a pattern classifier on data of one type and test how well the classifier generalizes to data recoded under different conditions is very useful for obtaining more compelling answers to several questions. By training a classifier on data from a subset of images from one category and then testing on data recorded when a different disjoint subset of images was shown, we were able to get a better estimate of how much abstract category information is contained in both ITC and PFC (for more information about PFC's role in other categorization tasks, see Nieder et al. 2002; Shima et al. 2007). Results from our analysis of abstract category information revealed that there is initially as much abstract category information in ITC as PFC, which was not seen in the original analyses by Freedman et al. (2003) due to the long length of the time periods used in their analyses as well as potential biases introduced by only using “selective” neurons when creating category-selective indices (see introduction).

The fact that there initially appears to be as much abstract category information in ITC as PFC (Fig. 3) raises several questions about ITC's role in categorization. One of the simplest explanations for the presence of abstract category information in ITC is that despite the morph paradigm used, the prototype images from the same category are more visually similar to each other than they are to the images from the other category (i.e., the 3 cat prototype images are more similar to each other than they are to the dog prototype images). If this was the case, then the classifier would be able to generalize across images from different prototypes from the same category based purely on visual information, which could explain the results (Sigala and Logothetis 2002). Analyses using a computational model of object recognition described in Serre et al. (2007) indeed suggest that prototype images are slightly more similar to each other than to prototypes from the opposite category. However, the level of similarity seems to be weaker than what is observed in the neural data. A direct test of whether visual image properties is giving rise to our findings could be done by running the same DMC experiment but using a different category boundary as was previously done for PFC (Freedman et al. 2001).

If indeed there is abstract category information in ITC that is not due to visual cues, this suggests that there is a “supervised” learning signal in ITC that is causing neurons in ITC to respond similarly to stimuli from the same category. One possible source of this supervised learning signal is that during the course of the sample presentation, PFC extracts category information from the signals arising in ITC and feeds this category information back to ITC (Tomita et al. 1999). However, with the resolution of our analyses, we could not detect any clear latency differences between the category information arising in PFC and ITC (see Supplemental Fig. S8). Given that there could be a single synapse between neurons in these two brain areas, the latency differences could be too small to detect (Ungerleider et al. 1989). Alternatively, ITC could have acquired abstract category information during the course of the monkey being trained in the task. In this scenario, which is similar to the model proposed by Risenhuber and Poggio (2000), the activity of “lower level” neurons that are selective to individual visual features present in particular stimuli are pooled together by “higher level” neurons through a supervised learning signal enabling these higher level neurons to respond similarly to all members of a given category irrespective of the visual similarity of individual members of the category. It should be noted that more recent models (e.g., Serre et al. 2007) propose a supervised learning signal is only present in PFC, while the presence of abstract category information in ITC suggests this supervised learning signal might be organizing the response properties of neurons earlier in the visual hierarchy (Mogami and Tanaka 2006); however these models could be easily modified to incorporate a supervised learning signal in stages before PFC. Because these monkeys have had an extensive amount of experience with these stimuli, it is also possible that a consolidation process has occurred when the monkey learned the task. For category grouping behavior that occurs on shorter time scales, it is possible that category signals would only be found in PFC.

By analyzing data over long time intervals, most physiological studies assume tacitly or explicitly that the neural code remains relatively static as long as the stimulus remains unchanged. We examined how stationary the neural code is by training the classifier using data from one time period and then testing with data from a different time period (Fig. 6). These analyses suggest that the pattern of activity coding for a particular stimulus or behaviorally relevant variable changes with time. Such results are consistent with the findings of Gochin et al. (1994), in whose study a paired-associate task was used to show that the pattern of activity in macaque ITC that is indicative of a particular stimulus during a sample period is different from the pattern of activity that is indicative of the same stimulus during a second stimulus presentation period. Also Nikolic et al. (2007) reported dynamic changes in the weights of separating hyperplanes for discriminating between visual letters using data from macaque V1. These observations suggest that the coding of particular variables through changing patterns of activity might be a general property of neural coding throughout the visual system. However, because adaptation or other nonlinear scaling of firing rates could potentially explain these results as an artifact of the decoding procedure in these studies, we further tested how stationary the neural code is by eliminating the best neurons from one time period and testing the classifier on data from another time period (Fig. 7). Results from this analysis show that there is only a temporally localized drop in classification accuracy, which indicates that different neurons carry information about the same variable at different time periods. Additionally, analyses of mutual information showed that most individual neurons are only selective for short time windows. These observations are consistent with the findings of Zaksis et al. (Zaksas and Pasternak 2006), who used an ROC analysis to show that many neurons in PFC and MT only have short time periods of selectivity. Baeg et al. (2003) also showed that past and future actions of rats can be decoded based on PFC activity during a delay period even when neurons with sustained activity are excluded from the analysis; this again agrees with our observations showing that the pattern of neural activity that codes information changes with time. While previous studies have concluded that neurons with short periods of selectivity play an important role in memory of stimuli, we also speculate that these dynamic patterns of activity might be important for the coding of a sequence of images so that the processing of new stimuli do not interfere with those just previously seen and could underlie the ability of primates to keep track of the relative timing of events.

An ongoing debate concerning the neural code is whether information is transmitted using a “rate code” in which all information is carried in the mean firing rate of a neuron within a particular time window, or whether a temporal code is used in which information is carried in by the precise timing of individual spikes (deCharms and Zador 2000). While the results in this paper cannot conclusively answer which coding scheme is correct, they do give some insight into this debate. First, because we decode mean firing rates over 150-ms bins (and shorter time bins tended to achieve lower decoding accuracies), our findings suggest that a large amount of information is still present even when the precise time of each spike is ignored (also see Hung et al. 2005). While it is possible that superior decoding performance could be achieved by using an algorithm that took exact spike times into account, considering the high performance level at certain time periods in the experiment (e.g., decoding of match versus nonmatch trial information is over 90% in PFC during the decision period, which is comparable to the 90% correct animals' performance), often there is not much more information left to extract. Second, because our results show that the pattern of neural activity that is predictive of a particular variable changes with time and that this change occurs on a faster time scale then changes in the stimulus, these findings argue against a strict rate based coding scheme in which all information about a stimulus is coded by the firing rate alone. Thus our findings suggest that neurons in ITC and PFC maintain information in their mean firing rates over time windows on the order of a few hundred milliseconds and that these periods of selectivity are time-locked to particular task events (with different neurons having different time lags), giving rise to a dynamic coding of information at the population level.

Applying feature selection methods prior to using pattern classifiers allowed us to characterize the compactness and redundancy of information in ITC and PFC. Results from these analyses revealed that at any one point in time, all the abstract category information available is contained in a small subset of neurons. However there still is a substantial amount of redundant information between this small highly informative subset of neurons and the rest of the more weakly selective neurons in the rest of the population. While other studies have examined sparse spiking activity in several different neural systems (Hahnloser et al. 2002; Perez-Orive et al. 2002; Quiroga et al. 2005; Rolls and Tovee 1995), and theoretical models have been proposed that analyze the implication of this sparse activity (Olshausen and Field 1997), our notion of compactness of information differs from these measures because we are not focused on whether neurons are firing, but rather we are focused on the information content that is carried by this spiking activity. It should also be noted that our notion of compactness of information differs the notion compactness described by Field (1994), because Field's notion of compactness implies that all neurons are involved in the coding for a stimulus, while our results suggest that only a small subset of a larger population of neurons contain the relevant information and that this subset of neurons changes in time (thus our notion of compactness could be equally well characterized as sparseness of information, however given the strong association in the literature between the term sparseness and firing rate, we found using this terminology to be confusing). Thus our measure adds a new and potentially useful statistic for understanding how information is coded in a given cortical region.

The neuronal responses studied here were not recorded simultaneously, and the creation of pseudo-populations can alter estimates of the absolute amount of information that a population contains because of noise correlations (Averbeck and Lee 2006; Averbeck et al. 2006). However, we were interested in relative information comparisons between different time periods or between different brain regions, so our conclusions would not be substantially altered by having data from simultaneous recordings. Furthermore, empirical evidence suggests that decoding using pseudo-populations returns roughly the same results as when using simultaneously recorded neurons (Aggelopoulos et al. 2005; Anderson et al. 2007; Baeg et al. 2003; Gochin et al. 1994; Nikolic et al. 2007; Panzeri et al. 2003). Our estimates of the absolute amount of information in the population could also be affected by the amount of data we have, the quality of the learning algorithms (however, see Supplemental Fig. S2, which suggests this is not an issue), and the features used for decoding. However, because in principle these issues affect all time points and brain areas equally, relative comparisons should be largely unaffected by them.

The ability to decode information from a population of neurons does not necessarily mean that a given brain region is using this information or that downstream neurons actually decode the information in the same way that our classifiers do. Our results using analyses in which the classifier is trained with one type of stimuli and must generalize to a different but related type of stimuli, supports the notion that the animal is using this information because such generalization implies a representation that is distinct from properties that are directly correlated with the stimuli, and having such an abstract representation coincidentally would be highly unlikely. For this reason, most of the analyses in this paper have focused on abstract category information (Figs. 3–7) because this information meets our criteria of being abstracted from the exact stimuli that are shown and hence is most likely utilized by the animal.

Using population decoding to interpret neural data is important because it examines data in a way that is more consistent with the notion that information is actually contained in patterns of activity across many neurons. By computing statistics on random samples of neurons, most analyses of individual neurons implicitly assume that each neuron is independent of all others and that neural populations are largely homogenous. However, such implicit assumptions are contrary to the prevailing belief that brain regions contain circuits of heterogeneous cells that have different functions and is inconsistent with empirical evidence (compact coding of information and activity) seen in this and other studies. The methods discussed in this paper can help align a distributed coding theoretical framework with analysis of actual empirical data, which should give deeper insights into the ultimate goal of understanding the algorithms and computations used by the brain that enable complex animals, such as humans and other primates, to make sense of our surroundings and to plan and execute successful goal-directed behaviors.

GRANTS

This research was sponsored by grants from: National Science Foundation, National Institute of Mental Health, and Darpa. Additional support was provided by: Children's Ophthalmology Foundation, Epilepsy Foundation, National Defense Science and Engineering Graduate Research Fellowship program, Honda Research Institute USA, NEC, Sony, and the Eugene McDermott Foundation. Additional supplementary material can be found at http://cbcl.mit.edu/people/emeyers/jneurophys2008/.