Using a Model to Assess the Role of the Spatiotemporal Pattern of Inhibitory Input and Intrasegmental Electrical Coupling in the Intersegmental and Side-to-Side Coordination of Motor Neurons by the Leech Heartbeat Central Pattern Generator

Abstract

Previously we presented a quantitative description of the spatiotemporal pattern of inhibitory synaptic input from the heartbeat central pattern generator (CPG) to segmental motor neurons that drive heartbeat in the medicinal leech and the resultant coordination of CPG interneurons and motor neurons. To begin elucidating the mechanisms of coordination, we explore intersegmental and side-to-side coordination in an ensemble model of all heart motor neurons and their known synaptic inputs and electrical coupling. Model motor neuron intrinsic properties were kept simple, enabling us to determine the extent to which input and electrical coupling acting together can account for observed coordination in the living system in the absence of a substantive contribution from the motor neurons themselves. The living system produces an asymmetric motor pattern: motor neurons on one side fire nearly in synchrony (synchronous), whereas on the other they fire in a rear-to-front progression (peristaltic). The model reproduces the general trends of intersegmental and side-to-side phase relations among motor neurons, but the match with the living system is not quantitatively accurate. Thus realistic (experimentally determined) inputs do not produce similarly realistic output in our model, suggesting that motor neuron intrinsic properties may contribute to their coordination. By varying parameters that determine electrical coupling, conduction delays, intraburst synaptic plasticity, and motor neuron excitability, we show that the most important determinant of intersegmental and side-to-side phase relations in the model was the spatiotemporal pattern of synaptic inputs, although phasing was influenced significantly by electrical coupling.

INTRODUCTION

Underlying many rhythmic activities such as walking, swimming, chewing, or breathing are rhythmically active neuronal networks that are capable of controlling the timing of these motor patterns in the absence of sensory input (Marder and Calabrese 1996). Analysis of these central pattern generators (CPGs) using both physiological and modeling approaches has helped to elucidate how motor patterns are controlled by the nervous systems as well as the general aspects of network function that carry over into all neuronal networks, both sensory and motor (Marder and Calabrese 1996; Marder et al. 2005). The hallmark of CPG action is that the isolated nervous system can produce a fictive motor pattern that mimics the pattern seen in the intact or semi-intact preparations.

In most cases, with the notable exception of the CPGs of the crustacean stomatogastric nervous system (Marder and Bucher 2007), motor neurons are not considered to participate in the production of fictive motor patterns, although their activity is driven and shaped by their synaptic input from premotor interneurons (e.g., Kiehn 2006). This is not to say that they are passive followers; they can feed back onto the pattern generator (e.g., Kiehn 2006; Kristan Jr et al. 2005), they may express voltage-dependent conductances that shape their output (e.g., Alaburda et al. 2002; Toledo-Rodriguez et al. 2005), and their electrical coupling may contribute to shaping their output (e.g., Kristan Jr et al. 2005; Marder and Bucher 2007). Recently, however, the importance of motor neuron intrinsic properties for fictive motor patterns has been called into question (Alaburda et al. 2005). Nevertheless, any assessment of the role of motor neurons in shaping fictive motor patterns must begin with a complete description of the spatiotemporal pattern of their synaptic drive and should involve realistic modeling.

In three preceding reports (Norris et al. 2006, 2007a,b), we presented a quantitative description of the spatiotemporal pattern of inhibitory synaptic input from the heartbeat CPG to segmental motor neurons that drive heartbeat in medicinal leeches and the resultant relative coordination of CPG interneurons and motor neurons. Here we begin the process of elucidating the relative roles of this pattern of input and intrasegmental electrical coupling of motor neurons in elaborating the heartbeat fictive motor pattern. We explore intersegmental and side-to-side coordination in an ensemble model of all heart motor neurons and their known synaptic inputs and electrical coupling (Fig. 1). In this model, motor neuron intrinsic properties were kept simple, so that we could determine the extent to which input and electrical coupling together can account for observed coordination in the living system in the absence of a substantive contribution from the motor neurons themselves.

FIG. 1.

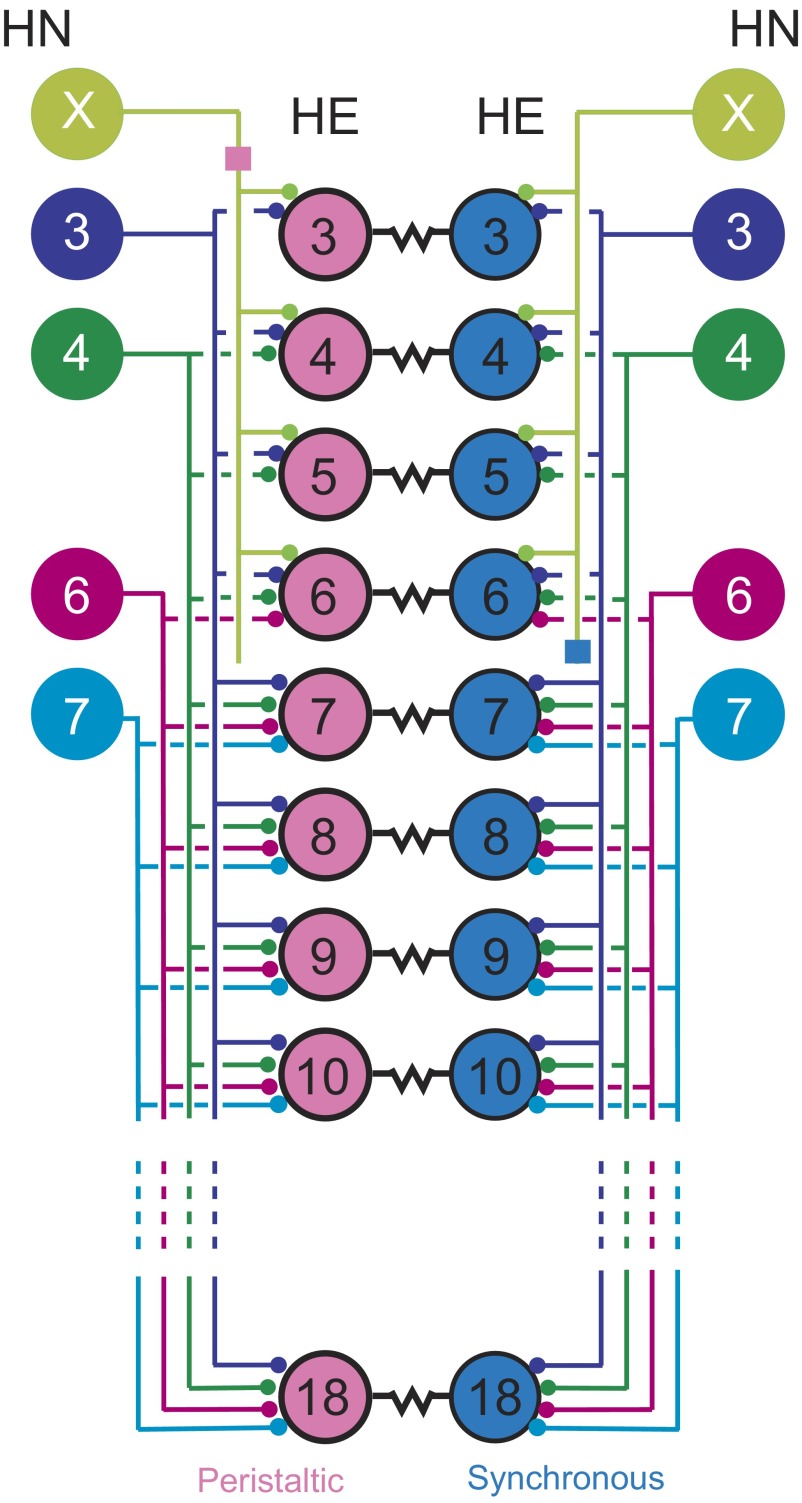
The leech heart motor neuron ensemble: inputs from the central pattern generator (CPG) and electrical coupling. A bilateral circuit diagram showing all the premotor heart (HN) interneurons [identified HN(3), HN(4), HN(6), HN(7), and unidentified HN(X)] of the CPG and their pattern of synaptic connections to ipsilateral heart (HE) motor neurons in HE(3)–HE(18). Large colored circles are cell bodies and associated input processes. Lines indicate cell processes; small colored/black circles indicate inhibitory chemical synapses; small colored boxes on the HN(X) interneurons' axons are putative spike initiation sites, peristaltic and synchronous; and resistors indicate electrical coupling between the bilateral heart motor neurons in the same segment. Standard colors for the identified interneurons are used throughout: lime green for the HN(X), blue for the HN(3), green for the HN(4), magenta for the HN(6), and cyan for the HN(7) interneuron. Peristaltically coordinated motor neurons are pink and synchronously coordinated motor neurons are light blue. The HN(X) interneuron is defined as one that gives rise to matched inhibitory postsynaptic potentials in ipsilateral HE(3)–HE(6) heart motor neurons and rectifying electrical coupling potentials in ipsilateral HN(3) and HN(4) interneurons (Calabrese 1977).

In two previous reports (Norris et al. 2007a,b), we provide detailed background on the leech heartbeat system; thus here we only briefly summarize (for a recent review see Kristan Jr et al. 2005). The two longitudinal heart tubes are innervated in each segment of the midbody (segments 3–18) by the ipsilateral member of a single electrically coupled (Peterson 1983) bilateral pair of heart [HE(3)–HE(18)] motor neurons (Maranto and Calabrese 1984). The heart motor neurons are rhythmically inhibited ipsilaterally by a set of four bilateral pairs of identified and one unidentified pair of premotor heart [HN(3), HN(4), HN(6), HN7), and HN(X) corresponding to segments 3, 4, 6, 7, and unknown] interneurons that are members of the heartbeat CPG (Fig. 1). The fictive motor pattern for heartbeat is bilaterally asymmetric; motor neurons on one side fire in a rear-to-front progression (peristaltic), whereas those on the other fire in near synchrony (synchronous) but with strict side-to-side coordination (Wenning et al. 2004). The asymmetry is not permanent, but rather the motor neurons of the two sides change roles (patterns) every 20–40 heartbeat cycles. We infer that there are no permanent asymmetries in the heartbeat motor network or its component neurons. The temporal pattern of the activity of the premotor interneurons has been described quantitatively and, like that of the motor neurons, is bilaterally asymmetric with strict side-to-side coordination and regular side-to-side switches of peristaltic and synchronous patterns (Norris et al. 2006). The pattern, strength, and intraburst synaptic plasticity of the inhibitory connections from the premotor interneurons to the motor neurons (spatial pattern) has also been quantitatively described and are not bilaterally asymmetric (Norris et al. 2007b). Moreover, we have also described in quantitative detail the relative phasing of heart motor neurons to one another and to their premotor inputs (Norris et al. 2007b; Wenning et al. 2004). Our model was designed to determine the extent to which the measured spatiotemporal pattern of synaptic input and intrasegmental electrical coupling of heart motor neurons can account for the intersegmental and side-to-side coordination of heart motor neurons observed during fictive heartbeat. Ultimately we seek to explain the relative phasing of each heart motor neuron with the premotor heart interneurons that provide its input.

METHODS

Heart motor neurons (HE) from HE(R,3) to HE(L,18) and heart interneurons (HN) from HN(R,1) to HN(L,7) are indexed by body side and midbody ganglion number. One unidentified heart interneuron is indexed HN(R/L,X) because its ganglionic origin is unknown. In our models, the left motor neurons always received a peristaltic input from the left interneurons and the right motor neurons always received synchronous input from the right interneurons, so we dispensed with body-side indexing and simply labeled the interneuron or motor neuron as peristaltic or synchronous.

General modeling strategy

The heart motor neuron ensemble model was implemented using GENESIS (GEneral NEural SImulation System) software (Bower and Beeman 1998). Each of the 32 heart motor neurons (16 bilateral pairs) (Fig. 1) was modeled as a single-compartment neuron with intrinsic conductances, inhibitory synaptic conductances, and a conductance for the electrical junctions linking bilateral segmental pairs. Inhibitory synaptic input onto the model motor neurons arises from ipsilateral premotor heart (HN) interneurons: four identified bilateral pairs—the HN(3), HN(4), HN(6), and HN(7) interneurons—and one unidentified bilateral HN(X) pair. The timing of these inputs (temporal pattern) was derived from 13 bursts of heart interneuron extracellular recordings in a particular living preparation and the strengths of each input (spatial pattern) and the intersegmental conduction delays, as well as the estimated time course of synaptic plasticity, were from averaged voltage-clamp recordings: both temporal and spatial patterns are subsequently described in detail. The simulation ran for 60 s with a time step of 0.0001 s, and the middle 10 bursts of the motor neurons (fictive motor pattern) sculpted from the 13 bursts of inhibitory input were used in the analysis. Each of the 16 segmental modules of our heart motor neuron ensemble model consisted of a bilateral pair of electrically coupled model motor neurons in one ganglion and their associated synaptic inputs.

Modeling intrinsic cellular properties

The current balance equation for the membrane potential (V) of each individual model heart motor neuron was

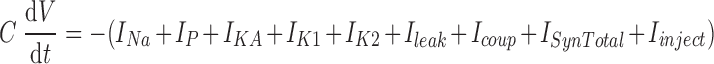(1)

where t is time, C is total membrane capacitance, I_leak is the leak current, I_coup is the junctional current for the electrical coupling, I_SynTotal is the sum of the synaptic currents for the inhibitory chemical synapses, and I_inject is any injected current. Each motor neuron contained five voltage-dependent ionic currents: 1) a fast Na⁺ current (I_Na), 2) a persistent Na⁺ current (I_P), 3) a fast transient K⁺ current (I_KA), 4) an inactivating delayed rectifier K⁺ current (I_K1), and 5) a noninactivating delayed rectifier K⁺ current (I_K2). The Hodgkin–Huxley equations (Hodgkin and Huxley 1952) describing these currents were those used for a model of an oscillator heart interneuron (Hill et al. 2001). The maximal conductances, ḡ_ion, of the currents were set empirically to match the general activity of heart motor neurons recorded intracellularly in the living system (ḡ_Na = 200 nS, ḡ_P = 8.5 nS, ḡ_KA = 50 nS, ḡ_K1 = 100 nS, ḡ_K2 = 80 nS). The specific membrane resistance was 1.1 Ωm²; the specific membrane capacitance was 0.05 Fm⁻². Each motor neuron was modeled as an isopotential cylinder with length and diameter equal (60 μm). With these cell proportions, the input resistance of each model motor neuron was 97 MΩ, which falls within the range measured in the living system (Opdyke and Calabrese 1995).

Modeling premotor inhibitory synaptic inputs

TEMPORAL PATTERN.

Sixty seconds of simultaneous extracellular recordings from ipsilateral HN(3), HN(4), HN(6), and HN(7) premotor interneurons in both the synchronous and the peristaltic coordination modes were used to generate a temporal pattern of synaptic inputs for the model motor neurons (like Fig. 2 in Norris et al. 2006). The peristaltic and synchronous input patterns were aligned to one another by assigning a phase of 0.0 to the middle spike of first peristaltic HN(4) burst (absolute phase marker) and a phase of 0.511 to the middle spike of the first synchronous HN(4) burst, which is the average side-to-side phase difference between the peristaltic and synchronous HN(4) activity observed in the living system (Norris et al. 2006). The period of the data set used for playback in our standard ensemble model was 4.3 s. The average period for the living system varies from 4.0 to 8.5 s (average 5.8 s) (Norris et al. 2006). Extracellular recordings of the spike times are not available for the HN(X) interneuron, so its temporal pattern was bootstrapped to conform generally to its pattern of inhibitory postsynaptic currents (IPSCs) recorded in heart motor neurons (Norris et al. 2006). Because we used recordings from living preparations to produce the temporal input pattern to the model, the temporal pattern is not precisely regular and each cycle of input to each model motor neuron is different. Therefore burst characteristics such as period and phase in the model show a certain variance.

FIG. 2.

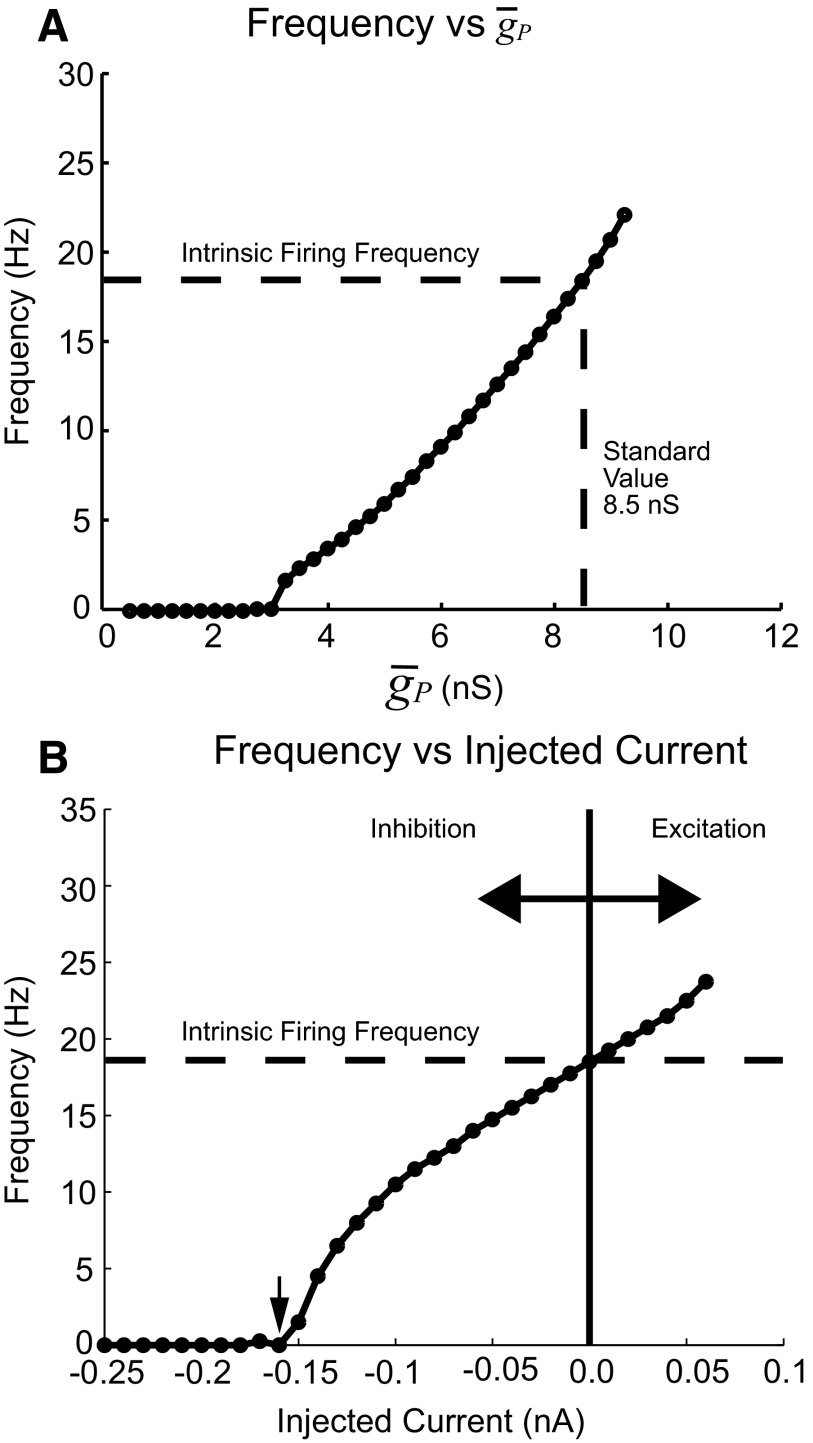
Intrinsic firing properties of model heart motor neurons in the absence of synaptic inputs and electrical coupling. A: I_P is a noninactivating depolarizing current producing tonic activity in the model motor neuron. The average firing frequency measured over 10 s increased with the maximal conductance of the persistent Na⁺ current (ḡ_P) and the relationship was nearly linear over the range from 4.75 to 10.25 nS. The value of ḡ_P (8.5 nS) used in the standard heart motor neuron ensemble model was chosen by matching the intrinsic firing frequency to the measured firing frequency observed in extracellular recordings (Norris et al. 2007b). B: frequency vs. injected current curve for a model motor neuron. The intrinsic firing frequency (ḡ_P = 8.5 nS) was 18 Hz. Applying −0.16 nA of current silenced the tonic spiking activity (arrow). When synaptic input was present, the motor neuron firing frequency varied from zero (0 Hz) to at or near the intrinsic firing frequency according to the amount of inhibition received by the model motor neuron (see text).

Intersegmental conduction delays were assigned to be 20 ms per segment, in conformity with measurements from the living system (Fig. 3B in Norris et al. 2007a). Spikes in the identified premotor neurons in both coordination modes and the HN(X) interneuron in the peristaltic mode travel rearward, whereas the HN(X) interneuron's spike in the synchronous mode travels frontward (Calabrese 1977). The temporal pattern of synaptic inputs was then constructed for each segmental module from the basic peristaltic (for left model motor neurons) and synchronous (for right model motor neurons) spike time patterns offset by the appropriate intersegmental conduction delays. (Figure 8 shows the temporal pattern of all of the inputs used in the model as a phase diagram.)

FIG. 3.

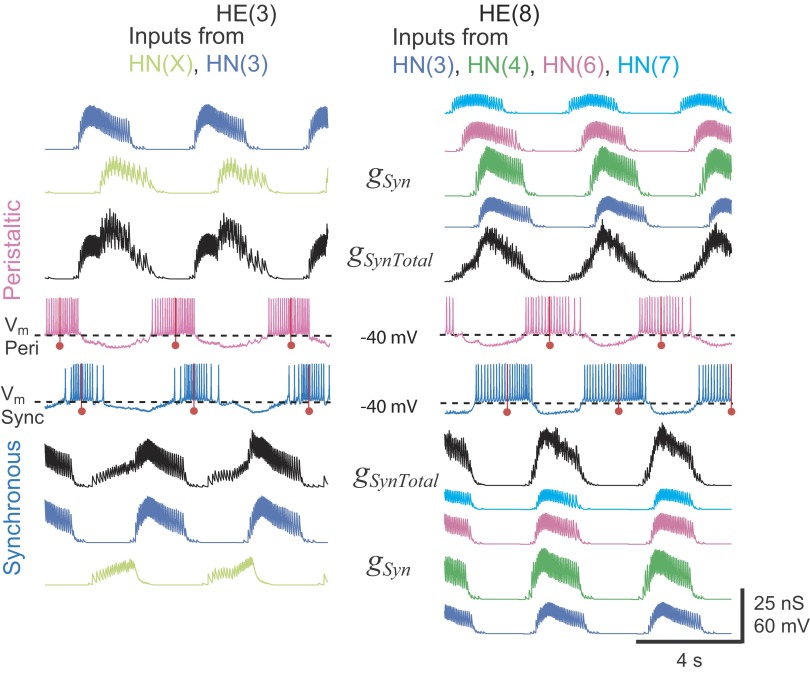
The spatiotemporal pattern of synaptic input to model heart motor neuron pairs. Simultaneous bilateral records of membrane potential (V_m: pink, peristaltic; blue, synchronous) and synaptic conductance of each independent input (g_Syn, color coded) and summed (_gSynTotal) in HE(3) and HE(10) model motor neuron pairs. The middle spikes in the heart motor neuron bursts are indicated by a red line with a ball. The HE(3) model motor neurons receive synaptic input from two sources: the ipsilateral HN(X) (lime green) and the HN(3) (blue) interneurons. The HE(10) model motor neurons receive input from 4 of the 5 ipsilateral premotor heart interneurons [HN(3), blue; HN(4), green; HN(6), magenta; and HN(7), cyan].

FIG. 8.

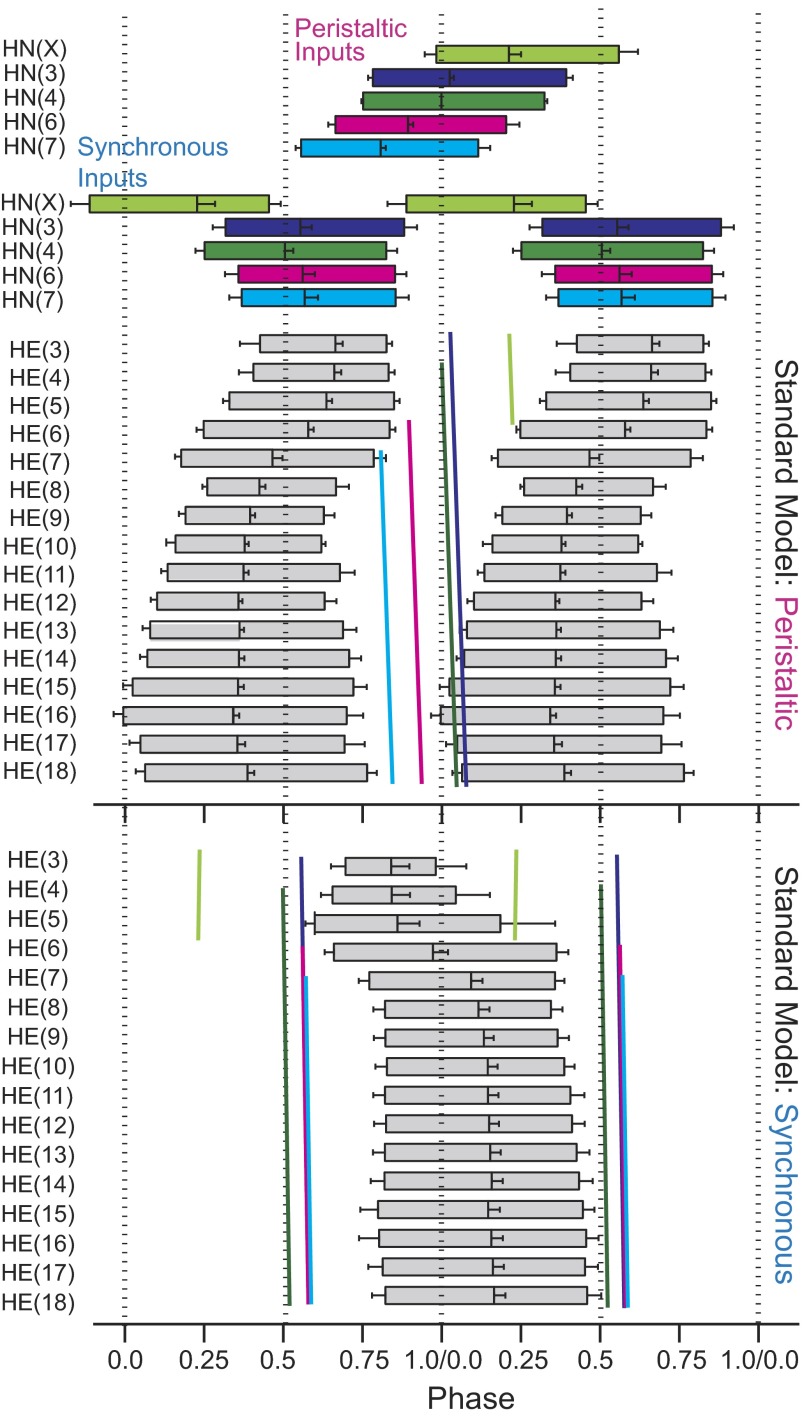
Summary phase diagram of the standard ensemble model: premotor synaptic inputs (top) and motor neuron activity (bottom). In these diagrams, the average timing of bursts in the heartbeat cycle is represented by boxes. The leftmost edge is the timing of the average first spike and the rightmost edge is the average timing of the last spike in the bursts. The middle spike (i.e., phase) is designated by the vertical line near the center of each box. Premotor inputs are color coded as in Fig. 1: HN(X), lime green; HN(3), blue; HN(4), green; HN(6), magenta; and HN(7), cyan. The peristaltic HN(4) premotor interneuron [in this case the HN(L,4) interneuron] was used as the phase reference (0.0 phase) for the activity of all model motor neurons and their premotor synaptic inputs. Slanted vertical lines represent the phase (middle spike) of each of the premotor inputs in peristaltic and synchronous coordination modes. The slope of the line reflects the conduction delay in each segment. From the average motor neuron bursts of the standard ensemble model, a pattern of duty cycles along the leech body axis is apparent.

SPATIAL PATTERN.

The relative synaptic weights of premotor inputs to each model motor neuron were assigned based on experimental data multiplied by a scaling factor. Thus we initially set the maximal synaptic conductance ḡ_Syn from each of the identified premotor inputs to each motor neuron for both coordination modes to the average conductance value from voltage-clamp data (Fig. 3A in Norris et al. 2007a). In the living system, for all the identified premotor interneurons, there was no statistical difference between the average synaptic conductance in the same motor neuron for the two coordination modes (Norris et al. 2007a). On the other hand, the synaptic weights appeared to be slightly different for the peristaltic and synchronous HN(X) inputs (Fig. 3A in Norris et al. 2007a). In our ensemble model, we used an approximate average value of ḡ_Syn for the HN(X) inputs to the model motor neurons of the two sides [HE(3), 6.5 nS; HE(4), 6.25 nS; HE(5), 5.75 nS; HE(6), 2.0 nS], except where noted. A uniform (see text for exceptions) scaling factor, σ, was then applied to these maximal conductances, producing a scaled g_Syn, to obtain appropriate duty cycles for model motor neuron activity as described in the text. For each synaptic input to each model motor neuron, the associated postsynaptic current synaptic current I_Syn was calculated as

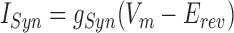(2)

where g_Syn is the instantaneous conductance (calculated as subsequently indicated from the scaled ḡ_Syn) of the specific premotor input, V_m is the instantaneous membrane potential of the model motor neuron, and E_rev is the reversal potential, assumed to be −62.5 mV (Angstadt and Calabrese 1991).

Each spike time in the temporal pattern triggered a synaptic activation function f_Syn(t) given by

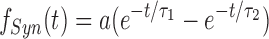(3)

where a is a normalization constant chosen so that the maximal value of f_Syn(t) = 1. Thus

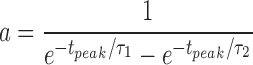(4a)

where

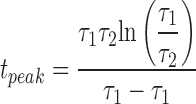(4b)

The time constants determine, respectively, the decay and rise times of the synaptic conductance (τ₁ > τ₂). In the model, the synaptic time constants for the premotor input originating from the HN(3), HN(4), HN(6), and HN(7) interneurons were set based on measurements from typical voltage-clamp records: τ₁ = 0.050 and τ₂ = 0.004 in Norris et al. (2007a). Greater summation in the synaptic input from the inputs from the HN(X) interneurons has been observed experimentally (Norris et al. 2007a), so τ₁ was increased to 0.1 for these synapses.

During each premotor interneuron burst, the postsynaptic currents show intraburst synaptic plasticity. During each premotor interneuron burst, initial IPSCs are very small. They increase to a nearly steady state for the majority of the burst and then decline toward the end of the burst (Norris et al. 2007a). This short-term synaptic plasticity was included in the ensemble model by modifying equations from Hill et al. (2001) for synaptic plasticity in a conductance-based heart interneuron model. M is a synaptic plasticity factor that in this case is an instantaneous function of presynaptic voltage, V_pre

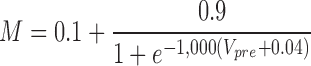(5)

Because only the spike times of the premotor interneurons are used as inputs to the model, we created a V_pre waveform for each premotor input that simulated the presynaptic membrane potential oscillation. This waveform increased exponentially from −50 to −30 mV for the first 75% of the premotor burst and then decayed exponentially from that point back to −50 mV. The rise and fall of V_pre was thus defined by two time constants—τ_plast-Rise and τ_plast-Decay—that effectively control the time course of M and thus the rise and fall of synaptic strength. Each of these time constants was set to 0.250 s, standard values that approximated the IPSC plasticity (synaptic enhancement early in a burst and synaptic depression late in the burst) observed in voltage-clamp recordings of Norris et al. (2007b).

SPATIOTEMPORAL PATTERN.

Combining the spatial and temporal patterns for each synaptic input, Eq. 2 becomes

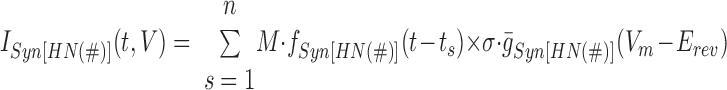(6)

where s is the numerical order of each presynaptic spike of the temporal pattern (n is the last such spike) for the given input and t_s is the time of occurrence of that spike and σ is the synaptic scaling factor defined earlier with reference to Eq. 2.

The I_SynTotal for each given model motor neuron in the current balance Eq. 1 is the sum of all synaptic inputs from each premotor interneuron

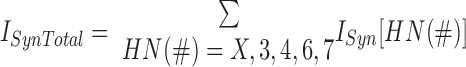(7)

where I_Syn(X) is the specific synaptic current onto that motor neuron from the HN(X) heart interneuron, I_Syn(3) is the specific synaptic current onto that motor neuron from the HN(3) interneuron, and so on. A snapshot of the resultant spatiotemporal pattern of synaptic inputs can be gained from the conductance plots of Fig. 3 for the independent g_Syn and combined g_SynTotal synaptic inputs to the HE(3) and HE(8) model motor neurons, peristaltic and synchronous.

Modeling electrical coupling

The basic equations for electrical coupling between the bilateral model heart motor neuron pairs were

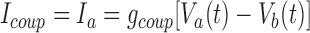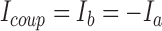(8)

where I_a is the current into motor neuron a and I_b is the current into motor neuron b; V_a and V_b are the membrane voltages of motor neurons a and b, respectively; and g_coup is the conductance of the electrical junction. The equations were adjusted to reflect measured coupling coefficient (average 0.34) and low-pass filtering (50-Hz cutoff frequency, −3 dB) gathered from experiments in the living system on isolated ganglia (Peterson 1983). This match was achieved by setting the conductance of the electrical coupling, g_coup, to 6 nS and filtering I_coup with a simulated RC circuit.

Data analysis

Simulation data were analyzed for period, intraburst spike frequency, duty cycle, and phase as described for the corresponding data from the living system in Norris et al. (2007b). Briefly, custom analysis programs were written in MATLAB and 10 full cycles of simulation data from a given model motor neuron were analyzed for each data point. Data points reported are means ± SD. Our burst marker for measuring period and phase was the middle spike of each burst. Our burst detection paradigm recognized a burst as groups of at least four spikes separated from other spikes by a minimum interburst interval of 300 ms. The minimum number of spikes per burst was waived for bursts of the HE(3) and HE(4) model motor neurons, which occasionally had as few as three spikes in each burst. In nearly all bursts, the middle spike of each motor neuron burst corresponded to the highest density of spikes in a burst and to the time of minimal synaptic inhibition. We calculated bilateral (absolute) phase of the model heart motor neurons using the middle spike of the HN(4) premotor interneuron input pattern in the peristaltic coordination mode (assigned 0.0 phase with no SD) in accordance with our convention for the living system (Norris et al. 2007b), thus facilitating comparisons between the model and the living system. Coordination mode-specific intersegmental phase differences between given ipsilateral model motor neurons were determined by the number of phase units between the leading motor neuron and the lagging motor neuron in the same activity wave progression. In some cases, this phase difference was expressed with a verbal indication of which motor neuron led or lagged. Side-to-side phase differences between bilateral model motor neurons were determined by counting the number of phase units separating bursts in the two motor neurons, left to right and right to left, and selecting the smaller. This side-to-side phase difference captured the minimum phase difference between the bursts regardless of which one led in absolute phase and was thus a measure of the degree of synchrony between the bursts in bilateral homologs. Burst period (T), phase (φ), and duty cycle (D) were calculated and bilateral phase diagrams constructed as described in Norris et al. (2007b).

RESULTS

Model strategy

Our model was designed to determine the extent to which the measured spatiotemporal pattern (pattern, strength, timing, and synaptic dynamics) of synaptic input and intrasegmental electrical coupling of heart motor neurons can account for the intersegmental and side-to-side coordination of heart motor neurons observed during fictive heartbeat (peristaltic and synchronous patterns of motor neuron coordination). We used model motor neurons with simple intrinsic properties compatible with spontaneous firing in the absence of inhibition and silence during bursts of interneuron-mediated inhibitory postsynaptic potentials. Such simple model motor neurons were used to enhance our ability to define the roles of synaptic input and electrical coupling and because motor neuron membrane currents, particularly inward currents, have not been adequately characterized. We pursued a step-by-step strategy in constructing the model: 1) construct a model of a heart motor neuron; 2) build 16 model segmental pairs of electrically coupled motor neurons; 3) provide each model segmental motor neuron pair with its unique spatiotemporal pattern of synaptic input from the CPG and tune appropriately to produce a “standard motor neuron ensemble model”; 4) examine the intersegmental coordination of motor neuron activity in the standard ensemble model and compare it to that from the living system; and 5) independently vary key parameters of the standard ensemble model to investigate their contributions to intersegmental and side-to-side coordination.

Heart motor neuron model: intrinsic firing

Model motor neurons were designed with minimal intrinsic properties: they fire at a constant frequency in the absence of input and fire in bursts only when interrupted at regular intervals by inhibitory synaptic input from premotor heart interneurons or hyperpolarizing current via intrasegmental electrical coupling.

The intrinsic firing frequency of a heart motor neuron model is largely determined by the maximal conductance (ḡ_P) of its persistent Na⁺ current (I_P) (Fig. 2A). The maximum intraburst firing frequency for experimental recordings of heart motor neurons in the middle segments varied between approximately 13 to 20 Hz (Table 1 in Norris et al. 2007b). The standard value of ḡ_P in the model was set to match this intrinsic firing frequency to 8.5 nS. At this value the intrinsic firing frequency of a model motor neuron (no synaptic input or electrical coupling) was 18 Hz and the model motor neuron is in the linear portion of the frequency versus ḡ_P curve (Fig. 2A).

TABLE 1.

Heart motor neuron (HE) duty cycles (D) for the standard ensemble model (σ = 1) and for the living system in the peristaltic and synchronous coordination modes

HE(#)	Peristaltic		Synchronous
	Standard model	Living system	Standard model	Living system
3	0.39	0.24	0.28	0.37
4	0.42	0.34	0.38	0.42
5	0.52	0.34	0.58	0.43
6	0.58	0.40	0.70	0.49
7	0.61	0.48	0.58	0.51
8	0.41	0.56	0.52	0.59
9	0.44	0.65	0.54	0.65
10	0.46	0.68	0.55	0.66
11	0.54	0.67	0.58	0.68
12	0.53	0.64	0.58	0.62
13	0.61	0.70	0.60	0.69
14	0.63	0.74	0.61	0.71
15	0.69	0.72	0.64	0.72
16	0.70	0.65	0.65	0.65
17	0.64	0.54	0.63	0.57
18	0.70	0.48	0.63	0.46

The duty cycle (D) is calculated as the difference between the mean first spike phase and the mean last spike and are thus without SD values (Norris et al. 2007a). Duty cycles for the living system are from Table 1 in Norris (2007a).

The relationship between firing frequency and current injected into the model motor neuron is also quasi-linear over an experimentally relevant range (Fig. 2B). The model motor neuron is tonically active (due to I_P) when no current is injected, but injecting −0.16 nA of current is sufficient to silence spiking activity entirely. With such model motor neurons, because of their simple intrinsic properties we may expect period, duty cycle, the intraburst spike frequency, and the timing of the burst with respect to these inputs (absolute phase) and to motor neurons in other segments (intersegmental phase differences) to be shaped primarily by their inhibitory premotor input and intrasegmental electrical coupling.

Tuning synaptic strength in the standard heart motor neuron ensemble model

Sixteen segmental pairs of electrically coupled heart motor neuron models were created to correspond to the entire heart motor neuron ensemble (Fig. 1). All the motor neuron models on one side received peristaltically timed inputs and all on the other side received synchronously timed inputs generated as described in methods to correspond to the summary phase diagram of Fig. 4 in Norris et al. (2006). On each side, peristaltic and synchronous, each model heart motor neuron received a unique segment-specific pattern of synaptic inputs corresponding to the synaptic weight diagram of Fig. 3A in Norris et al. (2007a) with synaptic dynamics corresponding to that described in Fig. 5 of Norris et al. (2007a). Because no two motor neurons received exactly the same spatiotemporal pattern of synaptic input, the resulting electrical activity of each model motor neuron was unique (Fig. 3).

FIG. 4.

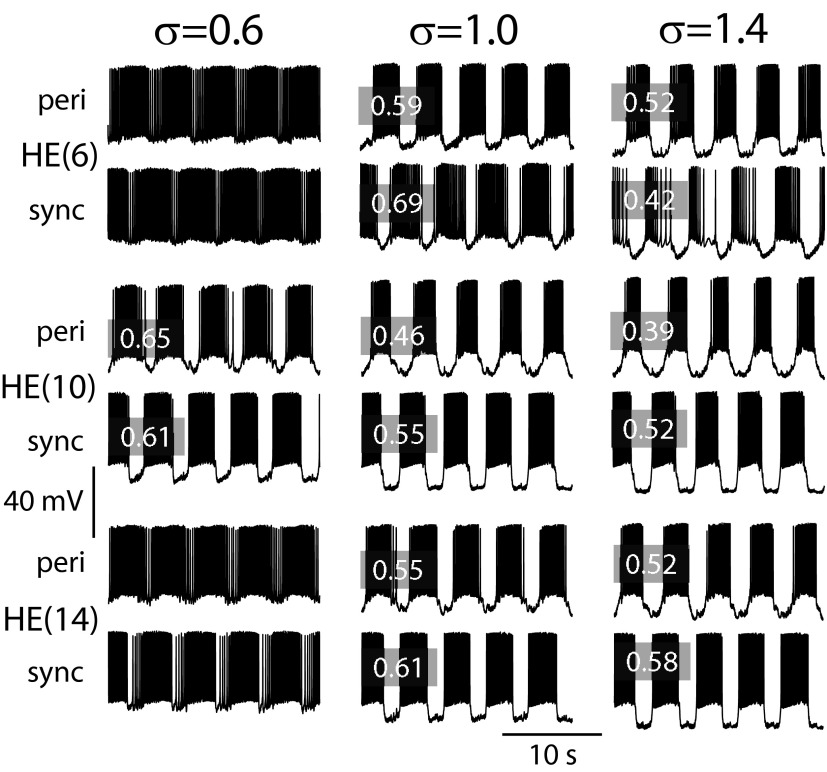
Adjusting the synaptic scaling factor σ (see methods, Eq. 6) for inhibitory synaptic input in the ensemble model to produce an optimal duty cycle of the model motor neuron activity across segments and sides. Membrane potential traces from three pairs of model motor neurons, representative of the front, middle, and rear model motor neurons—left side peristaltic and right side synchronous—as σ was varied. Duty cycles of the model traces illustrated are indicated in the gray boxes. At a low value of σ (σ = 0.6) the model heart motor neurons in the middle segments [HE(7)–HE(13)], represented in the figure by HE(10) model motor neuron pair [one receiving peri(staltic) and one sync(hronous) inputs], approximate the values for duty cycle observed in the living system (Norris et al. 2007), whereas front and rear model motor neurons do not receive enough inhibition [represented by the HE(6) and HE(14) model motor neuron pairs]. The unity σ used in the standard model results in good matching of the duty cycles between the living system and the ensemble model for the HE(14) model motor neuron pair and for the HE(6) model motor neuron receiving synchronous input (sync). This value for σ, however, results in smaller duty cycles for the middle [HE(10)] model motor neuron pair. For the duty cycle of the HE(6) model heart motor neuron receiving peristaltic input (peri) to match measured values requires an increase in σ (σ = 1.4). This larger value resulted in poor matching of the duty cycles of the majority of the model motor neurons in the ensemble model. Table 1 lists the duty cycles for the living system and the standard model.

FIG. 5.

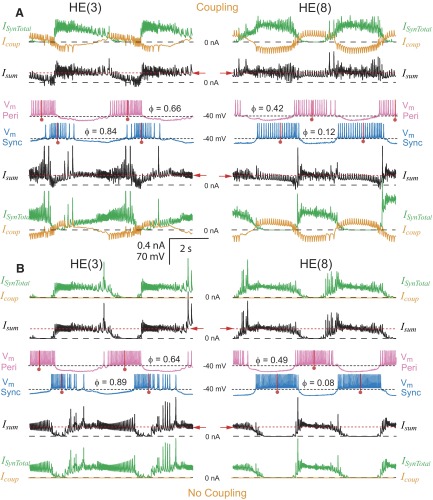
The interaction of synaptic input and electrical coupling in controlling the activity of model motor neurons. Simultaneous bilateral records of membrane potential (V_m: pink, peristaltic; blue, synchronous), total synaptic current (I_SynTotal, green), coupling current (I_coup, orange), summed synaptic and coupling current (I_sum, black), and absolute phase (φ) in HE(3) and HE(8) model motor neuron pairs. Corresponding currents are directly above (peristaltic) or below (synchronous) the membrane potential traces and approximately one heartbeat cycle is shown. A and B illustrate current and voltage records with (standard value of coupling) and without electrical coupling, respectively. Electrical coupling tends to synchronize the burst activity of the motor neurons and its effect is strongest when the synaptic inhibition from the premotor cells overlaps. See text for further explanation. The red dashed line and arrow indicate the level of outward current that suppresses spike activity in the model motor neurons (Fig. 2B).

The measured synaptic weights (average maximal synaptic conductances) were scaled by a constant factor in the model to establish the optimal level of inhibition effective at controlling the spiking activity in our model heart motor neurons, while preserving the relative weight of each interneuron's input to any given motor neuron. Figure 4 shows activity for three representative motor neuron pairs for three different synaptic scaling factors of the maximal synaptic conductances. With a small scaling factor (0.6), the bursts of the HE(6) and HE(14) model motor neurons have ill-defined beginnings and ends. The duty cycle in these cases was ≥0.95. However, the average duty cycles for the pair of HE(10) model motor neurons (indicated with gray boxes in Fig. 4) are comparable to the duty cycles observed in the living system (0.68 peristaltic and 0.66 synchronous, Table 1). Increasing the synaptic scaling factor decreased the duty cycle in all of the segmental pairs of model motor neurons. A synaptic scaling factor of 1 resulted in duty cycles for the HE(10) model motor neurons well below those observed in the living system in both coordination modes, although the duty cycle for the HE(14) model motor neurons in both coordination modes was nearer but below that of the living system (0.74 peristaltic and 0.71 synchronous, Table 1). The HE(6) model motor neuron's duty cycle was comparable in the synchronous mode but was longer in the peristaltic mode than that in the living system (0.40 peristaltic and 0.49 synchronous, Table 1). To match the duty cycle of the living system in the peristaltic mode for the HE(6) model motor neuron, the scaling factor had to be increased to ≥1.4. At this level, the duty cycles for most other model motor neurons in both coordination modes compared poorly (substantially shorter) with the values measured in the living system. Moreover, the HE(3) and HE(4) model motor neurons rarely fired any action potentials in either coordination mode (not shown). The duty cycles of the middle and rear motor neurons [those not receiving input from the HN(X) interneuron] were more robust to changes in the synaptic scaling factor. The synaptic scaling factor had no significant effect on the phase relation between the motor neurons (see Parameter variation in the following text). We thus chose a synaptic scaling factor of 1 as the best compromise for our standard motor neuron ensemble model. At none of the scaling factors assayed did the HE(17) or HE(18) model motor neurons fire with anything approximating their duty cycle observed in the living system. We had to increase the scaling factor of the HE(17) model motor neuron to 2 and that for the HE(18) model motor neuron to 3 to obtain duty cycles in the model comparable to those in the living system. This necessity suggests that the data on the synaptic input to these motor neurons from the living system are incomplete. For a complete comparison of motor neuron duty cycles between the living system and the standard model, see Table 1.

Activity of model segmental motor neuron pairs

INHIBITORY SYNAPTIC INPUT AND ELECTRICAL COUPLING SCULPTS OUT BURST ACTIVITY.

To elucidate how the different spatiotemporal patterns of the premotor input to segmental motor neuron pairs gives rise to segment-specific and coordination mode-specific motor neuron activity, we examined in detail the premotor inputs to the model motor neurons (Fig. 3) and the integration of these inputs with electrical coupling to produce model motor neuron bursts (Fig. 5). We focused on two different model motor neuron pairs, one from the front [HE(3) motor neurons] and one from the midbody [HE(8) motor neurons].

INHIBITORY SYNAPTIC INPUT.

The HE(3) model motor neurons each receive only two inhibitory synaptic inputs: one from the ipsilateral HN(3) and the other from the ipsilateral HN(X) interneuron, whereas the HE(8) model motor neurons each receive inhibitory input from ipsilateral HN(3), HN(4), HN(6), and HN(7) interneurons but not from the HN(X) interneuron (Fig. 1) The synaptic conductance traces (Fig. 3, g_Syn) illustrate the differences in the spatiotemporal input patterns between these two motor neuron pairs. Only input from the HN(3) interneurons is common to the two model motor neuron pairs, but it is reduced in the HE(8) compared with that in the HE(3) model motor neuron pair. The temporal pattern of inhibitory synaptic inputs (sequence of presynaptic spike times) is also different on the two sides: one side receives the peristaltic pattern and the other the synchronous, but on a given side the temporal pattern of common inputs to the two motor neuron pairs is identical except for conduction delays. For example, the HE(8) model motor neurons receive input from the ipsilateral HN(3) interneuron delayed by 100 ms compared with the HE(3) model motor neurons to account for the conduction time between segment 3 and segment 8.

The HE(3) model motor neurons are representative of the front motor neurons that receive synaptic input from the HN(X) interneuron. On the synchronous side, where input from the HN(X) interneuron is roughly antiphasic to the input from the HN(3) and HN(4) premotor interneurons, these front model motor neurons were inhibited throughout the entire heartbeat cycle (Fig. 3). Otherwise, inhibitory input to the motor neurons generally had distinct gaps, as illustrated by both peristaltic and synchronous HE(8) motor neurons and the peristaltic HE(3) motor neuron (Fig. 3). The gaps in synaptic inhibition with peristaltic input in front, middle and rear model motor neurons were shorter than the gaps with synchronous input in the middle and rear model motor neurons. As would be expected from the analysis of the effect of injected current on the firing frequency of the intrinsically active model motor neuron in Fig. 2B, small amounts of synaptic inhibition decreased the firing rate and large amounts stopped the firing of the heart motor neuron models. Model motor neurons often fired action potentials during periods of weak inhibition, and motor neuron bursts often overlapped with the premotor inhibitory input, albeit with decreased firing frequency. In model motor neuron bursts, the middle spike burst marker corresponded to the region of high spike frequency in the burst and to the time of low or absent synaptic inhibition.

ELECTRICAL COUPLING.

In the living system, the electrical junctions between heart motor neurons pass hyperpolarizing current somewhat better than depolarizing current (although it is not clear whether this rectification is due to rectification at the junction or in the extrajunctional resistance) and the frequency response of the coupling is very low, presumably due to the cable (AC filtering) properties of the neurites that lead to the actual gap junctions (Peterson 1983). Accordingly, we modeled the electrical junctions with low-pass filter characteristics, which reduced the depolarizing current through the junctions associated with spikes, but did not abolish it. Spikes are less effectively transmitted via electrical coupling in the living neurons, presumably because they are generated distal to the neuritic compartments where coupling occurs and only passively invade these compartments as they do the cell body. The model motor neurons are a single compartment, so spikes are large at the sites of coupling. This spike-associated inward current was transient and appeared not to have much effect on spike activity in the receiving model motor neuron.

Electrical coupling in a model motor neuron pair causes synaptic currents to be shared, allowing inhibitory input to the contralateral motor neuron to indirectly influence a given motor neuron, while diminishing the effectiveness of direct inhibitory synaptic input to that motor neuron. As subsequently argued, these two effects can have competing influences on when a neuron fires with respect to its input. The synchronizing effect of coupling is strongest when the two coupled neurons would fire at side-to-side phase difference intermediate between 0.0 (in phase) and 0.5 (in antiphase) in the absence of electrical coupling (i.e., because of their inhibitory input alone).

Figure 5A shows the coupling current through the electrical junctions (I_coup) and the total synaptic current (I_SynTotal) received by the HE(3) and HE(8) model motor neurons from the premotor cells that inhibit them. The sum of these two currents (I_sum) is also shown and the red dashed line indicates the level of steady outward current that causes complete cessation of firing (Fig. 2B). The driving force behind the coupling current is the difference in membrane potential between the coupled motor neurons of a pair. Each motor neuron received outward coupling current (I_coup) when its contralateral homologue was being inhibited and some inward current when its contralateral homologue was spiking.

Despite pauses in synaptic inhibition during the heartbeat cycle, the model motor neurons rarely achieved their maximal steady-state firing frequency because synaptic current was shared through their electrical coupling (Fig. 5A). Each motor neuron thus received net outward current during the entire heartbeat cycle (I_sum), except infrequently when a spike-mediated coupling potential transiently made the current net inward. When coupling was removed, spike frequency in the model motor neuron pairs increased (Fig. 5B) and there were now clear periods where each neuron received no outward current (I_sum). Electrical coupling also diminished the effect of direct inhibitory input because the contralateral model motor neuron acted as a current sink. Paradoxically, the total synaptic current appeared to decrease when coupling was removed (Fig. 5B), but this was an effect of driving force because the membrane potential achieved a greater hyperpolarization during the inhibition—i.e., the inhibition was more effective.

Sharing of synaptic current between electrically coupled model motor neurons was greatest when their respective synaptic inputs were in antiphase and least when they were in phase. The net result was that direct inhibition in phase with inhibition to the contralateral neuron was enhanced, whereas direct inhibition out of phase with inhibition to the contralateral neuron was diminished by the electrical coupling. For example, the inputs from the HN(X) interneuron pair are relatively in phase across the two sides, so their inhibitory influence on bilateral motor neuron pairs, like that in the HE(3) pair illustrated in Fig. 5A, was enhanced in their target (ipsilateral) motor neuron. Because they were near the same membrane potential during this concurrent inhibition, the bilateral motor neurons became functionally uncoupled. The summed current (I_sum) was nearly equal to the synaptic current (I_SynTotal), whereas the coupling current (I_coup) hovered near zero for much of the peristaltic HE(3) motor neuron's inhibited phase (Fig. 5A), when the synchronous HN(X), peristaltic HN(X), and peristaltic HN(3) inputs were all active together (Fig. 3). The inputs from the HN(3) and the HN(4) interneuron pairs were each in antiphase across the two sides (Fig. 3), so their direct inhibitory influence on coupled motor neuron pairs, like that in the HE(8) pair illustrated (Fig. 5A), was diminished in their target (ipsilateral) motor neuron because some of the inhibitory synaptic current was effectively leaked to the contralateral motor neuron via the electrical coupling. I_sum was substantially smaller than I_SynTotal during each motor neuron's inhibited phase and the coupling current I_coup underwent large oscillations during the model motor neurons' activity cycle. On the other hand, there was maximal sharing of synaptic input; I_sum was similar in the two motor neurons. The sharing of depolarizing current in the model may also have contributed to these effects because each motor neuron was spiking/active, whereas it received the contralateral inhibitory current via the electrical coupling.

These complex interactions between electrical coupling and inhibition at different phases in the two coupled motor neurons had a clear segment-specific effect on the phase of model motor neuron activity (Fig. 6A) and thus on intersegmental coordination. These effects on phasing were revealed by comparing model motor neuron pairs with and without coupling (Fig. 5, A vs. B). The absolute phase of the model motor neurons shifted measurably with the addition of coupling. In the HE(8) model motor neuron pair, because of the nearly antiphasic synaptic inhibition of the two neurons (Fig. 3), the uncoupled HE(8) model motor neurons fired at a side-to-side phase of 0.41, which shifted to 0.30 with coupling. The peristaltic HE(8) motor neuron shifted 0.07 phase unit and the synchronous HE(8) motor neuron shifted 0.04 phase unit toward one another; both shifted to be more synchronized with one another and less in antiphase with their predominant synaptic input, the ipsilateral HN(4) interneuron (Fig. 3). [Comparable side-to-side phase values for the HE(7) motor neuron pair were 0.44 uncoupled and 0.31 coupled; the synchronizing effect of coupling was less when the synaptic input would drive the neurons closer yet to antiphase.] The HE(3) model motor neurons also showed side-to-side phase shifts [the peristaltic HE(3) motor neuron shifted 0.02 phase unit and the synchronous HE(3) motor neuron shifted 0.05 phase unit toward one another] from 0.25 when uncoupled to 0.18 when coupled. Thus an important effect of electrical coupling was a reduction in the side-to-side phase difference, i.e., a partial synchronization of burst activity of the segmental model motor neuron pairs (Fig. 5, voltage traces).

FIG. 6.

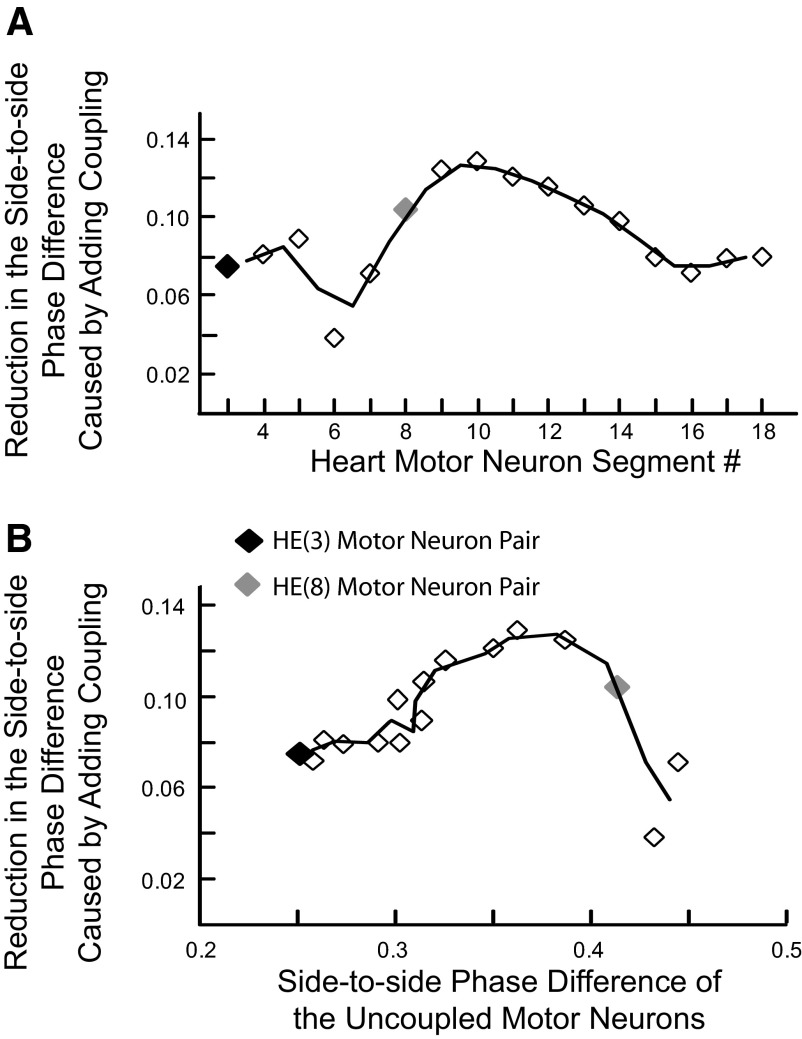
Segment-specific effects of electrical coupling on phasing of heart motor neurons reflect side-to-side differences in the phasing of synaptic inputs to each coupled pair of motor neurons. A: the side-to-side phasing of each segmental motor neuron pair was compared with and without electrical coupling and the difference plotted vs. heart motor neuron segment number. Electrical coupling reduces the side-to-side phase difference of each motor neuron pair by a segment-specific amount. B: the data points of A are now reordered and plotted vs. the side-to-side phase difference of the uncoupled motor neuron in each segment to illustrate how the side-to-side difference in synaptic input affects the synchronizing ability of electrical coupling. In A and B, the black diamond shows the data point derived from the HE(3) motor neuron pair and the gray diamond the data point derived from the HE(8) motor neuron pair that are both illustrated in Fig. 5. The trend lines plotted are the running average of the 2 points on either side of the line vertices.

The reduction in the side-to-side phase difference of the segmental model motor neuron pairs varied from segment to segment in a way that reflected the phase difference between their inputs and the competing effects the electrical coupling had on these inputs. In-phase inputs functionally uncoupled the motor neurons of the pair but were maximally effective in their respective motor neuron; out-of-phase inputs led to maximal sharing of synaptic current between the motor neurons of a pair but were minimally effective in their respective motor neuron. These effects were revealed by plotting the reduction in the side-to-side phase difference of the segmental model motor neuron pairs versus the side to-side phase difference of the uncoupled motor neurons of a pair (Fig. 6B). Uncoupled motor neurons fired solely in response to their direct synaptic input so the phase difference of an uncoupled segmental pair reflected the phase difference of the respective direct inputs to the motor neurons. The maximal effect of electrical coupling was seen when the uncoupled motor neuron fired with a phase difference of about 0.35 (i.e., when their inputs were substantially but not completely out of phase). In the model, this maximal effect of coupling occurred in the HE(9)–HE(11) motor neuron pairs (Fig. 6).

Because the absolute phase shifts seen in the four model motor neurons when coupling was removed were all different, changes in intersegmental coordination were produced. The HE(3) to HE(8) intersegmental phase difference decreased from 0.24 to 0.15 [HE(8) motor neuron leading] on the peristaltic side and from 0.28 to 0.19 [HE(3) motor neuron leading] on the synchronous side. Thus the effect of coupling when interacting with the spatiotemporal pattern of synaptic input to model heart motor neurons was to amplify intersegmental phase differences.

Motor neuron activity of the entire standard ensemble model

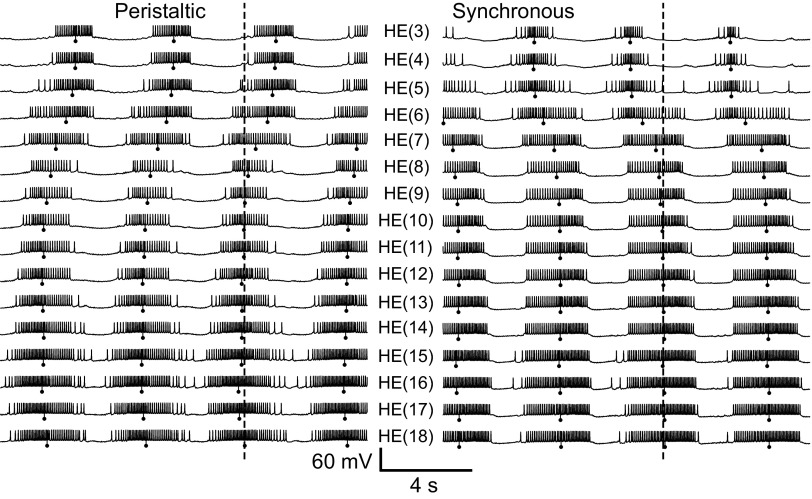
Figure 7 shows the coordinated bursting activity of all 16 bilateral pairs of motor neurons of the standard ensemble model. The middle spike, which is the phase marker for burst activity (see methods), is indicated on the figure for each model motor neuron. The model captures the general outlines of intersegmental coordination (unilateral phase relations) seen in the living system, for both coordination modes. In the peristaltic coordination mode, burst activity in the rear model motor neurons in general occurred before burst activity in front model motor neurons (i.e., the rear HE bursts led the front HE bursts in phase), whereas in the synchronous coordination mode, front model motor neuron bursts led those in rear model motor neurons in phase. In all motor neurons, interspike intervals were longer at the ends of the bursts and shorter in the center. This characteristic waxing and waning of spike frequency of model motor neuron bursts correspond well to the living system (Norris et al. 2007b).

FIG. 7.

Membrane potential traces for all 16 bilateral [HE(3)–HE(18)] motor neuron pairs in the standard ensemble model: left, peristaltic; right, synchronous. Vertical lines with balls indicate the middle spike of each model motor neuron burst and the dashed lines indicate the middle spike of the peristaltic HN(L,4) premotor synaptic input (phase reference). The general trends for intersegmental coordination observed in the living system are captured by the ensemble model, but the peristaltic phase progression in the model is too small and there is an abrupt jump in the synchronous phase progression between the HE(6) and HE(7) model motor neurons. This phase jump indicates a dominance of the inputs from the HN(X) interneuron in the front model motor neurons.

Duty cycle and intersegmental phase relations of the standard motor neuron ensemble model

The duty cycle and phase relations of the motor neuron bursts in the standard ensemble model are shown in the phase diagram of Fig. 8. The phase reference for this and subsequent bilateral phase diagrams is the peristaltically coordinated HN(4) interneuron, as it has been in our experimental analysis of the phase relations of heart interneuron burst activity (Norris et al. 2006). From front to rear, the duty cycles of the model motor neurons tended to increase, although there was a noticeable contraction of the duty cycle of the HE(8) motor neuron in the peristaltic coordination mode. This segmental progression is similar to the living system except for the rearmost segments where duty cycles are smaller (Norris et al. 2007b). The duty cycles of the HE(3)–HE(6) model motor neurons (particularly on the synchronous side) varied considerably from burst to burst, as reflected in the phase diagrams by larger error bars, again similar to the living system (Norris et al. 2007b). Table 1 gives the average duty cycle for every model motor neuron in the standard model and includes the corresponding data from the living system (Norris et al. 2007b) for comparison. In the synchronous coordination mode, the two frontmost model motor neurons have noticeably shorter duty cycles than the rest. The shorter duty cycles of the HE(3) and HE(4) model motor neurons occur because they receive synaptic inhibition throughout the heartbeat cycle during the synchronous coordination mode due to the influence of the HN(X) premotor interneuron (Figs. 3 and 5).

The simplified bilateral phase diagram of Fig. 9 makes comparison of the intersegmental phase differences in the living system and the standard model easier. In such simplified diagrams, the phasing of the motor neuron bursts is indicated only by plotting the phase of the middle spike (phase marker) of each burst and the phasing of the premotor interneuron inputs is represented only by the phase of the HN(4) interneurons adjusted in each segment by the intersegmental conduction delay.

FIG. 9.

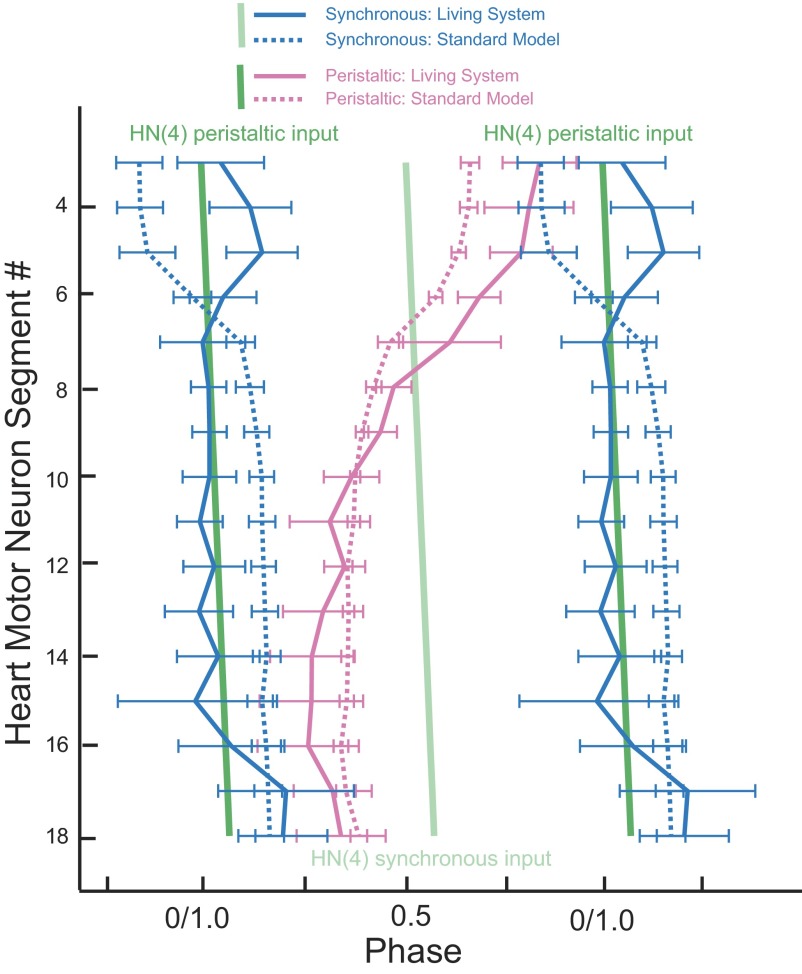
Simplified phase diagram comparing the standard ensemble model with the living system. The bilateral absolute phase relations of the standard model (dashed lines) compared with that of the living system (solid line) with the peristaltic HN(4) interneuron as the phase reference. Two synchronous (blue) and one peristaltic (pink) phase curves are shown for both the model and the living system. The phase of the peristaltic HN(4) interneuron is indicated with a slanted green straight line and the phase of its contralateral homologue, the synchronous HN(4) interneuron, is indicated with a slanted light green straight line. The slopes of these lines reflect the conduction delays from segment to segment. Although the intersegmental phase differences among the middle and rear synchronously coordinated motor neurons are similar for the model and the living system, use of a common phase reference illustrates that model motor neuron activity is not properly phased to the synaptic input. The intersegmental phase differences among the peristaltically coordinated motor neurons in the model match the general trend of the living system, but the standard model does not capture the large intersegmental phase differences of the living system. Again, the use of a common phase reference illustrates that model motor neuron activity is not properly phased to the synaptic input. The mismatch in absolute phase between the model and the living system is smallest in the middle motor neurons and gradually increases both frontward and rearward.

As in the living system, the peristaltic intersegmental phase progression was rear to front in the standard ensemble model but the magnitude of phase progression was smaller (Fig. 9). In model motor neurons receiving peristaltically coordinated inhibitory input, the motor neurons traverse a total of 0.28 of phase rear to front, considering all the segmental motor neurons, but 0.32 when considering motor neurons HE(16) through HE(3) where the phase progression is monotonic. These measures for the living system are 0.49 and 0.58, respectively (Norris et al. 2007b); the model has a substantially smaller peristaltic phase progression than that of the living system. As observed in the living system, these segmental phase changes in the ensemble model are not uniform. The rear-to-front progression starts at HE(16) and proceeds frontward with gradually increasing segmental phase steps to its maximum, 0.11, between HE(6) and HE(7). The largest phase difference between adjacent segments in the living system (0.07) also occurs between HE(6) and HE(7) (Norris et al. 2007b). The HE(3) and HE(4) model heart motor neurons fire in near synchrony; additionally, a slight front-to-rear progression can be observed in the HE(16)–HE(18) motor neurons (0.04). This deviation from the general trend in peristaltic phase progression for the rearmost model motor neurons is also observed in the phase relations measured in the living system for the peristaltically coordinated motor neurons in these same segments (0.08).

The near synchrony of the synchronous coordination mode was observed in the standard ensemble model from HE(18) to HE(7), but there was a large phase jump from HE(7) to HE(5) (Fig. 9). In the living system, near synchrony is observed from HE(16) to HE(6), with phase jumps at HE(6) going frontward and HE(16) going rearward (Norris et al. 2007b). In the model, the front phase jump is in a different direction and the rear phase jump is not present (Fig. 9). Model motor neurons receiving synchronously coordinated inhibitory input traverse a total of 0.32 of phase front to rear, considering all the segmental motor neurons, but only 0.05 of phase front to rear when considering motor neurons HE(7) through HE(15) where the phase progression is most synchronous (Fig. 7). These measures for the living system are 0.16 and 0.02, respectively, all front to rear (Norris et al. 2007b) (Fig. 9). Just as in the peristaltic coordination mode, intersegmental phase progression is not uniform in the standard model. The majority of the synchronous phase difference occurs between the HE(5) and HE(7) model motor neurons. The two largest segmental phase steps are between the HE(5) and HE(6) model motor neurons, 0.11 front to rear, and between the HE(6) and HE(7) model motor neurons, 0.12 front to rear. The phase differences between these same motor neurons in the living system [HE(5) and HE(6) motor neurons, 0.10 rear to front, HE(6) and HE(7) motor neurons 0.05 rear to front] are comparably large but in the opposite direction. This discrepancy in the intersegmental phase relations—arising in model motor neurons that receive inhibitory synaptic input from the synchronously coordinated HN(X) interneuron—is difficult to understand at present.

The maximal intersegmental phase difference between two motor neurons for either coordination mode in the standard ensemble model is smaller than the corresponding maximal phase difference in the premotor inputs (activity phases of the premotor interneurons) (Fig. 8). In other words, the outputs of model motor neuron ensembles do not fully express the phase difference available in its inputs.

Comparison of the phase relations of motor neurons with respect to their synaptic inputs in the standard ensemble model and the living system

Figure 9 emphasizes motor neuron firing with respect to inputs and permits a clear evaluation of model performance compared with that of the living system. The peristaltic model motor neurons from HE(10) forward fire progressively earlier than their living counterparts, leading to the reduced peristaltic phase progression of the standard ensemble model (Fig. 9). The synchronous model motor neurons from HE(7) to HE(16) fire consistently later and from HE(3) to HE(6) fire earlier than their living counterparts (Fig. 9). The causes of these mismatches are unclear but may be the result of inadequate representation of motor neuron intrinsic properties (e.g., postinhibitory rebound) and potential segmental differences in these properties in the model.

To control for unintended effects of the specific input pattern used in the standard model, two other premotor spike input patterns were “played back” into the standard model, yielding nearly identical results for phasing as the standard model (data not shown). These two other playback patterns had phase characteristics similar to those of the standard pattern [as would be expected since all of the input patterns were from typical recordings of premotor inputs in the living system (Norris et al. 2006)], but differed in period. Taken as a whole, the similarity of the general phase relations observed in peristaltic and synchronous coordination mode using these three different input patterns suggests that a range of inputs can produce similar outputs of the model and that the discrepancies between the model and the living system are not input specific.

We next explored the contribution of electrical coupling, intersegmental conduction delays, and synaptic plasticity to the phasing of heart motor neurons by removing them from the standard model.

Effects of removing electrical coupling on intersegmental and side-to-side coordination in the standard ensemble model

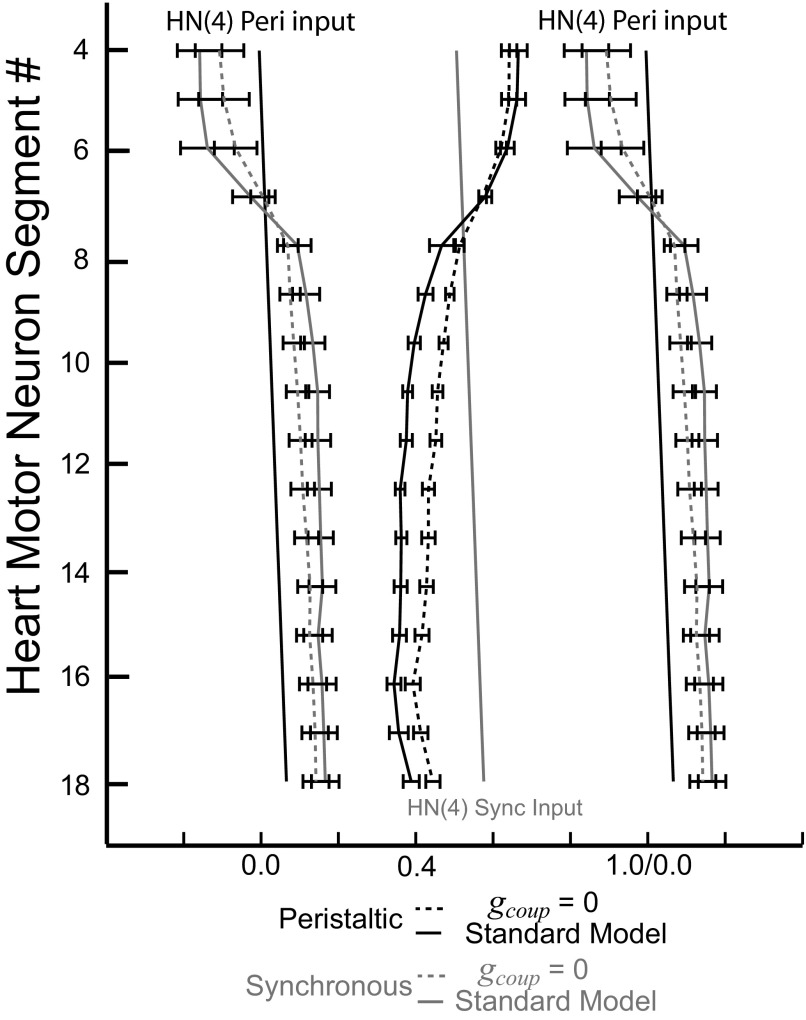
The effect of removing the electrical coupling in the standard ensemble model on the intersegmental phase relation of model motor neurons is shown in Fig. 10, where the phasing of the standard model motor neurons is compared with their phasing without electrical coupling. Here again, the peristaltically coordinated HN(4) interneuron was used as the phase reference. The characteristic rear-to-front progressions in the peristaltic coordination mode and the synchronous coordination mode were not changed with the removal of the electrical coupling. In each segment, removal of electrical coupling resulted in shifts in the absolute phase of the motor neurons and an increase in the side-to-side phase difference (minimum phase difference; see methods). These changes reflect the synchronizing effect of electrical coupling. Because the magnitude of the effect of electrical coupling on phasing (absolute and side-to-side) is segment specific (Figs. 5 and 6), removal of electrical coupling altered the intersegmental phase progressions in both coordination modes (Fig. 10). The maximal intersegmental phase difference in the peristaltic coordination mode [standard model considering motor neurons HE(16) through HE(3)] decreased from 0.32 rear to front to 0.25. The synchronous maximal phase difference [standard model considering the HE(7) through HE(15) motor neurons, which are most synchronous] slightly increased from 0.05 front to rear to 0.06. Compared with the living system and considering both intersegmental phase and absolute phase (firing with respect to input), the ensemble model without electrical coupling performed slightly better in the synchronous coordination mode and substantially worse in the peristaltic coordination mode.

FIG. 10.

Bilateral phase relations of the standard ensemble model with and without electrical coupling. As in Fig. 9, the phase diagram uses the peristaltic HN(4) interneuron as the phase reference. Its phase is indicated by the black slanted straight line and the phase of its contralateral homologue, the synchronous HN(4) interneuron, is indicated with a gray slanted straight line. Without electrical coupling, side-to-side phase differences increase in every segment.

The average firing frequencies of the model motor neuron bursts increased with the removal of coupling because sharing of inhibition between the motor neurons in the same segment was eliminated (complete data not shown but see Fig. 5 for an example). Similar effects of removing coupling from the ensemble model on absolute, side-to-side, and intersegmental phasing were seen when the maximal conductance of the persistent Na⁺ current (ḡ_P) was decreased from 8.5 to 7.5 nS, to control for the effect of removing electrical coupling on firing frequency (data not shown).

Effects of removing intersegmental conduction delays and synaptic plasticity on intersegmental coordination in the standard ensemble model

We also examined the contribution of intersegmental conduction delays in synaptic connections and of synaptic plasticity in producing the intersegmental phase relations by analyzing the output of the standard ensemble model with each of these synaptic properties removed. Changing the conduction delays from 20 ms per segment to 0 ms changed the intersegmental timing of the synaptic input while preserving the temporal phase relation among the premotor inputs for any given motor neuron (within a segment). Similarly, setting the synaptic plasticity factor (M Eq. 5) equal to 1 (see Hill et al. 2001) eliminated the amplitude dynamics of the synaptic input while preserving the experimentally derived spatial pattern of relative synaptic weights.

Removal of conduction delays had very little effect on the absolute phase of any motor neuron: the peristaltic and synchronous intersegmental phase progressions did not change much with the removal of the conduction delays from the standard model (data not shown). The intersegmental phase difference in the synchronous mode decreased slightly from 0.05 front to rear in the standard model [considering motor neurons HE(7) through HE(15)] to 0.04 without the conduction delays. This small decrease was expected because the conduction delays for these motor neurons increase proceeding rearward and their removal reduces the front-to-rear phase difference in the synchronous coordination mode. The maximal intersegmental phase difference in peristaltic coordination increased slightly when the conduction delays were removed from a 0.32 intersegmental phase difference [when considering motor neurons HE(16) through HE(3)] to 0.34 when the conduction delays are set to 0 ms. This small increase was expected because the conduction delays increase proceeding rearward, thus reducing the rear-to-front phase difference that can be realized in the peristaltic coordination mode of the standard model.

Removal of synaptic plasticity had very little effect on the absolute phase of any motor neuron. The peristaltic and synchronous intersegmental phase progressions did not change much with the removal of the synaptic plasticity from the standard model (data not shown). With this perturbation, each synaptic event throughout a premotor input burst occurs at maximal amplitude. The intersegmental phase difference in the peristaltic coordination mode increased slightly from 0.32 rear to front [standard model, when considering motor neurons HE(16) through HE(3)] to 0.33 with the removal of the synaptic plasticity. The intersegmental difference in synchronous coordination decreased from 0.05 front to rear [standard model, when considering motor neurons HE(7) through HE(15)] to 0.03 with the removal of the synaptic plasticity.

Parameter variation

We next systematically varied model parameters over a range of values to get a more complete picture of their mechanistic role in the standard model. We illustrate our results of parameter variations by examining three coupled pairs of model heart motor neurons from the middle segments 7, 10, and 13 that receive inhibitory input from the same premotor interneurons, but with different synaptic weights. The parameter variations manipulated key factors in synaptic function, excitability, and outward K⁺ currents. The synaptic parameters varied were the time constants of synaptic plasticity (τ_plast-Rise and τ_plast-Decay), the conductance of the electrical coupling (g_coup), and the length of the conduction delays (delay). The excitability factors were maximal conductance of the persistent Na⁺ current (ḡ_P), membrane resistance (R_m), and the scale factor of the inhibitory synaptic input (σ) (see Fig. 5). The maximal conductance of the inactivating K⁺ current (ḡ_K1), the noninactivating K⁺ current (ḡ_K2), and the fast transient K⁺ current (ḡ_KA) were also manipulated in the parameter variation. Each parameter was varied between 0 and 200% of the standard value in steps of 25%.

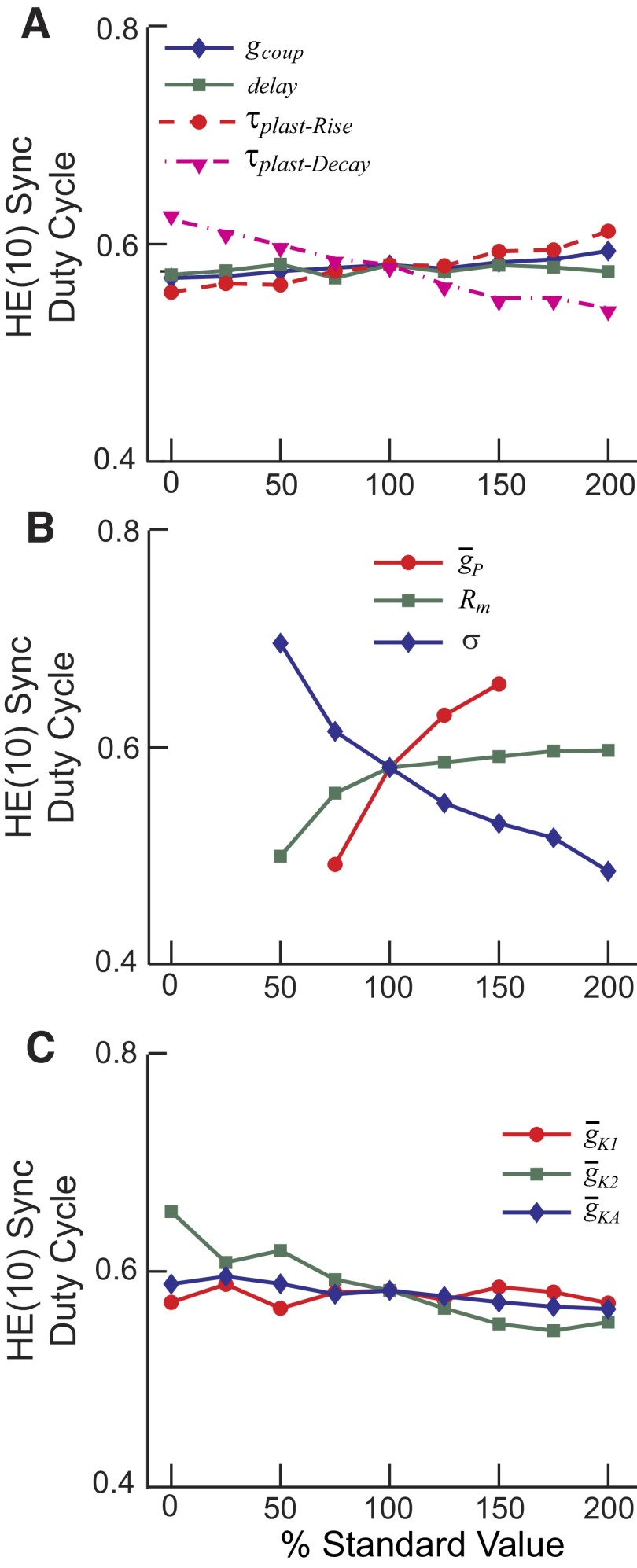
Figure 11 shows the results of this parameter variation on the duty cycle of the HE(10) motor neuron in synchronous coordination. The results for peristaltic coordination were similar, as were the results for the HE(7) and HE(13) motor neurons in both coordination modes. Duty cycle increased with increasing τ_plast-Rise and decreased more strongly with τ_plast-Decay; these effects were commensurate with their roles in synaptic termination of the burst and synaptic release for burst formation, respectively. Conduction delays and electrical coupling had little effect on duty cycle, although as noted earlier, electrical coupling did have an effect on spike frequency (reducing g_coup to zero increased spike frequency; Fig. 5). Duty cycle was greatly affected, as expected, by variations of the excitability factors. Increases in ḡ_P and in R_m gave rise to increases in duty cycle. As the synaptic scaling factor increased, the duty cycle decreased. Only small changes in duty cycle were observed with manipulation of the conductance of the K⁺ currents, except for the noninactivating I_K2, where there was a slight decline with increasing ḡ_K2. This decline is to be expected because increasing ḡ_K2 leads to a decrease in excitability of the motor neuron.

FIG. 11.

The effect of varying model parameters on the duty cycle of the synchronous HE(10) model motor neuron [in this case the HE(R,10) motor neuron]. A: the rise time of the synaptic plasticity (τ_plast-Rise and τ_plast-Decay), the conductance of the electrical coupling (g_coup), and the size of the conduction delays (delay) were varied from 0 to 200% of standard values. B: the maximal conductance of the persistent Na⁺ current (ḡ_P), the membrane resistance (R_m), and the scale factor for the inhibitory synaptic input (σ) were varied from 0 to 200% of standard values. Missing points in the graph indicate parameter values where the model motor neuron did not exhibit clearly recognizable bursts but fired nearly continuously. C: the maximal conductances of the delayed rectifier K⁺ current (ḡ_K1), the persistent K⁺ current (ḡ_K2), and the transient K⁺ current (ḡ_KA) were varied from 0 to 200% of standard values.

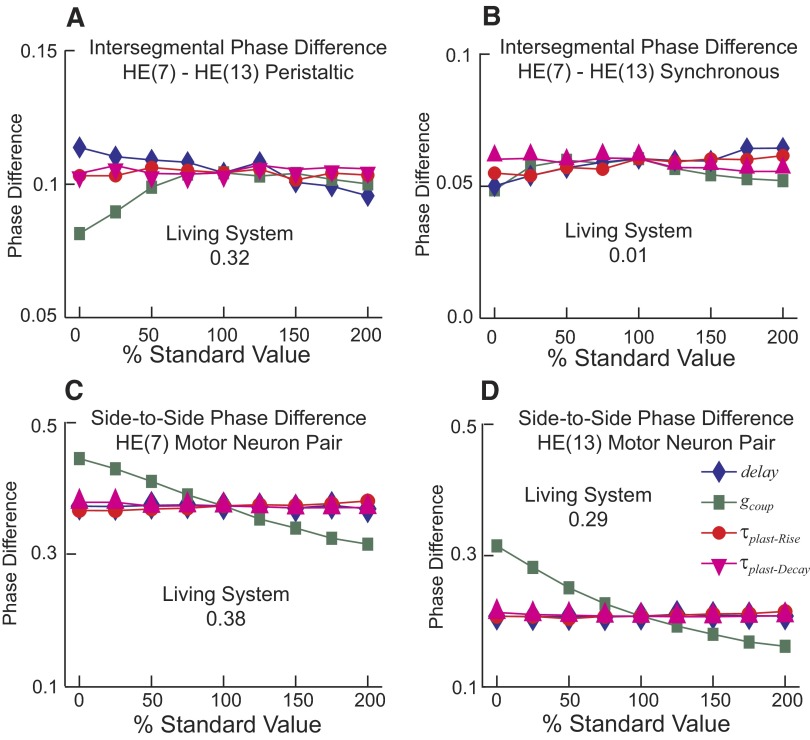
Figure 12, A and B shows the effect of varying synaptic plasticity (τ_plast-Rise and τ_plast-Decay), electrical coupling (g_coup), and delay (delay) parameters on the intersegmental phase difference between the HE(7) and HE(13) model motor neurons in each coordination mode. For comparison, the intersegmental phase difference between the HE(7) and HE(13) motor neurons is 0.32 rear to front for peristaltic mode and 0.01 front to rear for synchronous mode in the living system; the corresponding numbers for the standard ensemble model are 0.10 and 0.06. Variations of the K⁺ current and excitability parameters had little to no effects on phase progression in these motor neurons (data not shown). The intersegmental phase difference increased with increasing conduction delay for the synchronous coordination mode, but decreased for the peristaltic coordination mode. In synchronous coordination mode, increasing τ_plast-Rise had a slight increasing effect, whereas increasing the τ_plast-Decay had a slight decreasing effect on the intersegmental phase difference. In peristaltic coordination mode, increasing τ_plast-Rise or τ_plast-Decay had a negligible effect on the intersegmental phase difference. These observations suggest that a more accurate assessment of τ_plast-Rise and τ_plast-Decay in the living system is not critical because little amelioration of intersegmental coordination in the ensemble model can be expected, at least with the current motor neuron model.

FIG. 12.

The effects of varying synaptic plasticity (τ_plast-Rise and τ_plast-Decay), electrical coupling (g_coup), and delay (delay) parameters on the intersegmental phase difference and on the side-to-side phase difference of motor neurons in the ensemble model. A and B: the intersegmental phase difference between the ipsilateral HE(7) and HE(13) model motor neurons in the peristaltic (A) and synchronous (B) coordination modes is mildly affected by each of the varied parameters and does not approach the magnitude observed in the living system (indicated on graph) for any parameter value. C and D: the side-to-side phase difference between the HE(7) (C) and between the HE(13) (D) model motor neurons is affected by varying the electrical coupling (g_coup), but varying the other parameters (τ_plast-Rise, τ_plast-Decay, and delay) had little effect. Parameters were varied from 0 to 200% of the standard value. Coordination mode-specific intersegmental phase differences and side-to-side phase differences were determined as described in methods.

The intersegmental phase difference between the HE(7) and HE(13) motor neurons decreased when g_coup was decreased below the standard level in both coordination modes. Decreasing/removing electrical coupling from the ensemble model would improve the phase difference between these middle motor neurons in synchronous mode (0.06, standard model; 0.05, model with no coupling; 0.01, living system) but worsen it in peristaltic mode (0.10, standard model; 0.08, model with no coupling; 0.32, living system) with respect to the living system. These effects of electrical coupling appear to peak at approximately the standard value of g_coup and shallowly reverse direction with increasing g_coup. Moreover, increasing g_coup in the frontmost and rearmost motor neuron pairs (where the preceding analyses hint that increased electrical coupling might provide phase shifts needed to match the living system), while keeping the standard g_coup for middle motor neurons did not improve the intersegmental phase differences in peristaltic mode and worsened phase differences in synchronous mode (data not shown).

Figure 12, C and D shows the effect of varying synaptic plasticity (τ_plast-Rise and τ_plast-Decay), electrical coupling (g_coup), and delay (delay) parameters on the side-to-side phase differences of the bilateral HE(7) and HE(13) model motor neurons. The side-to-side phase differences changed very little with manipulations of conduction delay or synaptic plasticity, but electrical coupling had a clear synchronizing effect, especially in the HE(13) motor neurons, as expected from the analyses of Fig. 6. Without coupling, the side-to-side phase difference for the HE(7) model motor neurons was larger than that in the standard model and larger yet than that in the living system, and it was decreased monotonically by electrical coupling (0.43, standard model; 0.46, model with no coupling; 0.39, living system, minimum phase difference; see methods) (Fig. 12C). Without coupling, the side-to-side phase difference between the HE(13) model motor neurons was larger than that in the standard model and in fact became larger than the side-to-side phase difference in the living system; it was decreased monotonically by electrical coupling (0.22, standard model; 0.33, model with no coupling; 0.29, living system, minimum phase difference) (Fig. 12D). The absolute phase [with respect to the peristaltic HN(4) input] of the HE(7) motor neurons [peristaltic: 0.55, model; 0.58, model with no coupling; 0.62, living system; synchronous: 0.12, model; 0.12, model with no coupling; 0.0, living system (cf. Figs. 9 and 10)] was reasonably well represented in the standard model and improved on the peristaltic side by electrical coupling, but the absolute phase of the HE(13) motor neurons [peristaltic: 0.46, model; 0.52, model with no coupling; 0.30, living system; synchronous: 0.24, model; 0.19, model with no coupling; 0.01, living system (cf. Figs. 9 and 10)] were not well represented and were improved on the peristaltic side but worsened on the synchronous side by electrical coupling. These types of trade-offs observed with parameter variation indicate that the ensemble model cannot be ameliorated to capture the living system without substantial new information about the living motor neurons such as segmental differences in electrical coupling, more accurately determined intrinsic properties including segmental differences, additional unaccounted for synaptic inputs, and/or subtleties of synaptic integration and control of spiking not captured by a single-compartment model.

DISCUSSION

In an attempt to simulate the fictive heartbeat motor pattern observed in the isolated leech nerve cord, we have constructed and tested a model of the ensemble of heart motor neurons and their inhibitory synaptic inputs from the heartbeat CPG. This first-generation ensemble model uses very simple model motor neurons—single-compartment neurons, electrically coupled as segmental pairs, with no dynamic intrinsic properties such as postinhibitory rebound—and represents an attempt to determine how well our experimentally determined spatiotemporal pattern of synaptic input in each segment (Norris et al. 2006, 2007b) can account for the fictive motor pattern observed in the living system (Norris et al. 2007b). The ensemble model captures the general features of the fictive motor program: the bilateral asymmetry in intersegmental coordination, which we designate the peristaltic and synchronous coordination modes. The model output, however, does not quantitatively match the intersegmental phase differences observed in the living system, nor are motor neurons coordinated with respect to their inputs as observed in the living system. Nevertheless, the ensemble model enabled us to explore the impact of crucial model features such as electrical coupling between heart motor neurons in the same segment, intersegmental delays, and short-term synaptic plasticity in the inputs on intersegmental coordination, side-to-side coordination, and phasing with respect to input of the model motor neurons.

In evaluating the model, it is useful to consider which assumptions made during the model construction might limit the ability of the model to accurately capture the phasing of the living system. In the ensemble model, the most important determinant of the phase relations among the motor neurons was the spatiotemporal pattern of synaptic inputs. However, this pattern is not likely to be the cause of the discrepancies between the model and the living system; the input pattern is constrained by data: average data for synaptic strength and three different choices of temporal pattern from three different representative preparations. The spatial pattern (pattern of synaptic weights) observed in the living system seems well tuned (see following text for the rearmost motor neurons where the spatial pattern is inadequate) to exploit the phase differences in the temporal pattern of inputs to produce the synchronous and peristaltic coordination modes. Indeed the challenge we presented ourselves with here was capturing how this experimentally derived input pattern produces the experimentally observed fictive motor (output) pattern.

It seems likely to us that the mechanisms for integrating synaptic inputs are different in the model and living heart motor neurons. Such mechanisms might involve their intrinsic properties such as the morphology of the motor neuron, its membrane currents and their distribution, and how membrane currents and neuritic structure influence the integration of synaptic input and the rectification and filtering properties of electrical coupling between motor neurons.

Rearmost motor neurons in the ensemble model require enhanced inhibition, suggesting additional inputs in the living system

The observation that the two rearmost [HE(17) and HE(18)] motor neuron pairs in the ensemble model did not produce distinct bursts when their synaptic weights were set to the values measured in the living system (Norris et al. 2007a) but required a two- to threefold enhancement of the synaptic scaling factor, σ, to produce bursts with reasonable duty cycles (Fig. 8) suggested that additional synaptic input to these motor neurons might exist. Circumstantial evidence indicated the existence of additional premotor inputs to the rearmost heart motor neurons (Thompson and Stent 1976). We have now researched each of the segmental ganglia for additional heart interneurons and found new pairs in ganglia 15 and 16, which connect to ipsilateral motor neurons going rearward (A. Wenning, unpublished data). These new findings will not solve the major discrepancies between the model and the living system, but they increase our confidence in the completeness of our description of the inputs to motor neurons frontward of segment 15 and will improve the model's ability to capture the phasing of the rearmost motor neurons.

Our ensemble model suggests that sharing synaptic current via electrical coupling is an important influence on the phase relations of heart motor neurons

A characteristic feature of electrical coupling of neurons is synchronization of neural activity (Bennett 1966). This feature is evident in our results from varying the coupling strength (g_coup) or eliminating coupling in our standard ensemble model. Electrical coupling decreases the side-to-side phase differences (Fig. 12, C and D) and these differences increase when the coupling is removed (Fig. 10). Electrical coupling produces these synchronizing effects in heart motor neurons mainly through sharing of synaptic currents (Fig. 5). However, each motor neuron reacts to electrical coupling in a different way (Figs. 5 and 6) because the various segmental pairs of motor neurons receive different side-to-side spatiotemporal patterns of input (Figs. 1 and 3). Synaptic input and electrical coupling interact in competing ways with maximal shunting of out-of-phase inhibition and augmentation of in-phase inhibition versus no sharing of synaptic current for in-phase inhibition and maximal sharing of synaptic current for out-of-phase inhibition. Each motor neuron is shifted in absolute phase differently by the coupling (Fig. 5); thus each motor neuron pair's side-to-side phasing is synchronized differently by the coupling (Fig. 6) and the intersegmental phase relations are shifted (Fig. 10). The maximum shifting ability of coupling comes when the synaptic inputs are nearly out of phase (0.35–0.40) (Fig. 6).

The inclusion of the electrical coupling between bilateral paired motor neuron in our model led us to examine the activity of both segmental motor neurons in the pair as our fundamental unit and led us to consider side-to-side coordination. Interestingly, the side-to-side phasing among the pairs of segmental motor neurons from HE(7) to HE(18) is relatively well matched compared with the living system. As Fig. 9 shows, if the bursts of each of these motor neuron pairs were advanced in phase approximately 0.10–0.20 bilaterally with respect to our phase reference, the peristaltic HN(4) interneuron, the phasing of all segments of the standard model that did not involve input from the HN(X) interneuron would be well matched to the living system.

The peristaltic and synchronous intersegmental phase differences are larger in the presence of the electrical coupling than in its absence because intermediate phasing is made possible by sharing the current of the contralateral cell. This observation points to an apparent paradox of the model: the addition of electrical coupling improves the capture of the intersegmental phase relations of peristaltically coordinated motor neurons but worsens that of the synchronously coordinated motor neurons. Our analysis of electrical coupling in the ensemble model suggests that electrical coupling is an important determinant of phase and especially of the side-to-side phase difference. Electrical coupling thus warrants further study beyond the initial description of Peterson (1983), focusing on extent, functional rectification, filtering characteristics, and segmental differences.

Improvements in intrinsic membrane properties of the model motor neurons could improve phase relations in the ensemble model

In our ensemble model of heart motor neuron coordination, the HE(7)–HE(18) model motor neurons fire consistently later with respect to their inputs [and the HN(4) phase reference] than observed in the living system, whereas the HE(3)–HE(6) motor neurons, which receive HN(X)-mediated input, fire consistently earlier with respect to their inputs [and the HN(4) phase reference] than observed in the living system. Ameliorating the ensemble model and gaining further mechanistic insight into the generation of the fictive heartbeat motor pattern require that we develop new hypotheses for how motor neurons process synaptic input and electrical coupling.

The model motor neurons on which the ensemble model is based were purposefully kept simple, mainly because the intrinsic properties of these motor neurons are relatively unexplored. Our model motor neurons are identical in every segment. They spontaneously fire tonically at a specified rate and become silent when strongly inhibited. They respond quasi-linearly over a considerable range when subjected to negative injected or inhibitory synaptic current, although they are prone to precipitous transition between firing and silence (Fig. 2B). Such model motor neurons suited our aims in constructing this first-generation model of coordination of the ensemble of heart motor neurons because they allowed us to explore the potentialities of the synaptic input pattern and electrical coupling of motor neurons in producing the fictive heartbeat motor pattern.

There are clear indications that intrinsic properties of motor neurons in oscillatory networks influence phase relation with respect to the oscillatory input (Bose et al. 2004; Kiehn et al. 2000; Marder and Bucher 2007). In the well-characterized stomatogastric pattern generators of crustaceans, h-current can advance motor neuron bursts with respect to inhibitory input and A-current can retard bursts with respect to inhibitory input (Bose et al. 2004; Harris-Warrick et al. 1995a,b). Such intrinsic currents have not been well explored in heart motor neurons but potentially exist. Moreover, segmentally differential expression of motor neuron intrinsic properties could potentially account for why front motor neurons are relatively delayed with respect to their inputs, whereas rear motor neurons are relatively advanced. Indeed, the one voltage-clamp study of intrinsic currents in heart motor neuron indicates that K⁺ currents are differentially distributed among the heart motor neurons, with front motor neurons containing relatively more of the delaying A-current than rear motor neurons (Opdyke and Calabrese 1995). Moreover, the morphology of the heart motor neurons may influence their integration of synaptic and coupling currents and should be considered at least to the extent of expanding the current single-compartment model to a small number of compartments that separate the model into a spiking area (fast intrinsic currents), an integration area (slow intrinsic currents), a postsynaptic/coupling area, and the relatively inexcitable soma. A complete characterization of heart motor neuron intrinsic properties, including segmental differences, and development of a multicompartment motor neuron model constrained by verifying that its spiking activity is similar to that of the living neurons [e.g., with determination frequency vs. injected current (F–I) curves such as Fig. 2B] may help resolve some of the discrepancies between the ensemble model and the living system.

General implications

Our aim in constructing an ensemble model of motor neuron coordination in the fictive heartbeat motor pattern of the leech was to gain insight into how this intersegmental, asymmetric motor program is generated by input from the heartbeat CPG to the heart motor neurons. Such insight could be useful in understanding more complex motor systems. So far, however, the insights are limited to the realization that the fictive motor pattern is not a simple readout of the input pattern; motor neuron electrical coupling, and probably motor neuron intrinsic properties, transform this input pattern considerably. This insight is not surprising since these aspects of motor neurons have been implicated as important in other motor programs in both invertebrate (e.g., Marder and Bucher 2007; Rela and Szczupak 2003, 2004) and vertebrate systems (e.g., Alaburda et al. 2002; Bertrand and Cazalets 1998; Bou-Flores and Berger 2001; Toledo-Rodriguez et al. 2005; although for a caution on interpreting the functional implications of motor neuron intrinsic properties, see Alaburda et al. 2005; Berg et al. 2007).

The most important implication of this work is that, even for complex networks and activity patterns, ambitious model building when constrained by the available data effectively focuses our attention on mechanisms and suggests further experimental analyses. These benefits of a model are perhaps greatest, not when the model captures the desired activity, but when the model has clearly analyzable shortcomings.

GRANTS

This work was supported by American Psychological Association/Diversity Program in Neuroscience Predoctoral Fellowship 5 T06 MH-1882, funded by the National Institute of Mental Health, to T. M. Wright and by National Institute of Neurological Disorders and Stroke Grant NS-24072 to R. L. Calabrese.