Mechanisms of conduction slowing during myocardial stretch by ventricular volume loading in the rabbit

Abstract

Acute ventricular loading by volume inflation reversibly slows epicardial electrical conduction, but the underlying mechanism remains unclear. This study investigated the potential contributions of stretch-activated currents, alterations in resting membrane potential, or changes in intercellular resistance and membrane capacitance. Conduction velocity was assessed using optical mapping of isolated rabbit hearts at end-diastolic pressures of 0 and 30 mmHg. The addition of 50 μM Gd³⁺ (a stretch-activated channel blocker) to the perfusate had no effect on slowing. The effect of volume loading on conduction velocity was independent of changes in resting membrane potential created by altering the perfusate potassium concentration between 1.5 and 8 mM. Bidomain model analysis of optically recorded membrane potential responses to a unipolar stimulus suggested that the cross-fiber space constant and membrane capacitance both increased with loading (21%, P = 0.006, and 56%, P = 0.004, respectively), and these changes, when implemented in a resistively coupled one-dimensional network model, were consistent with the observed slowing (14%, P = 0.005). In conclusion, conduction slowing during ventricular volume loading is not attributable to stretch-activated currents or altered resting membrane potential, but a reduction of intercellular resistance with a concurrent increase of effective membrane capacitance results in a net slowing of conduction.

several experiments have linked volume overload or acute myocardial wall stretch with atrial and ventricular arrhythmias (46). Reentrant arrhythmias are the predominant phenotype associated with mechanical dysfunction in the diseased heart. Since reentrant circuits require excitable tissue ahead of the activation wavefront (an “excitable gap”), they are promoted and sustained by reduced refractoriness and slowed conduction. We have previously observed in isolated perfused rabbit hearts that passive ventricular loading by volume inflation slows epicardial conduction by ∼15–20% (47). This is comparable in magnitude to the 23–35% slowing observed in a mouse model in which connexin43 expression was reduced by 45% (13). This reduction in connexin43 expression is, in turn, comparable with the 47% reduction in membrane area staining for connexin43 gap junctions observed in tissue samples from patients with chronic myocardial ischemia (30). Other effects of mechanical stimuli on electrophysiology (broadly termed “mechanoelectric feedback”) are frequently associated with the activity of stretch-activated channels (SACs) (18).

Conduction velocity (CV) is influenced by membrane excitability, as a faster phase 0 of the action potential (AP) more quickly creates the electrical potential gradient that drives current flow along the membrane. The associated voltage-gated fast sodium conductances are affected not only by ligand gating and autonomic stimulation (34) but also by resting membrane potential. As resting potential depolarizes toward threshold, less charge is needed to achieve threshold, yet more sodium channels are trapped in the inactivated state (28), resulting in a biphasic relationship between conduction speed and resting potential (35). Myocardial stretch has been associated with a slight depolarization of resting membrane potential (15).

Passive conduction speed is also influenced by the resistive and capacitive properties of the myocardium (21). Although total myoplasmic resistance along a cell length is the primary resistance to longitudinal conduction (51), those gap junctions that colocalize with several cellular structural elements at the intercalated discs (17) further modulate longitudinal resistance to conduction (35); yet, these recurring resistances reduce the downstream electrical load on the depolarizing wavefront (42). Similarly, increased membrane capacitive load, which is governed by the membrane surface-to-cellular volume ratio (21), can slow conduction, since greater membrane capacitance requires more time for an upstream cell to charge its neighbor from resting potential to threshold.

The objective of the present study was to investigate the contributions of stretch-activated currents, alterations in resting membrane potential, or changes in intercellular resistance or membrane capacitance to conduction slowing during myocardial stretch by ventricular volume loading in isolated rabbit hearts. Our findings suggest that SACs or other stretch-dependent mechanisms that may alter resting membrane potential do not significantly contribute to conduction slowing during volume loading in this preparation. Intercellular resistance was actually decreased by volume loading, and the conduction slowing observed was predominantly attributable to increased effective membrane capacitance during tissue stretch.

METHODS

Isolated heart preparation and experimental protocol.

All experiments were performed using isolated Langendorff-perfused rabbit heart preparations as previously described (47) under animal use protocols approved by the University of California-San Diego Institutional Animal Care and Use Committee. Briefly, hearts from New Zealand White rabbits (2.5–3.0 kg) were isolated and retrogradely perfused with warmed (35–37°C) and oxygenated (95% O₂-5% CO₂) modified Tyrode solution composed of (in mM) 130 NaCl, 4.5 KCl, 1.3 CaCl₂, 1.1 MgCl₂, 25 NaHCO₃, 1.2 NaH₂PO₄, and 10.0 dextrose. The heart was paced from the left ventricular free wall near (∼5 mm from) the apex at twice diastolic threshold at a cycle length of 360 ms using an epicardial bipolar electrode (∼1-mm interelectrode separation). The left ventricle was passively volume loaded to an end-diastolic pressure of 30 mmHg by inflating and deflating an intraventricular latex balloon connected to a pressure transducer over a period of 30 s, with 1-min stabilization periods allowed between load state changes. We have previously shown that such loading causes a heterogeneous strain distribution across the left ventricular free wall that does not significantly vary from apical to basal regions, with an average epicardial anterior (region of greatest strain) fiber direction strain of 0.04 and cross-fiber strain of 0.03 (47). Optical mapping data were taken for triplicate 2-s runs in the “initial unloaded” (0 mmHg), “loaded” (30 mmHg), and “final unloaded” (0 mmHg) states, with replications taken within 1 min and an unload/load/unload series completed within 5 min. Reported data were acquired within 1–3 h after isolation, with preparations typically being stable for 3–4 h.

Optical mapping.

Optical mapping was performed as previously described (47). Briefly, after hearts had been stained with a 10-ml bolus of the voltage-sensitive dye di-4-ANEPPS (10.4 μM), the dye was excited at 516 ± 45 nm with light from a 300-W xenon arc lamp. Epifluorescence was passed through a >610-nm filter and focused with a high-numerical aperture lens (f/0.95, Navitar, Rochester, NY) onto an 8-bit charge-coupled device camera (model CA-D1-256, Dalsa, Waterloo, ON, Canada), which imaged an approximate 9-cm² area at 399 frames/s and a resolution of 128 × 126 pixels. Additional 5-ml dye injections were given as needed to maintain acquired fluorescent signal intensity. The electromechanical uncoupling agent 2,3-butanedione monoxime (BDM; 12.5 mM) was added to a secondary perfusate reservoir, which was used to perfuse the heart during data acquisition, and was washed out immediately after data acquisition, with 2–3 min of washin time and at least 10 min of washout. Although BDM has been shown to have electrophysiological consequences (1, 3), we have previously shown that activation times increase to a similar extent during volume loading when BDM is absent and that conduction slowing is reversible with the removal of loading despite the presence of BDM (47).

CV analysis.

Optical data were processed and phase shift filtered as previously described (48, 49). After data had been filtered, activation times at each pixel were extracted as the time of the maximum rate of rise of the optical AP upstroke. The global apparent epicardial CV vector field was calculated over the extent of the left ventricular free wall from the reciprocal gradient of the global activation time field as described by Bayly et al. (2).

CV is reported as the mean apparent epicardial magnitude from four consecutive APs and from the region of the left ventricular free wall near, but basal to, the pacing site. Although apparent epicardial conduction globally slows a similar relative amount (15–20%) with loading across the left ventricular free wall (47), reported values exclude the stimulus artifact region (<1 mm, ∼1 cross-fiber space constant) and also exclude the late-activated region distal from (>5 mm) the stimulating electrode, as apparent epicardial CV suddenly increases at distances greater than this, which may reflect a component of endocardial conduction [mean unloaded value of ∼25 cm/s at 1–4 mm but ∼50 cm/s at 6–10 mm (47)]. The remaining ∼5-mm-wide subset region provides an accurate estimate of apparent CV (48, 49) and reflects the consequence of epicardial stretch on epicardial CV (47). As a consequence of myofiber organization (52) and conduction anisotropy, epicardial fiber conduction from epicardial apical pacing quickly propagates out of view, and the resultant depolarization wavefront that activates the vast majority of the tissue in the region of interest is roughly parallel to the epicardial fiber direction; thus, reported velocity values are from the path of slowest propagation (47), reflecting epicardial cross-fiber conduction. Reported normalized CVs (and other parameters) are normalized by the mean initial unloaded value of the specific unload/load/unload series.

SACs.

CV was measured in n = 4 hearts before and after 50 μM Gd³⁺, a nonspecific blocker of SACs, was added to the perfusates. Since Gd³⁺ precipitates out of carbonate- and phosphate-buffered saline, the perfusate was modified to a HEPES-buffered solution, which contained (in mM) 140 NaCl, 4.5 KCl, 1.3 CaCl₂, 1.3 MgCl₂, 10 HEPES, and 10.0 dextrose and was titrated to a pH of 7.4 and oxygenated with 100% O₂. As a positive control of the effect of Gd³⁺, AP durations (APDs) at 30% and 60% repolarization levels (APD₃₀ and APD₆₀) were concurrently measured by taking the difference between repolarization time at 30% or 60% recovery from the peak value and activation time. At least 15 min of washin time was allowed.

Resting membrane potential from varied extracellular potassium concentration.

CV was measured in n = 5 hearts as a function of perfusate potassium concentration to manipulate resting membrane potential (28, 35). This relationship was evaluated at 2, 2.5, 3.5, 4.5 (normokalemic), 5.5, 6.5, and 8 mM, with at least 10 min of washin time allowed. The curve was also measured during volume loading. The statistical significance of an upward or downward shift relative to the CVs measured in the unloaded heart was analyzed by repeated-measures ANOVA of the measured CVs. The statistical significance of a leftward or rightward shift was tested by a paired Student's t-test of the slope of the relation at normokalemic perfusion, which was calculated as the mean of the slopes of the CV-log (extracellular potassium concentration) relation between 3.5 and 4.5 mM and between 4.5 and 5.5 mM perfusate potassium. In the unloaded heart, normokalemic perfusion resulted in a maximal CV such that a shift in the relation in either direction would cause the absolute magnitude of the slope to increase.

Effective space constants.

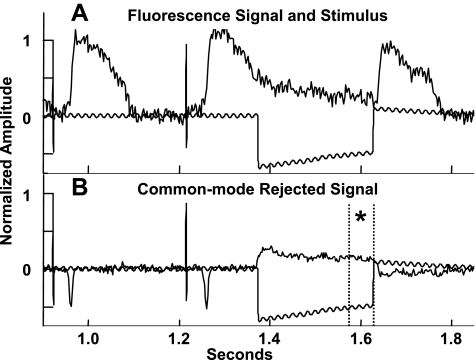
The effect of volume loading on effective fiber and cross-fiber space constants was assessed in n = 4 hearts using methods similar to those of Poelzing et al. (31) in conjunction with an assessment of CV. The magnification of the optical mapping system was increased to reduce the field of view to ∼2.25 cm², centered about a 125-μm-diameter Teflon-coated platinum wire contacting the midlateral left ventricular free wall. After steady-state pacing from the apical electrode (100 paced beats), a 1-mA (∼2× threshold) cathodal stimulus was delivered from the midlateral left ventricular free wall electrode for 250 ms, with the onset during phase 3 of the local AP, resulting in a cathodal-break stimulus during phase 4. This resulted in a significant transmembrane potential response that achieved steady-state before termination of the stimulus (Fig. 1A) without having to artificially depress membrane excitability to apply a nonactivating stimulus of sufficient duration to achieve steady state. Signals were normalized by baseline AP amplitude so that the tissue stimulus response could be compared across space. The common mode signal (mean signal distal from the stimulus site) was subtracted from every pixel, leaving only the transmembrane voltage response to the stimulus (Fig. 1B). The steady-state stimulus response field (mean of the last ∼75 ms of stimulus, phase 4 of the local AP) was fitted to the second-order steady-state approximate analytic solution to the bidomain equations (37). These equations were modified by multiplying all terms by the dimensionless radius (coordinates normalized by the transverse and longitudinal space constants), as this better reflects the temporal and spatial averaging inherent in the optical mapping technique and results in an apparent voltage decay that is accurately described by an exponential (31) rather than steeper functions (Bessel or error). The resulting equation when the coordinate system is rotated such that z is aligned with the local epicardial fiber direction and x with the cross-fiber is as follows:

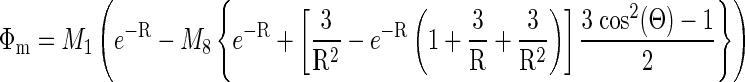(1)

where

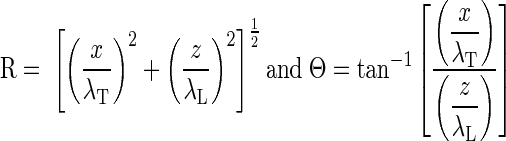where R is the space-constant normalized radius, Θ is the polar angle measured from the fiber axis, and Φ_m is the transmembrane potential. M₁ and M₈ are scaling parameters taken from the amplitude of the response at the center and nominal ratios of intracellular and extracellular conductivities (37, 38), respectively, whereas the free parameters are the transverse (cross-fiber) and longitudinal (fiber) space constants (λ_T and λ_L, respectively.

Fig. 1.

A: example fluorescence signal showing transmembrane voltage responses to a cathodal-break stimulus proximal to the electrode. B: the same signal after common mode rejection. *Steady-state region.

Mean strain induced by volume loading was used to correct loaded values of the effective space constant such that all reported values are in terms of unloaded length (a constant material description; uncorrected effective space constant values are ∼1.03× larger). Optical recordings of cardiac APs sample the emitted fluorescence of tissue up to ∼250 μm in depth (16). As the loading typically applied in this protocol resulted in epicardial fiber and cross-fiber strains of 0.04 and 0.03, respectively, in the regions of greatest strain (47), incompressibility suggests a maximum wall thinning strain of −0.07, or approximately one additional cell thickness in depth sampled during loading. Measurements of effective space constants were replicated in triplicate for each load state, and means were normalized by series mean initial unloaded values.

Effective membrane capacitance estimation from bidomain model analysis.

A bidomain model, as described by Skouibine et al. (44), was used to simulate the above technique for measuring the effective space constants. The two-dimensional mesh represented 13 fiber and cross-fiber space constants (at resting potential membrane resistance), discretized into one-fifth space constants, with 0.1-ms time steps. Baseline membrane capacitance was taken from Sokabe et al. (45) as 0.7 μF/cm², and baseline conductivities were taken as 2.5 × 10⁻³ Ω·cm fiber interior and exterior, 1.3 × 10⁻³ Ω·cm cross-fiber exterior, and 0.5 × 10⁻³ Ω·cm cross-fiber interior to approximate the nominal conductivity ratios of Roth (38) and concurrently approximate the initial unloaded measured effective space constants (see results). The membrane was coupled to the Saucerman et al. (40) implementation of the Puglisi-Bers rabbit ventricular myocyte ionic model (32), which is a modification of the Luo-Rudy model (25). A unipolar cathodal stimulus was applied at the center node of the mesh, which had the uniform initial condition of being in midrepolarization (at −18 mV, from the Saucerman ionic model cycling at 360 ms) and uniform boundary condition of normal repolarization. As with the experimental data, this boundary (distal, common mode) repolarization morphology was subtracted from that of the interior nodes to obtain the membrane potential response to the stimulus. This model was reevaluated after varying conductivities to modify the space constants in excess of the range of measured values (90–140%) and after varying membrane capacitance over the range of 90–190%. Absolute node spacing was covaried with the conductivities to maintain the baseline scaling, preventing the introduction of consequential edge effects. Stimulus current density was set to obtain a membrane response of similar magnitude to that measured and then was covaried with parameters so as to maintain a constant total injection current, as in the experimental study. The model steady-state membrane response was also fitted to the second-order steady-state approximate analytic solution to the bidomain equations as described above (without the modification for optical mapping) to measure the model effective membrane space constants. The model results were used to estimate changes in effective membrane capacitance from the same n = 4 dataset used to measure the effective space constants above (see results).

Multicellular fiber conduction model analysis.

A model of conduction along a monodomain multicellular fiber was developed as described by Shaw and Rudy (41), with 3 discretizations/cell, again using the Saucerman et al. ionic model. The 70-cell fiber was stimulated at the first cell, and CV was calculated as the distance covered between cell 20 and cell 50 divided by the difference in activation times, calculated from the maximum derivative of the upstrokes. Initial capacitance was again set at 0.7 μF/cm², after which intercellular resistance was iteratively modified until CV matched the case-specific measured initial unloaded CV. CV was again calculated after increasing membrane capacitance by the case-specific estimated change in capacitance and decreasing intercellular resistance by the amount calculated from the measured heart-specific change in cross-fiber space constant assuming that only intercellular resistance (rather than membrane resistance) changed so as to maximize the possible opposing effect (see results and Eq. 2).

Statistics.

All values are expressed as means ± SE. CV and effective space and time constants were analyzed using repeated-measures ANOVA with load state and the use of pharmacological agents as multiple within factors where appropriate. A post hoc Scheffè's F-test was used to differentiate load states when appropriate using a significance level α = 0.05. Power was calculated as described by Cohen (8).

RESULTS

Stretch-activated currents.

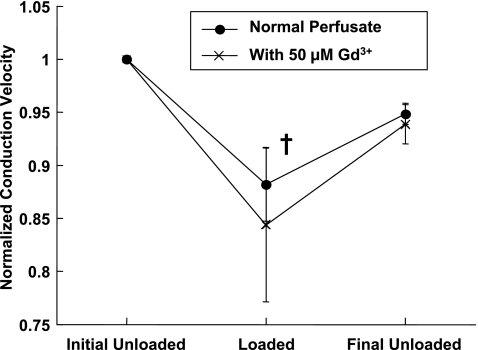
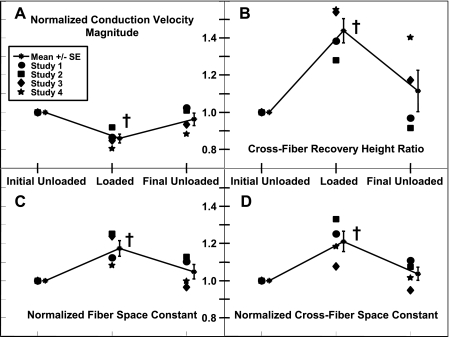
Gd³⁺ (50 μM) attenuated the increase in APD₃₀ and APD₆₀ during volume loading and inhibited recovery to unloaded values, but Gd³⁺ did not significantly alter the reversible conduction slowing during volume loading. Mean initial unloaded APD₃₀ was 103 ± 3 ms and increased 19 ± 3% (P = 0.001) during volume loading before recovering to 104 ± 2% of the initial value after the load was removed. With Gd³⁺ present, mean initial unloaded APD₃₀ was 105 ± 7 ms but increased only 6 ± 7% during volume loading and continued to increase to 113 ± 8% of the initial value after load was removed. This interaction of Gd³⁺ with the effect of loading on APD₃₀ was significant (P < 0.05). The attenuation of the increase in APD₆₀ during volume loading in the presence of Gd³⁺ was less pronounced, but the recovery of APD₆₀ when loading was removed was still inhibited, and this interaction effect of Gd³⁺ was significant as well (P < 0.01). CV decreased 12 ± 3% (P = 0.01) during volume loading and recovered to 95 ± 1% of the initial value of 30.8 ± 4.7 cm/s (Fig. 2). In the presence of Gd³⁺, similar changes during loading were observed: CV decreased 15 ± 7% during volume loading and recovered to within 94 ± 2% of the initial value of 29.9 ± 4.8 cm/s. The interaction effect of Gd³⁺ on load-dependent changes in CV was not significant, even though this experiment could detect a minimum 40% interaction effect (a 40% attenuation of slowing during loading due to the presence of Gd³⁺) with a power of 0.8 or greater.

Fig. 2.

Mean ± SE conduction velocities (CVs) without and with 50 μM Gd³⁺ as functions of the ventricular volume loading state. All values were normalized by the initial unloaded value. †P < 0.05 compared with the initial unloaded value.

Resting membrane potential from varied extracellular potassium concentration.

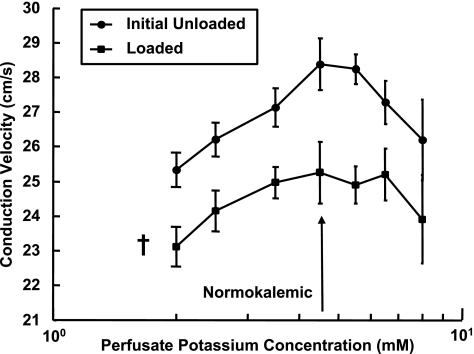
Varying the perfusate potassium concentration did not significantly alter the effect of volume loading on CV. Figure 3 shows that in the range of concentrations studied, increasing or decreasing perfusate potassium concentration from normokalemic slowed conduction, and the shape of this biphasic relationship was similar before, during, and after volume loading (“after” data are not shown for clarity). CV decreased 11 ± 3% from the mean unloaded value when normokalemic (28.4 ± 2.4 cm/s) and decreased at all potassium concentrations by an overall average of 9 ± 6% (P = 0.03). When load was removed, CV at normokalemia recovered to 94 ± 2% of the initial value and to 91 ± 5% averaged across all potassium concentrations. The mean initial unloaded slope of the relationship at the normokalemic point was not significantly altered (P = 0.19, power to detect the difference in mean slopes resulting from a leftward curve shift that resulted in an 11% CV reduction was 0.91), indicating that the relationship between CV and perfusate potassium concentration was not significantly left or right shifted by ventricular loading.

Fig. 3.

Mean ± SE CVs as a function of perfusate potassium concentration before and during volume loading. †P < 0.05 compared with the initial unloaded value.

Effective space constants and effective membrane capacitance.

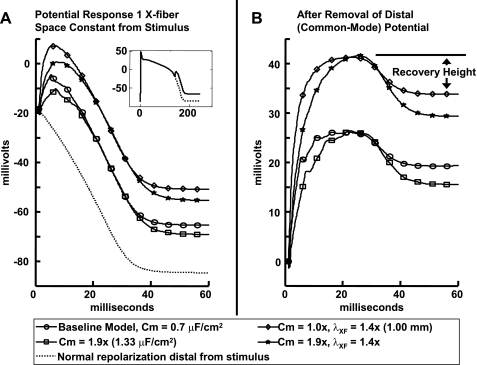
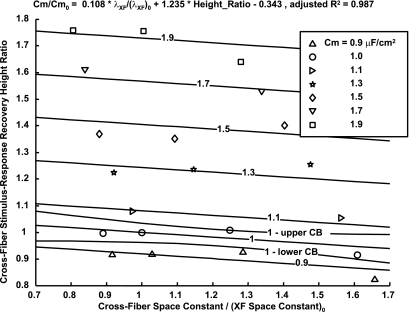
Because CVs measured from the region of interest primarily reflected cross-fiber conduction, the analysis of the bidomain modeling focused on measurable parameters in this direction. Figure 4 shows the effect of varying membrane capacitance and cross-fiber conductivities on the membrane response at the node closest to one effective (second-order steady-state approximate analytic solution of the bidomain equations) cross-fiber space constant from the stimulus. This model analysis revealed that the indicated response recovery height (Fig. 4B) at the same effective distance (normalized by fiber and cross-fiber space constants) from the stimulus is dependent on the variation of membrane capacitance and tissue conductivities. Specifically, the ratios of response recovery height and cross-fiber effective space constant to their baseline values can be used to predict the ratio of input membrane capacitance to the baseline capacitance. As the response recovery height ratio was similar within a region 0.5–1.5 space constants from the stimulus, this mean ratio was used, as this allowed pooling of data from the noisier experiments. Figure 5 shows contours of membrane capacitance as a function of these measurable quantities and the simultaneous functional confidence contours about a capacitance ratio of 1 (global root mean square error = 0.04).

Fig. 4.

A: bidomain model of transmembrane voltage responses to a stimulus application during repolarization (inset) at one effective cross-fiber (1 X-fiber) space constant (λ_XF) as measured using the methods for experimental data from the stimulus site, whereas distal from the stimulus (>6 space constants) showed no deviation from normal repolarization. B: after normal repolarization was subtracted, the remaining signal is the response to the stimulus, of which the recovery height (maximum to steady state) is dependent on membrane capacitance (C_m) and tissue conductivities.

Fig. 5.

A fit to model results so that changes in C_m can be predicted from measured changes in the cross-fiber stimulus-response recovery height and effective λ_XF, showing contours of constant C_m and simultaneous functional confidence boundaries about the 1 μF/cm² contour. C_m0, initial C_m; (λ_XF)₀, initial λ_XF.

Volume loading simultaneously slowed conduction and increased the effective space constants (Fig. 6A). CV decreased 14 ± 2% (P = 0.005) during volume loading and recovered to 96 ± 3% of the initial value (36.0 ± 3.3 cm/s) when the load was removed. The mean cross-fiber stimulus-response recovery height ratio was 1.44 ± 0.7 (P = 0.005) and recovered to 1.11 ± 0.11 (Fig. 6B). However, the tissue space constants increased during loading: in the fiber direction by 17 ± 4% (P = 0.02) and recovered to 105 ± 4% of the initial unloaded value (1.08 ± 0.08 mm; Fig. 6C) and in the cross-fiber by 21 ± 5% (P = 0.006) and recovered to 104 ± 4% of the initial unloaded value (0.74 ± 0.06 mm; Fig. 6D).

Fig. 6.

Individual data points and means ± SE of measured CV (A), the measured cross-fiber stimulus-response recovery height ratio (B), measured fiber space constant (C), and measured λ_XF (D). All parameters were measured concurrently within an individual experiment and loading state. All values are normalized by initial unloaded values. †P < 0.05 compared with the initial unloaded value.

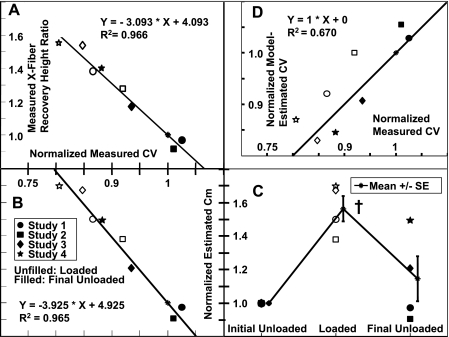
Changes in the measured mean cross-fiber stimulus-response recovery height ratio was inversely correlated with changes in measured CV (correlation coefficient = −0.98, P < 0.0001; Fig. 7A). Consequently, changes in effective membrane capacitance estimated from the recovery height ratio and cross-fiber space constant were also inversely correlated with changes in measured CV (correlation coefficient = −0.98, P < .0001; Fig. 7B). Estimated effective membrane capacitance increased 56 ± 8% (P = 0.004) and recovered to 115 ± 13% of the assumed initial value of 0.7 μF/cm² (Fig. 7C).

Fig. 7.

A: correlation between changes in concurrently measured CVs and cross-fiber stimulus-response recovery height ratios. B: correlation between changes in measured CVs and effective C_m values estimated from the fit to model data. C: individual data points and means ± SE of estimated C_m. D: correlation between changes in measured CVs and model-estimated CVs, with regression to unity. All values were normalized by initial unloaded values. †P < 0.05 compared with initial unloaded values.

Multicellular fiber conduction model analysis.

Modifying monodomain model capacitance and resistance by values computed for each heart from the measured space and time constants resulted in net conduction slowing that was well correlated with measured conduction slowing (correlation coefficient = 0.86, P = 0.003; Fig. 7D).

DISCUSSION

We investigated four possible mechanisms of conduction slowing measured by optical mapping during ventricular volume loading in isolated perfused rabbit hearts. This study supports the hypothesis that loading-related slowing of CV is a result of increased effective membrane capacitance rather than being mediated via the effects of SACs, stretch-dependent alteration of resting membrane potential, or changes in tissue electrical resistance associated with intercellular coupling.

Stretch-activated currents.

Changes in APD during stretch have been attributed to the action of SACs (53). Previously, we found that the nonspecific SAC blocker streptomycin did not significantly alter the effect of volume loading on CV but also did not alter the effect of loading on APD (47). In this study, we observed that the SAC blocker Gd³⁺ significantly attenuated the prolongation of APD₃₀ and APD₆₀ during volume loading but did not significantly attenuate concurrent conduction slowing. This suggests that Gd³⁺ was indeed inhibiting cation nonselective SACs, but these channels were not significantly contributing to conduction slowing during ventricular loading. Although Gd³⁺ inhibits sodium channels at the concentrations used here (23), Gd³⁺ had little apparent effect on measured, unloaded, cross-fiber CV values, and any effect of Gd³⁺ on sodium channels was accounted for by comparing normalized CV values. However, this study is limited in that potassium-selective SACs are insensitive to Gd³⁺ (5).

Resting membrane potential from varied extracellular potassium concentration.

Varying perfusate potassium concentration had the same previously reported biphasic effects on CV (35). Membrane excitability was significantly altered, as indicated by the large changes in CV. If loading caused conduction slowing primarily by altering resting membrane potential (whether by the activity of SACs or an independent mechanism such as alterations in intracellular calcium concentrations), then volume loading would have the effect of moving along the relationship between CV and perfusate potassium concentration; consequently, the relationship assessed during volume loading would be a leftward or rightward shift of the unloaded relationship. However, volume loading caused conduction slowing at all potassium concentrations, consistent with a downward shift of this relationship, and did not significantly alter the mean slope of the relationship at normokalemic perfusion, suggesting that load slows conduction independent of altered resting potential. Moreover, one model study (15) indicated that the slight depolarization from resting potential typically observed during stretch (and attributed to SACs) would tend to enhance excitability and, consequently, CV (33) rather than depress it. Additionally, it has been observed that stretch can switch human skeletal muscle sodium channels to faster current kinetics (50), and such an effect on cardiac sodium channels also would enhance membrane excitability.

Effective space constants and effective membrane capacitance.

Epicardial conduction slowing during volume loading was associated with increases in the effective space constants measured on the epicardium. The mean effective space constants we measured were similar to values previously reported for fiber and cross-fiber directions using optical methods [λ_L ∼ 1.58 and λ_T ∼ 0.73 mm (31)], although the cross-fiber data have significantly better agreement. Changes in CV, effective space constants, stimulus-response recovery height ratio (and consequently estimated effective membrane capacitance) were all incompletely reversible with removal of loading, and we (47) have previously shown that activation times increase with loading in the absence of BDM, indicating that these effects are not an artifact of BDM. Because epicardial and transmural strains are small (typically 0.04 and −0.07, respectively), and because the depth of sampling of the optical mapping technique [∼250 μm (16)] is small compared with the wall thickness, such that no more than an additional cell thickness in depth would be sampled during loading, the macrostructure measured by the optical technique is comparable without and with loading. We did not observe the classically described dogbone-shaped potential distributions; however, we measured tissue responses at steady state, 200 ms after the stimulus onset. Others (39) have reported that low stimulus strength induces an initial dogbone-shaped field that spreads out nonuniformly, such that it can no longer be easily detected after 10 ms.

Model-assisted estimation of changes in effective membrane capacitance based on the membrane response to a stimulus indicated a significant increase correlated with volume loading. Membrane patches placed under tension will stretch with a concomitant increase in capacitance of the patch itself (45), whereas passive ventricular volume loading to 30 mmHg causes unfolding of the slack membrane and an integration of caveolae into the sarcolemma (20). These mechanisms would lead to an increase in the effective cell membrane surface area-to-volume ratio, increasing effective membrane capacitance (14). These stretch-associated effects would result in increased capacitive electrical load (current sink) on the depolarization wavefront, slowing conduction. Furthermore, the varying dynamics of sarcolemmal lipid recruitment with stretch and endocytosis with relaxation, processes on the order of minutes (27), may partially explain the incomplete recovery of CV and other measured parameters at 1 min after unloading.

In one dimension, the effective space constant is proportional to membrane resistance (R_m) and inversely proportional to extracellular resistance (R_e), intracellular resistance (R_i), and the membrane surface-to-tissue volume ratio (β) (19), as follows:

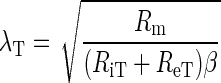(2)

Recently, it has been observed that shear stress of osteocytes induces opening of connexin43 hemichannels, the predominant connexin type expressed in ventricular myocytes, within 10 min from the onset of shearing (6). The increase in the effective space constant we measured is indicative of a decrease in longitudinal resistances and may specifically indicate that ventricular wall stretch caused increased intercellular coupling, possibly by a similar pathway. This may further explain our previous results, wherein we observed an unexpected decrease in the dispersion of repolarization during volume loading (47). Although an increase in intercellular coupling would be expected to lead to faster conduction, others have shown using computer simulations of propagation that CV is not very sensitive to changes in intercellular resistance at normal levels of cellular coupling and specifically showed that a decrease in CV of 7% required an increase in intercellular resistance of 43%, as most of the resistance to propagation in the fiber direction is composed of myoplasmic resistance (51). A related experimental study was unable to resolve a difference in CV between synthetic strands of wild-type neonatal cardiomyocytes and strands composed of cells from mice with a 43% reduction in connexin43 expression. Consequently, any gap junctional conductance downregulation due to increased intracellular calcium concentration during myocardial stretch (4) would be too moderate (10) to significantly impact conduction, and any significant effect would also decrease the effective space constant. Because extracellular resistance in the cross-fiber direction is ∼0.25 times that of the intracellular resistance (38), any effect of volume loading on extracellular resistance is expected to have a proportionally less significant effect on CV.

Multicellular fiber conduction model analysis.

The fiber model analysis indicated that an increase in membrane capacitance consistent with observations would significantly slow conduction more than any concurrent increase in intercellular conductivity would speed conduction, even if allowing for the maximal increase consistent with the change in space constant. This is most likely a consequence of conduction speed typically being more sensitive to changes in membrane capacitance (24) than intercellular coupling (51). The relative contributions of these two competing effects may explain some of the discrepant reports of faster conduction during stretch in several different isolated myocardial tissue preparations (9, 11, 29, 36), although the discrepancy may also lie in the definition of CV used (26), as several reports (7, 12, 43, 54) in whole chamber preparations have observed slowed conduction during stretch.

Clinical implications.

Conduction slowing is a well-recognized contributor to reentry (22), along with dispersion of recovery. Our results provide strong evidence for a new mechanism through which mechanical stretch may slow conduction and thus facilitate arrhythmogenesis in the mechanically dysfunctional myocardium. Further studies are required to understand the timecourse, recovery, and spatial preferences of changes in membrane capacitance; their interaction with regions of scar, which may further alter capacitance; and their direct effect on arrhythmogenesis.

Conclusions.

We have shown that slowing of apparent epicardial conduction during myocardial stretch by ventricular volume loading is not primarily attributable to SACs or depressed membrane excitability due to altered resting potential. We have further shown that volume loading is associated with an increase in the effective myocardial space constants, suggesting reduced intercellular resistance, and is also associated with changes in membrane response to a unipolar stimulus that is consistent with an increase in effective membrane capacitance. A one-dimensional conduction model analysis showed that increasing effective membrane capacitance and reducing intercellular resistance by amounts consistent with the measured changes in the effective cross-fiber space constant is sufficient to account for the net magnitude of conduction slowing we observed. These novel mechanisms of ventricular conduction slowing could contribute to reentrant arrhythmias associated with altered mechanical loading conditions in vivo.

GRANTS

This work was supported by National Science Foundation Grant BES-0506252, National Institutes of Health (NIH) Grants 5-P01-HL-4634and P41-RR-08605, and Grant 0265120Y. R. W. Mills was a trainee on NIH Training Grant T32-HL-07444.

DISCLOSURES

A. D. McCulloch is required by the University of California-San Diego (UCSD) Institutional Review Committee to disclose that he is a co-founder of Insilicomed, a licensee of UCSD-copyrighted software supported in part by a NIH grant acknowledged herein. That software was used in no part of the research described in this article.