An integrated mechanobiochemical feedback mechanism describes chromosome motility from prometaphase to anaphase in mitosis

Abstract

During mitosis, chromosomes undergo a series of movements while being end-on attached to the kinetochore microtubules (KMTs) from spindle poles. The mechanism underlying such movements and their physiological functions remains elusive. We describe a mechanobiochemical feedback model of chromosome motility. The key ingredient is a feedback mechanism between the local chemical reactions that control the dynamics of KMTs and the mechanical state of the chromosome via tension-sensitive proteins localized at the kinetochores. This model can recapitulate all of the essential and distinct features of chromosome motilities from prometaphase to anaphase in a coherent manner. We further show that this feedback mechanism provides robust and precise means of guiding the chromosome to the cell equator regardless of the initial conditions and uncertainty in velocity. Predictions of our model can be tested experimentally.

The essential function of mitosis is to ensure the precise partitioning of the replicated parental chromosomes into the two daughter cells. After entry into mitosis, the centromere regions of chromosomes build kinetochores, which act as the primary chromosomal end-on attachment sites for spindle microtubules (1). At first, chromosomes are end-on attached via kinetochores by microtubules from one of the spindle poles, resulting in a monooriented configuration. Subsequently, the sister kinetochore connects to microtubules from the opposite pole, resulting in biorientation. Bioriented chromosomes congress to the cell equator while their kinetochore-attached microtubules polymerize and depolymerize. After all of the chromosomes in the cell are bioriented and congressed, sister chromatids separate and segregate to opposite spindle poles. Surveillance mechanisms correct errors in chromosome–spindle interactions and coordinate the behavior of multiple chromosomes in the cell, thereby ensuring high-fidelity segregation.

In vertebrate somatic cells, chromosomes attached to spindle microtubules undergo a series of striking movements that have been subject to considerable study, but the underlying mechanism and functions remain obscure (2–4). Monooriented chromosomes oscillate with amplitudes of ≈3–4 μm and periods of ≈5 min near the attached spindle pole (3, 4). After capture by microtubules from the distal pole, bioriented chromosomes congress to the cell equator without much oscillation. Interestingly, after congression, bioriented chromosomes again oscillate vigorously and regularly around the cell equator, with amplitudes of ≈2–3 μm and periods of ≈3 min (3, 4). Chromosome segregation is triggered only after all sister chromatids are properly aligned at the cell equator, whereupon the bioriented chromosome oscillations are dampened (3, 4). Because the directional switch of the chromosomal motion during oscillations is very abrupt, it has been termed “directional instability” (3, 4).

Many aspects of chromosomal motility in mitosis remain unknown: What ensures that bioriented chromosomes always congress to the cell equator? Why don't the chromosomes oscillate during this congression process while they do oscillate vigorously and regularly both before (monooriented) and after (bioriented) congression? Why and how does the chromosome oscillation get dampened right before chromosome segregation? Because the timing for the dampening of chromosome oscillation coincides with the relief of mitotic checkpoint activity and chromosome segregation, the key question is: What is the relationship between chromosome motility and mitotic checkpoint signaling?

Experiments have provided important clues for the mechanism of chromosome movements. The regularity of chromosome oscillations makes them unlikely to stem from stochastic fluctuations. The independence in the movement of different chromosomes in the same cell suggests that it is the intrinsic local changes in the state of individual chromosome–spindle interactions that drive the oscillation, instead of global cellular changes (3, 4). Recent experiments have suggested also that, at least in vertebrate cells, chromosome oscillations in mitosis do not arise from the so-called microtubule flux mechanism (5, 6), in which the kinetochore microtubules (KMTs) move poleward (P) while polymerizing at the kinetochore (1, 7). Therefore, data point to a scenario in which chromosome movement in mitosis originates from intrinsic changes in the activity of the kinetochores that attach chromosome end-on to the KMT plus ends (1, 3, 4, 8).

Congressing a chromosome to the cell equator requires the guidance of spatial clue, which is nicely conferred by a spatial gradient in the away-from-pole (AP) ejection force from spindle poles (4). To pinpoint the cell equator, the opposing forces exerted on the bioriented chromosome have to be balanced. However, force balance is likely only a part of the mechanism controlling chromosome movement in mitosis (9). Because the chromosome remains end-on attached to the KMT plus ends during its movement, its P and AP movements must involve the shrinkage and the growth of the underlying KMTs, respectively (8, 9). It then follows that chromosome movement needs to be at least coordinated with, if not limited by, the local chemical reactions that regulate KMT plus-end dynamics (8–10). This expectation is supported by the observation that chromosome motions become largely stopped if one inhibits microtubule dynamics by treatment with a low dose of Taxol during mitosis (10). From a mechanical perspective, we note that because it is the growth and shrinkage of KMT plus ends (instead of viscous drag) that limit and, hence, determine the chromosome velocity (8, 9), the difference between the P and AP forces cannot be entirely balanced by the viscous drag arising from the moving chromosome (8, 9, 11). In other words, the chromosomes cannot move as fast as what their driving forces “command” (3, 4, 12), and the imbalance between the driving forces must be resisted by the chromosomes, resulting in a highly stretched configuration (3, 4).

Experiments suggest that this resistance, which we refer to as “kinetochore resistance,” tends to modulate the local levels of tension-sensor proteins (13–20). These tension sensors have been implicated in regulating the local chemical reactions that govern KMT plus-end dynamics and, hence, chromosome velocity (12, 19–25). Thus, through kinetochore resistance and tension-sensor proteins, a kinetochore-localized mechanobiochemical feedback loop may be realized individually for each chromosome pair. We propose that it is this feedback loop that controls the movement of individual chromosome pairs (9), instead of the pure mechanical models (26, 27) that focus on the direct balance between P and AP forces.

In previous work we have shown computationally that the proposed feedback loop is capable of generating the observed monooriented chromosome oscillation for parameters within the physiological range (9). Here, we generalize this mechanobiochemical feedback model to the motility of bioriented chromosome. We show that our model can coherently reproduce all of the key sequential events of bioriented chromosome movements in mitosis, including chromosome congression, the ensuing oscillation around the cell equator, the dampening of oscillation while located at the cell equator, and, finally, chromosome segregation. Below we first describe our model and present the main computational results together with their connections to in vivo observations. Then, we discuss the implications of the proposed feedback mechanism on physiological functions of some key cell-cycle proteins in mitosis. Detailed model derivations and additional results are given in the supporting information (SI) Figs. S1–7 and the SI Text.

Model

Qualitative Ingredients.

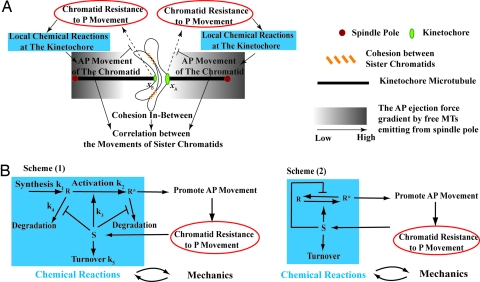
The model describes chromosome motility in which the sister kinetochores are end-on attached by the KMTs from both sides (see Fig. 1). The key ingredients are:

1. There is a regulator (R), likely a mitotic kinase, localized at sister kinetochores (23–25). At each kinetochore, when the activated regulator level (R*) is above a certain threshold, it promotes KMT plus-end growth (28) and activates AP movement by the AP ejection force, possibly via chromokinesin motor activities (12); below this threshold it would confer P movement of the chromatid (28).

2. The cohesion complex physically “glues” sister chromatids (29), dictating the correlation between the movements of sister chromatids (29, 30).

3. The level of activated regulator R* local to each kinetochore is determined by the synthesis of R, activation to R*, deactivation of R*, and degradation of R, R* (31, 32). The last two are further modulated by a kinetochore-localized “sensor protein,” S (33–35); two possible scenarios are sketched in Fig. 1B.

4. In addition to being activated by R*, the AP ejection force from either side has an increasing spatial gradient in the P direction (Fig. 1A) caused by the astral formation of the spare microtubules around the spindle pole and the associated chromokinesin distribution (4, 36).

5. The kinetochore resistance (i.e., the imbalance between the P and AP forces as manifested by chromosome stretching) tends to increase the local sensor-protein level S (see Fig. 1A) (13–20). The individual kinetochore resistance at the sister chromatids is affected by the modulation of AP ejection force in two ways: (i) as the sister chromatid approaches its associated pole, it encounters more and more resistance because of the increasing AP force gradient (4, 36); and (ii) the restoring force from the cohesion complex effectively increases the AP force on the sister chromatids as they move apart from each other (29, 30).

Fig. 1.

Schematics of the mechanobiochemical feedback mechanism. (A) Qualitative picture of the proposed mechanism. The sister-chromatid movements modulate the kinetochore resistance that results in chromosome stretching, which further affects the local chemical reactions that promote the AP movement of the chromatid. That, in turn, opposes the tendency of the P movement of the chromatid, leading to a closed feedback loop. (B) Two possible schemes of the local chemical reactions that govern feedback from the chromatid's mechanical state.

Mathematical Formulation.

We adopted the feedback mechanism of Fig. 1A and reaction scheme 1 in Fig. 1B. (Reaction scheme 2 yields similar results and, hence, is not described here.) The qualitative model is incorporated into equations below; detailed assumptions and derivations are given in the SI Text.

We define a one-dimensional coordinate x connecting the two spindle poles, with x = 0 being the cell equator, and x_A and x_B the positions of the two chromatids (A and B), respectively (see Fig. 1). The velocity of the chromatids, dx_i/dt, is given by

where i ∈ {A, B}, R_i* is the activated regulator level associated with chromatid i. V_A and V_B are constants related to the intrinsic strength of the proteins that depolymerize/polymerize the KMT plus end; it is important to note that chromatid velocity has to be modulated by the local regulator-level R_i*. Because of the opposite polarity of the sister chromatids, we have −V_A = V_B = V₀, where V₀ > 0. The signs of V_A and V_B are chosen such that the chromatid moves toward the cell equator (AP direction) when its R_i* > R₀; otherwise, it moves toward its associated pole (P direction). ξ_i represents the stochastic noise in velocity, taken to be Gaussian distributed with mean 〈ξ_i〉 = 0 and variant 〈ξ_i(t₁)ξ_i(t₂)〉 = ∣ξ̄∣² δ(t₁ − t₂).

Eqs. 2 and 3 represent the local chemical reactions that directly control the regulator levels at the sister chromatids:

Eqs. 2 and 3 include the synthesis, activation, and degradation of R_i (represented by the k₁, k₂, and k₄ terms, respectively), along with modulation of the activation and degradation rates by the sensor protein S. Here we neglected the diffusion of proteins between sister chromatids in accordance with the observation that the localization of kinetochore proteins is not dominated by diffusion (37).

Modulation of the sensor protein level S_i is modeled by Eq. 4:

Here, −k₅S_i is the turnover rate of the sensor protein. The last two terms represent the key couplings between mechanics and biochemistry. k₆·(1 + α_ix_i)·R_i* describes the increase in “sensor” level with kinetochore resistance, arising from the activation of the effective x-dependent AP ejection force by R* (Fig. 1; also see derivations in the SI Text). The spatial profiles of the AP force are chosen to be linear when the chromatid and its associated pole are on the same side of the equator and zero otherwise; that is, α_A < 0 for x_A > 0, α_A = 0 for x_A < 0, and α_B > 0 for x_B < 0, α_B = 0 for x_B > 0 (see Fig. 1). K̄·(x_A − x_B − l₀) describes modulation of the sensor level by the elastic restoring force from the cohesion between sister chromatids, which tends to pull them closer to each other and effectively increases the kinetochore resistance and, hence, the S level. l₀ is the resting interkinetochore distance, and K̄ is the spring constant. A hard-wall repulsion is imposed for x_A − x_B < l₀, preventing the crossing of sister chromatids.

Solutions of Eqs. 1–4 depend on the kinetic parameter values, which in turn depend on the identity of the regulator and sensor molecules. To that end, we take the regulator R as the Cdk kinase and the sensor S as the mitotic checkpoint proteins. This identification leads to parameter values listed in Table S1. We stress, however, that the main focus of our study is to demonstrate the feasibility of the mechanobiochemical feedback mechanism of chromosome motility, not to identify specific molecular players. By surveying the parameter space, we will show below that our results are robust to the variations in parameter values and, hence, not dependent on the specific characteristics of the molecular players used here. If not otherwise mentioned, the parameter values in the model are chosen as follows: k₁ = 0.1 nM·min⁻¹, k₂ = 0.06 min⁻¹, k₃ = 0.02 nM⁻¹·min⁻¹, k₄ = 0.25 min⁻¹, k₅ = 3.33 min⁻¹, k₆ = 3.33 min⁻¹, K_C = 0.2 nM⁻¹, V₀ = 20 μm·min⁻¹, ∣α∣ = 0.01 nm⁻¹, l₀ = 1.0 μm, K̄ = 0.001, and the relative noise level ∣ξ̄∣/V₀ = 0.1. We numerically integrated Eqs. 1–4 over time, starting from arbitrary initial conditions. We thus obtained the instantaneous dynamics, characterized by the positions and velocities of the sister chromatids along with their local protein levels and kinetochore resistance.

Results

Mechanobiochemical Feedback Mechanism Guarantees Bioriented Chromosome Congression.

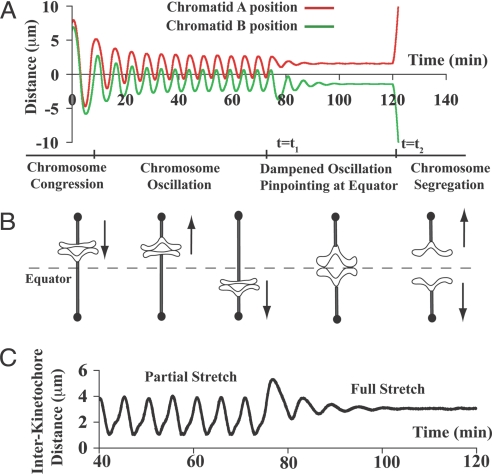
Fig. 2 shows that by sequentially changing the kinetic parameters in the model, the proposed mechanobiochemical mechanism can reproduce the distinct and essential patterns of chromosome motilities in a coherent manner akin to those in mitosis, which includes chromosome congression, its ensuing oscillation around the cell equator, oscillation dampening and pinpointing chromosome at the cell equator, and P movements after chromosome segregates.

Fig. 2.

Bioriented chromosome motility. (A) The mechanobiochemical feedback mechanism coherently captures all of the sequential changes of chromosome motilities during mitosis. The initial conditions for the sister chromatids are: x_A = 7.5 μm and x_B = 6.0 μm; R_A* = 5.0, S_A = 1.2, R_A = 0.1, R_B* = 1.0, S_B = 1.0, and R_B = 0.1. The parameters change sequentially: (i) t = 0, biorientation; (ii) t = t₁, S turnover rate k₅ changes from 3.3 min⁻¹ to 16 min⁻¹, and the oscillation gets damped; and (iii) t = t₂, the cohesion is broken (K̄ = 0.001 changes to K̄ = 0) and the feedback is completely disassembled (k₅ = 16 min⁻¹ and K_C changes from 0.2 nM⁻¹ to 0), and the chromosome segregates. (B) The schematics of sister-chromatid configurations during the process shown in A. Arrows in (B) represent the overall direction of chromosome movement. (C) The calculated interkinetochore distance change for A.

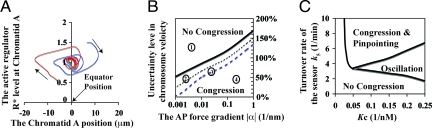
Fig. 2A shows that soon after being bioriented (t = 0), the positions of the sister chromatids (indicated by the vertical coordinates of the red and green curves) can move all the way from ≈10 μm away toward the cell equator (x = 0) within a few minutes. In vivo experiments also suggest that chromosome congression is very robust (3, 4); that is, despite the noisy intracellular environment, the chromosomes always manage to find their way to the cell equator regardless of the initial state. Such robustness entails a safeguard mechanism to guarantee congression. Can our proposed feedback provide such safeguard for chromosome congression? Fig. 3A shows a phase-space plot in which the position of a chromatid (x_A) is plotted against its local level of the active regulator (R_A*) over time from two different initial states (the blue and red trajectories). We see that with either initial state, the trajectory converges around the cell equator (x = 0). We verified this to be true for a large number of initial states (data not shown) in which the initial position of the chromosome can be tens of micrometers away from the cell equator and the initial local protein levels can differ ≈10-fold between sister chromatids. Therefore, this feedback mechanism can provide a robust means for chromosome congression.

Fig. 3.

The mechanobiochemical feedback mechanism ensures the chromosome congression and pinpointing at the cell equator. (A) The phase plot of the dynamic trajectories of the system characterized by the chromatid A position x_A and its active regulator level R_A* (the arrows represent the directions of the system evolution). (B) The phase diagram of chromosome congression characterized by the uncertainty level of velocity ∣ξ̄∣/V₀ and the AP force gradient ∣α∣. 1, No congression; 2, congression but no sustained oscillation; 3, congression and sustained oscillation but no reliable pinpointing to the cell equator; 4, reliable congression, oscillation, and robust pinpointing to the cell equator after S drops. (C) The phase diagram of pinpointing chromosome at the equator characterized by S turnover rate k₅ and the feedback strength K_C.

Fig. 3B shows the dependence of chromosomal congression on two critical ingredients in the model: the AP force gradient ∣α∣ and the degree of intrinsic fluctuation in chromosome velocity ∣ξ∣. Congression is obtained for the vast region of the parameter's space at large force gradient and relatively small fluctuation. The results demonstrate that the proposed mechanism can drive the chromosome to the cell equator in a robust manner, failing only when the uncertainty level of velocity is much higher than the intrinsic velocity of the KMT plus-end V₀, which seems highly unlikely. Of course, the chromosome congression also depends on the AP force gradients α_i, because ultimately it is the spatial profile of the AP ejection forces that encodes the location of the cell equator within the model. Although necessary, the spatial force gradient alone is never sufficient to guide chromosomes to the cell equator. We will return to discuss this point further below.

We next investigated the dependence of chromosome congression on the proposed feedback mechanism. Fig. 3C shows a phase diagram of chromosome motility characterized by the sensor turnover rate (k₅) and the sensor strength that prevents the regulator from degradation (K_C). Because the mechanical state of the chromosome modulates the local sensor level (Eq. 4), and the sensor further propagates such signal along the feedback loop by protecting the regulator degradation via the factor K_C (Eqs. 2–3 and Fig. 1), K_C reflects the mechanobiochemical feedback strength. As Fig. 3C shows, there is a threshold value of K_C, only above which the proposed feedback can guarantee chromosome congression; otherwise, the chromosome would not congress to the equator reliably from an arbitrary initial condition and could settle far away from the equator (exemplified by Fig. S2). Taking these results together, a fast mechanobiochemical feedback is pivotal in ensuring robust chromosome congression.

Bioriented Chromosome Oscillation After Congression.

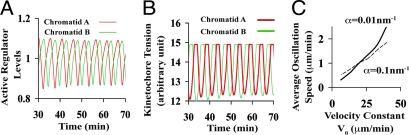
After congression, our model further predicted that the bioriented chromosome would subsequently oscillate around the cell equator with the amplitude ≈2 μm and the period ≈4 min (Fig. 2A for t < t₁), akin to those observed in in vivo experiments (3, 4). Because the chromosome movement is governed by mechanobiochemical feedback, the similar oscillations will reflect on both the chemical and mechanical states of sister chromatids.

Fig. 4A shows that the active regulator levels R* at the sister chromatids oscillate around the threshold level R₀ = 1 with the same periodicity as the chromosome oscillation. It is interesting to note that the active regulator levels R_A* and R_B* are largely anticorrelated; that is, R_A* is always above the threshold level R₀ (R_A* > R₀) when R_B* is below it (R_B* < R₀), and vice versa. According to our model (see Eq. 1 and Fig. 1), when R_A* > R₀, it will drive the chromatid A toward the cell equator; otherwise, chromatid A will tend to move toward its associated pole. Because of their opposite polarity, the anticorrelation of R_A* and R_B* around the threshold level R₀ simply reflects the tendency for the sister chromatids to move in the same direction synchronously; they seldom oppose each other's motion. Such synchronization also reflects on the mechanical states. Fig. 4B shows the kinetochore resistances for sister chromatids oscillating in a similar anticorrelated manner. It is because low R* implies a low S level that fails to protect R* from degradation (Eqs. 2 and 3), which is itself a reflection of a decrease in the kinetochore resistance (Eq. 4) and, hence, an increase in kinetochore tension by definition, resulting in a more stretched chromatid. Conversely, a high R* level reflects a less stretched chromatid. Therefore, the anticorrelation dictates that when one chromatid undergoes P movement (“leading”), the kinetochore tension at this chromatid is much enhanced, whereas the one at the other (“trailing”) chromatid is reduced, effectively following the leading chromatid movement without much effort, and vice versa (schematics in Fig. 2B). This synchronization effect in oscillation also leads to a smaller interkinetochore distance than that of the fully stretched case for dampened oscillation (Fig. 2C, and see below). These predicted features are consistent with the experimental observations (3, 4).

Fig. 4.

Characteristics of bioriented chromosome oscillation. (A and B) The chemical and mechanical states of the sister chromatids during chromosome oscillation. (C) The dependence of the average oscillation velocity of bioriented chromosome on the AP force gradient α and the velocity constant V₀.

Fig. 4C shows that the average velocity of the bioriented chromosome oscillation increases with the velocity constant V₀. (See Fig. S3 for the dependences of oscillation amplitude and period on the spatial gradient α and velocity constant V₀.) Fig. 4C further predicts that at a large velocity constant V₀, the average oscillation velocity is actually larger for a smaller spatial gradient (α = 0.01 nm⁻¹) than that for a larger one (α = 0.1 nm⁻¹). As the velocity constant V₀ drops off, the trend reverses. If the chromosome were purely driven by the mechanical force/gradient, one would expect a higher velocity for higher gradient, because it provides a steeper slope for the chromosome movement. We provide a detailed interpretation of this finding in Fig. S4. This result stems from the nature of mechanobiochemical feedback and distinguishes our model from pure mechanical models on the basis of a spatial force gradient. This prediction could also reconcile the controversy over chromosome oscillation changes in a Kif18 mutant (38, 39).

Dampening Bioriented Chromosome Oscillation Pinpoints the Chromosome at Cell Equator.

So far, we have shown that our proposed feedback mechanism can faithfully congress and oscillate the chromosome around the cell equator; and the predicted features of these sequential events are consistent with observations. However, some key questions have yet to be addressed: What is the advantage of such a complicated feedback mechanism if it does indeed control the chromosome motility in mitosis? And, how do we distinguish our model from the simple mechanical model from a functional standpoint? These questions are addressed in this section.

Once congressed around the cell equator, bioriented chromosomes form a tight metaphase plate, which may be crucial for avoiding chromosome entanglement during subsequent segregation (40). Surveillance by mitotic checkpoint proteins prevents chromosome segregation until all of the chromosomes in the mitotic cell are aligned at the metaphase plate (13). Therefore, simply bringing the chromosomes near the cell equator may not be enough for mitosis to progress; instead, they need to additionally form a tight metaphase plate by pinpointing at the equator.

As shown in Fig. 2A, the chromosome oscillation gets rapidly dampened if the sensor turnover rate (k₅ in Eq. 4) is enhanced (at t = t₁). Within minutes, the chromosome has exactly pinpointed the cell equator, across which the sister chromatids reside symmetrically. This predicted dampening oscillation is consistent with the observed transition in chromosome motility right before the metaphase/anaphase transition (3, 4). Moreover, we showed that pinpointing the chromosome to the cell equator can be realized over a wide range of parameter space from our model (Fig. 3C) and is largely insensitive to the initial conditions and stochastic fluctuation in chromosome velocity (Fig. 3B). Furthermore, as the sensor level S and, hence, the active regulator level R* drop at the cell equator, the tendency of poleward movement for individual chromatids can be balanced only at a position further away from the cell equator, where a larger AP force can be incurred by the spatial gradient ∣α∣ and R* can be maintained at ≈R₀. This leads to an enlarged interkinetochore distance and fully stretched configurations of both sister chromatids (Fig. 2B and C), consistent with the characteristics of metaphase/anaphase transition (41). In contrast, a simple mechanical force gradient obviously cannot provide the fidelity of pinpointing chromosome at the cell equator in a timely and robust manner in vivo because of the presence of the noisy cellular environment. Also, a mechanical force gradient on its own cannot account for the dampening in bioriented chromosome oscillation. Thus, the proposed feedback mechanism is capable of robustly pinpointing the chromosomes at the cell equator.

To trigger the transition from oscillation to pinpointing the chromosome to the cell equator within our model, it is necessary to partially disassemble the local chemical reactions, for example by increasing k₅ (Fig. 3C). What could modulate these local chemical reactions in vivo? We note that mitotic checkpoint proteins inhibit Cdk/cyclin B degradation (33–35), which is one of the major driving factors for mitosis progression. Degradation of Cdk/cyclin B and, hence, the decline in the activity of mitotic spindle checkpoints at the kinetochore strongly dictate anaphase onset (13, 37). It is intriguing that some of the checkpoint proteins are modulated by the mechanical state of the chromosome (14–20), although exactly how the modulation works has remained unclear. A possible pathway is that, once the chromosome is properly aligned at the cell equator, dynein/dynactin complex moves mitotic checkpoint proteins away from the kinetochore region and, thus, down-regulates checkpoint activity (42–44). These mitotic checkpoint proteins coincide with the notion of the sensor proteins in the model, and the regulator that controls the chromosome motility in our model is akin to one of the functions of Cdk/cyclin B. Naturally, according to our proposal, the sequential changes in the chromosome motility patterns reflect the evolving local chemical reactions that encode the different stages of mitosis progression.

Chromosome Segregation at the Metaphase/Anaphase Transition.

After the chromosomes are properly aligned at the cell equator, a mitotic cell will progress to chromosome segregation: the cohesion between sister chromatids is broken and the separated chromatids are pulled apart toward their respective poles (3, 4, 29). One might naively think that segregation would follow simply from the disassembly of the mechanical linkage between the sister chromatids (i.e., setting K̄ = 0 in Eq. 4). However, this action alone may not be sufficient for chromosome segregation according to our model. The segregated chromatid can move poleward persistently only if its local mechanobiochemical feedback is completely removed [e.g., with K_C = 0 and increased k₅ (at t = t₂ in Fig. 2A)]. Otherwise, as the separated chromatid moves poleward, it will encounter more and more AP force resistance, which would increase the active regulator level R* via the sensors in the feedback loop, thereby countering the P movement tendency. With partially impaired feedback (e.g., increased k₅, but intact K_C = 0.2 nM⁻¹), the separated chromatids will undergo damped oscillation at a distance away from the equator (Fig. S6). Fig. S7A shows that the final extent of such poleward movement depends on the impairment of the feedback: the more it is destroyed (e.g., the larger k₅), the farther can the chromatid move poleward. Fig. S7B shows that with the feedback intact, the segregated chromatid can even undergo sustained oscillation just like monooriented chromosome oscillations (9). The findings in Fig. S7 might explain the observed pseudoanaphase chromosome motility in nondegradable cyclin B mutant (45), where the segregated chromosome can stand still or oscillate depending on the dose of nondegradable cyclin B. Together, our results suggest that complete disassembly of the feedback is necessary for sustained chromosome segregation.

Discussion

Mitosis ensures that sister chromatids are precisely partitioned into daughter cells, which is critical for the fidelity of genetic inheritance (1, 13). To transport chromosomes with precision in a coordinated manner, both mechanical and chemical controls are used. From the mechanical perspective, spindle microtubules that emanate from the spindle pole provide the centrally important driving force for chromosome movement in mitosis (1). After their end-on attachments via kinetochores, the growth and the shrinkage of the KMT plus ends essentially regulate the chromosome P and AP movement (8, 10, 11). From the chemical standpoint, it is the local kinase–phosphatase reactions at the attached kinetochore that control the dynamics of the KMT plus ends (21–25) and, hence, control chromosome movement (28). Furthermore, the chromosome itself is highly stretched during its movement (3, 4, 46). This stretching is because the chromosome arms would encounter more and more resistance to move poleward because of the spare spindle microtubules that reach out in the astral form from the spindle pole and their associated chromokinesins (4, 36). Such resistance would highly stretch the chromosome (3, 4, 36, 46). In other words, there is a spatial gradient in the mechanical force impinging on the chromosome (4, 36). It is striking that the elastic force stored in the chromosome deformation modulates the level of the tension-sensitive protein at the attached kinetochores (14–20) as an intrinsic part of the local chemical reactions that regulate the chromosome movement (9). Therefore, a mechanobiochemical feedback mechanism regulates chromosome movement in mitosis.

In this article we have investigated theoretically this feedback mechanism on bioriented chromosome motility in mitosis. Our model captures all of the distinct and sequential changes in chromosome motility throughout mitosis in a coherent and timely manner. By sequentially varying several key kinetic parameters with molecularly justifiable mechanisms, the model can reproduce the chromosome congression to the cell equator, the ensuing chromosome oscillation, dampening oscillation that pinpoints the chromosome to the cell equator, and subsequent chromosome segregation (Fig. 2). Moreover, many features of sister-chromatid motility predicted by our model are consistent with experimental observations (3, 4) (Figs. 2 and 4).

From the functional viewpoint, our proposed mechanobiochemical feedback mechanism provides a robust means of congressing and tightly packing the bioriented chromosome at the cell equator. Also, it is largely insensitive to the stochastic fluctuations in the chromosome velocity and the initial chromosome state after biorientation, including the initial position of sister chromatids and the initial relative kinetochore protein distributions between sister chromatids (Fig. 3). Partially impairing the full feedback mechanism at improper timing would jeopardize pinpointing the chromosome to the cell equator (Fig. S2). Such precise location of the chromosome at the cell equator cannot be readily achieved from a simple model of pure mechanical force balance, because a pure mechanical “tug-of-war”-like mechanism is independent of the chromosome position and, hence, cannot possibly place it at the cell equator without fluctuation. Following this line of argument, we suggest that although the vigorous bioriented chromosome oscillation around the cell equator might not carry out any significant function, it could be reminiscent of the full feedback loop, which is the “price” that the cell needs to pay and which has to be disassembled later in mitosis. Alternatively, the sustained bioriented chromosome oscillation could be a checking process to even out the asymmetry between sister chromatids in terms of mechanical and chemical states, which could further check out if the chromosome is properly attached while waiting for the “proceeding signals” (13, 37). To that end, sustained oscillation requires the level of the active regulator R* at each sister chromatid to be ≈R₀ (Fig. 4). It necessitates the full strength of the feedback loop via the mechanical-sensitive proteins (Fig. 3), which coincides with the function of mitotic checkpoint proteins (13, 37). Consequently, the chromosome oscillation is a manifestation of the underlying mitotic surveillance mechanisms that ensure fidelity of segregation. In either case, the chromosome motility provides a diagnostic guidance to understand the governing mitotic signal-transduction pathways.

In our model, we have not addressed the issues of what dictates the timing of the disassembly of local chemical reaction pathways. Here, the suggested regulator and sensor resonate quite well with our proposed mechanism: right before the metaphase/anaphase transition, mitotic checkpoint proteins (the putative sensor in our model) are depleted from the kinetochores (42–44), leading to degradation of the local Cdk kinases (the active regulator) by APC/Cdc20 (37), which increases the P movement tendency for the sister chromatids, resulting in an enlarged interkinetochore distance (41). It would be interesting to find what coordinates the mitotic checkpoint inactivation in a timely manner for different pairs of sister chromatids to allow anaphase to proceed.