Flow induces loop-to-β-hairpin transition on the β-switch of platelet glycoprotein Ibα

Abstract

Interaction of glycoprotein Ibα (GPIbα) with von Willebrand factor (VWF) initiates platelet adhesion to injured vascular wall to stop bleeding. A major contact between GPIbα and VWF involves the β-switch region, which is a loop in the unliganded GPIbα but switches to a β-hairpin in the complex structure. Paradoxically, flow enhances rather than impedes GPIbα-VWF binding. Gain-of-function mutations (e.g., M239V) in the β-switch reduce the flow requirement for VWF binding, whereas loss-of-function mutations (e.g., A238V) increase the flow requirement. These phenomena cannot be explained by crystal structures or energy calculations. Herein we demonstrate that the β-hairpin is unstable without contacting VWF, in that it switches to a loop in free molecular dynamics simulations. Simulations with a novel flow molecular dynamics algorithm show that the loop conformation is unstable in the presence of flow, as it switches to β-hairpin even without contacting VWF. Compared with the wild-type, it is easier for the M239V mutant but harder for the A238V mutant to switch to β-hairpin in the presence of flow. These results elucidate the structural basis for the two mutants and suggest a regulatory mechanism by which flow activates GPIbα via inducing a loop-to-β-hairpin conformational transition on the β-switch, thereby promoting VWF binding.

Binding of glycoprotein Ibα (GPIbα) to von Willebrand factor (VWF) initiates a multistep platelet adhesion and signaling cascade of the hemostatic process (1, 2). Dysfunction of GPIbα-VWF interaction may cause bleeding disorders such as von Willebrand diseases (VWD) (3). A rapid kinetic on-rate of GPIbα-VWF binding is required for flowing platelets to tether to injured vessel wall. Counterintuitively, however, GPIbα-VWF binding is enhanced by blood flow, despite the fact that increasing flow shortens contact time for molecular interaction (4). A minimum flow is required for platelets to tether to VWF (4, 5). The kinetic rates of GPIbα-VWF binding and their mechanical regulation by flow can be altered by structural variations. Mutations may require higher or lower flows for platelet to tether to VWF compared with the wild-type (WT) GPIbα (6). The former is referred to as a gain-of-function (GOF) mutant, whereas the latter is a loss-of-function (LOF) mutant. GOF mutations G233V and M239V naturally occur in some patients with platelet-type (PT) VWD (5, 7, 8).

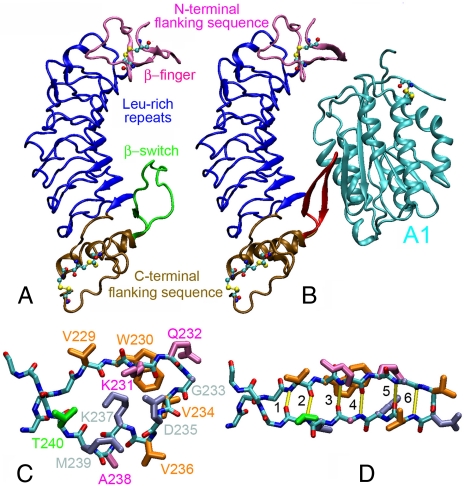
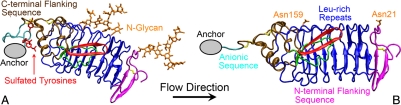
GPIbα consists of a glycosylated N-terminal domain (GPIbαN), a long mucin stalk, a transmembrane domain, and a cytoplasmic tail (9, 10). The binding site for VWF resides on GPIbαN, which contains eight tandem leucine-rich repeats (Fig. 1 A) (11). The monomeric subunit of VWF consists of multiple copies of A, B, C, and D type domains (12). The binding site for GPIbα resides on the A1 domain (Fig. 1 B, cyan) (13). Regions of GPIbαN at each end of the leucine-rich repeats bind, respectively, to the top and bottom of the A1 domain (Fig. 1 B) (14, 15).

Fig. 1.

Structures of GPIbα. Structures of unliganded GPIbαN (A) (PDB code 1QYY) (23) and GPIbαN in complex with VWF-A1 (cyan) (B) (PDB code 1SQ0) (15). The N-terminal flanking sequence (mauve), leucine-rich repeats (blue), C-terminal flanking sequence (ochre), and cysteine residues (balls and sticks) of the GPIbαN are shown. The loop conformation of the β-switch (residues 227–243) in A is shown in green, and its β-hairpin conformation in B is shown in red. The loop (C) and the β-hairpin (D) conformations are respectively zoomed in to show the side chains of residues 229–240 with colors according to their phenotypes when mutated to valine (pink for LOF, gray for GOF, and orange for residues that are already valine in the WT sequence or residues whose phenotypes are unknown when mutated to valine). The side-chains of residue Thr-240 are shown in green because different experimental assays showed different phenotypes. The β-hairpin conformation is stabilized by six H-bonds (marked yellow in D) numbering 1–6 from the near end of the β-hairpin outward (D).

Comparison of the unliganded (Fig. 1 A) and liganded (Fig. 1 B) GPIbαN structures (14, 15) reveals that the largest conformational change occurs in a region of the C-terminal flanking sequence (residues 229–240), which switches from a structureless loop (Fig. 1 C; green in Fig. 1 A) to a β-hairpin (Fig. 1 D; red in Fig. 1 B), hence the name β-switch. The β-hairpin aligns with the central β-sheet of the A1 to form a major interface of the complex (Fig. 1 B). Nearly every nonvaline residue in β-switch has been substituted by valine in mutagenesis studies (16). In addition to the naturally occurring PT-VWD mutations G233V and M239V, D235V and K237V also exhibit GOF phenotype (light blue in Fig. 1 C and D). By contrast, K231V, Q232V, and A238V (purple in Fig. 1 C and D) display LOF phenotype.

Comparison between the M239V (14) and WT (15) GPIbαN:A1 complexes did not reveal immediate insights for the GOF phenotype of M239V. Nor did energy calculations for the modeled mutants based on equilibrium structures. Because flow-enhanced GPIbα-VWF interaction is a nonequilibrium process, we hypothesized that flow induces a dynamic conformational change in β-switch that promotes GPIbα-VWF binding. We developed a novel all-atom flow molecular dynamics (FMD) algorithm to simulate how flow affects the WT and mutant structures. In contrast to the pressure-driven (17) or SLLOD (18) algorithm, our FMD algorithm generates flow by applying forces directly to the water molecules, which is easier to control. We examined how stable the loop and the β-hairpin conformations were, how readily they transitioned from one to another, whether flow could induce conformational transitions, and whether and how the GOF and LOF mutations might alter the flow regulation of conformational changes. The results support our hypothesis and provide insights for flow regulation of GPIbα-VWF binding. This work demonstrates computationally that fluid flow can induce transition from an unstructured to a structured conformation in a protein.

Results

The importance of the β-switch to VWF binding is supported by the observations that it forms a major contact surface with A1 and mutations in this region alter binding to VWF. To elucidate the structural bases of the phenotypes of these mutants, we compared the structures of GPIbαN:A1 complexes with the WT, M239V, and A238V β-switch [supporting information (SI) Fig. S1 A–C]. The respective structures of the GOF and LOF mutants were similarly modeled from the WT structure. The mutations do not alter the β-sheet interactions with A1, which are independent of the side chains (Fig. S1 A–C). We used free MD simulations to examine the stability and calculate the interaction energies of these structures. No conformational changes were observed. Surprisingly, regardless of their phenotype, the two mutants show similar interaction energies between A1 and the whole GPIbαN (Fig. S1 D) or the β-switch alone (Fig. S1 E), which are slightly lower than that of the WT. Thus, structural analyses and energy calculations did not offer immediate insights for the different phenotypes of these GOF and LOF mutants.

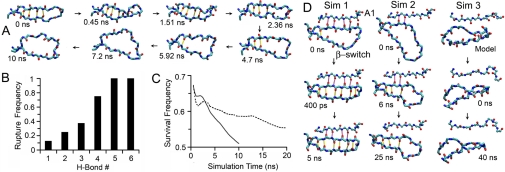
The crystallographic observation of the β-switch in two different conformations (Fig. 1 A and B) suggests that this region is structurally bistable. When GPIbαN was bound to A1, the β-hairpin conformation was stable during 20-ns free dynamics simulations. When the β-hairpin was isolated, however, it melted to a loop or showed a melting tendency in all 8 simulations of 10 ns (three runs) or 20 ns (five runs) (Fig. S2). This is illustrated in Fig. 2 A, which shows snapshots of the structure at indicated times in a representative simulation (see also Movie S1). Conformational transition from the β-hairpin to the loop is signified by progressive disruption of six hydrogen (H) bonds that connect the two legs of the β-hairpin (see Fig. 1 D for their numbering convention). To quantify this process, we plotted the distance between each of the six H-bond donor-acceptor pairs vs. time in Fig. S2 for each of the eight simulations and define a 3.5-Å cutoff beyond which the H-bond is considered disrupted. Despite variations in the trajectories from different simulations as a result of thermal fluctuations, a general trend is evident. Disruption of H-bonds began at the far end of the β-hairpin (i.e., H-bond no. 6), which was broken during equilibration in all simulations before free MD simulation was started (Fig. S2). Melting propagated inward toward the near end of the β-hairpin (i.e., H-bond no. 1), which was broken in 1 of 8 runs only. This decreased frequency of H-bond rupture with increasing distance from the far end of the β-hairpin is clearly shown in Fig. 2 B. It can also be seen by using an alternative metric—the survival frequency—that declines over time as shown in Fig. 2 C for the average curve of all six H-bonds over all simulations (solid) or over the five 20-ns runs (dashed). These results demonstrate that, without binding to A1, the β-hairpin is unstable and will spontaneously transition to a structureless loop.

Fig. 2.

β-Hairpin-to-loop transition of β-switch in the absence of force. (A) Snapshots of simulated isolated β-switch structures in a representative free MD simulation taken at consecutive times (indicated) when the next pre-existing H-bond was disrupted. The simulation started from the β-hairpin conformation (1SQ0) and ended 10 ns after all H-bonds (marked yellow) were disrupted and the β-hairpin became a loop. (B) Rupture frequency (number of simulations during which rupture was observed divided by eight, the total number of simulations) for each H-bond. (C) Survival frequency (sum of running fractions of time during which distances between all H-bond donor-acceptor pairs were below the 3.5-Å cutoff divided by the original number of six) averaged over all eight runs (solid curve) or only five 20-ns runs (dashed curve) as a function of time. (D) Test of the binding-induced fit model. Snapshots of three free MD simulations of the GPIbαN:A1 complex (only the β-switch and the A1 β-strand that it contacts are shown) after the β-hairpin was disrupted by force, whereas keeping its interaction with A1 completely (left column) or partially (center column) intact, or replacing the β-strands by the loop (taken from PDB code 1QYY) (right column).

Because the loop conformation seems unfavorable for docking with A1, we asked the question of whether the β-hairpin formation results from binding to A1 or the β-hairpin is preformed before A1 binding. The former possibility represents a “binding-induced fit” hypothesis, which we tested by using three simulations (SI Methods). In the first simulation, the two legs of the β-hairpin in the GPIbαN:A1 cocrystal structure was first separated by a force while keeping its interaction with the A1 central β-sheet intact; the system was then subjected to free dynamics to see whether the β-hairpin would reform. This was indeed observed in only 0.4 ns of simulation (Fig. 2 D, right column and Movie S2). The result suggests that binding of one leg of the loop to A1 would induce loop-hairpin transition of the β-switch. This also provides further support to our hypothesis that β-hairpin is a stable conformation when it is bound to A1. The second simulation is similar to the first except that two of the four H-bonds connecting the β-switch to the A1 were also disrupted. Three H-bonds between the two legs of the β-switch reformed in 3 ns, but no more H-bond formation was observed in the remaining of this 25-ns free dynamics simulation (Fig. 2 D, middle column and Movie S3). Interestingly, the two disrupted H-bonds between β-switch and A1 did not reform stably, and the two remaining H-bonds became weaker, as the distances between their donors and acceptors fluctuated above and below the cutoff line that defines the H-bond more than those did in the first simulation (Fig. S3 D and E). These results indicate an energy barrier hindering the binding of a disordered β-switch to A1 and suggest that, when β-switch is only partially bound to A1, the driving force that induced the β-hairpin reformation in the first simulation is greatly weakened. In the third simulation, the β-hairpin structure in the GPIbαN:A1 cocrystal was replaced by the loop structure of the isolated GPIbαN crystal, which was not bound to A1 at all. Note that GPIbαN remained bound to A1 via other contacts (e.g., through the β-finger region). No backbone interaction was observed between β-switch and A1, and no H-bond formation was observed between the two legs in the β-hairpin in 10-ns equilibration and in another 40-ns free dynamics (Fig. 2 D, right column and Movie S4). This indicates that, although we cannot exclude the existence of an “induced fit” pathway, its driving force is not detectable during the time in which our simulation was run. Fig. S3 plots the time courses of distances of H-bond donor-acceptor pairs between two legs of the β-switch (rows A-C) and between β-switch and A1 (rows D through F) for the three simulations. These results do not support the binding-induced fit hypothesis.

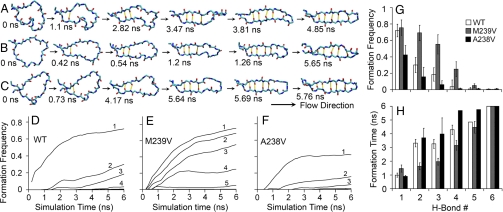
How could the β-hairpin be preformed before A1 binding? The observation that a minimum flow is required for platelet to tether to VWF prompted us to hypothesize that flow induces a loop-to-β-hairpin transition, which promotes VWF binding. To test this hypothesis, we developed a novel FMD algorithm and used it to examine the stability of the loop conformation in the presence of flow. The FMD algorithm is briefly described in Materials and Methods, and the rigorous tests of its validity are presented elsewhere (19). Remarkably, with flow, the isolated loop quickly transitioned toward the conformation of a β-hairpin in all six 6-ns independent simulations for WT (Fig. S4 A–F). Fig. 3A shows snapshots of the WT structure at indicated times in a representative simulation (see also Movie S5). Interestingly, conformational transition from the loop to the β-hairpin was characterized by the same events but followed a reversed time course to the transition from the β-hairpin to the loop. It is signified by progressive formation of the six H-bonds, thereby holding the two legs closer and closer. Similar to the previous analysis of the β-hairpin-to-loop transition, we plot the distance between each of the six H-bond donor-acceptor pairs vs. time and use the same 3.5-Å cutoff to define the H-bond (Fig. S4). Formation of H-bonds began at the near end of the β-hairpin (i.e., H-bond no. 1), which was formed in all simulations (Fig. S4). The process propagated outward toward the far end of the β-hairpin (i.e., H-bond no. 6), which had not formed at the end of any 6-ns runs but had clearly shown a tendency to form. This can be seen in Fig. 3 D, where the increasing frequency of H-bond formation with time is plotted for each of the six H-bonds (averaged over six runs). At a given time (e.g., 6 ns), the H-bond formation frequency decreased with increasing distance from the near end of the β-hairpin (Fig. 3 G). This can also be shown by using an alternative metric—the time required for H-bond formation—that increases with increasing distance from the near end of the β-hairpin (Fig. 3 H). These results support our hypothesis and demonstrate that flow can induce loop-to-β-hairpin conformational transition on the β-switch even without its binding to A1.

Fig. 3.

Flow-induced loop-to-β-hairpin transition of isolated β-switch. Snapshots of simulated structures of WT (A), M239V (B), and A238V (C) β-switches in representative FMD simulations taken at consecutive times (indicated) when the next new H-bond was formed. The simulations started from the loop conformations (1QYY or modeled after 1QYY by mutating residue 239 or 238 to a valine) and ended 6 ns after the first five H-bonds were formed and the loop almost became a complete β-hairpin. Formation frequencies (running fraction of time during which distance between each H-bond donor/acceptor pair was below the 3.5-Å cutoff) for the indicated H-bonds are averaged over six simulations and plotted vs. time for WT (D), M239V (E), and A238V (F). Some of the curves are obscure because they are too close to the x-axis. The end results at 6 ns are shown in G as a bar graph (mean ± SEM of six simulations) for WT (open bars), M239V (hatched bars), and A238V (solid bars). (H) Time required for each H-bond to form and survive for >50 ps the first time (mean ± SEM of six simulations) for WT (open bars), M239V (hatched bars), and A238V (solid bars).

Our simulations suggest that, for the isolated β-switch, the loop is stable but the β-hairpin is unstable in the absence of flow, whereas the loop is unstable but the β-hairpin is stable in the presence of flow. Thus, flow acts as a mechanical regulator that switches the GPIbα structure between two conformations, and the β-switch serves as a mechanical sensor. This is consistent with the experimentally observed flow enhancement of GPIbα-VWF binding, because a preformed β-hairpin should be more favorable for docking with VWF-A1. Because GOF/LOF mutants in the β-switch region lower/raise the flow requirement for GPIbα-VWF binding, they are predicted to require less/more time than WT to induce the loop-to-β-hairpin switch under identical flow conditions. We tested this prediction by FMD simulations with the GOF mutant M239V and the LOF mutant A238V. M239V was chosen because this naturally occurring PT-VWD mutant is located in the middle of the stands in the β-hairpin conformation (Fig. 1 C). A238V was chosen because it is adjacent to M239V, which makes comparison easier. Fig. 3 B and C show, respectively, snapshots of the M239V and A238V structures at indicated times in representative simulations (see also Movie S6 and Movie S7). The six snapshots in each row of Fig. 3 A–C are chosen such that the first corresponds to the beginning of FMD simulation and the remaining two to six snapshots correspond, respectively, to the instants when the first to the fifth H-bonds were formed. From the times in each column of Fig. 3 A–C we can see that, compared with WT, M239V took less time, whereas A238V took more time to form the same H-bond in most of the cases. Again, we quantify the loop-to-β-hairpin transition by the distance between each of the six H-bond donor-acceptor pairs, which is plotted vs. time in rows A through F of Fig. S5 and Fig. S6 for each of the six simulations for M239V and A238V, respectively. The respective time courses of formation frequency for each H-bond (averaged over six simulations) for M239V and A238V are plotted in Fig. 3 E and F. It is evident that compared with the WT, the M239V curves are shifted upward and leftward toward higher frequency and shorter time, whereas the A238V curves are shifted downward and rightward toward lower frequency and longer time. We compare the respective formation frequencies for M239V and A238V at 6 ns to that of the WT for each H-bond (Fig. 3 G) and the respective times required for H-bond formation for M239V and A238V to that of the WT for each H-bond (Fig. 3 H). It is evident that the frequency of H-bond formation is higher for M239V but lower for A238V, whereas the time required for H-bond formation is shorter for M239V but longer for A238V. Fig. 3 and Figs. S4–S6 clearly show that, compared with WT, M239V has a decreased flow requirement for the loop-hairpin switching, whereas that of M239V is increased. These results support our hypothesis and further demonstrate that flow can induce loop-to-β-hairpin conformational transition on the β-switch even without binding to A1.

The proceeding FMD applied a flow of several tens of meters per second to greatly speed up loop-to-β-hairpin transition for it to be observed in several nanoseconds of simulation time (Fig. S7 C and D), which is 2 orders of magnitude larger than the velocities of arterial blood flows (20). Flow velocities relative to a platelet above its membrane (experienced by the β-switch) are even smaller. To examine how flow velocity affects the conformational transition, we reduced the drag forces by half (thus reducing flow velocity) in several simulations. H-bond formation was still observed, although it occurred in a slower rate (row G of Figs. S4–S6).

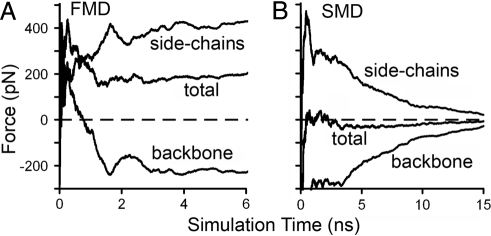
Can a concentrated force induce similar conformational changes in the β-switch? If so, which is more efficient, flow or concentrated force? To answer these questions, we used steered molecular dynamics (SMD) simulations to examine the effect of a 200 pN force pulling at the far end of the loop (C_α atoms of Val-234 and Asp-235). This pulling force was chosen for the SMD simulations to be comparable with the FMD simulations. In FMD, a 0.7-pN force was applied to each of the ∼300 atoms in a 2-Å think layer, which add up to ∼210 pN of total applied force. Results of these SMD simulations were shown in Figs. S4 H and I and S5H. Although H-bond formation was observed in these SMD simulations, they occurred in much lower frequency and lasted much shorter time compared with that observed in the FMD simulations. The different efficiencies for flow and concentrated force to induce the loop-to-β-hairpin transition are revealed by examining the interaction forces (running average over time) between water and the protein calculated from FMD (Fig. 4 A) and SMD (Fig. 4 B) simulations. The total interaction force is broken down into two parts: one acting on the side chains and the other acting on the protein backbone. In FMD, because the side chains extend into the flow field, these atoms are pushed by the water molecules with a stable positive force of ∼400 pN. The side chains pull the backbone forward, which drags the water molecules in the inner circle along, resulting in a stable negative force of approximately −200 pN. In SMD, because the force is directly applied to the far end of the loop, the water-protein interaction is caused by the motion of the protein atoms as a result of the elongation of the loop upon stretching, which has a net value of zero. The force is positive on the side chains and negative on the backbone: both decrease to nearly zero after 15-ns simulations when the protein atoms cease motion because the far end of the β-switch is stretched nearly as far right as possible. Thus, in SMD, the concentrated force applied to the two backbone atoms propagates mainly along the backbone. By contrast, in FMD, the drag forces applied through flowing water are dispersed over the side chains as well as the backbone. Because β-hairpin formation requires movement of side chains, flow is much more effective than concentrated force to induce the conformational transition.

Fig. 4.

Interaction forces between β-switch and surrounding water. Interaction forces between the side chains, backbone, or total β-switch (indicated) and surrounding water calculated from FMD (A) and SMD (B) simulations.

Discussion

A goal of this study was to elucidate the structural basis of the GOF and LOF mutations in the β-switch region of GPIbα. However, comparison of equilibrium structures and energetics of GPIbαN:A1 complexes with WT and mutant β-switches proved unrevealing. Although it may seem surprising at first glance, this result is consistent with experiment. Similar interaction energies predict similar affinities and stabilities of VWF-A1 bonds with WT and GOF/LOF mutant GPIbα. This prediction is supported by experimental observation that compared to the WT, M239V mutation increases the binding affinity for A1 by 6-fold, but the off-rate has little change (14). Thus, the phenotypical differences between the WT and GOF/LOF mutants lie in the on-rates. But what is the structural basis of the on-rate differences?

To answer this question, we considered the different β-switch conformations in the unliganded (Fig. 1 A) and liganded (Fig. 1B) GPIbα (15), the flow requirement for platelet to tether to VWF, and the changes of this requirement by the β-switch mutations (5). These considerations led us to the hypothesis that flow enhances the on-rate for GPIbα-VWF binding by inducing a loop-to-β-hairpin transition on the β-switch region. Significantly, this hypothesis implies a dynamic rather than static structural basis for the on-rate differences among the WT and GOF/LOF mutants. A dynamic structure can be stable but necessitates departure from equilibrium. Nonequilibrium processes can be produced by mechanical perturbations such as force and flow. Indeed, a recent study has demonstrated that force slows off-rate of GPIbα-VWF dissociation (an unusual characteristic called catch bonds), which underlies flow-enhanced platelet rolling on VWF and prevents platelet agglutination (21). GOF mutations in the A1 domain away from the binding site eliminate catch bonds, abolish the flow requirement for rolling, and cause platelet agglutination. SMD simulations suggest a structural basis for this such that force tilts the complex structure to allow sliding and rebinding on the binding interface, thereby slowing the off-rate for dissociation. By comparison, here we hypothesize that flow enhances on-rate for association by inducing a loop-hairpin transition on the β-switch region. These two mechanisms are complementary in that they regulate different aspects of the GPIbα-VWF binding kinetics that underlie different aspects of flow-enhanced platelet adhesion to VWF. We should note that although our simulations did not obtain support for the “binding-induced fit” mechanism, this mechanism cannot be excluded because of the limited time of the simulations.

To test our hypothesis, we developed a novel MD algorithm termed FMD to simulate the effects of fluid flow on protein conformation. Our hypothesis has been supported by FMD simulations of the loop-hairpin transition on the β-switch, which was observed in two flow velocities, suggesting that reduced velocity would prolong the time but still induce the transition. Comparing to WT, the GOF mutant M239V and LOF mutant A238V were observed to respectively decrease and increase the flow requirement for the loop-hairpin transition, in agreement with experiment. The fact that these expected differences were still observed imparts confidence to our results despite the fact that they were obtained by simulations with much higher velocities than reality to shorten the loop-hairpin transition time to the nanosecond range affordable by our computational resources.

How closely do our in silico simulations of an isolated β-switch mimic physiological conditions? To answer this question requires putting the β-switch in the context of the whole GPIbα and of the platelet. When plasma flows over a platelet, it applies a shear force to bend the long stalk of GPIbα toward the flow direction. The protein portion of the U-shaped GPIbαN is nearly symmetric about its long axis connecting the N and C termini, which is probably aligned with the flow direction (Fig. 5). In addition, flow exerts drags on two potential N-glycans on Asn-21 and Asn-159 (orange in Fig. 5A) located on the one side of this axis, which is likely to tilt this side slightly away from the flow direction to align the β-switch with the flow, making it an ideal flow sensor (Fig. 5A). Besides the anchoring residues 227–228 and 241–243, the β-switch sequence has little interaction with the rest of GPIbαN in both the loop and β-hairpin conformations. Therefore, it should be relatively flexible and its conformation may be easily influenced by the flow. These arguments are depicted in Fig. 5, where both the loop (green) and β-hairpin (red) conformations are shown. They extend our model by including flow alignment of GPIbαN as a prerequisite to the flow-induced loop-hairpin transition on the β-switch. The flow alignment of GPIbαN depends on how GPIbαN is anchored to the GPIbα stalk, which in turn depends on the conformation of the anionic sequence (residues 269–288). In the co-crystal structure, the anionic sequence was not solved, suggesting their lack of direct contact with A1 (14, 15). This sequence (cyan tube) was observed in another unliganded GPIbαN structure, where it interacted with the C-terminal flanking sequence (ochre) via three sulfated tyrosines (red sticks) and other negatively charged residues on the anionic sequence (Fig. 5) (11). It seems reasonable to assume that the interactions between the anionic sequence and GPIbαN regulate the flow alignment of GPIbαN (Fig. 5). This model can explain the experimental observation that replacing the three tyrosines with Phe (but not with Glu) reduces adhesion of cells expressing the mutant GPIbα to immobilized VWF under flow (22), which was previously unexplained because these residues are far away from the VWF-A1 binding site. Moreover, our model suggests that the two potential N-glycans on GPIbαN may affect flow alignment of GPIbαN such that deglycosylation of GPIbα may increase the flow requirement for VWF binding. Thus, the model of flow-induced loop-hairpin transition is supported by MD simulations and explains flow-enhanced platelet tethering and the phenotypes of the GOF and LOF mutants in the β-switch. The extended model with flow alignment further explains the phenotypes of the tyrosine mutants and provides a testable prediction regarding the effect of deglycosylation, which motivates future experiments.

Fig. 5.

Model for flow alignment of GPIbαN. Anchored to the end of a long stalk, the N-terminal domain of GPIbα extends ∼60 nm from the platelet membrane, making it an ideal flow sensor as the platelet circulates in the blood stream. Depending on the GPIbαN-stalk anchor, flow may exert different forces on the U-shaped protein (blue) and the presence/absence of two potential N-glycans (orange) at Asn-21 and Asn-259 to align GPIbαN with the flow direction (indicated) differently, as shown in A and B, respectively. The anchor is mediated by contacts of the anionic sequence (cyan) with other portion of the C-terminal flanking sequence (ochre) through three sulfated tyrosines (red sticks), which are likely to affect the alignment of GPIbαN and, in turn, the β-switch region in the flow field. Our model hypothesizes that the alignment in A exposes the β-switch [drawn in both loop (green) and β-hairpin (red) conformations] to the flow stream, which induces the loop-hairpin transition, thereby enhancing the on-rate for GPIbα-VWF binding. Mutations that replace the three sulfated tyrosines or remove the N-glycans may alter the GPIbαN alignment with flow as shown in B, which affects the exposure of the β-switch to the flow, thereby altering the flow enhancement of GPIbα-VWF binding.

Methods

Systems used in our simulations include GPIbαN in complex with A1 and isolated β-switch sequence. Four structures of β-switch (residues 227–243) were used: the WT sequence in the β-hairpin conformation [taken from Protein Data Base (PDB) code 1SQ0] (15), the WT sequence in the loop conformation (taken from PDB code 1QYY) (23), and the modeled M239V and A238V sequences in the loop conformation. The simulation methods for GPIbαN:A1 with these sequences are detailed in SI Methods. For simulations with an isolated β-switch, each sequence plus a Cl⁻ ion (to neutralize the system) was soaked into a 64 × 40 × 40-Å water box in such a way that the (to be formed) β-hairpin would align along the x-axis under flow (also along the x-direction) (Fig. S7 A and B). These structures served as the starting point for the MD simulations with NAMD (24) and the CHARMM22 force field (25). Structures and the Movies S1–S7 were generated by using VMD (26).

In all simulations, the N-terminal C_α atoms of residues 227 and 228 as well as the C-terminal C_α atoms of residues 242 and 243 were fixed to anchor the sequence. Periodic boundary conditions were used. A cutoff of 12 Å with a smooth switching from 10.5 Å was used for van der Waals interactions. The particle-mesh Ewald method was used for full electrostatic interactions. The system was first energy-minimized for 5000 steps with heavy atoms of the peptide fixed and then another 5000 steps with only the terminal C_α atoms fixed. After raising the temperature to 300 K in 50 ps, the systems were subjected to equilibration for 1.5 ns under NPT ensemble with the use of the Langevin piston method to control the pressure and Langevin dynamics to control the temperature. The Langevin coefficient was decreased every 0.5 ns from 5, 1, to 0.1 ps⁻¹. The equilibrated systems at 1.5 ns were taken for further simulations. The numbers of independent runs with different MD methods for different systems are summarized in Table S1. For each system, independent minimization, heat-up, and equilibration processes were used for different runs to ensure that the equilibrated structures are uncorrelated to provide meaningful statistics.

For FMD, a 0.7 or 0.35 pN force is applied along the x-direction to each of the ∼300 atoms within a 2-Å layer of the y-z plane (shown as larger spheres in Fig. S7A). This force accelerates the water molecules, which flow rightward and over the peptide in a later time (Fig. S7B). Because of the periodic boundary conditions, after exiting the water box at the right boundary, the water molecules reappear at the corresponding positions at the left boundary. When they re-enter the 2-Å layer, the force is applied to them again. Thus, a flow is generated with increasing velocity over time. The velocity depends on time and the distance from the x-axis, as shown in Fig. S7 C and D. The increase in flow velocity with increasing time limits the simulation time because the velocity becomes too large and the system temperature also increases to 350 K at 6 ns when 0.7 pN force is applied (as calculated from the kinetic energy), which causes the system to become unstable in long simulations. In a separate article (19), an improved FMD algorithm is described that allows simulations at constant mean flow and constant temperature for a much longer time, which confirmed the results of the present method. We observed no significant differences in the H-bonds' forming frequency or their durations between FMD and free MD simulations.