Abstract
Threatened species become increasingly difficult to detect as their populations decline. Managers of such cryptic threatened species face several dilemmas: if they are not sure the species is present, should they continue to manage for that species or invest the limited resources in surveying? We find optimal solutions to this problem using a Partially Observable Markov Decision Process and rules of thumb derived from an analytical approximation. We discover that managing a protected area for a cryptic threatened species can be optimal even if we are not sure the species is present. The more threatened and valuable the species is, relative to the costs of management, the more likely we are to manage this species without determining its continued persistence by using surveys. If a species remains unseen, our belief in the persistence of the species declines to a point where the optimal strategy is to shift resources from saving the species to surveying for it. Finally, when surveys lead to a sufficiently low belief that the species is extant, we surrender resources to other conservation actions. We illustrate our findings with a case study using parameters based on the critically endangered Sumatran tiger (Panthera tigris sumatrae), and we generate rules of thumb on how to allocate conservation effort for any cryptic species. Using Partially Observable Markov Decision Processes in conservation science, we determine the conditions under which it is better to abandon management for that species because our belief that it continues to exist is too low.
Keywords: conservation planning, decision theory, optimal monitoring, Sumatran tiger
Many of the most threatened species are cryptic, and their presence in an area can be uncertain because of the imperfect nature of most detection methods (1–3). Several enigmatic species have been assumed to be extinct for long periods before being rediscovered inadvertently (e.g., Jerdon's courser [Rhinoptilus bitorquatus] (4), the Mahogany glider [Petaurus gracilis] (5), the South Island Takahē [Porphyrio hochstetteri] (6), and the Madeiran land snail [Discus guerinianus], ref. 7). Even the persistence of large mammals, like the Sumatran rhinoceros, Dicerorhinus sumatrensis, can be uncertain in particular locations (8). Managers of cryptic threatened species are prone to 2 sorts of error. First, it is possible, if not likely, that some reserves are being managed to conserve a species that has already disappeared or become functionally extinct (e.g., the Ivory-billed woodpecker, Campephilus principalis) (9, 10). The second possible error is that managers could give up on a species too soon, failing to invest in sufficient surveying to be sufficiently sure further management is unwarranted. Managers of protected areas need to know how long they should continue investing in conservation management without strong evidence that the species is still present and when to shift their resources from saving a species to looking for that species, that is, surveying. Ultimately, if their belief in the persistence of the species continues to decline, when should managers surrender resources to another conservation problem?
The problem of how best to allocate conservation resources can be couched in terms of a trade-off between managing, surveying, or doing nothing (surrendering and redistributing resources to other problems). Whether to invest scarce management resources and time in surveying may be a difficult decision for managers to make, although some may argue that expenditure on determining the presence of a potentially viable population is a prerequisite to management. Just as difficult is the decision to give up on the species and stop management, especially if it is possible that the species may still be extant. These problems have not been addressed in a systematic manner within an optimization framework. The ecology and conservation literature present little guidance on how to approach such a problem, although some analogous problems in other fields have been tackled within a decision-theory framework (see refs. 11–13). Here, we build on lessons from these studies and theoretical frameworks for optimal conservation decision making proposed by other authors (14, 15) to develop and illustrate a coherent decision framework for allocating resources between 3 activities: managing, surveying, and doing nothing for, a cryptic threatened species.
The goal of efficient conservation planning and management is to find an optimal allocation of resources to actions that maximizes the net expected long-term benefit. In the problem presented here, the optimal strategy involves a trade-off between the value of a threatened species and the costs of managing and surveying. Without intervention the species is subject to a local probability of extinction. If the species remains extant, surveying enables detection with a particular probability. Thus, surveying provides information about the presence of the species but does not affect its probability of extinction. In contrast, managing decreases the probability of extinction without providing more information about the species' presence. We pose this problem as a Partially Observable Markov Decision Process (POMDP) (16, 17) and solve a multiple time-step version using the incremental pruning algorithm (18). The POMDP algorithm finds an optimal resource allocation each year given the current belief in the state of the species (i.e., extant or extinct) [see Methods and supporting information (SI) Appendix]. We also derive analytic approximations for the solution obtained from the POMDP algorithm. The analytic solutions approximate the critical probabilities of persistence at which we switch between managing, surveying, and doing nothing. We then determine the number of years of managing and surveying that are required for these critical probabilities to be achieved. The analytic approximations provide managers with direct insights into the form of the solutions without the need for specialist implementation of the POMDP algorithm. This article has 2 major aims: (i) to introduce POMDP as a coherent approach to optimal allocation of resources in a system with partially observable states (e.g., the current status of a cryptic species), and (ii) to use the POMDP as a comparative tool to generate consistent rules of thumb for optimal allocation of conservation effort that can be generalized for other cryptic species.
The Sumatran tiger, like all the tiger subspecies, has suffered dramatic population declines as a result of a reduction in prey abundance, habitat clearance, and illegal poaching (19). The 36,400 km2 Kerinci Seblat region of Sumatra has been designated an area of high priority for wild tiger conservation (20), and significant resources are spent annually to implement management strategies for this tiger population. Linkie, et al. (19) investigated how investment of resources in anti-poaching protection influenced the probability of losing Sumatran tigers from 4 core subpopulations in this region. The current conservation strategy for this species includes reducing the level of poaching by patrolling a subpopulation and assessing its status through surveying.
In this study, we focus on 1 of the 4 core areas in this region (i.e., core population 1, ref. 19). Implementing management at 50% intensity (or protection level) is assumed to secure this subpopulation of tigers (19). To ensure this level of protection, an estimated US$18,744 must be spent on management each year. The subpopulation core area is divided into grid cells that can be surveyed. We assume that 10% of these cells are surveyed annually at a cost of US$10,870. Thus, a total budget of approximately US$30,000 can be allocated between management and surveying in this study. We estimated the potential cost for failure to maintain viable subpopulations of tigers as US$175,134 a year based on the funding raised for tigers in the Kerinci Seblat region between 1998 and 2006 (Zoological Society of London 2007 IUCN cat projects database). We interpolated a yearly local extinction probability of 0.058 when the park is managed and 0.1 when it is not (18). Similarly, detectability of tigers living in the reserve was estimated at 0.78 per annum when surveyed and 0.01 when not surveyed (see Table S1).
We ask, what is the optimal management strategy for this highly valued species? When is it best to invest money managing the Sumatran tiger, when should we survey to assess the status of the population, and when, if ever, should we give up? We strive first to answer these questions for the Sumatran tiger and then to generalize the analysis to other threatened species. The response of the optimal strategy to changes in cost, values of extinction, and detection probabilities was assessed with an extensive sensitivity analysis.
Results
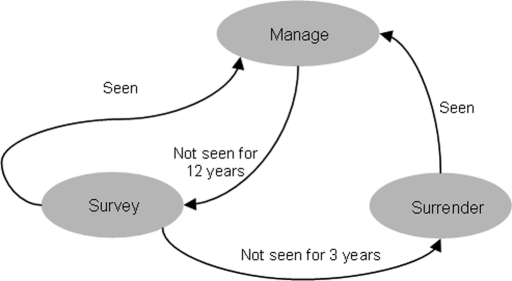
The optimal decision about whether to manage the species, survey, or surrender resources to other conservation actions depends on our belief that the species is persisting in the reserve (Figs. 1 and 2). If the Sumatran tiger is known to be present (i.e., it is detected in the reserve), the optimal strategy is to manage it for 12 years from this time. If the species is not observed during that 12-year period, it is optimal to switch all resources from managing to surveying. If the species remains unobserved for a further 3 years of dedicated surveying, the optimal strategy is to stop investing resources in conserving this species.
Fig. 1.
Decision graph representing the optimal strategy for Sumatran tigers. When the Sumatran tiger is observed, it is worthwhile to manage the species for 12 years, at which point surveying is recommended. If the tiger is not observed after a further 3 years of investment in surveying, the optimal strategy is then to surrender. These results are conditional on available estimates of detection and yearly local extinction probabilities.
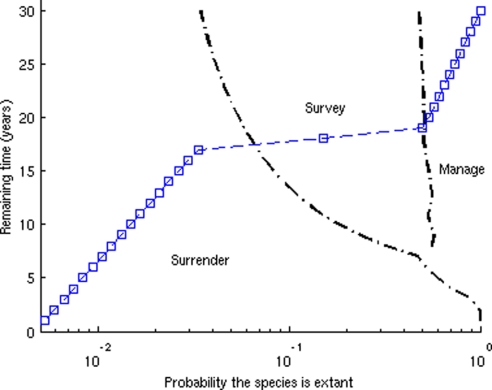
Fig. 2.
Optimal strategy versus belief over a 30-year time horizon. At each time step the optimal strategy maps an optimal action (manage, survey, or surrender) to each value of belief state. The plotted blue line illustrates an example of optimal management when the tiger is only seen at time horizon 30 and then remains unobserved. The belief that the species is extant varies proportionally over time.
Each year that tigers remain unobserved, our belief in their persistence declines (as represented by the line of blue squares in Fig. 2). The belief in persistence declines fastest when we survey but do not detect a tiger. If we observe a tiger at any time during this process, there no longer is uncertainty about its persistence (the probability of persistence increases to 1), and the optimal decision is to return to the start of the decision-making process and thus implement management.
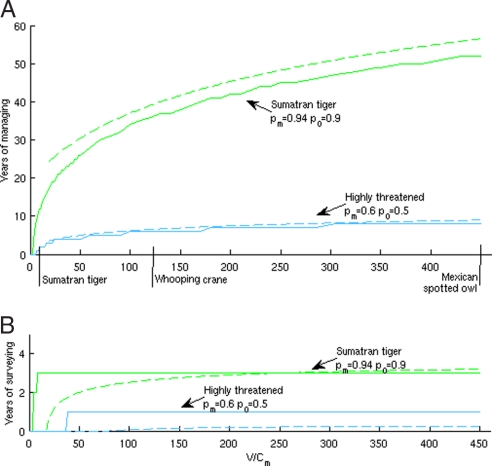
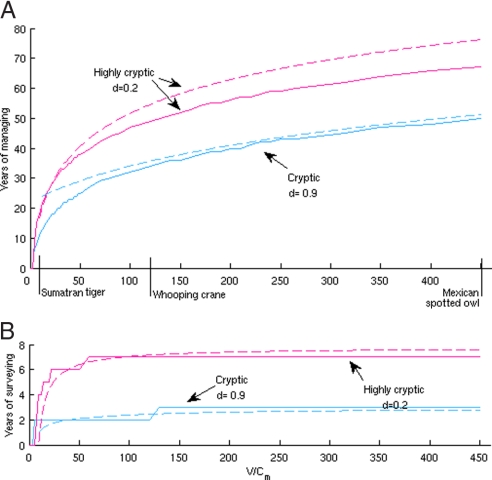
We generalize our findings to other species by investigating how key parameters affect the optimal management strategies. The same general pattern is observed. It always is optimal first to manage a species for Tm years before surveying it for Ts years. The value of the species (V) and the costs of managing (Cm) influence the optimal allocation of resources between management and monitoring. When the value of a species relative to the cost of its management (V/Cm) increases, the optimal time to spend on managing and surveying increases (Figs. 3 and 4). For small values of V/Cm, the investment priority is first managing and then surveying (Fig. 3). For high values of V/Cm, when the species is not highly threatened, the time spent managing, Tm, increases continuously (Fig. 3A). The time over which surveying is implemented, Ts, reaches an asymptote, suggesting that there is no benefit in surveying for more than Ts years, irrespective of this ratio (Fig. 3B). Similar results are observed when we consider difference in detection given surveying rather than persistence probabilities (Fig. 4). As value relative to cost increases, so too does, the time over which management should be implemented, a result consistent for varying detection probabilities (Fig. 4A). Further, as this ratio increases, the time over which surveying should be implemented remains relatively constant, irrespective of detection (Fig. 4B).
Fig. 3.
Comparison of optimal resource allocation for (A) managing and (B) surveying of approximate analytical solution (dashed lines) and exact solution (solid lines) for the Sumatran tiger and a hypothetical highly threatened species. po and pm represents the local probability of persistence if we do nothing and if we manage. The more threatened and valuable the species, the more we spend time managing for the species without surveying. The Whooping crane and the Mexican spotted owl are given as examples of V/Cm values using WTP (see SI Appendix and Table S2).
Fig. 4.
Comparison of optimal resource allocation for (A) managing and (B) surveying of an approximate analytical solution (dashed lines) and exact solution (solid lines) relative to cost of managing for different values of detectability (d). The more valuable and difficult to detect a species is, the longer is the time of management before surveying.
We investigated how the threat of extinction of a species affects the optimal management strategy for that species given its value (Fig. 3). Intuitively, if there is no benefit from implementing management (pm = po), then surrendering is optimal because doing so entails no monetary or conservation costs. When managing increases the local probability of persistence of the species (pm>po), our results again predict that we should manage a species even when it remains unobserved for some time (Fig. 3A). However, the more threatened a species is, the faster the belief in its persistence declines, and the less time should be spent managing and surveying. Indeed, when the species is severely threatened, it never is optimal to survey, regardless of the value of the species or cost of management (Fig. S1 and SI Appendix).
The optimal management strategy of a species also depends on the efficiency of surveying. When the probability of detection increases, and thus survey efficiency increases, we spend less time managing and surveying (1 year if surveying is perfect, Fig. S2 and SI Appendix). When the survey method is unreliable (e.g., probability of detection d = 0.2), however, the time spent managing and surveying increases regardless of the relative economic values (Fig. 4 A and B).
It is possible that the presence of surveyors in a population could deter poachers from acting in the area. Thus, surveying could improve the local probability of a species' persistence (pm>ps>po). Our study reveals that when effective surveying (high probability of detection) is cheaper and provides a relatively similar probability of extinction, ps, compared with management, pm, surveying is optimal. Conversely, the larger the difference in persistence between surveying and management (pm ≫ ps), the longer is the time that should be spent managing rather than surveying. Similar results are obtained if we assume that managing provides information about the presence of the species (d>dm>do). The analytical approximations of Tm and Ts provide guidance on how any set of parameters influences the optimal strategy (see Methods and SI Appendix).
Discussion
Our findings provide guidance for managers of cryptic threatened species in determining how long they should invest in managing and surveying before surrendering resources to other conservation decisions. We discovered that money should be invested first in management before engaging in any efforts to survey for the species. The best length of time to invest in management depends mainly on the current belief in a species' persistence, its value, its detectability, and its probability of extinction. When the risk of losing a species reaches a critical point, economic value has less affect on the optimal management time frame. Indeed, no matter the value of the species, the urgency of its status means we must invest time in increasing its chance of persistence or risk losing the species. Thus, the optimal strategy is to invest in active protection. It is comforting to think that continued investment in managing and surveying will increase a species' persistence, but for some highly threatened species there is a point at which the only optimal decision is to surrender resources to another conservation project. This result challenges the way resources currently are appropriated for endangered species, in which the more endangered the species is, the more money it tends to receive. A recent example of this phenomenon is the charismatic Ivory-billed woodpecker, which received more than US$20.2 million from donations and redirected U.S. Fish and Wildlife Service funds for conservation efforts in habitat protection and monitoring programs (9). In the case of wild tiger conservation, at least US$41 million was spent by nongovernmental organizations and international donors on wild tiger conservation projects between 1998 and 2005. Approximately 18% of the total (US$7.3 million) was spent on tiger monitoring (Zoological Society of London 2007 IUCN cat projects database).
Here, we provide a simple protocol for determining how cryptic threatened species should be managed to maximize the efficiency of any conservation strategy. Our protocol relies on the availability of data to estimate ecological parameters such as the probability of local extinction and the detectability of the species. Estimation of the probability of local extinction often is a key parameter required to inform conservation programs and can be derived through methods such as population viability analysis (see SI Appendix). The probability of detecting a cryptic species can be estimated by repeated sampling methods (21). In some circumstances, neither time nor money allows the use of such estimation methods, and parameter estimates are not be available. In these situations, deciding on the more profitable conservation decision remains a challenging process. The urgency of conservation problems worldwide means that managers are making decisions on the allocation of funds despite this lack of information. By providing a comprehensive and interpretable sensitivity analysis of our approach, we provide managers with a tool to evaluate current managerial decisions and enable them to elicit more appropriate management strategies, given their expertise and understanding of the species they manage.
Valuing species is a challenging and highly subjective endeavor. To illustrate our method, we used 2 types of values: 1 based on donations (the Sumatran tiger) and 1 based on willingness to pay (WTP) (22, 23). There are many other types of valuation that managers may access (e.g., ecotourism value) (22). We investigated the effect of these 2 valuation methods on the results for the Sumatran tiger. When the WTP values were used, the V/Cm ratio was estimated to be 265 (see SI Appendix), as opposed to a ratio of 9 when the donations value was used. This difference in ratios illustrates the enormous variability in valuation methods. An investigation of the interactions between different valuation methods and levels of rarity and protection is an important area of future research.
The approach used in this work raises many important questions about optimal conservation management when knowledge is uncertain. The influences of metapopulation structure and of uncertainty about the probabilities of persistence and detection on optimal management strategies are areas warranting further investigation. By formulating this problem of when to manage, survey, or surrender a threatened species in a transparent and rigorous manner, we provide a framework that allows conservation science to assess the role of these strategies for the protection of threatened species. Further, our framework provides a conceptual tool for investigating the effect of key ecological parameters on how management should proceed for individual threatened species. We have demonstrated that formal decision protocols provide a coherent approach to planning efficient conservation investments and dealing with uncertainty in complex resource allocation problems.
Materials and Methods
The first step in formulating the problem of allocating conservation resources is to define a quantifiable objective. Our objective is to find the optimal allocation of resources that maximizes the expected long-term benefits for the conservation of a cryptic threatened species. How long should we manage for a species? When should we survey for that species? When should we give up on that species?
POMDP is a convenient model for solving sequential decision-making optimization problems when there is uncertainty because the decision-maker does not have complete information about the current state of the system. Let S be the finite set of states representing the possible configuration of the system. S is defined by 2 states: S = {extinct, extant}. Let A be the finite set of actions controlling the state of the system: A = {survey, manage, do nothing}. The stochastic dynamic of the system is defined by a set of probability transition matrices denoted P, in which the function P : S × A → Pr(S) defines for each state-action pair a probability distribution over S. In our problem, we assume that when the species is extinct there is no recolonization process, and thus the population remains extinct indefinitely, P(Extinct|Extinct,·) = 1 (see Table S1). The reward/cost function R : A × S → ℜ defines for each pair action-state the cost of an action and the benefits of a state (see Table S1). To take into account the incomplete observability of the system, we also define the finite set of possible observations Z = {absent, present} and the corresponding observation function O that maps to each state-action pair a probability distribution over Z. In other words, the probability of detecting the species given that the species is extant and that the previous decision is to do nothing is defined by O(present|extant, do nothing) = do (see Table S1).
Because it is neither practical nor tractable to use the history of the action-observation trajectory to compute or represent an optimal solution, belief states are used to summarize and overcome the difficulties of incomplete detection. Indeed Aström (24) has shown that belief states are sufficient statistical tools to summarize all the observable history of a POMDP without loss of optimality. A POMDP can be cast into a framework of a fully observable Markov decision process in which belief states represent the continuous but fully observable state space. Here, a belief state is defined as a distribution probability over states extinct and extant.
In our case, solving a POMDP is finding a strategy π : B × τ → A mapping an allocation of resources given a current belief state (b ∈ B) and a time-step (t ∈ τ). An optimal strategy maximizes the expected sum of rewards over a finite time horizon, T. This expected summation also is referred to as the “value function”. A value function essentially ranks strategies by assigning a real value to each belief b. Although various algorithms from the operation research and artificial intelligence literatures have been developed during the past years, the computational complexity of exact algorithms remains intractable for most problems (refer to ref. 25).
We obtained an analytic approximation of the POMDP solution by noting that the solution identifies values of the probability of persistence that mark 2 boundaries, 1 between managing and surveying and the other between surveying and doing nothing (Fig. 2). The location of these boundaries depends on the time horizon, but over long time horizons, the boundaries are asymptotic.
The first boundary, between managing and surveying, is relatively insensitive to the time horizon and so can be solved by determining the level of belief at which we should switch strategies from managing the species to surveying for the species, bm/s, over 3 time steps (see SI Appendix for details). To do this we compare the expected value of managing the species Vm with the expected value of the species if we survey, Vs, by setting Vm = Vs and solving for bm/s. This leads to:
The number of years that we should manage a species after last seeing it can be determined by finding the time it takes for the probability that the species is extant to decline to bm/s. After Tm years of protection, the probability that the species is extant will equal pmTm. Therefore, setting bm/s = pmTm and solving for Tm leads to
The second boundary between surveying and surrendering is sensitive to the time frame of management, although as the time horizon increases, the boundary approaches an asymptote (Fig. 2). Therefore, we wish to obtain a relatively long-term solution for bs/n, the belief at which we should switch from surveying to surrendering. Using a sufficiently long time frame will approximate this asymptote. To determine when the value of surveying is the same as the value of doing nothing (Vn), we can solve Vs = Vn for bs/n over an appropriate time horizon T:
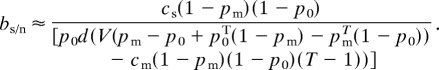 |
We can determine the number of years of surveying by evaluating the number of years of absence surveys that are necessary to reduce b from bm/s to bs/n. This can be obtained from an iterative evaluation of Bayes' rule, and we obtain:
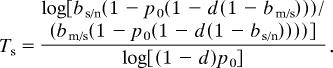 |
Supplementary Material
Acknowledgments.
Law enforcement data for this report were supplied by D. Martyr from Fauna & Flora International. We are grateful to T.G. Martin, O. Buffet, L. Peret, F. Garcia, and A. Cassandra for valuable discussions. Comments by N. Peyrard and T.G. Martin improved this manuscript. This work has been supported by the Institut National de la Recherche Agronomique (I.C.), Applied Environmental Decision Analysis Centre, an Australian Research Council Federation Fellowship, The Invasive Animals Cooperative Research Centre within the Detection, Prevention and Mitigation Program (E.M.), and a Mid Year University of Queensland Research Scholarship from the University of Queensland (E.M.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/cgi/content/full/0805265105/DCSupplemental.
References
- 1.MacKenzie DI, Kendall WL. How should detection probability be incorporated into estimates of relative abundance? Ecology. 2002;83(9):2387–2393. [Google Scholar]
- 2.MacKenzie DI, et al. Estimating site occupancy rates when detection probabilities are less than one. Ecology. 2002;83(8):2248–2255. [Google Scholar]
- 3.Tyre AJ, et al. Improving precision and reducing bias in biological surveys: Estimating false-negative error rates. Ecol Appl. 2003;13(6):1790–1801. [Google Scholar]
- 4.Baillie J, Groombridge B, editors. Rhinoptilus bitorquatus. 1996 IUCN Red List of Threatened Animals. Gland, Switzerland: International Union for the Conservation of Nature; 1996. [Google Scholar]
- 5.Maxwell S, Burbidge AA, Morris K, editors. Action Plan for Australian Marsupials and Monotremes. Gland, Switzerland: International Union for the Conservation of Nature/SSC Australasian Marsupial and Monotreme Specialist Group; 1996. Petaurus gracilis. [Google Scholar]
- 6.Baillie J, Groombridge B, editors. Gland, Switzerland: International Union for the Conservation of Nature; 1996. Porphyrio hochstetteri. 1996 IUCN Red List of Threatened Animals. [Google Scholar]
- 7.Nowak RM, editor. Walkers Mammals of the World. Sixth edition. Baltimore and London: The Johns Hopkins University Press; 1999. [Google Scholar]
- 8.Foose TJ, van Strien N, editors. Gland, Switzerland: International Union for the Conservation of Nature/SSC Asian Rhino Specialist Group; 1997. Asian Rhinos. Status Survey and Conservation Action Plan. [Google Scholar]
- 9.Stokstad E. U.S. announces recovery plan for a ghost bird. Science. 2007;317(5842):1158. doi: 10.1126/science.317.5842.1158b. [DOI] [PubMed] [Google Scholar]
- 10.U.S. Fish and Wildlife Service. Draft Recovery Plan for the Ivory-Billed Woodpecker (Campephilus principalis) Atlanta, GA: US Fish and Wildlife Service; 2006. [Google Scholar]
- 11.Gerber LR, Beger M, McCarthy MA, Possingham HP. A theory for optimal monitoring of marine reserves. Ecol Lett. 2005;8(8):829–837. [Google Scholar]
- 12.Martin TG, et al. Optimal conservation of migratory species. PLoS ONE. 2007;2(8):e751. doi: 10.1371/journal.pone.0000751. 710.1371/journal.pone.0000751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wilson KA, McBride MF, Bode M, Possingham HP. Prioritizing global conservation efforts. Nature. 2006;440(7082):337–340. doi: 10.1038/nature04366. [DOI] [PubMed] [Google Scholar]
- 14.Possingham HP, Andelman SJ, Noon BR ST, Pulliam HR. Making smart conservation decisions. In: Soule ME, Orians GH, editors. Conservation Biology: Research Priorities for the Next Decade. Washington, DC: Island; 2001. [Google Scholar]
- 15.Dorazio RM, Johnson FA. Bayesian inference and decision theory - A framework for decision making in natural resource management. Ecol Appl. 2003;13(2):556–563. [Google Scholar]
- 16.Kaelbling LP, Littman ML, Cassandra AR. Planning and acting in partially observable stochastic domains. Artificial Intelligence. 1998;101(1–2):99–132. [Google Scholar]
- 17.Monahan GE. A survey of Partially Observable Markov Decision Processes: Theory, models, and algorithms. Manage Sci. 1982;28(1):16. [Google Scholar]
- 18.Cassandra AR. pomdp-solve: POMDP solver software. 2005 Available at http://www.pomdp.org/
- 19.Linkie M, Chapron G, Martyr DJ, Holden J, Leader-Williams N. Assessing the viability of tiger subpopulations in a fragmented landscape. J Appl Ecol. 2006;43(3):576–586. [Google Scholar]
- 20.Wikramanayake ED, et al. An ecology-based method for defining priorities for large mammal conservation: The tiger as case study. Conserv Biol. 1998;12(4):865–878. [Google Scholar]
- 21.MacKenzie DI. Occupancy Estimation and Modeling: Inferring Patterns and Dynamics of Species Occurrence. Burlington, MA: Elsevier; 2006. [Google Scholar]
- 22.van Beukering PJH, Cesar HSJ, Janssen MA. Economic valuation of the Leuser National Park on Sumatra, Indonesia. Eco Econ. 2003;44:43–62. [Google Scholar]
- 23.Pearce D. Do we really care about biodiversity? Environmental and Resource Economics. 2007;37:313–333. [Google Scholar]
- 24.Aström KJ. Optimal control of Markov decision processes with incomplete state estimation. J Math Anal Appl. 1965;1:174–205. [Google Scholar]
- 25.Cassandra AR. Providence, RI: Brown University; 1998. Ph.D thesis. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.