Abstract
Using longitudinal data from urban Brazil, the authors track the employment patterns of thousands of children aged 10-16 during four months of their lives in the 1980s and 1990s. The proportion of children who work at some point during a four-month period is substantially higher than the fraction observed working in any single month. The authors calculate an intermittency multiplier to summarize the difference between employment rates in one reference week vs. four reference weeks over a four-month period. They conclude that intermittent employment is a crucial characteristic of child labour which must be recognized to capture levels of child employment adequately and identify child workers.
In spite of growing concern about child labour in developing countries, very little is known about the day-to-day and month-to-month movements of children into and out of the labour force. Since accurate assessment of the extent of child labour is needed for sound public policy, we must find out the extent to which child labour is characterized by long-term employment with high labour force attachment rather than by short-term employment spells with frequent movement into and out of the labour force. Though the specific nature of child labour undoubtedly varies with age, sex, region and household circumstances, a concern that there has been insufficient recognition of how volatile and intermittent child labour can be is the underlying motive for this article. Media portrayals - often focusing on children working long hours in steady, year-round work in factories or sweatshops - reinforce a view of child labour as relatively stable employment. Even in factory work, however, children may not be steady workers: one study has found a very high rate of child migration between garment firms in Bangladesh (Boyden and Myers 1995). Theoretical models of child labour (e.g. Basu and Van, 1998; Basu, 1999; Dessy, 2000) tend to treat children as either working or not, without considering the possibility that children’s work may be characterized by considerable intermittency.
However, case studies and fieldwork in small areas suggest that much of children’s labour force involvement is sporadic, opportunistic, quick to change and often informal.1 Cross-sectional surveys provide the bulk of our information about child labour, and have the advantage of providing information on large samples of children; however, they are not designed to measure transitions into and out of employment. They provide only a snapshot of children’s labour market experience, tempting analysts (ourselves included) to draw sharp distinctions between children identified as either working or not working at the time of the survey - much as analysts distinguish between economically active and inactive adults. These distinctions can be misleading when seeking to identify the potentially sizeable number of intermittently employed children.
There may be major implications for estimates of the proportion and total number of working children, if a significant proportion of children proves to be working intermittently. Consider the International Labour Organization’s estimates of the magnitude of child labour worldwide. The ILO’s 1996 estimate of child labourers in less developed countries has been repeatedly cited and used in reports and documents (Anker, 2000a and 2000b); the 2002 estimate and a follow-up estimate of 2006 are likely to be even more influential, given the increasing attention - and funding - being granted to child labour programmes and policies. According to the ILO (2002), there were 211 million child workers (aged 5 to 14 years) worldwide in 2000. This estimate declined to 191 million in 2004 (ILO, 2006). These figures are based on national household survey estimates (from countries in each region of the world) of the number of children employed during a reference week.
In this article, we show that many more children are identified as workers when panel data are used to record the intermittently employed. We use “intermittency multipliers” to summarize the size of this effect. As an example, we apply these multipliers to the ILO’s estimates for the year 2000. If intermittency in child employment were as prevalent worldwide as our study found it to be in metropolitan Brazil, the number of child workers worldwide would plausibly be between 364 million and 409 million. This means that if we were to ask children whether they are working during one week every month for four months in a row - instead of using only one reference week - and if the results for other countries are similar to those for urban Brazil, the ILO’s global estimate of economically active children would increase by between 72 and 94 per cent.2
As discussed in the ILO (2002) report, there are sound reasons for choosing the reference week method to define work, notably to maximize comparability with previous estimates and with the estimates of many national statistical agencies. (The most common alternative, a one-year reference period, is tainted by recall bias that is likely to be especially severe in the case of children.) We propose, however, that given the highly intermittent nature of children’s work, a measure based on activity in a single week may significantly understate the incidence of child labour. In choosing a time period to measure child labour, it is important to consider the purpose in defining a “child worker.” If it is to count and identify characteristics of children at risk of employment-related hazards or exploitation, a reference-week-based definition is too narrow; instead, a measure capturing employment in recent months in hazardous industries or occupations may identify children likely to take up those types of job again. If the goal is to increase human capital accumulation, it is worth noting that (depending on the school system) intermittent employment may take as great a toll on grade progression as regular employment. If the goal is to reduce the intensity of child work - for any of a number of reasons - it is important to understand the regularity and duration of employment as well as the number of hours worked in a reference week. Different combinations of work hours and job duration can have a range of implications for the well-being of young people (Anker, 2000b; Mortimer, 2003; Mortimer and Kirkpatrick Johnson, 1998). Thus, for most policy purposes, we argue that a reference period of one week is too short because it misses children’s frequent labour force entries and exits. The higher the incidence of intermittency, the greater the undercount of total child workers, broadly defined.
This article draws upon panel data to follow the month-to-month labour force movements of urban Brazilian children aged 10 to 16 in the 1980s and 1990s, capturing their employment status at the time of each month’s survey. We begin by reporting trends in youth employment from 1982 to 1999. We then present rates of employment entry and exit, the two components of employment transitions. The article concludes with evidence indicating that urban children’s employment is often of short duration and intermittent. To our knowledge, this has never before been documented for a large, representative sample.3 For children observed working at some point during a four-month period, the proportion of those working all four months is rarely as high as 50 per cent. For those aged under 15, that proportion is usually below 25 per cent. These results prove robust in sensitivity tests eliminating effects of the long school holidays. The implications of frequent entry and exit are summarized in an intermittency multiplier describing the extent to which child employment rates based on a reference week must be expanded if child labour estimates are to capture recent as well as current employment. For younger age groups, the multipliers are often as high as 2, meaning that a broader measure of child labour captures twice as many children as typical monthly surveys are able to identify.
Data and samples used
For a country with reasonably high levels of average production and income, Brazil has had relatively high levels of child employment. This may be due to Brazil’s marked income inequality4 or to the economic instability of recent decades. The country experienced rapid economic growth in the 1960s and 1970s, followed by a major recession in the early 1980s and continuing economic fluctuations that left per capita income in 1990 at about the 1980 level. Economic performance, though better in the 1990s, was still characterized by large fluctuations. Brazil is generally viewed as having under-performed in education relative to its level of income (Birdsall and Sabot, 1996). In 1995, for example, the mean years of completed schooling among 25- to 29-year-olds were less than seven (Lam, 1999).
The Pesquisa Mensal de Emprego (PME), or Monthly Employment Survey, was created by Brazil’s statistical agency (the Instituto Brasileiro de Geografia e Estatística, IBGE) to track employment and unemployment from month to month in six of Brazil’s largest metropolitan areas. These cities are: São Paulo, Rio de Janeiro and Belo Horizonte, in south-east Brazil; Salvador and Recife, in north-east Brazil; and Porto Alegre, in southern Brazil. For every household interviewed, the PME survey gathers standard demographic, schooling, labour force and earnings information about each household member aged 10 and over. Households are rotated in and out of short panels, so that a household will be interviewed once per month for four consecutive months, temporarily dropped out of the survey for eight months, then interviewed again once per month for four more months. Thus, household members, ideally, can be tracked over a 16-month period. In the part of our analysis that draws upon the longitudinal dimension of the PME, however, we use only the first four consecutive-month interviews for each household. Household rotation panels overlap, so about 35,000 households are interviewed each month, including 4,500 to 7,500 households from each of the six metropolitan regions.5 These sample sizes are large enough to allow us to analyse boys and girls separately for each city, month and year. For example, we observe, on average, about 190 girls and 190 boys aged 14 in São Paulo and about 150 girls and 150 boys aged 14 in Salvador in any given month.
The PME was first fielded in the early 1980s, and this article draws upon microdata for overlapping panels beginning in February 1982 and up to and including January 2000. Interviews conducted each month of each year during this period are included in our sample. The questionnaire is remarkably consistent over this time period. We briefly describe the overall trends in child employment for the entire period. Much of the following analysis focuses on three cities during two time periods: São Paulo, Salvador and Porto Alegre, from 1982 to 1984, at the beginning of the period, and from 1996 to 1998, at the end of the period.6 We limit ourselves to a few metropolitan regions because we present many of our results graphically, to show trends. Our choices were made to show the diversity of children’s experience in Brazil’s cities. São Paulo is Brazil’s largest metropolitan area by far, with a 1996 population of 9.8 million; São Paulo and the southern metropolitan area of Porto Alegre (1.28 million inhabitants in 1996) have strong labour markets, and cross-sectional surveys typically show relatively high child employment rates. Salvador, by contrast, is typical of the poorer north-east, with relatively weak labour markets; its population was 2.2 million in 1996.7 Any results we present that combine populations of different metropolitan areas are weighted by the inverse of the PME household sampling fraction for each area, so that our aggregate results are representative of the experience of the “average” household across these six largest metropolitan areas.
Observed children include all household members in the 10-16 years age range, regardless of the child’s relationship to the household head. Thus, children may be sons or daughters of the head (90.3 per cent), other relatives of the head (8.3 per cent), or non-relatives of the head, e.g. agregados8 and boarders (0.4 per cent), domestic servants (0.5 per cent) or relatives of domestic servants (0.1 per cent). Our sample of 10- to 16-year-olds also includes a small percentage of young people who are heads of households (0.1 per cent) or their spouses (0.3 per cent). Most of the analysis uses a subset (98.6 per cent) of this sample that includes only sons, daughters and other relatives of the household head. Because children’s activities change rapidly as they age, throughout this analysis as far as possible we report results for single years of age. Ages 14 and 16 are often highlighted in this article. This is because the minimum age for admission to employment or work specified by the ILO’s Minimum Age Convention, 1973 (No. 138), is 15 years (Article 2, para. 3). Thus, ages 14 and 16 are of particular interest as they are just below and above that cut-off line.
Throughout this article, the term “employed” is used to mean “in the labour force in the reference week of a particular month”, whether as an employee or self-employed.9 We also wish to point out that, in its narrow sense of labour force work, the term “work” ignores the substantial amount of non-labour-force domestic work done by children. We recognize that children do much work that is not captured by standard labour force surveys. Housework is rarely counted, with the result that girls’ contributions to family well-being in the form of housework are systematically neglected (Levison, 2000; Levison, Moe and Knaul, 2001). Moreover, surveys designed to capture adult work are not necessarily appropriate to measuring children’s work, much of which occurs in the informal economy. Levison (1991) estimates that the standard Brazilian survey question on employment missed at least 29 per cent of child employment in 1985. Finally, Knaul (1995) finds that parents systematically under-report child work to survey interviewers. For all of these reasons, we expect our estimates to under-report the labour of young people in Brazil.
Trends in child employment, 1982-99
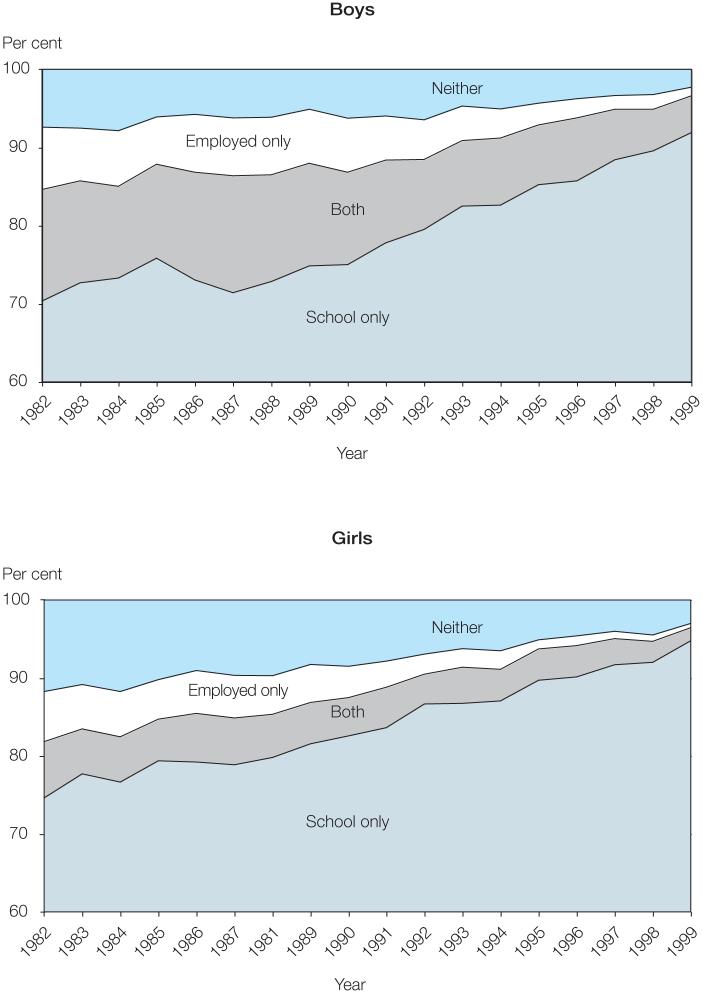
The employment of children and young people has been declining in Brazil’s cities for some time. To provide an overview of child activities in the 1980s and 1990s, figure 1 shows the aggregate trends in employment and school enrolment for the six metropolitan areas covered by the PME.10 The top panel reports the percentage of 14-year-old boys attending school who are not employed, and the percentages of those who combine school attendance and employment, those who work in the labour force and are not enrolled in school, and those who report neither activity. The bottom panel reports the same information for 14-year-old girls. The great majority of children are enrolled in school and do not work in the labour force, according to our data. A substantial proportion of the employed children also attends school. This is not surprising, as many schools are run in shifts of about four hours, which means that children are not at school for many hours each day. Children have many hours each day when they are not in classes. The proportion of employed children becomes very small in later years. Among girls, almost as many fall in the “neither school nor employment” category as are employed. Analysis of similar Brazilian cross-sectional data from 1985 shows that many of these girls are engaged primarily in domestic chores (Levison, 1991).
Figure 1.
Percentage of 14-year-old boys and girls who are only in school, only employed, doing both, or doing neither, six metropolitan areas, Brazil, 1982-99
Source: Brazil PME; authors’ calculations.
In developing countries, working children are generally assumed to be poor children. This assumption is not unreasonable for younger children engaged in labour market work; it becomes problematic for older children as they move into adulthood. Thus, analysis of child work status by socio-economic status (SES) is important in order to understand the structure of child work and its role in the lives of more or less privileged children and their families. As a rough measure of socio-economic status, we divide the sample into those above and below the median per capita household income.11 From this point on, we restrict our sample to the 98.6 per cent of children who are sons, daughters or other relatives of the household head. We use the term “mother” loosely: In this analysis, the “mother” is the female head or spouse of the head, while the 10- to 16-year-olds are the sons, daughters and other relatives of the head. Some sons and daughters of male heads are step-children of the head’s current spouse, for example.
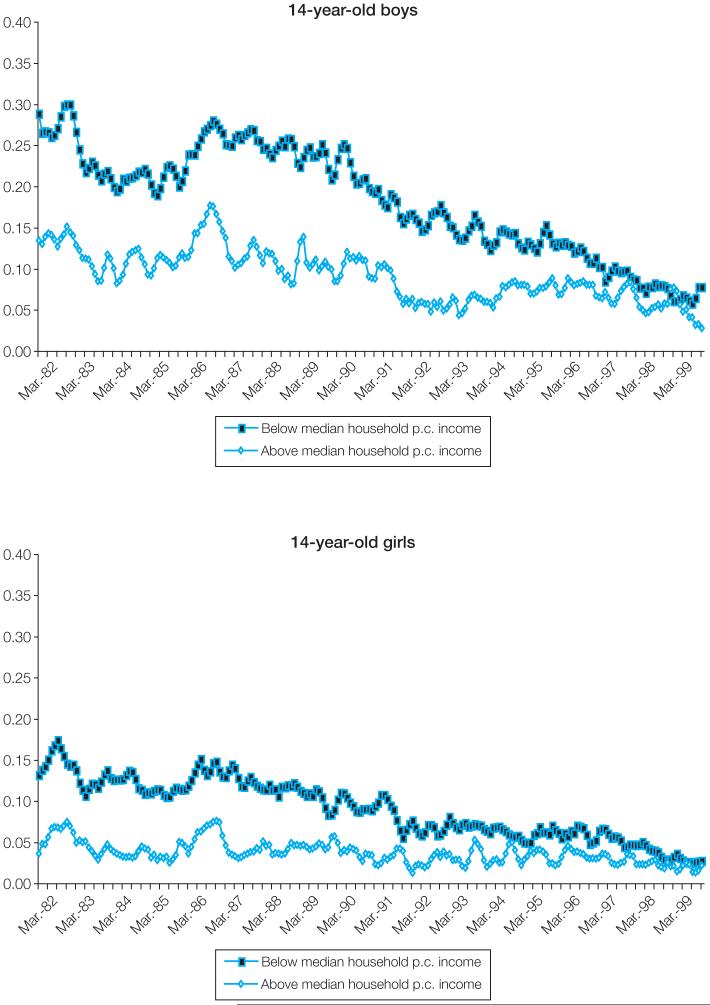
Figure 2 shows the proportions of employed 14-year-old boys and girls, in households with above and below median per capita income.12 In the 1980s, both boys and girls from lower-income households were roughly twice as likely to be employed as were children from higher-income households. The decline in employment rates was more rapid among children in the lower-income group, so that the gap between the two SES groups became much smaller. By the end of the 1990s, employment rates for children from lower-income households were only slightly higher than those for children from higher-income households. Similar patterns hold for 16-year-old boys and girls (not shown). Further information is required to determine what combination of factors has led to this change. Suspects include increasing demand for education by children of less-educated parents, greater availability of school openings, increased quality of public schools, and/or declining demand for child labour, especially in jobs traditionally held by children from lower-income households.
Figure 2.
Proportion of 14-year-olds employed, by household income, in six metropolitan areas, Brazil, 1982-99, 3-month moving averages
Source: Brazil, PME; authors’ calculations.
Measuring employment transitions: Entry and exit rates
Whatever the level of employment, there are always people moving into jobs and people leaving jobs. A decline in the overall employment level may occur because fewer people start new jobs, because those who start working leave their jobs more quickly, or both. In this section, taking advantage of the longitudinal feature of the PME data, we analyse employment entry and exit rates for children in order to better understand the trends described above.
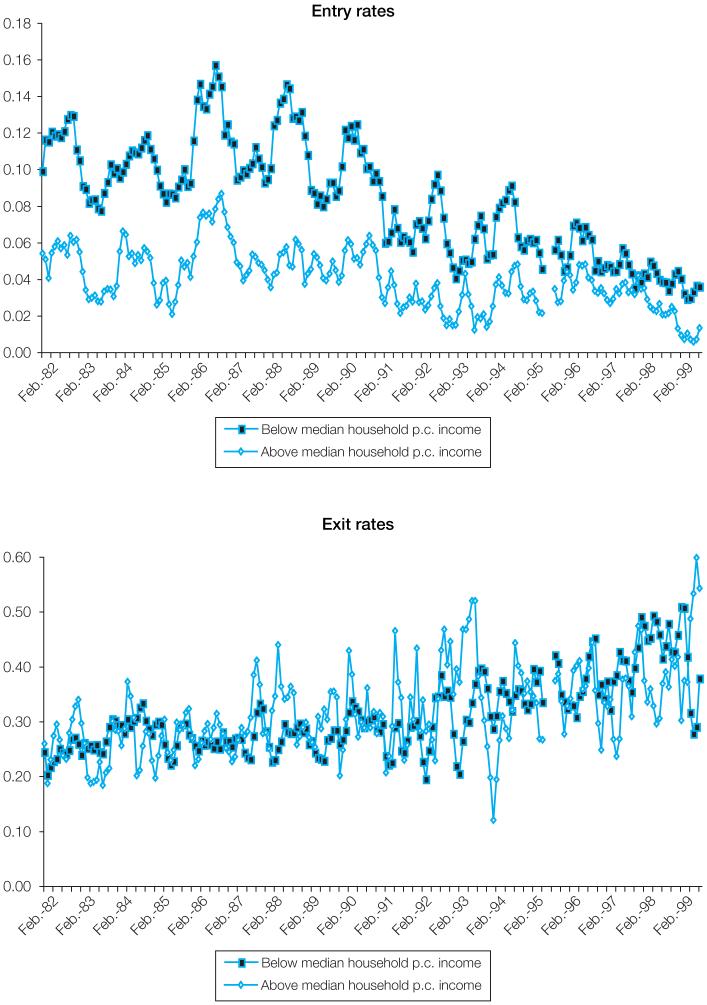
Our measure of the rate of entry into employment is the number of individuals who move from “not working” in month 1 to “working” in month 2, divided by the number of individuals who were “not-working” in month 1. The exit rate is defined analogously as the number of individuals who move from “working” in month 1 to “not-working” in month 2, divided by the number of individuals who were working in month 1. For 14-year-olds in São Paulo in the early 1980s, the probability that a boy not working in month 1 is observed working in month 2 is about 10 per cent; the corresponding probability for girls is about 5 per cent. The probability that a working boy has left employment by the following month is around 25 per cent, with fairly similar estimates for girls’ exit rates.
Duryea, Lam and Levison (2007) describe how entry and exit rates are related to each other and to the percentage of the population employed. Two important points are worth emphasizing. Firstly, systematic differences in employment between population groups or in changes over time in the level of employment can be linked to differences in entry or exit rates. In comparing male and female workers, for example, we can ask whether higher employment rates for male workers result from higher probabilities of entering employment, from lower probabilities of leaving employment, or some combination of the two. Secondly, some differences in entry or exit rates may result simply from differences in the overall level of employment. In general, there will be higher entry rates and lower exit rates among groups with higher levels of employment, although this tendency may be offset by other factors. For example, adult men aged 30 to 49 in metropolitan Belo Horizonte (a group with employment rates of over 90 per cent) had entry rates between about 0.40 and 0.68 from 1982 to 1998. By contrast, entry rates for adult women of similar ages (who have employment rates closer to 50 per cent) were between 0.15 and 0.40, a result that might be expected since on average women are less likely to be on the margin of entering employment.
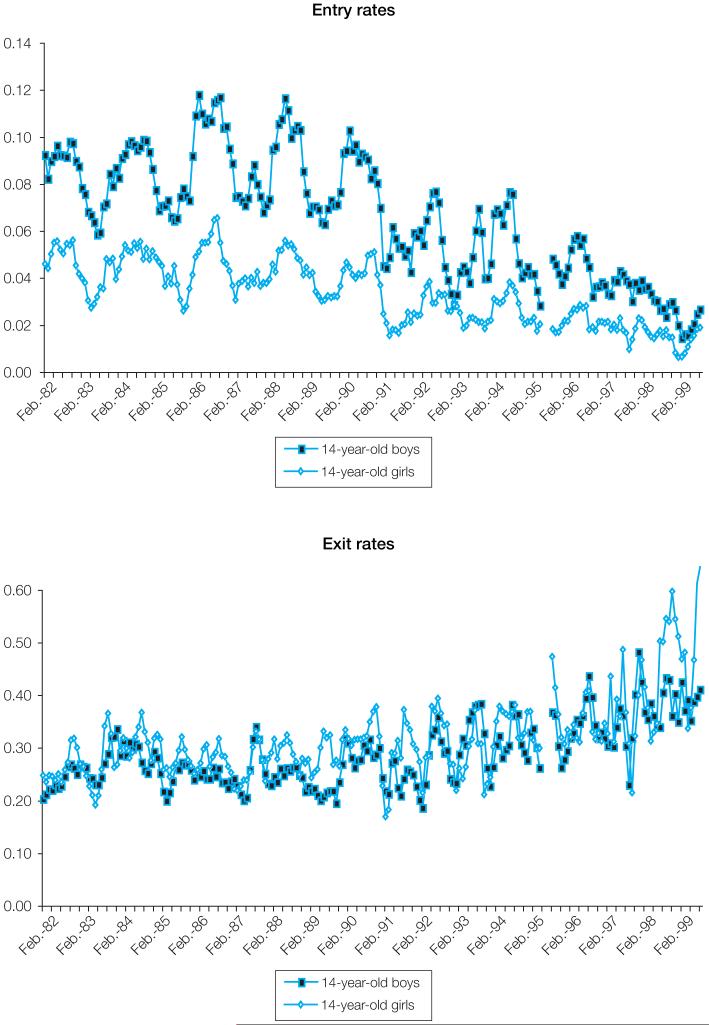
We documented above that child employment rates showed a downward trend over the 1980s and 1990s. Here we consider the components of that change. Have entry rates fallen, exit rates increased, or both? Because we observe relatively few entries and exits per city/month/sex/age group, in spite of observing many children, the figures on entry and exit rates discussed below combine data from all six metropolitan areas covered by the PME. Figure 3 shows that entry rates showed a downward trend throughout the 1980s and 1990s for both boys and girls aged 14, in spite of considerable volatility. In the 1980s, the probability that a non-employed boy began working in any given month fluctuated between 6 and 12 per cent; for girls, this probability fluctuated around 5 per cent. In the 1990s, boys’ and girls’ entry rates fell: for the first time, fewer than 5 per cent of 14-year-old boys moved into employment in some months, and girls’ entry rates dropped consistently below 5 per cent. Boys and girls showed similar patterns of peaks and troughs in entry rates (although girls’ were less pronounced), implying that they were responding to labour market conditions. For example, the first trough corresponds roughly to the onset of the economic crisis in the early 1980s, suggesting a pro-cyclical pattern of child employment.13
Figure 3.
Rates of entry into and exit from employment, 14-year-old boys and girls, in six metropolitan areas, 1982-99, Brazil, 3-month moving averages
Source: Brazil PME; authors’ calculations.
Exit rates for 14-year-olds are shown in the bottom panel of figure 3. Boys’ and girls’ exit rates are much more similar than are their entry rates. The probability that an employed child became non-employed in any month was between 20 and 30 per cent in the 1980s, and increased to between 30 and 40 per cent by the late 1990s. Again, a structural shift seems to have occurred in the early 1990s.
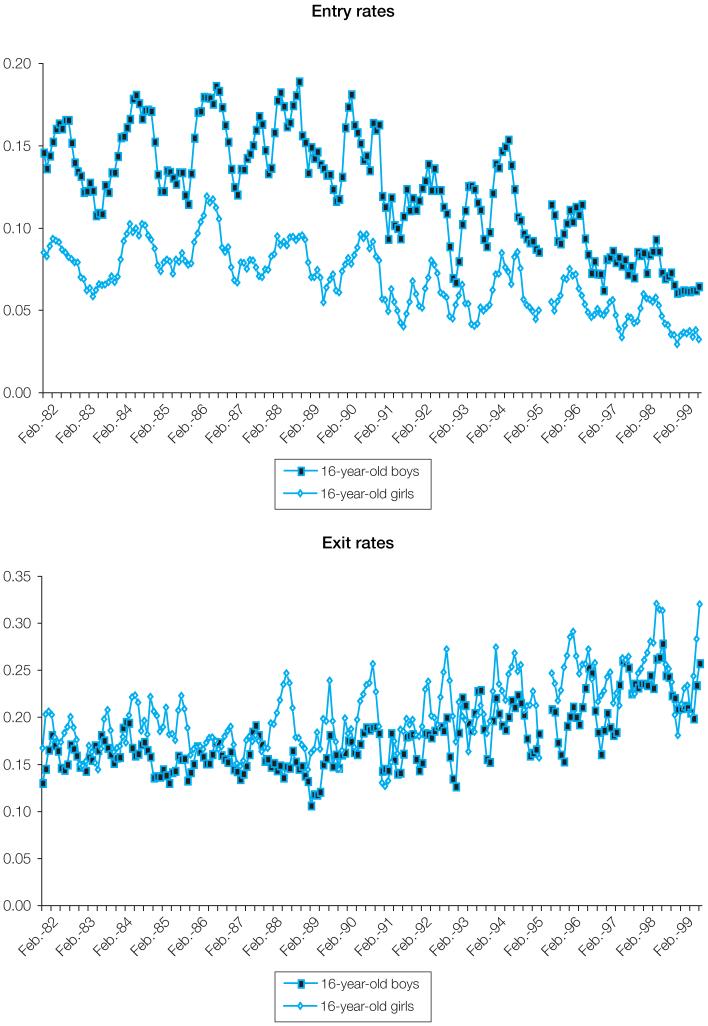
Figure 4 presents the entry and exit rates of 16-year-old boys and girls. Entry rates are higher and exit rates lower for 16-year-olds compared to 14-year-olds of the same sex. As was the case for 14-year-olds, entry rates of 16-year-olds are roughly twice as high for boys as for girls in all periods, with substantial declines in entry rates in the 1990s. As for 14-year-olds, the exit rates of boys and girls are very similar, indicating that, once employed, boys and girls are equally likely to leave a job (or, more precisely, become non-employed) in any particular month. Duryea, Lam and Levison (2007) show that, under certain assumptions, similar exit rates imply that boys and girls spend approximately the same amount of time in jobs (that is, employment duration is similar). Whatever motivates a move out of employment, the resulting patterns are similar for boys and girls. In contrast, the difference in entry rates by sex suggests that the incentives and disincentives to become employed may differ for girls and boys. A higher demand for boys’ labour is reflected in their higher wages (e.g. Levison, 1991), while girls tend to be assigned household and child-care responsibilities that can conflict with paid work. Lower rates of entry into employment imply that girls’ time in non-labour-force activities (such as school and household work) is steadier than boys’.
Figure 4.
Rates of entry into and exit from employment, 16-year-old boys and girls, in six metropolitan areas, Brazil, 1982-99, 3-month moving averages
Source: Brazil PME; authors’ calculations.
Analysis of the entry and exit rates of boys and girls by metropolitan region (not presented here) show that entry rates (separated by sex) are similar across regions, suggesting regional patterns of socio-economic constraints and incentives; by contrast, exit rates vary more across regions. Again, labour demand seems to play an important role in explaining regional differences.
Children’s rates of entry into and exit out of employment vary with socio-economic status. Figure 5 shows entry and exit rates for 14-year-old boys from higher- and lower-income households, again using median per capita household income as the threshold. The top panel shows that entry rates are consistently higher for boys in the lower SES group. In many months of the 1980s, the lower SES group was up to twice as likely to enter into employment; in the 1990s, the gap narrowed significantly. For example, the probability of a lower-SES 14-year-old boy entering employment in any given month was about 12 per cent in early 1982, compared with about 5 per cent for a higher-SES boy. Similar patterns hold for 14-year-old girls and 16-year-old boys and girls (not shown), although the previously observed pattern of lower entry rates for girls and 14-year-olds is maintained.
Figure 5.
Rates of entry into and exit from employment, 14-year-old boys, by household income, in six metropolitan areas, Brazil, 1982-99, 3-month moving averages
Source: Brazil PME; authors’ calculations.
The bottom panel of figure 5 shows that, in contrast to entry rates, exit rates are not clearly differentiated by socio-economic status. Rates for the higher-SES group show more volatility, but this is explained by the smaller number of observations of employed children in this group (since children must be employed in order to exit employment). Thus, poorer children are more likely to take up jobs than better-off children. Once employed, however, children in the upper-SES group are not likelier to stop being employed than children in the lower-SES group. Both SES groups repeat the overall pattern of a fall in entry rates and an increase in exit rates in the 1990s.
Evidence on employment intermittency
The evidence presented above on labour force entry and exit rates shows that many boys and girls move into and out of employment. That is, they have low rates of labour force attachment, at least at these young ages. However, from entry and exit rates it is impossible to discern whether most employed children have similar patterns of intermittent employment, or whether some children are steady, long-term workers while others move into and out of the labour force very frequently. Our final analysis, summarized in tables 1 and 2, sheds more light on these and related questions. The sample for this analysis, as previously stated, includes only children for whom we have information about the first four (consecutive) months of each interview cycle. We now analyse employment patterns across that four-month period.
Table 1.
Employment rates and employment transition rates for boys and girls aged 10-12, 13-14 and 15-16 years, in metropolitan Salvador, São Paulo and Porto Alegre, 1982-84
| Salvador |
São Paulo |
Porto Alegre |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Age: | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 |
| Boys 1982-84 | |||||||||
| Percentage employed 0 months | 85.6 | 68.0 | 51.6 | 92.0 | 69.9 | 36.8 | 91.6 | 71.1 | 38.5 |
| Average percentage employed each month | 7.1 | 18.4 | 32.5 | 4.2 | 18.4 | 49.7 | 4.7 | 20.8 | 48.1 |
| Low SES1 | 9.2 | 22.1 | 38.4 | 4.9 | 21.2 | 52.9 | 6.4 | 23.7 | 52.4 |
| High SES2 | 3.2 | 10.7 | 21.3 | 2.1 | 10.7 | 40.6 | 1.7 | 14.6 | 38.4 |
| Percentage employed at least 1 month | 14.4 | 32.0 | 48.4 | 8.0 | 30.1 | 63.2 | 8.4 | 28.9 | 61.5 |
| Low SES1 | 18.4 | 38.0 | 57.4 | 9.7 | 34.3 | 68.0 | 11.2 | 33.0 | 67.4 |
| High SES2 | 7.0 | 20.1 | 31.8 | 3.6 | 18.3 | 49.9 | 3.6 | 19.8 | 48.8 |
| Intermittency multiplier3 | 2.02 | 1.74 | 1.49 | 1.93 | 1.63 | 1.27 | 1.78 | 1.39 | 1.28 |
| Low SES1 | 2.01 | 1.71 | 1.50 | 1.97 | 1.62 | 1.28 | 1.74 | 1.40 | 1.29 |
| High SES2 | 2.19 | 1.88 | 1.49 | 1.70 | 1.71 | 1.23 | 2.05 | 1.35 | 1.27 |
| Sample size | 2 763 | 1 740 | 1 794 | 4 311 | 2 801 | 2 796 | 2 935 | 2 029 | 1 951 |
| Low SES1 | 1 763 | 1 125 | 1 135 | 3 117 | 2 062 | 2 032 | 1 870 | 1 384 | 1 307 |
| High SES2 | 991 | 602 | 635 | 1 183 | 734 | 755 | 1 058 | 640 | 631 |
| For those working at least 1 month: | |||||||||
| Sample size | 397 | 557 | 869 | 347 | 842 | 1 767 | 248 | 587 | 1 200 |
| Average hours worked per week4 | 29.3 | 32.1 | 36.4 | 30.4 | 37.8 | 42.7 | 31.5 | 37.4 | 41.1 |
| Percentage employed 1 month | 48.4 | 36.3 | 23.5 | 43.5 | 32.3 | 13.6 | 37.1 | 20.3 | 14.1 |
| Percentage employed 2 months | 20.9 | 21.0 | 18.5 | 22.2 | 19.8 | 13.9 | 24.6 | 17.4 | 15.5 |
| Percentage employed 3 months | 15.4 | 19.6 | 23.9 | 17.3 | 18.5 | 16.8 | 15.3 | 16.2 | 14.3 |
| Percentage employed 4 months | 15.4 | 23.2 | 34.1 | 17.0 | 29.3 | 55.7 | 23.0 | 46.2 | 56.2 |
| Percentage with 1 transition | 40.6 | 38.2 | 33.5 | 41.8 | 36.5 | 22.8 | 39.5 | 27.3 | 24.3 |
| Percentage with 2 transitions | 35.0 | 28.2 | 23.4 | 26.8 | 22.4 | 14.8 | 25.8 | 17.2 | 11.6 |
| Percentage with 3 transitions | 4.0 | 5.4 | 4.5 | 5.5 | 4.5 | 1.9 | 4.0 | 2.9 | 2.4 |
| Girls 1982-84 | |||||||||
| Percentage employed 0 months | 94.6 | 84.6 | 71.7 | 96.0 | 83.0 | 58.7 | 95.0 | 79.2 | 63.4 |
| Average percentage employed each month | 2.4 | 9.1 | 19.0 | 1.9 | 10.0 | 29.9 | 2.6 | 14.2 | 26.7 |
| Low SES1 | 2.2 | 7.5 | 16.0 | 2.2 | 11.5 | 33.9 | 3.3 | 16.9 | 30.6 |
| High SES2 | 1.2 | 3.3 | 9.7 | 0.7 | 4.3 | 17.0 | 1.4 | 7.7 | 15.0 |
| Percentage employed at least 1 month | 5.4 | 15.4 | 28.3 | 4.0 | 17.0 | 41.3 | 5.0 | 20.8 | 36.6 |
| Low SES1 | 5.6 | 15.4 | 27.3 | 4.8 | 19.8 | 46.9 | 6.2 | 24.5 | 42.2 |
| High SES2 | 3.3 | 6.6 | 17.4 | 1.5 | 7.6 | 24.9 | 2.9 | 12.6 | 21.2 |
| Intermittency multiplier3 | 2.23 | 1.70 | 1.49 | 2.11 | 1.70 | 1.38 | 1.92 | 1.47 | 1.37 |
| Low SES1 | 2.54 | 2.04 | 1.70 | 2.15 | 1.73 | 1.38 | 1.89 | 1.45 | 1.38 |
| High SES2 | 2.75 | 2.02 | 1.80 | 2.19 | 1.76 | 1.46 | 2.11 | 1.64 | 1.41 |
| Sample size | 2 724 | 1 836 | 1 828 | 4 207 | 2 796 | 2 741 | 2 815 | 1 818 | 1 867 |
| Low SES1 | 1 607 | 1 113 | 1 010 | 3 046 | 2 049 | 1 939 | 1 796 | 1 186 | 1 206 |
| High SES2 | 1 045 | 623 | 631 | 1 145 | 722 | 707 | 1 013 | 613 | 567 |
| For those working at least 1 month: | |||||||||
| Sample size | 147 | 282 | 518 | 167 | 474 | 1 132 | 142 | 378 | 683 |
| Average hours worked per week4 | 33.0 | 42.4 | 41.5 | 32.7 | 40.9 | 43.2 | 33.0 | 41.7 | 42.9 |
| Percentage employed 1 month | 59.2 | 34.8 | 28.8 | 50.3 | 37.1 | 21.3 | 42.3 | 25.9 | 22.1 |
| Percentage employed 2 months | 16.3 | 22.7 | 15.8 | 24.0 | 18.1 | 15.9 | 24.6 | 17.5 | 12.9 |
| Percentage employed 3 months | 10.2 | 14.5 | 13.5 | 12.0 | 17.1 | 15.1 | 15.5 | 15.1 | 16.3 |
| Percentage employed 4 months | 14.3 | 28.0 | 41.9 | 13.8 | 27.6 | 47.7 | 17.6 | 41.5 | 48.8 |
| Percentage with 1 transition | 42.9 | 31.2 | 26.6 | 43.1 | 34.6 | 29.1 | 39.4 | 31.5 | 30.5 |
| Percentage with 2 transitions | 38.1 | 32.6 | 22.6 | 34.7 | 28.5 | 14.9 | 28.2 | 17.5 | 14.5 |
| Percentage with 3 transitions | 0.7 | 2.5 | 3.7 | 2.4 | 3.4 | 2.9 | 5.6 | 2.9 | 1.9 |
Children living in households with below-median adult household income.
Children living in households with above-median adult household income.
Intermittency multiplier = percentage employed at least 1 month/average percentage employed each month.
Average hours worked excludes weeks for which the child did not work. A few cases reported being employed in a month while working zero hours; these were excluded from average hours worked, but not from the percentage employed.
Source: Brazil PME.
Table 2.
Employment rates and employment transition rates for boys and girls aged 10-12, 13-14 and 15-16 years, in metropolitan Salvador, São Paulo and Porto Alegre, 1996-98
| Salvador |
São Paulo |
Porto Alegre |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Age: | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 |
| Boys 1996-98 | |||||||||
| Percentage employed 0 months | 94.8 | 86.7 | 69.9 | 97.1 | 86.8 | 59.1 | 98.6 | 87.6 | 63.8 |
| Average percentage employed each month | 2.1 | 5.5 | 15.2 | 1.3 | 7.3 | 29.1 | 0.6 | 7.5 | 25.0 |
| Low SES1 | 2.3 | 6.5 | 17.0 | 1.6 | 8.2 | 29.9 | 0.6 | 9.1 | 28.6 |
| High SES2 | 1.5 | 3.3 | 11.2 | 1.1 | 6.1 | 28.0 | 0.7 | 5.5 | 19.7 |
| Percentage employed at least 1 month | 5.2 | 13.3 | 30.1 | 2.9 | 13.2 | 40.9 | 1.4 | 12.4 | 36.2 |
| Low SES1 | 6.1 | 15.4 | 33.6 | 3.6 | 14.8 | 43.5 | 1.3 | 15.3 | 41.3 |
| High SES2 | 3.6 | 8.8 | 22.5 | 2.0 | 11.1 | 37.6 | 1.6 | 8.7 | 28.7 |
| Intermittency multiplier3 | 2.53 | 2.44 | 1.98 | 2.14 | 1.81 | 1.41 | 2.16 | 1.65 | 1.45 |
| Low SES1 | 2.59 | 2.38 | 1.97 | 2.30 | 1.80 | 1.46 | 2.06 | 1.68 | 1.44 |
| High SES2 | 2.35 | 2.70 | 2.02 | 1.87 | 1.82 | 1.34 | 2.29 | 1.60 | 1.46 |
| Sample size | 2 376 | 1 756 | 1 817 | 3 143 | 2 241 | 2 337 | 2 351 | 1 668 | 1 735 |
| Low SES1 | 1 551 | 1 186 | 1 225 | 1 683 | 1 241 | 1 302 | 1 334 | 922 | 1 011 |
| High SES2 | 825 | 566 | 587 | 1 454 | 998 | 1 027 | 1 013 | 745 | 715 |
| For those working at least 1 month: | |||||||||
| Sample size | 124 | 234 | 547 | 90 | 295 | 956 | 33 | 206 | 628 |
| Average hours worked per week4 | 29.9 | 32.1 | 34.9 | 30.4 | 35.5 | 39.0 | 35.3 | 34.5 | 37.7 |
| Percentage employed 1 month | 60.5 | 58.1 | 41.5 | 52.2 | 37.3 | 23.4 | 57.6 | 31.6 | 24.4 |
| Percentage employed 2 months | 25.8 | 24.4 | 26.9 | 22.2 | 25.4 | 14.0 | 12.1 | 23.8 | 17.4 |
| Percentage employed 3 months | 8.9 | 12.8 | 19.6 | 12.2 | 15.9 | 17.3 | 18.2 | 15.5 | 15.6 |
| Percentage employed 4 months | 4.8 | 4.7 | 12.1 | 13.3 | 21.4 | 45.3 | 12.1 | 29.1 | 42.7 |
| Percentage with 1 transition | 37.1 | 45.7 | 41.7 | 50.0 | 40.7 | 29.7 | 36.4 | 35.9 | 30.6 |
| Percentage with 2 transitions | 42.7 | 37.2 | 32.5 | 25.6 | 26.1 | 18.9 | 48.5 | 24.3 | 18.2 |
| Percentage with 3 transitions | 9.7 | 7.7 | 6.9 | 5.6 | 4.1 | 1.9 | 0.0 | 4.9 | 2.7 |
| Girls 1996-98 | |||||||||
| Percentage employed 0 months | 97.9 | 94.3 | 84.8 | 98.5 | 93.1 | 75.9 | 98.9 | 94.3 | 76.9 |
| Average percentage employed each month | 0.7 | 2.4 | 7.2 | 0.6 | 3.7 | 15.8 | 0.5 | 3.2 | 15.6 |
| Low SES1 | 0.8 | 2.5 | 6.8 | 0.7 | 4.7 | 16.3 | 0.7 | 4.2 | 16.1 |
| High SES2 | 0.4 | 1.2 | 4.1 | 0.5 | 2.4 | 14.1 | 0.3 | 1.9 | 13.5 |
| Percentage employed at least 1 month | 2.1 | 5.7 | 15.2 | 1.5 | 6.9 | 24.1 | 1.1 | 5.7 | 23.1 |
| Low SES1 | 2.4 | 6.4 | 15.4 | 1.6 | 8.6 | 25.1 | 1.4 | 7.2 | 24.0 |
| High SES2 | 1.5 | 3.3 | 10.4 | 1.3 | 4.9 | 21.4 | 0.7 | 3.6 | 20.1 |
| Intermittency multiplier3 | 3.00 | 2.43 | 2.10 | 2.45 | 1.87 | 1.52 | 2.17 | 1.75 | 1.48 |
| Low SES1 | 2.86 | 2.58 | 2.26 | 2.40 | 1.82 | 1.54 | 2.17 | 1.71 | 1.49 |
| High SES2 | 3.69 | 2.67 | 2.57 | 2.48 | 2.02 | 1.51 | 2.15 | 1.93 | 1.50 |
| Sample size | 2 288 | 1 712 | 1 942 | 3 046 | 2 277 | 2 270 | 2 283 | 1 640 | 1 626 |
| Low SES1 | 1 478 | 1 135 | 1 299 | 1 699 | 1 236 | 1 209 | 1 318 | 920 | 926 |
| High SES2 | 793 | 553 | 585 | 1 343 | 1 034 | 1 021 | 961 | 716 | 656 |
| For those working at least 1 month: | |||||||||
| Sample size | 48 | 98 | 295 | 46 | 158 | 546 | 26 | 93 | 375 |
| Average hours worked per week4 | 28.9 | 35.0 | 36.0 | 27.1 | 34.5 | 36.4 | 29.3 | 33.7 | 35.9 |
| Percentage employed 1 month | 75.0 | 61.2 | 52.2 | 60.9 | 45.6 | 27.7 | 50.0 | 48.4 | 25.1 |
| Percentage employed 2 months | 16.7 | 22.4 | 18.6 | 19.6 | 17.7 | 17.9 | 23.1 | 7.5 | 18.9 |
| Percentage employed 3 months | 8.3 | 7.1 | 15.3 | 15.2 | 13.9 | 18.3 | 19.2 | 11.8 | 16.0 |
| Percentage employed 4 months | 0.0 | 9.2 | 13.9 | 4.3 | 22.8 | 36.1 | 7.7 | 32.3 | 40.0 |
| Percentage with 1 transition | 60.4 | 39.8 | 39.3 | 54.3 | 49.4 | 35.5 | 42.3 | 33.3 | 35.2 |
| Percentage with 2 transitions | 37.5 | 41.8 | 36.6 | 32.6 | 18.4 | 22.0 | 34.6 | 28.0 | 17.9 |
| Percentage with 3 transitions | 0.0 | 8.2 | 5.4 | 4.3 | 2.5 | 1.8 | 11.5 | 1.1 | 0.8 |
Children living in households with below-median adult household income.
Children living in households with above-median adult household income.
Intermittency multiplier = percentage employed at least 1 month/average percentage employed each month.
Average hours worked excludes weeks for which the child did not work. A few cases reported being employed in a month while working zero hours; these were excluded from average hours worked, but not from the percentage employed.
Source: Brazil PME.
Table 1 includes various kinds of employment rates and employment transition rates for three age groups of children (10-12, 13-14 and 15-16 years) in metropolitan Salvador, São Paulo and Porto Alegre, between 1982 and 1984. Table 2 includes the same information for the period almost 15 years later, that is, from 1996 to 1998. Rates for boys are presented in the top panel of each table, and those for girls in the bottom panel. Standard errors for the estimated employment rates are presented in the Appendix, tables B and C. The top row in each panel reports the percentage of the sampled children who were “never employed” during the reference week of four consecutive monthly interviews.14 The great majority of 10- to 12-year-olds fall into this category, with boys in Salvador displaying the lowest percentage: 86 per cent between 1982 and 1984 and 95 per cent between 1996 and 1998. The other groups of 10- to 12-year-olds of both sexes (including those from other cities) are between 92 and 96 per cent “never employed” in the four-month period in the early 1980s, and between 97 and 99 per cent in the 1996-98 period. The big transitions occurring in the teen years are reflected in the lower rates of “never employed” for 13- to 14-year-olds, and the even lower rates for 15- to 16-year-olds. In each case, more girls than boys are “never employed.” The estimates in tables 1 and 2 show large differences between the early 1980s and the late 1990s, and the relevant sample sizes are large enough that such differences are statistically significant. The decline in employment among older children is indeed quite dramatic. For example, 59 per cent of the girls aged 15 to16 had not been employed during any of the four months in São Paulo from 1982 to 1984; by the 1996-98 period this proportion had risen to 76 per cent. For 15- to 16-year-old boys in São Paulo, the percentage of those not employed in the four-month interval rose from 37 to 59 per cent.
We argued above that the intermittent employment of children, though important, has been difficult to discern using standard cross-sectional employment surveys. The next rows of each panel in tables 1 and 2 provide strong evidence further supporting this argument. The “average percentage employed each month” gives the employment rates observed using only the reference week in a given month - as in a standard, cross-sectional employment survey. The “percentage employed at least one month” out of the four consecutive months is the proportion of the observed children who could be considered labour-force workers by this broader measure of “employed recently.” The difference between these two measures is evidence supporting our argument. For example, although the average monthly employment rate for boys aged 10 to 12 in Salvador between 1982 and 1984 is 7 per cent, the proportion employed at least one month (or “employed recently”) is double that, at 14 per cent. The rates are also approximately double for boys aged 10 to 12 in the other cities as well as in the later period.15 For older boys in both periods and all cities, the percentage employed recently is 7 to 16 percentage points higher than the traditional monthly employment rate. Girls show a similar pattern of large differences in the proportion employed each month and the proportion employed recently. For example, while the monthly employment rate for girls aged 15 to 16 in Porto Alegre for the later period is 16 per cent, the percentage of girls who were employed at least one of the four months is 23 per cent. Overall, this evidence supports the contention that a substantial proportion of young workers is missed by standard cross-sectional employment surveys.
Do these patterns hold when children are differentiated by socio-economic status? Clearly, the answer is yes. Both SES groups show levels of recent employment that are substantially higher than their respective monthly employment rates. Among the levels of recent employment, those for children in households below the median per capita household income (“low SES”) are the highest ones reported in tables 1 and 2. Although employment rates are lower for children from higher-income households, the percentage employed in at least one month is often twice as high as the standard monthly employment rate for that group.
The difference between child employment rates based on a reference week and child employment rates based on a longer reference period - capturing part of the phenomenon of frequent transitions into and out of employment - can be summarized by an “intermittency multiplier.” If we observe an average monthly employment rate of 10 per cent and a “recent employment” rate of 20 per cent, the value of the multiplier is two.16 Thus, the intermittency multiplier is the factor by which the monthly employment rate must be multiplied in order to obtain the recent employment rate. Tables 1 and 2 present intermittency multipliers for each age group, with a breakdown for low and high SES groups. We see in table 1 that the intermittency multiplier for boys aged 10 to 12 in Salvador in the 1982-84 period was 2.02, a value fairly similar to those for the two separate SES groups. If applied to an estimate of the total number of children working, this multiplier means that the estimate based on asking about employment during a single week only would need to be multiplied by two in order to approximate the number of children who were recorded as working at some time during the four-month period. For older age groups the multiplier is lower, around 1.3 to 1.5 for 15- to 16-year-olds. This will be discussed in greater detail below.
The last nine rows of each panel in tables 1 and 2 describe the employment patterns of those aged 10 to 12, 13 to 14 and 15 to 16 years who were employed in the reference week of at least one month of the first four months of each interview cycle (“recently employed”). Since employment is relatively rare, especially among younger children and in the later time period, the number of children analysed in these rows is occasionally small enough to be problematic, in spite of our very large samples. This is most serious in the case of 10- to 12-year-olds in the 1996-98 period, where the sample sizes for those observed working are often well below 100.
For employed children, table 1 shows that even 10- to 12-year-old children spend a substantial number of hours working, averaging about 30 hours per week. According to tables 1 and 2, average weekly hours in employment increase steadily with age, up to approximately 40 hours per week for 15- to 16-year-olds. From 1982 to 1984, girls of all ages worked on average as many, or more, hours than their male counterparts. Girls’ hours exceeded those of boys by the greatest margin for 13- to 14-year-olds in Salvador, probably reflecting the intensity of domestic work carried out by girls employed as maids. By years 1996 to 1998, however, average hours worked by girls and boys had become quite similar.
The next four rows in each panel of tables 1 and 2 address the issue of employment intermittency and labour force attachment in greater detail. The repeated interview structure of the survey allowed us to measure the nature of employment attachment for children employed at least once in four months. We report the percentage of child workers who are employed during one month (not necessarily the first) of the four in the interview series, during any two of the four months (not necessarily consecutive), or during any three of the four months, as well as those employed during the reference week in all four months. The four measures add to 100 per cent within each city/sex/age/years group.
The percentages of children employed for one, two, three and four months reveal some interesting patterns that vary across age groups. The simplest pattern is apparent among 10- to 12-year-olds in Salvador and São Paulo: the percentages of children employed decline fairly steadily from one to four months of employment. In many cases, conditional on being employed, more children work either one month or four months than two or three months. Perhaps it takes young people a considerable amount of trial-and-error to find a position that will turn into a steady job.
One obvious question is what proportion of child workers is observed working in all four months, that is, the proportion of children with the kind of labour force attachment typical of adult workers. That proportion is never more than half of that of the children observed working during at least one month. For example, 29 per cent of ever-employed boys aged 13 to 14 are employed for all four months in Porto Alegre from 1996 to 1998. While it has long been established from cross-sectional data that employment rates increase with age, tables 1 and 2 demonstrate that employment intermittency generally falls with age, or, conversely, that labour force attachment increases with age. For instance, in São Paulo 4 per cent of employed girls aged 10 to 12 worked all four months in the 1996-98 period, compared with 23 per cent of 13- to 14-year-old girls and 36 per cent of 15- to 16-year-old girls. The levels are different both for girls in other cities and for boys, but the general pattern of work attachment increasing with age is observed.17
As we already noted in the figures, boys have higher employment rates than girls in all periods, cities and age groups. Tables 1 and 2 show that the percentage employed recently (“employed at least one month”) is also higher for boys everywhere and at all ages. In general, recently employed boys are more likely to be employed all four months than recently employed girls. There are a few exceptions. In the earlier period, presented in table 1, ever-employed girls aged 13 to 14 and 15 to 16 in Salvador are more likely than ever-employed boys to work all four months. In the later period, employed girls aged 13 to 14 in all three cities, as well as 15- to 16-year-old girls in Salvador, are more likely than boys to be employed all four months. This is probably related to the high prevalence of domestic workers among girls.18
As documented by Levison (1991) and Barros, Mendonça and Velazco (1996), employment rates for older children and percentages of child workers employed during all four months are higher in the cities offering better labour market opportunities (São Paulo and Porto Alegre) than in cities with fewer prospects (Salvador). For example, the monthly employment rate for 15- to 16-year-old boys is 15 per cent in Salvador compared with approximately 29 and 25 per cent in São Paulo and Porto Alegre, respectively, in the 1996-98 period. The employment rate for girls is also about twice as high in the other cities as in Salvador. For the youngest group of boys, however, monthly employment rates and ever-employed rates are higher in Salvador, suggesting that these boys are pushed into the labour force by poverty.
Overall, the large variation in these measures by city/sex/age group implies that different definitions of “child worker” will be very sensitive to the population studied and to the interval used in defining employment. The longer the period considered for “employed recently,” the greater the potential discrepancy with the traditional cross-sectional employment rate. The fact that these measures differ so much from the standard measure and from each other when considering only a four-month period implies that longer reference periods could result in counting even more children as “child workers” (recall bias aside).
The final three rows in each panel of tables 1 and 2 address transitions into and out of employment. Since we observe four consecutive months, it is possible for any given child to move between being employed and not being employed (or vice versa) up to three times. The statistics presented here show, for those employed at least one month, what percentage of children experience one, two or three transitions. Including the omitted category of zero transitions, these measures add up to 100 per cent for each city/sex/age group. These transition measures provide perhaps the most convincing evidence of employment intermittency. Although relatively few young workers made three transitions in a four-month period, the majority of 10- to 14-year-olds made one or two. One exception is Porto Alegre where this proportion (one or two transitions) is as low as 45 per cent (13- to 14-year-old boys in 1982-84); in most cases, over two-thirds of ever-employed 10- to 14-year-olds made one or two transitions. Again we see that transitions decline with age, but well over one-third of the ever-employed 15- to 16-year-olds in this analysis made one or two transitions in the four-month period.
It would be reasonable to hypothesize that many urban children become employed at the end of the school year, work during the long holidays and then quit when the next school year begins. Is there a structural reason driving our intermittency results? To address this question, we created a sub-sample including only children whose first four consecutive months of interviews fall entirely within the school year. The sensitivity analysis thus compares results for children interviewed between March and November (inclusive) with results for the previous (full-year) sample. We re-created tables 1 and 2 for this school-year-only sample but do not present them, because they report very similar results to the original tables 1 and 2. Changes due to ending or starting a school year explain a very small fraction of observed movements. This is also borne out in a sensitivity analysis of table 3, discussed below.
Table 3.
Intermittency multipliers for girls and boys aged 10-12, 13-14 and 15-16 years, in six metropolitan areas, Brazil, 1982-84 and 1996-98
| Age |
||||||
|---|---|---|---|---|---|---|
| 10-12 |
13-14 |
15-16 |
||||
| Girls | Boys | Girls | Boys | Girls | Boys | |
| Using all four-month periods | ||||||
| 1982-84 | 2.05 | 1.97 | 1.65 | 1.63 | 1.43 | 1.35 |
| Low SES1 | 2.09 | 1.97 | 1.69 | 1.62 | 1.45 | 1.36 |
| High SES2 | 2.21 | 1.95 | 1.77 | 1.68 | 1.52 | 1.31 |
| 1996-98 | 2.37 | 2.20 | 1.96 | 1.85 | 1.58 | 1.49 |
| Low SES1 | 2.39 | 2.31 | 1.94 | 1.83 | 1.59 | 1.51 |
| High SES2 | 2.37 | 2.04 | 2.08 | 1.87 | 1.60 | 1.45 |
| Using only four-month periods between March and November | ||||||
| 1982-84 | 2.04 | 1.95 | 1.61 | 1.62 | 1.43 | 1.35 |
| Low SES1 | 2.11 | 1.96 | 1.65 | 1.61 | 1.46 | 1.36 |
| High SES2 | 2.05 | 1.93 | 1.72 | 1.72 | 1.48 | 1.29 |
| 1996-98 | 2.21 | 2.12 | 1.88 | 1.78 | 1.57 | 1.47 |
| Low SES1 | 2.23 | 2.22 | 1.90 | 1.77 | 1.57 | 1.49 |
| High SES2 | 2.19 | 1.93 | 1.89 | 1.79 | 1.61 | 1.43 |
Children living in households with below-median adult household income.
Children living in households with above-median adult household income.
Source: Brazil PME, authors’ calculations.
Intermittency multipliers
The intermittency multipliers shown for the separate cities in tables 1 and 2 demonstrate the wide discrepancies that may be observed between a single snapshot estimate of child employment rates and a broader measure that captures shortrun movements into and out of employment. Table 3 presents similar intermittency multipliers for the combined six metropolitan areas included in the PME survey. The multipliers are calculated by age, sex, and socio-economic status for the time periods of 1982-84 and 1996-98. A number of patterns can be seen in table 3. Consider the top panel, calculated using the full-year sample. First, as noted in tables 1 and 2, the intermittency multipliers decrease with age. This is consistent with all of our evidence showing that intermittency is more important for younger children than for older youths and, presumably, adults. For 10- to 12-year-olds, multipliers are in the neighbourhood of 2.0. Second, multipliers for girls are almost always higher than those for boys. In other words, correcting employment estimates for intermittency will have a bigger effect on estimates for girls than on those for boys. Third, as child employment levels decline over time, the intermittency multipliers increase. All of these patterns are consistent with an underlying negative relationship between standard employment rates and intermittency.
The second panel of table 3 presents intermittency multipliers calculated for the school-year-only sub-sample. Totals for the 1982-84 period scarcely differ between the two samples. From 1996 to 1998, the school-year-only sub-sample has slightly lower multipliers than does the full-year sample. As employment becomes rarer among children and young people, school transitions may explain more - but still a very small fraction - of transitions into and out of employment.
It might be argued that children who work intermittently differ in some important ways from those whose work patterns are stable. In particular, are intermittent child workers just working a few hours to earn a bit of pocket money? We calculated average hours worked in the reference week for children employed for one, two, three or four months. Children employed during three or four months tended to work more hours per week than those employed during one or two months, but all groups averaged at least 20 hours per week - and often closer to 30 hours.
The high levels of intermittency that we estimate for child workers can be better appreciated if placed in the context of comparable estimates for adult workers. The fact that the multipliers drop significantly as we move from the 10- to 12-year-olds to the 15- to 16-year-olds suggests that multipliers for adult workers are likely to be even smaller. Although it is outside the scope of this article to analyse intermittency of adult workers in detail, exploratory analysis indicates that intermittency over a four-month period is much lower for adults than the estimates we show here for children. For example, comparable estimates for women aged 25 to 34 (a group we might expect to have relatively high intermittency) in São Paulo from 1982 to 1984 indicate that 52 per cent were working in any given month over a four-month period, while 62 per cent worked at some point over the entire four-month period. This implies an intermittency multiplier of 1.2 - that is, the total number of women found working at some point over the four-month period is 20 per cent higher than the number observed working in one single month. While this difference is well worth taking into account in studies of women’s labour force activity, it is much smaller than the intermittency multipliers of 1.9 and 2.1 that we estimate for 10- to 12-year-old boys and girls, respectively, in the same period. (Estimates for other adult groups and other time periods yield a similar picture.) While expanding the time period must always lead to higher estimated employment rates, since there is some degree of intermittency in all groups, the levels of intermittency observed for children are much larger than those for adults. While our estimates of child labour can often double when we use a four-month period rather than a single reference week, our estimates of adult employment only increase by 10 to 30 per cent, even among groups that might be expected to exhibit frequent work transitions.19
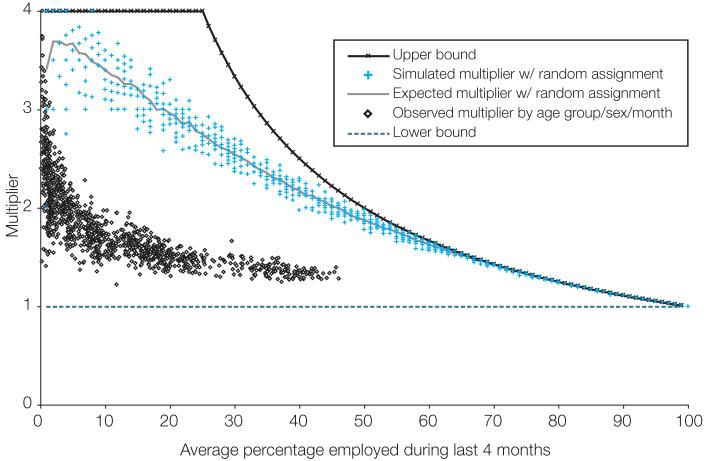
There must be some relationship between the intermittency multiplier we have defined and the overall employment rate. For example, if 75 per cent of some population group is working, an intermittency multiplier of 2.0 for that group would clearly be impossible. Figure 6 summarizes the relationship between intermittency multipliers and the cross-section estimate of employment. The figure presents a scatter plot of the observed intermittency multipliers in each month against the average employment rate, disaggregated by sex and age group. In order to give a better idea of where in “multiplier space” our observed multipliers lie, the upper and lower bounds of the multiplier are included in the figure, as well as a simulated multiplier when employment is randomly assigned across children over a four-month period. The lower bound of the multiplier is 1, corresponding to the case where a given amount of employment is concentrated among as few children as possible. That is, all employed children must be employed in each of four sequential monthly interviews. The lower bound is invariant to the average employment rate.
Figure 6.
Simulated intermittency multipliers when employment is random, and observed multipliers for boys and girls aged 10-12, 13-14 and 15-16 years, plotted against average percentage employed, 1982-99
Source: Brazil PME; authors’ calculations.
The upper bound of the multiplier is a function of the average employment rate, and the shape of this function will depend on the length of the panel. Since we observe children for four consecutive months, the multiplier can never be greater than 4. This is the case when a given amount of employment in the last four months is spread as evenly as possible across all children, so that no more than a quarter of them are observed to be working in each of the four months. For average employment rates above 25 per cent, however, more than a quarter of all children must work in each month, no matter how evenly the work is spread. Thus, the upper bound of the multiplier falls when average employment exceeds this level. In the limit, the upper bound converges to 1. For longer panels, the upper bound of the multiplier will increase, and its interpretation will change accordingly.
The series labelled “simulated multiplier” in figure 6 is the outcome of a simulation where employment is allocated randomly across all children over a four-month period. For example, if there are 100 children observed over four months and the average percentage of children employed during any month is 10 per cent, then the simulation randomly assigns 40 (= 100 × 4 × .1) months of employment across the 400 observed child-months. Figure 6 plots ten replications of the simulation for each percentage-point increment of average employment. At high levels of employment, random employment yields a multiplier very close to the upper bound, since randomly allocating many months of employment across the population will result in most children being employed in at least one month. The variance of the multiplier increases at lower average employment rates, since accidental concentration of multiple months of employment among some children causes large changes in the multiplier. Put differently, since the simulation assumes that employment is uncorrelated across months for a given child, random variation will produce cases where it is possible to spread the work more evenly, especially at lower employment rates. In order for the multiplier to reach the upper bound, employment must be negatively correlated across months for a given child.
Not surprisingly, our estimated multipliers fall well below the “random assignment” benchmark, indicating that employment is positively correlated across months. Figure 6 also illustrates that the average employment rate explains much of the variation in the multiplier. The lower average employment rates we observe for girls, younger children and higher-SES groups are strongly associated with higher intermittency multipliers for those groups. Essentially, lower employment rates leave a greater percentage of the population available for entry into employment in any given month.
Policy-makers and activists emphasize the numbers of child workers in particular contexts, yet the numbers that experts generate rarely correspond to the concept of “child labourer” being used. Intermittency multipliers provide a simple yet powerful tool for understanding the prevalence and patterns of child labour. The past few years have seen a proliferation of programmes to reduce labour-force work among children and young people. Examples include PETI (Eradication of Child Labour Programme) in Brazil and PAI (Programa de Atención Inmediata) in Costa Rica (Duryea and Morrison, 2004; Legovini and Regalia, 2001; Yap, Sedlacek and Orazem, 2001). However, as governments and international organizations have designed and expanded these programmes, they have probably underestimated the resources needed, especially for all girls and for all children aged under 15.
Implications for estimates of child labourers worldwide: A counter-factual exercise
As an illustration of the implications of intermittent employment on the overall estimate of child labour, we use our estimated intermittency multipliers to adjust the ILO’s estimate of the number of child workers worldwide in the year 2000 (for details of this estimate, see ILO, 2002). The ILO estimates are based on questions about employment in a reference week in 29 national household surveys. These counter-factual estimates are used to produce estimated numbers of working children by world region, sex, and age group. Since the measure of employment used by the ILO is identical to our one-month measure of employment (that is, it is based on work reported in a single reference week), it is interesting to consider how much larger the number of child workers in the world would be if the estimate had been based on a four-month period (with panel data) and if the relationship between estimates using a single reference week and those using a four-month period were the same as we observed in urban Brazil.
Applying our intermittency multipliers for the 1982-84 and 1996-98 periods to the ILO estimates, we produce two of many possible revised counts of the total number of child workers worldwide in 2000. Our primary assumption is that multipliers for metropolitan Brazil are positively correlated with unobserved (and perhaps unobservable) “global” multipliers by age and sex. An additional assumption is necessary because we do not observe 5- to 9-year-olds in the PME. Their employment levels are certainly lower than those of 10- to 12-year-olds, implying greater intermittency. To be conservative, however, we apply the multipliers for 10- to 14-year-olds to the numbers of 5- to 9-year-olds, by sex. Table 4 shows the details of our calculations. Since our intermittency multipliers range from 1.7 to almost 2, they have a large impact when applied to estimates of worldwide child labour. These adjusted estimates imply that the worldwide number of child workers aged 5 to 14 would range from 364 million to 409 million if workers were measured over a four-month period rather than a single reference week. Though these estimates are speculative, requiring the strong assumption that the pattern of work intermittency in the rest of the world is similar to that of metropolitan Brazil, we believe the estimates are instructive about the sensitivity of child labour estimates to the period of observation. Similar exercises could be done using many of the ILO’s Statistical Information and Monitoring Programme on Child Labour (SIMPOC) surveys, which include measures of work over a 12-month period in addition to the measure using a single reference week, although the impact of recall bias would be greater. Although the SIMPOC data do not permit the kind of detailed analysis of work transitions that we have presented here, our results suggest that the highly intermittent nature of children’s work calls for close attention to the impact of reference period on estimates of child labour. Different types of estimates may be needed for different policy and programmatic purposes.
Table 4.
Adjusted child workers worldwide, boys and girls aged 5-9 and 10-14 years
| Sex/age group | ILO estimate of children at work1 |
Intermittency multipliers from metropolitan Brazil2 |
Intermittency-adjusted estimates of children at work |
||
|---|---|---|---|---|---|
| (thousands) | 1982-84 | 1996-98 | (thousands) | ||
| Boys aged 5-9 years | 38 100 | 1.71 | 1.90 | 65 269 | 72 432 |
| Boys aged 10-14 years | 70 900 | 1.71 | 1.90 | 121 459 | 134 787 |
| Girls aged 5-9 years | 35 000 | 1.74 | 1.98 | 60 877 | 69 441 |
| Girls aged 10-14 years | 66 800 | 1.74 | 1.98 | 116 187 | 132 534 |
| Total 5-9 years | 73 100 | 126 146 | 141 873 | ||
| Total 10-14 years | 137 700 | 237 646 | 267 321 | ||
| Total 5-14 years | 210 800 | 363 792 | 409 194 | ||
ILO (2002), table 1, page 17.
The multiplier for the 10-14 age group was applied to the 5-9 age group, since the PME does not consider children aged 5-9 years.
Conclusion
A range of evidence constructed using panel data from metropolitan Brazil shows that the employment of 10- to 16-year-old boys and girls declined in the 1990s, compared with the 1980s. Both lower rates of entry into employment and higher exit rates from employment are responsible for the decline of the 1990s. Although boys and lower-SES children were employed to a greater extent than girls and higher-SES children, the employment gap by socio-economic status narrowed in the 1990s. By all appearances, by the late 1990s child employment affected only a small percentage of the metropolitan population. This documented decline in child employment is convincing, in so far as using the measure of employment typically used for adults can accurately reflect children’s employment experience.
The use of longitudinal data, even over a short, four-month period, convincingly demonstrates the inadequacy of traditional (adult) employment measures when applied to children. Traditional measures based on a single reference week substantially under-report child employment, due to the propensity of young workers to move into and out of the labour force. Measures of employment over four consecutive months show that relatively small proportions of young workers in urban Brazil remained employed for four months. Very high proportions of 10- to 16-year-olds made at least two transitions into and out of employment in a four-month period. This implies relatively short employment spells. Although scholars of child labour are familiar with case studies reporting that many children work intermittently, this is the first large-scale study to confirm this “stylized fact”.
While entry rates were higher for lower-SES children, exit rates did not differ by socio-economic status, implying that once employed, higher-SES children are as likely to continue working as are lower-SES children. The pattern is comparable when children are divided by sex: boys’ and girls’ exit rates are much more similar than are their entry rates.
The confirmation that many children moved rapidly into and out of employment does not negate the decline of child employment in urban Brazil in the 1980s and 1990s. The traditional measure of employment tells us that, on average, in the reference week of any given month or year, a substantially smaller percentage of children were employed in the late 1990s, compared with the early 1980s. (This trend appears to have continued up to 2004, as evidenced by the findings for Latin America in ILO (2006).) Our additional evidence shows that the percentage of children employed during the reference week of at least one month out of four observed months also fell substantially between 1982-84 and 1996-98. For example, about 30 per cent of 13- to 14-year-old boys in Salvador, São Paulo and Porto Alegre were employed at least one month in four in the 1982-84 period. By the 1996-98 period, this number had more than halved to about 13 per cent. Employment of 13- to 14-year-old girls during at least one month in four fell even more, from between 15 and 21 per cent to about 6 per cent.
In this case, using employment measures designed for adults has correctly indicated that child employment is declining in urban Brazil. However, although the direction of the trend is correct, the levels indicated by the traditional measure are highly misleading. One-time measures generally fail to identify many children who are in fact often found working in the labour force. Moreover, such measures inappropriately emphasize distinctions between employed and non-employed children, who are taken to represent ever-employed and never-employed children. This, then, gets to the heart of the problem: intermittent employment is a crucial characteristic of child work that is generally ignored and, therefore, not understood.
Our intermittency multipliers imply that, for children aged 10 to 12 in urban Brazil, more than twice as many children are likely to work during a four-month period as in any given reference week. If work intermittency were similar in magnitude for child workers around the world, there could be 409 million child workers worldwide. In order to estimate the number of children who work “often” or “frequently”, intermittency multipliers are needed for many countries and labour markets. There is no universal multiplier. While the patterns observed for the intermittency multipliers in metropolitan Brazil may well be characteristic of child employment, the size of multipliers should vary depending on labour market characteristics and reference periods. There may also be substantial differences between urban or rural residence. This can be predicted by the generally higher employment levels for children in rural areas.20
We suspect that high then decreasing intermittency is a feature of the normal growing-up process, whereby young people move on from school, play and unpaid work into paid adult-status employment. Some basic skills are acquired after initial labour force entry. For example, young people must learn to show up for work on time, day after day. Some learn this the hard way - by being fired for transgressions. For each new job, there must be a search process. Meanwhile, young people are learning how to identify good jobs, or jobs that are a reasonable fit. Some job acceptances will prove to have been a bad idea. Jobs that are intolerable, for one reason or another, should lead to higher quit rates, as young people learn to leave abusive or exploitative situations. While higher intermittency rates may have positive aspects for young adults, they also imply that more children than is generally recognized are putting in hours - sometimes many hours - into labour market activities each week, when their priority (especially for younger children) should be attending school regularly and learning.
The evidence presented here suggests that intermittent work is a fundamental feature of children’s work, with levels of short-term movement much higher than those observed for adults. This level of intermittency means that standard employment measures based on a single reference week miss important dimensions of children’s work experience, possibly giving a misleading picture of the prevalence of child labour. Our results suggest that most children who work, especially at younger ages, do not work all of the time, with many working one month but not the next. However, these same results imply that the total number of children engaged in work is much larger than the number seen working in any one month. A fuller and better informed view of the intermittent nature of children’s work will lead to better policies and better programmes to combat child labour.
Acknowledgments
This article is based on an earlier working paper, available at: http://www.pop.umn.edu/research/mpc-working-papers-series/2007-working-papers-1. This project was supported by funding from the National Institute of Child Health and Human Development, Grant R01HDHD031214, and the Andrew W. Mellon Foundation. We thank Olga Nieuwenhuys and the other organizers of the International Conference on Rethinking Childhood: Working Children’s Challenge to the Social Sciences (Paris, Nov. 2000) for their suggestions. We also acknowledge the helpful suggestions of three anonymous reviewers. All errors are the responsibility of the authors. Opinions expressed in this article are those of the authors and do not necessarily reflect the views of the United States Government or any of its agencies.
Responsibility for opinions expressed in signed articles rests solely with their authors and publication does not constitute an endorsement by the ILO.
Appendix
PME (Pesquisa Mensal de Emprego) Panel Design
Like many national employment surveys with rotating panel designs, the panel structure of the PME is designed primarily to reduce volatility in estimates of month-to-month and year-to-year changes in unemployment. The survey is not designed explicitly for purposes of analysing longitudinal transitions of individuals. Dwellings, rather than households, are the focus of the sample design, thus households only remain in the sample if they continue to reside in the dwelling that was originally included in the sample. Although public-release versions of the data are not designed for longitudinal analysis, they do contain household identification numbers that make it possible to track households across sample months. Individuals within households must be tracked using month and year of birth, a process that enables relatively straightforward matching for most individuals. We impose a set of filters on matches of both households and individuals across months, using variables such as sex, year of birth, month of birth and education.
Sample attrition
Given that the PME does not directly focus on following households longitudinally, sample attrition is relatively high. As shown in Appendix table A, about 82 per cent of children aged 10 to 16 observed in month 1 of a PME rotation group are also observed in months 2, 3 and 4, which makes them eligible for our analysis of intermittency. While this is relatively high attrition, we also show in the same table that those who remain in the sample differ very little from those who are missing for one or more months. For example, boys observed in all four months have a school enrolment rate of 89.2 per cent and an employment rate of 14.4 per cent in month 1, compared with an enrolment rate of 88.3 per cent and an employment rate of 14.7 per cent for all boys observed in month 1. Similarly, Appendix table A shows that the fraction of children whose mothers have more than four years of schooling is virtually identical in the full sample of children observed in month 1 and in the sample observed in all four months. While there are many reasons to expect non-random attrition in a dwelling-based survey such as this one, a large proportion of the attrition is truly random, because of such causes as sample size and design or incomplete identification numbers. While we can never know how the lost observations would have behaved in terms of changes in employment, it is reassuring that these lost observations were almost indistinguishable from the observations that remained in the sample based on the variables that were observable in month 1. Given the scarcity of panel data from developing countries, we believe the strengths of these employment data - their large sample size, long time-period coverage and detail - far outweigh their weaknesses, and provide a rare look at children’s actual transitions into and out of the labour force.
PME questions on work and school
The employment question in the PME - “O qué fez X na semana passada?” - means “What did X do last week?”, where X refers to each member of the household aged over 10. Typically, a single adult respondent answers the question for all household members. The interviewer reads the possible answers to this question - “worked, didn’t work but had a job, looked for a job, retired, student, domestic work, other” - and stops as soon as the interviewee responds in the affirmative. Thus, under this interviewing method, a child who both worked and went to school should be classified as working since the interviewer reads this option first. School enrolment for each household member is recorded in a separate question unrelated to employment status during the “registration” portion of the interview, along with other non-employment questions such as date of birth, relationship to the head and educational attainment. It is therefore possible to identify children who are both working and going to school.
Measurement error and entry/exit rates
Measurement error obviously affects our estimated entry and exit rates. Owing to a number of measurement reasons, overstatement or understatement of movement into and out of employment may occur. The inaccuracy of reported child employment in one or more months constitutes a problem that may be exacerbated by the fact that the reports are provided by adult respondents, who may differ from month to month. An inaccurate report in one month may lead to “false” transitions into or out of employment across several months. Poterba and Summers (1986) use re-interview surveys to show that reporting errors on employment states in panel data exaggerate the transitions into and out of employment for adults in the United States. Biasing our estimates in the other direction is the fact that we only observe employment in one reference week of each month. Our measures may underestimate movements into and out of the labour force if there are movements in weeks other than the weeks included in the survey. It is not possible to estimate the net effect of these offsetting, potential biases.
Appendix table A.
Evidence on attrition in Brazil PME: Sample means for boys and girls aged 10-16 years present in month 1 and in months 1-4 of PME, 1982-99
| Variable | Children observed in month 1 (1) | Children observed in months 1-4 (2) |
|---|---|---|
| Boys | ||
| Age of child in month 1 | 12.97 | 12.98 |
| Child enrolled in school in month 1 | 88.3% | 89.2% |
| Child working in month 1 | 14.7% | 14.4% |
| Years of schooling for child | 3.97 | 4.01 |
| Fraction of children whose mothers have 4+ years of education in month 1 | 63.5% | 63.5% |
| Sample size | 239,586 | 199,033 |
| Percentage of all those seen in month 1 | 100 | 83.1 |
| Girls | ||
| Age of child in month 1 | 13.01 | 13.00 |
| Child enrolled in school in month 1 | 88.0% | 89.4% |
| Child working in month 1 | 8.2% | 7.6% |
| Years of schooling for child | 4.37 | 4.42 |
| Fraction of children whose mothers have 4+ years of education in month 1 | 64.3% | 63.9% |
| Sample size | 239,340 | 196,683 |
| Percentage of all those seen in month 1 | 100 | 82.2 |
Appendix table B.
| Salvador |
São Paulo |
Porto Alegre |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Age: | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 |
| Boys 1982-84 | |||||||||
| Percentage employed 0 months | 0.67 | 1.12 | 1.18 | 0.41 | 0.87 | 0.91 | 0.51 | 1.01 | 1.10 |
| Average percentage employed each month | 0.55 | 1.15 | 1.52 | 0.35 | 0.93 | 1.40 | 0.46 | 1.17 | 1.64 |
| Low SES2 | 0.69 | 1.45 | 1.90 | 0.40 | 1.09 | 1.64 | 0.58 | 1.41 | 2.00 |
| High SES3 | 0.82 | 1.83 | 2.55 | 0.74 | 1.75 | 2.70 | 0.67 | 2.13 | 2.89 |
| Percentage employed at least 1 month | 0.67 | 1.12 | 1.18 | 0.41 | 0.87 | 0.91 | 0.51 | 1.01 | 1.10 |
| Low SES2 | 0.74 | 1.16 | 1.17 | 0.45 | 0.90 | 0.88 | 0.58 | 1.04 | 1.06 |
| High SES3 | 0.48 | 0.96 | 1.10 | 0.29 | 0.73 | 0.95 | 0.34 | 0.89 | 1.13 |
| Percentage employed 1 month | 2.51 | 2.04 | 1.44 | 2.66 | 1.61 | 0.82 | 3.07 | 1.66 | 1.00 |
| Percentage employed 2 months | 2.04 | 1.73 | 1.32 | 2.23 | 1.37 | 0.82 | 2.73 | 1.56 | 1.04 |
| Percentage employed 3 months | 1.81 | 1.68 | 1.45 | 2.03 | 1.34 | 0.89 | 2.29 | 1.52 | 1.01 |
| Percentage employed 4 months | 1.81 | 1.79 | 1.61 | 2.02 | 1.57 | 1.18 | 2.67 | 2.06 | 1.43 |
| Percentage with 1 transition | 2.46 | 2.06 | 1.60 | 2.65 | 1.66 | 1.00 | 3.10 | 1.84 | 1.24 |
| Percentage with 2 transitions | 2.39 | 1.91 | 1.44 | 2.38 | 1.44 | 0.85 | 2.78 | 1.56 | 0.92 |
| Percentage with 3 transitions | 0.99 | 0.96 | 0.70 | 1.22 | 0.72 | 0.33 | 1.25 | 0.69 | 0.44 |
| Girls 1982-84 | |||||||||
| Percentage employed 0 months | 0.43 | 0.84 | 1.05 | 0.30 | 0.71 | 0.94 | 0.41 | 0.95 | 1.11 |
| Average percentage employed each month | 0.31 | 0.81 | 1.17 | 0.22 | 0.69 | 1.17 | 0.34 | 1.03 | 1.36 |
| Low SES2 | 0.25 | 0.67 | 1.08 | 0.22 | 0.68 | 1.17 | 0.34 | 1.04 | 1.35 |
| High SES3 | 0.22 | 0.65 | 1.04 | 0.20 | 0.67 | 1.14 | 0.31 | 0.95 | 1.35 |
| Percentage employed at least 1 month | 0.43 | 0.84 | 1.05 | 0.30 | 0.71 | 0.94 | 0.41 | 0.95 | 1.11 |
| Low SES2 | 0.57 | 1.08 | 1.40 | 0.39 | 0.88 | 1.13 | 0.57 | 1.25 | 1.42 |
| High SES3 | 0.56 | 0.99 | 1.51 | 0.36 | 0.99 | 1.63 | 0.52 | 1.34 | 1.72 |
| Percentage employed 1 month | 4.05 | 2.84 | 1.99 | 3.87 | 2.22 | 1.22 | 4.15 | 2.25 | 1.59 |
| Percentage employed 2 months | 3.05 | 2.49 | 1.60 | 3.30 | 1.77 | 1.09 | 3.62 | 1.95 | 1.28 |
| Percentage employed 3 months | 2.50 | 2.10 | 1.50 | 2.51 | 1.73 | 1.06 | 3.04 | 1.84 | 1.41 |
| Percentage employed 4 months | 2.89 | 2.67 | 2.17 | 2.67 | 2.05 | 1.48 | 3.20 | 2.53 | 1.91 |
| Percentage with 1 transition | 4.08 | 2.76 | 1.94 | 3.83 | 2.18 | 1.35 | 4.10 | 2.39 | 1.76 |
| Percentage with 2 transitions | 4.01 | 2.79 | 1.84 | 3.68 | 2.07 | 1.06 | 3.77 | 1.95 | 1.35 |
| Percentage with 3 transitions | 0.68 | 0.93 | 0.83 | 1.18 | 0.83 | 0.50 | 1.93 | 0.86 | 0.52 |
This table presents standard errors corresponding to the percentages in table 1. The standard error for a given percentage 100p is calculated as sqrt{p*(1-p)/N}, where N is the sample size. The “average percentage employed each month” in table 1 is calculated as .25*(Percentage employed 1 month) + .5*(Percentage employed 2 months) + .75*(Percentage employed 3 months) + Percentage employed 4 months. Accordingly, the standard errors for this average are calculated as sqrt{.252*Var(Percentage employed 1 month) + .52*Var(Percentage employed 2 months) + .752*Var(Percentage employed 3 months) + Var(Percentage employed 4 months)}.
Children living in households with below-median adult household income.
Children living in households with above-median adult household income.
Appendix table C.
| Salvador |
São Paulo |
Porto Alegre |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Age: | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 | 10-12 | 13-14 | 15-16 |
| Boys (1982-84) | |||||||||
| Percentage employed 0 months | 0.46 | 0.81 | 1.08 | 0.30 | 0.71 | 1.02 | 0.24 | 0.81 | 1.15 |
| Average percentage employed each month | 0.26 | 0.51 | 0.96 | 0.22 | 0.64 | 1.26 | 0.18 | 0.78 | 1.37 |
| Low SES2 | 0.29 | 0.64 | 1.16 | 0.27 | 0.87 | 1.66 | 0.25 | 1.04 | 1.80 |
| High SES3 | 0.53 | 0.76 | 1.68 | 0.37 | 0.95 | 1.93 | 0.24 | 1.18 | 2.11 |
| Percentage employed at least 1 month | 0.46 | 0.81 | 1.08 | 0.30 | 0.71 | 1.02 | 0.24 | 0.81 | 1.15 |
| Low SES2 | 0.49 | 0.86 | 1.11 | 0.33 | 0.75 | 1.03 | 0.23 | 0.88 | 1.18 |
| High SES3 | 0.38 | 0.68 | 0.98 | 0.25 | 0.66 | 1.00 | 0.26 | 0.69 | 1.09 |
| Percentage employed 1 month | 4.39 | 3.23 | 2.11 | 5.27 | 2.82 | 1.37 | 8.60 | 3.24 | 1.71 |
| Percentage employed 2 months | 3.93 | 2.81 | 1.90 | 4.38 | 2.54 | 1.12 | 5.68 | 2.97 | 1.51 |
| Percentage employed 3 months | 2.55 | 2.19 | 1.70 | 3.45 | 2.13 | 1.22 | 6.71 | 2.52 | 1.45 |
| Percentage employed 4 months | 1.93 | 1.38 | 1.39 | 3.58 | 2.39 | 1.61 | 5.68 | 3.17 | 1.97 |
| Percentage with 1 transition | 4.34 | 3.26 | 2.11 | 5.27 | 2.86 | 1.48 | 8.37 | 3.34 | 1.84 |
| Percentage with 2 transitions | 4.44 | 3.16 | 2.00 | 4.60 | 2.56 | 1.27 | 8.70 | 2.99 | 1.54 |
| Percentage with 3 transitions | 2.66 | 1.74 | 1.09 | 2.41 | 1.15 | 0.44 | 0.00 | 1.50 | 0.65 |
| Girls (1982-84) | |||||||||
| Percentage employed 0 months | 0.30 | 0.56 | 0.81 | 0.22 | 0.53 | 0.90 | 0.22 | 0.57 | 1.04 |
| Average percentage employed each month | 0.10 | 0.36 | 0.65 | 0.13 | 0.46 | 0.97 | 0.15 | 0.51 | 1.14 |
| Low SES2 | 0.10 | 0.32 | 0.58 | 0.13 | 0.47 | 0.96 | 0.15 | 0.52 | 1.14 |
| High SES3 | 0.04 | 0.22 | 0.52 | 0.13 | 0.43 | 0.98 | 0.13 | 0.47 | 1.14 |
| Percentage employed at least 1 month | 0.30 | 0.56 | 0.81 | 0.22 | 0.53 | 0.90 | 0.22 | 0.57 | 1.04 |
| Low SES2 | 0.40 | 0.73 | 1.00 | 0.30 | 0.80 | 1.25 | 0.33 | 0.85 | 1.40 |
| High SES3 | 0.43 | 0.75 | 1.26 | 0.31 | 0.67 | 1.28 | 0.27 | 0.70 | 1.57 |
| Percentage employed 1 month | 6.25 | 4.92 | 2.91 | 7.20 | 3.96 | 1.91 | 9.81 | 5.18 | 2.24 |
| Percentage employed 2 months | 5.38 | 4.21 | 2.27 | 5.85 | 3.04 | 1.64 | 8.26 | 2.74 | 2.02 |
| Percentage employed 3 months | 3.99 | 2.60 | 2.09 | 5.30 | 2.75 | 1.66 | 7.73 | 3.35 | 1.89 |
| Percentage employed 4 months | 0.00 | 2.92 | 2.01 | 3.01 | 3.34 | 2.06 | 5.23 | 4.85 | 2.53 |
| Percentage with 1 transition | 7.06 | 4.94 | 2.84 | 7.34 | 3.98 | 2.05 | 9.69 | 4.89 | 2.47 |
| Percentage with 2 transitions | 6.99 | 4.98 | 2.80 | 6.91 | 3.08 | 1.77 | 9.33 | 4.65 | 1.98 |
| Percentage with 3 transitions | 0.00 | 2.77 | 1.32 | 3.01 | 1.25 | 0.57 | 6.27 | 1.07 | 0.46 |
This table presents standard errors corresponding to the percentages in table 2. The standard error for a given percentage 100p is calculated as sqrt{p*(1-p)/N}, where N is the sample size. The “average percentage employed each month” in table 2 is calculated as .25*(Percentage employed 1 month) + .5*(Percentage employed 2 months) + .75*(Percentage employed 3 months) + Percentage employed 4 months. Accordingly, the standard errors for this average are calculated as sqrt{.252*Var(Percentage employed 1 month) + .52*Var(Percentage employed 2 months) + .752*Var(Percentage employed 3 months) + Var(Percentage employed 4 months)}.
Children living in households with below-median adult household income.
Children living in households with above-median adult household income.
Footnotes
See, for example, Reynolds (1991). Boyden, Ling and Myers (1998, p. 162) write that “neglecting children’s work histories and careers can be misleading because the intensity of their work, their work schedules, and their activities and occupations are often quite variable even over short periods of time...Longitudinal research, then, is more likely to provide an accurate picture of the range, schedules, and intensity of work in different seasons or different phases of childhood.”
This calculation is discussed at the end of the article and the calculations are detailed in table 4.
The Brazilian monthly employment surveys used are representative samples of six metropolitan regions in Brazil.
Deininger and Squire’s (1996) compendium of inequality measures shows that in recent decades the level of income inequality in Brazil has been among the highest in the world.
Data issues related to matching across panels and attrition are discussed in the Appendix.
Because of the structure of the overlapping panels, many more households are rotated into the survey in even years than in odd years. To maximize sample sizes, tables focusing on data from the first four interviews do not include 1999 or January 2000.
Some of our results also include metropolitan Rio de Janeiro (with a population of 5.55 million in 1996) and Belo Horizonte (2.09 million), both in the south-east, and the metropolitan area of Recife (1.35 million inhabitants), in the north-east.
Agregados are not clearly defined by any source. Foster children seem to be included in this category, which covers a very small percentage of children.
More information on the PME questions about work and school enrolment is provided in the Appendix.
Disaggregated trends for 14- and 16-year-old boys and girls in Salvador, São Paulo and Porto Alegre can be found in Levison et al. (2007).
Only the income of adults is used in the calculation of household income, in order to help separate the income measure from the child labour decision. In results not shown, we have also used the mother’s education as a proxy for the socio-economic status of the household, classifying children whose mothers have four or more years of schooling as the high SES group. This may be a better measure of long-term household resources, being less sensitive to short-run volatility than is income. Comparisons of children in high and low SES groups when mother’s education is used as the measure of SES lead to results that are very similar to those shown here using per capita household income.
Some of the sample’s month/sex/age groups contain only small numbers of observations, leading to increased variability in the estimates of proportions employed. We use three-month moving averages to smooth this volatility in the remainder of the figures in this article. Thus, the average plotted for March 1996 is the average of February, March and April 1996.
Using 12 years of the annual household survey for Brazil (the Pesquisa Nacional por Amostra de Domicílios, PNAD), Duryea and Arends-Kuenning (2003) demonstrate that employment rates of 14- to 16-year-olds in urban areas increase as local wages increase, after controlling for household income.
Of course, children counted as “never employed” by this measure may have been employed before the four-month period in which they were interviewed, or they may have been employed during weeks other than the four reference weeks during the four-month period.
As can be seen in the Appendix, tables B and C, the standard errors for these estimates are relatively small. For example, the standard error for the estimate of 7.1 per cent employment for boys aged 10 to 12 in Salvador is 0.55 per cent.
We use the term “monthly employment rate” since that is the standard way of reporting employment and unemployment using the PME. Specifically, the “average employment rate” captures whether or not the child was reported to have worked in one reference week of one specific month, while the “recent employment rate” captures whether or not the child was reported to have worked in any of four reference weeks, one in each of four consecutive months.
One notable exception is the similarity of work attachment for 13- to 14-year-olds and 15- to 16-year-olds in Porto Alegre, especially in the later period. This may be due to the dominance of the shoe-making industry in that metropolitan area. We find that children ever-employed in shoe-making have much more stable employment than children in other industries: among the 13- to 14-year-olds, 50 per cent of boys and 42 per cent of girls were employed during all four months between 1996 and 1998, compared with 26 and 31 per cent, respectively, for boys and girls working in other industries. Moreover, among employed 13- to 14- and 15- to 16-year-olds, the proportions with jobs in shoe-making are greater for the younger age group than for the older (for both sexes) in both time periods.
The top ten industries for employed children in Salvador, São Paulo and Porto Alegre can be found in Levison et al. (2007).
Note that these estimates of labour force transitions for adult women also suggest that the high transition rates for children are not simply the result of imprecisely measured employment rates leading to spurious transitions. The employment rates of all household members are presumably measured with error, but transition rates for children are several times higher than those estimated for adults.
For example, in Brazil in 1999, Kassouf (2001) reports that about three times as many 5- to 9-year-olds worked in rural areas as in urban ones. For 10- to 14-year-old boys and girls, 1.5 times as many worked in rural areas as in urban areas.
References
- Anker Richard. The economics of child labour: A framework for measurement. International Labour Review. 2000a;139(3):257–280. [Google Scholar]
- Anker Richard. Conceptual and research framework for the economics of child labour and its elimination; International Programme for the Elimination of Child Labour Working Paper; Geneva, ILO. 2000b. [Google Scholar]
- Barros Ricardo Paes de, Mendonça Rosane, Velazco Tatiana. Economia Brasileira em Perspectiva. Vol. 2. IPEA; Rio de Janeiro: 1996. A pobreza é a principal causa do trabalho infantil no Brasil urbano? pp. 537–563. [Google Scholar]
- Basu Kaushik. Child labor: Cause, consequence, and cure, with remarks on international labor standards. Journal of Economic Literature. 1999 Sep.37(3):1083–1119. [Google Scholar]
- Basu Kaushik, Van PH. The economics of child labor. American Economic Review. 1998 June;88(3):412–427. [Google Scholar]
- Birdsall Nancy, Sabot Richard., editors. Opportunity foregone: Education in Brazil. Inter-American Development Bank; Washington, DC: 1996. [Google Scholar]
- Boyden Jo, Ling Birgitta, Myers William. What works for working children. UNICEF and Rädda Barnen, Save the Children Sweden; Stockholm: 1998. [Google Scholar]
- Boyden Jo, Myers William. Exploring alternative approaches to combating child labour: Case studies from developing countries. UNICEF; Florence: 1995. Innocenti Occasional Papers, Child Rights Series No. 8. [Google Scholar]
- Deininger Klaus, Squire Lyn. A new data set measuring income inequality. The World Bank Economic Review. 1996;10(3):565–591. [Google Scholar]
- Dessy Sylvain F. A defense of compulsory measures against child labor. Journal of Development Economics. 2000;62(1):261–275. [Google Scholar]
- Duryea Suzanne, Arends-Kuenning Mary. School attendance, child labor and local labor markets in urban Brazil. World Development. 2003 July;31(7):1165–1178. [Google Scholar]
- Duryea Suzanne, Lam David, Levison Deborah. Effects of economic shocks on children’s employment and schooling in Brazil. Journal of Development Economics. 2007 Sep.84(1):188–214. doi: 10.1016/j.jdeveco.2006.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duryea Suzanne, Morrison Andrew. The effect of conditional transfers on school performance and child labor: Evidence from an ex-post impact evaluation in Costa Rica. Inter-American Development Bank; Washington, DC: 2004. Research Department Working Paper No. 505. [Google Scholar]
- ILO The end of child labour: Within reach. Global Report under the follow-up to the ILO Declaration on Fundamental Principles and Rights at Work; International Labour Conference; Geneva. 2006; 2006. Report of the Director-General (Report I (B)) 95th Session. [Google Scholar]
- ILO Every child counts: New global estimates on child labour; International Programme on the Elimination of Child Labour; Geneva. 2002. [Google Scholar]
- ILO Child labour: Targeting the intolerable; International Labour Conference; Geneva. 1998; 1996. Report VI (1) 86th Session. [Google Scholar]
- Kassouf Ana Lucia. “Trabalho infantíl” (“Child work”) In: Marcos de Barros Lisboa, Naércio A. Menezes Filho., editors. Microeconomía e sociedade no Brasil. Vol. 1. Editora Contra Capa; Rio de Janeiro: 2001. pp. 117–150. [Google Scholar]
- Knaul Felicia. Young workers, street life and gender: The effect of education and work experience on earnings in Colombia. PhD thesis. Harvard University; Cambridge, MA: 1995. [Google Scholar]
- Lam David, Population Studies Center . Generating extreme inequality: Schooling, earnings and intergenerational transmission of human capital in South Africa and Brazil. University of Michigan; Ann Arbor, MI: 1999. Research Report No. 99-439. [Google Scholar]
- Lam David, Duryea Suzanne. Effects of schooling on fertility, labor supply, and investments in children, with evidence from Brazil. Journal of Human Resources. 1999 Winter;34(1):160–192. [Google Scholar]
- Legovini Arianna, Regalia Ferdinando, Sustainable Development Department . Targeted human development programs: Investing in the next generation. Inter-American Development Bank; Washington, DC: 2001. [accessed 19 Sep. 2007]. Best Practices Working Paper No. Pov-110. Sep. Available online at: http://www.iadb.org/sds/doc/POVTHDP.pdf. [Google Scholar]
- Levison Deborah. Children as economic agents. Feminist Economics. 2000 Spring;6(1):125–134. [Google Scholar]
- Levison Deborah. Children’s labor force activity and schooling in Brazil. PhD dissertation. University of Michigan; Ann Arbor, MI: 1991. [Google Scholar]
- Levison Deborah, Hoek Jasper, Lam David, Duryea Suzanne, Minnesota Population Center . Intermittent child employment and its implications for estimates of child labor. University of Minnesota; Minneapolis, MN: 2007. Working Paper No. 2007-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levison Deborah, Moe Karine, Knaul Felicia. Youth education and work in Mexico. World Development. 2001 Jan.29(1):167–188. [Google Scholar]
- Mortimer Jeylan T. Working and growing up in America. Harvard University Press; Cambridge, MA: 2003. [Google Scholar]
- Mortimer Jeylan T., Kirkpatrick Johnson Monica. New perspectives on adolescent work and the transition to adulthood. In: Richard Jessor., editor. New perspectives on adolescent risk behavior. Cambridge University Press; Cambridge: 1998. pp. 425–496. [Google Scholar]
- Reynolds Pamela. Dance civet cat: Child labour in the Zambezi Valley. Ohio University Press; Athens, OH: 1991. [Google Scholar]
- Poterba James M., Summers Lawrence H. Reporting errors and labor market dynamics. Econometrica. 1986 Nov.54(6):1319–1338. [Google Scholar]
- Yap Yoon-Tien, Sedlacek Guilherme, Orazem Peter F. [accessed 19 Sep. 2007];Limiting child labor through behavior-based income transfers: An experimental evaluation of the PETI Program in rural Brazil. 2001 Feb. updated 2002. Manuscript. Available online at: http://siteresources.worldbank.org/INTISPMA/Resources/383704-1153333441931/11375_orazem-peti-brazil.pdf.