Structure of Flexible Filamentous Plant Viruses

Abstract

Flexible filamentous viruses make up a large fraction of the known plant viruses, but in comparison with those of other viruses, very little is known about their structures. We have used fiber diffraction, cryo-electron microscopy, and scanning transmission electron microscopy to determine the symmetry of a potyvirus, soybean mosaic virus; to confirm the symmetry of a potexvirus, potato virus X; and to determine the low-resolution structures of both viruses. We conclude that these viruses and, by implication, most or all flexible filamentous plant viruses share a common coat protein fold and helical symmetry, with slightly less than 9 subunits per helical turn.

Flexible filamentous plant viruses include at least 19 recognized genera (22), almost all in three families of single-stranded, positive-sense RNA viruses, the Potyviridae, the Flexiviridae, and the Closteroviridae. Members of the family Potyviridae account for almost a third of the total known plant virus species (22) and are responsible for more than half the viral crop damage in the world (37), infecting most economically important crops (32). Members of the family Flexiviridae (2), and particularly of the large genus Potexvirus, are also of considerable significance to agriculture (42). Both families show great potential for biotechnological applications, including protein expression and vaccine production (12, 54). Despite their importance, however, little is known about the structures of any of the flexible filamentous plant viruses, in sharp contrast to the amount of data on the rigid tobamoviruses (48, 63) or the icosahedral plant viruses (15); flexibility, instability, and in many cases low levels of expression have made these viruses particularly intractable to structural studies. Structural and evolutionary relationships among the flexible filamentous plant viruses have been suggested (18, 47, 56, 60), but there is very little sequence homology between the coat proteins of viruses in the different families, and there has hitherto been no structural support for such relationships at the level of either viral symmetry or coat protein folding. Indeed, reports of viral symmetry until now appeared to contradict hypotheses of evolutionary relationships.

Soybean mosaic virus (SMV) is a potyvirus, that is, a member of the genus Potyvirus, the largest genus in the family Potyviridae (3). SMV is a major pathogen of soybeans, transmitted efficiently through seed and by aphids in a nonpersistent manner; yield losses as high as 35% have been reported (30). Despite dramatic morphological differences, members of the family resemble the icosahedral plant comoviruses and animal picornaviruses in genomic organization and replication strategy (32). Early electron microscopic observations found the potyviruses to be about 7,500 Å long and 120 Å in diameter, with helical pitches of about 34 Å (44, 60). A fiber diffraction study (51) of the tritimovirus wheat streak mosaic virus (WSMV) suggested that WSMV has 6.9 subunits per turn of the viral helix, but there was considerable ambiguity about that symmetry determination, which was made from a very poorly oriented sample. Almost nothing is known about the three-dimensional structures of members of the family at the atomic or even at the subunit level.

Potato virus X (PVX) is the type member of the genus Potexvirus. Virions of potexviruses are flexous rods, 4,700 to 5,800 Å long and about 130 Å in diameter (58). As early as the 1930s, Bernal and Fankuchen (8) used fiber diffraction methods to determine the helical pitch of PVX to be approximately 33 Å. All potexviruses are believed to share a common architecture, with slightly less than 9 protein subunits per helical turn (55). More-precise fiber diffraction studies (52) found the helical symmetry of PVX to be 8.9 protein subunits per turn and the helical pitch to be 34.5 Å. The virion was shown to have a deeply grooved surface. Fourier transform infrared spectroscopy studies of PVX suggest that the virion surface is highly hydrated and that the bound water molecules help to maintain the surface structure of the virion (6). Spectroscopic studies show that coat proteins of potexviruses and potyviruses have similarly high α-helical contents (5, 31).

We have obtained well-oriented fiber diffraction data from SMV. These data have enabled us to determine a radial density distribution for the virus and, together with data from scanning transmission electron microscopy (STEM) and cryo-electron microscopy (cryo-EM), to determine the viral symmetry. Cryo-EM data, interpreted using constraints from fiber diffraction, have allowed us to determine the virus structure, providing the first reconstructed image of a potyvirus showing subunit shape and arrangement at any resolution. For comparison, we have determined the structure of PVX at a comparable resolution and confirmed the PVX symmetry. Both the symmetries and the structures strongly indicate a relationship between the two families.

MATERIALS AND METHODS

Virus purification.

SMV strains G6 and G7 (16) were purified as previously described (11). The ratios of the optical densities at 260 and 280 nm were close to 1.2, confirming that coat protein and RNA were present in the expected ratios. Purified virus was stored at 4°C in 50 mM sodium phosphate, pH 7.6. Most experiments were carried out using the G7 strain, but fiber diffraction experiments used both strains, and because of the better orientation and higher quality of the diffraction data, data from the G6 strain were used in the analysis. The coat proteins of the two strains differ at only 3 amino acid residues (33), and the substitutions are all conservative and within 20 residues of the N terminus, known to be located at the outer surface of the virion and probably disordered (5, 56). PVX was purified and stored as previously described (52).

Fiber diffraction.

Dried fibers of SMV were prepared by suspending a 5-μl drop of virus solution (up to 40 mg/ml in concentration) between two glass rods ∼1.5 mm apart and allowing it to dry over a period of hours to days. Humidity control was essential during drying; even brief exposure to low humidity dramatically reduced order in the fibers. Fibers were made in closed chambers (46) in the presence of either saturated potassium sulfate or saturated sodium tartrate solution, producing 97% or 92% relative humidity, respectively.

Fiber diffraction data were collected at the BioCAT beam line of the Advanced Photon Source synchrotron, Argonne National Laboratory. Fibers were dusted with calcite, and wide-angle specimen-to-detector distances were determined from the 104 calcite diffraction ring at a 3.0355-Å resolution (19). Low-angle specimen-to-detector distances were determined by measuring diffraction patterns from tobacco mosaic virus (TMV) (35). Wide-angle (to about 4-Å resolution) and low-angle (to a lowest resolution of about 130 Å) data were collected and scaled together (34).

Diffraction patterns were analyzed using the program WCEN (9) to determine experimental parameters and the helical repeat, to apply corrections to the intensities, and to transform the data from detector to reciprocal space. Equatorial amplitudes were determined by the method of angular deconvolution (41, 49).

Radial density distributions were determined by applying a Fourier-Bessel transform to the equatorial data (14). This calculation requires that signs be applied to the diffraction data; these signs are not directly obtainable from the data. Signs were determined by the minimum-wavelength principle (10), assuming the radius determined by electron microscopy. The radius is not critical; in most cases, including that of SMV, large errors in the radius will have no effect on the sign determination. Essentially, the principle states that for a structure of a given linear dimension (in fiber diffraction, the particle radius), the Fourier transform (the Fourier-Bessel transform in fiber diffraction) cannot oscillate at a frequency higher than that calculated. In consequence, diffracted amplitude maxima that are sufficiently close together must have alternating signs. The minimum-wavelength principle was used by Caspar (13) in TMV studies, and the signs determined for TMV were subsequently shown by isomorphous replacement to be correct (26, 48).

Electron microscopy.

Cryo-EM grids were prepared by applying ∼3 μl of samples to 2/2 C-flat grids (ProtoChips Inc.). The excess liquid from the droplet was manually blotted away with filter paper, and the sample grid was immediately plunged into liquid ethane cooled by liquid nitrogen, using a homemade vitrification device. Cryo-EM images were collected using an FEI Tecnai 12 (120-kV) electron microscope equipped with a Gatan cryo holder and a Gatan UltraScan 1000 (2Kx2K) charge-coupled-device camera at a nominal magnification of ×67,000 (1.47 Å/pixel). The defocus values of the micrographs were determined using the program CTFIT from the EMAN program suite (40), and these values were used to correct for the phase component of the contrast transfer function by phase flipping (24). A low-pass filter that truncated the data at 7 Å was also applied.

Three-dimensional reconstruction of virion images from cryo-electron micrographs used iterative helical real-space reconstruction (IHRSR) (20, 21). The virions are well suited to helical reconstruction, being homogeneous and regular in structure. IHRSR, which is based on single-particle reconstruction methods, appears to be the most effective method of reconstruction for these viruses; the flexibility of the viral filaments makes Fourier-Bessel methods, which require straight particles with a high degree of order over long distances in the filament, less useful. Segments of virions were selected using the program BOXER, also from the EMAN suite; these segments were then used in IHRSR reconstructions using the SPIDER software package (25). Models were constrained to have minimum radii of 15 Å (based on the radial density distributions from fiber diffraction) and maximum radii at least 5 Å greater than maxima from the radial density distributions. The resolution of the final reconstructions was determined by Fourier shell correlation (29) of randomly generated half sets of the data, using a threshold value of 0.5. UCSF Chimera (53) was used to generate models and density maps.

For electron microscopy phase determination, particles were selected and processed using the Straighten algorithm (36), a part of the ImageJ software package (1). Diffraction patterns (Fig. 1) were calculated from selected filament segments, and the phase differences between symmetrically equivalent points in the first intensity peak on the first layer line were determined. Only patterns including clear, symmetric first-layer line intensities were used.

FIG. 1.

Example of a calculated diffraction pattern from a segment of SMV in a cryo-electron micrograph. The arrow indicates the first intensity peak in the first layer line. The position of this layer line corresponds to a spacing of about 165 Å; near-meridional layer lines corresponding to a spacing of 33 Å are also clearly visible. For phases to be used in symmetry determination, the first-layer-line intensities in the four quadrants were required to be clearly visible and symmetric in position and appearance.

STEM.

STEM was used to determine the mass per unit length of the SMV virions. Grids for STEM were prepared by the wet-film technique (61, 62). Briefly, titanium grids coated with a thick, holey film were placed on a floating thin carbon film prepared by ultrahigh vacuum evaporation onto freshly cleaved rock salt, picked up one at a time so that a thin layer of liquid was retained, and washed extensively. TMV was allowed to adsorb to the carbon film for 1 min. After further washings, the sample was allowed to adsorb for 1 min. After additional washes, the grid was blotted to a very thin layer of liquid, plunged into liquid nitrogen slush, transferred to an ion-pumped freeze drier, freeze dried overnight, and transferred under vacuum to the microscope. Images were analyzed using the PCMass software available from the Brookhaven STEM website (www.biology.bnl.gov/stem/stem.html). Mass-per-unit-length measurements were calibrated against measurements from the TMV internal standard.

Mass spectrometry.

Samples were mixed on-target with matrix containing 40 mg/ml ferulic acid in 60% acetonitrile, 0.1% trifluoroacetic acid, and subjected to matrix-assisted laser desorption/ionization-time-of-flight mass spectrometry using an Applied Biosystems Voyager DE-STR mass spectrometer. Data were acquired with delayed extraction (150 ns) in positive-ion mode (accelerating voltage, 25,000 V; grid voltage, 95%), using the linear geometry. Masses were externally calibrated using a protein standard mixture consisting of insulin, cytochrome c, apomyoglobin, aldolase, and albumin.

SDS-PAGE.

SMV coat protein was separated by sodium dodecyl sulfate-polyacrylamide gel electrophoresis (SDS-PAGE) using an 18% polyacrylamide gel and visualized by Coomassie blue staining. Gel analysis was performed with Bio-Rad Quantity One software, version 4.6.3.

RESULTS

Helical symmetry.

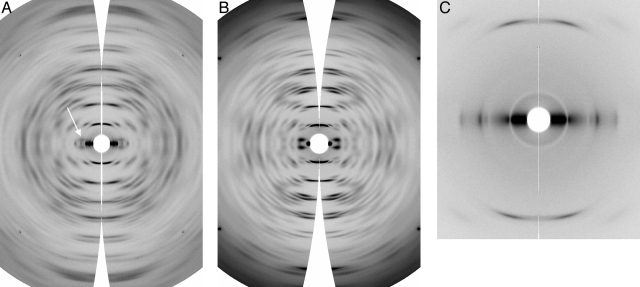
Fiber diffraction patterns from the G6 strain of SMV are shown in Fig. 2A and C. The patterns are well ordered, with disorientations of about 5° and data extending to resolutions of 4 Å or better. For comparison, a diffraction pattern from the potexvirus Narcissus mosaic virus (NMV) (34) is also shown (Fig. 2B). The patterns show that the fibers are noncrystalline, with continuous diffraction along layer lines. The noncrystallinity is confirmed by the absence of crystalline reflections in the low-angle diffraction pattern (Fig. 2C).

FIG. 2.

(A) and (B) Wide-angle fiber diffraction patterns from the potyvirus SMV (A) and the potexvirus NMV (B), with intensities corrected and data transformed into reciprocal space. The arrow in panel A indicates the first layer line. (C) Low-angle data from SMV, corrected and transformed.

The SMV diffraction patterns are characterized by a series of equally spaced near-meridional layer lines (seven are visible in Fig. 2A, and one is visible in Fig. 2C), whose spacing corresponds to a helical pitch p of 33.0 ± 0.2 Å. Numerous other layer lines are also present; the first (Fig. 2A) is at a reciprocal spacing of (0.2 ± 0.02)/p, corresponding to five times the helical pitch. All of the layer lines can be indexed using this spacing. If the number of subunits per turn of the viral helix (u) is u_i plus Δu, where u_i is an integer and Δu is between 0 and 1, these layer line spacings imply that Δu is 0.2 ± 0.02 or 0.8 ± 0.02. From the positions of the first maxima on the higher-order layer lines, it is immediately evident that Δu must be 0.8 rather than 0.2; this conclusion is particularly supported by the strength of the 19th and 24th layer lines near the meridian, making obvious pairs with the 20th and 25th layer lines (the crossover point in the characteristic “X” shape of helical diffraction). If Δu were 0.2, these pairs would include the 21st and 26th layer lines rather than the 19th and 24th (14, 34). Since the crossover is close to the fourth and fifth near-meridional layer lines, it follows from the selection rule for helical diffraction and the properties of Bessel functions (14, 17) that the integer u_i is close to 8.

More information about u_i can be obtained from diffraction patterns calculated from cryo-EM images (Fig. 1). The order of the Bessel function contributing to the first layer line in a diffraction pattern is the integer nearest to the number of subunits in each turn of the diffracting helix (14, 17). Its parity can be determined by measuring the phase difference between equivalent points in the first intensity maximum on opposite sides of the meridian. In the absence of noise, a phase difference of 0° implies that the Bessel order is even; 180° implies that it is odd.

Phase differences between equivalent points in a given diffraction pattern were measured for an average of 14 separate points within the prominent first intensity peak on the first layer line in each of five diffraction patterns from separate images of SMV. For every point, the difference was greater than 90°; only three points had phase differences less than 120°, and the mean phase difference for each image was greater than 145°. The overall mean phase difference was 155°. For PVX, the overall mean phase difference from 10 points in each of 10 diffraction patterns was 151°. The observed differences clearly indicate that for both viruses, the number of subunits per helical turn is closest to an odd integer. In the case of PVX, this confirms previous determinations of potexvirus symmetry as a little less than 9 subunits per turn (52, 55), although it is not consistent with the most recent determination (34) of the symmetry of NMV. The direct measurements from cryo-EM are unambiguous, whereas symmetry determination from fiber diffraction data alone can be very difficult, so it is most likely that the symmetry of NMV is 8.8 subunits per turn, close to the PVX symmetry of 8.9 subunits per turn.

An independent determination of helical symmetry is available from STEM measurements. Fiber diffraction and STEM are complementary experimental approaches; fiber diffraction leaves some ambiguity in the value of u_i but can determine Δu very precisely and accurately. STEM, in contrast, is not as precise but provides an unambiguous estimate of u. STEM calculations require an accurate estimate of molecular mass. From mass spectrometry, the dominant protein subunit mass was found to be 29,749 ± 43 Da. This mass is slightly smaller than the intact subunit molecular mass of 29,859 Da (33), suggesting that approximately one amino acid had been proteolytically removed. SDS-PAGE analysis of SMV (Fig. 3) showed that most of the protein was in a single band at approximately the mass of the intact protein. Minor bands were seen at about 92% and 88% of the major-band mass; these bands were estimated to contain 10.6% and 2.1% of the visualized protein, respectively. From these data, we estimate that the average subunit molecular weight is 98.9% of the major-band molecular mass. This percentage should be taken as a maximum value, since it does not consider smaller degradation products whose bands are too weak to observe, and it does not consider the possibility that the strongest SDS-PAGE band includes not only the dominant molecular species but also slightly smaller degradation products. We assume from the RNA sequence (GenBank accession no. AY216010) and the virion length that each protein subunit binds five nucleotides. For STEM analysis, the mass of one subunit was therefore taken to be 31,027 Da (98.9% of 29,749), with five nucleotides with an average molecular mass of 321 Da.

FIG. 3.

SDS-PAGE from SMV. Two bands from degradation products of SMV coat protein are clearly visible.

Mass per unit length was determined from STEM measurements of 735 segments of SMV particles to be 7880 ± 400 Da/Å. From this value, the subunit mass, and the helical pitch of 33.0 Å, u was determined to be 8.38 ± 0.5 subunits per turn of the viral helix. The helical pitch was taken from the fiber diffraction measurement because uncertainties in the calibration of the fiber diffraction measurements are much lower than those of the cryo-EM measurements, although it is possible that the pitch changed slightly under cryo-EM conditions. The value of 8.38 is probably a low estimate of u because of the effect of protein degradation on the average subunit molecular mass, so the STEM results strongly support the value of 8.8 for u.

This symmetry differs from the reported symmetry of another member of the family Potyviridae, WSMV (51), but the WSMV symmetry was determined using an almost completely disoriented fiber diffraction sample and was acknowledged at the time to be uncertain. The symmetry is in surprisingly good agreement with early estimates of 7 to 9, based solely on sedimentation coefficients of the coat protein (27, 45). By analogy with the observations reported here, we may conclude that all members of the family Potyviridae have slightly less than 9 subunits per turn of the viral helix.

Virus structures.

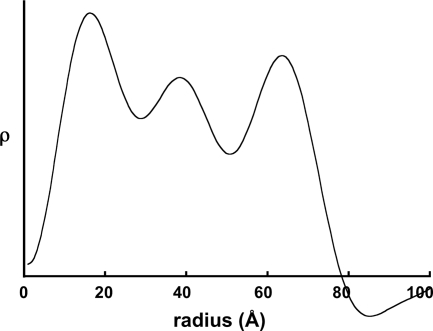
A radial density distribution for SMV at a resolution of 22 Å is shown in Fig. 4. This distribution was determined by the minimum-wavelength principle (10), using data from the low-angle diffraction pattern (Fig. 2C) at resolutions between 110 Å and 65 Å and the wide-angle pattern (Fig. 2A) at resolutions between 65 Å and 22 Å. The origin peak (data inside the equatorial node at 110 Å) was calculated from a solid cylinder, scaled in amplitude to the low-angle amplitudes and radially to the first node position (26, 34). The positions of the peaks in the distribution are probably influenced by series termination error; they remain even when very large temperature factors are imposed upon the equatorial amplitudes, but their positions depend on the resolution of the input data. The maximum and minimum radii, however, appear to be well determined.

FIG. 4.

Radial density distribution in SMV. Units of electron density (ρ) are arbitrary.

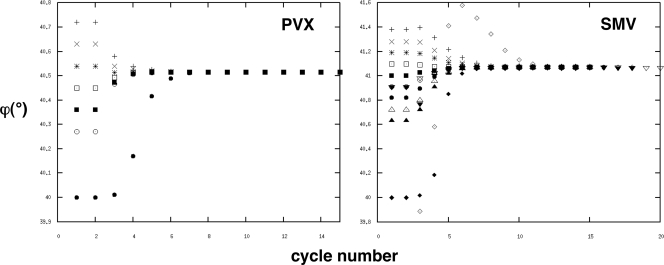
For IHRSR, 18,458 virion segments were selected from the SMV micrographs and 9,982 segments from PVX. Fewer segments of PVX were needed for analyses at a comparable resolution, perhaps because the PVX virions are better ordered than those of the more flexible SMV. For SMV reconstructions, data from 80 micrographs at defocus values between 0.31 and 1.31 μm were used. For PVX, 132 micrographs were used, with defocus values between 1.09 and 1.74 μm. Initial models were usually featureless cylinders (21) but also included completely unrelated structures (64). Reconstructions were started from many different initial symmetries and allowed to continue until convergence was achieved. Regardless of the initial model, the final refined symmetries converged to the same point (Fig. 5) and the refined models were indistinguishable in appearance.

FIG. 5.

Convergence of the rotation angle ϕ as a function of cycle number during IHRSR. Refinements were started from many different rotation angles; provided that the angle was not too far from the final refined angle (21), they all converged to the same value. Most of the refinements used solid cylinders as initial reference volumes, but for SMV, arbitrary unrelated density distributions (solid inverted triangles, open diamonds, and solid diamonds) were also used.

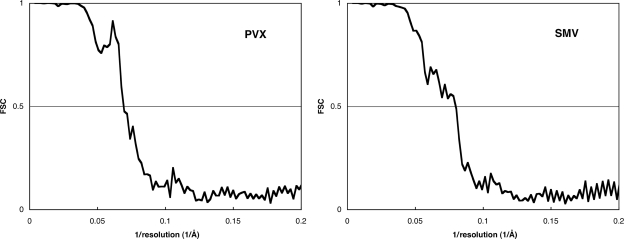
SMV reconstructions that were started with symmetries between 8.7 and 9.0 subunits per turn all converged to a symmetry of 8.77 subunits per turn (Fig. 5). This value differs from the fiber diffraction value by slightly more than the experimental error and may reflect a real difference in symmetry under different conditions. The difference is not, however, sufficiently large to affect conclusions about the virus structure. SMV reconstructions started with symmetries close to 7.8 or 9.8 subunits per turn were not stable, providing further support for the conclusion that u is close to an odd number. Reconstructions started close to the correct symmetry are expected to converge to that symmetry (21). PVX reconstructions started with symmetries between 8.84 and 9.0 subunits per turn converged to 8.89 subunits per turn, consistent with previous determinations (52, 55). Fourier shell correlation plots (29) (Fig. 6) suggest that the resolutions of both the SMV and PVX reconstructions are about 14 Å. The refined models are shown in Fig. 7, together with typical particle images of SMV and PVX.

FIG. 6.

Fourier shell correlation plots for the refined PVX and SMV models. In both cases, the correlations fall below 0.5 at a resolution of about 1/14 Å.

FIG. 7.

(A) Cryo-electron micrograph of SMV with contrast reversed. Scale bar, 250 Å. (B) IHRSR reconstruction of SMV, section normal to viral axis. Scale bar (also applies to panels C and D), 50 Å. (C) IHRSR reconstruction of SMV, outside surface view. (D) IHRSR reconstruction of SMV, section through viral axis. (E) Cryo-electron micrograph of PVX with contrast reversed. Scale bar, 250 Å. (F) IHRSR reconstruction of PVX, section normal to viral axis. Scale bar (also applies to panels G and H), 50 Å. (G) IHRSR reconstruction of PVX, outside surface view. (H) IHRSR reconstruction of PVX, section through viral axis. Color coding in panels B, C, D, F, G, and H is from red-orange (low density) to green-blue (high density).

The radial density distribution of SMV (Fig. 4) suggests that the virion has a central hole of radius about 15 Å, slightly smaller than the central holes of tobamoviruses (48) and potexviruses (34). The minimum radius is not clear from the cryo-EM reconstructions; the density maps are noisy at a very low radius. The maximum radius from both the radial density distribution and the cryo-EM reconstruction (Fig. 7B and C) is about 70 Å, greater than most, although not all, previously reported potyviral radii (37). Previous reports have been based on negative-stain electron microscopy, and it is likely that negative stain would penetrate the outer surface of the virus, leading to underestimates of the radius.

The maximum radius of PVX from the cryo-EM reconstruction (Fig. 7F and G) is about 65 Å, consistent with earlier estimates (52).

The protein subunits in both the SMV and the PVX reconstructions from cryo-EM (Fig. 7B, D, F, and H) are compact and well defined, with a major domain at high radius in the virion and smaller regions of density reaching into the viral center. The subunits have their longest dimensions running approximately radially, reminiscent of the TMV protein subunits (48) but much shorter and wider. The SMV subunits are about 55 Å long, 35 Å wide at the widest (high-radius contact) point, and 33 Å in the axial direction. The PVX subunits have similar azimuthal and axial dimensions but are only about 45 Å long. In both viruses, axial intersubunit contacts are almost entirely confined to the high-radius region of the structure. Azimuthal contacts extend more to low radii but are still predominantly at high radii. The viral structures are very open at low radius (Fig. 7D and H), consistent with flexibility.

The viral RNA is not expected to be distinguishable from the adjacent protein at this resolution. If there are five nucleotides bound to each protein subunit, and if the RNA chain is extended to about the degree found in TMV, we would expect it to be located at a radius of about 30 to 35 Å in both viruses, close to the middle of the protein subunit and at a slightly lower radius than the major high-radius density. The density in this region (Fig. 7B and F) is consistent with such a location for the RNA, but it would be inappropriate to draw any firm conclusions about RNA structure at the resolution of these reconstructions.

DISCUSSION

Structure determination of filamentous viruses.

In recent decades, there has been great progress in determining icosahedral virus structures. Studies of filamentous viruses, however, with the exception of the rigid tobamoviruses (63) and the filamentous bacteriophages (43), have made little progress. A hybrid methodological approach to structure determination such as we have described here appears to offer at least a partial solution to this problem. The combination of cryo-EM and X-ray fiber diffraction, supplemented by information from other sources, has allowed us to determine viral symmetries and begin the process of three-dimensional structure determination. Reconstruction from cryo-EM data has the potential to provide even higher-resolution models, which will be invaluable for phasing and eventually exploiting the full potential of the fiber diffraction data.

Structures of SMV and PVX.

We have determined the helical symmetry of SMV to be 8.8 subunits per turn; by implication, potyviruses in general are expected to have a little less than 9 subunits per helical turn. We have also confirmed that PVX has 8.9 subunits per turn. SMV and PVX have diameters of 140 Å and 130 Å, respectively, and share an open architecture, consistent with viral flexibility. The viruses have very similar density distributions at low resolution, but there are a number of small but significant differences.

The most distinct structural differences between the two viruses are near the outer surfaces of the virions, where the grooves in the SMV surface are shallower, the virion diameter is greater, and there is a distinct curvature in the shape of the subunit by comparison with the PVX subunit. The outer surface is the location of the N terminus of the coat protein (5, 7, 56), the region known to be involved in vector transmission of potyviruses (4, 37). The structural differences are therefore consistent with functional differences in this part of the virion.

Several groups have attempted to predict three-dimensional structures for both potex- and potyviral coat proteins (5, 50, 56). The predicted structures are variations and extensions of the four-helix bundle structure of TMV (48), consistent with the high α-helical content of the proteins and the known location of the N and C termini (5, 7, 56). The most detailed models (5, 50) consist of two domains, an inner four-helix bundle and an outer α/β domain, with extra β strands in the larger potyviruses. Although these models are similar in shape to the subunits that we observe, their lengths appear to be at least 70 Å, significantly too large to fit the observed dimensions of the virions or the subunits.

Structural relationships among filamentous plant viruses.

The SMV diffraction pattern is very similar to the PVX diffraction pattern (52) and remarkably similar to that of NMV (34), with similar intensity distributions extending to the limits of the patterns at a resolution of about 4 Å (Fig. 2). The striking similarities between potexvirus and potyvirus symmetry, low-resolution structural models, and higher-resolution fiber diffraction data provide direct evidence for a structural relationship between the coat proteins of members of the families Flexiviridae and Potyviridae.

It is reasonable to speculate that most or all flexible filamentous plant viruses are structurally related. We note that the helical pitches reported for the closteroviruses (59) and confirmed by our own unpublished results are similar to those of the potexviruses and potyviruses. A similar speculation can be applied to rigid, rod-shaped plant viruses, although there is little or no evidence that the flexible viruses and the rigid viruses have the same coat protein fold (18, 60). One apparent exception to these predictions might be the very different reported helical symmetries of the rigid tobamoviruses and tobraviruses (23, 28). However, reports of the tobravirus symmetry (about 25 subunits per turn) all appear to depend on a single early electron microscopic observation, whereas stoichiometric calculations similar to those that have been used for the potexviruses (38) and potyviruses (51) suggest that the tobraviruses have only about 16 subunits per turn, similar to the tobamoviruses. The existence of a common protein fold will greatly facilitate the design of modified coat proteins for use in peptide expression (12, 54) and conferral of resistance on hosts (39, 57) and has important implications for the taxonomy, evolution, and further structural study of filamentous viruses.