Abstract
To shed light on the driving force for the hydrophobic effect that partitions amphiphilic lipoproteins between water and membrane, we carried out an atomically detailed thermodynamic analysis of a triply lipid modified H-ras heptapeptide anchor (ANCH) in water and in a DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) bilayer. Combining molecular mechanical and continuum solvent approaches with an improved technique for solute entropy calculation, we obtained an overall transfer free energy of ∼−13 kcal mol−1. This value is in qualitative agreement with free energy changes derived from a potential of mean force calculation and indirect experimental observations. Changes in free energies of solvation and ANCH conformational reorganization are unfavorable, whereas ANCH-DMPC interactions—especially van der Waals—favor insertion. These results are consistent with an enthalpy-driven hydrophobic effect, in accord with earlier calorimetric data on the membrane partition of other amphiphiles. Furthermore, structural and entropic analysis of molecular dynamics-generated ensembles suggests that conformational selection may play a hitherto unappreciated role in membrane insertion of lipid-modified peptides and proteins.
INTRODUCTION
Transfer of nonpolar (hydrophobic or water-hating) compounds into lipid membranes is usually ascribed to the hydrophobic effect. The driving force for the hydrophobic effect is assumed to be entropic in origin (1). This is because the entropy change, ΔS, associated with the transfer of small nonpolar molecules such as benzene and hexane from the pure phase to water is large and negative at room temperature; the corresponding enthalpy, ΔH, is approximately zero or only slightly negative. The conventional molecular interpretation of this observation is that insertion of nonpolar molecules in water perturbs the hydrogen-bonding pattern of the surrounding water molecules. In the absence of water-solute interactions to compensate for this effect, stronger interaction among water molecules around the solute causes ordering into so-called “clathrates” (1), “icebergs” (2), or “flickering clusters” (3). The release and reorganization of these ordered water molecules upon the transfer of the solute to the pure phase explains the entropic origin of the hydrophobic effect (1). This transfer process is also characterized by a strong temperature dependence of the heat capacity change (ΔCp), which can be explained by the consumption of heat to “melt” the iceberg. Similarly, the connection between the formation of interfaces (such as water-membrane) and the hydrophobic effect for large solutes has been described by the displacement of water molecules away from nonpolar solute surfaces (4) or dewetting (5).
Partitioning of purely hydrophobic molecules into model or biological membranes is consistent with this “classical” picture of the hydrophobic effect, namely, solvent effects drive insertion. Indeed, the transfer of a series of hydrophobic tripeptides to lipid membrane is associated with large positive (favorable) entropy and (nearly) zero enthalpy (6). In contrast, the transfer of amphiphilic molecules from aqueous phase to lipid membrane can be either enthalpy or entropy driven. For instance, although entropy dominates the membrane transfer free energy of the positively charged local anesthetic dibucaine, the same calorimetric experiments found enthalpy-driven hydrophobic effects for the potential-sensitive dye 2-(p-toluidinyl)naphthalene-6-sulfonate, the membrane conductivity inducing anion tetraphenylborate, and the Ca2+ channel blocker amlodipine (7).
These data demonstrate that the driving force for the hydrophobic effect responsible for the partition of amphiphilic compounds between water and membrane cannot be generalized as arising from solvent reorganization. Enthalpy-driven hydrophobic effects have also been found in drug-protein associations (8). The conventional interpretation of the hydrophobic effect is further complicated by the difficulty of distinguishing between solute and solvent effects. First, the van der Waals (vdW) attraction energy between apolar molecules in the liquid phase can mask the hydration enthalpy (9). For example, whereas the overall room temperature enthalpy associated with the transfer of a benzene molecule to water is close to zero, the vdW interaction energy measured by the heat of vaporization is positive (∼+6 kcal mol−1), suggesting a negative hydration enthalpy (10). Second, it has long been appreciated that the solvent and solute contributions to entropy are hard to separate by experimental procedures (8,11) or by common computational techniques (12). In fact, the assignment of the entropy of transfer to water reorganization alone is valid only when the solute reorganization is negligible, which is typically not the case.
To shed light on these issues, we explicitly calculated the solute- and solvent-related contributions to the free energy of transfer (or insertion) of an amphiphilic lipopeptide into a 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) bilayer. A triply lipid-modified heptapeptide representing the H-ras membrane anchor (ANCH) was used as a model system. H-ras belongs to the family of Ras GTPases that are crucial regulators of cellular signaling. They mediate cell proliferation, development, and apoptosis when bound to membranes, especially the inner leaflet of the plasma membrane. Membrane targeting is achieved through posttranslational lipid-modification(s) (13). In H-ras, this involves farnesylation (modeled here by a hexadecyl group, HD) at the C-terminal CaaX signal (a usually represents aliphatic and X any amino acid) followed by palmitoylation (Palm) of two adjacent cysteine residues (Fig. 1). The distribution of the polar and charged side chains (Ser-183 and Lys-185) relative to the nonpolar Met-182 and the lipid-modified groups (Palm181, Palm184, and HD186) gives ANCH an amphiphilic character. However, the flexibility of its long lipid tails and lack of a defined geometry in solution makes ANCH unique when compared with common membrane-binding amphiphilic motifs, such as α-helices (14), Trp-containing peptides ((15) and references therein), and ring-carrying hydrophobic ions (7).
FIGURE 1.
Structure of ANCH in water (state 1 = s1, left) and in a DMPC bilayer (state 2 = s2, right). The models represent the centers of the first clusters from simulations s1 and s2 (see text). Carbon (green), oxygen (red), nitrogen (blue), and sulfur (yellow).
ANCH is an interesting system both in itself and as a model for studying the driving force of the hydrophobic effect for (lipo)peptide membrane partitioning. First, a detailed understanding of its membrane insertion thermodynamics is biologically and pharmacologically important with implications for cancer therapy. Second, its moderate size allows an extensive sampling of configurational space by computer simulations. Third, the structure and dynamics of membrane-bound ANCH, as well as the mechanism of insertion and the associated potential of mean force (PMF), have already been characterized in detail (16–18). Substantial experimental information is also available (19–21). Furthermore, the nonconventional structure and unique amphiphilicity of ANCH provide a fresh perspective into an old problem.
We used molecular dynamics (MD) simulations to generate structural ensembles of ANCH in water and in a DMPC bilayer. These ensembles were used to evaluate thermodynamic quantities. Solute configurational entropy was evaluated by a complete quasiharmonic analysis corrected for anharmonicities and pairwise correlations and external entropies by a probability distribution approach. Internal and solvation energies were estimated by molecular mechanical and continuum solvation models. We found that the hydrophobic effect responsible for the water-to-membrane transfer of ANCH is enthalpy driven. Furthermore, a combined structural and entropic analysis of ANCH suggests that conformational selection may play a significant role in membrane binding.
METHODS
The equilibrium distribution of ANCH at temperature T (310 K in this work) between water and membrane can be described by the insertion free energy, 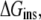 (Eq. 1),
(Eq. 1),
 |
(1) |
Changes in enthalpy (ΔH) and entropy (ΔS) arise from changes in interaction and reorganization of atoms within and between the heptapeptide ANCH, p, membrane, m, and water, w (Eq. 2).
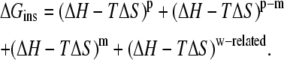 |
(2) |
Each of these terms can be calculated by sampling solute and solvent configurations at the initial state of ANCH in water (s1) and the final state in membrane (s2, Fig. 1). Here, the third term is assumed to be negligible (see Simulation details section) and peptide insertion is described by a two-step process (Eq. 3):
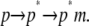 |
(3) |
The first step, 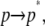 represents the conformational adaptation of p to its shape in membrane, p*. The second step,
represents the conformational adaptation of p to its shape in membrane, p*. The second step, 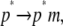 involves the association of p* and m. Note that all thermodynamic quantities can be computed in a single step involving the end states (
involves the association of p* and m. Note that all thermodynamic quantities can be computed in a single step involving the end states ( ). The advantage of the two-step scheme is that the free energy cost of peptide conformational reorganization,
). The advantage of the two-step scheme is that the free energy cost of peptide conformational reorganization, 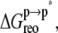 can be calculated separately from the association free energy,
can be calculated separately from the association free energy, 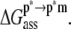 Their sum equals the total free energy of insertion,
Their sum equals the total free energy of insertion, 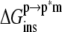 (Eq. 4).
(Eq. 4).
 |
(4) |
Ensemble-averaged intra-ANCH and ANCH-membrane potential energy and the corresponding polar and nonpolar solvation free energies were computed using the molecular mechanics Poisson Boltzmann solvent accessible surface area (MM-PBSA) approach (22,23) adapted to a membrane system.
MM-PBSA
In the MM-PBSA scheme,  and
and 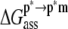 can be written as (Eqs. 5 and 6),
can be written as (Eqs. 5 and 6),
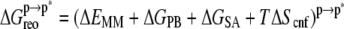 |
(5) |
 |
(6) |
The potential energy, (where
(where  represents either
represents either  or
or  ), is composed of covalent (bond, angle, dihedral,
), is composed of covalent (bond, angle, dihedral, 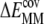 ) and nonbonded vdW (
) and nonbonded vdW (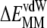 ) and electrostatic (
) and electrostatic (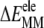 ) interaction energies:
) interaction energies:
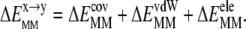 |
(7) |
Each of these terms was obtained from an ensemble-averaged difference of the corresponding CHARMM force field (24) energies at s1 and s2, computed without cutoff for the nonbonded terms.
The Poisson Boltzmann (PB) method of continuum electrostatics was used for the electrostatic solvation, 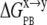 (Eq. 8).
(Eq. 8).
 |
(8) |
where 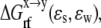 the reaction field energy, is the free energy of transferring a molecule from a medium of dielectric ɛs to one of dielectric ɛw. The PBEQ module of the CHARMM program (25) was used to solve the linear PB equation (by the successive overrelaxation method) in a cubic grid of 229 Å3. The default trilinear interpolation for charge distribution and Debye-Huckel approximation for boundary points (with the XY periodic boundary condition for membrane) were used. The dielectric boundary was smoothed within ±0.5 Å from atomic surface. The bilayer was treated as a dielectric slab with a hydrophobic thickness of ∼25 Å. The dielectric constants for water (ɛw) and membrane/ANCH (ɛs) were set to 80 and 2, respectively. A dilute salt concentration of 0.015 M with a Stern radius of 2 Å and a probe radius of 1.4 Å were used.
the reaction field energy, is the free energy of transferring a molecule from a medium of dielectric ɛs to one of dielectric ɛw. The PBEQ module of the CHARMM program (25) was used to solve the linear PB equation (by the successive overrelaxation method) in a cubic grid of 229 Å3. The default trilinear interpolation for charge distribution and Debye-Huckel approximation for boundary points (with the XY periodic boundary condition for membrane) were used. The dielectric boundary was smoothed within ±0.5 Å from atomic surface. The bilayer was treated as a dielectric slab with a hydrophobic thickness of ∼25 Å. The dielectric constants for water (ɛw) and membrane/ANCH (ɛs) were set to 80 and 2, respectively. A dilute salt concentration of 0.015 M with a Stern radius of 2 Å and a probe radius of 1.4 Å were used.
The nonpolar solvation, 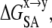 was computed using the change in the solvent accessible surface area (SASA) and a vacuum-water surface tension coefficient (γvw) of 0.0054 kcal mol−1 Å−2 (Eq. 9; see Gorfe and Jelesarov (26) and references therein).
was computed using the change in the solvent accessible surface area (SASA) and a vacuum-water surface tension coefficient (γvw) of 0.0054 kcal mol−1 Å−2 (Eq. 9; see Gorfe and Jelesarov (26) and references therein).
 |
(9) |
SASA was calculated with the CHARMM program and a probe radius of 1.4 Å, where the membrane was treated as single entity whose geometry is defined by the constituent lipids. Note that 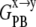 and
and 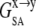 contain both enthalpic and entropic effects arising from water-water, water-ANCH, and water-membrane interactions.
contain both enthalpic and entropic effects arising from water-water, water-ANCH, and water-membrane interactions.
The MM-PBSA approach has been widely used in protein-protein (22,23), protein-DNA (26), and small molecule-protein (27,28) binding free energy calculations, as well as in alanine-scanning experiments (26). The PB approach, complemented by SA or in isolation, has also been used for the estimation of membrane binding solvation energies of model peptides and proteins (29–32). MM-PBSA requires extensive sampling of configurational spaces. Therefore, in addition to approximations inherent in continuum models, conformational sampling plays a crucial role in limiting the accuracy of MM-PBSA. For example, whether separate simulations for the reactants and complex or a single one for the complex provide a better agreement with experiment is still unclear (22,23,28,33). We used two 70 ns explicit water MD simulations with ANCH in water and in membrane.
Simulation details
A structural model of ANCH, constructed as described before (17,18), was solvated in a box of 56.5 × 40.7 × 38.9 Å3 containing 2642 water molecules and a Cl− ion. After setup of the systems through cycles of minimizations and equilibrations following standard protocols (see for example, Gorfe and Caflisch (34)), a production simulation was commenced with the program NAMD (35) under the same condition as previous simulations (16–18). The CHARMM27 force field (24) was used with constant temperature (310 K), normal pressure, and cross-sectional area. The full particle mesh Ewald electrostatics, a 12 Å cutoff for vdW interactions, a 14 Å cutoff for nonbonded list update, the SHAKE algorithm, and a 2 fs time step were used in all simulations. A simulation of the peptide in water was run for 70 ns and the resulting ensemble represented state s1. An earlier 20 ns simulation (17) of ANCH in a bilayer of 216 DMPC lipids was extended to 70 ns, and represented state s2. In each case, structural stabilization was achieved between 5 and 10 ns (16–18) but intramembrane and ANCH-membrane interactions continued to evolve until ∼35ns. Therefore, all except the first 10 ns structures (sampled every picosecond) were used for the solute entropy calculations but only the last 35 ns (sampled every 10 ps for MM and SA, and every 100 ps for the more expensive PB) for the MM-PBSA calculations.
Note that i) ANCH in the s2 state is structurally similar to a DMPC lipid (Fig. 1); and ii) a single lipid was removed from the ANCH-containing leaflet (17,18). As a result, peptide insertion did not significantly perturb the equilibrium structure of the bilayer (see Gorfe et al. (17) for details) suggesting that the contribution of 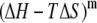 to
to 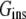 can be neglected.
can be neglected.
Solute entropy and membrane perturbation free energies
The solute configurational (or internal) entropy, 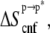 which contains the so-called conformational and vibrational entropies, was estimated based on a complete quasiharmonic analysis with corrections for anharmonicities and pairwise correlations (36). The quasiharmonic entropy upper-bound estimate (
which contains the so-called conformational and vibrational entropies, was estimated based on a complete quasiharmonic analysis with corrections for anharmonicities and pairwise correlations (36). The quasiharmonic entropy upper-bound estimate ( ) was calculated using the program entropy (37). Its corrections for anharmonicities in the quasiharmonic modes (
) was calculated using the program entropy (37). Its corrections for anharmonicities in the quasiharmonic modes (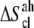 ) and for (supralinear) pairwise correlations among the modes (
) and for (supralinear) pairwise correlations among the modes ( ) were evaluated at the classical level as detailed elsewhere (36). These terms are additive,
) were evaluated at the classical level as detailed elsewhere (36). These terms are additive,
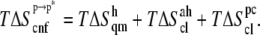 |
(10) |
Notice that 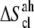 and
and 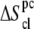 are in fact
are in fact 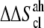 and
and 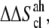 accounting for both differences between states s1 and s2 and corrections to the absolute
accounting for both differences between states s1 and s2 and corrections to the absolute 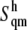 value (36). The same method has been recently applied to systems of different chemical natures (38–42). Single lipid tail configurational entropies were calculated as in Baron et al. (38).
value (36). The same method has been recently applied to systems of different chemical natures (38–42). Single lipid tail configurational entropies were calculated as in Baron et al. (38).
The external entropy (i.e., the loss of translational and rotational degrees of freedom of ANCH upon membrane binding,  ) was evaluated based on the numerical integration of the normalized probability distributions, p(q), of the rigid-body translation and rotation of ANCH at s2 (28,43),
) was evaluated based on the numerical integration of the normalized probability distributions, p(q), of the rigid-body translation and rotation of ANCH at s2 (28,43),
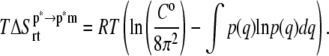 |
(11) |
C0 is standard concentration and q represents Cartesian or angular coordinates.
The free energy of membrane perturbation, 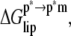 was estimated as follows. The structure of υ = 44 DMPC lipids was perturbed upon ANCH insertion when 10 Å was used as the coherence length (17). This perturbation has been characterized by the average change in the orientational order parameter of the bound lipids from the bulk (ΔSD ≈ 0.04). Together with
was estimated as follows. The structure of υ = 44 DMPC lipids was perturbed upon ANCH insertion when 10 Å was used as the coherence length (17). This perturbation has been characterized by the average change in the orientational order parameter of the bound lipids from the bulk (ΔSD ≈ 0.04). Together with 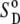 (∼0.2) of a pure DMPC bilayer, ΔSD can be used to estimate
(∼0.2) of a pure DMPC bilayer, ΔSD can be used to estimate 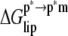 based on a simplified version of an expression due to Jähnig (44).
based on a simplified version of an expression due to Jähnig (44).
 |
(12) |
where μ = 0.27 kcal mol−1 is derived from the latent heat per lipid molecule at phase transition (Q = 5.4 kcal mol−1) and a theoretical temperature factor of 1/160 (44).
RESULTS AND DISCUSSION
To characterize the driving force for the partition of ANCH between water and membrane, the free energy of insertion (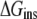 ) was parsed into enthalpy/entropy and solute/solvent contributions. The results (Table 1) indicate that membrane insertion is driven by the interaction enthalpy (
) was parsed into enthalpy/entropy and solute/solvent contributions. The results (Table 1) indicate that membrane insertion is driven by the interaction enthalpy (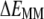 ≈ −136 kcal mol−1) and is opposed by solvation free energies (
≈ −136 kcal mol−1) and is opposed by solvation free energies ( ≈ + 87 kcal mol−1) as well as by solute entropy (
≈ + 87 kcal mol−1) as well as by solute entropy ( ≈ +36 kcal mol−1). The resulting overall free energy of insertion (∼−13 kcal mol−1) qualitatively agrees with estimates from PMF calculations (∼−30 kcal mol−1) and indirect experimental observations (∼−26 kcal mol−1) (16,45). This value is also comparable to the free energy cost of extracting a DMPC lipid from a bilayer as found by a recent PMF calculation (46).
≈ +36 kcal mol−1). The resulting overall free energy of insertion (∼−13 kcal mol−1) qualitatively agrees with estimates from PMF calculations (∼−30 kcal mol−1) and indirect experimental observations (∼−26 kcal mol−1) (16,45). This value is also comparable to the free energy cost of extracting a DMPC lipid from a bilayer as found by a recent PMF calculation (46).
TABLE 1.
Contributions to the water-membrane transfer free energy of ANCH (kcal mol−1)
| Process | Potential energy 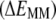
|
Solvation 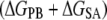
|
Nonwater entropy 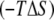
|
Free energy (sum) |
|---|---|---|---|---|
 |
24.3 (8) | 4.1 (7)* | 30.6 (9)† | 59.0 |
 |
−160.8 (65) | 83.3 (16)* | 5.5 (1) | −72.0 |
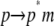 |
−136.5 (66)‡ | 87.4 (19)‡ | 36.1 (10) | −13.0 |
For brevity 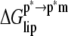 ≈ 0.6 kcal mol−1 is included in
≈ 0.6 kcal mol−1 is included in  although it contains an enthalpic component as well. Statistical errors obtained after block averaging over 7 ns subensembles of changes in energies are given as standard deviations (shown in parentheses).
although it contains an enthalpic component as well. Statistical errors obtained after block averaging over 7 ns subensembles of changes in energies are given as standard deviations (shown in parentheses).
Error was propagated as the sum of standard deviation values in  and
and 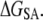
The average error on 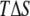 was obtained from a numerical error analysis for
was obtained from a numerical error analysis for 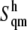 after propagating the error on the difference (see Supplementary Material, Fig. S1).
after propagating the error on the difference (see Supplementary Material, Fig. S1).
Standard deviation was computed directly from the  transition.
transition.
Peptide conformational adaptation
ANCH reorganization costs ∼59 kcal mol−1 in free energy ( Table 1). The major sources of the unfavorable
Table 1). The major sources of the unfavorable 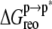 are the configurational entropy (
are the configurational entropy (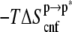 ≈ 31 kcal mol−1) and the loss of vdW interactions (
≈ 31 kcal mol−1) and the loss of vdW interactions (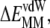 Fig. 2 A). Intra-ANCH electrostatic interactions (
Fig. 2 A). Intra-ANCH electrostatic interactions (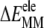 ) provided a modest favorable energy, whereas the covalent term (
) provided a modest favorable energy, whereas the covalent term ( ) is negligible (Fig. 2 A). These results can be rationalized by the dominant structure of ANCH (Fig. 1). In s1, ANCH is relatively compact with its hydrophobic lipid tails wound around each other. In s2, ANCH adopted an extended conformation with the lipid tails unwound (Figs. 1 and 3). This compact-to-extended
) is negligible (Fig. 2 A). These results can be rationalized by the dominant structure of ANCH (Fig. 1). In s1, ANCH is relatively compact with its hydrophobic lipid tails wound around each other. In s2, ANCH adopted an extended conformation with the lipid tails unwound (Figs. 1 and 3). This compact-to-extended 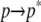 transition can be quantified by the ensemble averaged solvent accessible surface area, which is ∼1700 Å2 for p and ∼2500 Å2 for p*. Therefore, the unfavorable
transition can be quantified by the ensemble averaged solvent accessible surface area, which is ∼1700 Å2 for p and ∼2500 Å2 for p*. Therefore, the unfavorable 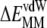 and the ∼5 kcal mol−1 nonpolar solvation (
and the ∼5 kcal mol−1 nonpolar solvation (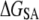 ) are largely due to the loss of vdW interactions and water exposure of the CH2 groups. The polar groups are solvent-exposed in both s1 and s2, explaining the modest electrostatic (interaction and solvation) contribution. That the largest contribution to
) are largely due to the loss of vdW interactions and water exposure of the CH2 groups. The polar groups are solvent-exposed in both s1 and s2, explaining the modest electrostatic (interaction and solvation) contribution. That the largest contribution to  arises from configurational entropy (Fig. 2 A) supports our earlier prediction of ANCH reorganization free energy being entropy dominated (16).
arises from configurational entropy (Fig. 2 A) supports our earlier prediction of ANCH reorganization free energy being entropy dominated (16).
FIGURE 2.
Energetic decomposition of  (a) and
(a) and 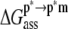 (b). Purely enthalpic (ΔEMM), purely entopic (
(b). Purely enthalpic (ΔEMM), purely entopic ( ), and mixed terms (
), and mixed terms (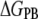 and
and  ) contribute to each of the
) contribute to each of the 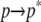 and
and 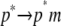 processes. Note that
processes. Note that 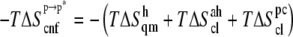 and the contribution of the (supralinear) pairwise correction (
and the contribution of the (supralinear) pairwise correction (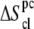 ) to the absolute entropy (
) to the absolute entropy (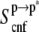 ) is large and similar in s1 (∼32%) and s2 (∼35%). Its contribution to
) is large and similar in s1 (∼32%) and s2 (∼35%). Its contribution to  is ∼3%, whereas the anharmonicity correction (
is ∼3%, whereas the anharmonicity correction (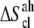 ) is small (∼0.1%).
) is small (∼0.1%).
FIGURE 3.
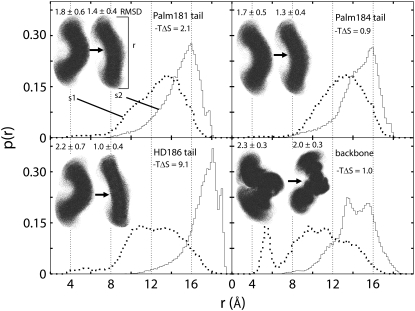
Probability (p(r)) distribution plots in s1 (dotted line) and s2 (solid line) of the end-to-end distances between the first and last carbon atoms of ANCH lipid tails (Palm181 (top left), Palm184 (top right), HD186 (bottom left)) and between the Cα atoms of residues 180 and 186 (backbone, bottom right). The corresponding structures are shown as dots (inset: s1 → s2) representing 1-ps-separated snapshots superimposed onto the first frame. The respective average RMSDs are depicted at the top of each structural model. Note that  represents the free energy difference (due to configurational entropy) between states s1 and s2.
represents the free energy difference (due to configurational entropy) between states s1 and s2.
The positive sign of 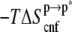 negates the conventional wisdom of associating structural relaxation with an increase in entropy. However, it is consistent with the notion that the bilayer reduces the configurational space available to ANCH by, among other effects, enforcing specific orientations (17,18,47,48). To have a qualitative understanding of this issue, we recomputed
negates the conventional wisdom of associating structural relaxation with an increase in entropy. However, it is consistent with the notion that the bilayer reduces the configurational space available to ANCH by, among other effects, enforcing specific orientations (17,18,47,48). To have a qualitative understanding of this issue, we recomputed  for each of Palm181, Palm184, and HD186 lipid tails as well as for the peptide backbone. We also calculated the probability distribution (p(r)) of the end-to-end distances, i.e., the distance between the first methyl and the last methylene carbon atoms of the lipid tails and the first and last Cα atoms of the backbone. The results are summarized in Fig. 3. The change in p(r) from s1 to s2 is modest in Palm184, intermediate in Palm181, and large in HD186. The corresponding (single-chain)
for each of Palm181, Palm184, and HD186 lipid tails as well as for the peptide backbone. We also calculated the probability distribution (p(r)) of the end-to-end distances, i.e., the distance between the first methyl and the last methylene carbon atoms of the lipid tails and the first and last Cα atoms of the backbone. The results are summarized in Fig. 3. The change in p(r) from s1 to s2 is modest in Palm184, intermediate in Palm181, and large in HD186. The corresponding (single-chain) 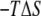 values mirror these variations (∼1, 2, and 9 kcal mol−1, respectively). In the case of the backbone, p(r) displays a approximately similar double-well distribution in both s1 and s2, which is again mirrored by the ∼1 kcal mol−1
values mirror these variations (∼1, 2, and 9 kcal mol−1, respectively). In the case of the backbone, p(r) displays a approximately similar double-well distribution in both s1 and s2, which is again mirrored by the ∼1 kcal mol−1 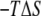 value. The same qualitative conclusions can be drawn by comparing the distribution of the superposed structures or the corresponding root mean-square deviations (RMSD, Fig. 3). These data demonstrate that insertion into the DMPC bilayer reduces the conformational space accessible to ANCH and thus explain the reduction in solute entropy.
value. The same qualitative conclusions can be drawn by comparing the distribution of the superposed structures or the corresponding root mean-square deviations (RMSD, Fig. 3). These data demonstrate that insertion into the DMPC bilayer reduces the conformational space accessible to ANCH and thus explain the reduction in solute entropy.
Peptide insertion
The reduction in configurational space and the loss in intra-ANCH vdW interactions are offset by the ∼−161 kcal mol−1 ANCH-membrane interaction energy change. The vdW interactions of ANCH lipid tails and Met-182 side chain with the DMPC lipids provided three-fourths of the potential energy; the rest is from Coulombic interactions (Fig. 2 B). Electrostatic solvation (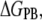 which is about twice the magnitude of
which is about twice the magnitude of  ) opposes binding. The value of
) opposes binding. The value of  is comparatively small but favorable. Together with the small contributions from external entropy, the overall association free energy (
is comparatively small but favorable. Together with the small contributions from external entropy, the overall association free energy (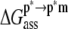 ) is therefore ∼−71 kcal mol−1.
) is therefore ∼−71 kcal mol−1.
The role of 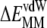 can be understood from the fact that i) as few as 5–7 initial vdW contacts lead to a fast and spontaneous insertion of the whole peptide (16,18,47), and ii) the progress of membrane insertion is accompanied by a steady increase of vdW contacts (16,17). The favorable
can be understood from the fact that i) as few as 5–7 initial vdW contacts lead to a fast and spontaneous insertion of the whole peptide (16,18,47), and ii) the progress of membrane insertion is accompanied by a steady increase of vdW contacts (16,17). The favorable 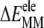 reflects the hydrogen-bond interactions involving amide groups and Ser-183/Lys-185 side chains with DMPC glycerol/phosphate oxygen atoms (16–18). The opposite effects of
reflects the hydrogen-bond interactions involving amide groups and Ser-183/Lys-185 side chains with DMPC glycerol/phosphate oxygen atoms (16–18). The opposite effects of  and
and 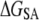 is consistent with the transfer of polar groups from water to the interfacial region being energetically costly compared to the transfer of nonpolar groups to the DMPC core. The loss of translational/rotational entropy also opposes binding by ∼5 kcal mol−1; ∼4 kcal mol−1 of this is from restrictions in rotational degrees of freedom. The magnitude of the translational entropy is small because only the z-dimensional (along the membrane normal) degree of freedom is restricted. In fact, the lateral mobility of ANCH is similar in water and in membrane. For example, the two-dimensional self-diffusion coefficient of ANCH is 10 × 10−8 cm2/s in s1 and 7.9 × 10−8 cm2/s in s2. The estimated free energy of membrane perturbation, arising from the disorder of DMPC lipids that are near ANCH, or bound lipids (17), is also very small (∼0.6 kcal mol−1). A similar value has been estimated before (44).
is consistent with the transfer of polar groups from water to the interfacial region being energetically costly compared to the transfer of nonpolar groups to the DMPC core. The loss of translational/rotational entropy also opposes binding by ∼5 kcal mol−1; ∼4 kcal mol−1 of this is from restrictions in rotational degrees of freedom. The magnitude of the translational entropy is small because only the z-dimensional (along the membrane normal) degree of freedom is restricted. In fact, the lateral mobility of ANCH is similar in water and in membrane. For example, the two-dimensional self-diffusion coefficient of ANCH is 10 × 10−8 cm2/s in s1 and 7.9 × 10−8 cm2/s in s2. The estimated free energy of membrane perturbation, arising from the disorder of DMPC lipids that are near ANCH, or bound lipids (17), is also very small (∼0.6 kcal mol−1). A similar value has been estimated before (44).
Backbone dynamics suggests conformational selection
The current calculations assumed an induced fit mechanism, i.e., ANCH conformational adaptation occurs after membrane binding. In a previous work (16), we anticipated that membrane insertion may be opposed by an entropy-dominated free energy of peptide reorganization. Based on the agreement between PMF calculations and experimental estimates, we further predicted that  would be small (16). Although they share the final state s2, the initial state in the previous work was somewhere between s1 and s2, which precludes direct comparison with the current data. Nevertheless, the large value of
would be small (16). Although they share the final state s2, the initial state in the previous work was somewhere between s1 and s2, which precludes direct comparison with the current data. Nevertheless, the large value of 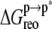 computed here requires an explanation. Distribution of the pairwise RMSD and cluster analysis (excluding the first 10 ns) provide interesting insights into this issue (Fig. 4).
computed here requires an explanation. Distribution of the pairwise RMSD and cluster analysis (excluding the first 10 ns) provide interesting insights into this issue (Fig. 4).
FIGURE 4.
Characterization of the ANCH backbone structure. (Main plot) normalized distributions of the pairwise (frame-by-frame) RMSD between structures sampled every 10 ps. (Inset) cluster-center structures of the first two clusters obtained by RMSD-based clustering with a cutoff of 2 Å, which is approximately the point of divergence from a normal distribution (calculated by WORDOM (62)). Note that although the first 10 ns of data were excluded, few structures cluster around 8 Å away from the dominant conformations. Color code: carbon in green, oxygen in red, nitrogen in blue.
The backbone structure of ANCH in s2 is characterized by a sharp and narrow Gaussian distribution of the pairwise RMSD and an average separation between ensemble members of 1 Å. The corresponding ensemble in s1 is characterized by a wide non-Gaussian distribution. Clustering of these structures resulted in one major cluster in s2 (94%) and two in s1 (76% and 21%). Remarkably, the second most populated cluster in s1 represents an extended conformation that closely mimics the most populated cluster in s2. Furthermore, the first cluster in s1 resembles the minor cluster in s2. An interesting outcome of this result is the possibility that membrane insertion involves conformational selection. This implies, in turn, that the inherent flexibility of ANCH in water generates conformers that would partition to membrane with lower energetic penalty. Conformational selection is a common theme in protein-protein, protein-ligand, and protein-nucleic acid associations (49–51), but membranes were often assumed to nonselectively shape proteins/peptides. Our data suggest that conformational selection may play at least a partial role in the transfer of ANCH to membrane. In such a case, the  value estimated here should represent an upper limit of the energetic penalty associated with the
value estimated here should represent an upper limit of the energetic penalty associated with the  transition, which is consistent with our previous PMF calculations (16).
transition, which is consistent with our previous PMF calculations (16).
Dynamics of the lipid tails supports conformational selection
The conformational reorganization of the ANCH lipid tails is crucial because, upon transfer from water, they need to straighten and adapt to the shape of the host lipids. This is evident from the distributions of the end-to-end distances (Fig. 3). Each of the lipid tails became stretched when inserted in the bilayer. The hexadecyl group (HD186) underwent the largest change, with an average chain length of ∼18 Å in s2 compared with ∼12 Å in s1. This allowed HD186 to insert deeper and to make a higher number of vdW contacts with the DMPC lipids (16,17). The chain length changes are comparatively small for Palm181 and Palm184 but are still significant.
Indirect experimental observations suggest that the removal of any of the ANCH lipids modulates the kinetics of membrane binding (45,52,53). General microscopy experiments showed that the cytosolic pool of H-ras is much smaller than the doubly lipid-modified N-ras or variants of H-ras with either Palm181 or Palm184 removed (21). Furthermore, PMF calculations found that the removal of the lipid tails results in a steep rise in the PMF upon membrane contact and that the largest contribution to the insertion free energy comes from HD186, followed by Palm181 and Palm184 (A. A. Gorfe and J. A. McCammon, unpublished). As discussed above, the extension of HD186 alone would cost ∼9 kcal mol−1 in configurational entropy (if treated as an isolated entity). We propose that instead of paying such an entropic penalty, structures with already extended lipids (see intersections of p(r) in s1 and s2) would selectively and spontaneously insert via the conformational selection mechanism.
Physicochemical considerations and earlier experiments
Some of the principles that hold for purely hydrophobic solutes highlighted in the introduction also apply to molecules containing some hydrophilic units (4). However, the accommodation of both hydrophilic and hydrophobic interactions restricts molecular configurations, resulting in additional entropic effects (4). Thus, the free energy of transferring amphiphilic molecules into a membrane with an oily interior has two major contributions. The first is the free energy contribution of the hydrophilic head, which favors the water-bilayer interface. The net contribution of this effect to the overall free energy can vary depending on the polarity (or charge content) and the shape of the headgroups. The second is the free energy contribution due to the transfer of the hydrophobic moiety to the oily interior of the membrane. The net contribution of this free energy is always favorable and is modulated by the size of the hydrophobic portion of the solute, which, for lipidated proteins, varies with the length (e.g., farnesyl versus geranyl geranyl) and saturation (e.g., farnesyl versus palmitoyl) of the lipid modification(s). Despite these differences, free energies due both to the headgroup and the hydrophobic tails have enthalpy and entropy components. The data presented in this work assign a dominant role to enthalpy. How general is this conclusion?
Consider two extreme cases: a highly charged hydrophilic head containing a small hydrophobic lipid tail and a singly charged hydrophilic head containing a large hydrophobic tail. The K-ras membrane ANCH, which contains eight Lys residues but only a single farnesyl group, represents the first. H-ras ANCH of this study represents the second. Because the dominant interactions of the K-ras ANCH are between the Lys residues and the (charged) lipid headgroups, electrostatic energy would dictate the water-membrane transfer process. The contributions of vdW interactions and solvent reorganization due to the single lipid tail may be significant but are not dominant. Therefore, attractive enthalpic interactions, not solvent reorganization or entropic effects, drive membrane incorporation of K-ras.
The difference between K- and H-ras would therefore be whether the source of enthalpy is electrostatic or vdW. In terms of polarity, most lipid modifications lie in between these two cases. Therefore, with the possible exception of the rare ring-carrying lipidations (such as glyceroylation), membrane insertion of most lipoproteins may be enthalpy driven. This conclusion is in accord with exothermic enthalpies measured for the following lipoprotein/membrane pairs: glucagon/DMPC (54), transcarbamylase leader peptide/phospholipid membranes (55), apolipoprotein A-II/DMPC (56), and apolipoprotein A-I/1,2-dimyristoyl-sn-glycero-3-phosphatidylglycerol (DMPG) (57). Other enthalpy-driven membrane transfers of amphiphiles include the potential-sensitive dye 2-(p-toluidinyl)naphthalene-6-sulfonate, the membrane conductivity inducing anion tetraphenylborate, and the Ca2+ channel blocker amlodipine (7).
In summary, the results in Table 1 and Fig. 2 (note the large standard deviation values) should be viewed as a first attempt toward a membrane insertion free energy computation of a lipopeptide in which all relevant contributions have been explicitly computed. Free energy calculations are notoriously difficult (58–61), even for relatively small systems. Therefore, a detailed and qualitatively sound thermodynamic picture, not a quantitative one, was anticipated. Large fluctuations and subtractions between very large numbers generally limit the quantitative accuracy of the results. Some improvement over the current data may be possible by the application of the principle of conformational selection, and/or the use of a double layer in the PB calculations (for the core and interfacial region of the bilayer).
Despite these limitations, the computed overall free energy of insertion is reasonably close to those derived from a PMF calculation and from indirect experimental observations. It thus allowed us to shed light on the membrane partition thermodynamics of lipoproteins by parsing the transfer free energy into solute/solvent and enthalpy/entropy contributions. Such a decomposition of the free energy demonstrated that the hydrophobic effect responsible for the membrane transfer of ANCH is enthalpy driven. Changes in solvation and peptide reorganization free energies disfavor membrane binding. The major source of the favorable enthalpy is the ANCH-membrane vdW interaction. Our results, therefore, provide atomistic structural and dynamical perspectives to earlier calorimetric observations on the role of enthalpy in the membrane partitioning of amphiphiles (see previous paragraph).
Furthermore, a detailed conformational and entropic analysis suggested that the dynamic behavior of ANCH in water allows the formation of extended conformations that would insert into membrane without a significant energetic penalty. A remarkable consequence of this observation is that conformational selection may play an important role in the membrane binding of lipoproteins, as it does in the association of other biomolecules.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Drs. Donald Hamelberg and Chia-en A. Chang for useful discussions.
The San Diego Supercomputer Center and the Center for Theoretical Biological Physics are acknowledged for computational resources. Additional support has been provided by the National Science Foundation, National Institutes of Health, Howard Hughes Medical Institute, National Biomedical Computation Resource, and Accelrys.
Editor: Peter Tieleman.
References
- 1.Tanford, C. H. 1980. The Hydrophobic Effect: Formation of Micelles and Biological Membranes. Wiley, New York.
- 2.Frank, H. S., and M. W. Evans. 1945. Free volume and entropy in condensed systems. 3. Entropy in binary liquid mixtures—partial molal entropy in dilute solutions—structure and thermodynamics in aqueous electrolytes. J. Chem. Phys. 13:507–532. [Google Scholar]
- 3.Nemethy, G., and H. A. Scheraga. 1962. Structure of water and hydrophobic bonding in proteins. 1. A model for thermodynamic properties of liquid water. J. Chem. Phys. 36:382–400. [Google Scholar]
- 4.Chandler, D. 2005. Interfaces and the driving force of hydrophobic assembly. Nature. 437:640–647. [DOI] [PubMed] [Google Scholar]
- 5.Hua, L., X. H. Huang, P. Liu, R. H. Zhou, and B. J. Berne. 2007. Nanoscale dewetting transition in protein complex folding. J. Phys. Chem. B. 111:9069–9077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jacobs, R. E., and S. H. White. 1989. The nature of the hydrophobic binding of small peptides at the bilayer interface—implications for the insertion of transbilayer helices. Biochemistry. 28:3421–3437. [DOI] [PubMed] [Google Scholar]
- 7.Seelig, J., and P. Ganz. 1991. Nonclassical hydrophobic effect in membrane binding equilibria. Biochemistry. 30:9354–9359. [DOI] [PubMed] [Google Scholar]
- 8.Homans, S. W. 2007. Water, water everywhere—except where it matters? Drug Discov. Today. 12:534–539. [DOI] [PubMed] [Google Scholar]
- 9.Privalov, P. L., and S. J. Gill. 1988. Stability of protein-structure and hydrophobic interaction. Adv. Protein Chem. 39:191–234. [DOI] [PubMed] [Google Scholar]
- 10.Privalov, P. L., and S. J. Gill. 1989. The hydrophobic effect—a reappraisal. Pure Appl. Chem. 61:1097–1104. [Google Scholar]
- 11.Cooper, A. 1999. Thermodynamic analysis of biomolecular interactions. Curr. Opin. Chem. Biol. 3:557–563. [DOI] [PubMed] [Google Scholar]
- 12.van Gunsteren, W. F., D. Bakowies, R. Baron, I. Chandrasekhar, M. Christen, X. Daura, P. Gee, D. P. Geerke, A. Glattli, P. H. Hunenberger, M. A. Kastenholz, C. Oostenbrink, M. Schenk, D. Trzesniak, N. F. van der Vegt, and H. B. Yu. 2006. Biomolecular modeling: goals, problems, perspectives. Angew. Chem. Int. Ed. Engl. 45:4064–4092. [DOI] [PubMed] [Google Scholar]
- 13.Hancock, J. F., A. I. Magee, J. E. Childs, and C. J. Marshall. 1989. All ras proteins are polyisoprenylated but only some are palmitoylated. Cell. 57:1167–1177. [DOI] [PubMed] [Google Scholar]
- 14.Huang, H. W. 2006. Molecular mechanism of antimicrobial peptides: the origin of cooperativity. Biochim. Biophys. Acta. 1758:1292–1302. [DOI] [PubMed] [Google Scholar]
- 15.Babakhani, A., A. A. Gorfe, J. Gullingsrud, J. E. Kim, and J. Andrew McCammon. 2007. Peptide insertion, positioning, and stabilization in a membrane: insight from an all-atom molecular dynamics simulation. Biopolymers. 85:490–497. [DOI] [PubMed] [Google Scholar]
- 16.Gorfe, A. A., A. Babakhani, and J. A. McCammon. 2007. Free energy profile of H-ras membrane anchor upon membrane insertion. Angew. Chem. Int. Ed. Engl. 46:8234–8237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gorfe, A. A., A. Babakhani, and J. A. McCammon. 2007. H-ras protein in a bilayer: interaction and structure perturbation. J. Am. Chem. Soc. 129:12280–12286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gorfe, A. A., M. Hanzal-Bayer, D. Abankwa, J. F. Hancock, and J. A. McCammon. 2007. Structure and dynamics of the full-length lipid-modified H-ras protein in a 1,2-dimyristoylglycero-3-phosphocholine bilayer. J. Med. Chem. 50:674–684. [DOI] [PubMed] [Google Scholar]
- 19.Abankwa, D., A. A. Gorfe, and J. F. Hancock. 2007. Ras nanoclusters: molecular structure and assembly. Semin. Cell Dev. Biol. 18:599–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Rotblat, B., I. A. Prior, C. Muncke, R. G. Parton, Y. Kloog, Y. I. Henis, and J. F. Hancock. 2004. Three separable domains regulate GTP-dependent association of H-ras with the plasma membrane. Mol. Cell. Biol. 24:6799–6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Roy, S., S. Plowman, B. Rotblat, I. A. Prior, C. Muncke, S. Grainger, R. G. Parton, Y. I. Henis, Y. Kloog, and J. F. Hancock. 2005. Individual palmitoyl residues serve distinct roles in H-ras trafficking, microlocalization, and signaling. Mol. Cell. Biol. 25:6722–6733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang, J. M., P. Morin, W. Wang, and P. A. Kollman. 2001. Use of MM-PBSA in reproducing the binding free energies to HIV-1 RT of TIBO derivatives and predicting the binding mode to HIV-1 RT of efavirenz by docking and MM-PBSA. J. Am. Chem. Soc. 123:5221–5230. [DOI] [PubMed] [Google Scholar]
- 23.Massova, I., and P. A. Kollman. 2000. Combined molecular mechanical and continuum solvent approach (MM-PBSA/GBSA) to predict ligand binding. Perspectives in Drug Discovery and Design. 18:113–135. [Google Scholar]
- 24.MacKerell, A. D., D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin, and M. Karplus. 1998. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 102:3586–3616. [DOI] [PubMed] [Google Scholar]
- 25.Brooks, B. R., R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan, and M. Karplus. 1983. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 4:187–217. [Google Scholar]
- 26.Gorfe, A. A., and I. Jelesarov. 2003. Energetics of sequence-specific protein-DNA association: computational analysis of integrase Tn916 binding to its target DNA. Biochemistry. 42:11568–11576. [DOI] [PubMed] [Google Scholar]
- 27.Zhou, Z., M. Bates, and J. D. Madura. 2006. Structure modeling, ligand binding, and binding affinity calculation (LR-MM-PBSA) of human heparanase for inhibition and drug design. Proteins. 65:580–592. [DOI] [PubMed] [Google Scholar]
- 28.Swanson, J. M., R. H. Henchman, and J. A. McCammon. 2004. Revisiting free energy calculations: a theoretical connection to MM/PBSA and direct calculation of the association free energy. Biophys. J. 86:67–74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ben-Tal, N., and B. Honig. 1996. Helix-helix interactions in lipid bilayers. Biophys. J. 71:3046–3050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ben-Shaul, A., N. Ben-Tal, and B. Honig. 1996. Statistical thermodynamic analysis of peptide and protein insertion into lipid membranes. Biophys. J. 71:130–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ben-Tal, N., A. Ben-Shaul, A. Nicholls, and B. Honig. 1996. Free-energy determinants of alpha-helix insertion into lipid bilayers. Biophys. J. 70:1803–1812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roux, B., T. Allen, S. Berneche, and W. Im. 2004. Theoretical and computational models of biological ion channels. Q. Rev. Biophys. 37:15–103. [DOI] [PubMed] [Google Scholar]
- 33.Wang, W., O. Donini, C. M. Reyes, and P. A. Kollman. 2001. Biomolecular simulations: recent developments in force fields, simulations of enzyme catalysis, protein-ligand, protein-protein, and protein-nucleic acid noncovalent interactions. Annu. Rev. Biophys. Biomol. Struct. 30:211–243. [DOI] [PubMed] [Google Scholar]
- 34.Gorfe, A. A., and A. Caflisch. 2005. Functional plasticity in the substrate binding site of beta-secretase. Structure. 13:1487–1498. [DOI] [PubMed] [Google Scholar]
- 35.Phillips, J. C., R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale, and K. Schulten. 2005. Scalable molecular dynamics with NAMD. J. Comput. Chem. 26:1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Baron, R., W. F. van Gunsteren, and P. H. Hunenberger. 2006. Estimating the configurational entropy from molecular dynamics simulations: anharmonicity and correlation corrections to the quasi-harmonic approximation. Trends in Physical Chemistry. 11:87–122. [Google Scholar]
- 37.Christen, M., P. H. Hunenberger, D. Bakowies, R. Baron, R. Burgi, D. P. Geerke, T. N. Heinz, M. A. Kastenholz, V. Krautler, C. Oostenbrink, C. Peter, D. Trzesniak, and W. F. van Gunsteren. 2005. The GROMOS software for biomolecular simulation: GROMOS05. J. Comput. Chem. 26:1719–1751. [DOI] [PubMed] [Google Scholar]
- 38.Baron, R., A. H. de Vries, P. H. Hunenberger, and W. F. van Gunsteren. 2006. Configurational entropies of lipids in pure and mixed bilayers from atomic-level and coarse-grained molecular dynamics simulations. J Phys Chem B. 110:15602–15614. [DOI] [PubMed] [Google Scholar]
- 39.Baron, R., and J. A. McCammon. 2008. (Thermo)dynamic role of receptor flexibility, entropy, and motional correlation in protein-ligand binding. ChemPhysChem. 9:983–988. [DOI] [PubMed] [Google Scholar]
- 40.Baron, R., D. Trzesniak, A. H. de Vries, A. Elsener, S. J. Marrink, and W. F. van Gunsteren. 2007. Comparison of thermodynamic properties of coarse-grained and atomic-level simulation models. ChemPhysChem. 8:452–461. [DOI] [PubMed] [Google Scholar]
- 41.Pereira, C. S., D. Kony, R. Baron, M. Muller, W. F. van Gunsteren, and P. H. Hunenberger. 2006. Conformational and dynamical properties of disaccharides in water: a molecular dynamics study. Biophys. J. 90:4337–4344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Pereira, C. S., D. Kony, R. Baron, M. Muller, W. F. van Gunsteren, and P. H. Hunenberger. 2006. Conformational and dynamical properties of disaccharides in water: a molecular dynamics study. Biophys. J. 90:4337–4344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Minh, D. D., J. M. Bui, C. E. Chang, T. Jain, J. M. Swanson, and J. A. McCammon. 2005. The entropic cost of protein-protein association: a case study on acetylcholinesterase binding to fasciculin-2. Biophys. J. 89:L25–L27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Jahnig, F. 1983. Thermodynamics and kinetics of protein incorporation into membranes. Proc. Natl. Acad. Sci. USA. 80:3691–3695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Silvius, J. R., and F. l'Heureux. 1994. Fluorimetric evaluation of the affinities of isoprenylated peptides for lipid bilayers. Biochemistry. 33:3014–3022. [DOI] [PubMed] [Google Scholar]
- 46.Tieleman, D. P., and S. J. Marrink. 2006. Lipids out of equilibrium: energetics of desorption and pore mediated flip-flop. J. Am. Chem. Soc. 128:12462–12467. [DOI] [PubMed] [Google Scholar]
- 47.Gorfe, A. A., R. Pellarin, and A. Caflisch. 2004. Membrane localization and flexibility of a lipidated ras peptide studied by molecular dynamics simulations. J. Am. Chem. Soc. 126:15277–15286. [DOI] [PubMed] [Google Scholar]
- 48.Huster, D., A. Vogel, C. Katzka, H. A. Scheidt, H. Binder, S. Dante, T. Gutberlet, O. Zschornig, H. Waldmann, and K. Arnold. 2003. Membrane insertion of a lipidated ras peptide studied by FTIR, solid-state NMR, and neutron diffraction spectroscopy. J. Am. Chem. Soc. 125:4070–4079. [DOI] [PubMed] [Google Scholar]
- 49.Berger, C., S. Weber-Bornhauser, J. Eggenberger, J. Hanes, A. Pluckthun, and H. R. Bosshard. 1999. Antigen recognition by conformational selection. FEBS Lett. 450:149–153. [DOI] [PubMed] [Google Scholar]
- 50.Sauve, S., J. F. Naud, and P. Lavigne. 2007. The mechanism of discrimination between cognate and non-specific DNA by dimeric b/HLH/LZ transcription factors. J. Mol. Biol. 365:1163–1175. [DOI] [PubMed] [Google Scholar]
- 51.Bosshard, H. R. 2001. Molecular recognition by induced fit: how fit is the concept? News Physiol. Sci. 16:171–173. [DOI] [PubMed] [Google Scholar]
- 52.Shahinian, S., and J. R. Silvius. 1995. Doubly-lipid-modified protein sequence motifs exhibit long-lived anchorage to lipid bilayer membranes. Biochemistry. 34:3813–3822. [DOI] [PubMed] [Google Scholar]
- 53.Silvius, J. R., and R. Leventis. 1993. Spontaneous interbilayer transfer of phospholipids: dependence on acyl chain composition. Biochemistry. 32:13318–13326. [DOI] [PubMed] [Google Scholar]
- 54.Epand, R. M., and J. M. Sturtevant. 1981. A calorimetric study of peptide-phospholipid interactions—the glucagon-dimyristoylphosphatidylcholine complex. Biochemistry. 20:4603–4606. [DOI] [PubMed] [Google Scholar]
- 55.Myers, M., O. L. Mayorga, J. Emtage, and E. Freire. 1987. Thermodynamic characterization of interactions between ornithine transcarbamylase leader peptide and phospholipid bilayer membranes. Biochemistry. 26:4309–4315. [DOI] [PubMed] [Google Scholar]
- 56.Massey, J. B., A. M. Gotto, and H. J. Pownall. 1981. Thermodynamics of lipid-protein interactions—interaction of apolipoprotein A-II from human-plasma high-density lipoproteins with dimyristoylphosphatidylcholine. Biochemistry. 20:1575–1584. [DOI] [PubMed] [Google Scholar]
- 57.Epand, R. M., J. P. Segrest, and G. M. Anantharamaiah. 1990. Thermodynamics of the binding of human apolipoprotein A-I to dimyristoylphosphatidylglycerol. J. Biol. Chem. 265:20829–20832. [PubMed] [Google Scholar]
- 58.Gilson, M. K., J. A. Given, B. L. Bush, and J. A. McCammon. 1997. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 72:1047–1069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Simonson, T., G. Archontis, and M. Karplus. 2002. Free energy simulations come of age: protein-ligand recognition. Acc. Chem. Res. 35:430–437. [DOI] [PubMed] [Google Scholar]
- 60.Lesyng, B., and J. A. McCammon. 1993. Molecular modeling methods. Basic techniques and challenging problems. Pharmacol. Ther. 60:149–167. [DOI] [PubMed] [Google Scholar]
- 61.Jorgensen, W. L. 2004. The many roles of computation in drug discovery. Science. 303:1813–1818. [DOI] [PubMed] [Google Scholar]
- 62.Seeber, M., M. Cecchini, F. Rao, G. Settanni, and A. Caflisch. 2007. WORDOM: a program for efficient analysis of molecular dynamics simulations. Bioinformatics. 23:2625–2627. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.